Mortality benefit of isoniazid preventive therapy in HIV-positive persons: a simulation study

SUMMARY

A meta-analysis of isoniazid preventive therapy (IPT) in human immunodeficiency virus-positive individuals failed to show a mortality benefit even though tuberculosis is a leading cause of death in this group. Results for purified protein derivative (PPD) positive patients were heterogeneous, however, and two of the included trials had many PPD-unknowns. When all PPD-unknowns were allocated to either PPD-positive or PPD-negative, the individual trial results were not robust, and simulated meta-analyses showed an overall reduction in all-cause mortality for PPD-positive individuals on IPT (relative risk 0.76; 95% credibility interval 0.6–0.95).

Isoniazid preventive therapy (IPT) in persons with human immunodeficiency virus/acquired immune-deficiency syndrome (HIV/AIDS) has been shown to prevent active tuberculosis¹ (TB), and is recommended by the World Health Organization (WHO).² Autopsy studies have demonstrated that TB is a leading cause of death in people with HIV/AIDS in TB-endemic areas such as sub-Saharan Africa; it would therefore stand to reason that IPT should reduce mortality.^3,4 However, only a non-significant trend of reduced mortality was found in a meta-analysis by Woldehanna et al. despite a number of large trials included from sub-Saharan Africa.¹

The aforementioned meta-analysis examines the mortality effect of IPT vs. placebo by appropriately subdividing individual study results into purified protein derivative (PPD) positive, PPD-negative and PPD-unknown subgroups to compute relative risks (RRs) for each as well as a grand mean for all persons. For PPD-negative persons, the individual trial results show RRs consistently around one, but for PPD-positive patients, the trial results are heterogeneous. The point estimates for three of the four studies suggest a decrease in mortality with isoniazid (INH), but the study by Mwinga et al. suggests the opposite. ⁵ On further inspection, however, in that trial 246/702 (35%) participants had an unknown PPD. Another study, by Hawken et al., also included 89/684 (13%) PPD-unknowns.⁶

Given that analyzing by PPD result when a large number of participants have an unknown PPD status may introduce systematic bias, we sought to examine via simulations the effect of allocating PPD-unknowns to either the PPD-positive or PPD-negative subgroup to test the robustness of the published RRs. We also sought to examine the sensitivity of the meta-analysis result to changes in these two studies. We focused on results for the PPD-positive group, which included fewer trials and displayed heterogeneity, in contrast to the result for PPD-negative individuals, which used a large number of trials, had little heterogeneity and was therefore unlikely to be significantly influenced by changes in the two studies.

METHODS

Data for the two studies in question^5,6 were extracted from the report by Woldehanna et al. from 2004.¹ For the initial individual analysis of each trial, we created all possible datasets where PPD-unknowns were allocated to PPD-positive or PPD-negative, preserving the actual number of total participants in each arm (i.e., INH or placebo) as well as the actual number of deaths in each arm. For example, one possible dataset included all PPD-unknowns as PPD-positive, another included all as PPD-negative, another included half as PPD-positive and half as PPD-negative, and so on. Each possible dataset was given equal weight because it was unknown why participants were missing PPD results. All studies defined PPD-positive as ≥5 mm induration.

We then performed a simulation of 100 000 meta-analyses to determine the effect that the PPD-unknowns might have on the meta-analysis result. In each iteration, all PPD-unknowns were allocated to either PPD-positive or PPD-negative using random numbers from a uniform distribution independently for each study. The RR of mortality with INH vs. placebo was then calculated for the two simulated studies and pooled with results from the studies by Pape et al.⁷ and Whalen et al.,⁸ using the Mantel-Haenszel method. The resulting distribution of 100 000 RRs is described using a Bayesian approach; the mean point estimate and the 95% credibility interval (CrI) (i.e., the probability that the mean lies within this interval is 95%) are reported.

Heterogeneity of the simulated meta-analyses was assessed using I², which describes the percentage of total variation across studies that is due to heterogeneity rather than chance.⁹ Meta-analytical formulae were obtained from documentation for the Review Manager software that was used in the original meta-analysis (the Cochrane Collaboration, Version 5.0, The Nordic Cochrane Centre, Copenhagen, Denmark). Statistical analyses were performed using SAS (SAS Institute, version 9.1, Cary, NC, USA).

RESULTS

All datasets were generated for the individual trials, and the mean and range of the RR of mortality were found. In Hawken et al.,⁶ 149 760 possible datasets were found and the mean RR of mortality was 0.58 (range 0.12–1.88), which is higher than the reported RR of 0.34. For Mwinga et al.,⁵ there were 5 559 840 possible datasets and the mean RR was 1.46 (range 0.13–14.46), lower than the published RR of 2.02 with a wide range.

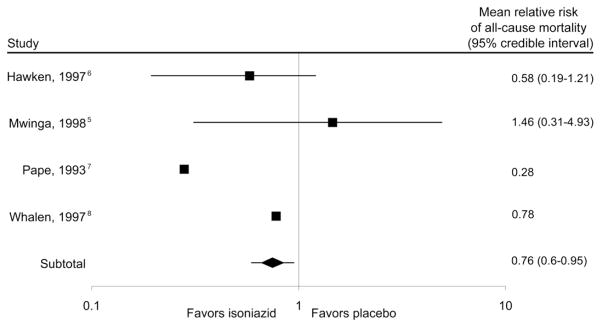
The results of the simulated meta-analyses are presented in an adapted Forest plot (Figure). The mean simulated RR for each of the two trials in question closely approximated those derived from averaging all possible datasets. When combining results from all studies, the total mean RR of mortality was 0.76, with a 95% CrI of 0.60–0.95, indicating a likely overall mortality benefit of IPT. The mean I² measurement was 42.9%, which is lower than the published I² of 54.7%, indicating less heterogeneity on average.

Figure.

All-cause mortality of tuberculosis preventive therapy with isoniazid vs. placebo in simulated studies and effect on meta-analysis result for PPD-positive persons; aggregate results after 100 000 simulations. The point estimate of the relative risk is the mean from all the simulations, while the 95% credibility interval is a numeric interval in which the mean lies with a 95% probability. In studies that were not simulated (i.e., Pape et al.⁷ and Whalen et al.⁸), only the published point estimate of the treatment effect is reported as the 95% confidence interval from these trials and 95% credibility interval from simulations are not comparable. PPD = purified protein derivative.

DISCUSSION

Subgroup analyses in clinical trials can be useful, but are often incompletely reported, which can affect subsequent meta-analyses.¹⁰ As it is unlikely that more large placebo-controlled trials of IPT will be undertaken because of the strong reduction of active TB already demonstrated, it is crucial to examine the existing evidence on mortality carefully.

In the current study, we showed that individual trial results analyzed by PPD subgroup are not robust or reliable when large numbers of participants have an unknown PPD, and conclusions should be drawn with caution. In addition, we demonstrated that allocating the PPD-unknowns had an overall effect on the meta-analysis results for PPD-positive participants, even though the two studies we examined were relatively small. The heterogeneity remained moderate, possibly due to differing study designs (i.e., Mwinga et al.⁵ studied twice-weekly IPT for 6 months and Pape et al.⁷ studied daily IPT for 12 months). However, when all PPD-unknowns were allocated, the mean heterogeneity from the simulations was less than the value from the original meta-analysis. The results from our simulated meta-analyses, indicating a likely mortality benefit of IPT in PPD-positive individuals, add strength to WHO recommendations that IPT be given as part of an initial package of care to people with HIV/AIDS.