UV Resonance Raman Investigation of the Aqueous Solvation Dependence of Primary Amide Vibrations

Abstract

We investigated the normal mode composition and the aqueous solvation dependence of the primary amide vibrations of propanamide. Infrared, normal Raman, and UV resonance Raman (UVRR) spectroscopy were applied in conjunction with density functional theory (DFT) to assign the vibrations of crystalline propanamide. We examined the aqueous solvation dependence of the primary amide UVRR bands by measuring spectra in different acetonitrile/water mixtures. As previously observed in the UVRR spectra of N-methylacetamide, all of the resonance enhanced primary amide bands, except for the Amide I (AmI), show increased UVRR cross sections as the solvent becomes water-rich. These spectral trends are rationalized by a model wherein the hydrogen bonding and the high dielectric constant of water stabilizes the ground state dipolar ⁻O—C=NH₂⁺ resonance structure over the neutral O=C—NH₂ resonance structure. Thus, vibrations with large C—N stretching show increased UVRR cross sections because the C—N displacement between the electronic ground and excited state increases along the C—N bond. In contrast, vibrations dominated by C=O stretching, such as the AmI, show a decreased displacement between the electronic ground and excited state, which result in a decreased UVRR cross section upon aqueous solvation. The UVRR primary amide vibrations can be used as sensitive spectroscopic markers to study the local dielectric constant and hydrogen bonding environments of the primary amide side chains of glutamine (Gln) and asparagine (Asn).

Graphical Abstract

INTRODUCTION

The primary amide functional group is of significant biological interest since it is found in the side chains of Gln and Asn. These side chains may be of structural and functional significance to peptides and proteins since they can participate in both intra- and intermolecular hydrogen bonding, which may be important to the formation and stabilization of prion and amyloid-like fibril aggregates that are involved in a number of protein diseases.^1–5 Given the importance of these primary amide groups, it is of great value to find spectroscopic markers that can be used to monitor the Asn and Gln hydrogen bonding and dielectric environments.

UV resonance Raman (UVRR) spectroscopy is a powerful tool for studying the conformations of proteins,⁶ as well as for determining hydrogen bonding, protonation states, and local dielectric environments of aromatic amino acids,⁷ arginine,⁸ and histidine^9,10 side chains. Deep UV excitation (~200 nm) selectively enhances the peptide bond secondary amide vibrations of the protein backbone⁶ and the primary amide vibrations of the Asn and Gln side chains.¹¹ Investigations of the secondary amide vibrations^12–18 have developed a deep understanding of the spectral dependence of the peptide bond secondary structure and its hydrogen bonding. This understanding has enabled incisive investigations of protein and peptide structure. The work presented here is developing a similar deep understanding of the structural, hydrogen bonding, and dielectric environmental dependence of primary amide vibrations.

We investigated propanamide, one of the simplest primary amide compounds with a structure similar to that of the Asn and Gln side chains. We assigned the vibrations observed in the infrared, non-resonance Raman, and UVRR spectra of crystalline propanamide with the aid of density functional theory (DFT). We then examined the solution behavior of the primary amide UVRR bands in mixtures of acetonitrile and water. The primary amide bands are very sensitive to their hydrogen bonding and dielectric environments. These bands will be useful as spectroscopic probes to monitor the side chain environment and structure of Gln and Asn.

MATERIALS AND METHODS

Materials

Propanamide (CH₃CH₂CONH₂, 97% purity) and acetonitrile (HPLC, far-UV grade) were purchased from Acros Organics. N-Methylacetamide (CH₃CH₂CONHCH₃, NMA, ≥99% purity) and sodium perchlorate (NaClO₄, ≥98% purity) were purchased from Sigma-Aldrich. D₂O (99.9% atom D purity) was purchased from Cambridge Isotope Laboratories, Inc.

Sample Preparation

The propanamide solid samples consisted of a crystalline powder, which was used without further purification or recrystallization. N-deuterated propanamide crystals were prepared by multiple recrystallizations in D₂O. Propanamide solutions were prepared in H₂O at 10 mM concentration. Samples prepared in mixtures of acetonitrile and water were prepared at 30 mM concentrations. For these experiments, NaClO₄ (200 mM) was used as an internal standard. The N-deuterated propanamide solution was prepared at 30 mM concentration in pure D₂O.

Infrared and Non-Resonance Raman Spectroscopy

The mid-infrared spectrum of propanamide crystals was measured in the 600–4000 cm⁻¹ region at 1 cm⁻¹ resolution. The data were collected using a PerkinElmer model Spectrum 100 series FTIR equipped with a Universal diamond ATR. The propanamide crystals were lightly ground for ~30 s using a mortar and pestle in order to ensure good optical contact between the sample and the diamond crystal. The sample was placed on the diamond crystal and a force of ~145 N was applied using a pressure arm.

The visible excitation Raman spectra of propanamide crystals were measured using a Renishaw inVia Raman spectrometer equipped with a research-grade Leica microscope. Spectra were collected using a 5× objective lens with a ~2 cm ⁻¹ resolution spectrometer. The 633 nm exciting line was generated by a HeNe laser. The 380 cm⁻¹, 918 cm⁻¹, 1376 cm⁻¹, 2249 cm⁻¹, and 2942 cm⁻¹ bands of acetonitrile¹⁹ were used for calibration.

UV Resonance Raman (UVRR) Spectroscopy

The UVRR spectra of crystalline propanamide were measured using cw 229 nm light generated by an Innova 300C FreD frequency doubled Ar⁺ laser.²⁰ Solid samples were spun by using a cylindrical brass rotation cell to prevent thermal degradation or photodegradation. A SPEX Triplemate spectrograph, modified for use in the UV, was utilized to disperse the Raman scattered light. A Spec-10 system charge-coupled device (CCD) camera (Princeton Instruments, Model 735-0001) was employed to detect the scattered light.

UVRR solution-state measurements were made using ~204 nm excitation. The UV light was generated by Raman shifting the third harmonic of a Nd:YAG Infinity laser (Coherent, Inc.) in H₂ gas (~30 psi) and selecting the fifth anti-Stokes line. Solutions were circulated using a thermostated (20°C) flow cell²¹ to prevent accumulation of photodegradation products. The scattered light was dispersed and imaged using a double monochromator, modified for use in the UV in a subtractive configuration,²² and detected with a Spec-10 CCD camera.

UV Absorption Measurements

Absorption spectra were taken of 30 mM propanamide and 10 mM N-methylacetamide solutions dissolved in acetonitrile and water. A Varian Cary 5000 spectrophotometer with a 0.2 mm path length quartz cuvette was used for all measurements.

Raman Cross Section Calculations

The UVRR scattering cross sections of the spectrally deconvoluted propanamide Raman bands (see Supporting Information for details) were calculated using the following equation:¹¹

$${\sigma }_i=\frac{I_i{k}_r{C}_r{\sigma }_r}{I_r{k}_i{C}_i}\left(\frac{{\mathrm{\epsilon }}_i+{\mathrm{\epsilon }}_{ex}}{{\mathrm{\epsilon }}_r+{\mathrm{\epsilon }}_{ex}}\right)$$ (1)

where σ_i is the cross section of the ith propanamide Raman band, and σ_r is the cross section of the 932 cm⁻¹ ClO₄⁻ stretching band from our internal standard. C_r and C_i are the concentrations of NaClO₄ and propanamide, respectively. The factors k_r and k_i are the spectrometer efficiencies at the 932 cm⁻¹ and ith propanamide Raman bands. Assuming only the analyte absorbs, the factors ε_i, ε_r, and ε_ex are the molar absorptivities at the ith propanamide Raman band, the 932 cm⁻¹ band, and the excitation wavelength, respectively. The expression in the parentheses corrects the cross section measurement for self-absorption.^23,24 The Raman cross section of the 932 cm⁻¹ reference band, σ_r, at 204 nm excitation, was estimated to be ~1.18 × 10⁻²⁷ cm ²· molecule ⁻¹· sr⁻¹ by extrapolating the Raman cross section measurements of Dudik et al.²⁵

DFT Calculations

The DFT calculations²⁶ were performed using the GAUSSIAN 09 package²⁷ with the M06-2X functional²⁸ and the 6-311++g** basis set. The calculated frequencies of the propanamide vibrations were calculated using a harmonic approximation and scaled linearly to the average band frequencies observed experimentally. The calculations simulated solvation implicitly by placing the propanamide molecule in an ellipsoidal cavity surrounded by a polarizable continuum dielectric modeled to simulate water. The potential energy distribution (PED) of each vibration was obtained from the GAUSSIAN output files by employing the GAR2PED program.²⁹

RESULTS AND DISCUSSION

Normal Mode Analysis

The infrared and Raman spectra of propanamide were reported previously.^30–35 The most detailed normal mode analysis and assignments were carried out by Kuroda et al.³⁴ and Nandini and Sathyanarayana.³⁵ Kuroda et al.³⁴ utilized semi-empirical calculations that employed modified Urey–Bradley and valence force fields, while Nandini and Sathyanarayana³⁵ employed ab initio Hartree–Fock calculations. The band assignments significantly differ between these studies, particularly in regard to the amide vibrations. In the work here, we performed a new normal mode analysis for propanmide using more accurate DFT calculations, and use these results to assign our infrared, normal Raman, and UVRR spectral bands.

Propanamide Molecular Structure

We determined the crystal structure of our propanamide crystals (see Supporting Information for details), and found it to be close to the structure reported previously.³⁶ The crystal unit cell is monoclinic (P2₁/c space group), with four molecules per unit cell (Figure S1). The measured crystallographic axes and angles are a = 8.851(4) Å, b = 5.750(2) Å, c = 9.766(3) Å, and β = 114.780(15)°.

We optimized the propanamide geometry (Figure 1) for the DFT calculations by taking the crystal structure as an initial starting point and determining the minimum energy geometry. As in the crystal, the calculated ground state equilibrium geometry of propanamide shows C₁ symmetry since the NCCC dihedral angle deviates from 180°. Our results agree with the calculated structure of Nandini and Sathyanarayana.³⁵ However, our calculated structure differs from that of Kuroda et al.,³⁴ who assumed a C_s symmetry for propanamide, since its crystal structure had not been determined at that time. Propanamide has 30 fundamental vibrations, which, for a C₁ point group are all both infrared and Raman active, and unlike in the C_s point group, there is no differentiation between in-plane (a′) and out-of-plane (a″) modes.

Figure 1.

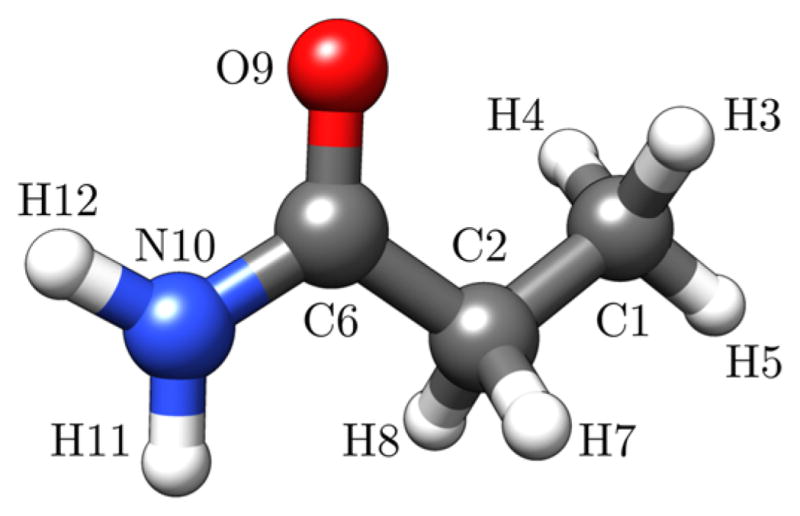
DFT-optimized structure of propanamide showing atomic numbering scheme used for normal mode analysis.

Tables S4–S6 enable comparisons between the structural parameters of the energy minimized structure used in our calculations and our measured crystal structure. The geometry and heavy atom bond lengths and angles of the minimized structure are close to the crystal structure, but not identical. This is most likely because the polarizable continuum model (PCM) employed in our calculations does not take into account crystal packing forces and hydrogen bonding.

Vibrational Band Assignments

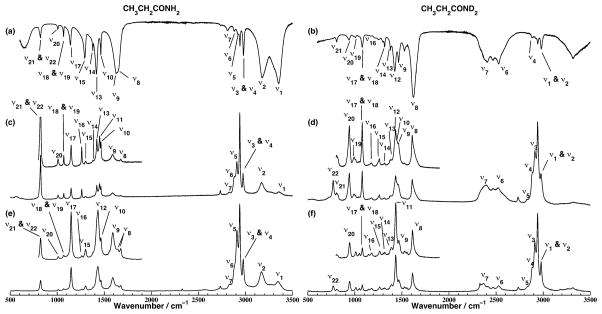
Figure 2 shows the infrared, visible Raman, and UVRR spectra of CH₃CH₂CONH₂ and CH₃CH₂COND₂. Table 1 compares the frequencies and relative intensities of the infrared and non-resonance Raman spectra. We utilized UVRR to help identify the primary amide Raman bands. The primary amide NV₁ electronic transition absorption band at ~180 nm resonance enhances the 204 nm excited UVRR spectra and pre-resonance enhances the 229 nm excited UVRR spectra. We expect that most resonance enhanced bands will consist of vibrations with large contributions of C–N stretching, since the excited state is expected to be expanded along this coordinate.³⁷ Tables 2 and 3 list the vibrational assignments, calculated, scaled frequencies, and PEDs for CH₃CH₂CONH₂ and CH₃CH₂COND₂, respectively.

Figure 2.

(a,b) Infrared, (c,d) non-resonance Raman (633 nm excitation), and (e,f) UVRR (229 nm excitation) spectra of crystalline CH₃CH₂CONH₂ and CH₃CH₂COND₂.

Table 1.

Infrared and Non-Resonance Raman Frequencies (cm⁻¹) of Crystalline CH₃CH₂CONH₂ and CH₃CH₂COND₂

CH3CH2CONH2a		CH3CH2COND2a,b
Infrared	Raman	Infrared	Raman
3356 vs, br	3356 s, br
3309 sh
	3265 sh
3177 vs, br	3171 s, br
2979 s	2975 s	2981 m	2977 s
2943 m	2940 vs	2943 w	2941 vs
2922 w	2909 s	2923 sh	2912 s
2882 w	2882 sh	2884 vw	2886 sh
2811 m	2827 vw		2833 sh
2737 sh	2734 m		2734 w
		2527 s	2523 s
		2407 s, br	2393 s, br
1643 sh, vs	1676 vw	1623 vs	1610 s
1628 vs	1588 m
1464 m	1464 s	1466 m	1464 m
	1450 s		1450 sh
			1434 s
1418 vs	1420 s	1425 s	1422 sh
1379 w	1381 w	1379 w	1378 sh
1294 s	1302 w	1318 w	1317 vw
	1260 s		1261 m
		1168 vw	1176 w
1141 s	1148 s
1068 m	1070 m	1079 m	1079 s
1007 w	1009 m	1007 w	1006 sh
		989 sh	992 m
		940 m	942 s
822 m	822 s		819 sh
811 sh	812 sh	807 m	806 m
			770 s
			731 sh
648 s, br	632 sh, br
	563 w, br		549 w, br
	471 s		441 m
	287 vw		274 w, br
	210 vw

^avs: very strong; s: strong; m: medium; w: weak; vw: very weak; br: broad; sh: shoulder.

^bBands that derive from the monodeuterated amide group are not reported.

Table 2.

Frequencies (cm⁻¹) and Assignments of Infrared and Raman Bands for Crystalline CH₃CH₂CONH₂

	Infrared	Raman	Calcd	δa (%)	PEDb (≥5% contribution)
ν1	3356	3356	3434	2.3	νNH (57), –νNH (43)
ν2	3177	3171	3319	4.6	νNH (57), νNH (43)
ν3	2979	2975	2906	2.4	νC1H (69), –νC1H (22)
ν4	2979	2975	2894	2.8	νC1H (49), –νC1H (45)
2ν10	2943	2940	–		–
ν5	2922	2909	2866	1.7	νC2H (75), –νC2H (19)
ν6	2882	2882	2830	1.8	νC1H (42), νC1H (32), νC2H (23)
ν7	2811	2827	2825	0.2	νC2H (76), νC2H (20)
2ν14	2737	2734	–		–
ν8	1643	1676	1667	0.5	νC=O (75), –νCN (7), δsNC(O)C (7)
ν9	1628	1588	1562	2.9	σNH2 (86), νCN (10)
ν10	1464	1464	1453	0.7	δas′CH3 (43), –δasCH3 (38), ρ′CH3 (8)
ν11	–	1450	1443	0.5	δasCH3 (51), δas′CH3 (39), –ρ′CH3 (8)
ν12	–	1430c	1393	2.6	ωCH2 (30), νC2C6 (20), –νCN (19), –βC=O (10), –νC1C2 (7), δas′CH3 (6)
ν13	1418	1420	1422	0.2	σCH2 (89)
ν14	1379	1381	1374	0.4	δsCH3 (89), νC1C2 (6)
ν15	1294	1302	1278	1.6	ωCH2 (31), νCN (28), –τCH2 (12), βC=O (8), ρNH2 (5)
ν16	–	1260	1271	0.9	τCH2 (61), ωCH2 (13), –ρ′CH3 (7), –ρCH2 (6)
ν17	1141	1148	1130	1.3	ρNH2 (30), –νC1C2 (19), ρ′CH3 (11), –ρCH3 (10), –νC=O (8), δsNC(O)C (7), δCCC (7)
ν18	1068	1070	1108	3.6	ρCH2 (27), –ρCH3 (21), –τCH2 (17), –ρ′CH3 (16), –ΠC=O (11)
ν19	1068	1070	1090	1.9	νC1C2 (38), ρNH2 (26), –νCN (16), ρCH3 (6)
ν20	1007	1009	1028	2.0	ρ′CH3 (28), ωCH2 (19), νC1C2 (18), –ρCH3 (11), –νC2C6 (9), –ρCH2 (8)
ν21	822	822	853	3.8	ρCH2 (23), ρ′CH3 (18), –ΠC=O (18), ρCH3 (15), τCH2 (10), νC2C6 (8)
ν22	811	812	850	4.7	νC2C6 (43), –ρCH3 (14), ρNH2 (11), –ρCH2 (7), νC1C2 (6)

^aδ = |ν_obs – ν_calc|/ν_obs × 100%.

^bν: stretch; δ_s: sym deformation; σ: scissoring; δ_as: asym deformation; ρ: rocking; ω: wagging; β: in-plane bending; τ: twisting; Π: out-of-plane bending.

^cFrequency obtained from 229 nm excitation UVRR data.

Table 3.

Frequencies (cm⁻¹) and Assignments of Infrared and Raman Bands for Crystalline CH₃CH₂COND₂

	Infrared	Raman	Calcd	δa (%)	PEDb (≥5% contribution)
ν1	2981	2977	2941	1.3	νC1H (69), –νC1H (22)
ν2	2981	2977	2929	1.7	νC1H (49), –νC1H (45)
2ν10	2943	2941	–	–	–
ν3	2923	2912	2900	0.6	νC2H (75), –νC2H (19)
ν4	2884	2886	2863	0.8	νC1H (42), νC1H (32), νC1H (23)
ν5	–	2833	2858	0.9	νC2H (76), νC2H (20)
2ν13	–	2734	–	–	–
ν6	2527	2523	2607	3.3	νND (54), –νND (45)
ν7	2407	2393	2458	2.4	νND (54), νND (45)
ν8	1623	1610	1662	2.8	νC=O (78), δsNC(O)C (7), –νCN (7)
ν9	1466	1464	1447	1.2	δas′CH3 (42), –δasCH3 (37), ρ′CH3 (8)
ν10	–	1450	1437	0.9	δasCH3 (52), δas′CH3 (38), –ρCH3 (8)
ν11	–	1434c	1401	2.3	νCN (33), –ωCH2 (19), –νC2C6 (19), βC=O (10), –δas′CH3 (6), δsND2 (5)
ν12	1425	1422	1415	0.6	σCH2 (89)
ν13	1379	1378	1367	0.8	δsCH3 (89), νC1C2 (8)
ν14	1318	1317	1295	1.7	ωCH2 (45), νCN (23), δsND2 (15)
ν15	–	1261	1261	0.0	τCH2 (75), –ρCH3 (9), –ρ′CH3 (5)
ν16	1168	1176	1134	3.2	δsND2 (60), βC=O (12), νC2C6 (8), –ωCH2 (5)
ν17	1079	1079	1093	1.3	νC1C2 (35), ρCH3 (19), –ρ′CH3 (11), –δCCC (7), –δsNC(O)C (5)
ν18	1079	1079	1091	1.1	ρCH2 (25), –ρ′CH3 (19), ρCH3 (17), –τCH2 (16), –ΠC=O (11), νC1C2 (7)
ν19	1007	1006	1019	1.2	νC1C2 (33), ρ′CH3 (20), ωCH2 (14), –νC2C6 str (9), –ρCH3 (6), δsND2 (5)
–	989	992	–	–
ν20	940	942	936	0.5	ρND2 (34), –νCN (15), –ρ′CH3 (11), δsNC(O)C (9), δsND2 (8), ρCH3 (6)
–	–	819	–	–	–
ν21	807	806	828	2.7	ρCH2 (29), ρCH3 (24), –ΠC=O (19), ρ′CH3 (13), τCH2 (12)
ν22	–	770	776	0.7	νC2C6 (51), ρND2 (25), –δCCC (7)

^aδ = |ν_obs – ν_calc|/ν_obs × 100%.

^bν: stretch; δ_s: sym deformation; σ: scissoring; δ_as: asym deformation; ρ: rocking; ω: wagging; β: in-plane bending; τ: twisting; Π: out-of-plane bending.

^cFrequency obtained from 229 nm excitation UVRR data.

2000–3500 cm⁻¹ Region

The high frequency region is dominated by N–H and C–H stretching bands. The N–H stretches show broad, strong peaks in both the infrared and Raman spectra that substantially downshift in frequency upon N-deuteration. The NH₂ asymmetric stretching band is located at ~3355 cm⁻¹, but downshifts to ~2525 cm⁻¹ upon N-deuteration. The NH₂ symmetric stretching band appears at ~3175 cm⁻¹, while its ND₂ counterpart appears at ~2400 cm⁻¹. The ~3320 cm⁻¹ feature observed in the CH₃CH₂COND₂ spectra derives from an N–H stretching vibration for mono-N-deuterated propanamide.

The bands located between 2700 and 3100 cm⁻¹ are insensitive to N-deuteration, which indicates that they are primarily C–H stretching modes. The ~2975 cm⁻¹ and ~2880 cm⁻¹ bands derive from CH₃ asymmetric and symmetric stretching modes, respectively. The CH₂ asymmetric stretching mode appears at ~2910 cm⁻¹ in the Raman, and at ~2920 cm⁻¹ in the infrared spectra. In contrast, the CH₂ symmetric stretching band appears at ~2830 cm⁻¹ and ~2810 cm⁻¹ in the Raman and infrared spectra, respectively.

The bands at ~2735 cm⁻¹ and ~2940 cm⁻¹ cannot be assigned to fundamentals. Neither band shifts upon N-deuteration, and according to Kuroda et al.’s³⁴ data, these bands also do not shift upon deuteration of the methlyene group. This indicates that they do not derive from overtone or combination of amide or methlyene bands. Therefore, we assign the ~2735 cm⁻¹ band to the first overtone of the ~1380 cm⁻¹ CH₃ symmetric deformation vibration. The ~2940 cm⁻¹ band is strong in both the non-resonance Raman and UVRR spectra, but is of only moderate intensity in the infrared. We assign this band to a Fermi resonance between the first overtone of the ~1460 cm⁻¹ CH₃ asymmetric deformation and the CH₃ symmetric stretching fundamental based on the suggestions of Kuroda et al.³⁴ and Nolin and Jones.³⁸ This assignment disagrees with Nandini and Sathyanarayana,³⁵ who attribute this band to a CH₂ asymmetric stretching mode. We disagree with the Nandini and Sathyanarayana³⁵ assignment since this band is upshifted beyond the typical frequency range (~2910–2930 cm⁻¹) observed for CH₂ asymmetric stretching vibrations.^39,40

1500–1800 cm⁻¹ Region

In this region there are two vibrations that involve the primary amide group, the Amide I (AmI) and Amide II (AmII) vibrations. The AmI at ~1640 cm⁻¹ and the AmII at ~1620 cm⁻¹ are strong and overlap in the infrared spectrum. In contrast, in the non-resonance Raman spectrum they are well-resolved, and show up as a moderately weak band located at ~1675 cm⁻¹ (AmI) and a stronger band at ~1590 cm⁻¹ (AmII). In the UVRR spectrum, the AmI band shows a ~1675 cm⁻¹ peak followed by an overlapping ~1640 cm⁻¹ feature. The AmII band is strong and occurs at ~1590 cm⁻¹.

The large frequency differences between the infrared and Raman bands for the AmI and AmII vibrations presumably derive from the coupling of molecular vibrations within the crystal lattice into phonons. The spectral frequency differences for the infrared, normal Raman, and resonance Raman spectra derive from their differing selection rules for the different phonon modes with different phasings of relative molecular motion.

Kuroda et al.³⁴ indicated that C=O stretching and NH₂ scissoring motions are both important to the PEDs of the AmI and AmII vibrations. In contrast, Nandini and Sathyanarayana’s³⁵ normal mode analysis, as well as other studies on acetamide,^41–43 indicate that the AmI vibration is mainly C=O stretching and the AmII is mainly NH₂ bending. Our analysis concludes that the AmI mode consists mostly of C=O stretching (~75%), with minor C—N stretching and NC(O)C in-plane bending (~7% each) components, while the AmII mode is essentially pure NH₂ scissoring (~86%) with a small C—N stretching component (~10%).

The spectral changes that are observed upon N-deuteration are consistent with our normal mode analysis of the AmI and AmII bands. The AmII band completely disappears, and a new band, which derives from ND₂ scissoring, appears at ~1170 cm⁻¹, supporting the notion that this mode is essentially pure NH₂ scissoring. In contrast, N-deuteration results in the AmI mode downshifting to ~1610 cm⁻¹ in the non-resonance Raman and UVRR spectra, and to ~1620 cm⁻¹ in the infrared spectrum. This behavior is similar to the AmI band in secondary amides, and strongly supports the idea that this mode is predominately C=O stretching.

1200–1500 cm⁻¹ Region

Most bands in this region are easily assigned to CH₃ or CH₂ deformations and bending vibrations. The bands at ~1464 cm⁻¹ and ~1450 cm⁻¹ derive from CH₃ asymmetric deformations, while the ~1380 cm⁻¹ band is assigned to the CH₃ symmetric deformation. In the non-resonance Raman and UVRR spectra, there is a weak band at ~1260 cm⁻¹ that is assigned to a CH₂ twisting mode.

C–N Stretching Modes

Our assignments of the remaining bands observed in the 1200–1500 cm⁻¹ region differ from Kuroda et al.³⁴ and Nandini and Sathyanarayana.³⁵ Kuroda et al.³⁴ previously assigned the ~1420 cm⁻¹ band to two fundamentals, a CH₂ scissoring mode and a C–N stretching mode. Nandini and Sathyanarayana³⁵ also assigned this band to two fundamentals, viz., a CH₂ bending mode and a CH₃ symmetric bending vibration. Nandini and Sathyanarayana³⁵ assigned a ~1300 cm⁻¹ band to a vibration that consists of ~30% C–N stretching and CH₂ wagging. They conflate this vibration with the C–N stretching mode that Kuroda et al.³⁴ assigned to the ~1420 cm⁻¹ band. In contrast, Kuroda et al.³⁴ assigns the ~1300 cm⁻¹ band to an almost pure CH₂ wagging vibration.

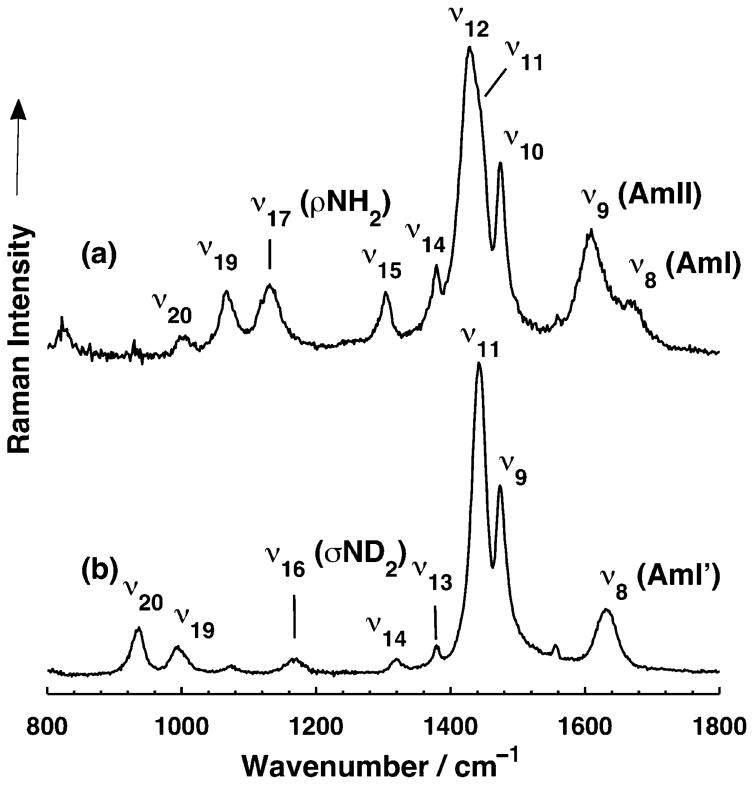
Our normal mode analysis and UVRR data lead to very different assignments of these two vibrations. In the UVRR spectrum of CH₃CH₂CONH₂, there is a very intense band at ~1430 cm⁻¹, which we assign to the ν₁₂ fundamental (Table 2) since it contains significant C–N stretching character. This band is not apparent in Kuroda et al.’s³⁴ or our non-resonance Raman spectra of CH₃CH₂CONH₂. The assignment of this resonance enhanced ~1430 cm⁻¹ mode allows us to unambiguously assign the ~1420 cm⁻¹ band to a CH₂ scissoring vibration. The ~1300 cm⁻¹ band, which appears weak in both the non-resonance Raman and UVRR spectra, is assigned to the ν₁₅ vibration, which appears to be related to the ν₁₂ mode.

Our normal mode analysis shows that the ν₁₂ and ν₁₅ amide vibrations contain significant C—N stretching. The largest ν₁₂ PED components are CH₂ wagging (~30%), C—CH₂ stretching (~20%), C—N stretching (~19%), and C=O in-plane bending (~10%). For ν₁₅, the major PED components are CH₂ wagging and C—N stretching (~30% each), followed by CH₂ twisting (~12%) and C=O in-plane bending (~8%).

1000–1200 cm⁻¹ Region

In this spectral region, we expect NH₂ rocking, CH₂ rocking, CH₃ rocking, and C–CH₃ stretching vibrations. The ~1141 cm⁻¹ infrared and ~1148 cm⁻¹ Raman bands are easily assigned to the NH₂ rocking vibration, since they downshift to ~940 cm⁻¹ upon N-deuteration. The C–CH₃ (ν₁₉) stretching vibration was previously assigned,³⁴ but our normal mode calculation suggests that this mode is more complicated and contains significant contributions of NH₂ rocking (~26%) and C–N stretching (~16%). The infrared and Raman spectra show only two bands located at ~1070 cm⁻¹ and ~1010 cm⁻¹. We assign the ~1070 cm⁻¹ band to both the CH₂ rocking (ν₁₈) and C– CH₃ stretching (ν₁₉) modes. In contrast, the ~1010 cm⁻¹ band shows a negligible change in frequency upon N-deuteration, and is thus assigned to the CH₃ rocking mode.

<1000 cm⁻¹ Region

The region below 1000 cm⁻¹ is dominated mainly by torsional motions, as well as extensively coupled skeletal stretching and deformation modes. This region is difficult to unambiguously assign, especially below 700 cm⁻¹. We assign the two bands at ~820 and 810 cm⁻¹ to CH₂ rocking and C–CH₃ stretching fundamentals, respectively. The C– CH₃ stretching mode shows a modest contribution of NH₂ rocking, which likely accounts for its ~42 cm⁻¹ downshift to ~770 cm⁻¹ upon N-deuteration.

Solvation Dependence of UVRR Bands

UVRR of Propanamide in Aqueous Solutions

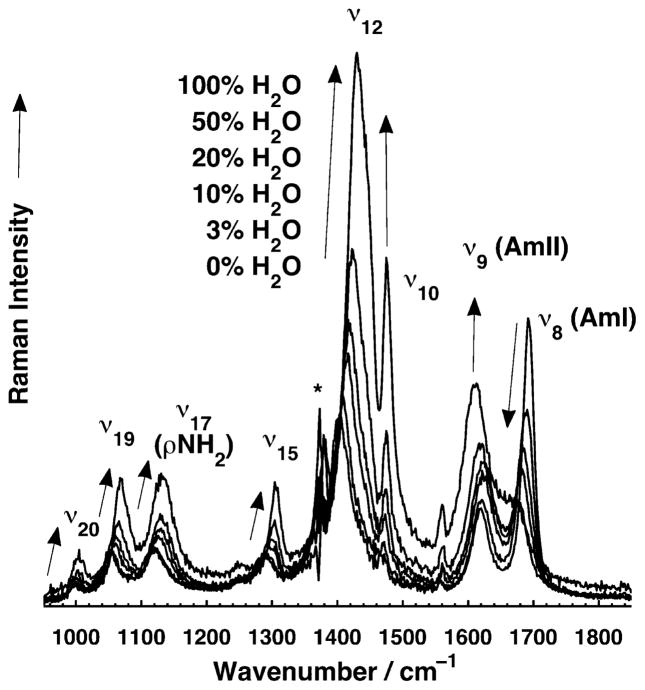
We measured the ~204 nm excited UVRR spectra of propanamide in mixtures of acetonitrile and water in order to determine the effects of solvation on the primary amide vibrations. The spectra of propanamide in aqueous solutions (Figure 3) differ from that of crystalline propanamide. Compared to crystalline spectra, propanamide in H₂O (Table 4) shows an AmI (ν₈) band that downshifts ~7 cm⁻¹ and appears as a shoulder, while the AmII (ν₉) band upshifts ~22 cm⁻¹. The ν₁₂ and C–CH₃ stretching (ν₁₉) bands do not change frequency, while the NH₂ rocking (ν₁₇) mode downshifts ~16 cm⁻¹.

Figure 3.

UVRR (204 nm excitation) spectra of propanamide (a) in H₂O and (b) in D₂O. The contribution of solvent was subtracted from both spectra. For (a) 200 mM NaClO₄ was used as an internal standard. The contribution of the ClO₄⁻ stretching band was also subtracted.

Table 4.

Measured Frequencies (cm⁻¹) and Cross Sections (σ, mbarns · molecule⁻¹· sr⁻¹) of UVRR Bands in CH₃CH₂CONH₂

vibration	crystala	waterb		acetonitrilec
	Freq	Freq	σ	Freq	σ
ν8 (AmI)	1676	1669 ± 1	3.5 ± 0.70	1692	9.8
ν9 (AmII)	1588	1610 ±1	18± 1.1	1619	4.9
ν12	1430	1428 ±1	30± 0.90	1403	9.1
ν17	1148	1132 ± 1	8.8 ± 0.24	1121	3.0
ν19	1070	1069 ± 1	6.0 ± 0.14	1051	2.3

^aUVRR cross sections were not calculated due to the lack of an internal standard.

^bValues measured from n = 4 sample size.

^cValues measured from n = 1 sample size.

The bands of propanamide in D₂O (Figure 3b) also show significant changes compared to their N-deuterated crystal spectra. The AmI′ (ν₈) band is broad and is located at ~1633 cm⁻¹. The AmII band disappears, and the ND₂ (ν₁₆) scissoring band occurs at ~1168 cm⁻¹, while the ν₁₁ band is at ~1443 cm⁻¹.

Effect of Solvation on UVRR Spectra

Figure 4 shows the dramatic effect of solvation on the UVRR bands of primary amides. The spectra show that all bands, except for the AmI, increase their Raman cross sections as the mole fraction of H₂O increases (Table 4). The AmII and ν₁₂ bands show the largest cross section increases (~3–4-fold), while the NH₂ rocking (ν₁₇) and the C–CH₃ stretching (ν₁₉) bands increase ~2–3- fold. The AmI band is the only band whose Raman cross section decreases as the mole fraction of H₂O increases.

Figure 4.

UVRR (204 nm excitation) spectra of propanamide (30 mM) in different acetonitrile and water mixtures. Arrows show frequency and intensity trends of UVRR bands as the fraction of H₂O increases. NaClO₄ (0.2 M) was used as an internal intensity and calibration standard in the solutions. Spectra were normalized to the integrated area of the 932 cm⁻¹ ClO₄ ⁻ stretching band. The spectral contributions of acetonitrile, ClO₄⁻, and water were subtracted. The asterisk indicates a spectral feature that is an artifact of subtracting out the ~1376 cm⁻¹ acetonitrile band.

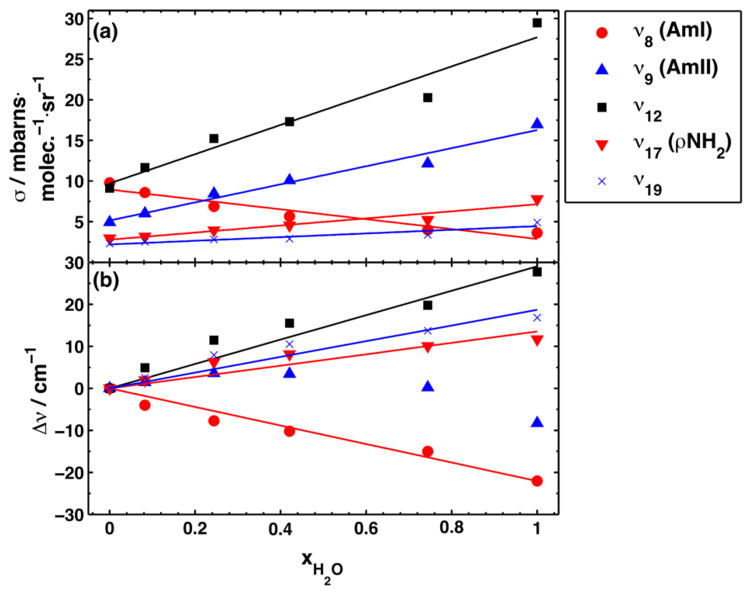
Figure 5 shows that there is a roughly linear cross section and frequency increase for most bands. The ν₁₂ band shows a ~29 cm⁻¹ per mole fraction H₂O frequency increase, the NH₂ rocking (ν₁₇) band shows a ~14 cm⁻¹ per mole fraction H₂O frequency increase, while the C–CH₃ stretching (ν₁₉) vibration shows a ~19 cm⁻¹ per mole fraction H₂O frequency increase. In contrast, the AmI band shows a ~22 cm⁻¹ per mole fraction H₂O frequency decrease. The AmII band shows only a modest frequency decrease with increasing water mole fractions.

Figure 5.

Dependence of UVRR propanamide band (a) cross sections and (b) frequencies on the mole fraction of water.

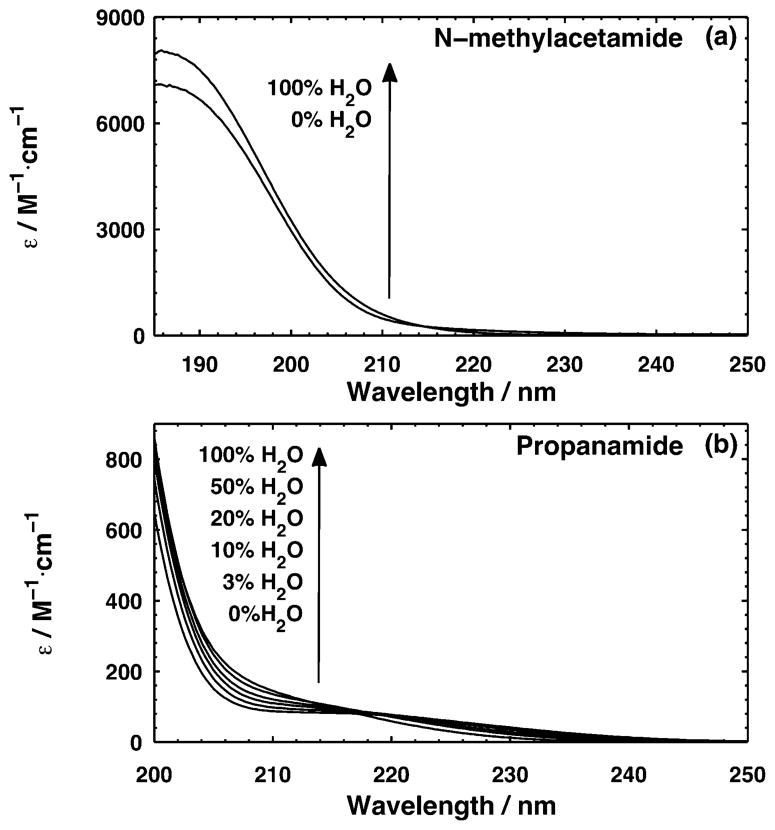
The dependence of the UVRR spectra of propanamide on the mole fraction of water shown in Figure 4 is very similar to that observed in valeramide₁₁ and NMA.^44–48 To understand this behavior, we compared the UV absorption spectra of propanamide and NMA in acetonitrile and in H₂O (Figure 6). The molar absorptivities of the ~200 nm NV₁ transitions increase for both propanamide and NMA as the solvent transfers from acetonitrile to H₂O. For NMA, the absorption peak maximum of the NV₁ transition redshifts going from acetonitrile to water. This is less clearly evident in the case of propanamide where the NV₁ absorption maximum lies deeper in the UV at ~180 nm. This trend is expected from the results of Nielsen and Schellman.⁴⁹ They observe redshifts in the absorption maxima of several primary and secondary amides going from cyclohexane to water. This increase in molar absorptivity of the NV₁ transition, upon aqueous solvation, is in part responsible for increasing the UVRR cross sections due to the fact that the Raman scattering cross section is proportional to the square of the molar absorptivity.

Figure 6.

UV absorption spectra of (a) NMA and (b) propanamide in acetonitrile and water. Arrows show trend of molar absorptivity as the fraction of water increases.

However, most of the cross section increase results from changes in the ground state structure. The effect of aqueous solvation on the UVRR secondary amide band intensities and frequencies has been traditionally rationalized by considering the effects of the solvent dielectric and direct hydrogen bonding on the amide group resonance structures.^44–48 We can invoke a similar argument for primary amides.

In low dielectric constant and hydrogen bonding environments, the primary amide O=C—NH₂ resonance form is typically dominant over the ⁻O—C=NH₂ ⁺ structure in the propanamide electronic ground state (Scheme 1). The dipolar resonance structure becomes more favorable in water due to the high dielectric constant and the stabilizing hydrogen bonding to propanamide’s C=O and NH₂ groups. These two effects increase the C—N bond order and decrease the C—O bond order of the primary amide group in the electronic ground state.

Scheme 1.

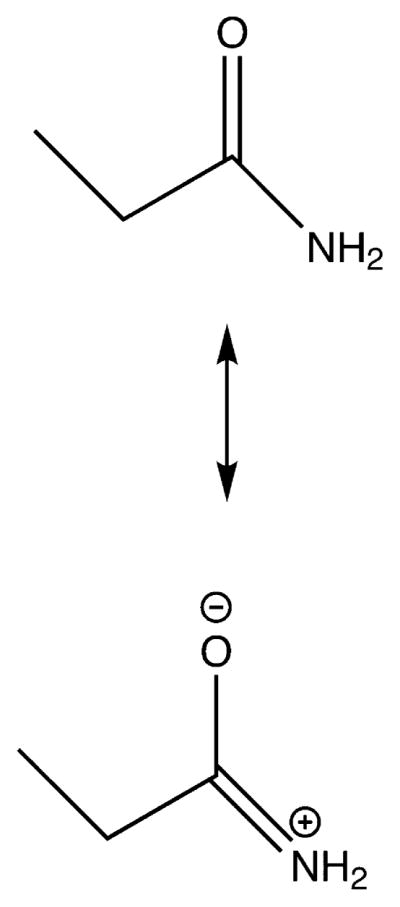
Resonance Structures of Propanamide

It is also important to note that the electronic excited state can also be impacted by solvation effects. For example, in NMA, Hudson and Markham⁴⁷ argued that their ab initio post- Hartree–Fock calculations indicate that the effects of hydrogen bonding due to solvation are greater in magnitude on the π → π* electronic excited state equilibrium geometry than for the ground state geometry. They argue that the changes in the C=O and C—N bond lengths in the excited state due to solvation were also in the opposite direction of the excited state bond length changes of unsolvated NMA; i.e., the C—N bond length is larger and the C=O bond length is smaller in the excited state for a NMA(H₂O)₃ cluster compared to an isolated NMA molecule.

The changes in C—O and C—N bond orders (and bond lengths) of the amide group going from acetonitrile to water profoundly affect the resonance Raman cross sections and the band frequencies. This is because resonance Raman cross sections scale with the square of the displacement along the enhanced vibrational normal coordinate between the equilibrium geometries of the electronic ground and excited states.⁵⁰ For example, the most resonance enhanced UVRR bands of NMA in water involve C—N stretching^{44–46,51,52} because of the large expansion of the electronic excited state along the C—N bond.^47,48,52 In contrast, there is a relatively small enhancement of the AmI band for NMA in water because the excited state expansion along the C=O bond is much less.

In the case of propanamide, the dramatic spectral changes observed in Figure 4 can likewise be explained by changes in C=O and C—N bond lengths upon solvation. The elongation of the C=O bond results in a decrease of the C=O stretching force constant. This results in a downshift in the AmI band frequency. The AmI band UVRR cross section also decreases because the magnitude of the displacement between the electronic ground and excited states along the C—O coordinate must decrease in water since the ground state C=O bond length elongates.

In contrast, for vibrations with significant C—N stretching, the contraction of the C—N bond length results in a vibrational frequency upshift due to the increase in the stretching force constant. This bond contraction also increases the magnitude of the displacement between the electronic ground and excited states along the C—N coordinate, which results in an increase in the Raman cross sections. It will be more difficult to explain the origin of the UVRR cross section increases for heavily coupled modes, such as the ~1430 cm⁻¹ ν₁₂ and the ~1300 cm⁻¹ ν₁₅ modes, which contain displacements of multiple atoms. The displacements of all of the primary amide atoms contribute to resonance enhancement. Phasing of this motion can be very important.⁵² However, we conclude that the C—N stretching motion in these vibrations is predominantly responsible for their UVRR intensity enhancements.

CONCLUSION

We utilized DFT calculations, infrared, non-resonance Raman, and UVRR spectra to assign the vibrational bands of crystalline propanamide. Our study resolves previous inconsistencies in the vibrational assignments and normal mode compositions of primary amide bands. We also studied the effect of aqueous solvation on the primary amide UVRR bands by examining the ~204 nm UVRR dependence as the solvent transfers from acetonitrile to water. The aqueous solvation dependence of primary amide UVRR bands can be rationalized by the stabilization between dipolar resonance structures of the ground electronic state of the amide group. Both hydrogen bonding interactions and the increased dielectric constant as the solvent transfers from acetonitrile to water contribute to the stabilization of the dipolar resonance structure in the ground state, which effectively increases the C–N bond order while decreasing the C–O bond order.

The resulting increased displacement between electronic ground and excited state geometries along the C–N coordinate increases the UVRR cross sections of vibrations that contain significant C–N stretching. In contrast, the decreased displacement between the electronic ground and excited state geometries along the C–O coordinate results in a dramatic decrease in the AmI band UVRR cross section. These results indicate that the AmI, AmII, and ν₁₂ band UVRR cross sections and their frequencies can be used as sensitive spectroscopic markers for hydrogen bonding and local dielectric environment of the side chains of Gln and Asn.