Mechanical properties of the tumor stromal microenvironment probed in vitro and ex vivo by in situ-calibrated optical trap-based active microrheology

Abstract

One of the hallmarks of the malignant transformation of epithelial tissue is the modulation of stromal components of the microenvironment. In particular, aberrant extracellular matrix (ECM) remodeling and stiffening enhances tumor growth and survival and promotes metastasis. Type I collagen is one of the major ECM components. It serves as a scaffold protein in the stroma contributing to the tissue’s mechanical properties, imparting tensile strength and rigidity to tissues such as those of the skin, tendons, and lungs. Here we investigate the effects of intrinsic spatial heterogeneities due to fibrillar architecture, pore size and ligand density on the microscale and bulk mechanical properties of the ECM. Type I collagen hydrogels with topologies tuned by polymerization temperature and concentration to mimic physico-chemical properties of a normal tissue and tumor microenvironment were measured by in situ-calibrated Active Microrheology by Optical Trapping revealing significantly different microscale complex shear moduli at Hz-kHz frequencies and two orders of magnitude of strain amplitude that we compared to data from bulk rheology measurements. Access to higher frequencies enabled observation of transitions from elastic to viscous behavior that occur at ~200Hz to 2750Hz, which largely was dependent on tissue architecture well outside the dynamic range of instrument acquisition possible with SAOS bulk rheology. We determined that mouse melanoma tumors and human breast tumors displayed complex moduli ~5–1000 Pa, increasing with frequency and displaying a nonlinear stress-strain response. Thus, we show the feasibility of a mechanical biopsy in efforts to provide a diagnostic tool to aid in the design of therapeutics complementary to those based on standard histopathology.

Introduction

Tumor development and dissemination into neighboring tissue parenchyma is characterized by loss of tumor-stroma demarcations at the invasive front of the growing mass(Provenzano et al., 2006; Weber et al., 2006). At this interface, presentation of tumor desmoplasia due to aberrant synthesis of many extracellular matrix (ECM) proteins, along with an imbalance of matrix remodeling and/or enzymatic degradation is indicative of poor prognosis and metastatic disease(De Wever & Mareel, 2003). Tumor growth is sustained by the co-evolution of transformed stromal and recruited immune cells within the transformed ECM microenvironment. As collagen type I is one of the most abundant ECM proteins in the stromal microenvironment, its microscale architecture and viscoelasticity provide biomechanical signals that in turn trigger a cascade of biological events that may convey tumor suppressive cues or enable tumor progression(Egeblad, Rasch, & Weaver, 2010; Friedl & Alexander, 2011). In skin cancers such as cutaneous melanoma and squamous cell carcinoma, desmoplasia is largely due to reactive fibroblasts, which are influenced in part by infiltrated leukocytes to drive copious production and assembly of fibrillar collagens(Kalluri & Zeisberg, 2006; van Kempen, Ruiter, van Muijen, & Coussens, 2003). In breast cancer, increased collagen deposition is also observed, accompanied by changes in both topographical and viscoelastic properties(Barcus, Keely, Eliceiri, & Schuler, 2013; Gilkes et al., 2013; K. R. Levental et al., 2009; Mouw, Ou, & Weaver, 2014; Ng & Brugge, 2009; Plodinec, Loparic, Monnier, Obermann, Zanetti-Dallenbach, Oertle, Hyotyla, Aebi, Bentires-Alj, H., et al., 2012). Specifically, normally curved fibers progressively thicken, lengthen and linearize to form stiffer bundles several micrometers in width and length that act as highways to facilitate tumor haptokinesis and dissemination(Conklin et al., 2011; Friedl & Wolf, 2009; Provenzano et al., 2006). At first glance, these highways also facilitate beneficial adaptive and innate immune responses where T cells and recruited monocytes have easier access to the tumor. However, T cell activation and macrophage polarization are regulated by substrate rigidity. Stiffer substrates abrogate tumor suppressive T cell function and promote pro-tumorigenic M2 polarization of macrophages(Leight, Wozniak, Chen, Lynch, & Chen, 2012; Pickup, Mouw, & Weaver, 2014). This suggests that the emergence of a pro-tumor microenvironment requires a delicate balance between the physical properties, topography and viscoelasticity of collagen. Thus, delineating the contributions of viscoelasticity from those due to topography is needed to understand how these signals may be involved in tumor progression.

Successful metastatic dissemination is also regulated by the physico-chemical properties of the collagen rich tumor microenvironment. Tumor cells adopt different modes of motility to traverse stromal and connective tissues based on the porosity, stiffness and linearity of the surrounding ECM milieu, as observed in surrogate biomimetic platforms and in murio(Alexander, Weigelin, Winkler, & Friedl, 2013; Brábek, Mierke, Rösel, Veselý, & Fabry, 2010; Entenberg et al., 2013; Pathak & Kumar, 2011; Patsialou et al., 2013). Namely, in vitro 3D cell migration is in part aided by nucleus-generated anisotropy in pressure, actomyosin-generated traction forces and/or proteolytic degradation to propel cells through surrogate or cell-derived ECM matrices(Friedl & Wolf, 2003; Petrie, Koo, & Yamada, 2014; Stroka et al., 2014). In addition, in vitro migration studies in reconstituted ECMs, including collagen I hydrogels, confirm that cell migration parameters such as speed, distance traveled and persistence also depend on physico-chemical properties such as protein density, pore size, fiber thickness, crosslinking, and alignment(Brábek et al., 2010; A D Doyle, Carvajal, Jin, Matsumoto, & Yamada, 2015; Entenberg et al., 2013; Fraley et al., 2015; Pathak & Kumar, 2011; Patsialou et al., 2013). These processes depend on physical and chemical factors of the cell including deformability, adhesion and contractility. Cellular and environmental factors are interdependent; moreover they are dynamic, as the cell cytoskeleton (CSK) and local ECM actively and passively modulate one another in a complex and reciprocal manner(Kasza et al., 2007; Kolahi & Mofrad, 2010; Xu, Boudreau, & Bissell, 2009). If the specific phenotypic characteristics facilitating metastasis could be identified, they could be exploited in anti-metastatic targeted therapies(Tanner & Gottesman, 2015). While some of the factors involved in successful migration have already been identified, the interdependence of physico-chemical variables has not been well characterized. Elucidating the cell-ECM interactions relevant to epithelial cancer cell motility in stromal matrices will further develop our emerging notion of the mechanical phenotype of metastasis.

At the single-cell level, mechanical cues can alter intracellular processes such as signal transduction, cell-cycle regulation, transcription, protein synthesis, and cell–extracellular matrix (ECM) crosstalk on a dynamic range spanning milliseconds to minutes and on length scales from nanometers to micrometers(Tanner & Gottesman, 2015). One such interaction, cells’ generation of traction forces on the ECM, is regulated by the mechanical properties of the surrounding ECM(Wolf, te Lindert, et al., 2013). Surrogate collagen type I hydrogels have been extensively used to mimic the fractal network of fibrillar and porous architecture observed in human tumors in vivo(Cukierman, Pankov, & Yamada, 2002; Wallace & Rosenblatt, 2003). The basic sub-unit of these self-assembled networks is the collagen molecule, a right-handed triple helix ~300 nm in length, composed of three intertwined left-handed proline helices stabilized by hydrogen bonds(Guthold et al., 2007). Collagen spontaneously polymerizes (the polymer is more thermodynamically stable than the monomer); triple helices interdigitate a characteristic 67 nm D-periodicity, forming a microfibril with ten surface and four core collagens(Shoulders & Raines, 2009). These fibrils may then further assemble into arrays of fibrils spanning 20 to 100s of nanometers in diameter (fibers). Collagen fibrils and fibers have elastic moduli in the GPa range, and show non-linear mechanical responses that vary with the magnitude of the stresses or strains applied(Carlisle, Coulais, & Guthold, 2010; Fratzl et al., 1998; Münster et al., 2013; Shen, Dodge, Kahn, Ballarini, & Eppell, 2008; Storm, Pastore, MacKintosh, Lubensky, & Jamney, 2005; Sun, Luo, Fertala, & An, 2002). Straightening of kinks, gliding of subunits in fibrils, stretching of subunits and disrupting fibril and fiber organization require different forces, giving rise to nonlinear stress-strain relationships characterized by the so-called toe, heel, linear and failure regimes for macroscopically deformed individual fibers(Fratzl et al., 1998; Roeder, Kokini, Sturgis, Robinson, & Voytik-Harbin, 2002). While individual fibers of collagen have Young’s moduli in the GPa range, bulk mechanical measurements of reconstituted collagen hydrogels are several orders of magnitude more compliant, in the Pa-kPa range(Gentleman et al., 2003; Roeder et al., 2002). Bulk mechanical properties of collagen gels are strongly influenced by network architecture and interactions. In reconstituted collagen hydrogels, rotational and translational degrees of freedom at crosslinks and entanglements between fibers play a dominant role, rather than individual fiber properties. Because of their hierarchical structure, viscoelasticity varies as a function of length and time scale measured. Additionally, cells receive and interpret mechanical cues from both the individual fibers as well as those from the bulk gel, it is imperative to determine the mechanical cues provided by collagen at different force, length and time scales in order to understand cellular mechanotransduction.

The collagen microarchitecture is determined by ligand density, fiber alignment, pore size, and intra- and extra-fibril crosslinking. For in vitro assembly of collagen type I gels, collagen concentration directly affects both matrix elasticity and pore size(Mickel et al., 2008; Motte & Kaufman, 2013). Additionally, changing the temperature at which the collagen is polymerized alters its fibril width, pore size, overall architecture, and local fibril stiffness(Raub et al., 2007a; Williams, Gelman, & Poppke, 1978). Modulating assembly conditions also affects mechanical properties, allowing formation of gels with elastic moduli ranging ~1–10⁴ Pa. Collagen can thus be tuned to simulate in vivo physical properties of tissue, ranging from normal, through neoplastic transformation, to full-blown tumor associated stroma. In fractal hydrogels, applied shear force can be used to align fibers parallel to the applied force. This reduces the macroscopic mechanical properties of the gel as compared to unaligned gel. In contrast, pre-alignment of collagen fibrils increases bulk gel stiffness(An, Sun, & Luo, 2004; Guthold et al., 2007; Pedersen & Swartz, 2005; Sun et al., 2002). Recently we and others have shown that topography alone may be sufficient to guide cells to align parallel to the direction of the nanofibril(Andrew D. Doyle, Wang, Matsumoto, & Yamada, 2009; Kim, Staunton, & Tanner, 2015). Because of these mechanical characteristics, an individual cell may receive different signals depending on the local architecture or stiffness of a particular fiber.

Atomic force microscopy (AFM) has been used to assess the elastic modulus of individual collagen fibers and collagen rich tumor stroma ex vivo. AFM micro- and nano-indentation gives a higher spatial resolution compared to bulk rheological methods, allowing examination of individual fibers and/or superficial mechanical mapping of tissues. Elegant studies have shown that an increase in Young’s modulus is indicative of the malignant transformation during human breast tumor progression with the largest value at the invasive front. Acerbi et al. showed a positive correlation, with increased stiffness at the invasive front with the more aggressive sub types of human breast cancers(Acerbi et al., 2015). Plodinec et al. used nano-indentation to map the stiffness of excised breast tumor tissue surfaces. However, AFM cannot probe the sample interior beyond a few micrometers, cannot measure forces below a several pN, and dynamic analyses are limited to hundreds of Hz. On the other end of the length spectrum, shear wave spectroscopy is able to distinguish benign from cancerous tissue, resolving intratumoral heterogeneities on the mm – cm length scale, comparable to tumors(Deffieux, Montaldo, Tanter, & Fink, 2009). Thus, to address the gap between AFM and bulk rheological methods we perform optical trap active microrheology using in situ calibration to assess the resistance to flow (viscosity) and the resistance to deformation (elasticity) in these complex viscoelastic materials as functions of the oscillation amplitude (2–20 nm) and frequency (2–15000 Hz)(Blehm, Devine, Staunton, & Tanner, 2015; Fischer & Berg-sørensen, 2007). Compared to passive techniques (observation of thermal fluctuations), active microrheology (observation of response to applied force) can measure nonlinear effects at different length and energy scales, and is less susceptible to thermal noise(Breedveld & Pine, 2003; M A Kotlarchyk et al., 2011; M A Kotlarchyk, Botvinick, & Putnam, 2010). The method involves the use of spherical beads that act as local mechanical sensors where spring-like harmonic forces are applied using an optical trap. The induced displacements in the tissue environment are then used to determine the local mechanical properties. Spatial resolution is determined by the size of the bead. Here we are able to achieve spatial resolution ~1 μm. A key step is determining the trap stiffness to correctly deduce the applied forces. We recently showed that when using optical trap based active microrheology, calibration of trap stiffness in proxy materials resulted in a discrepancy of viscoelasticity in as much as a 20 fold overestimation of complex modulus vis à vis in situ calibration performed at each bead(Blehm, Devine, Staunton, & Tanner, 2015). Here, we examine collagen fiber length, pore size and fiber width to determine the microscopic determinants of the collective bulk mechanical properties. In addition, we then apply the method to freshly excised murine tumors in an effort to map heterogeneities in tissue mechanical properties with high spatial resolution. We determined that mouse melanoma tumors and human breast tumors displayed elastic moduli ~5–1000 Pa, increasing with frequency and displaying a nonlinear stress-strain response. We show that direct calibration of trap stiffness at each probe allows us to determine absolute forces needed to resolve local heterogeneities in collagen fractal gels and in murine tumors. Thus, we show the feasibility of using optical based active microrheology to obtain a mechanical biopsy in efforts to provide a diagnostic tool to aid in the design of therapeutics complementary to those based on standard histopathology.

Materials and Methods

Microsphere PEGylation

Fluorescent 1 μm carboxylated polystyrene spheres conjugated to Rhodamine (Thermofisher #8821) were centrifuged and resuspended in 10% molar excess EDC (1-ethyl-3-(3-dimethylaminopropyl)-carbodiimide) for 1 h. The beads were centrifuged and resuspended in 50X molar excess ethylene diamine for 6 h and agitated on a shaker at medium speed overnight. Beads were then centrifuged and resuspended in a solution containing 2X molar excess mPEG-SVA adjusted to pH 8 with NaOH overnight, then agitated on a shaker overnight. Beads were centrifuged and resuspended in deionized water.

Collagen Gels

Sample Surface functionalization

Glass bottom dishes (Willco cat #GWST-5040) were immersed in 1 N NaOH for 10 minutes. This solution was aspirated and the dishes were then rinsed with deionized H₂O followed by a second wash step with ethanol, then 1% APTES in ethanol was added for an incubation time of 1 hour. APTES was removed and a second round of washing with ethanol followed by deionized H₂O was performed. Finally, 0.5% glutaraldehyde/PBS solution was added for 60 min followed by a wash step of deionized H₂O and air-drying for 20 min. This is necessary to ensure that collagen adheres to the surface, preventing any detachment upon hydration(Staunton, Doss, Lindsay, & Ros, 2016).

Hydrogel preparation

A stock solution of a 10X reconstitution buffer was prepared consisting of sodium bicarbonate (final concentration 2.2%) and HEPES (final concentration 0.2M) in ultrapure H₂O and kept at −20°C. A 10X DMEM solution was achieved by dissolving DMEM High Glucose (4.5 g/L, without L glutamine, with sodium Pyruvate 110 mg/L, phenol red free) into with 200 ml double deionized water (ddH2O) with pH balanced to 7.9–8.0. Both reagents were filter sterilized. Acid-soluble highly concentrated rat-tail collagen type I (BD Biosciences, San Jose, CA, USA) (stock concentration 8.23 mg/ml) was kept at 4°C at all times. All materials were placed on ice for half an hour prior to the preparation of the collagen hydrogels. Hydrogels were prepared as a function of final collagen concentration and conditions where the final concentration of collagen was kept constant but allowed to polymerize at different temperatures (at 4, 20 and 37°C). Final collagen concentrations of 2 mg/ml (low) and 6 mg/ml (high) were achieved by combining 100 μl of thawed aliquot of 10X reconstitution buffer and a 100 μl frozen aliquot of 10X DMEM and 20 μl of 1 μm rhodamine fluospheres (Thermofisher #F8821) in PBS at a final number of 10⁷ of beads, and supplemented with ddH20 to achieve a final volume of 1 ml. For example, for a hydrogel of 6 mg/ml final collagen concentration, 729 μl of collagen stock (original solution 8.23 mg/ml) was supplemented by 51 μl of ddH2O. 1 N NaOH was added to this solution on ice and the mixture thoroughly mixed and brought to a final pH of 7.6–7.8. Solutions were then pipetted onto functionalized 50 mm Willco glass bottom dishes (~1 ml) on a freezer pack and spread by pipette to evenly cover the surface (including edges). These solutions were either allowed to polymerize at 37°C for 45 mins, at 20°C for 45 mins or at 4°C for 24 hours before 4 ml of media was added to prevent dehydration.

Ex Vivo Tumors

Animal Handling and Cell Lines

Animal studies were conducted under protocols approved by the National Cancer Institute, and the National Institutes of Health Animal Care and Use Committee.

Tumor cell lines, a mouse melanoma cell line, B16F10 (cat. No. CRL-6475) and a human breast adenocarcinoma cell line, MDA-MB-231 (cat. No. HTB-26) were obtained from American Type Culture Collection (ATCC, VA). Briefly, both cell lines were cultured as monolayers in DMEM high glucose media (Life technologies, CA) supplemented with final volume of 10% Fetal Bovine Serum (FBS), 1% MEM non-essential amino acids, L-glutamine, penicillin and streptomycin. Medium was refreshed every 2–3 days.

Lentiviral Transduction

Cells were transduced with virus using the ExpressMag Transduction System (Sigma). Briefly, viral supernatant was incubated with magnetic beads at room temperature for 15 min, added to the adherent cells and placed on a strong magnetic plate at 37°C for 12 min. Media was replenished 16 hr. later and the viral mixture disposed of in compliance with NIH policy. Transduced cells were selected with 2 μg/ml puromyocin (InvivoGen, San Diego, CA). Flow cytometry was performed to isolate the GFP/luciferase positive cells from cells that did not the express these markers using the Cell Sorting feature on a BDFACS Aria (BD Biosciences).

In vitro Bioluminescence Activity Assay

Luciferase activity of pre-sorted cells was determined using VivoGlo^™ luciferin (Promega, Madison, WI), according to the manufacturer’s instructions. Briefly, 1×10⁴ of GFP/Luciferase and its parental cells were seeded on a white-walled 96-well plate (Corning, Corning, NY). Cells were washed with PBS and then mixed with 150 μl/ml of luciferin in IMDM media (Gibco). After 10 minutes, luciferase activity was measured by Infinit200^® Pro Luminometer (Tecan, San Jose, CA). For each experiment, 3 individual samples were prepared.

Tumor injections

Briefly, a cell and fluorescent bead suspension in PBS was injected subcutaneously in the flanks of 8–10 week old female nu/nu mice where the final cell number was 5×10⁵ cells and 10⁷ beads. Tumor burden was estimated by weekly physical and in vivo bioluminescence measurements and mice were euthanized as tumors approached 1 cm in diameter with no detectable metastasis, as determined from BLI imaging. Luminescence emitted by tumors in nude mice was measured weekly. Briefly, each mouse was injected intra-peritoneally with 100 μl of VivoGlo^™ luciferin at 3 mg/ml in PBS. After 15 min, the mice were sedated by 2.5% Isoflurane, following the animal protocol. Mice were imaged on the dorsal and ventral sides and the luciferase signals were captured by a Xenogen IVIS-200 system (Perkin-Elmer, Waltham, MA). The luminescence quantity was displayed by radiance and the units are displayed as photons/s/cm²/sr.

Ex vivo tumor preparation

Fresh tumors were excised and half of the sample was prepared for ex vivo imaging and the other for histological analysis. Half of the tumor was immediately placed in 4% paraformaldehyde solution for 12 h and then prepared for histological staining. Tumors were then embedded in paraffin prior to sectioning on a microtome. Serial sections, 8 μm thick were labeled for specific ECM stains as delineated by Masson trichrome, and Haematoxylin and eosin as previously described(Blehm et al., 2015). The second half was then thinly sliced and mounted on a No.0 Willco glass bottom dish to perform mechanical measurements.

Optical Trap-based Microrheology

Experimental apparatus

We used a home built instrument as described previously (Blehm et al., 2015). Briefly, the optical trap is comprised of two lasers: one that traps and one that detects. The trapping beam is steered by a 2D acousto-optic deflector (AOD). The trap beam motion and detection beam motion are tracked by quadrant photodiodes (QPDs). QPD signals are recorded at 80 kHz on a FPGA DAQ card that also sends control signals to the AOD. Control and data collection are conducted in custom Labview programs.

Beam Alignment

Before each experiment, alignment and functionality of the trap was determined using a control sample of carboxylated beads in PBS at a concentration of 10⁷ beads per mL. Briefly, the calibration involves trapping a bead, which is then oscillated using the AOD at magnitudes that can be easily observed on a charge-coupled device (CCD) camera (typically equivalent to 500 nm). The trap’s oscillation is detected on the trap QPD, and then the detection laser’s response is verified on the detection QPD. Maximum response to oscillations in both dimensions (x and y) is found by adjusting the detection laser mirror and dichroic mirror. This signal is then centered in the middle of the range where its response is optimal. The detection QPD is then adjusted such that the detection beam is centrally located in both x and y. Once this is accomplished, the trap is calibrated in water using the power spectrum method and then calibrated using the active-passive method described below. Finally, the bead position on the CCD is determined by centroid-fitting an image of the bead on the camera, and this position is used as the trap position in the trap-centering algorithm.

In situ Positional Sensitivity Calibration

Samples are loaded on the microscope stage and the condenser is adjusted for Köhler illumination. In consideration of Faxen’s law only probes > 30 μm from the coverslip are measured to minimize drag force due to boundary effects(Svoboda & Block, 1994). Typically, an image of 512 × 512 square pixels is recorded by the CCD camera, and then beads that are in focus on a given plane are manually selected. The software records the positions of each of these beads and the active oscillation is performed systematically. Data acquisition proceeds bead by bead. For each bead, an image of a subset of the original area encompassing 21 × 21 square pixels is acquired for each bead’s position, and then the centroid is estimated to determine the bead’s center. The trap laser is then centered to that bead’s location by the piezo-stage. A 49-image z stack comprised of images 100 nm apart is acquired, and the center of the bead in the axial direction (z axis) is determined by detection of the maximum bead intensity. It should be noted that axial centering is crucial to trapping the bead, and the intensity method used here is sensitive to fluorescence or brightfield illumination of the beads in the sample and at the prior time of trap position determination. With the trap laser off, a volt-to-nanometer conversion calibration for each bead is calculated by stepping the piezostage in X and Y (12 nm per step, 21 steps) through the bead(M.A. Kotlarchyk, Botvinick, & Putnam, 2010). The detection QPD’s voltage is recorded and normalized to the sum of the total voltage on the QPD for each dimension (x and y). A high NA condenser collects all scattered light from the bead and the conjugate image of the bead is mapped onto the back-focal plane and collected on the QPD(Farré & Montes-usategui, 2010; Gittes & Schmidt, 1998; Grange, Husale, Güntherodt, & Hegner, 2002; Jun, Tripathy, Narayanareddy, Mattson-hoss, & Gross, 2014). A line fit to the data is used to obtain a volt-to-nanometer conversion in both dimensions (x and y).

Measurements for in situ Trap Stiffness Calibration and Active Microrheology

With a bead positioned in the trap center with the volts-to-nanometer conversion factor of the position detection system calibrated, a series of recordings is then conducted from which both the complex modulus and the in situ trap stiffness are found(Berg-sørensen & Flyvbjerg, 2004; Fischer & Berg-sørensen, 2007). The technique consists of two steps: 1) detection of a trapped particle’s thermal motion(passive motion) and 2) detection of the applied oscillatory force induced bead oscillation amplitude and phase delay relative to the applied force (active motion). The trap is first oscillated for 1 s, followed by 1 s in which the trap is held stationary at the bead’s equilibrium position. During the active 1 s pulse, the trap position is oscillated by a multiplexed waveform consisting of the sum of sines spanning a broad band of frequencies. Measurements consisted of either a pair of separate sweeps at high (300–15700 Hz) and low frequencies (3–157 Hz), or a single broadband sweep (2–12809 Hz). Because the frequencies of the sines chosen are prime numbers (or multiples of different primes), the higher harmonics of each do not overlap with the others, which reduces crosstalk between frequencies(Blehm et al., 2015). This allows the frequencies to be recorded simultaneously, reducing measurement times. The amplitude of each component sine is equal (either 2, 5, 10 or 20 nm). To ensure that the amplitude of the resulting multiplexed waveform results in a maximum displacement of the probe that remains within the linear range of both the trap and detection beams, the component sines are given phase offsets. The effect of the phase offsets is to reduce the stacking of the peaks of (especially the lower) frequencies so the probe is never moved more than 200 nm from its equilibrium position. After the trap is displaced according to the waveform, the probe motion is recorded with trap stationary during the passive 1 s pulse. This active-passive sequence is repeated seven times for each bead. The measurement is conducted first with the low frequency multiplexed waveform, followed by the high frequency multiplexed waveform. This sequence of measurements was conducted at successively higher amplitudes, first with waveforms composed of sines with amplitudes 2 nm, then with 5 nm, 10 nm, and 20 nm. The data from the detection QPD was acquired at a sampling rate of 80 kHz.

Calculation of in situ Trap Stiffness and Complex Moduli from Active Measurements

For each bead, first the voltage time series are converted to position time series using the volts-to-nanometers conversion factor. The bead position time series x_U(t) of the undriven (passive) pulses are Fourier transformed to x̃_U(ω) to obtain the thermal power spectrum P_U(ω):

$$P_U(\omega )=\langle {\mid {\stackrel{\sim }{x}}_U(\omega )\mid }^2\rangle$$ (1)

where the angular frequency ω = 2πf, with f the linear frequency and <> denotes the time average. For the driven (active) pulses, the position time series of both the trap laser position x_L(t) and the bead position x_dr(t) are Fourier transformed to x̃_L(ω) and x̃_dr(ω), respectively. These are complex, accounting for both amplitude and relative phase of the bead and trap oscillations, and together give the active power spectrum R̃_L(ω):

$${\stackrel{\sim }{R}}_L(\omega )=\frac{{\stackrel{\sim }{x}}_{dr}(\omega )}{-i\omega {\stackrel{\sim }{x}}_L(\omega )}$$ (2)

where i² = −1. The trap stiffness is then determined from the active and passive spectra:

$$k_{\omega }=\frac{Re\{{\stackrel{\sim }{R}}_L(\omega )\}}{P_U(\omega )}$$ (3)

where Re{R̃_L(ω)} is the real component of the active power spectrum. The friction relaxation spectrum γ̃_D(ω) is then calculated:

$${\stackrel{\sim }{\gamma }}_D(\omega )+i\omega m=-\frac{k_{\omega }}{i\omega }\left(\frac{1}{i\omega {\stackrel{\sim }{R}}_L(\omega )}+1\right)$$ (4)

where m is the probe mass. Finally the complex modulus G^*(ω) is found:

$$G^{\ast }(\omega )=\frac{i\omega {\stackrel{\sim }{\gamma }}_D(\omega )}{6\pi a}$$ (5)

where a is the probe radius, the storage (elastic) shear modulus G′(ω) = Re{G^*(ω)}, and the loss (viscous) shear modulus G″(ω) = Im{G^*(ω)}.

Analysis of intracycle nonlinear elasticity and viscoelasticity by higher order harmonics

Following the approach of Ewoldt et al., we investigated the intra-cycle strain-stiffening or -softening and shear-thickening or -thinning(Ewoldt, Hosoi, & Mckinley, 2008; Ewoldt, Winter, Maxey, & Mckinley, 2010). The scaled second (n=2) and third (n=3) elastic and viscous Chebyshev coefficients were calculated as $\frac{e_n}{e_1}=\frac{I_{n}cos({\delta }_n)}{I_{1}cos({\delta }_1)}$ and $\frac{{\nu }_n}{{\nu }_1}=\frac{I_{n}sin({\delta }_n)}{I_{1}sin({\delta }_1)}$, respectively, where I_n and δ_n are the magnitude and phase angle at the nth harmonic of the driven frequency of the Fourier transform of the displacement vs. time signal of the probe during trap oscillation. The even (odd) order harmonic terms correspond to transient (steady-state) intra-cycle nonlinear response. The moduli G′, G″ were accordingly decomposed into series of terms G′ = G′₁ + G′₃ + ··· and G″ = G″₁ + G″₃ + ··· where e_n = G′_n(−1)^(n−1)/2 and v_n = G″_n/ω.

Data and Statistical Analysis

Custom Matlab programs were used for all of the data analysis as described in(Blehm et al., 2015; Fischer & Berg-sørensen, 2007). Means for each bead were calculated at each frequency to get Ḡ′(ω) and $\overline{G^{″}}(\omega )$. Bead means (n > 20 beads per sample) were pooled and from samples for each condition and averaged. Single exponent power law fits were performed in MATLAB using damped least squares, least absolute residuals fitting. GraphPad Prism was used for statistical analyses. Microrheology data were statistically compared using 2-way ANOVA with Tukey’s multiple comparison test; p-values listed are for pairs of datasets, and the largest p-value is listed when multiple pairs are compared. At least nine collagen gels were measured and analyzed per condition; 6 B16-F10 tumors were measured.

Confocal imaging

Confocal micrographs were recorded on a Zeiss LSM 780 using a pinhole size of 1 Airy unit and pixel size 60.2 nm. Collagen fibers were imaged with 405 nm excitation (in reflection mode) and embedded fluorospheres were simultaneously imaged with 532 nm excitation using a dichroic filter. LSM files were exported to ImageJ, binarized (the 75th percentile of the intensity histogram was chosen as the threshold for each image) and segmented (Watershed); pore sizes were then determined (Analyze Particles, Area). The binarized images were also exported to MATLAB for box counting analysis using the function lacunarity_glbox.m, (http://www.mathworks.com/matlabcentral/fileexchange/25261-lacunarity-of-a-binary-image/content/lacunarity_glbox.m) to determine the lacunarity(Tolle, McJunkin, & Gorsich, 2008). The binarized images were also processed using the CT-FIRE (Ver. 1.3 Beta 2) curvelet transform fiber extraction software in MATLAB(Bredfeldt, Liu, Pehlke, et al., 2014) (http://loci.wisc.edu/software/ctfire) to determine the distributions of fiber lengths and widths.

Bulk Rheology

Collagen type I hydrogel samples for bulk rheology measurements were prepared by pipetting 450 μl of solution on Willco wells (GWSB-5040) containing a 25 mm ID steel washer (1 mm thick), and spreading the solution to cover the fill the washer. The samples were then incubated at 37C, 5% CO₂ for 90 min and then 3 ml of PBS was gently added on top. The samples were then incubated overnight, and the PBS was aspirated immediately before measurement the next day. All bulk rheology measurements were carried out at Georgetown University Institute for Soft Matter Synthesis and Metrology using an Anton Paar Physica MCR 301 rheometer equipped with a PP-25 measuring plate (parallel, 25 mm diameter). The parallel plate was lowered into contact with the surface of each sample until the load reached 0.2 N. Then frequency sweeps (0.1–10 Hz, 5 points per decade) were conducted at 0.1% strain. An amplitude sweep (0.1%–30%) at constant frequency (1 Hz) was then performed to confirm the linear viscoelastic range of deformation. Measurements were carried out in triplicate.

Results

Polymerization temperature dependence of microarchitecture

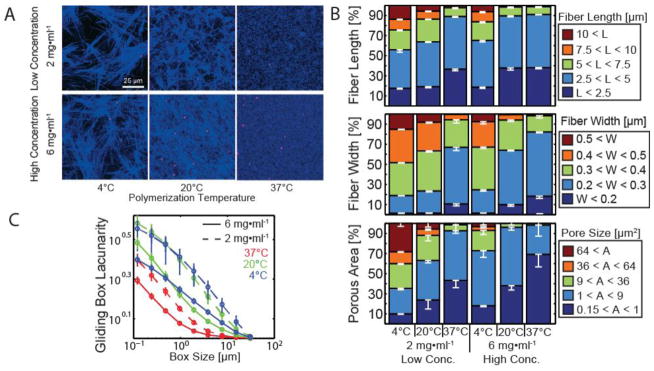
Acid solubilized collagen type I self assembles into fibrillar networks in vitro. These networks arise from lateral and end-to-end polymerization of collagen monomers roughly 1.5 nm in width and 300 nm in length. These then further assemble into fibrils ~15–200 nm wide, stabilized by both hydrophobic interactions and covalent bonds. Individual fibrils further bundle into fibers that form the intricate network of fibrillar and porous architecture. Microarchitecture and micromechanical properties of hydrogels are sensitive to the physical and chemical conditions under which they are polymerized. We tuned the properties of high concentration rat-tail type I collagen by controlling the initial collagen concentration and polymerization temperature (Figure 1A). Of these variables, polymerization temperature had the greatest effect on topological features. Figure 1A shows confocal reflection micrographs of gels formed by collagen at 2 mg/ml and 6 mg/ml polymerized at 4°C, 20°C, and 37°C. Lower temperatures reduce the number of nucleation events during polymerization, i.e. fewer polymers for monomers to interact with. This results in the formation of fewer, longer, thicker fibers, as well as larger pore sizes.

Figure 1. Tuning collagen I microarchitecture by temperature and concentration dependence.

(A) Confocal reflection micrographs of collagen type I hydrogels polymerized at different initial concentrations (2 mg/ml, top; 6 mg/ml, bottom) and temperatures (4°C, left; 20°C, center; 37°C, right). Fluorescent polystyrene microspheres were mixed into the solution before polymerization (magenta dots), to serve as mechanical probes. (B) Quantification of microscale topography of collagen type I hydrogels using curvelet transform fiber reconstruction (CT-FIRE) algorithms(Bredfeldt, Liu, Pehlke, et al., 2014). Stacked histograms of fiber length, fiber width and pore area distributions. (C) Gliding box lacunarity is a measure of spatial heterogeneity as a function of length scale; gels polymerized at 37°C are more homogeneous, 4°C gels are most heterogeneous at lengths > 1 μm, while 25°C gels are most heterogeneous at lengths < 1μm.

To quantify these features, oversampled images were collected and processed using a curvelet transform fiber recognition algorithm (CT-FIRE)(Bredfeldt, Liu, Pehlke, et al., 2014). Fiber length, width and pore area were quantified and the distributions were binned into stacked histograms. We determined that fiber architecture was dominated by fibers that were 2.5–5 μm in length. For hydrogels of low collagen concentration (2mg/ml) a broader distribution of fibers was measured than for hydrogels of higher collagen concentration (6mg/ml). Specifically, the largest distribution of fiber lengths where values ranged from L>2.5 – L<10 μm in length were measured for hydrogels polymerized at 4°C of collagen concentration of 2 mg/ml gels (Figure 1B). For hydrogels of higher concentration, fibers longer than 10 μm were only detected in gels polymerized at 4°C.

Here, we determined that collagen formed a meshwork of smaller fibers in hydrogels polymerized at higher temperatures and higher collagen concentration (37°C and 6mg/ml respectively). Instead, fiber width increases with decreasing polymerization temperature (Figure 1B) ranging in values from w > 0.2 μm to w < 0.5 μm. Fibers of width, w > 0.3 μm were most prevalent (>15%) in the hydrogels polymerized at 4°C for lower concentration of 2 mg/ml. However, some hydrogels showed similar distributions despite differing initial conditions as observed when comparing hydrogels polymerized at 4°C with final concentration of 6 mg/ml and those polymerized at 20°C with final concentration of 2 mg/ml gels.

Pore sizes on the order of the size of a cell nucleus (64 μm²) or greater were absent in hydrogels polymerized at 37°C at final concentrations of 2 or 6 mg/ml where the meshwork was largely dominated by smaller fibrillar network. Instead, these larger porous areas were found to more prevalent (as much as 25% of the distribution) for hydrogels polymerized at 4°C but in greater abundance for hydrogels of final concentrations 2mg/ml than for those with final concentration 6 mg/ml polymerized at 20 °C (Figure 1B). A similar trend holds for pore sizes on the order of a large cell protrusion (9–36 μm²). In addition, heterogeneity of spatial structure as a function of length-scale was assessed by performing gliding box scans on the images to find the (dimensionless) lacunarity, a measure of size-dependent self-similarity (Figure 1C). In such a plot, a straight line indicates structure generated by a single multiplicative process (monofractal); changes in slope occur at lengths at which a change in scaling occurs; and curvature suggests interaction between multiplicative processes at many scales (multifractal)(Plotnick, Gardner, Hargrove, Prestegaard, & Perlmutter, 1996). In the context of collagen network self-assembly, changes in slope might occur at critical length scales characteristic of competing polymerization processes, or e.g. a probable branching distance. Curves of gels with different concentrations but the same polymerization temperature exhibit similar slopes, indicating similar topography. Interestingly, both positive and negative curvature can be seen in the various gels. Hydrogels polymerized at 37°C have the lowest lacunarity, beginning at 3 μm to curve upwards with decreasing length scale. In contrast, hydrogels polymerized at 20°C with final concentration of 6 mg/ml have higher lacunarity but similar curvature whereas hydrogels polymerized at 4°C with final concentration of 6 mg/ml show similar lacunarity but with less curvature where the curves intersects at ~0.75 μm. Hydrogels polymerized at 4°C and 20°C with final concentration of 2 mg/ml displayed the highest lacunarity.

Comparison of Active microrheology and bulk rheology

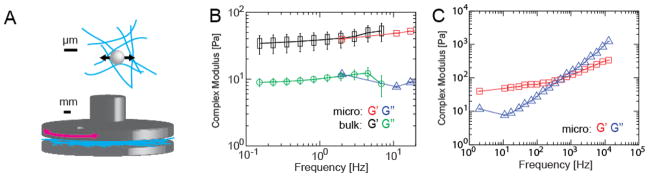
Collagen hydrogels may display microrheological properties that reflect the fractal network of the gel at the micrometer length scale, which may be distinct from the bulk rheological properties. We next sought to compare the rheological properties of the collagen gels using optical trap based active microrheology and small angle oscillatory shear (SAOS) bulk rheological measurements for overlapping frequencies (1–10Hz) of each technique (Figure 2A). We determined that hydrogels with final concentration of 2 mg/ml polymerized at 37°C showed an overall shear modulus of ~35–50 Pa and loss modulus of ~10 Pa across all frequencies as determined from small angle oscillatory shear (SAOS). In the overlapping frequencies, active microrheology measurements on the same gels gave remarkably similar results. (Figure 2B). Optical trap based active microrheology method can probe mechanical response at higher frequencies. From 2–200 Hz, an elastic plateau is present with storage moduli increasing only gradually 40–70 Pa. At higher frequencies, the slope increases, rising to ~350 Pa at frequencies greater than 10 kHz. The loss modulus was ~10 Pa at 2–30 Hz, increasing to ~1 kPa spanning the range of 30–10 kHz. The crossover frequency (at which storage and loss moduli are equal in magnitude) is ~500 Hz. The loss modulus has a local minimum at ~10 Hz, characteristic of entangled fiber networks (Abidine et al., 2015; Granek, Cates, Granek, & Cates, 2009)(Figure 2C).

Figure 2. Comparison of viscoelasticity obtained at different length scales is comparable for the overlapping frequencies obtained using bulk and microscale rheological methods.

Mechanical measurements at μm and mm length scales. (A) Schematics of active microrheology (top) and small angle oscillatory shear (SAOS) bulk rheology (bottom) of a fibrillar polymer network. (B) Comparison of bulk and active microrheology for overlapping frequencies: SAOS complex shear modulus (storage–black rectangles and loss-green circles) and active microrheology complex modulus (storage–red squares and loss-blue triangles) for vs. frequency of type I collagen hydrogel polymerized at 37°C at 2 mg/ml. (C) Complex modulus spanning frequencies from 2–12kHz, (storage–red, squares and loss-blue triangles) from optical trap based active microrheology measurements of collagen type I hydrogel polymerized at 37°C at 2 mg/ml with 1 μm diameter pegylated polystyrene microspheres, measured for beads firmly attached to fibers.

Using in situ calibration to determine rheological properties as a function of hydrogel polymerization temperature

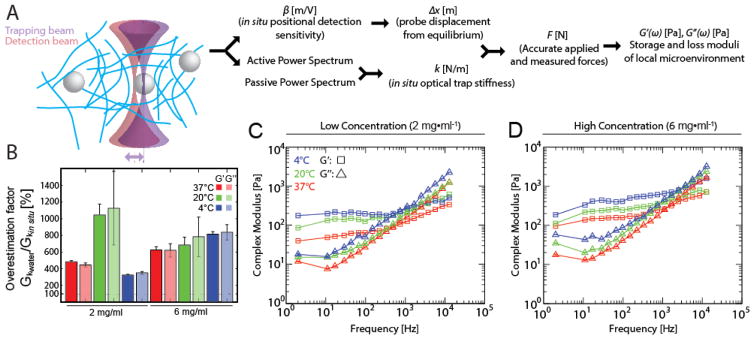
Calculation of the complex modulus from active microrheology measurements requires that the applied force, and thus the effective spring constant, or trap stiffness, is known. This trap stiffness is usually determined from proxy materials such as glycerol and water with known physical properties. However, trap stiffness will vary within a sample due to optical and mechanical heterogeneities, thus applying a trap stiffness that is determined in a proxy material may result in discrepancies in the measured mechanical properties. These optical heterogeneities also affect the sensitivity of the detection of the probe displacement (which is also needed to know the applied force), so this too must be calibrated for each measured probe. Together with this calibration, recording the passive and active spectra yield the trap stiffness and the moduli (see Materials and Methods for details). The approach is depicted in Figure 3A, and a schematic of the microscope is shown in (Blehm et al., 2015). We next used this technique to probe microscale mechanics at frequencies not readily accessible by SAOS. Using this in situ calibration, we then sought to determine the effect of polymerization temperature on micromechanical properties. To determine the differences between values determined from in situ and water trap stiffness calibration, we compared the moduli of the gels using the trap stiffness as determined from water to that obtained using in situ calibration. Comparison of storage and loss moduli using the values calibrated in water show that these values exceed the moduli calculated using an in situ calibration by 300–1000% as averaged across all frequencies (Figure 3B). We determined that for hydrogels of final concentration of 2 mg/ml, the storage modulus varied significantly (p<0.0001, 2-way ANOVA) as a function of hydrogel polymerization temperature, with moduli rising ~20–350 Pa (37°C), ~90–1500 Pa (20°C), and ~200–2500 Pa (4°C) over 2 Hz–12 kHz. On average across frequencies, storage moduli measured for hydrogels polymerized at 4°C gels were ~threefold and twofold greater than the storage moduli obtained for hydrogels polymerized at 37°C and 20°C respectively (Figure 3C). Similarly, for hydrogels of final concentration 6 mg/ml, storage moduli also differed significantly (p<0.0001), as a function of polymerization temperature. Hydrogels polymerized at 4°C and 20°C were 2.5- and 1.5-fold stiffer respectively than those polymerized at 37°C. Storage moduli showed an increase from ~100 to ~750 Pa for hydrogels polymerized at 37°C, from ~120 to ~900 Pa for hydrogels polymerized at 20°C, and from ~200 to ~2000 Pa for hydrogels polymerized at 4°C over the frequency range of 2–12 kHz (Figure 3D). A similar trend was observed where the loss moduli also varied significantly with temperature (p<0.0001, 2-way ANOVA). The loss moduli showed an increase from ~15 to ~1700 Pa for hydrogels polymerized at 37°C, from ~45 to ~2700 Pa for hydrogels polymerized at 20°C, and from ~60 to ~3500 Pa for hydrogels polymerized at 4°C (Figure 3D). These observations suggest that polymer network micromechanics depends on polymerization temperature.

Figure 3. In situ-calibrated optical trap based active microrheology resolves mechanical differences in collagen I gels polymerized at different temperatures and with different initial collagen concentrations.

(A) Active microrheology scheme. The positional detection sensitivity is calibrated for each probe. With the detection and trapping beams aligned, the passive power spectrum and then (by oscillating the trap laser position) the active power spectrum are recorded. From these measurements, the trap stiffness (which is sensitive to optical heterogeneities) can be found for each probe. The data is then used to compute forces and the storage and loss moduli of the probe’s local microenvironment. (B) A comparison of the storage modulus as calculated using the incorrect trap stiffness (determined in water prior to the experiment) and using the in situ calibrated trap stiffness. Using the value from water leads to overestimation. (C, D) Storage moduli (squares) and loss moduli (triangles) vs. frequency determined from optical trap based active microrheology of low concentration (2 mg/ml) (C) and high concentration (6 mg/ml) (D) collagen I hydrogels that were polymerized at different temperatures: 37°C (red), 20°C (green), and 4°C (blue). Measurements conducted from 2–12k Hz, with oscillation amplitude 20 nm with 100 mW laser power.

Nonlinear Stress/Strain Behavior

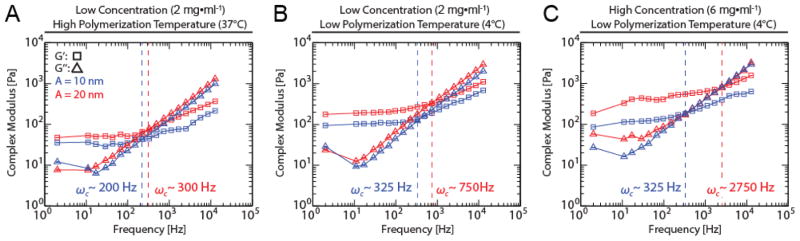
Cells respond to both chemical and physical cues of the microenvironment. The chemical cues are largely provided by ligand density that is governed by both the overall concentration of collagen and the local architecture. Thus, the signaling cues are intertwined with the architecture and mechanical cues imparted to cells. This makes decoupling the physical cues from those due to the physical properties non trivial. We sought to examine hydrogels of the same final collagen concentration but differing architectures (polymerized at different temperatures) and those of different final collagen concentration but comparable architectures (polymerized at same temperature). We next sought to determine the stress-strain behavior of these hydrogels using active microrheology. For an optical trap, there are two ways to vary the stress and strain applied to the probe’s microenvironment: 1) by changing the trap position oscillation amplitude or 2) by changing the laser power. The applied force F and the displacement of the bead from the trap center Δx are related to the trap stiffness k by F= −kΔx, altering the oscillation amplitude or trap stiffness changes both the stress and strain applied to the gel. Here, we keep the laser power constant but modulate the trap oscillation amplitude for the aforementioned hydrogel conditions. We observe an emergence of nonlinearity for the measured complex moduli across all frequencies when stress and strain were increased by changing oscillation amplitude from 10 to 20nm. Specifically, complex moduli measured at amplitudes of 10 nm and 20 nm were significantly different as determined by 2-way ANOVA (p=0.0001) (Figure 4). For hydrogels polymerized at 37°C with final concentration of 2mg/ml, complex moduli measured at a lower strain induced by an oscillation amplitude of 10 nm was ~60% of the value measured at a higher strain induced by an oscillation amplitude of 20 nm (Figure 4A). For hydrogels polymerized at 4°C with the same concentration of 2mg/ml, storage and loss moduli measured at a lower strain induced by an oscillation amplitude of 10 nm were ~60% and ~70% of the values obtained at higher strain respectively (Figure 4B). For hydrogels polymerized at same temperature of 4°C with final concentration of 6mg/ml, storage and loss moduli measured at lower strain were ~70% and ~90% of the values obtained at higher strain increasing to 750 Pa and 450 Pa at 12 kHz, respectively (Figure 4C).

Figure 4. In situ-calibrated optical trap based active microrheology resolves nonlinear stress-strain behavior in collagen I gels polymerized at different temperatures and with different initial collagen concentrations.

Storage moduli (squares) and loss moduli (triangles) vs. frequency determined from optical trap based active microrheology of collagen I hydrogels polymerized at low concentration (2 mg/ml) and high temperature (37°C) (A), high concentration (6 mg/ml) and high temperature (37°C) (B), and high concentration (6 mg/ml) and low temperature (4°C) (C) using different applied stress/strain by oscillating the trap position with displacement amplitudes of either 10 nm (blue) or 20 nm (red) each with 100 mW laser power. Dashed blue and red vertical lines indicate crossover frequencies at which the loss moduli first exceed the storage moduli.

For each of these conditions we determined that the crossover frequency, ω_c occurs at a higher frequency when higher strain is applied. The crossover frequency occurs at the transition from the elastic plateau regime to liquid-like behavior, which can be interpreted as a glass transition(Alcaraz et al., 2003; Sollich, Lequeux, Hébraud, & Cates, 1997; Wirtz, 2009). Interestingly, both the ω_c at lower and higher strains are increased between hydrogels with the same final collagen concentration but different architectures. However, when architecture is similar but collagen concentration is dissimilar, ω_c is the same at lower strains but increasing strain induces a greater shift in high collagen concentrations vs. lower concentrations (Figure 4).

Flexible polymer networks are predicted to have complex moduli that exhibit power law frequency dependence G^* ∝ ω^α with α = ½, whereas α = ¾ for semi-flexible polymers. We next sought to determine if these measured values show a power law frequency dependence. We determined that the hydrogels exhibit a weak power-law frequency dependence in G^* ∝ ω^α for all gels, with power law exponents α ranging 0.66–0.74 (fit lines not shown).

Theoretical works have also been developed that suggest intracycle nonlinearities in viscoelasticity can also be interrogated by examining the higher order harmonics of the elastic modulus, which by appropriate choice of basis functions can be decomposed such that adding higher order terms does not affect lower order terms(Ewoldt et al., 2008, 2010) (for details see Methods). The 2^nd order term reflects transient behavior, while the 3^rd order term reflects steady state behavior, with the sign of the term indicating intracycle strain stiffening (positive), softening (negative), or linearity (zero). Using this analysis approach, both 2^nd and 3^rd order terms from our data were approximately zero (Supplementary Figure S1).

Active Microrheology of murine melanoma tumors

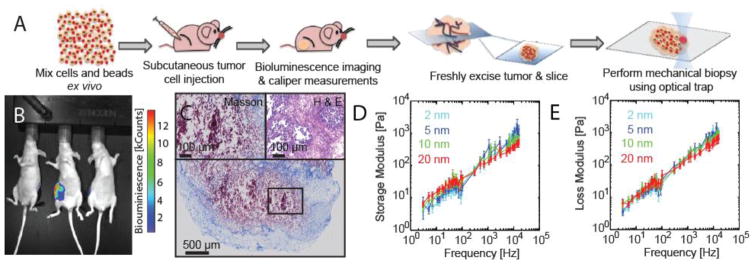
Type I collagen is one of the major ECM components and serves as a scaffolding protein in the stroma contributing to the tissue mechanical properties. Aberrant deposition and remodeling of the stroma is a hallmark of the presence of malignant tissue. Histological staining and confocal microscopy of ex vivo tumors confirm copious amounts of type I collagen in excised melanoma tumors. To confirm similar stages of tumor progression for each sample, we then confirmed that there was no distant metastasis as detected using bioluminescent imaging (BLI) (Figure 5A) and visual examination of organs at necropsy (data not shown). We then measured the complex moduli of the tumors using optical trap based active microrheology. B16-F10 melanoma tumors exhibited a nonlinear mechanical response; storage moduli differed significantly (p<0.004) with oscillation amplitude (2 nm, 5 nm, 10 nm, 20 nm). Complex moduli (G*) exhibited weak power law frequency dependence with power law exponents of 0.70, 0.63, 0.57, and 0.52 at amplitudes 2 nm, 5 nm, 10 nm, and 20 nm, respectively. Storage and loss moduli rise monotonically 5 Pa–1000 Pa over frequencies 3 Hz–15 kHz, (Figure 5C). MDA-MB-231 breast tumor samples had similar mechanical properties (Supplementary Figure S2).

Figure 5. In situ-calibrated optical trap based active microrheology resolves nonlinear stress-strain behavior in murine melanoma tumors.

Active microrheology of excised murine subcutaneous melanoma tumors. (A) Schematic of experiment. (B) Bioluminescence of mouse tumors. B16-F10 metastatic mouse melanoma cells were subcutaneously injected with fluorescent polystyrene microspheres into the flank and allowed to grow for 2 weeks. Animals were sacrificed and tumors were excised, rinsed, and thin sections (~70 μm) prepared on glass bottom dishes for measurements. (C) Haematoxylin and eosin histology stains. (D, E) Storage (D) and loss (E) moduli vs. frequency at oscillation amplitudes 2 nm (cyan), 5 nm (blue), 10 nm (green), and 20 nm (red).

Discussion

There is a strong clinical correlation between tissue mechanics and pathological disease(Keely, 2011; Mouw et al., 2014; Schedin & Keely, 2011; Tanner & Gottesman, 2015). Aberrant deposition and remodeling of the stromal ECM environment are indicative of a transformed and tumor permissive environment(Werb & Lu, 2015). Collagen type I contributes significantly to the biochemical signaling and mechanical cues that are imparted to both tumor and stromal cells within this ECM milieu(Lu, Weaver, & Werb, 2012). Thus, the signaling cues are intertwined with the mechanical cues imparted to cells. This makes decoupling these cues non-trivial. Here, we aimed to delineate the mechanical contributions of this important ECM scaffold on length scales that are needed for understanding cancer mechanosignaling. In the tumor microenvironment a broad range of biological processes occur including protein-protein interactions, molecular motor activity, cytoskeletal remodeling, signal transduction, cell motility, cell proliferation and the establishment of multicellular structures. These processes feature dynamics that occur over a broad range of time and force regimes. Identifying the governing principles of these phenomena remains challenging because they occur on overlapping scales and feature reciprocal interactions across these scales that give rise to emergent properties. Characterizing mechanical properties and responses of tissue and extracellular milieu for a wide range of frequencies and forces is therefore a prerequisite to decoding the complexities of cellular behaviors including mechanotransduction and motility in physically distinct microenvironments.

Mechanical properties of biomaterials including collagen hydrogels have been extensively studied using an array of instrumentation. Bulk rheometers, atomic force spectroscopy and nanoindentation, X-ray scattering, microelectromechanical systems, and others have been used to probe various properties(Arevalo, Urbach, & Blair, 2010; Carlisle et al., 2010; Fratzl et al., 1998; Gutsmann et al., 2004; Motte & Kaufman, 2013; Shen et al., 2008; Wenger, Bozec, Horton, & Mesquida, 2007). Bulk rheology integrates the mechanical contributions of network crosslinking and entanglement at the millimeter scale, with the assumption that the material acts as a continuum. This approach cannot resolve the mechanical properties of microdomains. However, cells adopt distinct strategies to migrate in a collagen environment. A tumor cell “crawling” along these fiber bundles will receive a signal different from the one received by a cell that “squeezes” through the pores. In addition, leukocytes migrating into the primary tumor site will receive their own distinct mechanical signals. Recently, it was found that 3D adhesion dynamics were locally regulated by ECM rigidity. Bundled, stiffer collagen fibrils increased single cell adhesion, whereas more pliant matrices favored adhesion retraction(A D Doyle et al., 2015). Thus, regional heterogeneities may also influence a cell’s ability to adhere to a de novo ECM milieu, a key requirement to facilitate metastatic spread. Hence, there is a need to resolve these microscale heterogeneities. The main attraction of microrheology methods in biology is that they probe the cellular length scale, and can access the local heterogeneous microenvironment directly in the presence of cells(Liu et al., 2006). Passive microrheology techniques determine mechanical properties including the complex modulus by tracking the thermal motion of tracer particles(Mak, Kamm, & Zaman, 2014; T. G. Mason & Weitz, 1995; T. Mason, Ganesan, van Zanten, Wirtz, & Kuo, 1997; Squires & Mason, 2010; Svoboda & Block, 1994). Previously, passive microrheology as well as active microrheology in conjunction with confocal microscopy, have been used to investigate fibrin gels(M A Kotlarchyk et al., 2011; M.A. Kotlarchyk et al., 2010).

Active Microrheology using an optical trap (aM-OT) is capable of probing physical properties of tissue and hydrogels, measuring both the resistance to flow (viscosity) and the resistance to deformation (elasticity). In aM-OT, the equations required to find the local viscoelasticity depend on the properties of the probe, including mass and radius. The spatial resolution is largely determined by the size of the bead. Here, using aM-OT, we resolved individual fiber bundles. Our probes, 1 μm microspheres, do not freely diffuse in any of our samples on our experimental time-scales, indicating that they are larger than the local microenvironment’s mesh size. Therefore, we are probing the protein polymer mesh that makes up the local ECM microenvironment of the cell, and not only the surrounding fluid phase. This allows us to resolve heterogeneities on micrometer length scales.

Microarchitecture and micromechanical properties of collagen hydrogels are sensitive to the physical and chemical conditions under which they are polymerized. Collagen assembly in vivo involves many factors, including enzymes and cellular activities, and in vitro hydrogels differ importantly from native collagen structures in many ways. Much work has been done toward defining the distinct roles of these parameters in the resulting collagen network, but their interrelation makes this a difficult task. Collagen assembly in vitro depends on pH, ionic strength, temperature, concentration, the presence of chemical crosslinkers, hydration state, and many other physical and chemical factors. During in vitro self-assembly, fibrillar architecture can be modulated by the final concentration of collagen (available ligand density), pH and polymerization temperature (Raub et al., 2007b, 2008), which presents the opportunity to tune gels to mimic normal and tumor tissue. There are several imaging modalities that are used to visualize collagen networks at different length scales, including electron microscopy, second harmonic generation imaging, two photon microscopy(Cox et al., 2003; Kadler, Holmes, Trotter, & Chapman, 1996; Zoumi, Yeh, & Tromberg, 2002). Reflection microscopy has the advantage of being non-invasive and label-free, considerable features for analysis of human tissue samples requiring rapid mechanical biopsies. However, the penetration depth is limited. For thicker samples, nonlinear multiphoton optical methods provide an alternative option. Another caveat is that fiber brightness is sensitive to fiber orientation(Jawerth, Munster, Vader, Fabry, & Weitz, 2010). Simultaneous fluorescence and reflectance microscopy revealed that some fibers are invisible when visualized in reflectance mode, hence some of our “pores” may not be simply fluid filled. Thus, we imaged between 10 μm and 50 μm from the coverslip to minimize glare and scattering. Using confocal reflection microscopy we achieved ~250 nm optical resolution (lateral). The ctFIRE algorithm employed here has been used extensively to quantify fiber properties(Bredfeldt, Liu, Conklin, et al., 2014; Bredfeldt, Liu, Pehlke, et al., 2014; Khanna, Wells, Puré, & Volk, 2015; Tilbury & Campagnola, 2015). Varying the initial collagen concentration regulated porosity, fiber width and fiber length and the microscale mechanics varied as a function of polymerization temperature (Figure 1). We found that pore area, fiber width, and fiber length decreased with increasing polymerization temperature and achieved distributions of fiber widths, lengths and porosity comparable to those described by others (Figure 1)(Bredfeldt, Liu, Conklin, et al., 2014; Bredfeldt, Liu, Pehlke, et al., 2014; Khanna et al., 2015; Tilbury & Campagnola, 2015).

For gels featuring a fine meshwork with pore sizes <1 μm², smaller than the probes used, we observed good agreement between bulk rheology and aM-OT for both storage and loss moduli for the overlapping frequencies probed by both methods (Figure 2A–B). Recently, complex moduli of polyacrylamide gels calculated from bulk rheology and AFM based microrheology measurements also showed good agreement in the overlapping frequency range(Abidine et al., 2015). The method used here is capable of probing a broadband frequency range spanning 1 Hz – 15 kHz (Figure 2C). This enables interrogation of the frequency-dependent viscoelasticity beyond most alternatives. One limitation is that below ~1 Hz, low frequency acoustic noise becomes problematic in most experimental conditions; for these time scales other methods are better suited. Across all probed frequencies for low and high concentration collagen gels chosen to mimic normal and tumor tissue, the complex moduli were inversely related to the polymerization temperature (Figure 3C–D). This result is opposite to what had been previously observed with bulk rheological measurements. Raub and colleagues found that gels became stiffer as they increased the polymerization temperature(Raub et al., 2007b, 2008). This discrepancy can simply be due to the resolution of each technique. Gels polymerized at 4°C form large fibril bundles on the order of several μm. Hence, a bead of diameter 1 μm will sense a stiffer fiber and those gels will seem stiffer than the gels polymerized at 37°C where the fibers are much smaller. In the case of bulk rheology, the porosity will also influence the overall tissue mechanics, so if there are larger porous cavities, hydration effects may result in an overall decrease in complex moduli, as observed for gels polymerized at 4°C with large average pore size.

When combined with a high numerical aperture and long working distance water objective, this optical trap based microrheology is able to probe thick specimens. A caveat when using aM-OT in optically and mechanically heterogeneous tissues is that the optical trap stiffness varies throughout the sample and thus must be calibrated for each probe. We and others have shown that in situ calibration at each probe sufficiently improves accuracy, temporal and spatial resolution necessary to resolve in vivo tissue mechanical heterogeneities (Berg-sørensen & Flyvbjerg, 2004; Blehm et al., 2013, 2015; Fischer & Berg-sørensen, 2007). Briefly, the fluctuation-dissipation theorem (FDT) method is used to calibrate the trap stiffness in situ. By taking a passive and an active measurement, we measure the three unknowns in the cellular trapping environment: the local elasticity, the local viscosity, and the trap stiffness. The passive measurement records the trapped bead’s amplitude of thermal motion in the trap. The active measurement involves oscillating the trap laser and simultaneously measuring the bead’s response at multiple frequencies (f_n). By combining the phase delay and the amplitude measured in the active calibration with the amplitude measured during the passive calibration at every frequency f_n, we can obtain the three unknowns and calibrate the trap in vivo. Here, we confirm that in collagen samples there is a discrepancy of as much as an order of magnitude overestimation of complex moduli calculated with trap stiffnesses calibrated in water (κ_ω) over those calibrated in situ (Figure 3B). The advantage of in situ calibration is that we can probe materials without a priori knowledge of local optical and/or mechanical properties of the microenvironment. This may be useful e.g. to predict establishment of a lesion by measuring the mechanical properties of the tumor permissive organ “soil” during the early stages of colonization of distal organs, following Paget’s seed and soil hypothesis(Fidler, 2003; Paget, 1989).

Another particular appeal of active microrheology is the ability to exert forces and thus explore the stress-strain relation beyond thermal perturbations in order to measure nonlinear effects at different length and energy scales. As biomaterials are very often nonlinear, this is especially relevant in the context of cell migration and other active processes(I. Levental, Georges, & Janmey, 2007). Compared to passive techniques, active microrheology is less susceptible to thermal noise(Breedveld & Pine, 2003). Notably, discrepancies in frequency dependence have been observed in active and passive measurements(Brau, Ferrer, Lee, Castro, & Tam, 2007). For an optical trap, there are two ways to vary the stress and strain applied to the probe’s microenvironment: 1) by changing the trap position oscillation amplitude or 2) by changing the laser power. For the first parameter, we are limited to a maximum of 200 nm for the oscillation amplitude to ensure that we are still probing in the linear regime. For the latter, we are restricted by local heating effects where increasing the laser power may locally denature and soften gels or tissues(Peterman, Gittes, & Schmidt, 2003). Using this approach, we measured the nonlinear mechanical response of collagen gels as a function of architecture and ligand density. Collagen is more thermodynamically stable as a polymer than a monomer, giving rise to many different forms of networks. Collagen forms fractal networks with microdomains having distinct microrheological properties. Such complex hierarchical structures exhibit distinct mechanical properties from one another, and furthermore distinct mechanical responses to perturbations at different force scales. We found in collagen that doubling the stress amplitude resulted in nearly doubling the complex modulus (Figure 4). The frequency dependence of the complex modulus tends toward values predicted for semi-flexible polymers (MacKintosh, Käs, & Janmey, 1995; Storm et al., 2005). While the frequency dependence was similar at high frequency among different gels, differences at low and intermediate frequencies became apparent as a function of applied stress and strain. Some viscoelastic materials exhibit a characteristic crossover frequency at which the loss modulus equals the storage modulus, marking a transition between a low frequency elastic plateau regime and a high frequency liquid-like regime characterized by power-law frequency dependence indicative of complex dynamics without a characteristic timescale. Such materials are often well-described by structural damping models in which the viscous component is directly coupled to the elastic component(Alcaraz et al., 2003; Fabry et al., 2003; Mofrad Kamm, Roger D., 2006). The same behavior can also be modeled as obeying the dynamics of a soft glass beyond the crossover frequency(Sollich et al., 1997; Sollich, 1998). Fitting of our collagen data to the structural damping model revealed good fits at frequencies just below the crossover and beyond, but in the elastic plateau region the actual storage and loss moduli were respectively higher and lower than those predicted by the model (data not shown)(Alcaraz et al., 2003). The discrepancy may owe in part to the local minima in G″ characteristic of entangled fiber networks(Abidine et al., 2015; Granek et al., 2009). A concentration dependence of the crossover frequency in polyacrylamide gels has previously been observed(Abidine et al., 2015). Here, we observe in gels of equal concentration but distinct topography (tuned by polymerization temperature) similar crossover frequencies at low stress, suggesting that fiber size and architecture and not only density play a role (Figure 4). Scale free rheological behavior at high frequencies has also been linked to the type of fractal topographical structure observed in the collagen gels(Fabry et al., 2003). Gels with longer, thicker fibers, larger pores, and greater lacunarity possess structural features across a greater range of length scales, and were here observed to exhibit elastic plateaus that extend to higher frequencies, but with a slightly greater slope in the elastic plateau regime. Furthermore, these gels exhibited relatively greater shifts in the crossover frequency whereby the onset of liquid-like behavior occurs at higher frequencies in response to greater applied stress and strain. In vitro hydrogels are excellent surrogates for in vivo tissue but they may differ from native collagen structures in many important ways such that there may be different mesh topologies in ordered tissues in vivo. Acid-extracted telopeptide-intact collagens more readily allow polymerization of hydrogels from reconstituted protein due to improved ability to polymerize and crosslink, whereas pepsin is commonly used for extraction of collagen structures from tissue. Recent studies have shown that the source, (bovine vs. rat vs. cell-derived tissue explants) and preparation of the collagen (acid solubilized vs. pepsin extracted) regulates the resultant stiffness and porous architecture of hydrogels(Wolf, Te Lindert, et al., 2013). Hence, our findings may be specific to acid-solubilized rat-tail collagen used in these studies. The ability to probe ECM mechanics directly in vivo or ex vivo on fresh tissue is therefore desirable. To date, few mechanics measurements have been conducted on tumor tissue material at the microscale. Plodinec at al. used AFM nanoindentation on murine breast tumor tissue sections, measuring the Young’s modulus of different regions in small force maps(Plodinec, Loparic, Monnier, Obermann, Zanetti-Dallenbach, Oertle, Hyotyla, Aebi, Bentires-Alj, Lim, et al., 2012). Acerbi et al. recently used AFM microindentation to measure 20 μm cryopreserved thin sections of human breast tissue from cancer patients of different molecular subtypes(Acerbi et al., 2015). Staunton et al. recently used AFM indentation with spheroconical probes to measure elasticity of cells embedded in 3D collagen I matrices(Staunton et al., 2016). For tumor samples, the sectioning process itself may alter the superficial surfaces measured in AFM indentation. With microrheology analysis, mechanical properties can be probed ~10–400 μm beneath the sheared surface. However, the use of multiple techniques is important to provide complementary and supplementary information, e.g. over different force and frequency ranges. The active microrheology measurements described here of the murine tumor microenvironment are the first of their kind to our knowledge. We used fluorescent beads and fluorescence microscopy to positively identify them in order to avoid inadvertent measurement of vesicles and other small round objects in the tumor. Such objects can be trapped and measured, but careful consideration of their surface moieties and size is needed to determine accurate displacement-viscoelasticity conversions. Plodinec and co-workers conducted AFM indentation measurements with sharp tips on human breast tumors measured at frequencies ~0.8 – 1 Hz, finding a trimodal distribution of Young’s moduli with peaks at ~1, 2, and 6 kPa(Plodinec, Loparic, Monnier, Obermann, Zanetti-Dallenbach, Oertle, Hyotyla, Aebi, Bentires-Alj, H., et al., 2012). AFM indentation measurements on human breast tumors measured at 20 μm/s with a 5 μm spherical probe showed Young’s moduli ~1 kPa(Acerbi et al., 2015). Interestingly mouse melanoma cell and human breast cancer cell tumors measured by am-OT here were as much as two orders of magnitude softer at comparable frequencies. We determined that mouse melanoma tumors also exhibited nonlinear stress-strain behavior, with frequency dependence shifting from semi-flexible to flexible behavior with increasing stress-strain amplitude, as obtained for collagen hydrogels. In addition, we determined that mouse melanoma tumors and human breast tumors displayed elastic moduli ~5 to ~1000 Pa, increasing monotonically with frequency. Mouse melanoma tumor samples also exhibited nonlinear stress-strain behavior in the tumor, with frequency dependence shifting from semi-flexible to flexible behavior with increasing stress-strain amplitude. While collagen hydrogels showed distinct properties between the elastic and viscous moduli, tumor samples showed relatively equal elastic and viscous moduli monotonically increasing as a function of frequency. In the future, implementation of multichannel fluorescence will enable specific labeling of cancer cells, ECM proteins, or microvasculature. How these mechanical properties compare with standard histopathological analyses may help to uncover the role of tumor progression and ECM mechanics.

Conclusion

We examined the effects of polymerization temperature and collagen concentration on the network architecture and microscale complex shear moduli of type I collagen hydrogels at two magnitudes of stress-strain amplitude at Hz-kHz frequencies. We found that decreasing polymerization temperature correlated with increasing pore area, fiber width, and fiber length distribution. Lower temperatures resulted in stiffer gels, as measured at the microscale. Using in situ calibration, we can obtain absolute rheological measurements in optically heterogeneous materials such as tissue that may not be readily resolves using calibration techniques in proxy materials. Modulating stress-strain amplitude by a factor of two significantly changed the response of all gels. We also observed that the complex modulus tended toward values predicted for semi-flexible polymer networks. We then determined that mouse melanoma tumors and human breast tumors displayed elastic moduli ~5 to ~1000 Pa, increasing with frequency. Mouse melanoma tumor samples also exhibited nonlinear stress-strain behavior in the tumor, with frequency dependence shifting from semi-flexible to flexible behavior with increasing stress-strain amplitude. Thus, we show the feasibility of a mechanical biopsy as a diagnostic tool to aid in design of therapeutics that would be complementary to those based on standard histopathology.

Biography

Kandice Tanner received her doctoral degree in Physics at the University of Illinois, Urbana-Champaign under Professor Enrico Gratton. She completed postdoctoral training at the University of California, Irvine specializing in dynamic imaging of thick tissues. She then became a Department of Defense Breast Cancer Post-doctoral fellow jointly at University of California, Berkeley and Lawrence Berkeley National Laboratory under Dr. Mina J. Bissell. Dr. Tanner joined the National Cancer Institute as a Stadtman Tenure-Track Investigator in July, 2012, where she integrates concepts from molecular biophysics and cell biology to learn how cells and tissues sense and respond to their physical microenvironment, and to thereby design therapeutics and cellular biotechnology. For her work, she has been awarded the 2013 National Cancer Institute Director’s Intramural Innovation Award, the 2015 NCI Leading Diversity award and the 2016 Young Fluorescence Investigator award from the Biophysical Society, She currently serves on the Membership Committee of the American Society of Cell Biology, the Minority Affairs Committee of the Biophysical Society and is a Member at large for the Division of Biological Physics of the American Physical Society