Quasi-particle interference of heavy fermions in resonant x-ray scattering

Probing the quasi-particle interference of heavy fermions by resonant x-ray scattering and scanning tunneling spectroscopy.

Abstract

Resonant x-ray scattering (RXS) has recently become an increasingly important tool for the study of ordering phenomena in correlated electron systems. Yet, the interpretation of RXS experiments remains theoretically challenging because of the complexity of the RXS cross section. Central to this debate is the recent proposal that impurity-induced Friedel oscillations, akin to quasi-particle interference signals observed with a scanning tunneling microscope (STM), can lead to scattering peaks in RXS experiments. The possibility that quasi-particle properties can be probed in RXS measurements opens up a new avenue to study the bulk band structure of materials with the orbital and element selectivity provided by RXS. We test these ideas by combining RXS and STM measurements of the heavy fermion compound CeMIn₅ (M = Co, Rh). Temperature- and doping-dependent RXS measurements at the Ce-M₄ edge show a broad scattering enhancement that correlates with the appearance of heavy f-electron bands in these compounds. The scattering enhancement is consistent with the measured quasi-particle interference signal in the STM measurements, indicating that the quasi-particle interference can be probed through the momentum distribution of RXS signals. Overall, our experiments demonstrate new opportunities for studies of correlated electronic systems using the RXS technique.

INTRODUCTION

The quest to understand strongly correlated electronic states has pushed the frontiers of experimental measurements of solids to the development of new experimental techniques and methodologies. Understanding these exotic electronic states, such as those in heavy fermions, cuprates, and pnictides, requires precise knowledge of their low-energy excitations. Angle-resolved photoemission spectroscopy (ARPES) and spectroscopic imaging with the scanning tunneling microscope (SI-STM) have provided a great deal of information on the nature of these low-energy states through precise measurements of their energy dispersion and interference properties (1–4). In the past decade, advances in resonant x-ray scattering (RXS) have provided a new tool to probe orbital-specific ordering phenomena in condensed matter systems, such as the charge order in the cuprates (5–20). Recently, theoretical investigations led by Abbamonte et al. (21), and subsequently by Dalla Torre et al. (22), proposed the extension of this technique to probe band structure effects, in resemblance to the quasi-particle interference signal measured using SI-STM. Remarkably, these theoretical studies demonstrate a simple and direct relation between the RXS intensity and SI-STM. Although this relation can be used to reinterpret (22) RXS measurements of charge order in the high-temperature superconducting cuprates (5–20), the equivalence between RXS and SI-STM is expected to hold more generally. Moreover, the element-specific sensitivity to the bulk electronic structure gives RXS a fundamental advantage over the surface-sensitive STM and ARPES probes. To test these hypotheses, we carried out complementary RXS and STM studies to assess the impact and significance of the quasi-particle interference in RXS experiments.

Here, we investigate these proposed ideas on an archetypical correlated heavy fermion system and further our understanding of heavy quasi-particle formation through RXS measurements. Unconventional superconductivity and quantum criticality in f-electron materials develop as a consequence of heavy quasi-particle excitations emerging through the hybridization of f-orbitals with conduction electrons (23–29). Understanding these remarkable phenomena requires probing the energy-momentum structure of the emergent narrow heavy bands near the Fermi energy (E_F) with high precision. The CeMIn₅ (M = Co, Rh) family of heavy fermion compounds (30, 31) is an ideal system for this task, because STM measurements can be carried out on these materials (32–34) and the energies of the Ce-M_4,5 edges (3d-to-4f transition) allow RXS measurements to be performed in the currently available state-of-the-art synchrotron soft x-ray end stations. In these Kondo lattice systems, the hybridization between the f-orbitals of the Ce atom and the itinerant spd conduction electrons leads to the formation of a narrow heavy band at the Fermi energy, below a characteristic coherence temperature T* (Fig. 1A). As a result, the heavy f-like band and its associated quasi-particle interference can be markedly suppressed above T*, allowing temperature to be used as a control parameter. Alternatively, isovalent substitution of the transition metal site M between Rh and Co controls the hybridization strength and, consequently, the large density of f-electron states near E_F (27). Finally, the ground state of CeCoIn₅ can be modified between superconductivity and antiferromagnetism by hole doping with Cd, which enables us to study the low-energy electronic states in the vicinity of different ordered phases (35, 36). Overall, the CeMIn₅ system allows the band structure to be easily tuned as a function of temperature and doping, providing an ideal test bench for the impact of band structure effects on the RXS experiment and its connection to SI-STM.

Fig. 1. STM studies on heavy fermion CeCoIn₅.

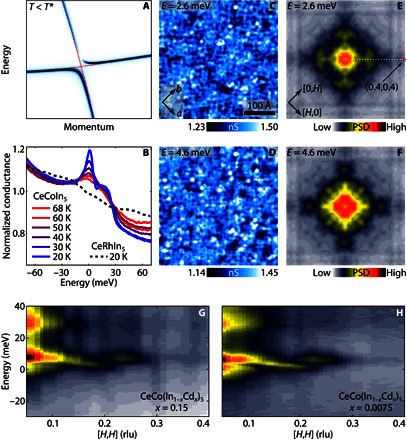
(A) Illustration of heavy fermion band formation as a result of hybridization below the T* coherence temperature of the Kondo lattice. (B) Temperature dependence of the averaged tunneling spectra on surface B of pure CeCoIn₅ and CeRhIn₅ (dashed line). Data are from Aynajian et al. (32). (C and D) Real-space conductance map near the Fermi energy on surface B of CeCo(In_1−xCd_x)₅ at x = 0.15 doping level, which shows clear heavy–quasi-particle interference waves (V_bias = −100 mV, I_{set point} = 1.6 nA). (E and F) Fourier transforms of the real-space conductance maps at the corresponding energies, which display dispersing peaks in the [H,H] direction. Red dot indicates the (0.4,0.4) point in the reciprocal space. (G and H) Energy-momentum cuts of the Fourier transforms in the [H,H] direction [dashed line on (E)] for x = 0.15 and x = 0.0075. The heavy fermion band formation and quasi-particle interference are unaffected by the Cd doping. rlu, reciprocal lattice units; PSD, power spectral density.

RESULTS

Our earlier STM studies (32, 33) showed that the cleaved (001)-oriented surfaces of CeCoIn₅ expose three different chemical terminations: surfaces A, B, and C. In these previous works, we demonstrated the surface-dependent sensitivity to the heavy fermion excitations: The light quasi-particles were detected on surface A, whereas surface B predominantly showed the heavy quasi-particles of the hybridized band structure. Here, we carried out spectroscopic measurements in the normal state (T = 10 K) on surface B of CeCo(In_1−xCd_x)₅ to study the heavy f–quasi-particle interference and compare it with the 4f-sensitive RXS data. Previously (32), the hallmark of heavy-band formation was observed through the temperature-dependent large density of states in the STM spectra (Fig. 1B). Here, we use SI-STM to visualize its energy-momentum structure. Figure 1 (C and D) shows the real-space conductance map (x = 0.15) at specified energies near E_F. The Fourier transforms of the conductance maps (Fig. 1, E and F) reveal an enhancement of local density of states modulations along the [H,H] crystallographic direction. The energy-momentum structure of these quasi-particles in the [H,H] direction signals the presence of rapidly dispersive bands as a function of energy (Fig. 1G). Similar results were obtained for the x = 0.0075 Cd-doped sample (Fig. 1H). Therefore, both results reveal the formation of heavy quasi-particle bands near the chemical potential, which are independent of the Cd doping: The quasi-particle interference is unaffected by the underlying ground state at this temperature. Overall, the dispersive nature of the modulations in the STM conductance maps, with the absence of nondispersive features, relates its origin to the quasi-particle interference of heavy f-electrons. The quasi-particle interference that originates from the heavy bands and the hybridization energy scale agree with ARPES measurements of heavy f–quasi-particles close to the Fermi energy (37, 38). However, from the experimental perspective, because both RXS and STM are momentum-transfer (Q-space) probes, the comparison between them becomes more direct.

We now move to our RXS measurements performed on CeCo(In_1−xCd_x)₅ samples (x = 0 and x = 0.1) and on CeRhIn₅. To enhance the sensitivity of our scattering measurements to the f-electron states, we tuned the photon energy near the Ce-M_4,5 edges, as determined by the x-ray absorption spectrum (XAS). The XAS in Fig. 2A displays peaks due to the 3d-to-4f transition, with two main regions separated by Δ^3d_SOC ~ 17 eV, which is the spin-orbit splitting of the J = 3/2 and J = 5/2 states of the 3d core hole, and corresponding to the M_4,5 edges, respectively (39, 40). Recent dynamical mean field theory calculations (41, 42) show the f–quasi-particle peak near the Fermi energy (also seen in our STM data in Fig. 1) to be entirely of J = 5/2 character, whereas the J = 7/2 f-band is located about 280 meV above the chemical potential. These strongly dispersing f-bands near the Fermi energy have been experimentally observed by ARPES measurements (37, 38) and STM measurements (33, 34). Dipole selection rules (ΔJ = 0, ±1) dictate that whereas at the M₅ edge both J = 5/2 and J = 7/2 unoccupied 4f states can be reached, only the J = 5/2 state can be reached at the M₄ edge. Therefore, we conclude that the RXS measurement at the M₄ edge is selectively sensitive to the narrow heavy f–quasi-particle peak at E_F and thus allows a direct comparison to the SI-STM data of Fig. 1 in an energy window smaller than the XAS broadening. In the following, therefore, we focus on RXS measurements at the Ce-M₄ edge.

Fig. 2. Resonant transition of the heavy 4f state.

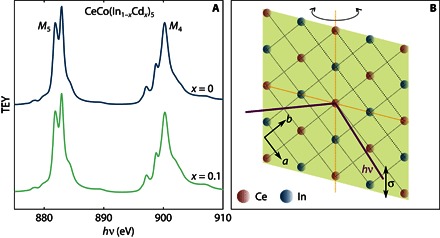
(A) Linearly polarized XAS spectra [measured through the total electron yield (TEY)] on CeCo(In_1−xCd_x)₅ at x = 0 (blue) and x = 0.1 (green) doping level at 10 K, which demonstrates the transition between the 3d and 4f states. The curves are shifted vertically for clarity. (B) RXS scattering geometry, with the scattering plane lying at 45° relative to the a and b axes.

The RXS measurements were performed using a standard scattering geometry (Fig. 2B) in the (HHL) plane with σ polarization and using a photon energy of E_ph = 900.3 eV in resonance with the Ce-M₄ edge, unless otherwise noted. Because of the geometric limitations imposed by this small photon energy, the momentum scans are not restricted to a single value of momentum transfer L along the crystallographic c axis (see the Supplementary Materials), similar to previous works on the cuprates (5–11).

Figure 3A shows momentum scans plotted as a function of in-plane momentum transfer along the two high-symmetry directions [H,0] and [H,H] in CeCoIn₅ at the Ce-M₄ edge and also at the Co-L₂ edge (corresponding to a 2p-to-3d transition). All scans exhibit a sharp increase (decrease) of intensity for small H < 0.15 rlu (large H > 0.4 rlu) related to the geometry of the RXS experiment, where we defined rlu as 2π/a = 1.36 Å⁻¹, with a = 4.6 Å, the tetragonal in-plane lattice constant. The momentum scans reveal a broad scattering enhancement residing on top of a temperature-independent fluorescence background in the 0.2 < H < 0.4 rlu range, along the [H,H] direction when tuned to the Ce-M₄ edge, but there was no enhancement along the [H,0] direction. Similar momentum scans, with the x-ray photon energy tuned to the Co-L₂ absorption edge, show the absence of the scattering enhancement along [H,H]. Furthermore, momentum scans for photon energies finely tuned around the Ce-M₄ resonance (Fig. 3B) demonstrate that the scattering enhancement near H = 0.35 rlu is resonant with the M₄ edge. These results indicate that the scattering enhancement observed at the M₄ edge along the [H,H] direction originates from heavy quasi-particles of f-character just above E_F.

Fig. 3. RXS measurements on CeCoIn₅.

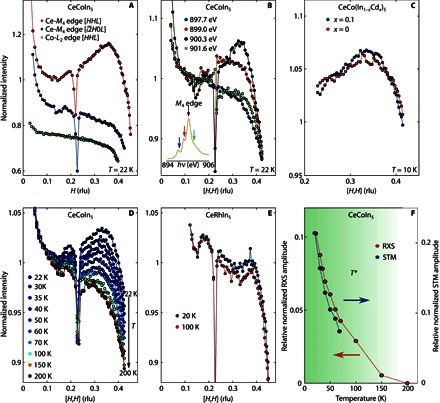
(A) On-resonance θ scans showing the RXS diffraction signal on pure CeCoIn₅ at the Ce-M₄ edge in both the [H,H] and [H,0] directions and as a comparison at the Co-L₂ edge in the [H,H] direction at T = 22 K. The curves are shifted vertically for clarity. (B) Energy dependence of the RXS spectrum on and off the Ce-M₄ edge. Inset shows the XAS around the M₄ edge, with arrows indicating the energies where RXS spectra were measured. (C) Comparison of the RXS cross section at the M₄ edge on CeCo(In_1−xCd_x)₅ at x = 0 (red) and x = 0.1 (blue) doping level at T = 10 K. The RXS signal exhibits the same shape independently from the doping level. (D) Detailed temperature evolution of the RXS peak on pure CeCoIn₅, which reveals strong temperature dependence. (E) RXS scans measured on CeRhIn₅ at T = 20 and 100 K. The cross sections display no significant temperature dependence. (F) Comparison of the RXS peak height with the hybridization peak height measured by STM (from Fig. 1B) as a function of temperature. Both signals exhibit a sharp uprise at the T* Kondo temperature, suggesting the common origin of the features.

Typically, resonant enhancement in scattering experiments is associated with electronic ordering. In this context, it must be noted that CeCo(In_1−xCd_x)₅ is located close to an antiferromagnetic (AFM) quantum critical point (35, 36), with Cd doping driving the system toward the AFM ground state (T_N ~ 3 K at x = 0.10). Hence, although all our measurements were performed in the absence of static order, it would be conceivable that at 10 K our RXS measurements, which are energy-integrated and therefore also sensitive to inelastic processes, could be picking up fluctuations of an ordered state. However, this possibility is repudiated by the insensitivity of the RXS scattering enhancement to Cd doping (Fig. 3C), demanding an alternative explanation.

To further investigate the origin of this resonant scattering enhancement, we next consider its temperature and material dependences. Figure 3D displays momentum scans along the [H,H] direction for several temperatures at the Ce-M₄ edge. The data reveal a significant temperature dependence, with a rapid suppression of the scattering enhancement up to 100 K and its saturation above. Identical measurements carried out on the isostructural material CeRhIn₅, where heavy f–quasi-particles are expected to be absent from the Fermi surface at 20 K (32), show no temperature-dependent scattering features in the same temperature window (Fig. 3E). These temperature- and material-dependent RXS measurements provide a direct connection to the STM measurements (Fig. 1B) and further provide an important finding. The robust presence of the heavy fermion band in CeCo(In_1−xCd_x)₅ (for x = 0.1 and 0.15) and its absence in CeRhIn₅ from STM and RXS indicate that the AFM ground state, which forms at lower temperatures in both compounds, has different origins, presumably related to the itinerant or localized character of the Ce’s f-moments. This is an important piece of information in the context of Kondo destruction and quantum criticality in heavy fermions (43) and deserves further investigation.

Figure 3F displays the amplitude of the scattering peak enhancement in RXS obtained at a given temperature as the difference between the area under the momentum scan at that temperature and at 200 K. Comparison to the temperature dependence of the f-weight from STM spectra shows a good agreement with the RXS results, indicating not only a strong correspondence between the two techniques but also that RXS can be a momentum-resolved probe of the band structure of materials beyond ordering phenomena.

Exactly how this sensitivity to the band structure occurs remains an open question in the field. To illustrate one possible scenario, in which a strongly dispersing (flat) band above the Fermi energy can give rise to a broad scattering enhancement in the RXS measurement, we follow the procedure proposed by Abbamonte et al. (21) and Dalla Torre et al. (22), using the experimentally obtained quasi-particle interference information rather than simulated data. The derived phenomenological picture relates the Fourier transform of STM conductance maps, g(q,ω), to the RXS intensity

$${\mathit{I}}_{\mathit{R}\mathit{X}\mathit{S}}(\mathit{q},{\mathit{E}}_{\text{ph}})={|{\displaystyle \underset{0}{\overset{\infty }{\int }}}\frac{\mathit{g}(\mathit{q},\mathrm{\omega }\prime )}{{\mathit{E}}_{\text{ph}}-\mathrm{\omega }\prime -{\mathit{E}}_{\mathrm{h}}+\mathit{i}{\mathrm{\Gamma }}_{\mathrm{h}}}\mathit{d}\mathrm{\omega }\prime |}^2$$ (1)

where the integral runs only over unoccupied states, whereas E_h and Г_h refer to the core-hole energy and broadening, respectively. At the resonant condition (that is, E_ph = E_h), this integral effectively relates I_RXS to the sum of g(q,ω) inside an envelope of width Г_h, which is typically ~200 meV.

Before applying Eq. 1 to our experimental data, we discuss the approximations and assumptions that it entails. First, we point out that choosing the proper integration boundaries is critical to the result of Eq. 1. Naturally, the limited energy range (few hundreds of millielectron volts) of an STM measurement requires us to introduce a cutoff energy for the upper bound of the integral. However, as we discussed earlier, because of dipole selection rules, the Ce-M₄ edge is expected to represent only the J = 5/2 heavy-electron states near E_F. Therefore, we restrict the integration only up to 20 meV, where we detect the strongly dispersing f-band, which is also the energy window where the tunneling spectrum exhibits a temperature dependence (Fig. 1B). Extending the integration to higher energies would suppress the strength of the signal associated with the heavy band relative to the background intensity of g(q,ω) and would also introduce spurious contributions from bands that may not play a role in the RXS measurement.

Second, it is important to note that the quasi–three-dimensional nature of the band structure of CeCoIn₅ is not accounted for in Eq. 1. Both STM and RXS techniques are sensitive to the Q_x and Q_y (or H and K in reciprocal lattice units) in-plane components of the Q = k_i – k_f momentum transfer, as well as the Q_z (or L) out-of-plane component. Generally, quasi-particle interference maps measured by STM in a material with three-dimensional band structure can be approximated by the weighted average quasi-particle interference over k_z slices (44), though the exact nature of this sum is not known. On the other hand, the scattering geometry in RXS measurements precisely determines the value of L (see the Supplementary Materials), but not the initial and final values of k_z. Therefore, because the sensitivity to k_z may be different in the two techniques, an exact connection between RXS and STM using Eq. 1 may not hold. The calculations below should be interpreted as a qualitative description.

Figure 4 shows the calculated RXS intensity based on our STM conductance maps acquired on surface B along the [H,H] direction. We observe that the flat band indicated by the dashed area in Fig. 4A leads to a broad scattering enhancement in the 0.2 < H < 0.3 rlu range (Fig. 4B). Quantitatively, the momentum range of enhanced quasi-particle interference in the STM data is smaller than that seen in the RXS measurements (Fig. 4C). This difference could be the result of the quasi–three-dimensionality of the CeCoIn₅ band structure as discussed above. Regardless, because the integration is taken over fast dispersing (heavy) bands, the RXS scattering signal predicted using Eq. 1 is expected to be broad in momentum space, similar to the RXS data in Fig. 3.

Fig. 4. Quasi-particle interference and RXS.

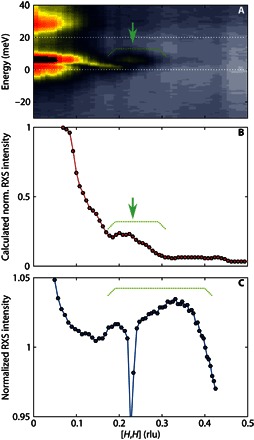
(A) Energy-momentum structure of the quasi-particle band in the [H,H] direction on surface B, with white dashed lines indicating the boundary of the integral (Eq. 1) used to calculate the RXS intensity. (B) Calculated RXS intensity, which exhibits a broad kink starting around H = 0.2 rlu. The momentum range, where the broad peak appears, is indicated by green dashed lines on both (A) and (B). (C) Experimentally measured RXS intensity on CeCoIn₅ at T = 22 K, which shows a broad peak around 0.2 < H < 0.4 rlu. The corresponding momentum range is indicated by dashed lines.

DISCUSSION

Here, we showed the results of a complementary SI-STM and RXS study that probes the significance of band structure effects in RXS scattering measurements. The temperature, material, and photon energy dependences of the RXS data indicate their sensitivity to the formation of the Kondo lattice in the CeMIn₅ system. On the basis of the experimental data, our model calculations show that the strongly dispersing f-bands can give rise to an enhancement of the RXS in a similar momentum range. These observations suggest that the bulk quasi-particle interference, as proposed by Abbamonte et al. (21) and Dalla Torre et al. (22), is responsible for the RXS signal in the present measurements. We should emphasize that although the quasi-particle interference in STM conductance maps arises from native defects, atomic step edges, and impurities, it may have an additional contribution in RXS measurements. When an x-ray photon excites a core electron to the valence band, it creates a localized core-hole potential, which can act as a scattering center. Therefore, this perturbation can also lead to the scattering and interference of the itinerant quasi-particles (45).

It must also be noted that orbital degrees of freedom and their structure factors play a key role in RXS and SI-STM measurements, as in the case of the d-wave form factor of the charge order in the cuprates (12, 13). To obtain the relation between RXS and SI-STM expressed in Eq. 1, Abbamonte et al. (21) purposely disregarded the atomic orbital components of the electronic wave function. This is a particularly inappropriate approximation for f-electron systems, where the atomic multiplet structure is usually well defined in core-hole spectroscopies. This opens the possibility, for example, that the broad scattering enhancement in the RXS is related to how the polarized light couples to particular orbitals (39), which might only become available to the x-ray scattering process after band hybridization below T*. In our experiments, this scenario seems unlikely, given that all our measurements were done in σ-scattering geometry (that is, light polarization constantly in the a-b plane of the sample throughout the momentum scans, as Fig. 2B shows). This suggests that the momentum structure observed in our RXS data is likely related to the band structure of CeCoIn₅, as supported by the temperature-dependent measurements and their similarity to the SI-STM signal. Nevertheless, given the complexity of the RXS cross section, a comprehensive treatment of the scattering process, which takes into account the atomic multiplets in f-electron systems, would provide a more natural explanation to our results.

Our experiments, which demonstrate the relevance of quasi-particle interference in RXS, may also be relevant to the cuprates. In the past few years, a universal charge-order instability emerged as the most exciting progress in the study of high-temperature superconductivity in cuprates (5–20). The ubiquitous nature of this electronic phenomenon in the bulk of hole- and electron-doped cuprates came from RXS experiments on (Y,Nd)Ba₂Cu₃O_y, Bi-2201, Bi-2212, HgBa₂CuO_4+δ, and Nd_2−xCe_xCuO₄ (6–11). These measurements reveal an incommensurate scattering peak, with correlation lengths ranging from 20 to 75 Å, depending on the material and doping. Making a parallel between our RXS experiment on CeCoIn₅ and those on the cuprates suggests that the bulk quasi-particle interference features might be present in the RXS signal of the latter, perhaps even in coexistence with the charge-order peak. At this point, only further experiments can clarify the impact of quasi-particle interference to the RXS measurements in the cuprates.

Our experiments demonstrate that RXS can be a powerful momentum- and energy-resolved probe of the bulk band structure of materials, even in the absence of any ordering phenomena. These results not only pave the way to future RXS experiments on f-electron materials but also support the complementary relationship between RXS and STM measurements.

MATERIALS AND METHODS

Sample growth, STM, and RXS measurement technique

The single-crystal samples used for the measurements were grown from excess indium at the Los Alamos National Laboratory. Small, flat crystals were oriented along the crystallographic axes and cut into sizes suitable for STM and RXS measurements (0.5 to 2 mm × 0.5 to 2 mm × 0.2 mm). The samples used for the STM measurements were cleaved perpendicular to the c axis in ultrahigh vacuum at room temperature and immediately inserted into our homebuilt variable-temperature STM. Differential conductance measurements were performed using standard lock-in techniques, with bias applied to the sample.

The reported RXS experiments were performed at the REIXS (Resonant Elastic and Inelastic X-ray Scattering) beamline of the Canadian Light Source using a four-circle diffractometer in the temperature range of 22 to 200 K (46) and at the UE46_PGM-1 beamline of the Helmholtz-Zentrum Berlin at BESSY II (Berliner Elektronenspeicherring für Synchrotronstrahlung) with a two-circle diffractometer between 10 and 200 K. Reciprocal-space scans were acquired by rocking the sample angle (θ) at a fixed detector position (θ_det = 170°). The samples were preoriented using Laue diffraction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/10/e1601086/DC1

STM measurements and data analysis

RXS comparison on Cd-doped sample

L dependence of the RXS enhancement

Anomalous drop in the RXS signal

fig. S1. STM measurements on CeCo(In_1−xCd_x)₅.

fig. S2. Symmetrization of the conductance map.

fig. S3. Comparison of the RXS cross section on CeCo(In_1−xCd_x)₅.

fig. S4. L dependence of the RXS measurement.