GWIS: Genome-Wide Inferred Statistics for Functions of Multiple Phenotypes

Abstract

Here we present a method of genome-wide inferred study (GWIS) that provides an approximation of genome-wide association study (GWAS) summary statistics for a variable that is a function of phenotypes for which GWAS summary statistics, phenotypic means, and covariances are available. A GWIS can be performed regardless of sample overlap between the GWAS of the phenotypes on which the function depends. Because a GWIS provides association estimates and their standard errors for each SNP, a GWIS can form the basis for polygenic risk scoring, LD score regression, Mendelian randomization studies, biological annotation, and other analyses. GWISs can also be used to boost power of a GWAS meta-analysis where cohorts have not measured all constituent phenotypes in the function. We demonstrate the accuracy of a BMI GWIS by performing power simulations and type I error simulations under varying circumstances, and we apply a GWIS by reconstructing a body mass index (BMI) GWAS based on a weight GWAS and a height GWAS. Furthermore, we apply a GWIS to further our understanding of the underlying genetic structure of bipolar disorder and schizophrenia and their relation to educational attainment. Our analyses suggest that the previously reported genetic correlation between schizophrenia and educational attainment is probably induced by the observed genetic correlation between schizophrenia and bipolar disorder and the previously reported genetic correlation between bipolar disorder and educational attainment.

Main Text

Genome-wide association studies (GWASs) play a major role in quantifying and understanding the genetic effects on a given human phenotype. GWASs are typically meta-analyzed across multiple cohorts. When the phenotype of interest is defined in terms of several other phenotypes, this requires all of these phenotypes to be measured in all cohorts (and participants) that participate in the meta-analysis. We propose a method of genome-wide inferred study (GWIS), which allows one to approximate GWAS summary statistics for a phenotype that is a function of other phenotypes. This approximation is based on a linearization of the function in question and GWAS summary statistics for the phenotypes on which the function depends. We replicate a body mass index (BMI) GWAS using a GWIS based on a height (MIM: 606255) GWAS and a weight GWAS. This GWIS is shown to be accurate when compared to the original GWAS. We proceed to use a GWIS to show that the observed genetic correlation between schizophrenia (MIM: 181500) and educational attainment is probably caused by the observed genetic correlation between schizophrenia and bipolar disorder (MIM: 125480) and the observed genetic correlation between bipolar disorder and educational attainment.

We start by providing a rigorous derivation of the GWIS. Let V = f(P₁,…, P_k) be a function of the k phenotypes P₁,…, P_k. Let S ∼ bin(n = 2, q) be a binomially distributed variable corresponding to the number of effect alleles (EA) of a biallelic SNP, where q denotes the effect allele frequency. Let N denote the sample size. We assume we have a multivariate linear regression model

$$\left[\begin{array}{cccc}{P}_{11}& P_{21}& \dots & P_{k1}\\ P_{12}& P_{22}& \dots & P_{k2}\\ ⋮& ⋮& & ⋮\\ P_{1N}& P_{2N}& \dots & P_{kN}\end{array}\right]=\left[\begin{array}{cc}1& S_1\\ 1& S_2\\ ⋮& ⋮\\ 1& S_N\end{array}\right]\left[\begin{array}{cccc}{\beta }_{01}& {\beta }_{02}& \dots & {\beta }_{0k}\\ {\beta }_{11}& {\beta }_{12}& \dots & {\beta }_{1k}\end{array}\right]+\mathit{ϵ},$$ (Equation 1)

which we write as

$$P=S\beta +\mathit{ϵ}.$$ (Equation 2)

P is a N × k matrix, S is a N × 2 matrix, β is a 2 × k matrix, and ϵ is a N × k matrix. We assume that each row of ϵ follows a multivariate normal distribution with zero mean vector and covariance matrix Σ and that the rows of ϵ are pairwise independent. Now assume that only an estimate for the matrix β (denoted by $\hat{\beta }$) is known, along with the standard errors of each of the $\widehat{{\beta }_{1j}}$, the covariance matrix between the phenotypes P₁,…, P_k, and the mean of each phenotype. This is equivalent to having the summary statistics of the GWASs of each of the k phenotypes and their phenotypic covariances.

The goal is to estimate ${\lambda }_0,{\lambda }_1$ in

$$f\left(P_{1i},\dots ,P_{ki}\right)=:V_i={\lambda }_0+{\lambda }_1{S}_i+e_i$$ (Equation 3)

with e_i normally distributed with zero mean. This is equivalent to performing a GWAS of V. To do this, we use a first-order Taylor approximation of V around the point

$$\mathcal{E}\left(s\right):=\left(\mathbb{E}\left[P_{1i}|S_i=s\right],\dots ,\mathbb{E}\left[P_{ki}|S_i=s\right]\right)$$

for s = 0,1,2. The point $\mathcal{E}\left(s\right)$ corresponds to the mean of the phenotypes of the individuals who have s effect alleles on this SNP. The first-order Taylor approximation is of the form

$$L_i:=f\left(\mathcal{E}\left(s\right)\right)+\sum _{l=1}^k\frac{\partial f\left(\mathcal{E}\left(s\right)\right)}{\partial P_l}\left(P_{li}-\mathbb{E}\left[P_{li}|S_i=s\right]\right),$$

where $\partial f\left(\mathcal{E}\left(s\right)\right)/\partial P_l$ denotes the partial derivative of f with respect to P_l, evaluated in the point $\mathcal{E}\left(s\right)$. Then, it follows that

$$\mathbb{E}\left[L_i|S_i=s\right]=\mathbb{E}\left[f\left(\mathcal{E}\left(s\right)\right)|S_i=s\right]=f\left(\mathcal{E}\left(s\right)\right),$$ (Equation 4)

since for each l in 1,…, k,

$$\mathbb{E}\left[P_{li}-\mathbb{E}\left[P_{li}|S_i=s\right]|S_i=s\right]=0$$

by the linearity of the expectation operator. Equation 4 shows that the mean of the linear approximation is equal to the function evaluated in the phenotypic mean of individuals that have s effect alleles. The error incurred in the linearization process takes the form

$$\frac{1}{2}\sum _{j=1}^k\sum _{l=1}^k\frac{{\partial }^{2}f\left(\tilde{\mathcal{E}}\right)}{\partial P_j\partial P_l}\left(P_{ji}-\mathbb{E}\left[P_{ji}|S_i=s\right]\right)\left(P_{li}-\mathbb{E}\left[P_{li}|S_i=s\right]\right)$$

for some $\tilde{\mathcal{E}}$ in between the two points (P_1i,…, P_ki) and $\mathcal{E}\left(s\right)$.

Note that the linearization is possible only if f satisfies certain regularity conditions on the relevant space of phenotype values. Notably, division by 0 is not allowed. This can be avoided by linear transformation of the observed phenotypes, and the parameters in the β matrix.

We now derive a linear model for our approximate expression for $\mathbb{E}\left[V_i|S_i=s\right]$. We write

$$\mathbb{E}\left[L_i|S_i=s\right]={\lambda }_0+{\lambda }_{1}s$$

and note that if s is 0, we have a direct approximation for ${\lambda }_0$:

$$\widehat{{\lambda }_0}=\mathbb{E}\left[L_i|S_i=0\right].$$

However, as we have shown, $\mathbb{E}\left[L_i|S_i=s\right]=f\left(\mathcal{E}\left(s\right)\right)$, so our approximation for ${\lambda }_0$ becomes

$$\widehat{{\lambda }_0}=f\left(\mathcal{E}\left(0\right)\right)$$

$$=f\left({\beta }_{01},{\beta }_{02},\dots ,{\beta }_{0k}\right),$$

i.e., the function f evaluated at the intercepts of our linear regression model. We can also estimate ${\lambda }_1=\left(\mathbb{E}\left[L_i|S_i=s\right]-{\lambda }_0\right)/s$ by evaluating this expression for s = 1,2 and weighing the results by their (estimated) relative population frequencies. The expression for $\widehat{{\lambda }_1}$ is given by

$$\widehat{{\lambda }_1}=\frac{2q\left(1-q\right)}{2q\left(1-q\right)+q^2}\left(f\left(\mathcal{E}\left(1\right)\right)-\widehat{{\lambda }_0}\right)+\frac{q^2}{2q\left(1-q\right)+q^2}\frac{f\left(\mathcal{E}\left(2\right)\right)-\widehat{{\lambda }_0}}{2}$$

$$=\frac{2q\left(1-q\right)}{2q\left(1-q\right)+q^2}\left(f\left({\beta }_{01}+{\beta }_{11},{\beta }_{02}+{\beta }_{12},\dots ,{\beta }_{0k}+{\beta }_{1k}\right)-\widehat{{\lambda }_0}\right)$$

$$+\frac{q^2}{2q\left(1-q\right)+q^2}\frac{f\left({\beta }_{01}+2{\beta }_{11},{\beta }_{02}+2{\beta }_{12},\dots ,{\beta }_{0k}+2{\beta }_{1k}\right)-\widehat{{\lambda }_0}}{2}.$$

To test our estimates for ${\lambda }_0$ and ${\lambda }_1$, we require their standard errors. Because we do not have the covariance matrix of $\hat{\beta }$, we must first estimate the covariance between each of the $\widehat{{\beta }_{ij}}$. With the theory of multivariate linear regression, we know that the least-squares estimator of β in the model $P=S\beta +\mathit{ϵ}$ is given by

$$\hat{\beta }={\left(S^{T}S\right)}^{-1}{S}^{T}P$$

with corresponding variance-covariance matrix

$$\text{Var}\left(\hat{\beta }\right)={\left(S^{T}S\right)}^{-1}\otimes \text{Σ,}$$ (Equation 5)

assuming that columns of ϵ have zero mean and the rows of ϵ are pairwise uncorrelated.¹ The matrix Σ is a k × k matrix with the elements ${\text{Σ}}_{jl}=\text{Cov}\left({\mathit{ϵ}}_j,{\mathit{ϵ}}_l\right)$, the covariance between the errors in the linear regressions of the phenotypes P_j and P_l on S. This is under the assumption of complete sample overlap. However, this specific solution requires one to analyze all phenotypes at the same time, which is not the case here. Because we are interested in $\text{Var}\left(\hat{\beta }\right)$ but (S^TS)⁻¹ and Σ are unknown, we must find a suitable approximation of these. We assume that the effect of each of the individual SNPs is small, so $\text{Var}\left({\mathit{ϵ}}_j\right)\approx \text{Var}\left(P_j\right)$ and $\text{Cov}\left({\mathit{ϵ}}_j,{\mathit{ϵ}}_l\right)\approx \text{Cov}\left(P_j,P_l\right)$. Expanding S^TS gives

$$S^{T}S=\left[\begin{array}{cc}N& \sum S_i\\ \sum S_i& \sum \left(S_i^2\right)\end{array}\right]$$

with inverse

$${\left(S^{T}S\right)}^{-1}=\frac{1}{N\sum \left(S_i^2\right)-{\left(\sum S_i\right)}^2}\left[\begin{array}{cc}\sum {\left(S_i\right)}^2& -\sum S_i\\ -\sum S_i& N\end{array}\right].$$

From this, we can infer

$$\text{Cov}\left(\widehat{{\beta }_{1j}},\widehat{{\beta }_{1l}}\right)=\frac{N\text{Cov}\left(P_j,P_l\right)}{N\sum \left(S_i^2\right)-{\left(\sum S_i\right)}^2}$$

$$=\frac{\text{Cov}\left(P_j,P_l\right)}{N\text{Var}{S}_i}$$

$$=\frac{\sqrt{\text{Var}\left(P_j\right)}}{\sqrt{N\text{Var}{S}_i}}\text{Cor}\left(P_j,P_l\right)\frac{\sqrt{\text{Var}\left(P_l\right)}}{\sqrt{N\text{Var}{S}_i}}$$

$$\approx \frac{\sqrt{\text{Var}\left({\mathit{ϵ}}_j\right)}}{\sqrt{N\text{Var}{S}_i}}\text{Cor}\left(P_j,P_l\right)\frac{\sqrt{\text{Var}\left({\mathit{ϵ}}_l\right)}}{\sqrt{N\text{Var}{S}_i}}$$

$$={\text{SE}}_j\cdot \text{Cor}\left(P_j,P_l\right)\cdot {\text{SE}}_l.$$

In case there is only partial sample overlap, $\text{Cov}\left(\widehat{{\beta }_{1j}},\widehat{{\beta }_{1l}}\right)$ may also be approximated as

$${\text{SE}}_j\cdot \text{Cor}\left(P_j,P_l\right)\frac{N_{\cap j,l}}{\sqrt{N_j{N}_l}}\cdot {\text{SE}}_l.$$ (Equation 6)

Here, $N_{\cap j,l}$ is the number of individuals that is present in both the GWAS of P_j and the GWAS of P_l, N_j is the number of individuals in the GWAS for P_j, and N_l is the number of individuals in the GWAS for P_l. If one cannot determine Cor(P_j, P_l) directly or the sample overlap between the GWASs is unknown, it is possible to use LD score regression based² on the summary statistics to estimate $\text{Cor}\left(P_j,P_l\right)\left(N_{\cap j,l}/\sqrt{N_j{N}_l}\right)$. Note that in the absence of sample overlap, $N_{{\cap }^{j,l}}$ is zero and thus $\text{Cov}\left(\widehat{{\beta }_{1j}},\widehat{{\beta }_{1l}}\right)$ is zero.

Having obtained the covariance matrix for $\hat{\beta }$, we can apply the Delta-method³ to find the standard errors of $\widehat{{\lambda }_0}$ and $\widehat{{\lambda }_1}$. The derivation above is based on linear regression assuming a continuous response variable. However, a link function may be used to apply this to other response variables.

Body mass index (BMI) is a well-known example of a variable that is a (non-linear) function of multiple phenotypes, defined as weight over height squared. Here we apply a GWIS to BMI. Let μ_w, μ_h denote the means of weight and height, respectively, and let ${\beta }_{w0},{\beta }_{h0},{\beta }_{w1},{\beta }_{h1}$ denote the intercepts of weight and height and the regression coefficients in the regression of weight and height on the SNP, respectively. We assume all of these parameters are known. As shown above, the mean of our approximated BMI is equal to

$$\frac{{\mu }_w}{{\mu }_h^2},$$ (Equation 7)

i.e., BMI calculated for the mean weight and mean height. In our case, the GWAS summary statistics pertained to standardized weight and height but were destandardized before computing the GWIS. The destandardization is based on information on population averages and standard deviations obtained from the Netherlands Twin Register (NTR).⁴ The destandardization involves multiplying the effect sizes by the standard deviation and using the population mean as a substitute for the intercept. The mean of the approximation is in general going to be equal to the function evaluated in the means of the phenotypes. The linear regression of BMI on the number of effect alleles of a given SNP is

$${\text{BMI}}_i={\beta }_{\text{BMI}0}+{\beta }_{\text{BMI}1}\cdot S_i+{\delta }_i,$$ (Equation 8)

where ${\beta }_{\text{BMI}0}$ is the intercept of the linear regression, ${\beta }_{\text{BMI}1}$ is the regression coefficient, and ${\delta }_i$ is the residual of the linear regression for the i^th subject.

Then, the derived values for the intercept and the regression coefficient become

$${\beta }_{\text{BMI}0}=\frac{{\beta }_{w0}}{{\beta }_{h0}^2}$$ (Equation 9)

and

$$\begin{array}{c}{\beta }_{\text{BMI}1}=\frac{2q\left(1-q\right)}{2q\left(1-q\right)+q^2}\left(\frac{{\beta }_{w0}+{\beta }_{w1}}{{\left({\beta }_{h0}+{\beta }_{h1}\right)}^2}-{\beta }_{\text{BMI}0}\right)\\ +\frac{1}{2}\cdot \frac{q^2}{2q\left(1-q\right)+q^2}\left(\frac{{\beta }_{w0}+2{\beta }_{w1}}{{\left({\beta }_{h0}+2{\beta }_{h1}\right)}^2}-{\beta }_{\text{BMI}0}\right)\end{array},$$ (Equation 10)

where q is the effect allele frequency of the SNP.

We demonstrate the accuracy of the GWIS for BMI by performing type I error rate and power simulations, both for the case where all required parameters are given and for the case where the parameters are mildly misspecified. There was no observed increase in type I error rate for GWIS, relative to a traditional BMI GWAS, with a GWIS having power comparable to a GWAS when all parameters were known; larger misspecification of the population parameters did not influence either the power or the type I error rate. However, when there is no sample overlap between the constituent height and weight GWASs, there is an approximate 15%–20% loss of power but no increase in type I error rate (see Table 1). It should be noted that the scale of the GWIS effect sizes and standard errors with misspecified population parameters may not be the same as that of the original GWAS. However, as shown by our simulations, inference based on the GWIS does not appear to suffer from misspecified population parameters. We have used a linear approximation to perform the GWIS. In Appendix A we outline the second-order approximation of BMI, which should be used in conjunction with a second-order Delta-rule. As can be seen in Table 1, the second-order approximation of BMI does provide an increase in power relative to the first-order approximation.

Table 1.

Type I Error Rates and Power for GWAS and Several GWIS Scenarios

Simulated Effect	Sample	R2	GWAS	GWIS	GWIS No Intercept	GWIS 50% Sample Overlap	GWIS 10% Sample Overlap	GWIS 0% Sample Overlap	GWIS Destandardized	GWIS Misspecified Height Mean	GWIS Second Order
Type I Error
0.00000	10,000		0.051	0.0509	0.0497	0.0523	0.0466	0.0461	0.0524	0.0512	0.0456
Power
0.5477	1,000	0.00192	0.166	0.162	0.182	0.141	0.12	0.099	0.165	0.148	0.185
0.5477	2,000	0.00128	0.251	0.251	0.278	0.219	0.196	0.167	0.278	0.283	0.276
0.5477	3,000	0.00128	0.394	0.398	0.392	0.289	0.228	0.252	0.359	0.391	0.382
0.5477	4,000	0.00116	0.475	0.474	0.484	0.39	0.311	0.317	0.473	0.496	0.464
0.5477	5,000	0.00114	0.573	0.578	0.548	0.441	0.39	0.392	0.577	0.599	0.583
0.5477	6,000	0.00110	0.671	0.677	0.625	0.497	0.465	0.445	0.658	0.647	0.642
0.5477	7,000	0.00105	0.702	0.712	0.691	0.611	0.482	0.496	0.698	0.717	0.714
0.5477	8,000	0.00099	0.764	0.764	0.759	0.648	0.568	0.538	0.776	0.804	0.761
0.5477	9,000	0.00103	0.806	0.81	0.832	0.709	0.632	0.633	0.826	0.811	0.819
0.5477	10,000	0.00101	0.862	0.872	0.851	0.746	0.642	0.661	0.842	0.868	0.86
0.5477	11,000	0.00100	0.898	0.901	0.899	0.79	0.7	0.682	0.883	0.899	0.898
0.5477	12,000	0.00098	0.901	0.904	0.91	0.81	0.75	0.75	0.925	0.91	0.922
0.5477	13,000	0.00096	0.934	0.932	0.942	0.853	0.789	0.767	0.934	0.951	0.923
0.5477	14,000	0.00096	0.936	0.936	0.942	0.852	0.798	0.79	0.955	0.951	0.953
0.5477	15,000	0.00098	0.968	0.968	0.952	0.921	0.853	0.807	0.962	0.96	0.961
0.5477	17,000	0.00099	0.986	0.987	0.979	0.928	0.881	0.859	0.968	0.979	0.971
0.5477	19,000	0.00094	0.988	0.987	0.988	0.943	0.909	0.903	0.984	0.983	0.981

The table reports power estimates and type I error for simulated body mass index (BMI) genome-wide inferred statistics (GWIS) for several sample sizes and effect sizes, under several different circumstances. GWAS refers to a linear regression of BMI on the simulated genetic variant, GWIS is an approximation of the same linear regression based on the technique outlined in the paper. We reduce sample overlap between the height and weight sample that are used in GWIS and we explore the effect of substituting the regression intercept with the population mean and standardization of height and weight and subsequent destandardization in the GWIS. These results indicate that GWIS provides similar power to genome-wide association study (GWAS) when the intercepts and scaling of the original GWASs are known. In case the original samples have little to no overlap, the GWIS suffers from approximately 15%–20% power loss for moderate effect and sample sizes. On the other hand, a second-order approximation of BMI gives a similar or higher power to a GWAS of the original BMI GWAS.

We apply GWIS by reconstructing a BMI GWAS based on publicly available height and weight GWAS summary statistics⁵ (see Web Resources). For each SNP included in the height and weight GWAS with a minor allele frequency (MAF) larger than 0.05 (as obtained from the HapMap Consortium⁶), we infer estimates and standard errors of these estimates for the association between the SNP and BMI. In a GWAS, BMI must be ascertained for all participants, whereas in a GWIS, we rely on parameter estimates that reflect the genetic effects on height and weight. Note that the original GWASs of height and weight do not have to be performed in a common set of individuals.

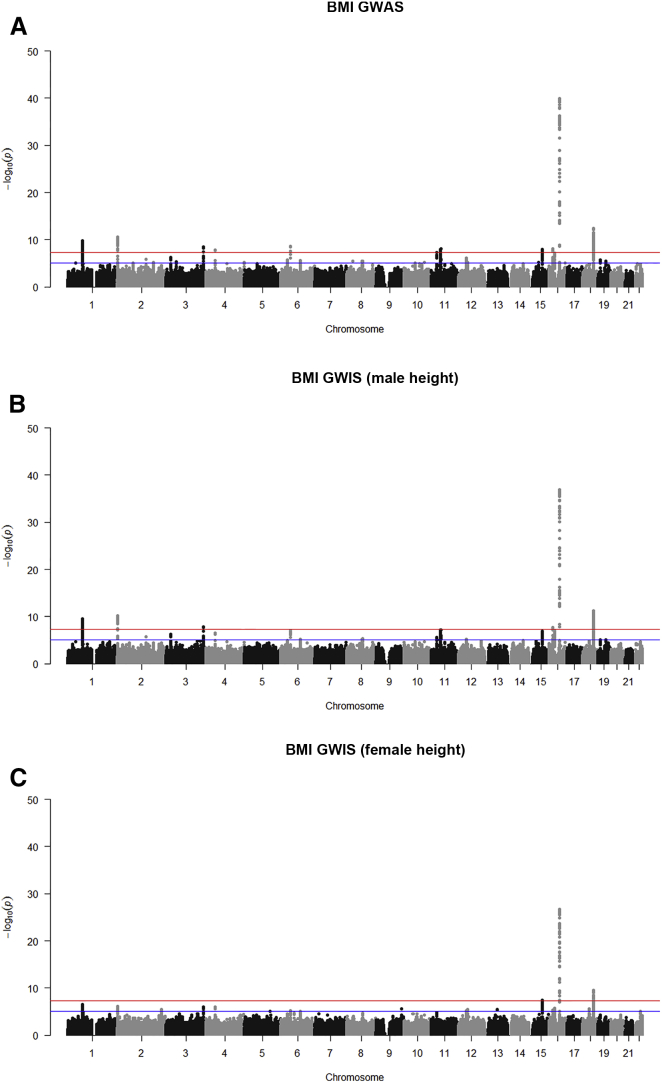
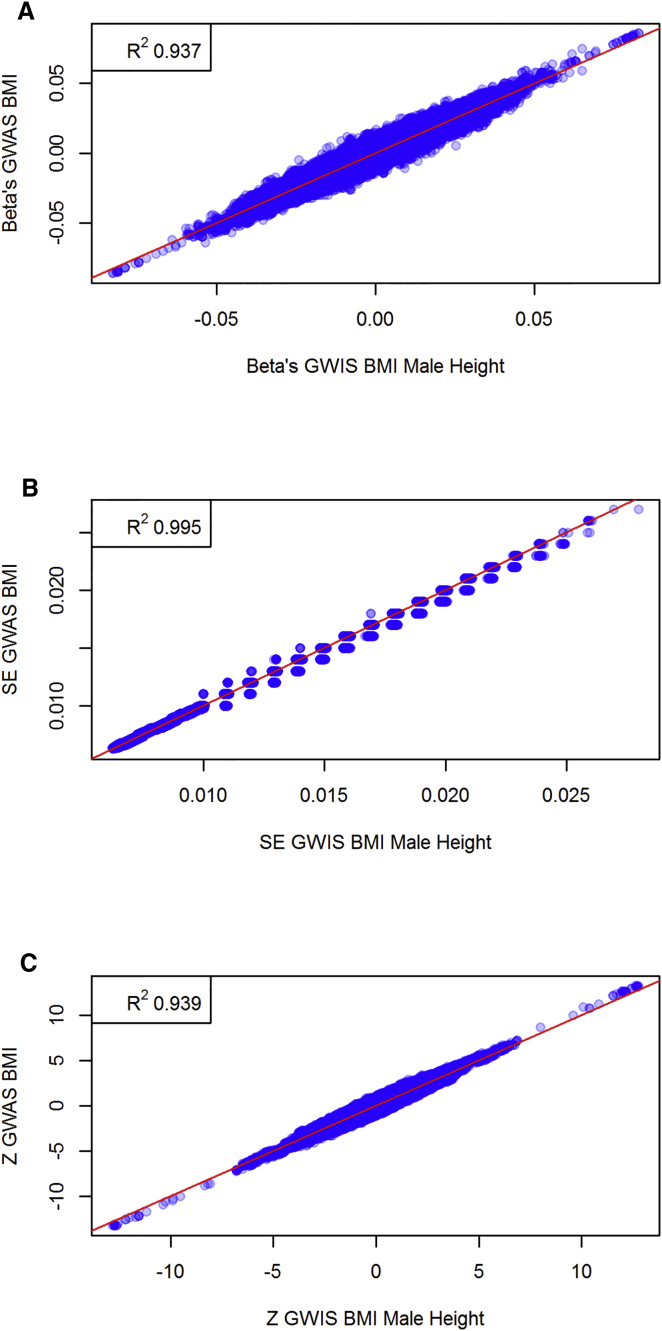
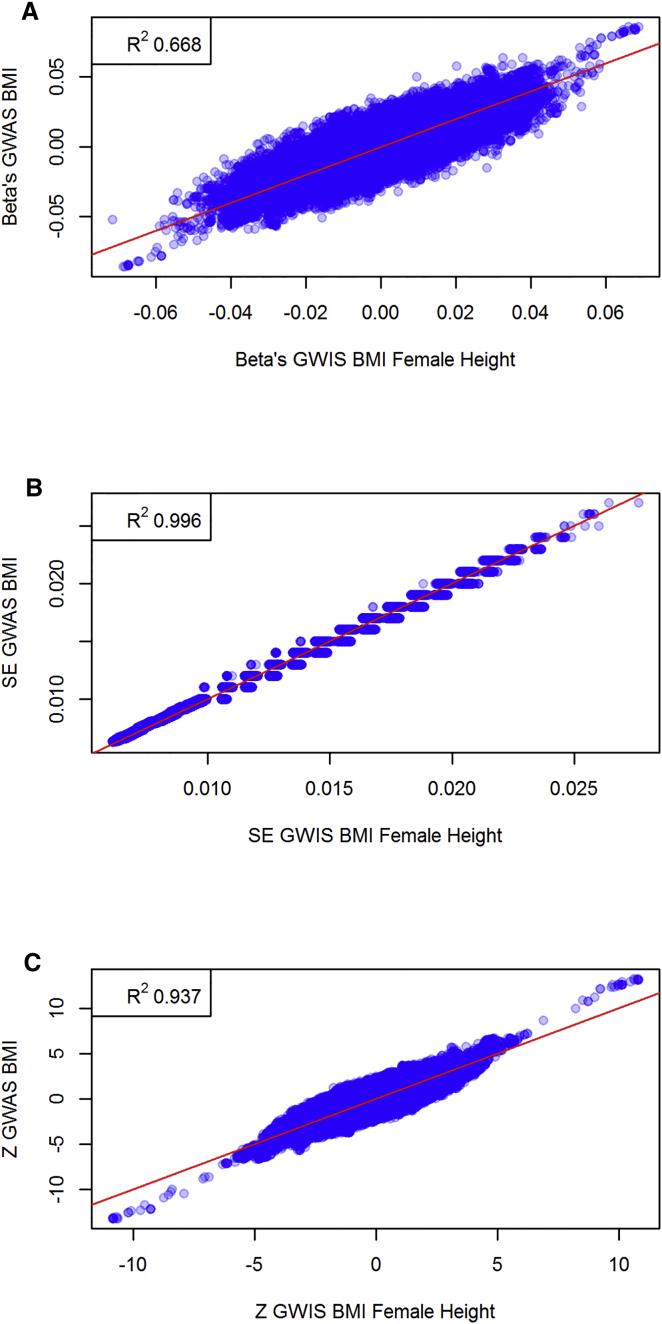
Based on the summary statistics of GWASs of standardized male height and weight,⁵ our GWIS replicated 310 out of 356 genome-wide hits (a 87.1% replication rate) and produced three false-positive results (see Table S1) when compared to a true BMI GWAS performed in the same sample. To demonstrate the method when the constituent phenotypes (i.e., weight and height) are measured independently, we substituted the male height GWAS results for the female height results. Here we assumed that the male and female genetic architecture for height in males and females are identical, i.e., the true effect sizes of each SNP on height is the same for males and females.⁷ The GWIS based on independent height and weight samples replicated 135 out of 356 genome-wide significant signals (a 37.9% replication rate) and yielded no false-positive associations. The corresponding Manhattan plots are shown in Figure 1. We constrain the set of SNPs to those SNPs for which at least 58,000 individuals were genotyped for either height or weight, and we plot the GWIS effect size versus the GWAS effect size, the GWIS standard error versus the GWAS standard error, and the GWIS Z score versus the GWAS Z score (see Figure 2 for the GWIS based on male height and Figure 3 for the GWIS based on female height). Even though the Manhattan plots and the replication rate reveal a loss of power, both forms of GWIS and the original BMI GWAS implicate associations in the same genomic regions. The fact that the GWIS based on female height has less power than the GWIS based on male height is consistent with the power simulations. Furthermore, we have also simulated a scenario (under the null hypothesis of no SNP effect) where the sample size of the original weight GWAS and height GWAS differ by up to two orders of magnitude. These simulations showed that there was no inflation in the type I error rate, even when one of the two SNPs was measured in 100,000 individuals and the other was measured in 1,000 individuals.

Figure 1.

Manhattan Plot of BMI GWAS and GWIS

Manhattan plots of −log p values for the (A) BMI GWAS as performed by Randall et al.⁵, (B) BMI GWIS using male height data, and (C) BMI GWIS using female height data. The location on the x axis corresponds to the genomic location of the SNP. In each figure, the blue line corresponds to p = 1 × 10⁻⁵ and the red line corresponds to p = 5 × 10⁻⁸.

Figure 2.

Comparison of BMI GWAS and BMI GWIS Summary Statistics Based on Male Height Data

Scatterplots of BMI GWAS effect sizes versus GWIS (male height) (A) effect sizes, (B) standard errors, and (C) Z scores. The top left corner for each figure reports the squared correlation.

Figure 3.

Comparison of BMI GWAS and BMI GWIS Summary Statistics Based on Female Height Data

Scatterplots of BMI GWAS effect sizes versus GWIS (female height) (A) effect sizes, (B) standard errors, and (C) Z scores. The top left corner for each figure reports the squared correlation.

Using LD score regression,² we computed the genetic correlations between BMI based on the GWAS summary statistics, the GWIS using male height data, and the GWIS using female height data. Because LD score regression requires information on the number of participants available per SNP, we assume the sample size for the BMI GWIS to be the lowest per-SNP sample size of either the height or weight GWAS used. As expected, the genetic correlation between BMI as measured in GWAS, BMI as approximated in GWIS using male height data, and BMI as approximated in GWIS using female height data is close to unity (see Table 2). Next, we estimated genetic correlations between BMI based on the GWAS, BMI based on GWIS using male height data, BMI based on GWIS using female height data and educational attainment,⁸ LDL cholesterol,⁹ age at menarche,¹⁰ rheumatoid arthritis¹¹ (MIM: 180300), and coronary artery disease¹² (MIM: 607339). Inference made on the genetic correlates of BMI based on GWIS closely mirror the inference made based on BMI GWAS summary statistics.

Table 2.

Estimated Genetic Correlations

	BMI GWIS (Female Height)	BMI GWAS	Rheumatoid Arthritis	Age at Menarche	LDL	Educational Attainment	Coronary Artery Disease
BMI GWIS (male height)	0.967 (0.012)	1.007 (0.002)	0.029 (0.045)	−0.338 (0.035)	0.019 (0.058)	−0.145 (0.053)	0.153 (0.063)
BMI GWIS (female height)	–	0.974 (0.013)	0.018 (0.053)	−0.371 (0.041)	−0.003 (0.061)	−0.157 (0.062)	0.150 (0.071)
BMI GWAS	–	–	0.039 (0.042)	−0.332 (0.032)	0.013 (0.050)	−0.160 (0.047)	0.173 (0.061)

Genetic correlation and standard errors between a BMI GWAS, two BMI GWISs (for male and female height), and multiple related traits. Correlations are estimated using LD score regression.

Ruderfer et al.¹³ performed GWASs of bipolar disorder (BIP), schizophrenia (SCZ), the pooled bipolar and schizophrenia case subjects versus the pooled control subjects (BIP + SCZ), and a GWAS in which the bipolar case subjects featured as control subjects and the schizophrenia case subjects as case subjects (SCZ − BIP) (see Web Resources). The latter two studies can be reproduced with a GWIS. The primary interest of these studies is to identify overlap and contrast between SCZ and BIP. SCZ and BIP are two psychiatric disorders with substantially correlated genetic underlying liabilities.¹⁴ This correlation prohibits the investigation of genetic variants that are specifically linked to either SCZ or BIP, as well as the investigation of genetic overlap between tertiary traits and SCZ or BIP. As a more exotic application of GWIS, we determine whether the genetic correlation between SCZ or BIP and a third trait is specific to either SCZ or BIP. To this end, we defined a function that decomposes the genetic SCZ liability into a part shared with the genetic liability of BIP and a residual, referred to as unique genetic SCZ liability (unique SCZ). In a similar manner, we defined a function that decomposes the genetic BIP liability into a part shared with the genetic liability of SCZ and a residual, referred to as unique genetic BIP liability (unique BIP). These functions are given by

$$\mathrm{Unique}\mathrm{SCZ}:=\left(1+c\right)\mathrm{SCZ}-\left(1-c\right)\mathrm{BIP}$$

$$\mathrm{Unique}\mathrm{BIP}:=\left(1+d\right)\mathrm{BIP}-\left(1-d\right)\mathrm{SCZ}$$

where

$$c=\frac{h_{\text{BIP}}^2-\text{Coh}\left(\text{BIP},\text{SCZ}\right)}{h_{\text{BIP}}^2+\text{Coh}\left(\text{BIP},\text{SCZ}\right)}d=\frac{h_{\text{SCZ}}^2-\text{Coh}\left(\text{BIP},\text{SCZ}\right)}{h_{\text{SCZ}}^2+\text{Coh}\left(\text{BIP},\text{SCZ}\right)}.$$

Here, Coh(BIP,SCZ) denotes the coheritability between BIP and SCZ (i.e., $h_{\text{SCZ}}\cdot r_{\text{BIP},\text{SCZ}}\cdot h_{\text{BIP}}$ with $r_{\text{BIP},\text{SCZ}}$ the latent phenotypic correlation between bipolar disorder and schizophrenia) and $h_{\text{BIP}}^2,h_{\text{SCZ}}^2$ denote the heritabilities of BIP and SCZ, respectively. Note that we cannot measure unique SCZ or unique BIP in individuals. Furthermore, the functions themselves depend on estimated heritability and coheritabilities, which leads to less accurate estimates of genetic effects on unique SCZ and unique BIP. This definition of unique BIP and unique SCZ is similar but not equivalent to a conditional analysis of BIP corrected for SCZ and SCZ corrected for BIP. In a conditional regression analysis of BIP corrected for SCZ, BIP is first regressed on SCZ. The residuals of this regression are then regressed on the SNP. However, the decomposition of BIP into unique BIP and a genetic component shared with SCZ is equivalent to regression BIP on the genetic component of SCZ, and then regressing the residuals on the SNP. It should be noted that a conditional analysis can be performed only in a fully phenotyped sample, which is difficult or even impossible for mutually exclusive dichotomous traits such as BIP and SCZ.¹⁵ Because effect sizes for SCZ and BIP are reported in terms of odds ratios, we take their logarithms to obtain effect sizes on the liabilities. Even though the genetic effects on the latent variables is unknown, for small effect sizes, the effects on the latent variables are approximately a constant multiple of the log(odds ratios) obtained from logit regression. We verified this by simulating a bivariate threshold model with moderately high genetic correlation and performing GWASs of both the latent variable and dichotomous variables. Then, we perform GWISs of the latent GWAS effect sizes and the dichotomous GWAS effect sizes. Table 3 shows that the latent and dichotomous GWASs and latent and dichotomous GWISs differ only by a constant multiple (for reasonably small effect sizes).

Table 3.

Accuracy of GWIS Based on GWAS of Dichotomous Traits

R-squared	SNP effect	Latent GWAS	Dichotomous GWAS	Ratio 1	Latent GWIS	Dichotomous GWIS	Ratio 2
0.0001	0.0050	0.0048	0.0089	1.8383	0.0059	0.0101	1.7147
0.0001	0.0100	0.0109	0.0167	1.5263	0.0125	0.0179	1.4290
0.0002	0.0150	0.0167	0.0279	1.6740	0.0179	0.0300	1.6766
0.0002	0.0200	0.0198	0.0346	1.7509	0.0234	0.0421	1.8034
0.0003	0.0250	0.0241	0.0430	1.7855	0.0281	0.0514	1.8283
0.0004	0.0300	0.0285	0.0511	1.7951	0.0324	0.0590	1.8210
0.0006	0.0350	0.0350	0.0638	1.8226	0.0410	0.0741	1.8089
0.0007	0.0400	0.0393	0.0706	1.7971	0.0460	0.0834	1.8122
0.0009	0.0450	0.0452	0.0814	1.8027	0.0514	0.0933	1.8152
0.0010	0.0500	0.0494	0.0881	1.7848	0.0562	0.1002	1.7830
0.0013	0.0550	0.0559	0.1013	1.8104	0.0646	0.1178	1.8237
0.0014	0.0600	0.0588	0.1058	1.7995	0.0682	0.1224	1.7950
0.0017	0.0650	0.0660	0.1193	1.8073	0.0751	0.1367	1.8197
0.0019	0.0700	0.0699	0.1249	1.7853	0.0806	0.1443	1.7914
0.0023	0.0750	0.0760	0.1337	1.7594	0.0862	0.1529	1.7742
0.0025	0.0800	0.0797	0.1402	1.7597	0.0915	0.1609	1.7591
0.0028	0.0850	0.0851	0.1533	1.8022	0.0970	0.1743	1.7969
0.0032	0.0900	0.0907	0.1633	1.8000	0.1028	0.1844	1.7935
0.0035	0.0950	0.0949	0.1691	1.7812	0.1093	0.1935	1.7709
0.0038	0.1000	0.0986	0.1763	1.7884	0.1137	0.2032	1.7874
0.0085	0.1500	0.1495	0.2671	1.7861	0.1707	0.3039	1.7806
0.0149	0.2000	0.1969	0.3506	1.7804	0.2259	0.4018	1.7790
0.0232	0.2500	0.2453	0.4375	1.7833	0.2829	0.5030	1.7777
0.0325	0.3000	0.2890	0.5188	1.7950	0.3356	0.6014	1.7920
0.0442	0.3500	0.3356	0.6060	1.8059	0.3914	0.7064	1.8046
0.0565	0.4000	0.3765	0.6917	1.8370	0.4416	0.8115	1.8377
0.0707	0.4500	0.4184	0.7725	1.8464	0.4936	0.9118	1.8474
0.0862	0.5000	0.4581	0.8589	1.8749	0.5431	1.0204	1.8787

Results obtained from simulated GWAS on a dichotomous outcome and simulated GWIS performed on the continuous latent variable produces effect sizes that differ approximately by a constant multiple, relative to the dichotomous GWAS and dichotomous GWIS. The reported values here are means over 500 runs, each containing N = 10,000 individuals. Ratio 1 reflects the ratio of the mean effect size from the dichotomous GWAS divided by the mean effect size of the latent GWAS, and ratio 2 reflects the mean effect of the dichotomous GWIS divided by the mean effect of the latent GWIS. Given small effects, the results are approximately equal up to a multiplicative constant. For very large SNP effect sizes, much larger than is usual for polygenic traits, these ratios no longer appear to be constant.

These functions are derived as follows. Given two phenotypes A and B, we can use our method to define a new trait as

$$X:=\left(1+c\right)A-\left(1-c\right)B$$ (Equation 11)

for a specific constant c. In our case, this constant is chosen such that the genetic correlation between X and B becomes zero. However, one may also choose the constant such that the environmental or phenotypic correlation between X and B becomes zero.

In terms of linear regression, this can be seen as

$$\left(1+c\right)A=\left(1-c\right)B+X$$

so that X is the residual of the linear regression (with fixed coefficients) of (1 + c)A on (1 − c)B.

Note that zero correlation does not imply that X and B are independent; rather, they have only become linearly independent. The expression for c is

$$c:=\frac{\text{Var}B-\text{Cov}\left(A,B\right)}{\text{Var}B+\text{Cov}\left(A,B\right)}$$ (Equation 12)

where Cov and Var denote the covariances and variances that are specific to the type of correlation that is considered. For example, in our case of genetic correlation, Cov denotes the coheritability and Var denotes the heritability of the traits.

We derive c by solving Cov(X,B) = 0, so

$$\mathrm{Cov}\left(X,B\right)=0$$

$$\left(1+c\right)\mathrm{Cov}\left(A,B\right)-\left(1-c\right)\mathrm{Cov}\left(B,B\right)=0$$

$$\left(\mathrm{Cov}\left(A,B\right)+\mathrm{Cov}\left(B,B\right)\right)c=\mathrm{Cov}\left(B,B\right)-\mathrm{Cov}\left(A,B\right)$$

$$c=\frac{\text{Var}\left(B\right)-\text{Cov}\left(A,B\right)}{\text{Var}\left(B\right)+\text{Cov}\left(A,B\right)},$$

which is well-defined if and only if $\text{Var}\left(B\right)\ne -\text{Cov}\left(A,B\right)$, that is, B is not equal to −A.

An equivalent expression for c is

$$c=\frac{1-\text{Cor}\left(A,B\right)\frac{{\sigma }_A}{{\sigma }_B}}{1+\text{Cor}\left(A,B\right)\frac{{\sigma }_A}{{\sigma }_B}}.$$

The term $\text{Cor}\left(A,B\right)\left({\sigma }_A/{\sigma }_B\right)$ corresponds to the slope of the linear regression of B on A. Thus, X is actually the distance between the data points in a 2-dimensional plane and their projection onto the linear regression line of A on B, rather than the vertical distance between the predicted value of A and the data point. This allows for error in the assessment of both A and B, rather than only measurement error in A. This is important because X is analyzed in a GWIS and the estimates for the association between both A and B and a SNP have a certain standard error.

We performed a GWIS of unique SCZ and a GWIS of unique BIP. For our analysis of unique SCZ and unique BIP in a GWIS, we included SNPs with information values between 0.9 and 1.1 as reported by Ruderfer et al. and minor allele frequencies larger than 0.05 (as obtained from the HapMap Consortium⁶). Both inclusion criteria reflect common practice in GWASs.¹⁶ We used LD score regression² to estimate genetic correlations between unique SCZ, unique BIP, and educational attainment. We checked that the genetic correlations were zero between unique BIP and SCZ and between unique SCZ and BIP by applying LD score regression. Further investigation suggests that unique BIP is, but unique SCZ is not, genetically correlated with educational attainment (Table 4). This suggests that the observed genetic correlation between schizophrenia liability and educational attainment is fully explained by its genetic correlation with bipolar disorder liability. We verify the correctness of our analysis by simulating a bivariate threshold model containing both genetic and environmental effects, where we show that substituting the logarithm of the odds-ratio is approximately correct for small SNP effect sizes. We also show that the unique traits are genetically uncorrelated.

Table 4.

Genetic Correlations between GWISs of Unique Schizophrenia, Unique Bipolar Disorder, and GWASs for Bipolar Disorder, Schizophrenia, and Educational Attainment

	Unique SCZ	Unique BIP	SCZ	BIP
Educational attainment	0.041 (0.082)	0.218 (0.102)	0.148 (0.050)	0.273 (0.067)
BIP	0.106 (0.110)	0.816 (0.031)	0.572 (0.063)	–
SCZ	0.882 (0.026)	−0.016 (0.101)	–	–

Genetic correlations along with their standard errors between schizophrenia, bipolar disorder, unique schizophrenia, unique bipolar disorder, and educational attainment. These correlations are obtained with LD score regression.

As shown by the replication of the BMI GWAS, GWIS provides an accurate approximation of GWAS summary statistics. GWIS can yield significant insight in the genetic architecture of phenotypes that can be expressed as (non-linear) function of phenotypes. This is demonstrated by the application of a GWIS to a function of bipolar disorder and schizophrenia, which decomposes these traits into a part that is shared between the two and a part that is unique to each of the traits. We have used this decomposition to show that it is likely that the genetic correlation between schizophrenia and educational attainment originates in the substantial genetic overlap between bipolar disorder and schizophrenia and the genetic correlation between bipolar disorder and educational attainment. However, GWISs have a more general domain of application. A GWIS can, for example, be performed for equations describing the steady-state kinetics of (bio-)chemical reactions involving metabolites of which the concentrations have been analyzed in a GWAS or for equations describing (active) membrane transport of proteins or metabolites given that GWAS summary statistics are available for their concentrations on both sides of the barrier. Another application of GWISs is increasing the effective sample size for the GWAS of a complex function. If not all constituent phenotypes have been measured in genotyped cohorts, these cohorts are excluded from the GWAS but can still contribute to a GWIS.

Successful application of a GWIS depends on the availability of sufficiently accurate GWAS summary statistics, the number of phenotypes involved in the function, as well as the degree of approximation. The accuracy of the summary statistics of each of the individual GWASs affects the accuracy of the GWIS results. Furthermore, the error of the GWIS statistics is likely to increase as more phenotypes are included, due to accumulation of the error in the GWAS results of each of these phenotypes. The degree of approximation used also affects the GWIS results, as the quadratic approximation of a function generally fits better than a linear approximation (see Appendix A for a quadratic approximation of BMI). As the number of GWASs increases, GWISs become applicable to a broader domain of functions. Increases in sample size allows GWISs to yield more accurate results. We note that our type I error analyses were based on BMI. We assume that these results will generalize to similar functions, but may require verification given more complex functions.

We recommend removing SNPs with low allele frequencies or poor imputation quality and SNPs available in a limited number of participants in the original GWASs (for height and weight) before performing GWIS. Although GWIS requires knowledge of the intercept of each linear regression of the original phenotypes on the SNP, substituting the population mean works reasonably well. Our simulations show that in the best case scenario, GWISs can be as powerful as GWASs. On the other hand, the empirical results for BMI show that GWIS remains a correct approximation of a GWAS, even when a very limited amount of information on the population parameters is available. A heuristic technique for performing a GWIS is available in the Web Resources.

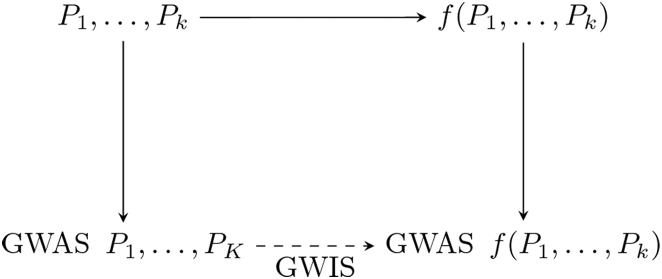
With these caveats in mind, however, our method provides a means of obtaining the GWAS summary statistics of a variable that is a function of phenotypes when GWAS summary statistics for these phenotypes are available in (not necessarily overlapping) samples, as outlined in Figure 4. This remains possible even when this variable is difficult or impossible to measure in individual participants. This shows that GWIS can yield significant insight in the genetic architecture of a large domain of phenotypes.

Figure 4.

A Schematic Representation of the Role of GWISs in Relation to Traditional GWASs

A GWIS provides a connection between several GWASs of phenotypes and a GWAS of a function of these phenotypes, without requiring access to the actual phenotypical data.

Published: September 8, 2016

Appendix A. A Second-Order Approximation of BMI

The second-order Taylor approximation of BMI is given by

$$Q_i=\frac{\mathbb{E}\left[W_i|S_i=s\right]}{\mathbb{E}{\left[H_i|S_i=s\right]}^2}+\frac{W_i-\mathbb{E}\left[W_i|S_i=s\right]}{\mathbb{E}{\left[H_i|S_i=s\right]}^2}+\frac{-2\mathbb{E}\left[W_i|S_i=s\right]\left(H_i-\mathbb{E}\left[H_i|S_i=s\right]\right)}{\mathbb{E}{\left[H_i|S_i=s\right]}^3}$$

$$+\frac{1}{2}\left(0+\frac{-4\left(W_i-\mathbb{E}\left[W_i|S_i=s\right]\right)\left(H_i-\mathbb{E}\left[H_i|S_i=s\right]\right)}{\mathbb{E}{\left[H_i|S_i=s\right]}^3}+\frac{6\mathbb{E}\left[W_i|S_i=s\right]{\left(H_i-\mathbb{E}\left[H_i|S_i=s\right]\right)}^2}{\mathbb{E}{\left[H_i|S_i=s\right]}^4}\right)$$

so that

$$\mathbb{E}\left[Q_i|S_i=s\right]=\frac{\mathbb{E}\left[W_i|S_i=s\right]}{\mathbb{E}{\left[H_i|S_i=s\right]}^2}-\frac{2\text{Cov}\left(W_i,H_i|S_i=s\right)}{\mathbb{E}{\left[H_i|S_i=s\right]}^3}+\frac{3\mathbb{E}\left[W_i|S_i=s\right]\text{Var}\left(H_i|S_i=s\right)}{\mathbb{E}{\left[H_i|S_i=s\right]}^4}.$$

Then, using this for our linear regression

$$\mathbb{E}\left[Q_i|S_i=s\right]={\lambda }_0+{\lambda }_{1}s$$

together with s = 0 gives

$$\widehat{{\lambda }_0}=\frac{{\beta }_{w0}}{{\beta }_{h0}^2}-\frac{2\text{Cov}\left(W,H\right)}{{\beta }_{h0}^3}+\frac{3{\beta }_{w0}\text{Var}\left(H\right)}{{\beta }_{h0}^4}$$

under the assumption that $\text{Cov}\left(W_i,H_i|S_i=s\right)=\text{Cov}\left(W,H\right)$ and a similar assumption for the variance of height. Then,

$$\begin{array}{l}\widehat{{\lambda }_1}=\frac{2q\left(1-q\right)}{2q\left(1-q\right)+q^2}\left(\frac{{\beta }_{w0}+{\beta }_{w1}}{{\left({\beta }_{h0}+{\beta }_{h1}\right)}^2}-\frac{2\text{Cov}\left(W,H\right)}{{\left({\beta }_{h0}+{\beta }_{h1}\right)}^3}+\frac{3\left({\beta }_{w0}+{\beta }_{w1}\right)\text{Var}\left(H\right)}{{\left({\beta }_{h0}+{\beta }_{h1}\right)}^4}-\left(\frac{{\beta }_{w0}}{{\beta }_{h0}^2}-\frac{2\text{Cov}\left(W,H\right)}{{\beta }_{h0}^3}+\frac{3{\beta }_{w0}\text{Var}\left(H\right)}{{\beta }_{h0}^4}\right)\right)\\ +\frac{1}{2}\cdot \frac{q^2}{2q\left(1-q\right)+q^2}\left(\frac{{\beta }_{w0}+2{\beta }_{w1}}{{\left({\beta }_{h0}+2{\beta }_{h1}\right)}^2}-\frac{2\text{Cov}\left(W,H\right)}{{\left({\beta }_{h0}+2{\beta }_{h1}\right)}^3}+\frac{3\left({\beta }_{w0}+2{\beta }_{w1}\right)\text{Var}\left(H\right)}{{\left({\beta }_{h0}+2{\beta }_{h1}\right)}^4}-\left(\frac{{\beta }_{w0}}{{\beta }_{h0}^2}-\frac{2\text{Cov}\left(W,H\right)}{{\beta }_{h0}^3}+\frac{3{\beta }_{w0}\text{Var}\left(H\right)}{{\beta }_{h0}^4}\right)\right)\end{array}$$

To demonstrate the usefulness of a second-order approximation, we perform type I error rate and power simulations for a GWIS based on the second-order approximation of BMI. The results in Table 1 indicate that a second-order approximation causes a significant increase in power for moderate samples sizes and moderate effect sizes, while not showing an increase in type I error rate.

Web Resources

• GIANT Consortium Data Files, http://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files

• GWIS, https://sites.google.com/site/mgnivard/gwis

• PGC summary statistics, https://www.med.unc.edu/pgc/results-and-downloads

• SSGAC (Rietveld et al. data), http://www.thessgac.org/data