How Well Can We Detect Lineage-Specific Diversification-Rate Shifts? A Simulation Study of Sequential AIC Methods

Abstract

Evolutionary biologists have long been fascinated by the extreme differences in species numbers across branches of the Tree of Life. This has motivated the development of statistical methods for detecting shifts in the rate of lineage diversification across the branches of phylogenic trees. One of the most frequently used methods, MEDUSA, explores a set of diversification-rate models, where each model assigns branches of the phylogeny to a set of diversification-rate categories. Each model is first fit to the data, and the Akaike information criterion (AIC) is then used to identify the optimal diversification model. Surprisingly, the statistical behavior of this popular method is uncharacterized, which is a concern in light of: (1) the poor performance of the AIC as a means of choosing among models in other phylogenetic contexts; (2) the ad hoc algorithm used to visit diversification models, and; (3) errors that we reveal in the likelihood function used to fit diversification models to the phylogenetic data. Here, we perform an extensive simulation study demonstrating that MEDUSA (1) has a high false-discovery rate (on average, spurious diversification-rate shifts are identified $\approx 30\%$ of the time), and (2) provides biased estimates of diversification-rate parameters. Understanding the statistical behavior of MEDUSA is critical both to empirical researchers—in order to clarify whether these methods can make reliable inferences from empirical datasets—and to theoretical biologists—in order to clarify the specific problems that need to be solved in order to develop more reliable approaches for detecting shifts in the rate of lineage diversification. [Akaike information criterion; extinction; lineage-specific diversification rates; phylogenetic model selection; speciation.]

Many evolutionary phenomena entail differential rates of diversification (speciation rate – extinction rate); adaptive radiation, diversity-dependent diversification, key innovations, and mass extinction. Phylogeny-based statistical methods have been developed to detect shifts in diversification rate through time, such as tree-wide shifts in diversification rate associated with episodes of mass extinction or adaptive radiation (Morlon et al. 2011; Stadler 2010; 2011; Höhna et al. 2015; May et al. 2016), or diversity-dependent decreases in diversification rate associated with ecological limits on speciation (Rabosky and Lovette 2008; Morlon et al. 2010; Etienne and Haegeman 2012; Etienne et al. 2012; Höhna 2014; Leventhal et al. 2014). Other methods seek to identify correlations between rates of diversification and some other variable, such as the evolution of discrete or continuous traits (Maddison et al. 2007; FitzJohn 2010) or episodes of biogeographic or climatic change (Moore and Donoghue 2009; Goldberg et al. 2011). Here, we focus on a third class of methods that seek to detect shifts in diversification rate along lineages of a phylogenetic tree (Moore et al. 2004; Chan and Moore 2005; Rabosky et al. 2007; Alfaro et al. 2009; Rabosky 2014).

The detection of lineage-specific diversification rates is often pursued using the approach proposed by Alfaro et al. (2009): Modeling Evolutionary Diversification Using Stepwise AIC (MEDUSA), implemented in the R (R Development Core Team 2009) package GEIGER (Pennell et al. 2014). The popularity of MEDUSA stems from several advantages it offers relative to alternative approaches: (1) rather than requiring complete species-level phylogenies, MEDUSA allows unsampled species to be included within unresolved terminal subclades; (2) rather than requiring the location of diversification-rate shifts to be specified a priori, MEDUSA agnostically evaluates diversification-rate shifts along all branches of the tree; (3) rather than assuming a pure-birth (Yule 1924) model (c.f., Chan and Moore 2005), MEDUSA is based on a more realistic birth-death model that accommodates extinction, and; (4) in addition to inferring the location(s) of diversification-rate shifts, MEDUSA also provides estimates of the diversification-rate parameters for each branch of the tree.

The statistical behavior of this popular method, however, is unknown. This is particularly disconcerting, as the use of the AIC for model selection has been shown to be problematic in other phylogenetic contexts (Alfaro and Huelsenbeck 2006; Boettiger et al. 2012), where it is biased toward overly complex models. Additionally, we demonstrate that the likelihood function used by MEDUSA to fit diversification models to the phylogenetic data is incorrect, which has the potential to impact the accuracy of parameter estimates and the reliability of the model-selection procedure. With these considerations in mind, we performed an extensive simulation study to characterize the statistical behavior of MEDUSA.

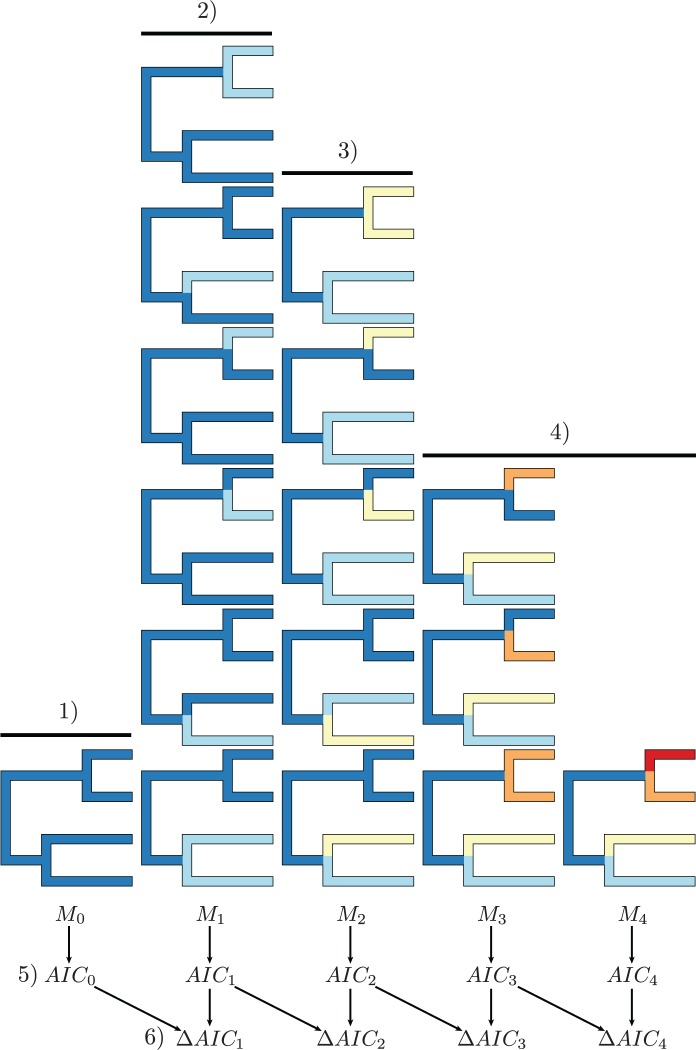
The MEDUSA algorithm.—MEDUSA begins by fitting a constant-rate birth-death process to an ultrametric phylogeny (i.e., where branch lengths and node heights are rendered proportional to time, and all species are contemporaneous) by means of maximum likelihood [using equation (3), detailed in the next section]. Each possible two-rate model—where a two-rate model includes a separate set of speciation- and extinction-rate parameters for a particular subclade of the tree—is then evaluated. If the difference in the AIC scores between the one-rate model and the best two-rate model exceeds a specified threshold ($\Delta {\text{AIC}}_{\text{crit}}$), the two-rate model is accepted. If the two-rate model is accepted, the process is repeated for each possible three-rate model. This procedure iteratively adds diversification-rate shifts to the phylogeny until additional diversification-rate shifts do not confer a sufficient improvement in the AIC score (Fig. 1). We provide a more detailed description of the MEDUSA algorithm in Section S1 of the Supplementary Material available on Dryad at http://dx.doi.org/10.5061/dryad.61q64.

Figure 1.

The MEDUSA algorithm. 1) The one-rate model, $M_0$, is first fit to the data using maximum likelihood. 2) Every possible two-rate model is then fit to the data, and the models are ranked by their likelihood score (with the best model, $M_1$, at the bottom). 3) Every possible three-rate model that is consistent with the best two-rate model is then fit to the data, and the models are ranked as in the previous step. 4) Step 3 is repeated for increasingly complex models until the most complex model has been evaluated. 5) The AIC score is computed for the best model in each index (i.e., with $0,1,\dots$ rate shifts). 6) The $\Delta$AIC value is calculated for each pair of adjacent models (as the difference in their AIC scores). Each of the $\Delta {\text{AIC}}_i$ comparisons are evaluated in succession, where the more complex model is selected if the computed $\Delta$AIC value exceeds some prespecified threshold, $\Delta {\text{AIC}}_{\text{crit}}$. This process continues until either the most complex model is accepted or the improvement in the AIC score is too small to exceed the $\Delta {\text{AIC}}_{\text{crit}}$ threshold.

There have been several versions of the MEDUSA algorithm that differ primarily in how they specify $\Delta {\text{AIC}}_{\text{crit}}$: the first version adopted a fixed (and conventional value) $\Delta {\text{AIC}}_{\text{crit}}$ of 4, whereas more recent versions of MEDUSA compute $\Delta {\text{AIC}}_{\text{crit}}$ based on the number of terminal lineages. In this article, we present results using the version of MEDUSA—available in the R package GEIGER (Pennell et al. 2014)—that we found to exhibit the best overall statistical behavior, which is also the version that has been used most frequently in empirical studies (we provide results for the other versions of the program in the Supplementary Material available on Dryad).

The Likelihood Function in MEDUSA is Incorrect

The likelihood function computes the probability of the data—typically a molecular phylogeny with estimated divergence times—given the parameters of the model. We assume the phylogeny, $\Psi$, with $k$ terminal lineages was generated by a birth-death process with a set of branch-specific speciation rates, $\lambda =\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{2k-2}\}$, and a vector of branch-specific extinction rates, $\mu =\{{\text{μ}}_1,{\text{μ}}_2,\dots ,{\text{μ}}_{2k-2}\}$, where ${\lambda }_i$ and ${\text{μ}}_i$ are the speciation and extinction rates for branch $i$, respectively.

The likelihood of observing the data is calculated piecewise (c.f., Rabosky et al. 2007). First, the function computes the likelihood of the internal branches, then computes the likelihood of the terminal lineages, and finally combines these two likelihoods. The probability density of observing an internal branch of length $t_i$ that arose at time $t_i^b$ used by MEDUSA is:

$$\begin{array}{l}P(t_i\mid {\lambda }_i,{\text{μ}}_i,t_i^b)=\frac{({\lambda }_i-{\text{μ}}_i)\exp (-({\lambda }_i-{\text{μ}}_i)t_i)}{1-\frac{{\text{μ}}_i}{{\lambda }_i}\exp (-({\lambda }_i-{\text{μ}}_i)t_i^b)}.\hfill \end{array}$$ (1)

The probability of observing terminal lineage $i$ with $n_i$ species, conditional on it having descendants at the present is

$$\begin{array}{lll}P(n_i\mid t_i^b,{\lambda }_i,{\text{μ}}_i)\hfill & =\hfill & \left(1-\frac{\exp (({\lambda }_i-{\text{μ}}_i)t_i^b)-1}{\exp (({\lambda }_i-{\text{μ}}_i)t_i^b)-\frac{{\text{μ}}_i}{{\lambda }_i}}\right)\hfill \\ \hfill & \hfill & \times {\left(\frac{\exp (({\lambda }_i-{\text{μ}}_i)t_i^b)-1}{\exp (({\lambda }_i-{\text{μ}}_i)t_i^b)-\frac{{\text{μ}}_i}{{\lambda }_i}}\right)}^{n_i-1}.\hfill \end{array}$$ (2)

Parsing the tree into $\mathcal{T}$ terminal lineages and $ℐ$ internal branches, the likelihood for the phylogeny and species richness data is calculated as

$$\begin{array}{l}P(\Psi \mid \lambda ,\mu )=\left({\displaystyle \prod _{i\in \mathcal{T}}P}(t_i\mid t_i^b,{\lambda }_i,{\text{μ}}_i)\right)\times \left({\displaystyle \prod _{i\in ℐ}P}(n_i\mid t_i^b,{\lambda }_i,{\text{μ}}_i)\right),\hfill \end{array}$$ (3)

as proposed by Rabosky et al. (2007).

This likelihood function, however, is incorrect in a number of ways. First, equation (1) is the probability density of the next birth event [equation (1)], rather than the probability density of an internal branch of length $t_i$. Second, it conditions on the survival of each of the terminal lineages. Typically, likelihoods under birth-death process models are conditioned on the survival of the entire process to the present (i.e., the total number of species present, $N$, must be greater than 0). The rationale for the condition is simple: if the process had not survived to the present, we would not have observed the tree. In the context of the present likelihood function, conditioning on the survival of every terminal lineage is different from conditioning on the survival of the entire process: in order for the process to survive, it is simply necessary that at least one terminal lineage survives, not that all terminal lineages survive.

This derivation of the likelihood function also suffers from a more fundamental—and more difficult—issue. Specifically, it requires that we are able to assign a set of speciation- and extinction-rate parameters to each lineage that arose during the evolution of the tree (extant or otherwise). Under a birth-death process, some lineages may go extinct before the present, and so are unobserved. Accordingly, it is not possible to coherently assign diversification parameters to extinct lineages. Consequently, this likelihood function implicitly assumes that diversification-rate shifts cannot occur along extinct lineages. When diversification-rate shifts occur along lineages that ultimately went extinct, the likelihood function will be incorrect. We discuss the provenance and derivation of these probability functions in more detail in Appendix.

Use of the AIC to Select Diversification Models may be Problematic

Use of the AIC to choose among models in other phylogenetic settings is known to be problematic (e.g.,Alfaro and Huelsenbeck 2006; Boettiger et al. 2012). Specifically, there is little theory to guide the specification of an appropriate critical threshold ($\Delta {\text{AIC}}_{\text{crit}}$) for preferring one model to another, and arbitrarily specified thresholds may strongly bias the model-selection procedure. Moreover, the AIC assumes that the sample size (in this case, the number of sampled lineages) is large. In practice, however, MEDUSA is generally applied to trees with a small number of incompletely sampled terminal lineages. Accordingly, the large sample size assumption of the AIC is apt to be violated, which may compromise the ability of MEDUSA to reliably choose the correct model.

Methods

Simulation Study

These considerations—regarding errors in the likelihood function and the reliability of the AIC as a means of selecting diversification models—motivated a simulation study to determine how well MEDUSA recovers the correct diversification-rate model under a variety of realistic conditions. All simulations were performed in R (R Core Team 2013) using the packages ape and TreeSim (Paradis et al. 2004; Stadler 2013); trees were subsequently manipulated with custom R scripts.

To ensure that our simulation study targeted an empirically relevant region of parameter space, we conducted a survey of all published studies that applied MEDUSA to empirical trees (Table S1 available on Dryad). From these empirical studies, we summarized relevant metadata, including: (1) the total number of species encompassed by the phylogeny (regardless of whether they were actually sampled), $N$; (2) the number of terminal lineages (i.e., unresolved subclades) included in the phylogeny, $k$, and; (3) speciation- and extinction-rate estimates provided by MEDUSA. We then designed our simulation study to reflect the characteristics of empirical MEDUSA studies (Fig.S2 available on Dryad).

We simulated constant-rate trees with a fixed speciation rate, $\lambda =0.01$, under various extinction rates, $\text{μ}=\lambda \times \{0,0.1,\dots ,0.9\}$, and of various sizes, $N=\{100,1000,10,000\}$. We simulated 1000 trees for each combination of these settings, and then collapsed each tree to various numbers of terminal lineages, $k=\{10,15,20,25,30,40,100\}$, by retaining the oldest $k-1$ nodes and assigning the pruned species to their corresponding terminal lineages; this protocol is equivalent to the “diversified-sampling” strategy described by Höhna et al. (2011). We then analyzed each tree with MEDUSA. For each analysis, we recorded(1) whether a rate shift was inferred, and; (2) the parameter estimates under the preferred diversification model. We computed the false-discovery rate as the fraction of analyses that inferred at least one diversification-rate shift. For analyses that correctly selected the constant-rate model, we computed the bias for each diversification-rate parameter as the estimated value divided by the true value. When MEDUSA incorrectly rejected the constant-rate model, we computed the magnitude of the inferred diversification-rate shift as the “derived rate” (i.e., the net-diversification-rate estimated for the subclade that experienced the diversification-rate shift) divided by the “initial” net-diversification rate (i.e., estimated for the remainder of the tree); $\delta =r_{\text{shift}}/r_{\text{initial}}$. We performed a pilot study to determine the number of replicate simulations required to ensure precise estimates of the false-discovery rate, which indicated that 500 replicate simulations were sufficient to ensure negligible Monte Carlo error (results not shown). To be conservative, we based our inferences regarding the statistical behavior of MEDUSA on 1000 replicate simulations for each unique parameter combination that we explored in our study.

We also performed additional simulations to comprehensively explore the parameter space defined by our empirical survey, and used multiple versions of the MEDUSA algorithm to accommodate implementation-specific effects. Overall, the results of these simulations are qualitatively and quantitatively similar to the simulation study described above; we refer the reader to the Supplementary Material available on Dryad for detailed descriptions (and results) of these additional simulation experiments.

Results

We focus on two primary aspects of the statistical behavior of MEDUSA: (1) the propensity to identify spurious diversification-rate shifts (i.e., the false-discovery rate), and; (2) the accuracy of diversification-rate parameter estimates (i.e., the estimator bias).

MEDUSA has a High False-Discovery Rate

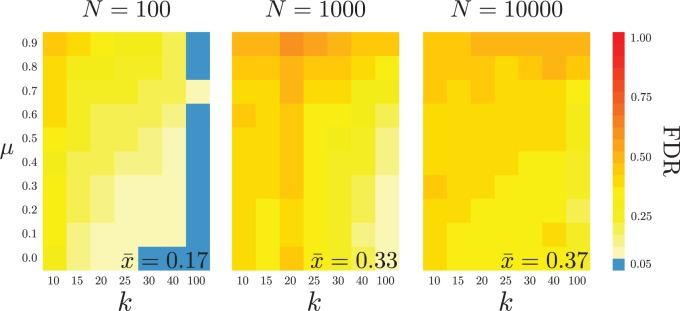
The overall false-discovery rate (FDR)—calculated as the unweighted average overall of simulated trees—is $29\%$ (Fig. 2), which is $\approx 6$ times higher than the nominal significance level, $\alpha =0.05$. Additionally, the FDR increases as the proportion of the species in unresolved terminal clades increases; in fact, when there are no unresolved clades (i.e., $k=N$; Fig. 2, left panel, right column), the false-discovery rate is approximately $5\%$. The FDR appears relatively insensitive to the true extinction rate, $\text{μ}$, although higher extinction rates tend to have higher FDR, on average. These patterns are consistent with violation of the large-sample assumptions of the AIC driving the inflated false-discovery rate: as $k$ decreases, the sample size decreases, exacerbating the bias toward overly complex models.

Figure 2.

False-discovery rate. We simulated constant-rate trees with a fixed speciation rate, $\lambda =0.01$, under various extinction rates, $\text{μ}=\lambda \times \{0,0.1,\dots ,0.9\}$ ($y$-axis), and of various sizes, $N=\{100,1000,10,000\}$ (left to right panels). We simulated 1000 trees for each combination of these settings, and then collapsed each tree to various numbers of terminal lineages, $k=\{10,15,20,25,30,40,100\}$ ($x$-axis of each panel), by retaining the oldest $k-1$ nodes and assigning the pruned species to their corresponding terminal lineages. We then analyzed each tree with MEDUSA, and recorded the fraction of trees in which at least one diversification-rate shift was inferred (the false-discovery rate; FDR).

MEDUSA Provides Biased Parameter Estimates

The ability of MEDUSA to estimate parameters of the birth-death process represents an important advantage over competing methods. This allows users to not only identify the number and phylogenetic distribution of diversification-rate shifts, but also to estimate the magnitude of corresponding changes in the speciation and extinction rates. Accordingly, even if—as we have demonstrated above—MEDUSA does not provide reliable estimates of the number and location of diversification-rate shifts, it may nevertheless prove useful for estimating parameters of the birth-death process. Moreover, if most of the spurious diversification-rate shifts are inferred to involve relatively minor shifts in diversification rate, then it might be possible to use the diversification-rate parameter estimates to distinguish between spurious and bonafide diversification-rate shifts. We focus on estimates of the net-diversification rate, $r=\lambda -\text{μ}$, as this compound parameter is expected to be considerably easier to estimate compared to the speciation and extinction rates (Kubo and Iwasa 1995; Rabosky et al. 2007). Our results agree with this expectation; estimates of the relative-extinction rate, $\text{μ}/\lambda$, are more severely biased than are estimates of the the net-diversification rate (see Supplementary Material available on Dryad).

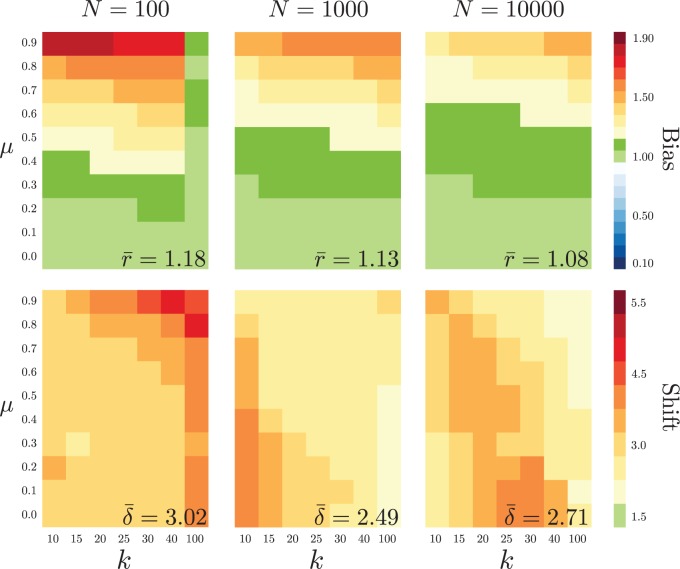
Our simulation study reveals that—even when MEDUSA selects the correct (constant-rate) model—the net-diversification rate estimate is $1.13$ times the true value, on average (Fig. 3, top row). As with the false-discovery rate, this bias is exacerbated as $k$ decreases. The severity of the bias also increases as the true extinction rate, $\text{μ}$, increases. When MEDUSA incorrectly selects a two-rate model, it infers a 2.7-fold change in the net-diversification rate, on average (Fig. 3, bottom row), with the upper 95% quantile of diversification-rate shifts entailing 7.7-fold increases in the net-diversification rate. Thus, when MEDUSA incorrectly identifies a diversification-rate shift, the magnitude of the spurious diversification-rate shifts is apt to be large.

Figure 3.

Parameter estimates. We simulated constant-rate trees and analyzed them as described in Figure 2. We binned the trees into categories: (1) where the (correct) constant-rate model was selected (top row), and; (2) where the constant-rate model was rejected (bottom row). Top row: We computed the bias in the estimated net-diversification rate, $r=\lambda -\text{μ}$, as $r_{\text{estimated}}/r_{\text{true}}$. Bottom row: We computed the magnitude of inferred diversification-rate shifts, $\delta$, as the estimated net-diversification rate for the subclade with the shift divided by the estimated net-diversification rate for the remainder of the tree, $\delta =r_{\text{shift}}/r_{\text{initial}}$.

Dicussion

The Statistical Behavior of MEDUSA

Biologists are clearly interested in identifying shifts in diversification rate across lineages, and have enthusiastically embraced MEDUSA as an approach for addressing this problem (Table S1 available on Dryad). Nevertheless, our simulation study reveals that MEDUSA is unreliable. For almost 30% of the trees that we simulated in our study—where rates were strictly constant across lineages of the tree—MEDUSA identified strong support for one or more diversification-rate shifts. This result applies to all versions of the algorithm (see Supplementary Material available on Dryad), and holds over a wide range of absolute parameter values that broadly encompass the conditions encountered in the analyses of actual empirical data sets (Table S1, Fig. S2 available on Dryad).

MEDUSA also provides biased estimates of diversification-rate parameters. Even when MEDUSA correctly identified the (true) constant-rate model, the net-diversification estimates were on average $1.13$ times their true values (Fig. 3, top row; see also Table S3 available on Dryad), and the relative-extinction rate estimates were on average $0.20$ times their true values (Table S4 available on Dryad). Similarly, when MEDUSA identified the (incorrect) multi-rate model, the spurious diversification-rate shifts were inferred to involve large rate shifts. On average, spurious diversification-rate shifts were estimated to involve a $2.7$-fold shift in net-diversification rate (Fig. 3, bottom row; see also Table S5 available on Dryad), with a large spread of values (the upper $95\%$ quantile had an average 7.7-fold shift in net-diversification rate, Table S6 available on Dryad). Similarly, these spurious diversification-rate shifts were estimated to entail an average $3.1$-fold shift in relative-extinction rate (Table S7 available on Dryad), with a correspondingly large spread of values (the upper $95\%$ quantile had an average 6.7-fold shift in relative-extinction rate, Table S8 available on Dryad).

Prospects for Addressing the $\Delta$AIC Threshold in MEDUSA

The high false-discovery rate exhibited by MEDUSA stems from: (1) the use of an arbitrary $\Delta {\text{AIC}}_{\text{crit}}$ threshold (the improvement in model fit necessary to justify selecting a more complex model), and; (2) the comparison of a large number of alternative diversification models. The earliest applications of MEDUSA iterated over several fixed values $\Delta {\text{AIC}}_{\text{crit}}$ to assess the sensitivity of biological inferences to this arbitrary threshold (c.f., Alfaro et al. 2009), but generally interpreted results for a fixed $\Delta {\text{AIC}}_{\text{crit}}$ of 4, a conventional threshold value advocated by Burnham and Anderson (2003). Recent versions of MEDUSA address multiple-testing concerns by computing the $\Delta {\text{AIC}}_{\text{crit}}$ threshold based on the number of terminal lineages, $k$, in the observed phylogeny, which is directly related to the number of models being compared. The function relating the number of lineages to $\Delta {\text{AIC}}_{\text{crit}}$ was derived from a simulation study performed with completely sampled (i.e., $k=N$), constant-rate birth-death trees (Pennell et al. 2014). As a result, the false-discovery rate is acceptable when $k=N$ (Fig. 1).

Unfortunately, the complex relationship between the false-discovery rate and aspects of the data ($N$, $k,\lambda$, and $\text{μ}$) displayed in Figure 1 makes it clear that multiple testing is not the sole pathology, and that there is no generic solution for specifying a value for $\Delta {\text{AIC}}_{\text{crit}}$ that will ensure appropriate statistical behavior. Fortunately, Monte Carlo simulation has proven to be an effective solution to similar problems (c.f., Moore et al. 2004; Boettiger et al. 2012), and we are optimistic that such a solution could be incorporated in the MEDUSA framework. However, developing an efficient and reliable Monte Carlo solution to this problem is nontrivial, and is an area for future work.

Prospects for Resolving Issues with the Likelihood Function of MEDUSA

We identified three issues with the MEDUSA likelihood function derived by Rabosky et al. (2007). First, the likelihood function uses an incorrect probability density for internal branches [equation (1)]; we provide the correct equation in the Appendix, equation (A.6). Second, the likelihood function incorrectly conditions on the survival of the process. In lieu of a stochastic model that explicitly describes diversification-rate shifts (see below), it may be more reasonable not to condition on survival. However, the consequences of removing this incorrect condition—e.g., on parameter estimates—are unknown.

The third—and more challenging—issue is the inability to account for diversification-rate shifts along lineages that ultimately go extinct. In order to accommodate these unobserved diversification-rate shifts, we must be able to compute the probability that a diversification-rate shift occurred along an extinct lineage, which in turn requires a model that describes how diversification-rate shifts occur through time and across (extant or extinct) lineages of the tree. MEDUSA, however, does not explicitly model the occurrence of diversification-rate shifts. Instead, MEDUSA compares a very explicit set of diversification-rate models while remaining agnostic about how the diversification-rate shifts arise (i.e., the diversification-rate shifts themselves are not described as events that occur with some probability). In the absence of a formal stochastic model of the diversification process, it is unclear how to accommodate diversification-rate shifts along extinct lineages within the MEDUSA framework. It is possible that a Monte Carlo approach using a rate-shift model (e.g., where rate shifts occur as a continuous-time Markov process along lineages, similar to the compound Poisson process model implied by BAMM;Rabosky 2014) could be devised to account for diversification-rate shifts along extinct lineages, but the feasibility and general applicability of such an approach requires further study.

Conclusions

In summary, many of the advances that make MEDUSA an attractive approach for detecting rate shifts appear to be problematic. For example, the ability to accommodate incompletely sampled trees with MEDUSA is a useful feature of the method. In fact, most applications ($82.5\%$) of this method involve incomplete trees. Nevertheless, the pathological behavior of MEDUSA is most extreme under these conditions (Fig. 2). Likewise, the adoption of a birth-death model is presented as an important advantage of MEDUSA over competing methods that do not accommodate extinction. However, (relative) extinction-rate estimates obtained using MEDUSA are extremely unreliable (Table S4 available on Dryad). This finding is relevant to the general debate regarding whether (relative) extinction rates can be reliably estimated from phylogenies (Rabosky 2010; Pyron and Burbrink 2013).

The primary conclusion of our simulation study—that the MEDUSA approach is unreliable—might be viewed as a “negative” result. After all, our findings cast considerable doubt on the conclusions of the many empirical studies that have used MEDUSA, and argue strongly against the application of this approach in future empirical studies. Nevertheless, we believe that it is important to be aware of the limitations of a method if it is likely to provide spurious results. Moreover, beyond demonstrating that MEDUSA is unreliable, the results of our simulation study provide insights into the reasons why the method is unreliable. Understanding the nature of these problems can focus theoretical efforts to develop more reliable methods. Accordingly, far from discouraging, we view the findings of this study as cause for optimism. We are hopeful that future efforts will resolve issues afflicting the MEDUSA framework for identifying diversification-rate shifts that—coupled with rigorous evaluation of these new methods—will continue to enhance our ability to explore a broad range of fundamental evolutionary processes.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.61q64.

Funding

This research was supported by National Science Foundation (NSF) [grants DEB-0842181, DEB-0919529, DBI-1356737, and DEB-1457835 awarded to BRM]. Computational resources for this work were provided by NSF XSEDE [grant TG-DEB140025].

Appendix 1

The likelihood functions used by MEDUSA are based on equations derived in Rabosky et al. (2007). For completeness, we present those equations and the equations from which they were derived. We note that these probabilities are not formally derived for a birth-death process model that allows among-lineage rate variation. Instead, these probabilities are derived for constant-rate birth-death processes, and then (incorrectly) applied to a variable-rate birth-death process by simply substituting different speciation and extinction rates for different branches of the tree.

Rabosky et al. (2007) derived equation (1) from Nee et al. (1994), equation (17), which is (substituting our notation):

$$\begin{array}{lll}P(t_i\mid n,\lambda ,\text{μ},t_i^b)\hfill & =\hfill & n(\lambda -\text{μ})\exp (-n(\lambda -\text{μ})t_i)\hfill \\ \hfill & \hfill & \times \frac{{(1-\frac{\text{μ}}{\lambda }\exp (-(\lambda -\text{μ})t_i))}^{n-1}}{{(1-\frac{\text{μ}}{\lambda }\exp (-(\lambda -\text{μ})t_i^b))}^n},\hfill \end{array}$$ (A.1)

where $n$ is the number of species alive at time $t_i^b$. For the special case in which $n=1$ (i.e., we consider a single branch that starts with a single species), the above equation simplifies to

$$\begin{array}{l}P(t_i\mid \lambda ,\text{μ},t_i^b)=\frac{(\lambda -\text{μ})\exp (-(\lambda -\text{μ})t_i)}{1-\frac{\text{μ}}{\lambda }\exp (-(\lambda -\text{μ})t_i^b)}.\hfill \end{array}$$ (A.2)

Allowing the rates of speciation and extinction on branch $i$ to be ${\lambda }_i$ and ${\text{μ}}_i$ produces equation (1). We note that, in its original context, this equation describes the probability density of times between birth events, rather than of internal branches of particular lengths. We describe the correct equation in the following section.

Kendall (1949) derived the probability of realizing $n$ species from a single species that starts at time $t_i^b$, which is [substituting our notation into his equation (21)]:

$$\begin{array}{lll}P(n\mid t_i^b,\lambda ,\text{μ})\hfill & =\hfill & \left(1-\frac{\text{μ}}{\lambda }\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)\hfill \\ \hfill & \hfill & \times \left(1-\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)\hfill \\ \hfill & \hfill & \times {\left(\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)}^{n-1},\hfill \end{array}$$ (A.3)

which is equivalent to equation (A17) in Raup (1985)and equation (8.46) from Bailey (1964). Conditioning probability (A.3) on the survival of the clade, which happens with probability

$$\begin{array}{ll}P(n>0\mid t_i^b,\lambda ,\text{μ})=\hfill & \left(1-\frac{\text{μ}}{\lambda }\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)\hfill \end{array}$$ (A.4)

gives

$$\begin{array}{lll}P(n\mid t_i^b,\lambda ,\text{μ})\hfill & =\hfill & \left(1-\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)\hfill \\ \hfill & \hfill & \times {\left(\frac{\exp ((\lambda -\text{μ})t_i^b)-1}{\exp ((\lambda -\text{μ})t_i^b)-\frac{\text{μ}}{\lambda }}\right)}^{n-1}.\hfill \end{array}$$ (A.5)

Again, allowing rates of speciation and extinction for clade $i$ to be ${\lambda }_i$ and ${\text{μ}}_i$ produces equation (2).

The Probability Density of an Internal Branch

Following Stadler (2010), the probability density of a branch of length $t_i$ is:

$$\begin{array}{l}P(t_i\mid \lambda ,\text{μ},t_i^b)=P(1\mid t_i^b,\lambda ,\text{μ})/P(1\mid t_i^e,\lambda ,\text{μ}),\hfill \end{array}$$ (A.6)

where $t_i^e$ is the time at the end of the branch, and $P(1\mid t,\lambda ,\text{μ})$ comes from equation (A.5).