Abstract
C60 fullerene crystals may serve as important catalysts for interstellar organic chemistry. To explore this possibility, the electronic structures of free-standing powders of C60 and (C59N)2 azafullerenes are characterized using X-ray microscopy with near-edge X-ray adsorption fine structure (NEXAFS) spectroscopy, closely coupled with density functional theory (DFT) calculations. This is supported with X-ray photoelectron spectroscopy (XPS) measurements and associated core-level shift DFT calculations. We compare the oxygen 1s spectra from oxygen impurities in C60 and C59N, and calculate a range of possible oxidized and hydroxylated structures and associated formation barriers. These results allow us to propose a model for the oxygen present in these samples, notably the importance of water surface adsorption and possible ice formation. Water adsorption on C60 crystal surfaces may prove important for astrobiological studies of interstellar amino acid formation.
Membrane production is considered to be one of the critical steps in the formation of amino acids in the interstellar medium, and ultimately to the earliest stages of life1. However, the molecular interactions between carbon, nitrogen and oxygen in space remain enigmatic. Recent studies from the Spitzer radio telescope2 have identified large amounts of crystalline C60 in interstellar outflows. Midinfrared bands at 7.0, 8.5, 17.4 and 19.0 μm match those for neutral C603,4, which has been suggested as a candidate for templating simple nucleobases in interstellar environments5. C60 crystal surfaces are a potential interstellar reaction membrane candidate; thus detailed characterization of the surface chemistry of fullerene crystal surfaces is required. However, quantitative analysis of spectroscopy data is complicated due to the potential ambiguity caused by carbonaceous impurities. For this reason it would be advantageous to also consider fullerene structures containing chemical markers, such as heterofullerenes.
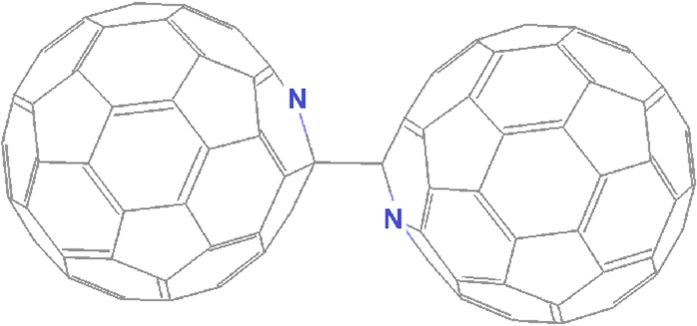
Amongst heterofullerenes, the best-known and most studied species are the nitrogen-substituted azafullerenes, notably the mono aza[60]fullerene (C59N)6,7,8,9,10,11,12,13,14, where a single carbon atom is replaced by nitrogen. The resultant carbon radical is stabilized by forming an intermolecular sp3-like bond with a similar radical carbon in a neighboring azafullerene, with a predicted binding energy on the order of 0.65 eV15. Thus the preferred structure at room temperature or below is the (C59N)2 dimer (Fig. 1)16. Little is known about the spontaneous oxidation behavior of azafullerenes as compared to C6017, and even the nature and origin of C60 oxidation itself upon exposure to air remains controversial18,19.
Figure 1. Structure of the azafullerene dimer (C59N)2.
Here we investigate the spectroscopic fingerprint of suspended clusters of C60 and (C59N)2 using near-edge X-ray adsorption fine structure (NEXAFS) spectroscopy and X-ray photoelectron spectroscopy (XPS) combined with a range of density functional theory (DFT) modeling approaches.
Previous near-edge X-ray adsorption fine structure (NEXAFS) spectroscopy studies of fullerenes have relied on thin film samples deposited on surfaces20,21,22. However, during fullerene film preparation, the thermal evaporation step can influence the formation as well as the interaction of the film with the substrate surface, especially in the case of azafullerenes. In addition, surface contamination can have a strong impact on NEXAFS spectra. For this reason, for the NEXAFS analysis, the azafullerene and fullerene powders were sonically dispersed in ethanol, and a drop of each solution was deposited onto lacey carbon films supported on copper transmission electron microscopy (TEM) grids. This allows us to study indirectly supported material located above holes in the lacey carbon film grid, avoiding the interaction of the measured sample region with the substrate.
We model the structures, possible oxidation products and pathways, and simulate spectra of pristine and oxidized fullerene and azafullerene species. Collectively these results allow us to establish a detailed picture of the morphology, electronic structure, and chemistry of these materials, notably including their interaction with water and other oxygen impurities.
Results and Discussion
NEXAFS Spectroscopy
Before considering the interaction between oxygen and fullerenes, we first properly characterize the carbon and nitrogen spectroscopic signatures of C60 and (C59N)2.
The experimental and theoretical carbon 1s spectra of C60 and a projection of the theoretical spectrum onto p-components either orthogonal (π*) or tangential (σ*) to the C60 cage surface are shown in Fig. 2. The spectrum is characterized by discrete peaks, and in general there is excellent agreement between theory and experiment, both for peak separations and intensities. Our experimental spectrum of C60 is very similar to those reported previously in the literature14,21,23,24. In order to account for electron-hole interactions we introduced a core-hole in the C 1s orbital of the excited carbon atom. Figure 2 shows the effect of removing either 0 (“initial state”), 0.5 (“Slater transition state”25) or 1 (“final state”) electron from this 1s (C) core orbital (panels a–c, respectively). The best agreement comes from the half core-hole approximation (Fig. 2b), which is used in the rest of our study.
Figure 2. Carbon 1s spectrum of C60.
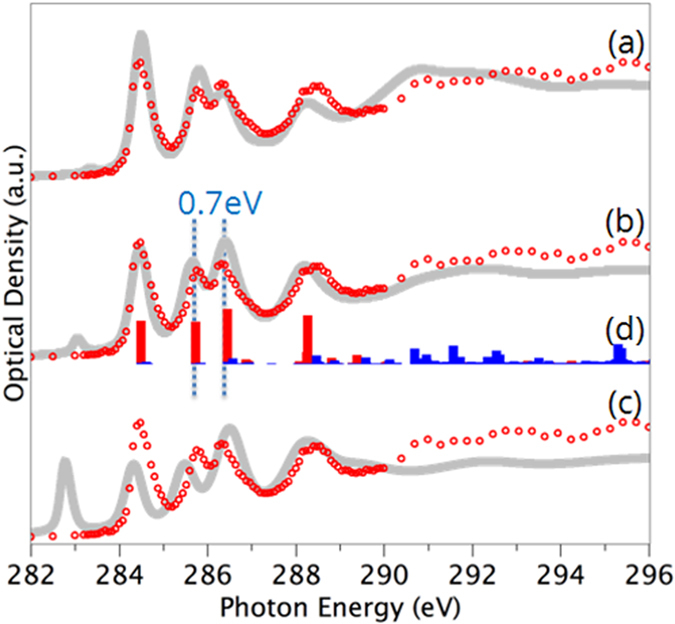
The experimental scanning transmission X-ray microscopy (STXM) data is plotted in red circles while the calculated spectra are gray lines. Calculations were performed with (a) full-core hole (final state), (b) half-core hole (Slater transition state) and (c) zero-core hole approximation (initial state). (d) Breakdown of calculated spectrum into π* (red) and σ* (blue) components.
The spectral decomposition in Fig. 2d reveals that the peaks in the low energy range (284–289 eV) have C 1s excitation to final states of π* character, while the higher energy spectral features are due to C 1s excitation to final states of σ* character. Specific σ* peaks seen in the experimental spectrum from 290–296 eV stand out clearly in the theoretical spectrum decomposition. From this analysis, the first three peaks below 287 eV are assigned to C 1s excitations to the four degenerate π* molecular orbitals t1u, t1g, t2u and ag, where the latter two are energetically very close26. The last peak at 288.5 eV also corresponds to an ag orbital27. We note that the small pre-peak seen in the modeling at around 283 eV is a screening artifact introduced by the half core-hole approximation28,29 as can be seen by its absense in the full core-hole data. Earlier GGA full core-hole modelling also gave good agreement to experiment29, with some variation from our calculated spectra (see Supplementary Information), notably in peak spacings, probably due to differences in basis set construction (the previous study including reduced four-electron effective core potentials for all non-excited carbon atoms, and non-diffusive basis sets for minimization with added diffuse functions for the static exchange Hamiltonian).
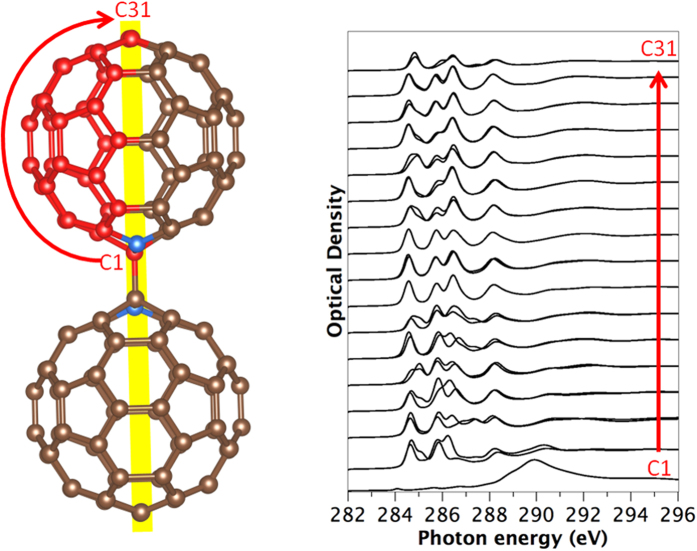
We next turn to the C 1s spectrum of (C59N)2. The symmetry breaking from nitrogen substitution and fullerene dimerization means there are now 31 symmetrically inequivalent carbon sites, and it is necessary to calculate the spectrum for each of these (Fig. 3). There are 28 inequivalent carbon sites with a multiplicity of four and 3 with multiplicity of two (these lie on the central mirror plane marked in yellow). Of these three, site C1 corresponds to the sp3 4-fold coordinated atoms covalently linking the two fullerene cages together, which is clearly visible in its associated spectrum which lacks the π* related peaks from 284–288 eV.
Figure 3. Calculated carbon 1s spectra using the Slater transition state, of (C59N)2 azafullerene for the symmetry inequivalent carbon atoms C1 to C31.
Atom colors: Blue: Nitrogen, Red: inequivalent C atoms, Brown: other carbon atoms.
If we now average these spectra using the appropriate weighting from their multiplicity, we obtain the averaged calculated spectrum, which is shown in Fig. 4 in comparison to the experimental C 1s spectrum of (C59N)2 measured by scanning transmission X-ray microscopy (STXM). Our experimental spectrum of (C59N)2 is very similar to those reported previously in the literature14,20,22. The experimental C 1s spectrum of (C59N)2 is in general very similar to that of C60, apart from additional broadening of the spectral features, notably around 286 eV. These are accurately reproduced by the calculations. This indicates that the perturbation induced by the nitrogen atoms is not very strong, and that the two extra electrons of (C59N)2 in comparison with C60 do not lead to significant occupation of the C-derived low-lying unoccupied states of C60.
Figure 4. Carbon 1s spectrum of (C59N)2.
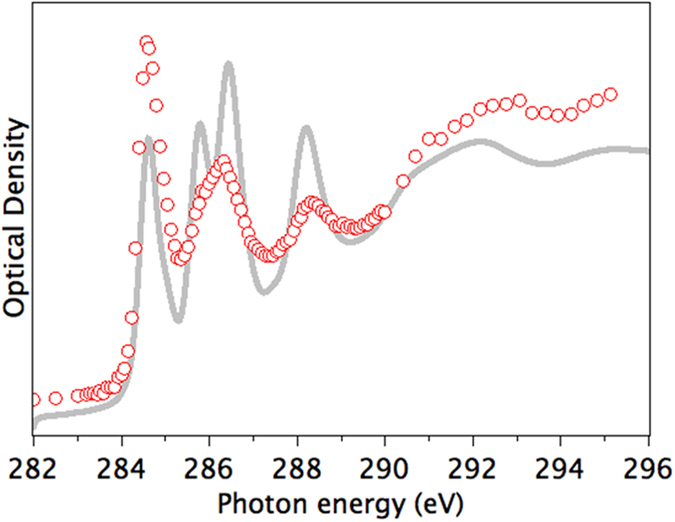
Experimental STXM data in red circles, calculated spectrum using the Slater transition state in gray is a weighted sum of individual atom spectra shown in Fig. 3.
The nitrogen 1s spectrum of (C59N)2 is shown in Fig. 5. It exhibits a primary component centered at 401.5 eV and a larger, broader feature at 406 eV consistent with nitrogen neighboring sp3-coordinated carbon30. When compared to the N 1s spectrum of (C59N)2 reported by Schulte et al.14 there is considerable disagreement, in particular the separation of the two main peaks is different (4.8 eV in this work, 5.2 eV in ref. 14) and there is a major difference in the width and relative intensity of the first peak which can not be explained by instrumental differences. In particular the N 1s spectrum of (C59N)2 reported by Schulte et al.14 has a rather sharp peak at 401.5 eV (fwhm ~1 eV), whereas the corresponding feature on our spectrum is much broader (fwhm ~2 eV). We explored the possibility the signal in the Schulte et al. spectrum14 could be from trapped gaseous N2. Subtraction of N2 gas signal to remove this sharp peak does result in a much broader first peak, closer to that we have measured, but there is still a poor match to our result.
Figure 5. N 1s spectra of (C59N)2 azafullerene.
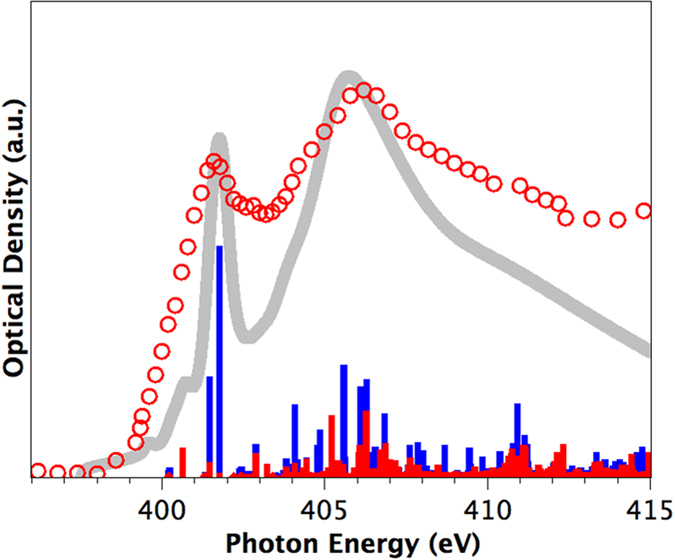
Experimental STXM data in red circles, calculated spectrum using the Slater transition state in gray, projection of calculated spectrum into π* (red) and σ* (blue) components.
By contrast good agreement is found between our measured and calculated N 1s spectra, notably in the features in the extended σ* states and the low energy shoulder to the 401.5 eV peak. We note that our theoretical and experimental data correctly reproduces the key spectral features found in a recent simulated (C59N)2 NEXAFS N 1s spectrum31, including primary peak spacings and the presence of the small pre-peak shoulder. This gives us additional confidence in our results
A key difference between the N 1s and C 1s spectra is that while the primary C 1s peak has strong π* character, the primary N 1s peak is mainly σ* in character. This is consistent with previous findings for EELS spectroscopy of nitrogen doping in single-walled carbon nanotubes28. In the current study we can see however that some π* character is responsible for the low energy shoulder of this peak, due to slight deviation from full tetrahedral configuration imposed by the fullerene cage environment.
The spectroscopic influence of nitrogen substitution in the fullerene cage is twofold: first, the stronger core potential offered by the nitrogen atom manifests itself in a low-binding energy shoulder split-off from the highest occupied molecular orbital (HOMO), carrying significant nitrogen character32. This is, however, not to be associated with simple filling of the lowest unoccupied molecular orbital (LUMO) of the C60, as the excess electronic charge stays relatively localized on the nitrogen sites. The substitutional nitrogen atom in C59N is sp3-bonded, i.e. forms three σ bonds with its carbon neighbors, with its remaining two valence electrons forming a stable lone pair. This means the loss of a π bond in the associated hexagon-hexagon double bond, creating a neighboring carbon radical with an unpaired pz-electron. The carbon radicals of neighboring cages combine to form a σ bond between them. Thus, in terms of bonding, the conversion from C60 to (C59N)2 involves the elimination of only one π bond per fullerene, and some structural modification of nearby σ bonds around the substitutional and cross-linking sites (Supplementary Figure 3).
The heteroatom introduces changes to the electronic structure of the fullerene cage, observed as spectral broadening and the appearance of two structures in between the three highest valence band peaks in photoemission32. As compared to the energy gap of C60 (∼1.86 eV), the energy gap between occupied and unoccupied states is smaller in (C59N)2 at 1.4 eV (ref. 22).
To summarise this section, we find good agreement between theory and experiment for the C 1s and N 1s spectra of C60 and (C59N)2. Small differences in peak positions and intensity are observed between these two species, caused by the relatively localised disruption to the fullerene bonding in the azafullerene dimer. While the first peak in the C 1s spectrum has π* character, in the N 1s spectrum this peak has primarily σ* character with a small low energy π* shoulder. It should be noted that the use of a statically screened electron-hole interaction via the Slater transition state allows accurate reproduction of the present NEXAFS data for both C60 and (C59N)2. Additionally, such an approach means that for the carbon 1s spectrum for (C59N)2, a weighted spectrum based on 31 half core-hole spectra for each inequivalent carbon site can be determined, allowing analysis of the contribution of each carbon atom to the resulting experimental spectrum. This demonstrates that while the static approach does not allow an explicit treatment of core-hole interactions, it is nonetheless a very powerful tool for the analysis of complex spectra.
X-Ray Photoelectron Spectroscopy
The discussion thus far has concerned the quantitative agreement between modeling and spectroscopy for C 1s and N 1s NEXAFS spectra. We next compare calculated C 1s and N 1s core level binding energies to those measured with XPS. An absolute energy comparison is essential to understand the interactions between molecules and (aza)fullerenes.
We find that although carbon atoms near the nitrogen site(s) do exhibit different calculated C 1s energies than those from pristine “bulk” C60, the binding energies are less than 40 meV higher already for next-nearest neighbors away from the N. Thus while the experimental C 1s spectrum is in theory a convolution of several peaks, within the experimental accuracy it is well described by the bulk value. For the dimer, we obtained N 1s–C 1s energy separations of 115.65 eV (ΔSCF) and 115.73 eV (ΔKS), in excellent agreement to our experimentally measured separation of 115.5 eV. This demonstrates the strength of this approach for the quantitative determination of relative core-level energies, with the ΔSCF method featuring the additional benefit of having the same atomic reference energies for both the N 1s and C 1s calculations.
We note further that although it is not experimentally accessible due to dimerization, the calculated N 1s–C 1s energy separation for the single C59N radical is 116.10 eV, implying that the interaction in the dimer lowers the N 1s level by about 0.4 eV (with the Kohn-Sham eigenvalues approximating the initial state energies showing a slightly larger difference of 0.7 eV). This is presumably due to slight differences in the chemical environment of the N atom and core-hole screening in the two systems.
Calculated Interaction with Atomic Oxygen Species
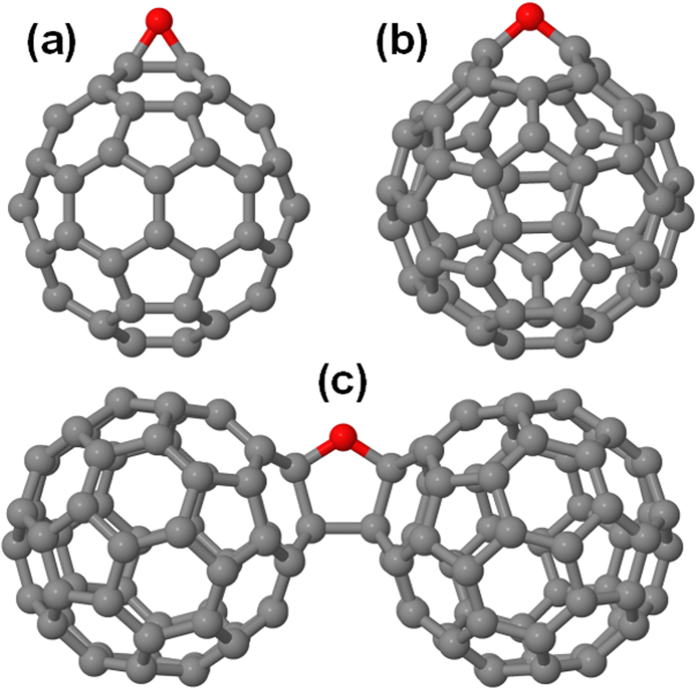
We next turn our attention to the nature of oxygen contamination in fullerene and azafullerene samples, which remains an open question in the literature. Both epoxide and annulene fullerene structures (Fig. 6a,b) have been successfully synthesized33,34. Density functional theory (DFT) studies of single oxygen addition to heterofullerenes found that C59N and C59HN showed similar epoxide formation and binding energies as C60 (ref. 17). However, it is not obvious how epoxides and annulenes would be produced via spontaneous O2 incorporation in C60 crystals upon air exposure. The most stable configuration for a single oxygen atom is cross-linking a fullerene dimer35,36,37,38 via a 2 + 2 cycloaddition reaction combining double bonds in neighboring C60, where the oxygen atom adopts an ether configuration in one of the cross-linked bonds (Fig. 6c). Dry air studies have suggested the presence of interstitial oxygen molecules sitting in the octahedral voids of the crystal18, and modeling has confirmed the octahedral site as the most stable for O2 incorporation38.
Figure 6.
Stable oxygen-fullerene complexes: C60O with oxygen in the (a) epoxide and (b) annulene configurations (c) ether-oxygen-bridged fullerene dimer C60-O-C60. Carbon atoms are shown in grey, oxygen in red.
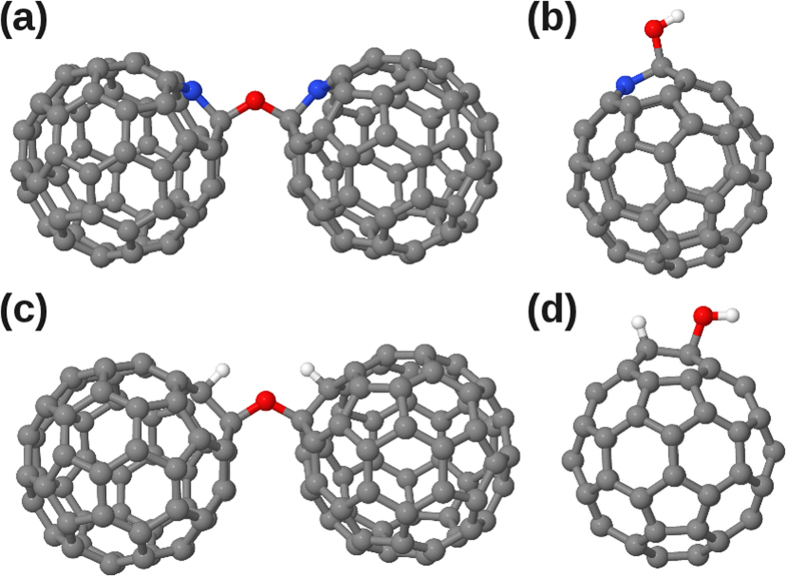
The most stable configuration that we found for a single oxygen atom in (C59N)2 structures is the analogue of the bridging configuration of C60 dimers, i.e. an oxygen atom in an ether configuration in the cross-linking bond between (C59N) pairs in the dimer (Fig. 7a). As compared to C60-O-C60 (Fig. 6c), replacing the sp3-cross-linked carbon atoms with two non-bonded nitrogen atoms removes the second cross-linking bond between the fullerene cages and relieves significant strain.
Figure 7.
Structures of (a) C59N-O-C59N (b) C59N(OH), (c) C6OH-O-C60H and (d) C60H(OH). Carbon atoms are shown in grey, oxygen in red, nitrogen in blue and hydrogen in white.
Calculated Interaction with Water
FTIR spectra have demonstrated the presence of both O2 and H2O in C60 crystals exposed to air19, and testing C60 in air with varying humidity has suggested that the observed O 1s XPS signal was caused by H2O exposure39. Indeed, C60 has a high affinity for water, as shown by its high free energy of hydration (−90.5 mJ/m2)40.
Before analyzing our experimental data, we first explore theoretically the feasibility of molecular H2O interaction with fullerenes and azafullerenes. To the best of our knowledge, there is little modeling of the H2O-C60 interaction. Tsetseris et al. showed that C60H(OH), i.e. H2O dissociated to saturate a C60 double bond, is 0.1 eV less stable than H2O in an octahedral void in the C60 crystal38, and models have been proposed of hydration cages forming around C60 when in solution41,42,43.
We calculate the binding energy of H2O to isolated “gas-phase” C60 to be 0.34 eV, increasing to 0.56 eV when the H2O molecule is placed in the octahedral interstitial void in fcc C60. The binding energy of H2O to gas phase (C59N)2 is 0.32 eV, very similar to that for H2O binding to C60. Since the nitrogen atoms are close to the cross-linked carbon atoms, they are spatially inaccessible to the H2O molecule, which is forced to sit further away on the cage surface and does not interact strongly with the nitrogen. The result again reflects the earlier finding that the perturbation of the fullerene cage caused by nitrogen substitution remains localized around the nitrogen and its neighbors, with the rest of the cage closely resembling pristine C60.
Considering potential reactions of (C59N)2 with water, one possibility is that H2O could saturate the C-C cross-linking bond between the cages, creating a C59NH/C59N(OH) pair. However, we found this structure to be 0.27 eV less stable than C59N-C59N with a neighboring H2O molecule. Additionally, we calculate an extremely high reaction barrier of 3.94 eV for this process, due to the difficulty in forcing the H2O molecule between the two fullerene cages in close proximity. We hence conclude that water is likely to remain molecular in interstitial voids if present within the bulk azafullerene sample.
Considering now possible reactions involving H2O and C60, a new structural analogue to C59N-O-C59N can be proposed, namely C60H-O-C60H (Fig. 7c). This is 0.13 eV more stable than H2O sitting in the interstitial space between two C60 molecules (which we find isoenergetic with C60 neighboring C60H(OH) (Fig. 7d), close to the result of Tsetseris et al.38). C60H-O-C60H thus represents the lowest total energy structure we obtained with a single H2O molecule and C60. However, entropic considerations will not favor this structure at finite temperatures, and similarly to the azafullerene case, there is a significant reaction barrier of 2.40 eV that needs to be overcome to form this structure from H2O + 2C60. It is possible such a process could be catalyzed, either by doping (in a -1 charge state this barrier drops to 1.66 eV with C60H-O-C60H now 0.24 eV more stable) or photocatalyzed (in the triplet state the calculated barrier drops to 1.67 eV).
Thus, even if catalyzed, the reaction barriers remain high enough that under conventional room temperature conditions we expect H2O in the presence of C60 crystals to remain in molecular form, as in azafullerenes.
Oxygen X-Ray Photoelectron Spectroscopy
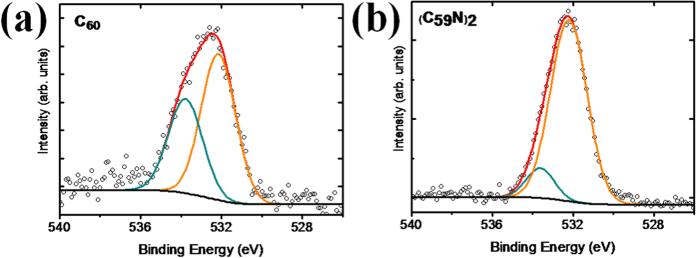
We next turn to our experimental oxygen data and its interpretation. Figure 8 shows the O 1s XPS signal of our fullerene and azafullerene samples (with the C 1s found at 284.6 eV). While both samples show a high intensity component at 532.2 eV, the C60 sample also shows another prominent oxygen component at 533.8 eV, only weakly present in the azafullerene sample despite the overall oxygen concentration being slightly higher there. In general, the oxygen concentration is comparable with previous studies39. The elemental compositions of the samples are shown in Table 1.
Figure 8.
O 1s XPS signal for (a) C60 and (b) (C59N)2 powders.
Table 1. Elemental compositions (±0.5%) determined by XPS for (a) C60 and (b) (C59N)2 powders.
| Sample | C | N | O | O (532.2 eV) | O (533.8 eV) |
|---|---|---|---|---|---|
| C60 | 97.0% | — | 3.0% | 1.8% | 1.2% |
| (C59N)2 | 94.5% | 1.5% | 4.0% | 3.5% | 0.5% |
The spatial resolution of STXM means we are able to collect NEXAFS spectra exclusively from single, indirectly supported crystalline regions. Notably we can compare our NEXAFS measurements, which are dominated by the bulk response of the crystallites, with the surface-dominated XPS data. In the individual C60 crystallites we did not detect any O 1s signal with NEXAFS. The azafullerene sample, which is more porous and less crystalline, did show a weak O 1s NEXAFS signal; however, comparison with theoretical modeling suggests this is due to ethanol contamination (see Supplementary Materials), which was used as a dispersant for the NEXAFS sample preparation.
The STXM-NEXAFS result therefore suggests that the observed O 1s XPS signal does not come from the bulk of the fullerene and azafullerene materials. There are thus two possible explanations for the signal. The first is that it comes from amorphous regions present elsewhere in the sample. The second is that it comes from surface/sub-surface adsorbed species, to which XPS is particularly sensitive, but which would be masked by the NEXAFS signal of the bulk. It is important to note that there can be no XPS signal corresponding to ethanol, since solvent was not used to make the XPS samples.
In order to assign the two peaks at 532.2 and 533.8 eV identified by XPS, we calculated the O 1s energies for all the structures shown in Figs 6 and 7 using the ΔSCF method (the ΔKS method yielded slightly lower binding energies for both the C 1s and O 1s levels, but their separation was almost identical between the two methods in all cases), with the results given in Table 2. Considering first the experimental O 1s XPS peak at 532.2 eV, the energy given in Table 2 for the OH group in C60H(OH) is close to this value at 532.53 eV. However, the calculated O 1s binding energies of ether-bound oxygen in C59N-O-C59N and C60H-O-C60H are also very similar; hence, we cannot conclusively assign the measured energies to one specific bonding, but suggest it corresponds to either hydroxyl- or ether-bonded oxygen in the sample.
Table 2. Calculated O 1s core-level binding energies for the different structures in Figs 6 and 7.
| Structure | Calculated O 1s [correction] (eV) |
|---|---|
| C60H-O-C60H | 532.56 [+0.39] |
| C60-O-C60 | 532.69 [+0.39] |
| C60-O- (annulene) | 533.43 [+0.39] |
| C60 > O (epoxide) | 533.00 [+0.39] |
| C60H(OH) | 532.53 [+0.39] |
| C59N(OH) | 533.01 [+0.26] |
| C59N-O-C59N | 532.49 [+0.26] |
The energies are shifted so that the C 1s energy of the corresponding unmodified structure (C60 or (C59N)2) matches the experimental value of 284.6 eV, with the applied corrections given in brackets.
The second experimental peak at 533.8 eV has a higher binding energy than any of our calculated structures in Table 2, and indeed, such a high value is strongly indicative of water. Onoe et al. measured XPS for C60 crystals exposed to humid air39, and found an O 1s peak at 533.5 eV, in good agreement with our value. They attributed this to water bound on the surfaces of the fullerene crystals. Given the ultra-high vacuum (10−9 mbar) in our XPS apparatus, we can safely assume that gas-phase H2O is unlikely (and would have an even higher O 1s of 535.75 eV)44. In other studies of water on metal and oxide surfaces, a downshift for surface adsorbed H2O to as low a value as 532.8 eV has been reported44, but screening on such surfaces is likely stronger than in the fullerene crystal. Since NEXAFS has excluded the presence of significant amounts of H2O within the crystal, the bound H2O observed in XPS must necessarily be near the crystal surface (the estimated maximum escape depth of our photoelectrons is ~2–3 nm). The lower intensity of the 533.8 eV O 1s signal in the C59N sample, arising from water, is also consistent with its decreased crystallinity as compared to C60 (see Supplementary Materials).
To directly simulate the core level binding energy of bound water, we created a model of eight C60 molecules taken from the infinite FCC lattice containing the relevant pore, surrounded by 15 Å of vacuum on all sides. Then, we ran two core level calculations using the ΔKS method: one with a H2O molecule in the pore, and another with the H2O placed at the corner of the simulation cell, far from the fullerenes. Thus the contents of the cell were the same in both cases (483 atoms with a total of 1928 valence electrons), and any error in screening our method makes for molecules is likely of similar magnitude. We should note that these are the largest core hole calculations ever reported to the best of our knowledge.
After correcting the resulting O 1s values so that both C 1s levels again match the experimental value, we found adsorption of H2O into the pore to downshift its O 1s level by 1.0 eV. Although this is not quite as much as the 2 eV difference between our higher BE component (533.8 eV) and a reference value for gas-phase H2O (535.75 eV), it is of similar magnitude and in the correct direction. Additional calculations for a hydration shell41 of 80 H2O molecules around C60 gave nearly the same O 1s binding energy for H2O at the C60 surface as for the single H2O molecule in the C60 FCC crystal pore. Thus the calculations are consistent with the assignment of this peak to surface or sub-surface water.
The O 1s XPS results strongly resemble findings for surface bound water on metals, where two O 1s peaks in XPS are commonly observed (for a review see ref. 45), and assigned to H2O and hydroxyl groups in the surface water layer, respectively. The presence of bound hydroxyl groups enhances water binding46. For example, two XPS peaks at 530.8 and 532.4 eV are observed for Cu(110) cleaned in UHV and then exposed to water at room temperature46, similarly, water on Ru{0001} shows two O 1s XPS peaks at 531.0–530.8 eV and 532.7–532.3 eV (the precise position varies with coverage)47. There is also precedent for water layer formation on carbon nanomaterials; for example, bilayer water formation has been observed on the surface of graphene under UHV conditions48. Thus our calculations, the XPS data, and comparison to the literature strongly supports the interpretation that our higher binding energy component is due to a surface water layer, resistant to evaporation even in the spectroscope vacuum, with the lower binding energy component due to hydroxyl groups present in this layer. We note as further evidence of the strong layer binding that when we applied an annealing step at 70 °C within the XPS chamber prior to measurement, the resultant O 1s signal remained unchanged.
In our case there was no deliberate introduction of water to the samples, which was rather adsorbed by the samples from the humid air of the laboratory over time. Daylight exposure in the laboratory can also help explain the presence of the strong hydroxyl signal, since it has been demonstrated that exposure of C60 to UV light in the presence of water leads to hydroxyl radical creation49.
Discussion and Conclusions
Isolated suspended clusters of C60 and (C59N)2 were analyzed by a combination of nanoscale NEXAFS, XPS and various DFT approaches. Our study clearly shows the benefit of combining different complementary theoretical and experimental techniques in order to characterize such complex samples as completely as possible.
We show that the extra electron in the azafullerene is predominantly localized on the N atom, and interpret the primary low energy peaks in the C 1s as coming from carbon π* states, whereas the primary low energy peak in the N 1s are from σ* states. Interpretation of the observed oxygen signal is complicated, but we propose that NEXAFS identifies the presence of ethanol solvent within the azafullerene crystals. In contrast, as more surface-sensitive, the XPS characterization identifies the presence of a surface water layer containing hydroxyl groups on both samples, with lower concentrations in the azafullerene sample. The water must necessarily be rather strongly bound given the ultra-high vacuum conditions used for XPS, which is corroborated by the large O 1s downshift of around 2 eV as compared to gas-phase water. This wetting behaviour strongly resembles that observed on many metal surfaces.
The presence of high levels of surface/subsurface adsorbed water in fullerene crystals, even under ultra-high vacuum conditions, has many important implications. One in particular is in the field of astrochemistry and astrobiology. Recent studies from the Spitzer radio telescope have identified large amounts of crystalline C60 in interstellar outflows3. We propose here that the C60 crystal surfaces may serve as substrates facilitating the formation of amino acids in the interstellar medium, and ultimately the earliest stages of life.
If water is strongly surface bound to C60, we could speculate that this may also be the case for other gaseous species. Surface reactions with water could then be catalyzed by kinetic confinement on the two-dimensional C60 crystal surface, with further mechanical confinement brought about by the surface rugosity. Surface reactions could be additionally catalyzed by UV-adsorption and energy transfer from the underlying fullerene crystal. C60 is known to be a highly efficient UV-absorber that promotes radical formation, for example converting triplet O2 to the singlet state with very high quantum yield50, and can in the presence of water and UV generate hydroxyl radicals49. Thus C60 crystals would be able to absorb the large amounts of available high energy UV-light present in and around such interstellar outflows, and direct it towards catalyzing surface reactions.
Methods
C60 was purchased from Bucky USA (99.5% grade), stored in the lab for several months and used as received. The details of azafullerene (C59N)2 synthesis have been reported elsewhere51. Briefly, starting from C60, [60]-N-MEM ketolactam is isolated following a two-step procedure. A degassed solution of the ketolactam in o-dichlorobenzene is refluxed under argon for 15 min with an excess of p-toluenesulfonic acid. After the reaction mixture is cooled, flash column chromatography using silica gel with toluene as eluent afforded azafullerene (C59N)2 as the least polar fraction. The material was further purified by high-performance liquid chromatography (Buckyprep column 20 × 250 mm, toluene eluent, 20 mL/min flow rate, 333 nm UV detection). The final HPLC trace shows only a single peak after recycling, the profile indicating the purity is >99.99%. The azafullerene samples after purification by HPLC, were stored in flat clear vials (4 mL/14.75 × 45 mm), with screw neck and with clear screw cap closed top Teflon, 1.5 mm (purchased from MACHEREY-NAGEL GmbH & Co. KG) at 25 °C and humidity 20%. They were prepared and transported between synthesis and characterization laboratories over a period of a few months. Storage in characterization laboratories was far from other chemical products.
STXM spectromicroscopy was used to analyze selected regions of the sample, taking advantage of its nanoscale spatial resolution52,53. The carbon 1s spectra were recorded using the ambient STXM on the 10ID-1 soft X-ray spectromicroscopy (SM) beamline at the Canadian Light Source (CLS) in Saskatoon, Canada. This beamline has an energy resolving power E/ΔE > 500054. In STXM monochromatic X-rays of different energies are focused onto the sample by a Fresnel zone plate55 and the transmitted X-rays detected. The spectra were obtained by (x, y) raster-scanning the sample at the focus of the X-rays over a range of photon energies so that a sequence of images at different energies was acquired, known as a “stack”56. The nitrogen 1s spectra were recorded on a different region of the same sample with the STXM on beamline 5.3.2.2 at the Advanced Light Source in Berkeley, USA. Data processing was similar in both cases. The oxygen 1s spectra were measured with the full field transmission X-ray microscope (TXM) at the U41-FSGM beamline, BESSY II electron storage ring, Berlin, Germany57. The spectra were recorded at room temperature in transmission mode by taking a sequence of images over a range of photon energies covering the investigated adsorption edges with a spectral resolution larger than 5000. The zone plate used provided a spatial resolution of 25 nm. Stack alignment, conversion to optical density, and extraction of NEXAFS spectra from small, free-standing regions were performed using the aXis2000 software58. Since the photon flux at the sample varies as a function of energy and time, the aligned image sequences were converted to optical densities by dividing the transmitted signal recorded on the sample region by the incident photon flux recorded in a sample-free region. Thus, the ultimately acquired image sequences at different energies provide spatially resolved NEXAFS spectra.
X-ray photoelectron spectroscopy (XPS) measurements were performed in a VG Escalab 220i XL with background pressure of 1×10−10 Torr, equipped with a source of monochromatic Al Kα X-rays (hν = 1486 eV). The escape depth of the photoelectrons is typically 2–3 nm, and the energy resolution was 0.6 eV. An electron gun (~1 eV) was used to compensate built-up charge on the specimen surface during the measurements. The samples for the XPS measurements were prepared by pressing the specimen into a pellet, avoiding the need for a solvent. A conductive double-face tape was used to attach the pellet to a sample holder.
Density functional theory calculations of different fullerene and azafullerene structures, their complexes with oxygen and water, and associated formation barriers were performed using the LDA-PW91 exchange-correlation functional59 as implemented in the AIMPRO code60,61,62. Spin-polarized calculations were carried out using supercells, fitting the charge density to plane waves with an energy cutoff of 150 Hartrees. Relativistic pseudopotentials generated by Hartwigsen, Goedecker and Hutter were used63. 28, 40 and 40 independent Gaussian functions were used as basis sets for carbon, nitrogen and oxygen respectively. Periodic boundary conditions were applied, with supercell sizes checked and chosen to be sufficiently large (vacuum distance between all structures being larger than 13 Å) to avoid interactions between fullerenes in neighboring cells. Electronic level occupation was obtained using a Fermi occupation function with kT = 0.04 eV. Absolute energies were converged in the self-consistency cycle to better than 10−8 Ha. Atomic positions were geometrically optimized until the maximum atomic position change in a given iteration dropped below 10−5 Bohr radii. Diffusion barriers were calculated using the climbing nudged elastic band method, with typically 20 images between the initial and final structure.
Simulated X-ray adsorption spectra were calculated using the WIEN2k program package64 with the LDA functional and using the GGA-PBE optimised atomic structures. The GGA functional is better suited for the geometry optimisation, whilst our test calculations demonstrated that LDA gave slightly better C 1s peak seperations for C60 than GGA for NEXAFS simulations (see Supporting Materials). In order to describe properly the impact of the two-particle electron-hole interactions on the XAS spectra, one should go beyond DFT by using the Bethe-Salpeter approach65 or time-dependent DFT66. Here, due to the size of the systems, we have chosen to mimic these many-body effects by considering a static screened electron-hole interaction using the Slater transition state, i.e. a half-reduced occupation in the C 1s and N 1s core levels when calculating the the C and N 1s NEXAFS of C60 and (C59N)2. A half-electron uniform background was added to perform these calculations. The broadening of our theoretical spectra was done in two steps by first considering a Lorentzian to account for the core-hole lifetime using tabulated values67, and adding an energy-dependent broadening to account for the excited state lifetimes68. For the energy-dependent broadening we considered a plasmon frequency of 8 eV for both C 1s and N 1s spectra. In order to compare our theoretical spectra with experiment, an energy shift which depends on the system and level of theory is needed. For the three C 1s spectra of C60 using 0, 0.5 and 1 core-holes, energy shifts of 282.7, 283.0 and 283.3 eV were used, respectively. For (C59N)2 energy shifts of 284.0 and 399.5 eV were used for the N 1s and C 1s spectra, respectively.
For calculations of the C, N and O 1s core-level binding energies, we utilized two methods based on density functional theory total energy differences, as implemented in the grid-based projector-augmented waves (PAW) simulation package GPAW69,70: a standard delta Kohn–Sham (ΔKS) calculation with a projector-augmented wave dataset including an explicit core-hole on an atom of interest71, and a novel all-electron extension of the delta self-consistent field (ΔSCF) method72. In the latter, the core electrons are included in the valence, enabling an explicit all-electron calculation within the PAW scheme73. Exchange and correlation for these calculations were estimated by the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation74, yielding significantly more accurate core level binding energies than the LDA72. In each case, we calculated via total energy differences the respective 1s energy and compared this to the C 1s energy for a carbon atom far away from the N site(s).
Additional Information
How to cite this article: Erbahar, D. et al. Spectromicroscopy of C60 and azafullerene C59N: Identifying surface adsorbed water. Sci. Rep. 6, 35605; doi: 10.1038/srep35605 (2016).
Supplementary Material
Acknowledgments
We would like to acknowledge the following funding bodies and computing resources: (D.E.) TUBITAK-2219 Abroad Post-Doctoral Research Funding Programme (1059B191301289); (C.B., M.S.) the Belgian Fund for Scientific Research (FRS-FNRS) under FRFC contract 2.4577.11 (Chemographene); (T.S.) the Vienna Scientific Cluster and the Austrian Science Fund (FWF) grants P 28322-N36 and M 1497-N19; (G.R., N.T.) the Greek General Secretariat for Research and Technology and the European Commission through the European Fund for Regional Development, NSRF 2007–2013 action “Development of Research Centers – ΚΡΗΠΙΣ” (POLYNANO), the European Commission under contract CALIPSO Transnational Access, and grants 642742 (Enabling Excellence), 612577 (NanoCF), 226716 (ELISA) and 312284 (CALIPSO). TXM measurements were performed at the Bessy-II facility, which is financially supported by the Helmholtz-Zentrum Berlin für Materialien und Energie GmbH. We thank HZB for the allocation of synchrotron radiation beamtime at the undulator beamline U41-TXM at the BESSY II electron storage ring, Berlin. STXM measurements were performed at the Canadian Light Source, which is funded by the Canada Foundation for Innovation, the Natural Sciences and Engineering Research Council of Canada, the National Research Council Canada, the Canadian Institutes of Health Research, the Government of Saskatchewan, Western Economic Diversification Canada, and the University of Saskatchewan. STXM measurements were also performed at the Advanced Light Source, which is supported by the Director of the Office of Science, Department of Energy, under Contract No. DE-AC02–05CH11231. The numerical calculations reported in this paper were partially performed at TUBITAK ULAKBIM, High Performance and Grid Computing Center (TRUBA resources).
Footnotes
Author Contributions C.B. initiated the project, N.T. and G.R. synthesized the (C59N)2 samples. C.B., A.P.H., M.S. and X.Z. performed the CLS experiments and associated data analysis. A.P.H. and X.Z. performed the ALS experiments and analysis. C.B. and P.G. performed the BESSY II experiments. C.B. and M.S. performed the XPS studies. X.R. and P.B. performed the NEXAFS simulations. T.S. performed the XPS core-level shift calculations. D.E. and C.P.E. performed the structural DFT calculations and proposed the structural and astrochemical models. D.E., C.P.E., X.R., T.S., C.B. and M.S. analyzed the data and wrote the paper. All authors contributed corrections and modifications.
References
- Allamandola L. J. & Hudgins D. M. In Solid State Astrochemistry Nato Science Series I. I. (eds Valerio Pirronello Jacek Krelowski & Giulio Manicò) 251–316 (Springer Netherlands, 2003). [Google Scholar]
- Werner M. W. et al. The Spitzer Space Telescope mission. Astrophysical Journal Supplement Series 154, 1–9 (2004). [Google Scholar]
- Cami J., Bernard-Salas J., Peeters E. & Malek S. E. Detection of C-60 and C-70 in a Young Planetary Nebula. Science 329, 1180–1182 (2010). [DOI] [PubMed] [Google Scholar]
- Sellgren K. et al. C-60 in Reflection Nebulae. Astrophysical Journal Letters 722, L54–L57 (2010). [Google Scholar]
- Goodman G., Gershwin M. E. & Bercovich D. Fullerene and the origin of life. Isr Med Assoc J 14, 602–606 (2012). [PubMed] [Google Scholar]
- Hetzel R., Manning T., Lovingood D., Strouse G. & Phillips D. Production of Fullerenes by Microwave Synthesis. Fullerenes Nanotubes and Carbon Nanostructures 20, 99–108 (2012). [Google Scholar]
- Tamuliene J., Tamulis A., Tamulis V., Balevicius V. & Balevicius L. M. NMR parameters of aza-fullerene and its derivatives. Fullerenes Nanotubes and Carbon Nanostructures 13, 61–72 (2005). [Google Scholar]
- Andreoni W. et al. Unconventional bonding of azafullerenes: Theory and experiment. J Am Chem Soc 118, 11335–11336 (1996). [Google Scholar]
- Brown C. M. et al. Effects of pressure on the azafullerene (C59N)(2) molecular solid to 22 GPa. J Am Chem Soc 118, 8715–8716 (1996). [Google Scholar]
- Brown C. M. et al. On the crystal structure of azafullerene (C59N)(2). Chemistry of Materials 8, 2548–2550 (1996). [Google Scholar]
- Yagi H. et al. Photoemission study of the electronic structure of azafullerene encapsulated single-walled carbon nanotubes. Chemical Physics Letters 570, 100–103 (2013). [Google Scholar]
- Rotas G. et al. Azafullerene C59N-Phthalocyanine Dyad: Synthesis, Characterisation and Photoinduced Electron Transfer. Chemphyschem 13, 1246–1254 (2012). [DOI] [PubMed] [Google Scholar]
- Iizumi Y. et al. Host-guest interactions in azafullerene (C59N)-single-wall carbon nanotube (SWCNT) peapod hybrid structures. Chemical Communications 46, 1293–1295 (2010). [DOI] [PubMed] [Google Scholar]
- Schulte K., Wang L., Moriarty P. J., Prassides K. & Tagmatarchis N. Resonant processes and Coulomb interactions in (C59N)(2). J Chem Phys 126, 184707 (2007). [DOI] [PubMed] [Google Scholar]
- Andreoni W. Computational approach to the physical chemistry of fullerenes and their derivatives. Annual Review of Physical Chemistry 49, 405–439 (1998). [DOI] [PubMed] [Google Scholar]
- Arcon D. et al. Stability, thermal homolysis and intermediate phases of solid hydroazafullerene C59HN. Chemical Communications, 3386–3388 (2007). [DOI] [PubMed] [Google Scholar]
- Ewels C. P., El Cheikh H., Suarez-Martinez I. & Van Lier G. Oxidation and reactivity of nitrogen- and phosphorus-doped heterofullerenes. Physical Chemistry Chemical Physics 10, 2145–2148 (2008). [DOI] [PubMed] [Google Scholar]
- Wohlers M., Werner H., Belz T., Ruhle T. & Schlogl R. C-60: A host lattice for the intercalation of oxygen? Mikrochimica Acta 125, 401–406 (1997). [Google Scholar]
- Werner H. et al. Reaction of molecular oxygen with C60: spectroscopic studies. Journal of the Chemical Society, Faraday Transactions 90, 403–409, 10.1039/FT9949000403 (1994). [DOI] [Google Scholar]
- Pichler T. et al. On-ball doping of fullerenes: The electronic structure of C59N dimers from experiment and theory. Phys Rev Lett 78, 4249–4252 (1997). [Google Scholar]
- Itchkawitz B. S. et al. Photoemission and C-1s near-Edge Absorption from Photopolymerized C-60 Films. Chemical Physics Letters 243, 211–216 (1995). [Google Scholar]
- Haffner S. et al. The electronic structure of (C59N)(2) from high energy spectroscopy. European Physical Journal B 1, 11–17 (1998). [Google Scholar]
- Maxwell A. J. et al. Electronic and geometric structure of C-60 on Al(111) and Al(110). Phys Rev B 57, 7312–7326, 10.1103/PhysRevB.57.7312 (1998). [DOI] [Google Scholar]
- Krummacher S., Biermann M., Neeb M., Liebsch A. & Eberhardt W. Close Similarity of the Electronic-Structure and Electron Correlation in Gas-Phase and Solid C-60. Phys Rev B 48, 8424–8429, 10.1103/PhysRevB.48.8424 (1993). [DOI] [PubMed] [Google Scholar]
- Mizoguchi T. et al. Core-hole effects on theoretical electron-energy-loss near-edge structure and near edge x-ray absorption fine structure of MgO. Phys Rev B 61, 2180–2187, 10.1103/PhysRevB.61.2180 (2000). [DOI] [Google Scholar]
- Kelly M. K., Etchegoin P., Fuchs D., Kratschmer W. & Fostiropoulos K. Optical-Transitions of C-60 Films in the Visible and Ultraviolet from Spectroscopic Ellipsometry. Phys Rev B 46, 4963–4968 (1992). [DOI] [PubMed] [Google Scholar]
- Wastberg B. et al. Is X-Ray-Absorption Spectroscopy of C-60 - the Effects of Screening and Core-Hole Relaxation. Phys Rev B 50, 13031–13034, 10.1103/PhysRevB.50.13031 (1994). [DOI] [PubMed] [Google Scholar]
- Arenal R. et al. Atomic Configuration of Nitrogen-Doped Single-Walled Carbon Nanotubes. Nano Letters 14, 5509–5516 (2014). [DOI] [PubMed] [Google Scholar]
- Nyberg M., Luo Y., Triguero L., Pettersson L. G. M. & Agren H. Core-hole effects in x-ray-absorption spectra of fullerenes. Phys Rev B 60, 7956–7960, 10.1103/PhysRevB.60.7956 (1999). [DOI] [Google Scholar]
- Schmidt N., Fink R. & Hieringer W. Assignment of near-edge x-ray absorption fine structure spectra of metalloporphyrins by means of time-dependent density-functional calculations. J Chem Phys 133, 054703 (2010). [DOI] [PubMed] [Google Scholar]
- Deng Y. F., Gao B., Deng M. S. & Luo Y. A comparative theoretical study on core-hole excitation spectra of azafullerene and its derivatives. J Chem Phys 140, 124304, 10.1063/1.4868717 (2014). [DOI] [PubMed] [Google Scholar]
- Patnaik A. et al. Polarized near-edge x-ray-absorption fine structure spectroscopy of C-60-functionalized 11-amino-1-undecane thiol self-assembled monolayer: Molecular orientation and evidence for C-60 aggregation. J Chem Phys 122, 154703–154709 (2005). [DOI] [PubMed] [Google Scholar]
- Heymann D. & Weisman R. B. Fullerene oxides and ozonides. Cr Chim 9, 1107–1116, 10.1016/j.crci.2006.02.003 (2006). [DOI] [Google Scholar]
- Taylor R. Oxides and oxidation of fullerenes. Elec Soc S 97, 281–289 (1997). [Google Scholar]
- Lebedkin S., Ballenweg S., Gross J., Taylor R. & Kratschmer W. Synthesis of C120o - a New Dimeric [60]Fullerene Derivative. Tetrahedron Letters 36, 4971–4974 (1995). [Google Scholar]
- Smith A. B. et al. Synthesis of Oxo-Bridged and Methylene-Bridged C-60 Dimers, the First Well-Characterized Species Containing Fullerene-Fullerene Bonds. J Am Chem Soc 117, 9359–9360 (1995). [Google Scholar]
- Taylor R., Barrow M. P. & Drewello T. C-60 degrades to C120O. Chemical Communications 22, 2497–2498 (1998). [Google Scholar]
- Tsetseris L. & Pantelides S. T. Oxygen and water-related impurities in C-60 crystals: A density-functional theory study. Phys Rev B 82, 045201–045206 (2010). [Google Scholar]
- Onoe J., Takeuchi K., Ohno K. & Kawazoe Y. X-ray photoelectron spectroscopy of air-exposed C-60 films: Origin of the O1s core peak. Journal of Vacuum Science & Technology a-Vacuum Surfaces and Films 16, 385–388 (1998). [Google Scholar]
- Ma X., Wigington B. & Bouchard D. Fullerene C-60: Surface Energy and Interfacial Interactions in Aqueous Systems. Langmuir 26, 11886–11893 (2010). [DOI] [PubMed] [Google Scholar]
- Chaplin M. In Nato Sci Ser Ii Math (eds Blitz Jonathan P. & M. Gun’ko Vladimir) pp 1–10 (Springer Netherlands, 2006). [Google Scholar]
- Hernandez-Rojas J., Breton J., Llorente J. M. G. & Wales D. J. Global potential energy minima of C-60(H2O)(n) clusters. Journal of Physical Chemistry B 110, 13357–13362 (2006). [DOI] [PubMed] [Google Scholar]
- Ohno K., Maruyama Y. & Kawazoe Y. Stability and reactivity of C-60 studied by all-electron mixed-basis molecular-dynamics simulations at finite temperatures. Phys Rev B 53, 4078–4082 (1996). [DOI] [PubMed] [Google Scholar]
- Yamamoto S. et al. In situ x-ray photoelectron spectroscopy studies of water on metals and oxides at ambient conditions. Journal of Physics-Condensed Matter 20, 184025–184039 (2008). [Google Scholar]
- Carrasco J., Hodgson A. & Michaelides A. A molecular perspective of water at metal interfaces. Nat Mater 11, 667–674, 10.1038/NMAT3354 (2012). [DOI] [PubMed] [Google Scholar]
- Yamamoto S. et al. Hydroxyl-induced wetting of metals by water at near-ambient conditions. J Phys Chem C 111, 7848–7850, 10.1021/jp0731654 (2007). [DOI] [Google Scholar]
- Weissenrieder J., Mikkelsen A., Andersen J. N., Feibelman P. J. & Held G. Experimental evidence for a partially dissociated water bilayer on Ru{0001}. Phys Rev Lett 93, 196102–196104, 10.1103/Physrevlett.93.196102 (2004). [DOI] [PubMed] [Google Scholar]
- Kimmel G. A. et al. No Confinement Needed: Observation of a Metastable Hydrophobic Wetting Two-Layer Ice on Graphene. J Am Chem Soc 131, 12838–12844, 10.1021/ja904708f (2009). [DOI] [PubMed] [Google Scholar]
- Yamakoshi Y. et al. Active oxygen species generated from photoexcited fullerene (C-60) as potential medicines: O-2(-center dot) versus O-1(2). J Am Chem Soc 125, 12803–12809 (2003). [DOI] [PubMed] [Google Scholar]
- Arbogast J. W. et al. Photophysical properties of sixty atom carbon molecule (C60). The Journal of Physical Chemistry 95, 11–12, 10.1021/j100154a006 (1991). [DOI] [Google Scholar]
- Hummelen J. C., Knight B., Pavlovich J., Gonzalez R. & Wudl F. Isolation of the Heterofullerene C59n as Its Dimer (C59n)(2). Science 269, 1554–1556 (1995). [DOI] [PubMed] [Google Scholar]
- Ade H. & Hitchcock A. P. NEXAFS microscopy and resonant scattering: Composition and orientation probed in real and reciprocal space. Polymer 49, 643–675 (2008). [Google Scholar]
- Stöhr J. NEXAFS Spectroscopy. (Springer-Verlag Berlin Heidelberg, 1992). [Google Scholar]
- Kaznatcheev K. V. et al. Soft X-ray spectromicroscopy beamline at the CLS: Commissioning results. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment 582, 96–99 (2007). [Google Scholar]
- Keskinbora K. et al. Ion beam lithography for Fresnel zone plates in X-ray microscopy. Optics Express 21, 11747–11756 (2013). [DOI] [PubMed] [Google Scholar]
- Jacobsen C., Wirick S., Flynn G. & Zimba C. Soft X-ray spectroscopy from image sequences with sub-100 nm spatial resolution. Journal of Microscopy-Oxford 197, 173–184 (2000). [DOI] [PubMed] [Google Scholar]
- Guttmann P. et al. Nanoscale spectroscopy with polarized X-rays by NEXAFS-TXM. Nature Photonics 6, 25–29 (2012). [Google Scholar]
- Hitchcock A. P. aXis2000: A software written in Interactive Data Language (IDL) available free for non-commercial use, Hitchcock Group, Hamilton, ON, Canada. http://unicorn.mcmaster.ca/aXis2000.html (2014).
- Perdew J. P. & Wang Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation-Energy. Phys Rev B 45, 13244–13249 (1992). [DOI] [PubMed] [Google Scholar]
- Briddon P. R. & Jones R. LDA calculations using a basis of Gaussian orbitals. Physica Status Solidi B-Basic Solid State Physics 217, 131–171 (2000). [Google Scholar]
- Rayson M. J. & Briddon P. R. Highly efficient method for Kohn-Sham density functional calculations of 500–10 000 atom systems. Phys Rev B 80, 205104–205111 (2009). [Google Scholar]
- Briddon P. R. & Rayson M. J. Accurate Kohn-Sham DFT with the speed of tight binding: Current techniques and future directions in materials modelling. Physica Status Solidi B-Basic Solid State Physics 248, 1309–1318 (2011). [Google Scholar]
- Hartwigsen C., Goedecker S. & Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys Rev B 58, 3641–3662 (1998). [DOI] [PubMed] [Google Scholar]
- Blaha P., Schwarz K., Madsen G., Kvasnicka D. & Luitz J. WIEN2k: An Augmented Plane Wave + LO Program for Calculating Crystal Properties, Vienna, Austria. URL http://www.wien2k.at/ (2001)
- Vinson J., Rehr J. J., Kas J. J. & Shirley E. L. Bethe-Salpeter equation calculations of core excitation spectra. Phys Rev B 83, 115106–115107 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Biggs J. D., Healion D., Govind N. & Mukamel S. Core and valence excitations in resonant X-ray spectroscopy using restricted excitation window time-dependent density functional theory. J Chem Phys 137, 194306–194310 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unoccupied Electronic States - Fundamentals for Xanes, Eels, Ips and Bis. Vol. 69 (Springer Berlin Heidelberg, 1992). [Google Scholar]
- Muller D. A., Singh D. J. & Silcox J. Connections between the electron-energy-loss spectra, the local electronic structure, and the physical properties of a material: A study of nickel aluminum alloys. Phys Rev B 57, 8181–8202 (1998). [Google Scholar]
- Mortensen J. J., Hansen L. B. & Jacobsen K. W. Real-space grid implementation of the projector augmented wave method. Phys Rev B 71, 035109–035111 (2005). [Google Scholar]
- Enkovaara J. et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. Journal of Physics-Condensed Matter 22, 253202–253224 (2010). [DOI] [PubMed] [Google Scholar]
- Ljungberg M. P., Mortensen J. J. & Pettersson L. G. M. An implementation of core level spectroscopies in a real space Projector Augmented Wave density functional theory code. Journal of Electron Spectroscopy and Related Phenomena 184, 427–439 (2011). [Google Scholar]
- Susi T., Mowbray D. J., Ljungberg M. P. & Ayala P. Calculation of the graphene C 1s core level binding energy. Phys Rev B 91, 081401–081405 (2015). [Google Scholar]
- Ojanpera A., Krasheninnikov A. V. & Puska M. Electronic stopping power from first-principles calculations with account for core electron excitations and projectile ionization. Phys Rev B 89, 035120–035125 (2014). [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple (vol 77, pg 3865, 1996). Phys Rev Lett 78, 1396–1396 (1997). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.