Causal Clustering for 1-Factor Measurement Models

Abstract

Many scientific research programs aim to learn the causal structure of real world phenomena. This learning problem is made more difficult when the target of study cannot be directly observed. One strategy commonly used by social scientists is to create measurable “indicator” variables that covary with the latent variables of interest. Before leveraging the indicator variables to learn about the latent variables, however, one needs a measurement model of the causal relations between the indicators and their corresponding latents. These measurement models are a special class of Bayesian networks. This paper addresses the problem of reliably inferring measurement models from measured indicators, without prior knowledge of the causal relations or the number of latent variables. We present a provably correct novel algorithm, FindOneFactorClusters (FOFC), for solving this inference problem. Compared to other state of the art algorithms, FOFC is faster, scales to larger sets of indicators, and is more reliable at small sample sizes. We also present the first correctness proofs for this problem that do not assume linearity or acyclicity among the latent variables.

1. INTRODUCTION

Psychometricians, educational researchers, and many other social scientists are interested in knowing the values of, or inferring causal relations between, “latent” variables that they cannot directly measure (e.g. algebra skill, or anxiety, or impulsiveness). One study attempted to learn the causal relations between depression, anxiety, and coping, for example [7]. A common strategy is to administer survey or test “items” that are thought to be measures or indicators of the latent variables of interest, e.g. by asking for a survey respondent’s level of agreement with the statement, “I felt that everything I did was an effort”. Unfortunately, it is rare that a latent variable is measured perfectly by any single measured indicator because any number of other factors may also influence the value of the indicator.

Researchers attempt to resolve this problem by estimating each latent of interest from the values of multiple indicators, rather than just one. A model in which each latent variable of interest is measured by multiple indicators is called a multiple indicator model [1]. In the above-mentioned study, for example, approximately 20 questions are used to estimate each investigated latent variable, in order to obtain more accurate estimates of the latent variables [7].

In many cases, despite significant care in the design of the indicator variables, the true model generating the data is not known. In particular, the measurement model, the part of the multiple indicator model that relates the indicators to the latent variables, is not known. It can be difficult to ascertain how many other factors might be influencing particular indicators or sets of indicators, or whether some of the indicators might be directly influencing other indicators, given just the survey design and background domain knowledge. Algorithms such as MIMBuild [6] can learn the causal relations between the latent variables if they are given a correct measurement model along with the indicator data, but correct output is not guaranteed if the measurement model is wrong. Incorrect measurement models result in incorrect inferences about the latent variables. Learning a correct measurement model is thus a critical step in learning a multiple indicator model. This paper addresses the problem of learning correct measurement models.

The space of all possible measurement models for a set of indicator variables is very large, and involves latent variables. It is much larger than the space of directed graphs over the indicator variables.¹ Instead of searching the entire space, researchers look for measurement models that have a particular form. Specifically, they look for measurement models where each indicator is a function only of the latent variable it measures, and an independent noise term that doesn’t correlate with any other indicator. This transforms the structure learning problem to a clustering problem: indicators should be clustered together if they measure the same indicator, and clustered apart if they do not.

Factor analysis is the most commonly used method for identifying multiple indicator models, but simulation studies have shown that factor analysis performs poorly when there are sources of covariation among the indicators other than the factor being measured [6]. If the way participants answer one survey item influences how they answer another survey item, for example, then factor analysis will often not cluster the indicators correctly. The BuildPureClusters (BPC) algorithm [6, 8] solves this problem by leveraging higher order algebraic constraints on the covariance matrix of the indicators. Intuitively, BPC uses a theorem stating that under conditions such as linearity, certain products of values in the covariance matrix will be equal if and only if the data was generated by the kind of measurement model we are looking for. This class of measurement models is described in detail in section 1.2. Unfortunately, BPC is slower than factor analysis and does not perform optimally on smaller data sets, such as those that social scientists often work with.

In this paper, we introduce the FindOneFactorClusters (FOFC) algorithm, a clustering method for discovering measurement models that is orders of magnitude faster than BPC and has improved accuracy on smaller sample sizes. This advantage in speed allows FOFC to be used on data sets that are too large for BPC to produce results within a practical amount of time. FOFC’s improved performance on small sample sizes is also important, as such data sets are common in social science domains. Factor analysis methods are still widely used by practitioners, so we also compare FOFC to a typical factor analysis method, though they are already known to perform worse than BPC in many situations [6, 8]. Finally, we use FOFC to analyze real sociometric survey data. By leveraging FOFC’s speed and accuracy, we are able to find multiple factor models that pass chi-square tests for this data set, rather than just a single model. The discovered models also incorporate many mores indicators than the model discovered using BPC, and are thus more informative.

1.1 Structural Equation Models

We represent causal structures as structural equation models (SEMs), described in detail in [2]. SEMs are frequently employed for this purpose [5, 10]. We denote random variables with italics, and sets of random variables with boldface. In a SEM the random variables are divided into two disjoint sets: substantive variables are the variables of interest, while error variables summarize all other variables that have a causal influence on the substantive variables [2]. Each substantive random variable V has a unique error variable ϵ_V. A fixed parameter SEM S is a pair ⟨φ, θ⟩, where φ is a set of equations expressing each substantive random variable V as a function of other substantive random variables and a unique error variable, and θ is the joint distribution of the error variables. The equations in φ represent what happens if variables in the system are manipulated, while θ represents the random external noise when there is no manipulation. φ and θ collectively determine a joint distribution over the substantive variables in S. We call that distribution the distribution entailed by S.

A free parameter linear SEM model replaces some real numbers in the equations in φ with real-valued variables and a set of possible values for those variables, e.g. X = a_X,LL + ϵ_X, where $a_{X,L}\in \mathbb{R}$. In addition, a free parameter SEM can replace the distribution over ϵ_X and ϵ_L with a parametric family of distributions, e.g. the bi-variate Gaussian distributions with zero covariance. The free parameter SEM is also a pair ⟨Φ, Θ⟩, where Φ contains the set of equations with free parameters and the set of values the free parameters are allowed to take, and Θ is a family of distributions over the error variables. We make the 4 following assumptions. 1) There is a finite set of free parameters. 2) All allowed values of the free parameters lead to fixed parameter SEMs such that each substantive variable X can be expressed as a function of the error variables of X and the error variables of its ancestors. 3) All variances and partial variances among the substantive variables are finite and positive. 4) There are no deterministic relations among the substantive variables.

This paper includes several figures showing path diagrams (or causal graphs). A path diagram is a directed graph representing a SEM: it contains an edge B → A if and only if B is a non-trivial argument of the equation for A. By convention, error variables are not included in a path diagram if they are not correlated. A fixed-parameter acyclic structural equation model with uncorrelated errors is an instance of a Bayesian Network ⟨G, P(V)⟨, where the path diagram is G, and P (V) is the joint distribution of the variables in G entailed by the set of equations and the joint distribution of the error variables [10].

The work in this paper makes heavy use of “structural entailment”. A polynomial equation Q, where the variables represent covariances, is entailed by a free-parameter SEM when all values of the free parameters entail covariance matrices that are solutions to Q. In such cases, Q is true as a consequence of the SEM’s structure alone. For example, a vanishing tetrad difference holds among {X, W} and {Y, Z}, iff cov(X, Y)cov(Z, W)–cov(X, Z)cov(Y, W) = 0, and is entailed by a free parameter linear SEM S in which X, Y, Z, and W are all children of just one latent variable L.

1.2 Pure 1-Factor Measurement Models

There are many kinds of measurement models that one might look for, but in this paper we focus on finding pure 1-factor measurement models. 1-Factor measurement models are a widely used type of multiple indicator model, where each measure (indicator variable) has precisely 1 latent (unmeasured) parent in addition to its “error” variable. There is often no guarantee, however, that the measures do not have unwanted additional latent common causes, or that none of the measures are causally influenced by any other measures. For a 1-factor measurement model to be easily used for making inferences about the latents, the model must be “pure” [6].

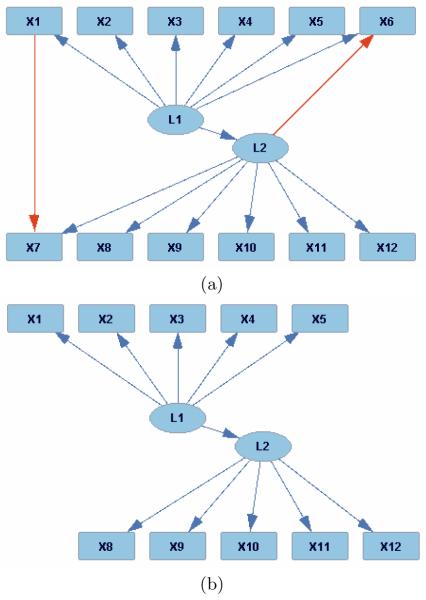
A set of variables V is causally sufficient when every cause of any two variables in V is also in V. Given a set of measured indicators O, and a causally sufficient set of variables V containing O such that no strict subset of V containing O is causally sufficient, then a 1-pure measurement model for V is a measurement model in which each observed indicator has at most 1 latent parent, no observed parents, and no correlated errors. Any model whose measurement model is pure is a pure model. Figure 1 shows two 1-factor measurement models, one impure and one pure. There are two sources of impurity in Figure 1 (a): X1 causes X7, and X6 has two latent causes, L1 and L2. However, note that the sub-model shown in Figure 1 (b) is a 1-pure measurement model, because when the variables X6 and X7 are removed, there are no edges between measured indicators, and each measured indicator has at most 1 latent cause.

Figure 1.

(a) Impure 1-Factor Model; (b) Pure Sub-model

Any subset S of O that contains four variables and for which every member of S is a child of the same latent parent, is adjacent to no other member of O, and has a correlated error with no other member of V is 1-pure; otherwise the subset is 1-mixed. In Figure 1 (a), {X2, X3, X4, X5} is a 1-pure quartet, but {X1, X2, X3, X4} and {X6, X7, X8, X9} are not 1-pure quartets.

2. TREK SEPARATION

Our algorithm utilizes trek separation theorems that were originally proven by Sullivent [11], and then extended by Spirtes [9]. In order to understand why our algorithm works, it is first necessary to understand the trek separation theorems.

A simple trek in directed graph G from i to j is an ordered pair of directed paths (P₁; P₂) where P₁ has sink i, P₂ has sink j, and both P₁ and P₂ have the same source k, and the only common vertex among P₁ and P₂ is the common source k. One or both of P₁ and P₂ may consist of a single vertex, i.e., a path with no edges. There is a trek between a set of variables V₁ and a set of variables V₂ iff there is a trek between any member of V₁ and any member of V₂. Let A, B, be two disjoint subsets of vertices V in G, each with two vertices as members. Let S(A, B) denote the sets of all simple treks from a member of A to a member of B.

Let A, B, C_A, and C_B be four (not necessarily disjoint) subsets of the set V of vertices in G. The pair (C_A; C_B) t-separates A from B if for every trek (P₁; P₂) from a vertex in A to a vertex in B, either P₁ contains a vertex in C_A or P₂ contains a vertex in C_B; C_A and C_B are choke sets for A and B [9]. Let ∣C∣ be the number of vertices in C. For a choke set (C_A; C_B), ∣C_A∣ + ∣C_B∣ is the size of the choke set. We will say that a vertex X is in a choke set (C_A; C_B) if X ∈ C_A ∪ C_B.

The definition of linear acyclicity (LA) below a choke set is complicated and is described in detail in [9]; for the purposes of this paper it suffices to note that, roughly, a directed graphical model is LA below sets (C_A; C_B) for A and B respectively, if there are no directed cycles between C_A and A or C_B and B, and each member of A is a linear function with additive noise of C_A, and similarly for B and C_B.

For two sets of variables A and B, and a covariance matrix over a set of variables V containing A and B, let cov(A, B) be the sub-matrix of Σ that contains the rows in A and columns in B. In the case where A and B both have 2 members, if the rank of the cov(A, B) is less than or equal to 1, then the determinant of cov(A, B) = 0. In that case the matrix satisfies a vanishing tetrad constraint since there are four members of A ∪ B if A and B are disjoint. For any given set of four variables, there are 3 different ways of partitioning them into two sets of two; hence for a given quartet of variables there are 3 distinct possible vanishing tetrad constraints. The following two theorems from [9] (extensions of theorems in [11]) relate the structure of the causal graph to the rank of the determinant of sub-matrices of the covariance matrix.

Theorem 1 (PETS1)

(Peter’s Extended Trek Separation Theorem): Suppose G is a directed graph containing C_A, A, C_B, and B, and (C_A;C_B) t-separates A and B in G. Then for all covariance matrices entailed by a fixed parameter structural equation model S with path diagram G that is LA below the sets C_A and C_B for A and B, rank(cov(A, B)) ≤ ∣CA∣ + ∣CB∣.

Theorem 2 (PETS2)

For all directed graphs G, if there does not exist a pair of sets ${\mathrm{C}}_{\mathrm{A}}^{\prime }$, ${\mathrm{C}}_{\mathrm{B}}^{\prime }$, such that (${\mathrm{C}}_{\mathrm{A}}^{\prime }$; ${\mathrm{C}}_{\mathrm{B}}^{\prime }$) t-separates A and B and $\mid {\mathrm{C}}_{\mathrm{A}}^{\prime }\mid +\mid {\mathrm{C}}_{\mathrm{B}}^{\prime }\mid \le r$, then for any C_A, C_B there is a fixed parameter structural equation model S with path diagram G that is LA below the sets (C_A; C_B) for A and B that entails rank(cov(A, B)) > r.

Theorem 1 guarantees that trek separation entails the corresponding vanishing tetrad for all values of the free parameters, and Theorem 2 guarantees that if the trek separation does not hold, it is not the case that the corresponding vanishing tetrad will hold for all values of the free parameters. If the vanishing tetrad does not hold for all values of the free parameters it is still possible that it will hold for some values of the free parameters, but the set of such parameter values will have Lebesgue measure 0. See [9].

This paper focuses only on 1-factor models, but note that the PETS theorems can be applied in the manner we describe in the following section for any n-factor model (in particular, see [4] for 2-factor models).

3. ALGORITHM

Before describing the FindOneFactorClusters (FOFC) algorithm, we will illustrate the intuitions behind it using Figure 1 (a). Let a vanishing quartet be a set of 4 indicators in which all 3 tetrads among the 4 variables are entailed to vanish by the PETS theorems. In general, pure sets of 3 variables (pure triples) can be distinguished from non-pure sets of 3 variables (mixed triples) by the following property: a triple is pure only if adding each of the other variables in O to the triple creates a vanishing quartet. For example, in Figure 1(a), T₁ = {X₂, X₃, X₄} is a pure triple. Adding any other variable to T₁ creates a quartet of variables which, no matter how they are partitioned, will have one side t-separated from the other side by a choke set ({L₁} : Ø). In contrast, T₂ = {X₁, X₂, X₃} is not pure, and when X₇ is added to T₂, the resulting quartet is not a vanishing quartet; when X₁ and X₇ are on different sides of a partition, at least 2 variables (including L₁, and X₁ or X₇) are needed to t-separate the treks between the variables in the two sides of the partition.

The algorithm first calls FindPureClusters, which tests each triple to see if it has the property that adding any other member of O creates a vanishing quartet; if it does have the property it is added to the list PureList of pure triples. FindPureClusters tests whether a given quartet of variables is a vanishing quartet by calling PassesTest, which takes as input a quartet of variables, a sample covariance matrix, and the search parameter α that the user inputs to FOFC. PassesTest can use any test of vanishing tetrad constraints; we use the Wishart test [12].² The list of pure triples at this point is every subset of X₂ through X₅ of size 3, and every subset of X₈ through X₁₂ of size 3. X₁, X₆, and X₇ do not appear in any pure triple. GrowClusters then initializes CList to PureList.

If any two pure sets of variables overlap, their union is also pure. FOFC calls GrowClusters to see if any of the pure triples in PureClusters can be combined into a larger pure set. Theoretically, GrowClusters could simply check whether any two subsets on PureClusters overlap, in which case they could be combined into a larger pure set. In practice, however, in order to determine whether a given variable o can be added to a cluster C in CList, GrowClusters checks whether a given fraction (determined by the parameter GPar) of the sub-clusters of size 3 containing 2 members of C and o are on PureList. If they are not, then GrowClusters tries another possible expansion of clusters on CList; if they are, then GrowClusters adds o to C in CList, and deletes all subsets of the expanded cluster of size 3 from PureList. GrowClusters continues until it exhausts all possible expansions.

Finally, when GrowClusters is done, SelectClusters goes through CList, iteratively outputting the largest remaining cluster C still in CList, and deleting any other clusters in CList that intersect C (including C itself).

FindPureClusters dominates the algorithm’s complexity, which in the worst case requires testing n choose 4 sets of variables, and each quartet requires testing 2 of the 3 possible vanishing tetrad constraints in order to determine if they all vanish. In practice, we have found that it can be easily applied to hundreds of measured variables at a time. On a personal laptop, running FOFC on a data set of 200 measured variables took only a few seconds, and a data set of 500 measured variables took approximately one minute. We believe that running FOFC on data sets with thousands or tens of thousands of variables should be feasible, but further testing is required to identify the upper bounds of FOFC’s scalability in practice.³

Algorithm 1.

FindOneFactorClusters

Data: Data, V, GPar, α

Result: SelectedClusters

Purelist = FindPureClusters(Data, V, α)

CList = GrowClusters(Purelist, GPar)

SelectedClusters = SelectClusters(CList)

Algorithm 2.

FindPureClusters

Algorithm 3.

GrowClusters

4. CORRECTNESS

The main theorems in this section are more general and abstract than the correctness and completeness of FOFC. They are included here so that they might be utilized directly for future theorems and algorithms. FOFC’s correctness and completeness under appropriate assumptions follows as a corollary of these other theorems, and is stated and proven after the more general theorems. The general theorems make use of terms and concepts that are not necessary for understanding the problem we focus on in this paper, or how FOFC functions. The appropriate transitions from these abstract concepts to those related to FOFC’s correctness and completeness are made within the corollary proof.

4.1 Definitions and Assumptions

Let SEM $\mathcal{G}$ have measured variables O and unmeasured variables L. A set of variables M ⊆ O is a 1-separable cluster relative to O iff every M ∈ M has no zero partial correlations with any other O ∈ O conditional on any set S ⊆ O \ ({O} ∪ M), but for which there is a L ∈ L, re ferred to as a key latent for M in O, such that all M ∈ M have zero partial correlations with all O ∈ O conditional on L. In graphical terms, this means that the key latent L d-separates the members of M from the members of O. A set of measures C ⊆ O is a swappable tetrad cluster iff all tetrads over variables in O that include at least 3 variables in C are entailed to vanish, and ∣C∣ ≥ 3 (to prevent vacuously satisfying the universal quantifier).

We assume that there is a trek between every pair of indicators and that there are no entailed vanishing partial correlations within O conditional on any subset of the other members of O. It is easy to check in practice whether this assumption is satisfied, and variables that violate this assumption can be removed from the data in pre-processing. In analogy to the Causal Faithfulness Assumption [10], we assume that tetrad constraints vanish only when they are entailed to vanish by the structure of the graph, and thus for all values of the free parameters. In the linear case and other natural cases, the set of parameters that violates this assumption is Lebesgue measure 0. In all of the following, we assume that all the indicators have a linear relationship with their latent parents.

4.2 Theorems and Proofs

Theorem 3 (Uniqueness of Key Latents)

If ∣M∣ ≥ 2, ∣O∣ ≥ 3, and there are no entailed zero partial correlations in O, then: if L₁ ∈ L is a key latent for M in O, then there can be no L₂ ∈ L, L₂ ≠ L₁, Corr(L₂, L₁) ≠ 1, such that L₂ is a key latent for M in O.

Proof

Assume ∣M∣ ≥ 2, ∣O∣ ≥ 3, that there are no zero partial correlations in O, and that there is a L₁ ∈ L such that all M ∈ M are independent of all O ∈ O conditional on L₁.

By contradiction, assume that there is an L₂ ∈ L, L₂ ≠ L₁, Corr(L₂, L₁) ≠ 1, such that all M ∈ M are independent of all O ∈ O conditional on L₂.

Both L₁ and L₂ must lie on every trek from each member of M to each member of O. Since M has at least two distinct members, and there is at least one additional member in O, let M₁ and M₂ be distinct members of M, and let X ∈ O be an additional distinct variable. L₁ and L₂ must both lie on every trek between M₁ and M₂, M₁ and X, and M₂ and X. Since we’ve assumed there are no entailed zero partial correlations in O, then there must be at least one trek for each pair.

Let an O-unblocked ancestor of A be an ancestor of A with at least one directed path to A without any member of O in it. Similarly, let an O-unblocked trek be a trek without any member of O on it, with the possible exception of the endpoints.

Since there is at least one trek between each pair, and L₁ must lie on each of those treks, L₁ must be an O-unblocked ancestor of at least two of M₁, M₂, and X. To see this, note that since L₁ lies on all treks from M₁ to M₂, and since there is at least one such trek, then L₁ must be an O-unblocked ancestor of M₁ or M₂. WLOG let it be M₁. By similar reasoning, L₁ must also be an O-unblocked ancestor of M₂ or X.

WLOG let L₁ be an O-unblocked ancestor of M₁ and M₂. Then there is an O-unblocked trek of the form {M₁, … ← …, L₁, … → …, M₂}. Since this is a trek between M₁ and M₂, L₂ must also be on this trek, and since L₂ ≠ L₁, L₂ must be be on either the M₁ or the M₂ side of L₁. WLOG, let the trek be of the form {M₁, … ← …, L₁, … → …, L₂, … → …, M₂}.

L₁ must also be on an O-unblocked trek from X to M₁, entailing that there is a (possibly trivial) O-unblocked trek from L₁ to X. L₂ either does or does not lie on this trek. If L₂ does not lie on this trek, then there is a trek from X to M₁ that does not include L₂, violating the assumption that L₂ is on all such treks. If L₂ does lie on this trek, then there is a trek from X to M₂ which does not include L₁, violating the assumption that L₁ is on all such treks. Thus, both parts of the disjunct lead to contradiction.

Theorem 4

If M is a 1-separable cluster relative to O with key latent L, and ∣M∣ ≥ 3, then M is a swappable tetrad cluster.

Proof

Let M be a 1-separable cluster relative to O with key latent L, with ∣M∣ ≥ 3. If ∣O∣ = 3 then M is vacuously a swappable tetrad cluster since there are no tetrads, vanishing or otherwise, so assume ∣O∣ ≥ 4. Since ∣M∣ ≥ 3 we have at least three distinct measures in M, M₁, M₂, and M₃; and since ∣O∣ ≥ 4 there is at least one more distinct variable, X.

By the definition of 1-separable cluster, every M ∈ M has no entailed zero partial correlations with any other O ∈ O, and all M ∈ M are independent of all O ∈ O conditional on L. It follows that there are no direct edges between any M ∈ M and any O ∈ O, that there are treks from ever M ∈ M to every O ∈ O, and that L lies on all those treks.

M₁, M₂, M₃, and X were chosen arbitrarily, and there are three distinct tetrads formed with those variables. WLOG, consider the tetrad {{M₁, M₂}, {M₃, X}}. In order to apply PETS1 to show that this tetrad vanishes, we need to show that either L is on the {M₁, M₂} side of every trek from {M₁, M₂} to {M₃, X}, or L is on the {M₃, X} side of every trek from {M₁, M₂} to {M₃, X}. By contradiction, assume otherwise, entailing that one of those treks has its source only on the {M₁, M₂} side of L, and another trek has its source only on the {M₃, X} side of L (with L not being the source for either trek). But this entails that there’s a nontrivial trek from a member of {M₁, M₂} into L and a nontrivial trek from {M₃, X} into L, which collectively form an active path from a member of {M₁, M₂} to a member of {M₃, X_g} with L as either the sole collider on the path, or a descendent of the sole collider on the path. This would make the path active when we condition on L and thus violate the assumption that all M ∈ M are independent of all O ∈ O conditional on L.

We can now apply PETS1 (see section 2) to show that all tetrads formed from {M₁, M₂, M₃, X} must vanish. Since those variables were chosen arbitrarily, it follows that all tetrads consisting of 3 variables from M and 1 from O will vanish, and so M is a swappable tetrad cluster.

Theorem 5

If ∣O∣ ≥ 4 and M is a swappable tetrad cluster relative to O, then M is a 1-separable cluster relative to O.

Proof

This theorem is a corollary of Lemma 9 in [6]. Silva’s Lemma 9 states: “Let G(O) be a linear variable model, and let C = {X₁, X₂, X₃, X₄} ⊂ O be such that all tetrads over C vanish. If all members of C are correlated, then a unique node P entails all the given tetrad constraints, and P d-separates all elements in C.” In particular, note that the unique node P mentioned in the lemma will satisfy the requirements for being a key latent of C.

The proof of Lemma 9 given by Silva doesn’t require assumptions beyond those we’re using in this paper; in particular it does not make use of linearity above the choke sets. As such, it can be applied in our setting.

Theorem 6 (FOFC is sound and complete)

FOFC outputs cluster M if and only if: ∣M∣ ≥ 3, and there is a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in M, and no other cluster N s.t. M ⊂ N and there is a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in N.

Proof

The proof proceeds by proving each direction of the “if and only if” separately. First, let ∣M∣ ≥ 3, and let there be a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in M, and let there be no other cluster N, with M ⊂ N, s.t. there is a pure 1-factor measurement submodel wit one latent variable using all and only those measured variables in N. Since there is a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in M, it follows that M is a 1-separable cluster (the one latent variable is the key latent). By theorem 4, M is a swappable tetrad cluster. Since M is a swappable tetrad cluster, every subset of size 3 will be in PureList (see section 3). By theorem 5 and using the assumption that M’s pure 1-factor measurement model is not contained by another pure 1-factor measurement model, M is not contained by another swappable tetrad cluster. It follows that during the GrowClusters step of FOFC, some member of PureList will be grown up to M, and stop growing at that point. M will then be a cluster output by FOFC.

For the other direction, assume FOFC outputs cluster M. For M to be in the output of FOFC, it must have been grown from some member of PureList, meaning that it contains that member of PureList (see section 3). All members of PureList are sets of at least 3 distinct indicators, so ∣M∣ ≥ 3. By how FOFC constructed PureList and then M, M is a swappable tetrad cluster. By theorem 5, M is a 1-separable cluster. By theorem 3, there is exactly 1 key latent separating the indicators in M. It follows that there is a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in M. There can be no other cluster N with a pure 1-factor measurement submodel with one latent variable using all and only those measured variables in N s.t. M ⊂ N, since this would lead to FOFC continuing to grow M into N during the GrowClusters step, contradicting the assumption that FOFC outputs cluster M.

5. SIMULATIONS

We simulated data from 4 different data generating models with free parameters. The base graph has 4 factors, with 48 measures divided evenly among them, e.g. factor L1 is measured by X1 – X12. The latent structure is L1 → L2, L1 → L3, L2 → L4, L3 → L4.

Case 1 is a linear SEM with free parameters, Gaussian noise, and no impurities. In all cases, the Gaussian noise variables have mean 0 and variance drawn from U(0.5, 1), and in cases 1-3 the edge parameters are drawn from a uniform distribution with support split between (−2, −1 and (1, 2). To account for sensitivity to variable order, we randomized the order of the measures before applying the search procedures.⁴

Case 2 adds impurities to Case 1. Specifically, we add the following edges: {X1 → X2, X2 → X3, X1 → X3, X2 → X4, X1 → X13, X2 → X14, L4 → X15, X25 → X26, X25 → X27, X25 → X28, X37 → X40, X38 → X40, X39 → X40}.

Case 3 modifies Case 2 s.t. L2, L3 and L4 are nonlinear functions of their parents: each latent L was set to the sum over its parents of 0.5 * c₁ * P + 0.5 * c₂ * P² plus an error, where P is one of the parents of L, and c₁ and c₂ are edge parameters. We tested the data for non-linearity with a White test in R, and the null hypothesis test of linearity was rejected.

Case 4 modifies the latent structure of Case 2 to be a cycle of length 4: L1 → L3 and L3 → L4 were removed and replaced with L4 → L3 and L3 → L1. The parameters on all 4 resulting latent structure edges are drawn from U(0.1, 0.3) to guarantee that the values of the latents will converge. All other edge parameters were as in cases 1-3.

Using these 4 cases, we evaluated FOFC alongside BPC [6] and factor analysis (FA) [1]. The versions of FOFC and BPC we used can be found in our publicly available implementation, noted in section 3. Note that our implementation of BPC is a well-optimized version of the code used by [6]. For FA, we used factanal() from R 3.1.1 with the oblique rotation promax. Data was generated from each free parameter SEM described above, at n = 100, 300, and 1000. The FOFC and BPC algorithms were run with significance level (for the vanishing tetrad tests) of 1/n where n is the sample size.⁵ FA was run with 4 factors and a cutoff threshold of 0.5. For all methods, we ignore and treat as unclustered any output cluster of size < 4; in our experience, very small clusters are unreliable and uninformative.

All simulations were run on the same Macbook Air (2Ghz CPU, 8g RAM). In terms of run time, FOFC was almost an order of magnitude faster than FA, and was two orders of magnitude faster than the computationally optimized implementation of BPC. FOFC’s speed is perhaps its primary advantage over BPC.

For each of the three methods and three sample sizes, we calculated the average cluster precision, recall, and accuracy of the inferred latent structure. We first evaluate these methods on precision: the proportion of output clusters that are pure, to the total number of output clusters. A cluster in a clustering is considered pure if there exists a latent in the true model that d-separates every member of that cluster from every over measure included in some cluster in the clustering.

Figures 2, 3, and 4 show the mean (over 50 runs) of the precision, recall, and Structural Hamming Distance (SHD), respectively, of the clustering output for each simulation case. In Figure 2, the error bars show the standard deviation of the precision. The blue, red and green bars represent the performance of FA, BPC and FOFC respectively. The bars are grouped by sample size: n =100, 300, and 1000 respectively. We generated 50 models for each of Cases 1-4.

Figure 2.

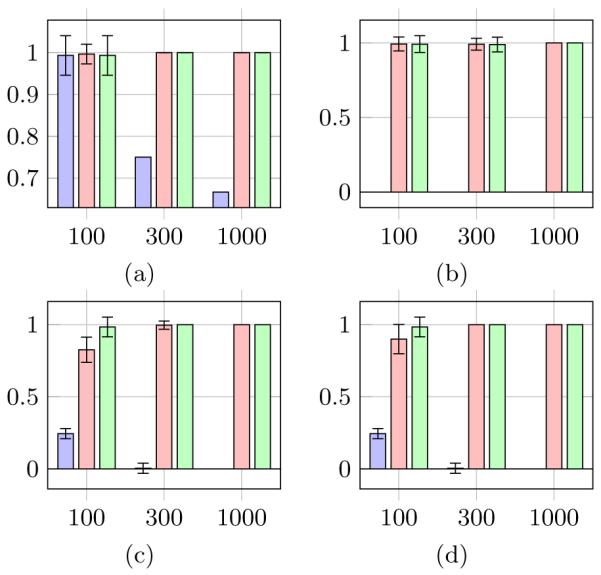
(a-d) Average Precision of FA (blue), BPC (red), and FOFC (green) Clustering Output for Cases 1-4

Figure 3.

(a-d) Average Recall of FA (blue), BPC (red), and FOFC (green) Clustering Output for Cases 1-4

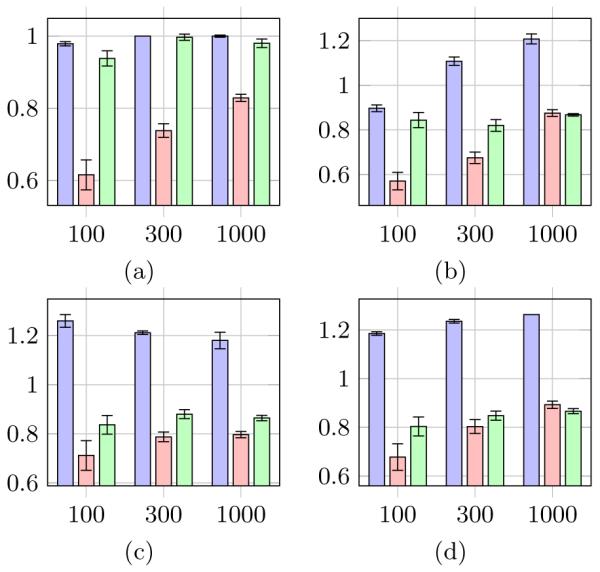
Figure 4.

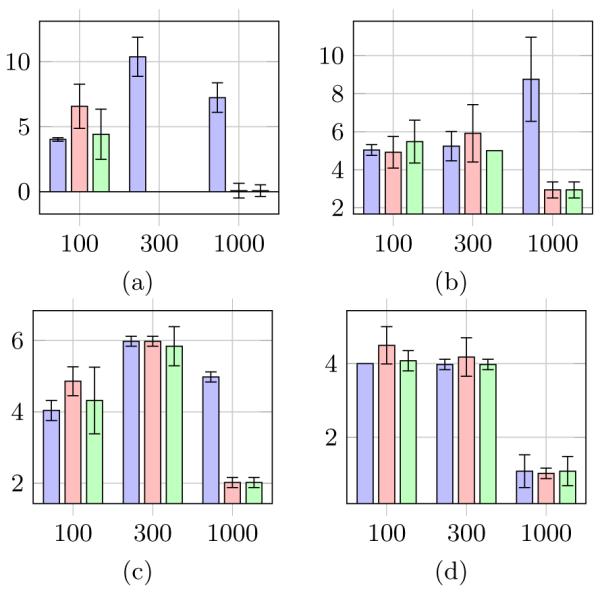
(a-d) Average SHD of FA (blue), BPC (red), and FOFC (green) MIMbuild Output for Cases 1-4

For some practitioners, precision may be the most important evaluative criterion, as it measures the how reliably output clusters can be trusted. FOFC and BPC both excelled in precision, while FA did worse than expected. FA did worse as the sample size increased, while BPC and FOFC improved when there was room to do so. It is possible that the excellent performance of FOFC and BPC is due to these algorithms creating very little output, however the results for the next evaluative criterion, recall, show that this is not the case.

We define recall to be the ratio of the number of output measures used in the output clustering to the number of output measures in a maximal pure clustering. A maximal pure clustering is a clustering composed of only pure clusters such that no other clustering composed of pure clusters uses more measures than it. For Case 1, a maximal pure clustering uses all 48 measures, while for Cases 2-4 a maximal pure clustering has 38 measures in it.

Unlike typical recall metrics, this kind of recall can have a value greater than 1. The ideal recall is 1; recall greater than 1 entails that there are impure clusters in the output; recall less than 1 means that fewer measures are being utilized by the output clusters than is optimal. These plots show that FOFC and BPC produce outputs that are large but not too large, while FA outputs too many variables. FOFC and BPC have similar recall for most circumstances, but FOFC has some advantages at smaller sample sizes.

To evaluate the accuracy of the structural models inferred by the three methods, we first used the output clusters as inputs to the MIMbuild algorithm [6] for inferring structural models from measurement models. We then created a mapping from the latent variables in the inferred structural models to those of the true structural models in the same manner as [6]. Finally, we computed the Structural Hamming Distance (SHD) between the inferred structural model and the true structural model, using the mapping from the previous step to identify inferred latents with their respective true latents (when they exist).

FOFC and BPC have very similar SHD in all cases and at all sample sizes. In most cases, FOFC and BPC improve with sample size. It is somewhat surprising that the SHD is as small as it is for cases 3 and 4, since the MIMBuild algorithm assumes that the causal relations amongst the latents are linear and acyclic. In those cases, even with perfect clusters, MIMBuild is not guaranteed to find the correct structure amongst the latents.

For some cases and sample sizes, the SHD of FA is comparable to that of BPC and FOFC, however in other cases it is dramatically worse. Unlike BPC and FOFC, FA often does not improve with sample size, and in case 2 actually significantly worsens at sample size 1000. FA’s performance is surprisingly good, considering its poor precision, but this is due to the way in which SHD is being calculated: actual structural nodes can be associated with hypothesized structural nodes even if the hypothesized clusters are impure [6]. FA is also benefitting from using the correct number of factors as input, unlike BPC and FOFC. Overall, BPC and FOFC have improved SHD compared to FA, as expected.

6. REAL DATA

We applied the current implementation of FOFC to Lee’s depression data [7], which has 61 indicator variables and a sample size of 127. Lee’s model fails a chi-square test: p = 0. Silva analyzed the same data set, using BPC to infer the existence of 1-pure measurement models [6]. The 1-pure measurement models are then used to construct a factor model over the variables in the measurement models, using the prior knowledge that Stress is not an effect of other latent variables. That factor model passes a chi square test with p = 0.28. However, that factor model includes only 5 out of 21 measures of Stress, 4 out of 20 measures of Coping, and 3 out of 20 measures of Depression, which is only barely enough indicators to informatively measure the factors in the model.

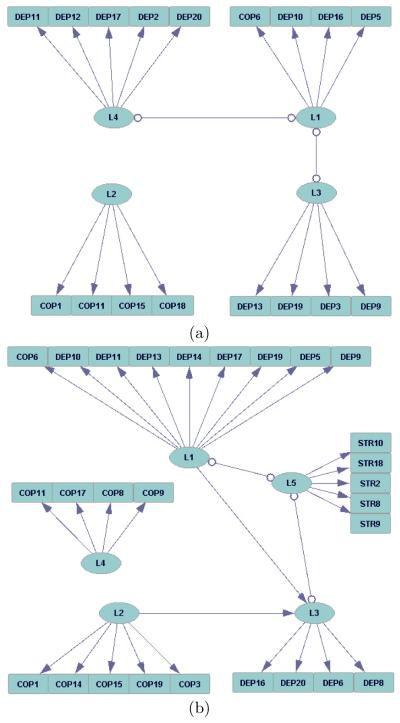
Since FOFC is fast, we reran it numerous times using different parameters and randomly reordering the measure variables for different results. We kept track only of discovered models that passed a chi square test. The highest scoring model that was found (p = 0.297) is shown in Figure 5 (a). The graphical model in this figure includes edges with “o” symbols at both ends, meaning that MIMBuild could not determine how those edges should be oriented. Such models represent an equivalence class of directed acyclic graphs, and are described in more detail in [10]. That model contains 4 factors (3 for depression, 1 for coping, 0 for stress) and uses a total of 17 measures. Another discovered model, shown in Figure 5 (b), does not pass a chi square test at as high of a p-value (p = 0.155), but is still notable due to its large size. That model contains 5 factors (2 for depression, 2 for coping, and 1 for stress) and uses 27 of the 61 measures recorded in Lee’s data set.

Figure 5.

Factor Models Inferred From Lee’s Data

A few features shared by both graphs are worth discussing. First, both graphs include a cluster of measured variables, and their latent parent, which is disconnected from the rest of the graph. Looking at the sample correlation matrix this appears to be warranted: many coping variables have near-zero correlations with non-coping variables, but moderate correlations with other coping variables. Both of these features of the distribution can be explained by the presence of an independent measurement model applying to some or all of the coping variables in the output graph.

Second, both models include multiple clusters for depression variables whose latents are connected. This suggests that it might be productive to reconceptualize depression as having a multi-dimensional value rather than a single number. Or, one might hypothesize that there is still a uni-dimensional depression value, but that it is more diffcult to measure than previously thought. In particular, it may be the case that a person’s level of depression is actually expressed via multiple more fine-grained properties, which are themselves also latent variables. The absence of an edge between L3 and L4 in Figure 5 (a) suggests that this hypothesis may not be correct, as the presence of such a higher-order latent variable causing L1, L3, and L4 would induce an edge between L3 and L4 if, as in this graph, it is not explicitly represented. Nonetheless, it may be worth further investigation.

Third, all the clusters identified by the algorithm accord very strongly with the background knowledge of the expert who designed the survey and identified which variables were, e.g., “coping” variables, and which were, e.g. “depression” variables. The sole exception is that COP6 reliably clusters with depression variables, rather than with other coping variables. According to [7], COP6 is the respondent’s reported degree of agreement with the following statement: “I feel that stressful situations are God (high power)’s way of punishing me for my sins or lack of spirituality”. We leave it to the reader to decide whether it is plausible that this item could cluster with depression indicators, rather than coping indicators.

The two models diverge regarding how depression relates to the other two factors of interest (coping and stress). Figure 5 (a) identifies no links between the depression factors and the coping factor it identifies, and identifies no stress factor at all. One can unfortunately conclude relatively little from this. This model suggests that there is at least some dimension of coping which is independent of a person’s depression, but remains agnostic as to whether there may be another dimension of coping which is causally connected to depression, especially because a large number of coping measures remain unclustered and are thus absent from the model. Since the model identifies no stress factor, it remains agnostic regarding its potential causal connections with the other factors.

Figure 5 (b) finds two coping factors, which are independent of each other. One of these coping factors has an edge oriented towards L3, a depression factor, but does not have any other connections to any other factors, and in particular is not connected to the other depression factor or to the stress factor. This suggests that some aspect of coping may causally influence some aspect of depression, but that the two are not connected as strongly as one might think. The edge from L3 to L5 is undirected, so it is unclear whether the coping factor is a causal ancestor of the L5 factor or not: an aspect of coping may or may not have a causal effect on stress mediated by an aspect of depression. L5, the stress factor, is connected by undirected edges to both L1 and L3, and so the graph is relatively agnostic about whether stress causes the depression factors. If L1 and L3 were both parents of L5, however, there would be no unoriented edges, so the graph does at least suggest that it is not the case that both aspects of depression cause stress.

Lee’s original hypothesis was that stress, coping, and depression each have a single factor, and that the stress and coping factors both cause the depression factor, and would also be correlated, although Lee was agnostic about whether that correlation would be due to the stress or coping factor causing the other one, or to the stress and coping factors having correlated error terms. Neither of the two models presented here, however, include a direct edge between a coping variable and a stress variable, and both models suggest that at least depression is better represented with multiple factors than with one. Both models also suggest that Lee’s data is relatively agnostic regarding whether stress causes depression or not, as a stress factor does not occur in model (a), and the edges between the stress factor and the depression factors in model (b) are unoriented. Model (b) partially corroborates Lee’s hypothesis that a coping factor causes a depression factor, as one of the two coping factors in that model is a direct cause of one of the two depression factors in the model. Overall, it is not a bad sign that the models found here do not align closely with Lee’s hypothesis, as Lee’s model does not pass a chi square test: p=0.

Silva used the BPC algorithm on Lee’s data, and found a model with a single stress factor, a single depression factor, and a single coping factor, with the stress factor being a direct cause of the depression factor, and the depression factor being a direct cause of the coping factor [6]. These edge orientations were identified by constraining their model such that the stress factor could not be a descendent of the other latent variables. Their model passes a chi square test with p=0.28, however it is also very small, incorporating only 12 observed variables. In contrast, the model in Figure 5 (a) has more variables and passes a chi square test at a higher p value, although it does not tell a story as compelling as the one told by Silva’s model. In terms of their structural differences, the models found here do not find an edge from a depression factor to a coping factor. The model in Figure 5 (a) finds no connection at all, while the one in 5 (b) actually finds the opposite: an edge from a coping factor to a depression factor. Further, this edge orientation is made without making any structural assumptions about the factors, unlike the corresponding edge in Silva’s model. Model (a) does not find a stress factor at all, but model (b) finds a stress factor with edges connecting it to both depression factors. If we also assumed that stress cannot be a descendent of depression, then that information could be used to orient these edges in accord with Silva’s model.

7. FUTURE WORK

We are currently exploring additional approaches for making FOFC even more reliable and efficient. FOFC’s principle benefit over BPC is speed, but the degree of the advantage is such that not only can FOFC be applied to much larger problems, but it is feasible to incorporate FOFC as part of a more complex algorithm for improved stability and reliability. We also believe FOFC’s recall could be improved by removing impure variables from the input variables given to it, which could be done in pre-processing or as part of a more complex process between iterations of FOFC. It would also be beneficial to develop a better understanding of the space of possible search procedures involving pure quartets, of which this implementation of FOFC is only one type of greedy search. Finally, we would like to generalize this method to arbitrary number of factor parents, rather than just 1.

Table 1.

Run Times On Simulated Data (ms)

METHOD	MEAN	SE
FA	642	222
BPC	9482	4953
FOFC	94	68