MODEL AVERAGING BASED ON KULLBACK-LEIBLER DISTANCE

Abstract

This paper proposes a model averaging method based on Kullback-Leibler distance under a homoscedastic normal error term. The resulting model average estimator is proved to be asymptotically optimal. When combining least squares estimators, the model average estimator is shown to have the same large sample properties as the Mallows model average (MMA) estimator developed by Hansen (2007). We show via simulations that, in terms of mean squared prediction error and mean squared parameter estimation error, the proposed model average estimator is more efficient than the MMA estimator and the estimator based on model selection using the corrected Akaike information criterion in small sample situations. A modified version of the new model average estimator is further suggested for the case of heteroscedastic random errors. The method is applied to a data set from the Hong Kong real estate market.

1. Introduction

Model averaging is an alternative to model selection for dealing with model uncertainty. By minimizing a model selection criterion, such as C_p (Mallows (1973)), AIC (Akaike (1973)), and BIC (Schwarz (1978)), one model can be chosen from a set of candidate models, but we end up “putting all our inferential eggs in one unevenly woven basket” (Longford (2005)). Model averaging often reduces the risk in regression estimation, as “betting” on multiple models provides a type of insurance against a singly selected model being poor (Leung and Barron (2006)). Additionally, it is often the case that several models fit the data equally well, but may differ substantially in terms of the variables included and may lead to different predictions (Miller (2002)). Combining these models seems to be more reasonable than choosing one of them. Averaging weights can be based on the scores of information criteria (Buckland, Burnham and Augustin (1997), Hjort and Claeskens (2003), Claeskens, Croux and van Kerckhoven (2006), Zhang and Liang (2011), Zhang, Wan, and Zhou (2012)). Other model averaging strategies that have been developed include, for example, the adaptive regression by mixing of Yang (2001), the Mallows model averaging (MMA) of Hansen (2007) (see also Wan, Zhang, and Zou (2010)), and the optimal mean squared error averaging of Liang et al. (2011).

The C_p and AIC are both widely used criteria in model selection. The former was developed from prediction of “scaled sum of squared errors” (Mallows (1973)), and the latter was produced by an approximately unbiased estimator of the expected Kullback-Leibler (KL) distance (Akaike (1973)). In addition, GIC (Konishi and Kitagawa (1996)), KIC (Cavanaugh (1999)), and RIC (Shi and Tsai (2004)) were also developed from the KL distance. Recently, Hansen (2007) utilized the C_p criterion in model averaging (called Mallows’ criterion) and presented the asymptotic optimality of the resulting MMA estimator. Motivated by these facts, proposing a novel model averaging approach from estimating the expected KL distance seems to be feasible and potentially interesting. From Shao (1997), C_p and AIC can be classified into the same class according to their asymptotic behaviors. Thus, the new approach is expected to have the same asymptotic optimality as MMA.

Hurvich and Tsai (1989) proposed a corrected version of AIC, AICc, that is an exactly unbiased estimator of the expected KL distance in linear models with normally homoscedastic error and thus has advantages over AIC and C_p under small sample situations. Following this observation, our approach is based on an unbiased estimator of the expected KL distance from the averaging model (the model with parameters estimated by model averaging) to the true data generating process, thus our approach is further expected to have advantages over MMA under small sample situations, which is verified by our simulation study. A referee mentioned that the choice of weights via a Kullback-Leibler distance was proposed in an entirely different context by Rigollet (2012), in which non-random vectors are aggregated and risk inequalities were proved.

More recently, to average estimators under a heteroscedasticity setting, Hansen and Racine (2012) proposed a jackknife model averaging (JMA) method. Liu and Okui (2013) suggested a Mallows’ C_p-like criterion for a heteroscedasticity setting and referred to their method as heteroscedasticity-robust C_p model averaging. In the current paper, we further modify our approach for averaging estimators for a heteroscedasticity setting.

The remainder of this paper is organized as follows. Section 2 introduces a weight choice criterion from estimating the KL distance and proves the asymptotic optimality of the resulting model average estimator. Section 3 extends the new method to the setting with heteroscedastic errors. Section 4 investigates the finite sample performance of the proposed model average estimators through extensive simulation studies. Section 5 applies the model average estimators to an empirical example. Section 6 has concluding remarks. Assumptions for the theoretical properties are provided in an Appendix and the proofs are reported in the Supplementary Material.

2. Weight Choice Criterion from KL Distance

Consider the data generating process

$$y=\mu +e,$$ (2.1)

where y = (y₁, …, y_n)^T is an n×1 vector of observations, μ = (μ₁, …, μ_n)^T is the mean vector of y, and e = (e₁, …, e_n)^T with the e_i’s independent with mean zeros and variance σ². We assume that e has a multivariate normal distribution when developing weight choice criteria, but the normality assumption is unnecessary when proving asymptotic optimality of the resulting model average estimators.

Assume that there are S candidate models used to approximate the data generating process given in (2.1). Write μ̂ ^(s) as the estimator of μ based on the s^th candidate model. Let the weight vector w = (w₁, …, w_S)^T, belonging to the set $\mathcal{W}=\{w\in {[0,1]}^S:{\sum }_{s=1}^S{w}_s=1\}$. The model average estimator of μ is written as $\widehat{\mu }(w)={\sum }_{s=1}^S{w}_s{\widehat{\mu }}_{(s)}$. Denote σ̂² as an estimator of σ².

Let f and g be the true density of the distribution generating the data y, and the density of the model fitting the data, respectively. The KL distance between them is given by I(f, g) = E_f(y){log f(y)} – E_f(y){log g(y|θ)}, where θ includes unknown parameters. Suppose that θ̂(y) is an estimator of θ. Then, the expected KL distance is

$$E_{f(y)}\{I(f,g_{\widehat{\theta }(y)})\}=E_{f(y^{\ast })}\{logf(y^{\ast })\}-E_{f(y)}(E_{f(y^{\ast })}[logg\{y^{\ast }\mid \widehat{\theta }(y)\}]),$$

where y^* is another realization from f and independent of y. Ignoring the constant E_f(y^*){log f(y^*)}, the fit of g{y|θ̂ (y)} can be assessed using the Akaike information (AI): AI = −2E_f(y)(E_f(y^*)[log g{y^*|θ̂(y)}]). Here, the fitting model is assumed to be normally distributed and the unknown parameters in (2.1) are estimated by θ̂ (y) = {μ̂ (w), σ̂ ²}. Thus, we write the Akaike information as

$$\begin{array}{l}\text{AI}(w)=-2E_{f(y)}(E_{f(y^{\ast })}[logg\{y^{\ast }\mid \widehat{\theta }(y)\}])\\ =E_{f(y)}[E_{f(y^{\ast })}\{nlog2\pi +nlog{\widehat{\sigma }}^2+{\Vert y^{\ast }-\widehat{\mu }(w)\Vert }^2{\widehat{\sigma }}^{-2}\}]\\ =E_{f(y)}\{nlog2\pi +nlog{\widehat{\sigma }}^2+{\Vert \mu -\widehat{\mu }(w)\Vert }^2+{\sigma }^{2}n{\widehat{\sigma }}^{-2}\}.\end{array}$$ (2.2)

Define

$$\begin{array}{l}\mathcal{B}(w)=nlog2\pi +nlog{\widehat{\sigma }}^2+{\Vert y-\widehat{\mu }(w)\Vert }^2{\widehat{\sigma }}^{-2}+2{\sigma }^2{\widehat{\sigma }}^{-2}\text{trace}\left(\frac{\partial \widehat{\mu }(w)}{\partial y^{\mathrm{T}}}\right)\\ +\frac{2{\sigma }^2}{{\widehat{\sigma }}^4}{\{y-\widehat{\mu }(w)\}}^{\mathrm{T}}\frac{\partial {\widehat{\sigma }}^2}{\partial y}+\frac{2{\sigma }^4}{{\widehat{\sigma }}^6}\text{trace}\left(\frac{\partial {\widehat{\sigma }}^2}{\partial y}\frac{\partial {\widehat{\sigma }}^2}{\partial y^{\mathrm{T}}}\right)-\frac{{\sigma }^4}{{\widehat{\sigma }}^4}\text{trace}\left(\frac{{\partial }^2{\widehat{\sigma }}^2}{\partial y\partial y^{\mathrm{T}}}\right).\end{array}$$

Although the definition of ℬ(w) appears complicated, the idea behind it is simple. For the purpose of selecting good weights, one should minimize AI(w) with w ∈ 𝒲. But AI(w) involves unknown moments of various random variables. So, we attempt to find an unbiased estimator of AI(w), which is just ℬ(w).

Theorem 1

If σ̂² and ∂σ̂²/∂y are continuous functions with piecewise continuous partial derivatives with respect to y, the expectation of ℬ(w) exists, and e has a multivariate normal distribution, then for any w ∈ 𝒲, E{ℬ(w)} = AI(w).

We focus on the case that μ̂ _(s) is linear with respect to y, μ̂ _(s) = P_(s)y, where the matrix P_(s) is not related to y. This class of estimators includes least squares, ridge regression, Nadaraya-Watson and local polynomial kernel regression with fixed bandwidths, nearest neighbor estimators, series estimators, and spline estimators (Hansen and Racine (2012)). Let $P(w)={\sum }_{s=1}^S{w}_s{P}_{(s)}$, so that μ̂ (w) = P(w)y.

When σ² is known, ℬ(w) can be simplified to

$$nlog2\pi +nlog{\sigma }^2+{\sigma }^{-2}{\Vert y-\widehat{\mu }(\omega )\Vert }^2+2\text{trace}\{P(w)\},$$

which, in the sense of weight choice, is equivalent to the Mallows’ criterion of Hansen (2007) for the situation with known σ².

In practice, σ² is unknown. We can estimate it directly by σ̂², which is required to satisfy Assumptions (A.4)–(A.5) in the appendix. For simplicity, we further assume that σ̂² is unrelated to w, which means that σ̂² is not from model averaging as in the existing literature, such as Hansen (2007) and Liang et al. (2011). After removing the terms unrelated to w and multiplying by σ̂², ℬ(w) reduces to

$${\mathcal{B}}^{\ast }(w)\equiv {\Vert y-P(w)y\Vert }^2+2{\widehat{\sigma }}^2\text{trace}\{P(w)\}-2y^{\mathrm{T}}{P}^{\mathrm{T}}(w)\frac{\partial {\widehat{\sigma }}^2}{\partial y},$$ (2.3)

which can be taken as a criterion for choosing weights. We let $w^{\ast }=\underset{w\in \mathcal{W}}{argmin}\{{\mathcal{B}}^{\ast }(w)\}$, the resulting weights by minimizing the criterion ℬ^*(w).

The predictive squared error in estimating μ is L_n(w) = ||μ̂ (w) – μ||². We can show the asymptotic optimality of μ̂(w^*) in the sense that μ̂ (w^*) yields a squared error that is asymptotically identical to that of the infeasible optimal model average estimator. Unless otherwise stated, all limiting processes discussed are with respect to n → ∞.

Theorem 2

If Assumptions (A.1) – (A.5) in the Appendix are satisfied, then

$$L_n(w^{\ast }){\{\underset{w\in \mathcal{W}}{inf}{L}_n(w)\}}^{-1}=1+o_p(1).$$

The direct use of σ̂² in ℬ^* (w) instead of σ² makes ℬ^*(w) not unbiased for estimating AI, up to a term unrelated to w. In what follows, we consider a situation where AI can be estimated unbiasedly using data, up to a term unrelated to w.

As in such model averaging papers as Hansen (2007), Wan, Zhang, and Zou (2010), Liang et al. (2011), and Hansen and Racine (2012), we now focus on least squares estimation with $P_{(s)}=X_{(s)}{(X_{(s)}^{\mathrm{T}}{X}_{(s)})}^{-}{X}_{(s)}^{\mathrm{T}}$, where X_(s) is the covariate matrix in the s^th candidate model and ${(X_{(s)}^{\mathrm{T}}{X}_{(s)})}^{-}$ is a generalized inverse of $X_{(s)}^{\mathrm{T}}{X}_{(s)}$. Let X = (X₍₁₎, …, X_(S)), m = rank(X), and P = X (X^TX)⁻ X^T. We adopt σ̂²(y, k) = y^T(I_n – P)y/k to estimate σ², where k is a positive constant. Consider the situation of μ being a linear function of X, μ = Xβ. Then, σ̂²(y, n) is the maximum likelihood estimator of σ² and σ̂²(y, n – m) is an unbiased estimator of σ². Substitute σ̂²(y, k) for σ̂² in (2.2) and denote the resulting AI(w) as AI_k(w). Define

$$\mathcal{C}(w)\equiv nlog2\pi +nlog{\widehat{\sigma }}^2(y,k)+2k{(n-m-2)}^{-1}\text{trace}\{P(w)\}+{\Vert y-\widehat{\mu }(w)\Vert }^2{\widehat{\sigma }}^{-2}(y,k)+4{\sigma }^2{\widehat{\sigma }}^{-2}(y,k)-2k^{-1}(n-m-4){\sigma }^4{\widehat{\sigma }}^{-4}(y,k).$$

Because AI_k(w) involves unknown moments of various random variables, in a manner similar to that leading to Theorem 1, we derive its unbiased estimator, which is just 𝒞(w).

Theorem 3

Suppose e has a multivariate normal distribution and μ is a linear function of X. For any k > 0, if the expectation of 𝒞(w) exists, then E {𝒞(w)} = AI_k(w).

By removing the terms unrelated to w and multiplying by σ̂²(y, k), 𝒞(w) simplifies to

$${\mathcal{C}}^{\ast }(w)\equiv {\Vert y-\widehat{\mu }(w)\Vert }^2+2y^{\mathrm{T}}(I_n-P)y{(n-m-2)}^{-1}\text{trace}\{P(w)\},$$

which we refer to as the KL model averaging (KLMA) criterion. Let $\widehat{w}=\underset{w\in \mathcal{W}}{\text{argmin}}\{{\mathcal{C}}^{\ast }(w)\}$. The resulting model average estimator is called the KLMA estimator.

Remark 1

By comparing the criterion 𝒞^* (w) and the Mallows’ criterion of Hansen (2007), the only difference is that n – m – 2 is used here, while n – m is used in Mallows’ criterion. The quantity n – m – 2 is from calculating the mean of the inverse Chi-squared distribution; see (S3.1) of the Supplementary Material. So the KLMA estimator will have the same large sample properties as the MMA estimator, and thus the asymptotic optimality of the MMA estimator presented by Hansen (2007) and Wan, Zhang, and Zou (2010) also holds for the KLMA estimator. In particular, our Assumptions (A.1) and (A.4) are sufficient for the asymptotic optimality of the KLMA estimator and Assumptions (A.2), (A.3), and (A.5) are not necessary.

Remark 2

Let c(w) = e′ I_n – P(w)}μ+σ²trace{P(w)} – e′P(w)e. Obviously, |E{c(w)}| = 0, but our weight vector ŵ is determined by data, so that |E{c(ŵ)}| may not be zero. We show in the Supplementary Material that

$$E\{L_n(\widehat{w})\}\le {inf}_{w\in \mathcal{W}}E\{L_n(w)\}+\mid E\{c(\widehat{w})\}\mid ,$$ (2.4)

which means that the expected predictive squared error by using ŵ is upper-bounded by the minimum expected error of model averaging estimators plus the term |E{c(ŵ)}|. This result holds for finite sample sizes. Similar results have been developed by Yang (2001) and Zhang, Lu and Zou (2013). If inf_w∈𝒲 E{L_n(w)} → ∞, then the term |c(ŵ)| is of order lower than inf_w∈𝒲 E{L_n(w)} under some regularity conditions (Wan, Zhang, and Zou (2010)).

3. The KLMA Estimator under a Heteroscedastic Error Setting

When the covariance matrix of e, Ω, is a general diagonal matrix, it follows from (2.2) that the Akaike information is

$$\begin{array}{l}{\text{AI}}_{\mathit{hetero}}=E_{f(y)}\left(E_{f(y^{\ast })}\left[nlog2\pi +log\mid \widehat{\mathrm{\Omega }}\mid +{\{y^{\ast }-\widehat{\mu }(w)\}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}^{-1}\{y^{\ast }-\widehat{\mu }(w)\}\right]\right)\\ =E_{f(y)}\left[nlog2\pi +log\mid \widehat{\mathrm{\Omega }}\mid +{\{\mu -\widehat{\mu }(w)\}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}^{-1}\{\mu -\widehat{\mu }(w)\}+\text{trace}({\widehat{\mathrm{\Omega }}}^{-1}\mathrm{\Omega })\right],\end{array}$$

where Ω̂ is an estimator of Ω and is also diagonal. Using similar conditions to those of Theorem 1 and the same argument as in the proof of Theorem 1, we see that

$$\mathcal{D}(w)\equiv nlog2\pi +log\mid \widehat{\mathrm{\Omega }}\mid +{\{y-\widehat{\mu }(w)\}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}^{-1}\{y-\widehat{\mu }(w)\}+2\text{trace}\left\{\mathrm{\Omega }{\widehat{\mathrm{\Omega }}}^{-1}\frac{\partial \widehat{\mu }(w)}{\partial y^{\mathrm{T}}}\right\}+2{\{y-\widehat{\mu }(w)\}}^{\mathrm{T}}\mathrm{\Omega }{\widehat{\mathrm{\Omega }}}^{-2}\widehat{a}+\widehat{\delta }$$ (3.1)

has expectation AI_hetero, where â = (â₁, …, â_n)^T, â_i = ∂Ω̂_ii/∂y_i, Ω̂_ii is the i^th diagonal element of Ω̂, and δ̂ is a scale related to ∂Ω̂_ii/∂y_i and ${\partial }^2{\widehat{\mathrm{\Omega }}}_{ii}/\partial y_i^2$, but unrelated to w.

We focus on the case with μ̂ (w) = P(w)y. After removing some terms unrelated to w and estimating Ω by Ω̂ in (3.1), 𝒟(w) reduces to

$${\mathcal{D}}^{\ast }(w)\equiv {\{y-\widehat{\mu }(w)\}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}^{-1}\{y-\widehat{\mu }(w)\}+2\text{trace}\{P(w)\}-2y^{\mathrm{T}}{P}^{\mathrm{T}}(w){\widehat{\mathrm{\Omega }}}^{-1}\widehat{a}.$$

It is straightforward to show that when Ω̂ = σ̂²I_n, 𝒟^*(w) simplifies to ℬ^* (w). Let ${\widehat{w}}_{\text{hetero}}=\underset{w\in \mathcal{W}}{\text{argmin}}\{{\mathcal{D}}^{\ast }(w)\}$, the resulting weights by minimizing 𝒟^* (w).

Under the heteroscedastic error setting, we define the predictive squared error in estimating μ as L_hetero,n(w) = {μ̂ (w) – μ}^TΩ⁻¹{μ̂ (w) – μ}. A result is the asymptotic optimality of μ̂ (ŵ_hetero) in the sense of minimizing L_hetero,n(w).

Theorem 4

If Assumptions (A.2) and (A.3), and Assumptions (B.2)–(B.5) in the Appendix are satisfied, then

$$L_{\text{hetero},n}({\widehat{w}}_{\text{hetero}}){\{\underset{w\in \mathcal{W}}{inf}{L}_{\text{hetero},n}(w)\}}^{-1}=1+o_p(1).$$ (3.2)

When the structure of Ω is known and it is related to an unknown parameter vector η, Ω = Ω(η), we can estimate Ω by the maximum likelihood (ML) approach based on the model with the largest number of covariates. Let η̂ be the ML estimator of η. Then â_i = ∂Ω̂_ii/∂y_i = ∂η̂^T / ∂y_i(∂Ω̂_ii / ∂η̂). The Supplementary Material provides some formulas for calculating ∂η̂^T/∂y. The resulting estimator is referenced as version 1 modified KLMA (mKLMA₁) estimator.

When the structure of Ω is unknown, we use residuals from model averaging to estimate Ω. Specifically, we use a two-stage procedure to get the weights.

Stage 1

Estimate μ using the methods developed in Sections 2, then use the residual vector y – μ̂(w^*) for the estimation of Ω, where w^* is the weight vector minimizing ℬ^*(w). Specifically, let Ω̂_ii = {y_i – μ̂ (w^*)_i}², where y_i and μ̂ (w^*)_i are the i^th elements of y and μ̂ (w^*), respectively. Ignoring the randomness of w^*, we have â_i = ∂Ω̂_ii/∂y_i = 2{y_i – μ̂ (w^*)_i}{1 – P(w^*)_ii}, where P(w^*)_ii is the i^th diagonal element of P(w^*). When focusing on least squares model averaging, we utilize ŵ instead of w^*.

Stage 2

To obtain the weights, minimize

$$\mathcal{E}(w)\equiv {\{y-\widehat{\mu }(w)\}}^{\mathrm{T}}{\widehat{\mathrm{\Omega }}}^{-1}\{y-\widehat{\mu }(w)\}+2\text{trace}\{P(w)\}-4y^{\mathrm{T}}{P}^{\mathrm{T}}(w){\widehat{\mathrm{\Omega }}}^{-1}\times {[\{y_1-\widehat{\mu }{(w^{\ast })}_1\}\{1-P{(w^{\ast })}_{11}\},\dots ,\{y_n-\widehat{\mu }{(w^{\ast })}_n\}\{1-P{(w^{\ast })}_{nn}\}]}^{\mathrm{T}}.$$

The resulting estimator is termed the version 2 modified KLMA (mKLMA₂) estimator.

4. Simulations

4.1. Homoscedastic error setting

We conducted simulation experiments to compare the small sample performance of the KLMA estimator and the MMA estimator under the homoscedastic error setting. The results from the estimator selected by AICc, a method that has been shown to perform better than C_p, AIC and BIC in model selection in small sample situations (see, for example, Hurvich and Tsai (1989) and Hurvich, Simonoff and Tsai (2002)), are also presented. In the first example, the number of covariates was fixed, while in the second example, it increased with the sample size n.

Example 1 (the fixed number of covariates)

This example is based on the setting of Hurvich and Tsai (1989): the model (2.1) with

$$\mu =X\beta ,\beta ={(1,2,3,0,0,0,0)}^{\mathrm{T}},\text{and}{X}_j~\text{Normal}(0,I_n),j=1,\dots ,7,$$

where X_j is the j^th column of X. Seven candidate models were considered with X_(s) = (X₁, …, X_s), s = 1, …, 7, respectively. Let R² = Var (μ_i)/Var (y_i) = Var (μ_i)/{Var (μ_i) + σ²} = 14/(14 + σ²), controlled by σ². We varied σ² such that R² varied in the range [0.1, 0.9]. The estimator μ̂ was evaluated in terms of its risk under the loss function L_μ = ||μ̂ – μ||², the predictive loss of μ̂. We did this by computing the average across 1,000 replications. The sample size n was 20 and 50.

The simulation results are shown in Figure 1. For clearer comparison, we normalized the risk by dividing by the risk of the infeasible optimal least squares estimator. It is encouraging that the KLMA has a lower risk than the MMA in the entire range of R² we considered, and the superiority is more obvious for n = 20. When n = 50, the two model average estimators have similar performance, which is expected as they have the same large sample properties. In most situations, the model averaging outperforms model selection by the AICc.

Figure 1.

Results for Example 1: risk comparisons under L_μ as a function of R².

The estimators were also evaluated in terms of risk under the loss function L_β = ||β̂ –β||^2. The simulation results are presented in Section S8 of the Supplementary Material. The comparison results are analogous to those under L_μ and support our proposed KLMA.

Example 2 (an increasing number of covariates)

This example is based on the setting in Hansen (2007): $y_i={\mu }_i+e_i={\sum }_{j=1}^{\infty }{\theta }_j{x}_{ji}+e_i$, x_1i = 1, all other x_ji are Normal(0, 1), e_i is Normal(0, 1), independent of x_ji, all x_ji are mutually independent, ${\theta }_j=c\sqrt{2\alpha }{j}^{-\alpha -1/2}$, R² = c²/(1 + c²) ∈ [0.1. 0.9], controlled by c, and α is set to 0.5, 1.0, and 1.5. Like Hansen (2007), we considered S = [3n^1/3] nested approximating models with the s^th model comprising the first s regressors, where [3n^1/3] returns the nearest integer from 3n^1/3. As in Example 1, we focused on the small sample cases, with n = 20 and 50. Following Hansen (2007), our evaluation was based on the predictive loss function L_μ with 1,000 replications.

The simulation results with α = 1 are depicted in Figure 2 and all simulation results are shown in Section S9 of the Supplementary Material. It is seen that the MMA estimator typically yields better estimates than the model selection estimator, which is in accordance with what was observed by Hansen (2007). The KLMA estimator is found to be superior to the MMA estimator in a large region of the parameter space, and this superiority is most marked when R² is small and α is large. This performance is particularly encouraging in view of the fact that this experiment is performed under the setting of Hansen (2007), where it has been shown that the MMA estimator performs better than many commonly used model selection and averaging methods. When R² is large, MMA can be slightly better than KLMA. When n increases, they perform more similarly.

Figure 2.

Results for Example 2: risk comparisons under L_μ as a function of R².

4.2. Heteroscedastic error setting

We conducted simulation experiments with heteroscedastic errors to compare the mKLMA₁ and mKLMA₂ estimators with the JMA estimator in Hansen and Racine (2012). The weight vector of the JMA estimator was obtained by minimizing a jackknife criterion.

Example 3

This example is based on the same setting as in Example 1 except that n varied in {20, 50, 150, 400}, and e ~ Normal[0, diag{exp(ηX_2,1), …, exp(ηX_2,n)}], where X_2,i is the i^th element of X₂ and η > 0. We changed the value of η such that R² = Var (μ_i)/Var (y_i) ≈ Var (μ_i)/[Var (μ_i) + E{exp(ηX_2,i)}] = 14/{14 + exp(η²/2)} varied in the range [0.1, 0.9].

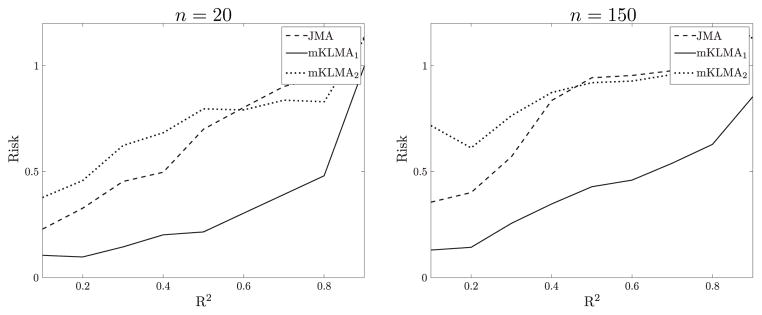
The risk comparison results of mKLMA₁, mKLMA₂, and JMA estimators under L_μ loss are presented in Figure 3 with n = 20 and 150 (the results with n = 50 and 400 are shown in Figure S.3 of the Supplementary Material). It is clear that mKLMA₁ generally leads to the lowest risk. The mKLMA₂ and JMA methods perform comparably; the latter has been shown to have advantages over the MMA estimator and other estimators selected by AIC, BIC, and cross-validation (Hansen and Racine (2012)). When R² is small, JMA produces a lower risk than mKLMA₂, while mKLMA₂ is superior to JMA when R² is large. The risk comparison under L_β loss is presented in Figure S.4 of the Supplementary Material. As in Example 1, the patterns under L_μ and L_β are almost the same.

Figure 3.

Results for Example 3: risk comparisons under L_μ as a function of R².

We also evaluated estimators in terms of risk under the loss function L_hetero,μ = (μ̂ − μ)Ω⁻¹(μ̂ − μ). Figure 4 shows risk comparison results with n = 20 and 150 (other results are shown in Figure S.5 of the Supplementary Material), from which, we see that mKLMA₂ and JMA are still comparable, and that mKLMA₁ performs much better.

Figure 4.

Results for Example 3: risk comparisons under L_hetero,μ as a function of R².

In Sections S11–S13 of the Supplementary Material, for a robustness check, we provide some more simulation examples. It is seen that our method is still superior to the other methods when the errors are not normally distributed or the coefficients depend on the sample size.

5. Empirical Example

We applied our methods to a data set from the Hong Kong residential property market. The data set consists of 560 transactions of the housing estate ‘South Horizon’ located in the South of Hong Kong, recorded by Centaline Property Agency Ltd. from January 2004 to October 2007. The model from Magnus, Wan and Zhang (2011) is adopted to analyze this data set:

$$\begin{array}{l}{\mathit{LPRICE}}_t={\beta }_1+{\beta }_2{\mathit{LAREA}}_t+{\beta }_3{\mathit{LFLOOR}}_t+{\beta }_4{\mathit{GARV}}_t+{\beta }_5{\mathit{INDV}}_t\\ +{\beta }_6{\mathit{SEAVF}}_t+{\beta }_7{\mathit{SEAVS}}_t+{\beta }_8{\mathit{SEAVM}}_t+{\beta }_9{\mathit{MONV}}_t\\ +{\beta }_{10}{\mathit{STRI}}_t+{\beta }_{11}{\mathit{STRN}}_t+{\beta }_{12}{\mathit{UNLUCK}}_t+e_t\end{array}$$ (5.1)

for t = 1, …, 560, where LPRICE is the natural logarithm of the sales price per square foot, and the twelve regressors, including the constant term, are shown in Table 1. As in Magnus, Wan and Zhang (2011), we treated the first six variables as focus regressors and the other six variables as auxiliary regressors, and so we combine 2⁶ = 64 models.

Table 1.

Regressors in application. See Magnus, Wan and Zhang (2011) for a detailed description of these variables.

Index	Regressor	Explanation
1	INTER.	Constant term
2	LAREA	Size of dwelling in square feet (natural logarithm)
3	LFLOOR	Floor level of dwelling (natural logarithm)
4	GARV	1 if garden view; 0 otherwise
5	INDV	1 if industry view; 0 otherwise
6	SEAVF	1 if full sea view; 0 otherwise
7	SEAVS	1 if semi sea view; 0 otherwise
8	SEAVM	1 if minor sea view; 0 otherwise
9	MONV	1 if mountain view; 0 otherwise
10	STRI	1 if internal street view; 0 otherwise
11	STRN	1 if no street view; 0 otherwise
12	UNLUCK	1 if located on floors 4, 14, 24, 34 or in block 4; 0 otherwise.

We used indices of the six auxiliary regressors to indicate these candidate models. For example, (7, 8) indicates the model including SEAV S and SEAVM. We examined the predictive power of the six model selection and averaging methods used in the simulation study: AICc, MMA, KLMA, JMA, mKLMA₁, and mKLMA₂, the last three of which are developed for the heteroscedastic setting. Magnus, Wan and Zhang (2011) has found that the heteroscedasticity structure of this data set is

$$\mathrm{\Omega }=\text{diag}\{exp(\eta {\mathit{STRN}}_1),\dots ,exp(\eta {\mathit{STRN}}_n)\},$$

so we also used this structure when implementing mKLMA₁.

Table 2 shows weights for all model averaging methods. We list only the models whose largest weights for all model averaging methods are not smaller than 0.01. In each column, the largest weight is indicated by an asterisk. It is seen that MMA and KLMA perform very closely and both put the largest weights on model (8, 10, 12). JMA, mKLMA₂, and mKLMA₁ put the largest weights on models (7, 10, 11, 12), (7, 8, 12) and (7), respectively. The model selected by AICc is (7, 8, 10, 12).

Table 2.

Weights estimated by model averaging methods.

Model	MMA	KLMA	JMA	mKLMA2	mKLMA1
(7)	0.06	0.06	0.01	0.18	0.52*
(8)	0.00	0.00	0.00	0.00	0.14
(7,8)	0.00	0.00	0.16	0.00	0.08
(7, 10)	0.22	0.22	0.16	0.16	0.00
(8, 9)	0.11	0.11	0.15	0.02	0.00
(8, 10)	0.00	0.00	0.00	0.00	0.16
(7, 8, 12)	0.21	0.20	0.08	0.31*	0.00
(7, 10, 12)	0.09	0.10	0.00	0.04	0.00
(8, 10, 12)	0.25*	0.25*	0.18	0.27	0.11
(7, 10, 11, 12)	0.06	0.06	0.25*	0.01	0.00

In many applications, it is often the case that a prediction may be sensitive to the sample that is used to estimate the forecasting model. Too early observations may not be useful or even lead to worse results in prediction, so we used a moving window of samples for estimation. We let n = 50 and 400. For each n, we did 560 – n one-step-ahead predictions.

To make comparison results easily detected, in each prediction, we subtracted minimum squared prediction error (SPE) of the six methods, from all SPEs. The corresponding values are called SPE distances. Table 3 displays mean SPE distances (MSPEDs) and their standard errors based on 560 – n predictions. Again, it is seen that KLMA performs better than MMA for relatively small sample size situation and they have very similar performance for the large sample sizes. We also find that mKLMA₁ performs best, and JMA and mKLMA₂ are comparable.

Table 3.

MSPEDs by model averaging and selection methods and their standard errors in forecasting Hong Kong estate price (×10⁻³).

n		AICc	MMA	KLMA	JMA	mKLMA2	mKLMA1
50	MSPED	1.522	1.175	1.164	1.276	1.309	1.081
	s.e.	0.152	0.092	0.090	0.115	0.156	0.092
400	MSPED	0.771	0.690	0.690	0.684	0.682	0.654
	s.e.	0.099	0.063	0.063	0.065	0.081	0.083

6. Concluding Remarks

We have developed a novel weight choice criterion based on the KL distance. Like the well-known MMA estimator, the resulting KLMA estimator is asymptotically optimal. More importantly, for finite sample situation, the KLMA estimator has been observed to be generally superior to the MMA estimator. We have further extended the KLMA estimator to the setting with heteroscedasticity and proved the corresponding asymptotic optimality. The simulation study and application have shown the promise of the proposed model average estimators.

For the purpose of statistical inference, it is necessary to obtain the limiting distribution of a model average estimator. Under the commonly used models with the local misspecification assumption, the limiting distribution theory of model average estimator using weights with an explicit form has been established in the literature such as Hjort and Claeskens (2003). Deriving the limiting distributions of our model average estimators, whose weight vectors have no explicit expressions, warrants further investigation.

Lastly, we remark that unbiasedness built in Theorems 1 and 3 are based on the normality assumption of e. Although a robustness check in the simulation study shows that our method still outperforms its competitors when e follows a uniform or Chi-squared distribution, we cannot conclude that our approach can be generally applied to other error distribution cases. Developing specific weight choice criteria for other distributions is an interesting open question for future studies.

Appendix: Assumptions

Let λ_max(A) denote the maximum singular value for a matrix A, R_n(w) = E {L_n(w)}, ξ_n = inf_w∈𝒲R_n(w), $w_s^0$ be an S × 1 vector in which the s^th element is one and the others are zeros, and T̂ be a matrix such that ∂σ̂²/∂y = T̂y.

• Assumption A.1. For a constant κ₁ and some fixed integer 1 ≤ G < ∞, $E(e_i^{4G})\le {\kappa }_1<\infty$, i = 1, …, n, and $S{\xi }_n^{-2G}{\sum }_{s=1}^S{R}_n^G(w_s^0)=o(1)$.

  Assumption A.2. max_{s∈{1,…,S}} λ_max(P_(s)) = O(1).

  Assumption A.3. ||μ||²n⁻¹ = O(1).

• Assumption A.4. ${sup}_{w\in \mathcal{W}}[\mid ({\widehat{\sigma }}^2-{\sigma }^2)\text{trace}\{P(w)\}\mid R_n^{-1}(w)]=o_p(1)$.

• Assumption A.5. $n{\lambda }_{max}(\widehat{T}){\xi }_n^{-1}=o_p(1)$.

Assumptions (A.1)–(A.3) are commonly used in such literature on model selection and model averaging as Li (1987), Andrews (1991), Shao (1997), Hansen (2007), and Wan, Zhang, and Zou (2010). The normality of e required in Theorem 1 is not necessary for asymptotic optimality. In Section S7 of the Supplementary Material, we present a discussion on Assumption (A.1) and its relationship with the normality of e.

Assumption (A.4) restricts the estimator σ̂². In Hansen (2007) and Wan, Zhang, and Zou (2010), the model with the largest rank of regressor matrix, denoted as r, is used to estimate σ². In this case, Assumption (A.4) is implied by Assumptions (A.1)–(A.3) and r₂n⁻¹ = O(1). See the proof of Theorem 2 in Wan, Zhang, and Zou (2010) for the derivation.

Assumption (A.5) places a constraint on the robustness of the estimator σ̂². Under any candidate model s, a natural estimator of σ² is σ̂² = ||y − μ̂_(s)||²/n = y^T(I_n − P_(s))^T(I_n − P_(s))y/n, and then Assumption (A.5) is obviously implied by Assumptions (A.1)–(A.2).

Let R_hetero,n(w) = E{L_hetero,n(w)}, ξ_hetero,n = inf_w∈𝒲R_hetero,n(w), Â be a matrix such that â = Ây, and P̃(w) = Ω^−1/2P(w)Ω^1/2.

• Assumption B.1. For a constant κ₂ and some fixed integer 1 ≤ G₁ < ∞, $E(e_i^{4G_1})\le {\kappa }_2<\infty$, i = 1, …, n, and $S{\xi }_{\text{hetero},n}^{-2G_1}{\sum }_{s=1}^S{R}_{\text{hetero},n}^{G_1}(w_s^0)=o(1)$.

  Assumption B.2. There exist two constants c₁ and c₂ such that 0 < c₁ ≤ min_{i∈{1,…,n}} Ω_ii ≤ max_{i∈{1,…,n}} Ω_ii ≤ c₂ < ∞.

• Assumption B.3. ${({max}_{i\in \{1,\dots ,n\}}\mid {\widehat{\mathrm{\Omega }}}_{ii}-{\mathrm{\Omega }}_{ii}\mid )}^{2}n{\xi }_{\text{hetero},n}^{-1}=o_p(1)$.

• Assumption B.4. ${max}_{i\in \{1,\dots ,n\}}\mid {\widehat{\mathrm{\Omega }}}_{ii}-{\mathrm{\Omega }}_{ii}\mid {sup}_{w\in \mathcal{W}}[R_{\text{hetero},n}^{-1}(w)\text{trace}\{\stackrel{\sim }{P}(w){\stackrel{\sim }{P}}^{\mathrm{T}}(w)\}]=o_p(1)$

• Assumption B.5. $n{\lambda }_{max}(\widehat{A}){\xi }_{\text{hetero},n}^{-1}=o_p(1)$.

Assumptions (B.1) and (B.5) are similar to Assumptions (A.1) and (A.5), respectively. Assumptions (B.3)–(B.4) restrict the estimator Ω̂. When the structure of Ω is known and it is related to a parameter vector η, Ω = Ω(η), we generally have ||η̂ − η|| = O_p(n^−1/2) and max_{i∈{1,…,n}} |Ω̂_ii − Ω_ii| = O_p(n^−1/2) under some regularity conditions and, in this case, Assumptions (B.3)–(B.4) are implied by Assumption (B.1) and formula (S5.4) in the Supplementary Material, respectively.