In vivo Diffusion-Tensor MRI of the Human Heart On a 3T Clinical Scanner: An Optimized Second Order (M2) Motion Compensated Diffusion-Preparation

Abstract

Purpose

The aim of this study was to optimize a diffusion-prepared balanced steady-state free precession cardiac MRI (CMR) technique to perform diffusion-tensor CMR (DT-CMR) in humans on a 3T clinical scanner.

Methods

A previously developed second order motion compensated (M2) diffusion-preparation scheme was significantly shortened (40%) yielding sufficient SNR for DT-CMR imaging. In 20 healthy volunteers and 3 heart failure (HF) patients, DT-CMR was performed comparing no motion compensation (M0), first order motion compensation (M1), and the optimized M2. Mean diffusivity (MD), fractional anisotropy (FA), helix angle (HA), and HA transmural slope (HATS) were calculated. Reproducibility and success rate (SR) were investigated.

Results

M2-derived left ventricular (LV) MD, FA, and HATS (1.4±0.2 um²/ms, 0.28±0.06, −1.0±0.2°/%trans) were significantly (p<0.001) less than M1 (1.8±0.3 um²/ms, 0.46±0.14, −0.1±0.3°/%trans) and M0 (4.8±1.0 um²/ms, 0.70±0.14, 0.1±0.3°/%trans) indicating less motion corruption and yielding values more consistent with previous literature. M2-derived DT-CMR parameters had higher reproducible (ICC>0.85) and SR (82%) than M1 (ICC=0.20-0.85, SR=37%) and M0 (ICC=0.20-0.30, SR=11%). M2 DT-CMR was able to yield HA maps with smooth transmural transition from endocardium to epicardium.

Conclusion

The proposed M2 DT-CMR reproducibly yielded bulk motion robust estimations of mean LV MD, FA, HA, and HATS on a 3T clinical scanner.

INTRODUCTION

Diffusion cardiac MRI (CMR) is a non-invasive, contrast-free technique capable of yielding unique tissue microenvironment characterization. It has the potential to detect myocardial fibrosis (1-4), myocardial edema in myocarditis (5), acute myocardial infarction (5), and myocardial fiber disarray (6-11). The latter of these applications can be achieved with diffusion-tensor (DT) CMR (12-14), which can map the underlying myofiber architecture of the heart. Despite the potentially powerful capability of yielding fiber orientation, clinical translation of DT-CMR remains elusive due to technical challenges including but not limited to bulk motion sensitivity inherent to diffusion MRI encoding, requirement for high signal-to-noise ratio (SNR), and long scan times.

Two main classes of diffusion encoding for in vivo diffusion CMR have been developed to address the motion sensitivity challenges: (i) stimulated echo (STE) encoding at identical cardiac phases over two successive heart beats (15-19) and (ii) spin echo with motion compensation encoding over a short period (<100ms) within a single heart beat (20-23). Currently, STE is more widely available due to its ability to encode diffusion with small gradient strengths by leveraging the periodicity of the heart. Despite innovative efforts to include a dual gated prospective respiratory navigation (19), STE is largely limited to a series (>6 per slice) of lengthy breath-holds, which is clinically not ideal. In comparison, spin echo diffusion encoding with motion compensation was originally introduced with first order motion compensation (M1) with research-grade ultrahigh gradient strengths (87 mT/m) (20). It was later demonstrated at 1.5T that increasing motion compensation to second order (M2) allowed for diffusion-weighted (DW) CMR with significantly lower clinical-grade gradient strengths (40 mT/m) (21). However due to the long diffusion encoding time (~100ms), severe T₂ decay resulted in low SNR, thus requiring long scan times (15 min for whole LV) of a 3D multi-shot readout to gain back sufficient signal and reliance on the averaging of apparent diffusion coefficient (ADC) maps to yield the final trace ADC. To achieve sufficient SNR to perform DT-CMR, scan times with this approach would need to be further increased in addition to doubling the number of diffusion directions to construct the self-diffusion tensor. Therefore, DT-CMR was not clinically feasible with this approach. Recent work in humans (23,24) and in mice at 7T (22) demonstrated that the combination of M2 and ultrahigh gradient strengths (80 mT/m and 400 mT/m, respectively) can drastically decrease the diffusion encoding time yielding robust DT-CMR. Using only clinically available gradient strengths (43 mT/m) at 3T, we hypothesize that the optimization of M2 for a shorter diffusion encoding time and higher main magnetic field can yield sufficient SNR for DT-CMR acquisition in a clinically feasible imaging time.

To achieve shorter M2 diffusion encoding, we proposed the use of single composite adiabatic refocusing pulse (BIR-4 (25) plus two hard pulses in the MLEV configuration (26)) with two balanced M1 gradient modules on either side of the refocusing pulse. The novel M2 diffusion encoding was integrated into a diffusion preparation scheme (4,21) modified for 3T imaging with crusher gradients to mitigate both B0 and B1 inhomogeneities as well as T1 contamination (27,28). 2D single-shot balanced steady-state free precession (bSSFP) was used to ensure that total scan times were clinically feasible (<15 minutes). Prospective respiratory navigator gating was employed to allow for free-breathing acquisition.

METHODS

Pulse Sequence Design

The pulse sequence design aimed at significantly reducing the duration of diffusion preparation module by changing a previously designed second order motion compensation (M2) diffusion quadra-bipolar pulse (21) (TE_prep = 110 ms) to a dual-M1 pulse (TE_prep = 67 ms) (Fig. 1), with major B₀/B₁ inhomogeneity considerations. A shorter diffusion preparation time minimizes the significant T2 decay allowing for higher SNR, which is critical for DT-CMR reconstruction. In addition, the proposed M2 pulse maintains many of the attractive features of the M2 quadra-bipolar pulse. Both M2 gradient designs offer gradient moment nulling (GMN) for zero (M0), first (M1), and M2 moments assuming ideal refocusing. Note that nulling of higher order moments implies nulling of lower orders (e.g. M1 represents both zero and first order gradient moments are nulled). Furthermore, both M2 pulses are composed of symmetric gradients (same gradient structure before and after the refocusing pulse) to counter the generation of concomitant fields, which can be significant at high (>40 mT/m) gradient strengths even at 3T (29). Similar to the M2 quadra-bipolar pulse, the proposed M2 pulse maintains partial alternation in gradient polarity to combat the formation of eddy current fields (30). Beyond the significant reduction in diffusion encoding time, the main difference between the two M2 pulses is the susceptibility to B1 inhomogeneity.

Figure 1.

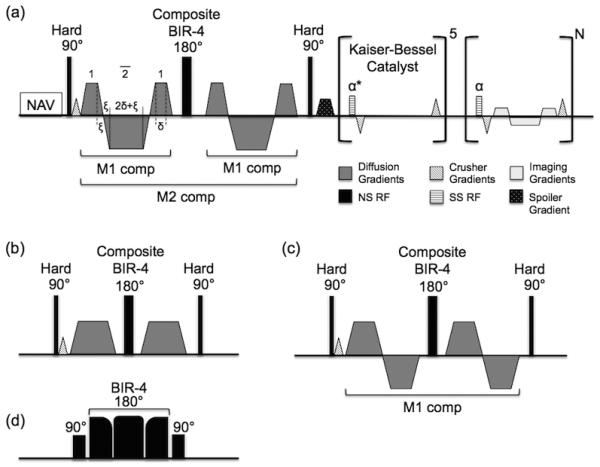
The proposed pulse sequence diagram of the proposed M2 B1-resistant diffusion-prepared bSSFP sequence for DT-CMR acquisition. (a) Respiratory navigator precedes the M2 B1-resistant diffusion preparation. The M2 B1-resistant diffusion encoding consists of two M1 pulses around a composite adiabatic refocusing pulse. M0 and M1 are independently nulled before and after the refocusing pulse and only M2 nulling depends on the integrity of the refocusing. A crusher gradient is placed before the refocusing pulse to select out only the spin echo pathways increasing the diffusion preparation’s robustness to B0 and B1 imperfections. This same crusher gradient with opposite polarity is played out for each TR of the bSSFP readout (during the 5 TR’s of catalyst ramp-up and N TR’s of single shot readout) and is balanced appropriately before the next TR. (b) M0 and (c) M1 gradient moment nulled designs used in this study to compare the effects of order of bulk motion compensation (M0 to M2) vs duration of diffusion encoding period (35 ms to 67ms). (d) Composite adiabatic refocusing pulse is a conventional composite MLEV pulse with the exception of the 180° being a BIR-4 adiabatic pulse.

The proposed M2 pulse has the additional benefit of B1 resistant GMN diffusion encoding, which is conducive for 3T CMR imaging. Nulling of M0 and M1 are achieved through gradient design and do not depend on ideal refocusing (Fig. 1). However, nulling of M2 will depend on both gradient design and the integrity of the refocusing pulse. This is contrary to the quadra-bipolar pulse that depends on sufficient refocusing to null both M1 and M2 (M0 is nulled through gradient design alone).

Numerical simulation of M0, M1, and M2 with considerations of imperfect refocusing reveals that the residual phase of the proposed M2 pulse is significantly less B1 dependent than that of the quadra-bipolar pulse (Supp. Fig. S1). Gradient waveforms of both M2 pulses were numerically integrated to calculate M0, M1, M2, and residual phase (ϕ) using the following equations:

$$\mathrm{M}0=\gamma {}_0^{TE∕2}Gtdt-g{}_{TE∕2}^{TE}Gtdt$$

$$\mathrm{M}1=\gamma {}_0^{TE∕2}tGtdt-g{}_{TE∕2}^{TE}tGtdt$$

$$\mathrm{M}2=\gamma {}_0^{TE∕2}{t}^{2}Gtdt-g{}_{TE∕2}^{TE}{t}^{2}Gtdt$$

$$\varphi =\mathrm{M}0+v\mathrm{M}1+\frac{1}{2}a\mathrm{M}2$$

Residual phase was calculated for varying levels of B1 (0.5 to 1.0) using the following relationship that relates the scaling of gradient amplitude after the refocusing pulse, g, to B1 amplitude, B:

$$\mathrm{g}=\cos \pi B$$

The proposed M2 pulse had 5 times less residual phase than the quadra-bipolar pulse (0.08π vs 0.4π, respectively) for a ~15% B1 inhomogeneity and quiescent cardiac motion (v = 1.5 cm/s, a = 10 cm/s² (21,31)). For peak cardiac motions (v = 15 cm/s, a = 100 cm/s² (21,31)) and ~15% B1 inhomogeneity, the discrepancy between the M2 quadra-polar and the proposed M2 pulse is much more drastic (0.6π vs 3π, respectively) with the quadra-bipolar theoretically yielding a completely dephased residual phase (>2π) that effectively results in a signal void in the image.

To further increase the B1 robustness of the proposed M2 pulse, a crusher gradient is played before a newly proposed non-selective “composite adiabatic (BIR-4 (25))” refocusing pulse and during the balanced steady-state free precession (bSSFP) readout. The crusher gradient scheme used in this work (Fig. 1) utilizes the crusher gradient scheme optimized for T2 preparation of the heart (27). The crusher gradient scheme offers robustness to both B0 and B1 inhomogeneity due to the placement of the first dephasing crusher before the refocusing pulse and also minimization of T1 contamination that may accrue during the SSFP readout. This is distinctly separate from previous work that employed a crusher scheme for selecting out stimulated echo pathways that uses the crusher gradients themselves as a means for stimulated-echo based strain (28) and diffusion (32) encoding, which also demonstrated similar robustness to B0 and B1 inhomogeneity. In contrast, the crusher gradient used in this work guides the echo pathway to remove stimulated echoes that may generate from imperfect B1 and B0 during both refocusing and tip-up by sufficiently dephasing (2π; M0 = 8 mT*ms and Δz = 10mm) the transverse magnetization before the refocusing pulse and rephasing it during each steady-state TR. However, the penalty of using a crusher gradient is a loss in signal and consequently signal-to-noise ratio (SNR) since the contaminating longitudinal magnetization is removed and only the desired transverse magnetization remains. The proposed “composite adiabatic” refocusing pulse (Fig. 1b) is a single BIR-4 adiabatic 180° pulse with two surrounding 90° hard pulses in a MLEV composite configuration (90°_x-180°_y-90°_x) (26). The inclusion of the proposed spin-echo crusher scheme with the composite adiabatic refocusing pulse should together compensate for using a single refocusing pulse instead of multiple pairs of refocusing pulses used in conventional T2-based preparations (4,33). Altogether, these features result in an optimized “M2 B1-resist” diffusion preparation more suitable for 3T imaging than the M2 quadra bipolar.

For all DT-CMR measurements, the diffusion preparation pulse was placed at the center of the most quiescent cardiac phase determined manually by CINE imaging. For a b-value = 350 s/mm², M0 (TE_prep = 35ms) and M1 (TE_prep = 46ms) diffusion preparations were always much less than the duration of the typical quiescent period (50-100ms). In comparison with the proposed M2 B1-resist diffusion preparation duration (TE_prep = 67ms), the shorter durations of M0 and M1 diffusion preparations would give an inherent advantage to bulk motion sensitivity. The 2D single-shot bSSFP readout modified with the proposed crusher gradients and conventional centric encoding was played after the diffusion preparation (34). Single shot imaging was chosen to minimize scan time with consideration of the six diffusion measurements needed to reconstruction the diffusion tensor. The optimized steady-state catalyst consisted of 6 RF pulses following a Kaiser-Bessel ramp-up envelop to the α pulse of the bSSFP readout (35).

Imaging Protocol

Phantom Experiments

Imaging in a 200mm radius spherical isotropic agar gel phantom with known ADC (1.3 um²/ms measured with gold standard DW SE(36)) was performed at 3T (MAGNETOM Verio, Siemens Healthcare, Erlangen, Germany) to demonstrate the refocusing robustness of the proposed M2 B1-resist diffusion preparation. The proposed M2 gradient scheme with single shot 2D bSSFP readout (TR/TE = 2.7/1.5ms, TR_g = 2s, FOV = 350×270 mm², α = 90°, 128 × 102 matrix, 10 mm slice thickness, 20 slices) was used for all measurements with b-value (b = 350 s/mm²), total diffusion preparation time (TE_prep=67ms), and diffusion direction ([1,1,1]) held constant. Four refocusing schemes were tested: (i) no crusher gradient with composite MLEV hard pulse, (ii) crusher gradient with composite MLEV hard pulse, (iii) no crusher gradient with composite adiabatic pulse, and the proposed (iv) crusher gradient with composite adiabatic pulse. A total of 20 measurements were repeated for each scheme with all four schemes being played before another repeated measurement was acquired (e.g. meas#1 = i, ii, iii, iv; meas#2 = i, ii, iii, iv; …).

In Vivo Experiments

Imaging on 20 healthy volunteers (39±14yo, 11 males) was performed at 3T (MAGNETOM Verio, Siemens Healthcare, Erlangen, Germany) with clinical gradient strengths of 43 mT/m. Localizers, CINE imaging (TR/TE = 4.5/1.31ms, 50 cardiac phases, FOV = 225 × 300 mm², α = 60°, 168 × 224 matrix, 8 mm slice thickness, horizontal long axis), and a series of DT-CMR scans were acquired during the quiescent period determined by the acquired CINE. For the DT-CMR scans, M0, M1, and M2 (TE_prep=35ms, 46ms, and 67ms, respectively) diffusion-prepared 2D single-shot bSSFP (TR/TE = 2.7/1.5ms, TR_g = 2RR, FOV = 350×270 mm², α = 90°, 128×102 matrix, 10mm slice thickness, 3 slices, 5 Kaiser-Bessel ramp up pulses, short axis) were acquired three times in a single session. The first and third DT-CMR acquisitions (3 slices, 4 NEX) were identical to test for intra-session reproducibility. The second acquisition was designated to test for the “success rate” (see “image analysis” section for detailed definition) of the proposed M2 DT-CMR technique filling up the rest of the total scan time (1 hour) and focusing on repeating a single slice multiple times (at least 8 NEX were acquired). In 3 heart failure patients (dilated cardiomyopathy, 71±5yo, 2 males) only a single set of DT-CMR acquisitions of M0, M1, and M2 were acquired using the same hardware and software set-up.

The DT-CMR scans were all acquired under free-breathing conditions using a prospective slice-following respiratory navigator and motion correction (37) to co-register all the DW images to their respective least DW image (b = 30 s/mm²). Recorded scan time for the first DT-CMR acquisition ranged from 10 to 17 minutes with respiratory navigator efficiency ranging from 30% to 45%. Two gradients at max gradient strength (43 mT/m) were simultaneously played out to achieve an effective gradient strength of 67 mT/m and 6 diffusion directions were acquired in a non-collinear fashion ([±1, 1, 0], [0, ±1, 1], [±1, 0, 1]) at a b-value of 350 s/mm². All subjects were recruited, consented, and scanned with the approval of Cedars-Sinai Medical Center Institutional Review Board (IRB).

Image Analysis

Refocusing Scheme Comparisons

Apparent diffusion coefficient (ADC) maps were generated for all four refocusing schemes with a single point mono-exponential fit. The normalized root mean square ADC error (NRMSE_ADC) and coefficient of variation (CV_ADC = ADC_σ/ADC_μ) were computed for each slice. NRMSE is calculated as follows:

$${\text{NRMSE}}_{\text{ADC}}=\frac{\frac{\overline{\stackrel{N}{i=1}AD{C}_i-u{}^2}}{N}}{u}$$

where N is the total number of voxels and u is the assumed ground truth ADC value (1.3 um²/ms). The mean NRMSE_ADC and CV_ADC for the four refocusing schemes were statistically compared using a two tailed paired t-test with significance being defined as p<0.05. SNR of the least diffusion-weighted images was also calculated for each scheme simply using the mean and standard deviation across all 20 measurements.

DT-CMR Parameters

Pixel-wise calculation of MD, FA, and HA were calculated using custom software in Python built off the diffusion imaging in Python (DIPY) platform (www.dipy.org) (38). Tensor reconstruction was calculated using a weighted least squares fit (39). Eigenvalue decomposition yielded eigenvectors to calculate fiber orientation and eigenvalues to calculate MD and FA (40). HA was calculated using the same geometric definition as Streeter, et al (41), with the local tangent vector, u, being defined from the center of mass of the LV blood pool to the voxel of interest for each short axis.

The left ventricle (LV) was manually segmented for the mean LV estimates for MD and FA. Mean LV HA transmurality (HATS) or the slope of mean HA vs transmural depth was reported in lieu of the mean LV HA. For each short axis slice, HAT was calculated by automatically segmenting the LV into five transmural concentric rings. Then, the slope was extracted from the linear regression of the mean HA for each ring against the transmural depth.

Success Rate

Success rate was determined for M0, M1, and M2 measurements using the second DT-CMR acquisition (1 slice, 6 diffusion directions, 8 NEX) in healthy volunteers. Success rate was defined as the percentage of all single average DW images (n=48) that were free of bulk motion artifacts. DW images were considered motion artifact-free when at least 90% of the LV was not affected by signal fall out (MD<3.0 μm²/ms) (42) or severe ghosting due to incoherent phase errors (43). Success rates were also plotted against heart rate.

Statistics

Mean differences were statistically tested with two tailed paired t-test statistics with significance defined as p<0.05 unless otherwise specified above. To test for reproducibility, Bland-Altman plots (44) and intra-class correlation (ICC) (45) were analyzed.

RESULTS

Refocusing Scheme Comparisons

Refocusing scheme iv that utilized both a crusher gradient and the BIR-4 adiabatic pulse presented with significantly (p<0.05) less NRMSE_ADC and CV_ADC (0.02±0.03 and 0.02±0.02, respectively) when compared to the three other refocusing schemes (i: 0.35±0.05 and 0.29±0.04; ii: 0.05±0.03 and 0.04±0.04; iii: 0.24±0.06 and 0.20±0.04) (Supp. Fig. S2). Qualitatively, schemes without crusher gradients (i and iii) resulted in large stark banding artifacts, while the schemes with crusher gradients (ii and iv) were subject to minimal banding and overall less SNR. SNR of the least diffusion-weighted images was reduced in schemes using a crusher gradient (ii: 52 and iv: 64) than schemes without (i: 76 and iii: 81).

DT-CMR Parameters

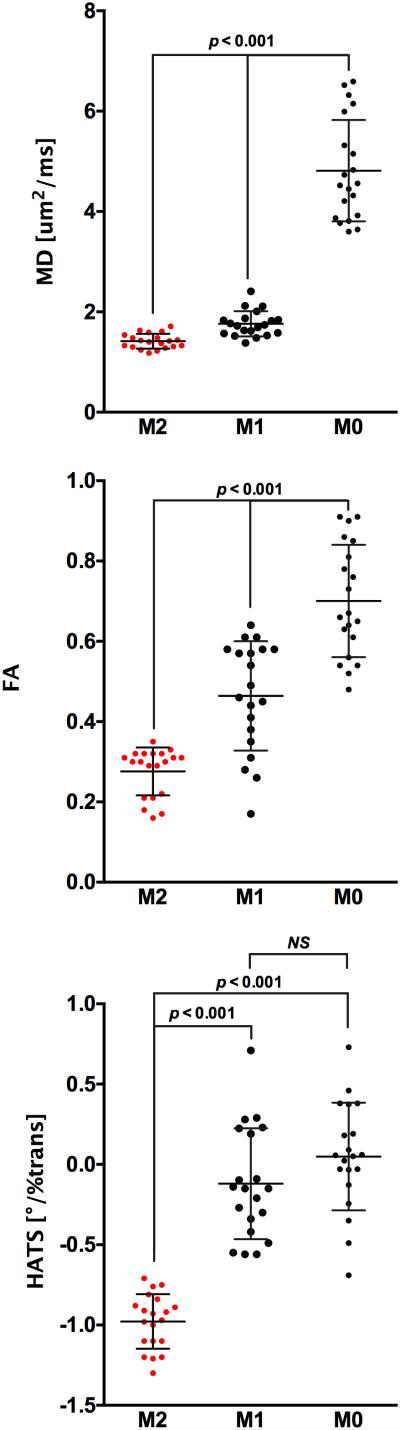
In healthy volunteers, M2-derived mean LV MD, FA, and HATS (1.4 ± 0.2 um²/ms, 0.28 ± 0.06, −1.0 ± 0.2°/%trans) were significantly (p<0.001) less than those derived using M1 (1.8±0.3 um²/ms, 0.46±0.14, −0.1±0.3°/%trans) and M0 (4.8 ± 1.0 um²/ms, 0.70 ± 0.14, 0.1±0.3°/%trans). M1-derived mean LV MD and FA were also significantly (p<0.001) less than M0-derived parameters, while M1-derived HATS was not significantly different than M0-derived HATS (Fig. 2). Severe signal loss was regularly observed in raw DWI of M0 (89%) and M1 (62%) measurements (Fig. 3). M0 derived LV MD was well above that of free water (3.1 um²/ms) at 37°C (46). All M0 and M1 measurements were not able to yield expected normal HA maps with a decreasing transition of HA from endocardium to epicardium (Fig. 4). Furthermore, M0 and M1-derived mean LV HATS were close to 0 indicating almost no helix structure existed. In regions of severe signal loss, HA values were completely dominated by the direction of the corrupted diffusion encoding. In comparison, M2 resulted in less severe signal loss (13%) in raw DWI and a majority (82%) of M2-derived HA maps exhibited expected normal smooth decreasing transition from endocardium to epicardium (right to left handed helix).

Figure 2.

Mean LV MD, FA, and HATS were significantly (p<0.001) decreased when comparing the proposed M2 B1-resistant with M1 and M0 DT-CMR measurements. M0-derived mean LV MD (4.8 um²/ms) was well above the self-diffusion of free water at 37°C (3.1 um²/ms) (46) indicating M0 measurements were substantially bulk motion corrupted. M1-derived mean LV MD and FA were also significantly (p<0.001) decreased compared with M0-derived measures demonstrating better bulk motion corruption. However, mean LV HATS for both M0 and M1 DT-CMR was centered on zero indicating that underlying fiber orientation had no helix fiber architecture, which is counter to the expected helix structure in normal fiber architecture (12,13,16,41,51,64). Therefore, M0 and M1 diffusion encoding did not predominantly reflect underlying fiber orientation. In contrast, the proposed M2 B1-resistant yielded a mean LV HATS that was negative representing a decrease in HA from endocardium to epicardium, which is consistent with the aforementioned literature.

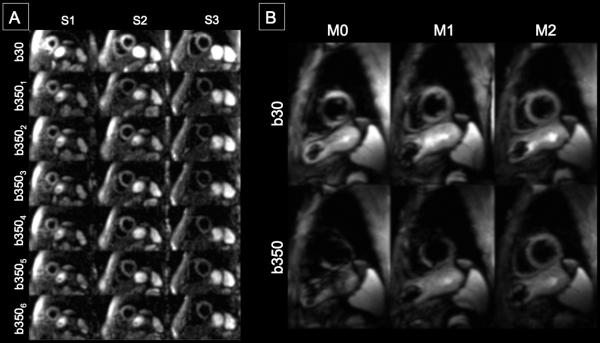
Figure 3.

(A) Representative single average raw DW-CMR measurements of the proposed M2 B1-resistant DT-CMR technique in a healthy volunteer. Three short axis slices with b30+six b350 diffusion directions were acquired. No severe signal loss can be observed. (B) Representative single average raw b30 and b350_(1,1,0) comparing M0, M1, and M2 B1-resistant at a single short axis slice in another healthy volunteer. Signal loss was observed in the anteroseptal and anterior LV segments of the M0 and M1 DW-CMR measurements. Note that even for the low b-value reference b30, M0 and M1 diffusion encoding yielded signal loss. In comparison, M2 B1-resistant DW-CMR measurement did not qualitatively show any severe signal loss.

Figure 4.

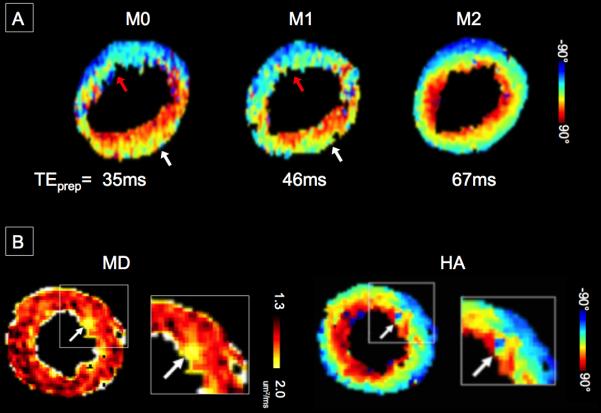
(A) Representative HA maps in a healthy volunteer demonstrating the proposed M2 B1-resistant DT-CMR technique can yield a continuous transmural change in HA from endocardium to epicardium. The M2-derived HATS for this slice was −1.2°/%trans. M0 and M1 DT-CMR measurements had partial continuous transmural change in the lateral wall (white arrows) with regional HATS of −0.6°/%trans and no transmural change in the anteroseptal wall (red arrows) with a regional HATS of −0.1°/%trans. (B) Representative MD and HA map in a heart failure patient reconstructed using the proposed M2 B1-resistant DT-CMR technique.

For HF patients, only the proposed M2 DT-CMR measurement was able to yield bulk motion robust mean LV MD, FA, and HATS values (1.8 ± 0.3 um²/ms, 0.24 ± 0.04, −0.6 ± 0.3°/%trans). Suspicious regions of elevated MD were found to correspond well with regions of abnormal HA (Fig. 4). FA maps were observed to be qualitatively uniform. In comparison, complete signal fallout was observed for M0 and M1 DT-CMR measurements with no detectable signal yielding mean LV MD, FA, and HATS values (M0: 4.9 ± 0.7 um²/ms, 0.74 ± 0.13, −0.1 ± 0.3°/%trans; and M1: 2.7 ± 0.5 um²/ms, 0.64 ± 0.11, −0.1 ± 0.4°/%trans).

Intra-scan Reproducibility

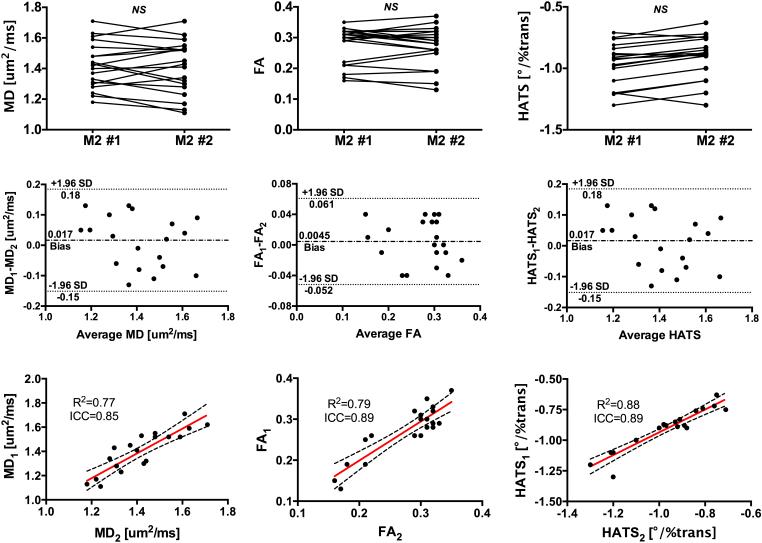
In healthy volunteers, M2 DT-CMR measurements were highly reproducible in yielding MD, FA, and HATS with good correlation (ICC: 0.85, 0.89, and 0.89; R²: 0.77, 0.79, and 0.88, respectively) and Bland-Altman plots were free of proportional and heteroscedastic errors (Fig. 5). Estimated biases for MD, FA, and HATS were near null (0.017 um²/ms, 0.0045, and 0.017°/%trans, respectively) and all differences were within ±1.96 standard deviations. In addition, there were no significant differences between the means of the intra-scan measurements.

Figure 5.

The proposed M2 B1-resistant DT-CMR technique was highly reproducible in yielding mean LV (left column) MD, (middle column) FA, and (right column) HATS. (Top row) Line plots of MD, FA, and HATS showed no significant differences between the first and second M2 B1-resistant DT-CMR measurements. (Middle row) Bland-Altman plots of MD, FA, and HATS demonstrated small biases and absence of proportional and heteroscedastic errors. (Bottom row) Correlation plots of MD, FA, and HATS illustrate substantial agreements between the first and second measurements.

M1 DT-CMR measurements were reproducible for MD (ICC: 0.81, R²: 0.72) with a small bias (−0.036 um²/ms) and Bland-Altman plots did not reveal any proportional and heteroscedastic errors. However, it had poor reproducibility and moderate biases for FA and HATS (ICC: 0.42 and 0.35; R²: 0.33 and 0.28; bias: 0.17 and 0.24°/%trans respectively). M0 DT-CMR measurements exhibited poor reproducibility (ICC: 0.25, 0.19, and 0.26; R²: 0.13, 0.06, and 0.11, respectively) for MD, FA, and HATS with moderate biases (0.27 um²/ms, 0.25, and 0.16°/%trans, respectively) and heteroscedastic error for MD (i.e. larger MD yielded larger differences).

Success Rate

Overall in healthy volunteers, the proposed M2 DT-CMR demonstrated significantly (p<0.01) higher success rate (82±18%) than M1 (37±15%) and M0 (11±10%) DT-CMR. For mild heart rates (HR) (< 75 BPM), the proposed M2 DT-CMR also exhibited significantly (p<0.01) higher success rates (87±8%) than M1 (41±17%) and M0 (18±16%) DT-CMR (Fig. 6). For higher HR (> 75 BPM), M2 DT-CMR was still significantly (p<0.01) higher in success rate (57±8%) than M1 (23±7%) and M0 (7±15%).

Figure 6.

Dependency of success rates on resting HR in normal volunteers. For HR < 75 BPM, success rates were above 80% for the proposed M2 B1-resistant, 20-70% for M1, and 0-30% for M0 DT-CMR techniques. For higher HR, the success rates were lower overall for M0, M1, and M2.

DISCUSSION

We have demonstrated that optimizations in diffusion gradient design and refocusing scheme can shorten the diffusion encoding time of a previously developed M2 DW-CMR technique (21) and inherently provide B0 and B1 robustness suitable for 3T DT-CMR imaging. Experiments in phantom, healthy volunteers, and heart failure patients on a clinical scanner with standard gradient strengths (43 mT/m) demonstrated the feasibility and potential of the proposed M2 B1-resistant DT-CMR technique.

Diffusion-prepared CMR at 3T is challenging because of the increased B0 and B1 inhomogeneities compared with 1.5T. Therefore, four refocusing schemes were compared to estimate the impact of using both a crusher gradient to guide the desired spin echo pathway and a B1 resistant adiabatic refocusing pulse. Among the four refocusing schemes tested in phantoms, the proposed combination of a crusher gradient with an adiabatic refocusing pulse (composite BIR-4) yielded the least NRSME_ADC and CV_ADC. A majority of the reduction in NRSME_ADC and CV_ADC can be attributed to the use of the crusher gradient with almost an order of magnitude decrease in error. In contrast, the use of an adiabatic refocusing pulse provided only 30%-50% reduction in NRSME_ADC and CV_ADC. The SNR penalty observed in this study of about 20-30% when utilizing a crusher gradient refocusing scheme was consistent with previous studies (27). This SNR penalty could be mitigated with acquisition of more diffusion directions and/or averages.

Both mean LV MD and FA for M0 and M1 diffusion prepared DT-CMR measurements in the presence of bulk motion resulted in an upward bias due to signal fallout. This is consistent with previous DT-MRI studies in the brain in which low SNR was associated with a positive bias of FA (47) and MD (42). Furthermore, the signal fallout was commonly (~40%) observed in one or two of the diffusion directions for M1 measurements as opposed to uniform signal fallout for M0 measurements. This would artificially cause the estimated tensor to have increased anisotropy resulting in a upward bias of FA despite the increase motion compensation of M1 compared with M0. A more rigorous study is needed to further tease out the relationship of bulk motion-induced signal fall out and the artificial increases in MD and FA.

Conversely, mean LV MD and FA for the proposed M2 diffusion prepared DT-CMR were consistent with previous studies (ADC: 1.3-1.8 um²/ms, FA: 0.2-0.5) using a M2 motion compensation approach (21,22,24,48,49). In addition, the proposed technique demonstrated higher intra-session reproducibility with substantial correlations between the repeated measures and acceptable Bland-Altman plots compared with M0 and M1 DT-CMR. The proposed M2 B1-resistant diffusion preparation was capable of yielding the histologically-validated (41,50) and previously reported (13,41,51) continuous transmural change in HA from endocardium to epicardium in volunteers. The transmural change in HA quantified by HATS was consistent with previous literature (−1.3 to −0.8°/%trans) for both STEAM-based and spin echo-based DT-CMR (13,19,23,49,51-55). Therefore, the proposed M2 B1-resistant DT-CMR technique principally reflected the underlying LV fiber orientation overcoming the adverse effects of bulk motion corruption.

In a small group of HF patients, the proposed M2 DT-CMR technique was able to yield raw DWI free of bulk motion-induced artifacts while M0 and M1-derived DWI exhibited complete signal fall out. Suspicious abnormal regions with elevated MD had corresponding changes in HA, which is consistent with previous literature citing myocardial disarray existing in the presence of myocardial fibrosis (6,56-58). Future pre-clinical studies are needed to validate with histology these findings with follow-up clinical studies to contextualize the proposed DT-CMR technique’s role with established CMR techniques.

Success rate in combatting bulk motion-induced signal loss was reported to be significantly higher for the proposed M2 B1 resist DT-CMR technique with a rate of ~90% for mild HR (<75 BPM) than M0 and M1 DT-CMR scans with rates of ~60% and ~30%. Despite the much shorter TE_prep time (35ms and 46ms), M0 and M1 diffusion encodings proved to have significant residual phase from bulk motion inducing partial or complete signal loss. This signal loss resulted in artificially inflated MD, FA, and HATS values. More importantly, it adversely disrupted the presentation of HA maps disrupting the smooth expected transmural transition from endocardium to epicardium mimicking disease. Future studies comparing various DT-CMR techniques should consider quantifying success rate as an important factor in measuring the robustness to bulk motion. More crucially, it can be a surrogate indicator of how well the techniques will fare in the clinical setting.

The bSSFP readout used in this study has several potential advantages over SS EPI readouts including reduction of susceptibility artifacts, decreased geometric distortion, and use of non-Cartesian trajectories. Currently, SS EPI readouts require a shorter readout to combat magnetic susceptibility and geometric distortion, which is achieved through reduced FOV, partial Fourier acquisition, and parallel imaging (19,20,23). bSSFP readouts do not require these compromises because of the short TR employed. For this reason, non-Cartesian trajectories can be used such as 2D radial or stack of stars opening a new avenue for respiratory navigator and ECG free acquisition (59,60). This would result in better clinical translation of DT-CMR given the current long scan times (>10 min) required to acquire enough diffusion directions to reconstruct the self-diffusion tensor.

Study Limitations

Though the diffusion encoding time has been greatly reduced (105 ms to 67 ms) compared to the original M2 pulse introduced for DW-CMR (21), it remains challenging to identify a sufficiently long quiescent period for diffusion encoding when HR is above 75 BPM. This is a key practical limitation that may explain the low to moderate success (40% to 70%) of the proposed M2 DT-CMR technique since the choice of trigger delay is determined by visual inspection of CINE. According to the numerical simulation outlined in the methods (Supp. Fig. 2), poor B1 refocusing coupled with significant bulk motion due to non-ideal choice in trigger delay can result in significant residual phase despite the attempt to null M2. Furthermore, the determination of an appropriate trigger delay could be difficult in the presence of arrhythmia or even simply HR drift, where a fixed trigger delay would be non-ideal. Despite all these practical issues found in healthy volunteers, this was not seen in our preliminary study of HF patients who had HR well above 75 BPM. The success of the proposed M2 DT-CMR in these patients can likely be attributed to their poor ejection fraction (less pumping bulk motion) and medical regiment of beta blockers. The practical issues of choosing the correct trigger delay or combatting arrhythmia can be potentially alleviated by further shortening the diffusion encoding period with potentially high gradient systems for reliable systolic imaging, shorter total scan times to reduce HR drift, or administration of beta-blockers just prior to imaging (61). Further studies are needed to further develop the proposed M2 DT-CMR to address these practical limitations using standard MRI gradient systems (~40 mT/m).

In this study, only six diffusion directions were acquired with a modest b-value of 350 s/mm² due to the simultaneous usage of two gradient systems at the same time. Though the proposed M2 DT-CMR technique was able to yield reasonable MD, FA, and HA maps, the DT-CMR imaging parameters used in this study are far from ideal compared with ex vivo studies (13,62,63) and in vivo mouse studies (9) that use 12 or more diffusion directions and b-values > 500 s/mm² to characterize myocardial fiber architecture. Future studies will need to be performed in patients comparing the use of higher b-values and more diffusion directions with the protocol used in this study to further elucidate the limits of using such modest DT-CMR parameters in detecting and characterizing abnormalities in the myocardial microstructure.

Another technical limitation is the lack of a ground truth validation of the proposed M2 B1-resistant DT-CMR technique. However, the proposed technique yielded fiber orientations that were consistent to normal organization of the human heart, which is composed of helix-oriented transmural layers that range from right handed (endocardium, HA>0) to left handed (epicardium, HA<0) helix fiber populations or a HATS that is negatively sloped (12,13,16,41,51,64). Though the presence of residual bulk motion sensitivity cannot be ruled out, it is clear that the all-or-nothing “signal drop out” bulk motion artifacts (42) did not dominate the estimated fiber orientation. Animal studies are required to quantify how much of the residual phase can be attributed to bulk motion and determine if the technique can accurately measure the underlying fiber orientation of the heart.

CONCLUSION

We developed an optimized M2 B1-resistant diffusion-prepared DT-CMR technique that allows for myocardial fiber orientation mapping on a 3T clinical MR scanner with conventional gradient system (~40mT/m). The technique demonstrated higher success rates, higher intra-scan reproducibility, and more consistent estimation of DT-CMR parameters than M0 and M1 pulses despite their significantly lower diffusion encoding periods. The technique also exhibited initial feasibility in potentially yielding robust fiber orientation mapping in a small group of HF patients.