Model parameters for simulation of physiological lipids

Abstract

Coarse grain simulation of proteins in their physiological membrane environment can offer insight across timescales, but requires a comprehensive force field. Parameters are explored for multicomponent bilayers composed of unsaturated lipids DOPC and DOPE, mixed‐chain saturation POPC and POPE, and anionic lipids found in bacteria: POPG and cardiolipin. A nonbond representation obtained from multiscale force matching is adapted for these lipids and combined with an improved bonding description of cholesterol. Equilibrating the area per lipid yields robust bilayer simulations and properties for common lipid mixtures with the exception of pure DOPE, which has a known tendency to form nonlamellar phase. The models maintain consistency with an existing lipid–protein interaction model, making the force field of general utility for studying membrane proteins in physiologically representative bilayers. © 2016 The Authors. Journal of Computational Chemistry Published by Wiley Periodicals, Inc.

Introduction

Coarse‐grained (CG) force fields enable the study of molecular level dynamics without the computational expense and sampling limitations inherent in atomistic molecular dynamics simulations. Coarse graining has proven useful for studying protein folding mechanisms in large part due to the success of energy landscape theory, which states that interactions present in the native state also determine the overall energetic landscape.1, 2, 3 When used in conjunction with all‐atom sampling, CG models can bridge disparate length and time‐scales to reveal the comprehensive picture of dynamics and existing structural ensembles.4, 5, 6, 7

Lipid membranes are a popular choice for coarse graining because of the size of the fully solvated system and the slow lateral diffusion of its components.8, 9, 10, 11 In an explicit lipid bilayer model, two‐tailed phospholipids interact via a CG description of head and tail functional groups, each of which are connected by flexible virtual bonds.12, 13 The overall effect of the surrounding water can be captured implicitly13, 14, 15, 16, 17 in the set of lipid and protein nonbond interaction potentials, assuming the parameterization is self‐consistent. More complex schemes represent individual groups of coordinated waters with explicit solvent particles. The well‐known MARTINI force field assigns a van der Waals interaction site for each grouping of four real water molecules.18 Incorporating a three‐bead polarizable site was found necessary to capture electrostatic screening in the CG water and did not affect oil/water partitioning.19, 20

Lu and Voth developed CG parameters for a mixed bilayer13 using the multiscale coarse graining (MS‐CG) method21 to derive a self‐consistent set of nonbond potentials.22 Whereas MARTINI optimizes Lennard–Jones terms empirically to fit macroscopic observables and can exhibit unphysical bond fluctuations,3, 23, 24, 25 MS‐CG employs tabulated potentials to maintain consistency in the pairwise site distributions compared to the atomistic reference ensemble. The Lu and Voth bilayer model was obtained from matching the forces generated by atomistic molecular dynamics simulation (MD) of a 64:64 mix of dioleoly‐phosphatidyl‐choline (DOPC) and dioleoyl‐phosphatidyl‐ethanolamine (DOPE) lipids. The reference simulation used the united‐atom lipid parameters of Berger et al.26 and SPC water. The bilayer exhibited an average area per headgroup of 56.7 Ų, which is smaller than estimates by others.27, 28 Corresponding CG simulations at constant volume (NVT) yielded general agreement with the atomistic behavior for 128‐ and 512‐lipid bilayers.

The present work adapts these and other parameters to simulate lipids common in eukaryotic and prokaryotic membranes. To explore the phase properties of various CG bilayers, simulations are conducted at constant surface tension29, 30 to determine the equilibrated area per lipid. Minimal changes are made to the model scheme so that protein‐lipid potentials previously developed by Ward et al.15 remain compatible for simulations of membrane proteins.31 Stable CG bilayer simulations of realistic geometry are demonstrated for membranes containing DOPC, DOPE, 1‐palmitoyl‐2‐oleoyl‐phosphatidyl‐choline (POPC), 1‐palmitoyl‐2‐oleoyl‐phosphatidyl‐ethanolamine (POPE), phosphatidylglycerol (POPG), cholesterol (Chol), and cardiolipin (CL).

Methods

Atomistic reference simulations

Two 20‐ns atomistic simulations are performed in Gromacs32 for comparison. A 64:64 ratio of DOPC:DOPE lipids were randomly distributed in a 6.5 nm bilayer with 4142 SPC water molecules and simulated using united‐atom Berger parameters.26 Second, a 128‐lipid POPC bilayer was simulated with united‐atom parameters33 and 2460 SPC waters in a 6.7 nm box. Both parameter sets were combined with updated chain torsions accommodating skew states28, 34 to better reproduce the experimental area per lipid. Long‐range dispersion corrections for energy and pressure and a 1.4 nm van der Waals cutoff were found necessary to approximate the experimental area per lipid in constant pressure (NPT) simulations at 1 bar.

Simulation parameters include a 2 fs timestep, 298 K temperature, and Particle‐Mesh Ewald electrostatics. All bonds are constrained using LINCS. The Nosé‐Hoover thermostat with 0.5 ps time constant is used for DOPC:DOPE, while Berendsen temperature coupling with 0.1 ps constant is used for POPC. The pressure is maintained using semiisotropic coupling with a 2 ps time constant and 4.5 × 10⁻⁵ bar⁻¹ compressibility for both x/y and z directions. Parrinello–Rahman pressure coupling is employed for DOPC:DOPE and the Berendsen barostat is used for POPC.

Consistent with the liquid‐disordered phase, the POPC simulation exhibited an average area per lipid of 69.8 ± 0.7 Ų and a hydrophobic thickness of 26.7 Å, defined by the distance between ester carbons. The DOPC:DOPE simulation had an area per lipid of 66.3 ± 1.0 Ų and a hydrophobic thickness of 27.4 Å, defined by the distance between ester sites.

CG model construction

Atomistic snapshots are converted to their corresponding CG representation by determining the mass centers of the atoms assigned to each CG site. Lipid models are constructed as follows. The nine site type assignments for DOPE and DOPC and their harmonic bonds and angles are unchanged from Lu and Voth (Fig. 1).13 The tabulated nonbond potentials for the nine sites are used for lipid‐lipid interactions. The transmembrane peptide K₂L₂₄K₂ 35 is placed in all CG bilayer simulations to examine whether any particular lipid model is destabilized in the vicinity of protein. The sidechain‐centric model of Hills et al. is used to represent protein–protein interactions,24 which maintains a similar mapping of heavy atoms to CG sites. Tabulated lipid–protein protein interactions were developed previously using MS‐CG.15 Transmembrane peptide is weakly biased to α‐helical structure by assigning harmonic springs (K = 150 kJ mol⁻¹ nm⁻²) between α‐carbons pairs within 10.5 Å separated by two or more bonds. The time‐averaged area per lipid molecule of each membrane‐peptide system is computed by subtracting the effective cross‐sectional area of the K₂L₂₄K₂ helix: 144.9 Ų, determined by comparing the box size of an equilibrated POPC bilayer in the presence and absence of peptide.

Figure 1.

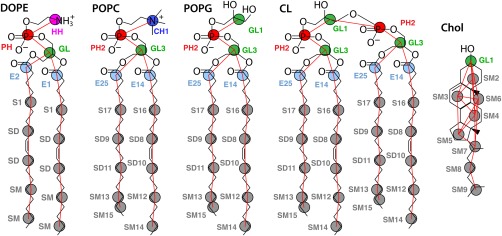
Final CG representation of lipids (v.2). Pairwise nonbond interactions are defined for nine unique site types: choline (blue), ethanolamine (pink), phosphate (red), glycerol (green), esters E1 and E2 (light blue), and nonpolar sites S1, SD, and SM (gray). Pseudobonds between CG sites are drawn as red lines. Pseudoatom numbers for each molecule are appended to the site name for palmitoyl‐oleoyl (PO) lipids and cholesterol. Analogous DOPC and POPE are not shown.

CG‐MD simulations

Single‐component bilayer simulations for each of DOPC, DOPE, POPC, POPE and POPG contained 1148 lipids with starting x = y box dimensions of 19.8, 18.8, 19.2, 18.8, and 18.8 nm, respectively. Mixed bilayer simulations consisted of randomly distributed lipids for: 574DOPC:574DOPE, 574POPC:574POPE, 918POPC:230Chol, 472POPC:446POPE:230Chol, and 784POPE:260POPG:52CL with starting x = y dimensions of 19.3, 18.7, 17.6, 17.4, and 18.8 nm, respectively.

Berendsen pressure coupling with a 2 ps time constant is used to apply a lateral surface tension to equilibrate isotropically the x = y box dimensions and maintain a model's preferred area per lipid. Maintaining a constant area with surface tension is analogous to fixing the box edge length in the NVT ensemble.29 Fixing too small or large an area, however, can destabilize the bilayer, causing tails to protrude from the nonpolar core. The effect can be more noticeable with smaller box sizes (6–9 nm), making equilibrating the area per lipid necessary. The temperature is maintained using Langevin dynamics with a 2 ps inverse friction constant. A CG simulation temperature of kT = 2.2 kJ mol⁻¹ was chosen for the best behavior across all liquid phase systems studied.

As in previous work, stiff protein bonds are relaxed to the harmonic equivalent of K = 10⁵ kJ mol⁻¹ nm⁻² to enable a 5 fs timestep, better reproducing the underlying atomic fluctuations than the force constants used for the 20 fs MARTINI timestep.3, 19 Each 17,000‐atom membrane system is simulated for 50 ns, requiring 10 h on a 48‐core node. The neighbor list is updated every step for the 1.2 nm nonbonded interaction cutoff.

Results and Discussion

Parameter improvement

Two improvements are made on the original bilayer model parameters of Lu and Voth.13 First, the geometry is restrained about the hydrocarbon cis double bond in oleoyl tails for DO/PO lipids. A four‐body periodic type proper dihedral potential was fit to the atomistic MD ensemble observed for both POPC and 1:1 DOPC/DOPE bilayers (Fig. 2). The same force constant of K_ϕ = 4.5 kJ/mol is used for the two double bonds in DOPC and DOPE and for each unsaturated chain in POPC, POPE, POPG, and CL.

Figure 2.

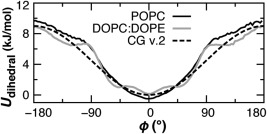
The probability distributions of the unsaturated S1‐SD‐SD‐SM pseudotorsion, Boltzmann‐inverted using U = kT ln p(ϕ). A single dihedral potential (dashed) is found to maintain the distribution observed in atomistic bilayer simulations (solid lines).

Second, when attempting to simulate a pure DOPE bilayer it was discovered that ethanolamine headgroup (HH) interactions were too attractive, formed a nonlamellar phase, and exposed the nonpolar tails, under both NVT and constant surface tension simulations. CG interaction potentials are compared in Figure 3. The solution employed was to replace the original HH‐HH term with the comparable, but more repulsive, potential developed for the CH‐HH interaction. Headgroup self‐association is assessed using the three‐dimensional (3D) radial distribution functions (RDFs) for HH, CH, and PH sites in 1DOPC:1DOPE bilayer simulations. The current model, denoted version 2 (v.2), is in better agreement with atomistic MD results than the original model (Fig. 4).

Figure 3.

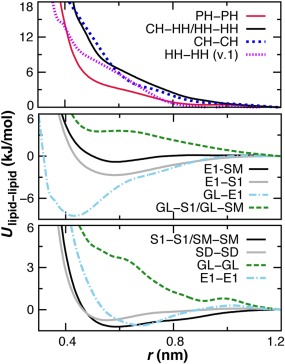
Comparison of select tabulated nonbond potentials of Lu and Voth used for all lipids.13 Nine unique site types are employed with the modification that the CH‐HH term is substituted for the repulsion between ethanolamine head groups (HH‐HH). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 4.

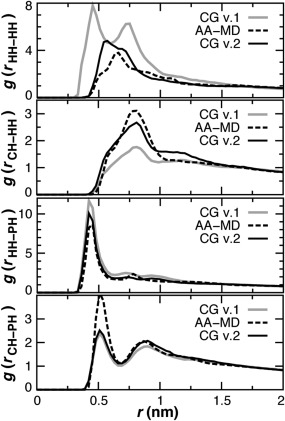
Head group radial distribution functions (RDF) in CG versions (solid) and atomistic (dash) DOPC:DOPE bilayer simulations. The 3D CG RDFs are scaled by 0.33 to account for the larger box size.

Treatment of phospholipids

Existing bond and angle terms for DOPC and DOPE functional groups were previously developed by Lu and Voth.13 Iterative Boltzmann inversion36 was found necessary due to the coupling of terms and the effect of local environment, as with electrostatic interactions between phospholipid headgroups.37, 38, 39 Corresponding geometric terms are adapted to construct models for PG and CL headgroups. The new terms for GL1‐PH2, GL1‐PH2‐GL3, and PH2‐GL1‐PH2 are labeled v.2 in Table 1. Bonds and angles for the unsaturated oleoyl chain are unchanged, but the pseudoatom numbers are appended to the site types to distinguish between the saturated palmitoyl chain (Fig. 1). Bonds and angles for saturated SD9 and SD11 sites in palmitoyl are taken from analogous segments in the oleoyl chain.

Table 1.

Comparison of bonded stretching parameters implemented for palmitoyl‐oleoyl lipid sites.

Harmonic bonds	r min (nm)	K bond (kJ mol−1 nm−2)
CH PH (v.1)a	0.435	7914.7
HH PH (v.1)	0.328	19,707.8
GL1 PH2 (v.2)	0.328	7914.7
PH2 GL3 (v.1)	0.347	13,304.3
SD8 SD10 (v.1)	0.331	11,681.5
SD9 SD11 (v.2)	0.338	7773.9
SD SM (v.1)	0.338	7773.9
SM12 SM14 (v.1)	0.345	8026.5
SM13 SM15 (v.2)	0.1	8026.5
Harmonic angles	θ 0 (degrees)	Kθ (kJ mol−1 rad−2)
CH PH GL (v.1)	127.9	33.9
HH PH GL (v.1)	115.8	74.6
GL1 PH2 GL3 (v.2)	115.8	33.9
PH2 GL1 PH2 (v.2)	115.8	33.9
S16 SD8 SD10 (v.1)	146.6	40.2
S17 SD9 SD11 (v.2)	158.2	23.5
SD8 SD10 SM12 (v.1)	145.0	36.2
SD9 SD11 SM13 (v.2)	158.2	23.5
SD SM SM (v.1)	158.2	23.5
Proper dihedrals	ϕ 0 (degrees)	Kϕ (kJ mol−1)	nb
S16 SD8 SD10 SM12 (v.2)	180	4.5	1

^aVersion 1 denotes terms parameterized from a DOPC:DOPE bilayer.^[13]

^bPeriodic multiplicity.

The palmitoyl chain contains two fewer carbon atoms than the oleoyl tail, but we were unable to obtain a stable bilayer model of POPC using only five tail sites40 for palmitoyl. The six tail sites (E2/E1, S1, SD, SD, SM SM) were then used for palmitoyl and oleoyl. POPC simulations were tested using equilibrium bond distances between SM13 and SM15 of 0.5, 1.0, and 1.7 Å. The 1‐Å bond resulted in the best agreement with the experimental values for the area per lipid and hydrophobic thickness (Table 2). Indeed, all palmitoyl‐oleoyl (PO) lipid mixtures simulated with these parameters for SM15 compare well with data available in the literature.27, 40, 41, 42, 43, 44, 45, 46 The pure POPG bilayer had the largest deviation in area per lipid, while pure DOPE had the largest deviation in hydrophobic thickness.

Table 2.

Constant surface tension CG v.2 simulations.^a

		Tension		Experiment (303 K)
Bilayer	(mN/m)	Area/Å2 b	E‐E (Å)c	Area/Å2	2D C (Å)
DOPC	50	69.2	28.8	67.4d	28.8d
DOPE	60	63.5	30.0	60–65[e,f]	32.3[e,k]
1:1 DOPC/PE	60	66.3	29.5	54–63f	‐
POPC	50	63.2	28.5	64.3g	28.8g
POPE	60	56.4	30.6	56.6e	32.6[e,k]
1:1 POPC/PE	60	59.9	29.4	–	–
POPG	70	61.2	28.9	66.0h	27.9h
4:1 POPC/Chol	60	53.4	30.5	53i	–
2:2:1 POPC/PE/Chol	60	50.8	31.3	–	–
15:5:1 POPE/PG/CL	70	58.3	29.9	–	–

^a1148‐lipid system at kT = 2.24 kJ/mol.

^bStandard deviation < 0.2.

^cHydrophobic thickness calculated as mean distance between ester CG sites.

^dKucerka et al., 2008.41

^eSee Jambeck and Lyubartsev, 2012.42

See Orsi and Essex, 2013.43

^fSee de Vries et al., 2004.27

^gKucerka et al., 2011.44

^hKucerka et al., 2012.45

ⁱ30 mN/m surface pressure (Smaby et al., 1997).46

All‐atom MD.

Cholesterol

Cholesterol was added to the model to represent the major components of eukaryotic membranes.47, 48, 49 The systematically improved nine‐site model of Daily et al.40 is employed for the site definitions and bonding interactions, including all harmonic bonds, constraints, cosine‐based angle potentials, and harmonic dihedrals to maintain planarity. The nine‐site model constitutes a significant improvement over the original eight‐site MARTINI representation.18 The position of site 6 was elevated to properly account for the role of the rough face methyl groups in limiting first‐shell cholesterol self interactions.50

Different model site types were explored for treating the nonbond lipid interactions involving cholesterol. CG simulations are tested in POPC‐only bilayers to compare to previous studies,40, 46 with a physiological mole concentration of 20% cholesterol (4 POPC: 1 Chol). Initial tests performed with nonpolar SD sites spanning positions 3–6 or 2–9 resulted in excessive first‐shell cholesterol association. SM sites were therefore employed for positions 2–9, which made cholesterol more attracted to the PO lipid chains due to a favorable SM‐SM interaction (Fig. 3). A single S1 site was tested at position 2, but its stronger attraction for ester sites E1 and E2 gave rise to smaller cholesterol tilt angles than has been observed in atomistic MD.40, 51

For the cholesterol headgroup, E1 and GL site types were investigated. The self‐association of cholesterol molecules in the bilayer plane was compared for 9‐site models containing the following site types (Fig. 5): E1‐S1‐SM(3‐9), E1‐S1‐SD(3‐6)‐SM(7‐9), and GL‐SM(2‐9). Incorporating the GL headgroup results in the best agreement with previous studies.40, 50 The repulsive GL‐GL potential (Fig. 3) limits first‐shell association near 0.6 nm, whereas the attractive E1–E1 potential promotes it.

Figure 5.

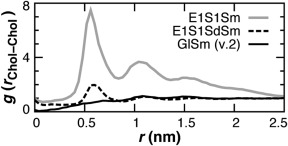
Cholesterol mass center self‐association 2d‐RDFs in the bilayer plane for three different CG cholesterol models tested in a 4:1 POPC:Chol bilayer. The repulsive GL‐GL nonbond potential (solid black) was found to successfully limit first‐shell association near 0.6 nm.40

The angle of cholesterol tilt is computed as a function of headgroup bilayer depth (Fig. 6). GL head groups cluster at a height z = 1.0 nm from the bilayer midplane, closest to the S17 acyl positions of POPC. The tilt of cholesterol molecules predominantly remains below 50 degrees and is larger for the more buried molecules. Cholesterol molecules are not observed to invert within the membrane, as has been seen with eight‐site models.40 These observations for 0.2 mole fraction cholesterol are consistent with prior atomistic MD studies at varied cholesterol concentrations.40, 51

Figure 6.

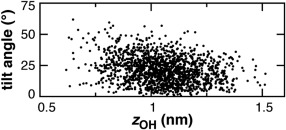
Cholesterol tilt angle versus distance of head group from bilayer midplane.51 Selected snapshots are shown for 4POPC:Chol CG v.2 simulation. Angle of tilt relative to the bilayer normal was computed using the SM7‐SM2 vector.40

CG molecular dynamics

Simulation of a pure DOPE bilayer is performed as a rigorous test of the model since unlike DOPC, DOPE has a marked propensity to form inverted hexagonal phases.43, 52 Experimentally, DOPE forms bilayers rather than hexagonal phase only at intermediate concentrations in water below 25°C.52 The revised HH‐HH potential limits the nonlamellar behavior of DOPE lipids. The DOPE bilayer is stable under CG‐MD, an improvement over v.1 simulations in which the pure DOPE bilayer breaks apart. Examination of the DOPE v.2 bilayer trajectory does reveal several transiently formed patches at the bilayer interface that are devoid of headgroups (Fig. 7A). This tendency highlights the attractive nature of the ethanolamine headgroups (Fig. 4), due to hydrogen bonding of the amine with phosphate.43 The HH‐PH tabulated potential, developed from atomistic reference simulations,13 has an attractive well depth of 14.9 kJ/mol, compared to 7.2 kJ/mol for that of CH‐PH. An applied surface tension of 60 mN/m was found to best minimize headgroup defects in DOPE simulations. The pure DOPE simulation exhibited an area per lipid of 63.5 Ų, comparable to data available in the literature (Table 2).42, 43

Figure 7.

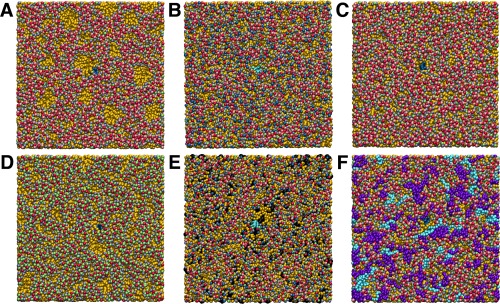
Final snapshot of CG bilayer simulations. The color scheme in Figure 1 is used for DOPE (A), DOPC:DOPE (B), POPE (C), and POPG (D) systems with tail sites shown in gold. Cholesterol is colored black for the 2POPC:2POPE:Chol bilayer (E). POPG and CL are colored purple and cyan, respectively, for 15POPE:5POPG:CL (F). For clarity, the transmembrane peptide is centered in each frame and colored blue (A,C,D,F) or cyan (B,E).

Headgroup defects are not observed in CG simulations of pure DOPC or pure POPC either in the bilayer bulk or in the vicinity of transmembrane peptide. A reduced surface tension of 50 mN/m resulted in good agreement with the experimental area per lipid and thickness for the pure DOPC and pure POPC CG simulations (Table 2).41, 44 It is noteworthy that the CG POPC area (63.2 ± 0.1 Ų) agrees better with experiment (64.3 Ų) than atomistic33 MD (69.8 ± 0.7 Ų). Similarly, POPC hydrophobic thickness is 28.5 Å (CG‐MD), 28.8 Å (experiment),44 and 26.7 Å (AA‐MD).

CG simulation of the DOPC:DOPE mixed bilayer at 60 nM/m is nearly devoid of defects across the entire membrane (Fig. 7B), illustrating the complete mixing of the two components and the rescue of DOPE's nonlamellar tendency by equimolar DOPC. The mean area per lipid (66.3 Ų) is intermediate between that of pure DOPC and pure DOPE, comparable to other estimates,27 and is identical to the reference atomistic simulation.

Simulation of a pure POPE bilayer with the same lateral pressure results in a smaller area per lipid than in DOPE (Table 2), given its shorter saturated tail.53 Even though the PE headgroup parameters are identical, the bilayer defects observed with pure DOPE are not present in POPE (Fig. 7C). Enhanced packing of the POPE saturated chain promoted lamellar behavior. Unlike DOPE, POPE is a major component of eukaryotic and prokaryotic membranes.

The anionic lipid POPG, abundant in prokaryotic membranes, was modeled using the glycerol site type at positions 1 and 3. A higher surface tension of 70 mN/m was needed to minimize defects in the headgroup region (Fig. 7D).38 The bilayer was not stretched or thinned beyond experimental values for the area and thickness (Table 2).45

Physiological bilayers

To create an environment representative of the plasma membrane,49, 54 a ternary mixture is simulated containing 2POPC:2POPE:1Chol, corresponding to erythrocytes in humans. As expected,40 cholesterol at a concentration of 0.2 mole fraction noticeably reduces the area per lipid from the value observed for 1POPC:1POPE and increases the hydrophobic thickness, determined from the mean separation between ester sites E1 and E2 (Table 2). Excessive clustering is not observed between cholesterol molecules during the simulation (Fig. 7E).

The double phospholipid cardiolipin is modeled using PO tails to develop a system for the inner membrane of gram‐negative bacteria. The acyl structure of E. coli cardiolipin is highly variable, with a predominant range of 64–68 carbons and 1–3 total unsaturations or even cyclopropane groups.55 The most abundant fatty acids in E. coli are 16:0 and 18:1, consistent with using PO tails to model cardiolipin.56 In contrast, other MD studies have focused on mitochondrial cardiolipin containing dioleoyl (DO)38, 57 or even diunsaturated58 chains. A system of 15POPE:5POPG:1CL was simulated for the E. coli inner membrane. The area per lipid is intermediate between that of pure POPE and pure POPG (Table 2). The pairwise RDFs are compared using only the x and y components of the distance between phosphate sites for each component lipid (Fig. 8). Self‐association is observed at 0.5 nm. By comparison, RDFs from MARTINI simulations in DOPE and DOPC peaked at 0.5 and 1.0 nm across cardiolipin concentrations.38 The present model limits self‐association in both eukaryotic and prokaryotic membranes (Figs. 7E–7F), suggesting commonalities in their dynamical behavior.59

Figure 8.

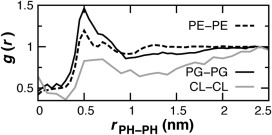
Lipid‐lipid 2D association RDFs computed in the bilayer plane for phosphate sites in 15POPE:5POPG:CL.38

Conclusions

A model of general utility for simulations of membrane systems was explored using physiological lipid bilayer compositions. The applied surface tension was calibrated to approximate experimental values known for the area per lipid rather than values obtained from a given atomistic force field.39 The bilayer structure remained stable for lamellar lipids other than DOPE. The present working model established for lipids abundant in eukaryotic and prokaryotic membranes will find future application in studies of lipid and protein interactions.60 Integrating out the water degrees of freedom makes the model of promising utility for systems with large cytoplasmic domains, as previously demonstrated with the MsbA transporter.15

The equilibrated area per lipid was recently determined for a wide selection of phospholipids in the MARTINI model.16 Traditional explicit water Martini simulations were simulated using semi‐isotropic pressure coupling of 1 bar parallel and normal to the bilayer. Bilayers were also equilibrated at zero tension using the Dry Martini model, which adapts purely attractive Lennard–Jones potentials to simulations in the absence of CG water. The implicit solvent simulations were conducted with 0 bar pressure in the bilayer plane. Approximate structural properties such as the area per lipid were reproduced with both models, but the permeation energetics of protein sidechains with multiple sites, including aromatic residues, suffered in Dry Martini. The lipid areas at 310 K are similar to the values in Table 2, albeit with a larger standard deviation of 0.8 Ų. Wet and Dry areas were 66 and 64 for POPC, 66 and 64 for DOPC, and 62 and 63 for DOPE, respectively. The water‐free force field we have developed thus better captures the difference in area between PO and DO tails, and exhibits agreement with experiment better than some atomistic simulations.

Exploration of bilayer permeation energetics with model amino acid site types will be described in a separate publication to further develop the protein component of the force field. In developing such models for biomolecules, the assignment of CG particle interaction centers, their bonded and nonbonded representations, and atom‐to‐CG mapping are crucial to obtaining a robust and transferrable model.3, 5, 40, 61 The models developed and explored for mixed bilayers and their interactions will serve as a guide for future parameterization efforts.

How to cite this article: Hills Jr. R. D., McGlinchey N.. J. Comput. Chem. 2016, 37, 1112–1118. DOI: 10.1002/jcc.24324