Shape-programmable magnetic soft matter

Significance

At small scales, shape-programmable magnetic materials have significant potential to achieve mechanical functionalities that are unattainable by traditional miniature machines. Unfortunately, these materials have only been programmed for a small number of specific applications, as previous work can only rely on human intuition to approximate the required magnetization profile and actuating magnetic fields for such materials. Here, we propose a universal programming methodology that can automatically generate the desired magnetization profile and actuating fields for soft materials to achieve new time-varying shapes. The proposed method can enable other researchers to fully capitalize the potential of shape-programming technologies, allowing them to create a wide range of novel soft active surfaces and devices that are critical in robotics, material science, and medicine.

Abstract

Shape-programmable matter is a class of active materials whose geometry can be controlled to potentially achieve mechanical functionalities beyond those of traditional machines. Among these materials, magnetically actuated matter is particularly promising for achieving complex time-varying shapes at small scale (overall dimensions smaller than 1 cm). However, previous work can only program these materials for limited applications, as they rely solely on human intuition to approximate the required magnetization profile and actuating magnetic fields for their materials. Here, we propose a universal programming methodology that can automatically generate the required magnetization profile and actuating fields for soft matter to achieve new time-varying shapes. The universality of the proposed method can therefore inspire a vast number of miniature soft devices that are critical in robotics, smart engineering surfaces and materials, and biomedical devices. Our proposed method includes theoretical formulations, computational strategies, and fabrication procedures for programming magnetic soft matter. The presented theory and computational method are universal for programming 2D or 3D time-varying shapes, whereas the fabrication technique is generic only for creating planar beams. Based on the proposed programming method, we created a jellyfish-like robot, a spermatozoid-like undulating swimmer, and an artificial cilium that could mimic the complex beating patterns of its biological counterpart.

Shape-programmable matter refers to active materials that can be controlled by heat (1–5), light (6, 7), chemicals (8–13), pressure (14, 15), electric fields (16, 17), or magnetic fields (18–33) to generate desired folding or bending. As these materials can reshape their geometries to achieve desired time-varying shapes, they have the potential to create mechanical functionalities beyond those of traditional machines (1, 15). The functionalities of shape-programmable materials are especially appealing for miniature devices whose overall dimensions are smaller than 1 cm as these materials could significantly augment their locomotion and manipulation capabilities. The development of highly functional miniature devices is enticing because, despite having only simple rigid-body motions (34–36) and gripping capabilities (37), existing miniature devices have already been used across a wide range of applications pertaining to microfluidics (38, 39), microfactories (40, 41), bioengineering (42, 43), and health care (35, 44).

Among shape-programmable matter, the magnetically actuated materials are particularly promising for creating complex time-varying shapes at small scales because their control inputs, in the form of magnetic fields, can be specified not only in magnitude but also in their direction and spatial gradients. Furthermore, as they can be fabricated with a continuum magnetization profile, $\mathbf{m}$, along their bodies, these magnetic materials can also generate deformations with very high spatial resolutions. A continuum $\mathbf{m}$ can be approximated as a collection of magnetic dipoles continuously distributed within a material, where each dipole can produce locally varying stress when it interacts with the actuating fields. The actuating fields can deform the materials by either exerting magnetic forces (27, 30) or torques (18, 19) on these dipoles.

Although shape-programmable magnetic soft materials have great potential, previous work can only rely on human intuition to approximate the required m and actuating fields for these materials to achieve their desired time-varying shapes. As a result, such heuristic and unsystematic methods can only program these materials for a limited number of applications, demonstrating only either simple deformations (21, 24–28) or very specific functionalities (18–20, 22, 23, 29–33).

Here, we present a universal programming methodology that can automatically generate the required $\mathbf{m}$ and actuating fields for small-scale soft matter to achieve desired time-varying shapes (Fig. 1A). This universal method therefore has the potential to inspire a wide variety of miniature devices that could transform robotics, material science, and biomedicine. The proposed method consists of theoretical formulations, computational strategies, and fabrication procedures. Although the theory and computational method are universal for programming 2D or 3D time-varying shapes (S2. Programming Materials with 3D Time-Varying Shapes), our fabrication technique is only generic for making planar beams. Despite the limitations of our current fabrication technique, it is still significantly better than existing techniques, which at most can only create direction-varying $\mathbf{m}$ that have a uniform magnitude (18, 19). As we can fabricate continua $\mathbf{m}$ that have desirable nonuniform magnitude and orientation profiles, the potential of shape-programmable magnetic beams can now be fully realized.

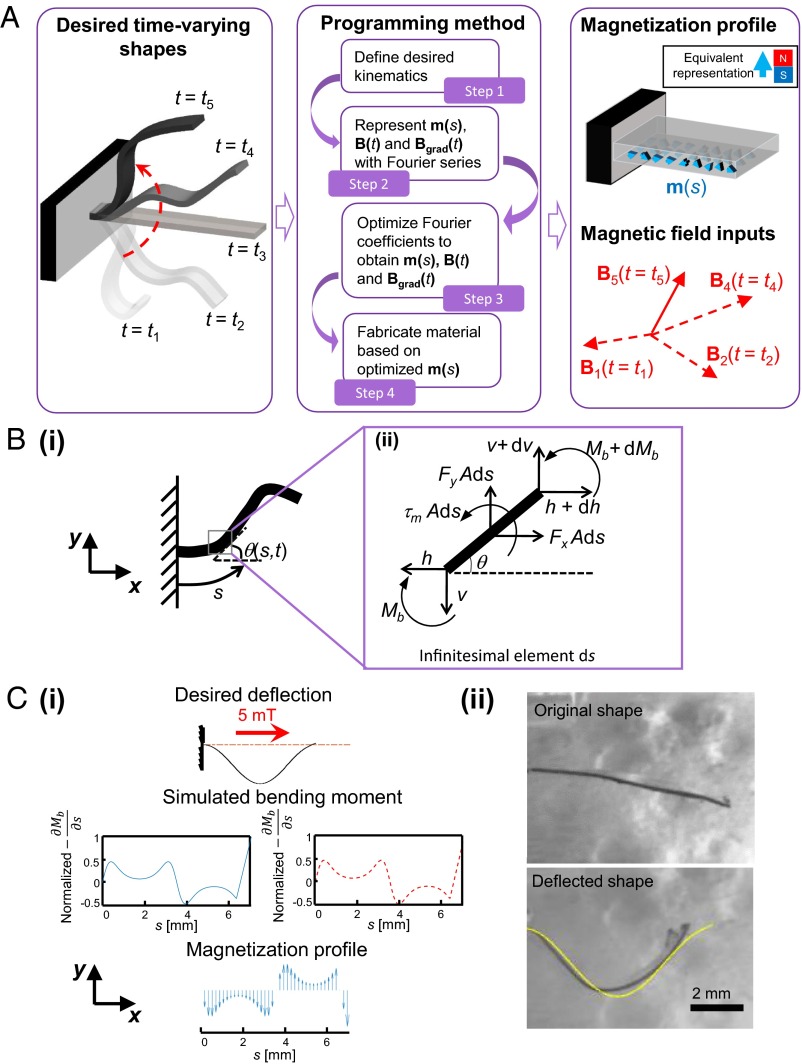
Fig. 1.

The programming methodology and a simple proof of concept. (A) The programming method for magnetic soft elastomeric composite materials to achieve the desired time-varying shapes. We illustrate this concept with an arbitrary beam that can be programmed to achieve the desired shapes shown on the Left. By using our proposed programming method (shown in the Center), we can automatically generate the required magnetization profile, $\mathbf{m}\left(s\right)$, and magnetic field control inputs, $\mathbf{B}\left(t\right)$, for the material (shown on the Right). The given $\mathbf{m}\left(s\right)$ and $\mathbf{B}\left(t\right)$ are only used as an illustration. (B) A graphical illustration for the theoretical formulations. Based on the desired kinematics in i, a quasistatic analysis can be conducted on ii. (C) A simple proof of concept of the proposed method in which a beam is programmed to create a shape resembling a cosine function when it is subjected to a 5-mT uniform magnetic field input. (i) Desired shape, simulated first derivative of the bending moment, and necessary magnetization profile along the beam. The desired first derivative of the bending moment is represented by the blue curve, whereas the dotted red curve represents the first derivative of the bending moment generated by magnetic actuation. As the blue and dotted red curves will totally overlap one another, they have been separated into two plots for clarity. The plotted magnetization profile is along the predeformed beam (see Fig. S6 for a more quantitative representation for the magnetization). Additional parameters for this device can be found in S9. Parameters for Each Case and Table S1. The obtained experimental results are shown in ii. The yellow line represents the desired programmed shape for this demonstration. The beam achieved its programmed shape when it was subjected to a 5-mT magnetic field.

Programming Methodology

We demonstrate our programming methodology with a large deflecting beam subjected to quasistatic conditions (Fig. 1B). For practical considerations, we have also considered $\mathbf{m}$ to be time invariant and actuating fields to be uniform in space. These constraints are necessary because it is challenging both to remagnetize the device in situ and to create position-variant actuating fields at such small scale with our electromagnets (Fig. S1).

Fig. S1.

A custom electromagnetic coil system that has eight coils is used for generating the actuating fields. The programmed beams will be placed in a container filled with liquid(s), and the container will in turn be placed at the center of the workspace. During the experiments, the camera will record the time-varying shapes of the beams.

To simplify our discussion, we constrain the cross-sectional area of this beam to be uniform and allow it to bend in a plane. Furthermore, although we have provided the generic discussions for the beam’s boundary conditions in S1. Boundary Conditions (see also Fig. S2), here we simplify the boundary conditions to fixed-free (Fig. 1Bi). Without any loss in generality, the bending axis of the beam is described by the z axis of the global frame shown in Fig. 1B.

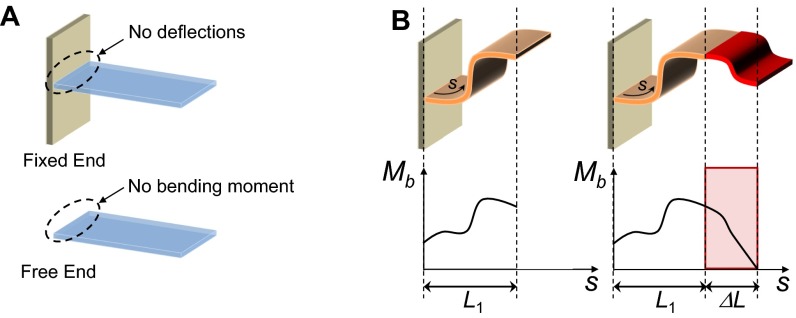
Fig. S2.

Necessary boundary conditions. (A) For a fixed end, there should not be any deflections. By contrast, there should be no bending moment at the free end. (B) Adding a physical extension to satisfy the boundary conditions for the free ends. At all of the time instants, the bending moment at the free end should be zero, as achieved by introducing an extension at the free end (indicated by the red portions). The bending moment along this extension will be fitted by a polynomial function so that its bending moment at the new free end will always be zero.

Theoretical Formulation.

Following the steps in Fig. 1A, we first define the desired deformations along the beam’s length, s. Because such deformations can vary with time, t, the kinematics can be mathematically represented with the rotational deflections along the beam, $\theta \left(s,t\right)$ (Fig. 1Bi). After the kinematics are specified, we establish the torque balance equation for an arbitrary infinitesimal element (Fig. 1 B, ii), ds, at any time, t, to be as follows:

$${\tau }_{m}A+v\hspace{0.17em}\cos \hspace{0.17em}\theta -h\hspace{0.17em}\sin \hspace{0.17em}\theta =-\frac{\partial M_b}{\partial s}.$$ [1]

The variables ${\tau }_m\left(s,t\right)$, $M_b\left(s,t\right)$, and A represent the applied magnetic torque (per volume), the beam’s bending moment, and its cross-sectional area, respectively. The other variables, $h\left(s,t\right)$ and $v\left(s,t\right)$, correspond to the x- and y-axis internal forces within the beam, respectively. Similarly, the force balance equations of the infinitesimal element can be expressed as follows:

$$F_x=-\frac{1}{A}\frac{\partial h}{\partial s},\hspace{0.17em}\hspace{1em}{F}_y=-\frac{1}{A}\frac{\partial v}{\partial s},$$ [2]

where $F_x\left(s,t\right)$ and $F_y\left(s,t\right)$ represent the applied magnetic forces (per volume) along the x and y axes, respectively. Thus, by using the Euler–Bernoulli equation and substituting Eq. 2 into Eq. 1, the desired deflections (i.e., required first derivative of bending moment) can be expressed explicitly by the actuating magnetic forces and torques as follows:

$${\tau }_m+{\displaystyle {\int }_s^L{F}_y\hspace{0.17em}\text{d}s}\cos \theta -{\displaystyle {\int }_s^L{F}_x\hspace{0.17em}\text{d}s}\sin \theta =-\frac{EI}{A}\frac{{\partial }^2\theta }{\partial s^2}.$$ [3]

The variables E, I, and L represent the Young’s modulus, the second moment of area, and the length of the beam, respectively. Eq. 3 implies that the material’s desired time-varying shapes can be achieved if the magnetic torques and forces can be programmed to balance the desired first derivative of bending moment, across the entire length of the beam at all times. To determine the necessary $\mathbf{m}\left(s\right)$ and actuating fields for the desired $\theta \left(s,t\right)$, we first give their mathematical relationship with the applied magnetic torques and forces:

$$\begin{array}{l}{\tau }_m\left(s,t\right)=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\left\{\left[\mathbf{R}\left(s,t\right)\mathbf{m}\left(s\right)\right]\times \mathbf{B}\left(t\right)\right\},\\ F_x\left(s,t\right)=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\left\{\left[\mathbf{R}\left(s,t\right)\mathbf{m}\left(s\right)\right]\cdot \nabla \right\}\mathbf{B}\left(t\right),\\ F_y\left(s,t\right)=\left[\begin{array}{ccc}0& 1& 0\end{array}\right]\left\{\left[\mathbf{R}\left(s,t\right)\mathbf{m}\left(s\right)\right]\cdot \nabla \right\}\mathbf{B}\left(t\right).\end{array}$$ [4]

The magnetic torque is a function of $\mathbf{m}\left(s\right)$ and the magnetic field, $\mathbf{B}\left(t\right)$, whereas the magnetic forces are dependent on $\mathbf{m}\left(s\right)$ and the spatial gradients of $\mathbf{B}\left(t\right)$. The rotational matrix, $\mathbf{R}\left(s,t\right)$, is used to account for the orientation change of magnetization profile due to the beam’s large deflection, and it is given as the following:

$$\mathbf{R}=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right].$$ [5]

Computational Method.

In contrast to previous magnetic programming studies, we do not use human intuition to speculate the necessary $\mathbf{m}\left(s\right)$ and the actuating fields. Instead, they are automatically generated by computers, and this is achieved by first representing them with corresponding sets of 1D Fourier series (step 2 in Fig. 1A):

$$\begin{array}{l}\mathbf{m}\left(s\right)=\left[\begin{array}{c}{\displaystyle {\sum }_{i=0}^n{a}_i\cos \left(i{w}_{s}s\right)+b_i\sin \left(i{w}_{s}s\right)}\\ {\displaystyle {\sum }_{i=0}^n{c}_i\cos \left(i{w}_{s}s\right)+d_i\sin \left(i{w}_{s}s\right)}\\ 0\end{array}\right],\\ \mathbf{B}\left(t\right)=\left[\begin{array}{c}{\displaystyle {\sum }_{j=0}^m{\alpha }_j\cos \left(j{w}_{t}t\right)+{\beta }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\gamma }_j\cos \left(j{w}_{t}t\right)+{\eta }_j\sin \left(j{w}_{t}t\right)}\\ 0\end{array}\right],\\ {\mathbf{B}}_{\text{grad}}\left(t\right)=\left[\begin{array}{c}\frac{\partial B_x}{\partial x}\left(t\right)\\ \frac{\partial B_y}{\partial x}\left(t\right)\\ \frac{\partial B_y}{\partial y}\left(t\right)\end{array}\right]=\left[\begin{array}{c}{\displaystyle {\sum }_{j=0}^m{\mathit{ϵ}}_j\cos \left(j{w}_{t}t\right)+{\delta }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\lambda }_j\cos \left(j{w}_{t}t\right)+{\mu }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\rho }_j\cos \left(j{w}_{t}t\right)+{\sigma }_j\sin \left(j{w}_{t}t\right)}\end{array}\right].\end{array}$$ [6]

The significant benefit of such representation is that Fourier series is inclusive of all possible discrete or continuous mathematical functions, enabling our proposed method to be universal. The vector ${\mathbf{B}}_{\text{grad}}\left(t\right)$ represents the spatial gradients of $\mathbf{B}\left(t\right)$ necessary for generating $F_x$ and $F_y$. The angular frequencies, ${\omega }_s$ and ${\omega }_t$, are given as $2\pi /L$ and $2\pi /T$, respectively, and T represents the total time to complete the shape trajectory. The other variables $a_i,b_i,c_i,d_i,{\alpha }_j,{\beta }_j,{\gamma }_j,{\eta }_j,{\mathit{ϵ}}_j,{\delta }_j,{\lambda }_j,{\mu }_j,{\rho }_j,\hspace{0.5em}\mathrm{and}\hspace{0.5em}{\sigma }_j$ are the 1D Fourier coefficients, and their subscripts i and j are integers that range from 0 to n and 0 to m, respectively. Thus, by substituting Eq. 6 and Eq. 4 into Eq. 3, we can obtain the following equation:

$$\left[{\mathrm{ℱ}}_1\hspace{0.17em}\text{cos}\hspace{0.17em}\theta -{\mathrm{ℱ}}_2\hspace{0.17em}\text{sin}\hspace{0.17em}\theta \right]+\left[{\displaystyle {\int }_s^L{\mathrm{ℱ}}_3\hspace{0.17em}\text{cos}\hspace{0.17em}\theta +{\mathrm{ℱ}}_4\hspace{0.17em}\text{sin}\theta \hspace{0.17em}\text{d}s}\right]\text{cos}\theta -\left[{\displaystyle {\int }_s^L{\mathrm{ℱ}}_5\hspace{0.17em}\text{cos}\hspace{0.17em}\theta +{\mathrm{ℱ}}_6\hspace{0.17em}\text{sin}\theta \hspace{0.17em}\text{d}s}\right]\text{sin}\theta =-\frac{EI}{A}\frac{\partial {}^2\theta }{\partial s^2},$$ [7]

where the left side is a function that represents the magnetic actuation and the right side represents the desired first derivative of bending moment. Each of these symbols, ${\mathrm{ℱ}}_1$ to ${\mathrm{ℱ}}_6$, corresponds to a set of 2D Fourier series expressed in s and t, with each 2D Fourier coefficients created from the 1D Fourier coefficients in $\mathbf{m}\left(s\right)$, $\mathbf{B}\left(t\right)$, and ${\mathbf{B}}_{\text{grad}}\left(t\right)$. Although the detailed mathematical description for ${\mathrm{ℱ}}_2$ to ${\mathrm{ℱ}}_6$ are shown in S6. Additional Discussion, we will show the mathematical representation of ${\mathrm{ℱ}}_1$ here as an example:

$$\begin{array}{c}{\mathrm{ℱ}}_1={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\gamma }_j-c_i{\alpha }_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\eta }_j-c_i{\beta }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\gamma }_j-d_i{\alpha }_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\eta }_j-d_i{\beta }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}.\end{array}$$ [8]

By following step 3 in Fig. 1A, a computational optimization method is then used to determine the optimal values of the 1D Fourier coefficients to satisfy Eq. 7. This optimization method is implemented by first discretizing the motion of the beam into p time frames, that is, $t=t_1$;$\dots$; $t=t_p=T$. Meanwhile, the beam is divided into q segments in length, that is, $s=s_1$;$\dots$; $s=s_q=L$. Thus, we create q new equations for each time frame by substituting different values of s along the beam into Eq. 7. By assembling all of the equations across all time frames, there are a total of $p\times q$ linear equations that can be written in matrix form as follows:

$$\mathbf{K}\mathbf{u}={\mathbf{M}}_{\mathbf{b}},$$ [9]

where $\mathbf{u}$ and ${\mathbf{M}}_{\mathbf{b}}$ are vectors containing the 2D Fourier coefficients and the desired first derivative of the bending moment across these $p\times q$ equations, respectively.

Subsequently, the optimal 1D Fourier coefficients in $\mathbf{m}\left(s\right)$, $\mathbf{B}\left(t\right)$, and ${\mathbf{B}}_{\text{grad}}\left(t\right)$ can be solved by performing the following optimization process:

$$\begin{array}{l}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\text{minimize}\hspace{1em}\hspace{1em}{\left(\mathbf{K}\mathbf{u}-{\mathbf{M}}_{\mathbf{b}}\right)}^{\text{T}}\mathbf{Q}\left(\mathbf{K}\mathbf{u}-{\mathbf{M}}_{\mathbf{b}}\right)\\ \text{subjected}\hspace{0.17em}\text{to}:\hspace{1em}\hspace{1em}\left|\mathbf{m}\left(s\right)\right|\le m_{\text{max}},\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\left|\mathbf{B}\left(t\right)\right|\le B_{\text{max}},\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\left|{\mathbf{B}}_{\text{grad}}\left(t\right)\right|\le B_{\text{grad}\hspace{0.17em}\text{max}},\end{array}$$ [10]

where $\mathbf{Q}$ is a matrix that gives higher weightings to time frames that are deemed to be more important. Physically, the optimization process in Eq. 10 minimizes the difference between the magnetic actuation and the desired first derivative of the bending moment while subjected to the physical constraints of our systems. After this optimization process has been solved numerically by solvers such as genetic algorithm (45) and gradient-based solvers (46), the optimal $\mathbf{m}\left(s\right)$, $\mathbf{B}\left(t\right)$, and ${\mathbf{B}}_{\text{grad}}\left(t\right)$ will be obtained.

Fabrication Technique.

Based on the magnitude profile of $\mathbf{m}\left(s\right)$ determined above, we use a two-step molding process to embed a heterogeneous distribution of ferromagnetic and aluminum microparticles into a silicone rubber. A large magnitude of magnetization is created by locally increasing the concentration of ferromagnetic particles, whereas a desired orientation profile for $\mathbf{m}\left(s\right)$ can be created by magnetizing the material when it is sandwiched between two jigs of a specified curvature. This curvature can be represented by the following integral:

$$\begin{array}{l}{x}_{\text{jig}}\left(s\right)={\displaystyle {\int }_0^s\cos \left(\varphi \left(s\right)\right)\text{d}s},\\ y_{\text{jig}}\left(s\right)={\displaystyle {\int }_0^s\sin \left(-\varphi \left(s\right)\right)\text{d}s},\end{array}$$ [11]

where $\varphi \left(s\right)={\tan }^{-1}\left(\left(m_y\left(s\right)\right)/\left(m_x\left(s\right)\right)\right)$, and $m_x$ and $m_y$ are the x- and y-axis components of $\mathbf{m}\left(s\right)$ when the material is undeformed. After magnetizing the material, its desired $\mathbf{m}\left(s\right)$ can be obtained (step 4 in Fig. 1A; see Materials and Methods for more details).

Results

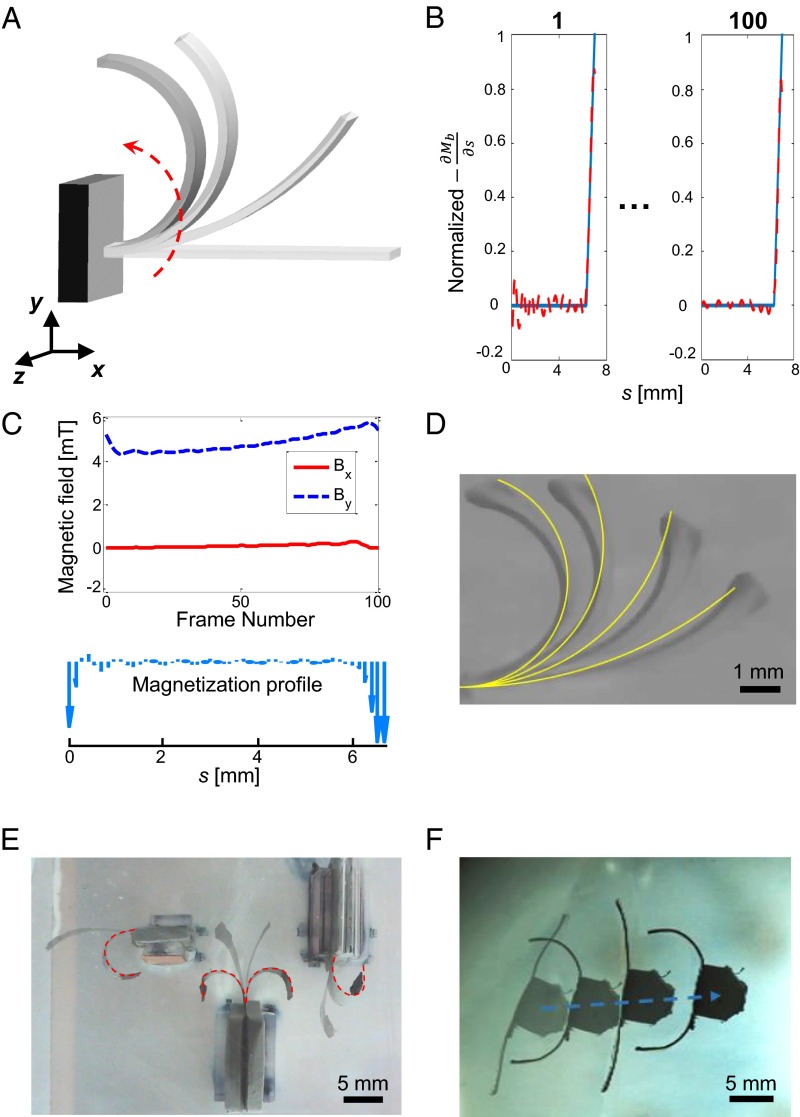
For the first experimental demonstration of our shape-programming methodology, a millimeter-scale beam was programmed to create a shape that resembled a cosine function when it was actuated by a constant magnetic field (Fig. 1 C i and ii). Next, we programmed a beam to produce a simple sequence of time-varying shapes with 100 discrete time frames. In each time frame, a uniform curvature was held over the beam, gradually increasing between each frame, until the beam curled into a semicircle (Fig. 2A). Despite the large number of time-varying shapes, we obtained a simple $\mathbf{m}\left(s\right)$ as well as actuating fields that satisfied Eq. 7 (Fig. 2 B and C). The beam was then fabricated and experimentally manipulated to achieve its desired shapes (Fig. 2D). Because the required magnetization profile and actuating fields were relatively simple, we extended this concept to simultaneously control multiple beams that have similar motions. By properly configuring several such beams, we were able to reversibly bend them into a “CMU” logo shape (Fig. 2E and Movie S1). We further extended this concept by using two similar beams to form the tentacles of a jellyfish-like robot. These tentacles could generate a fast power stroke and a slow recovery stroke for the robot to swim against the slope of an oil–water interface (average speed, 1.8 mm/s; see also Fig. 2F, Movie S2, and S6. Additional Discussion, for controlling the stroke speeds). The jellyfish-like robot was also steerable, and these steering strategies are discussed in S3. Steering Strategies and Fig. S3.

Fig. 2.

Programming soft composite materials that can gradually fold up into a semicircle. (A) Schematic of a soft beam programmed to fold up under magnetic excitation. Although we illustrated this motion with only four shapes, there were a total of 100 distinct shapes throughout this motion. (B) Optimization results for the desired first derivative of the bending moment. Each plot represents the desired first derivative of the bending moment of the beam for one time frame. The frame number for each time frame is represented by the number at the Top. In the simulations, the time difference between each time frame is 0.01 s. The blue lines in the time frames represent the desired first derivative of the bending moment, and the dotted red lines represent the obtained first derivative of the bending moment created by the magnetic actuation. The x axis of each plot represents the length of the beam, which ranges from s = 0 to 7 mm. (C) The required magnetization profile, $\mathbf{m}\left(s\right)$, and the magnetic field, $\mathbf{B}\left(t\right)$, to achieve the desired time-varying shapes. This magnetization profile is along the predeformed straight beam (see Fig. S6 for a more quantitative representation for the magnetization profile). Using the coordinate system in A as a reference, the variables $B_x$ and $B_y$ in the magnetic field plot represent the x- and y-axis components of the magnetic field, respectively. (D) Snapshots of a single beam curling up under magnetic excitation. The yellow lines represent the corresponding desired time-varying shapes. (E) Four soft beams made of the programmable material are shown deforming into a reversible CMU logo under magnetic excitation. To visualize the logo better, we highlighted the final CMU shape with dotted red lines. (F) A jellyfish-like robot equipped with two soft tentacles made of the programmable soft composite material. The robot could propel itself on an oil–water interface by bending its tentacles back and forth under magnetic excitation. Additional parameters for this device can be found in S9. Parameters for Each Case and Table S1.

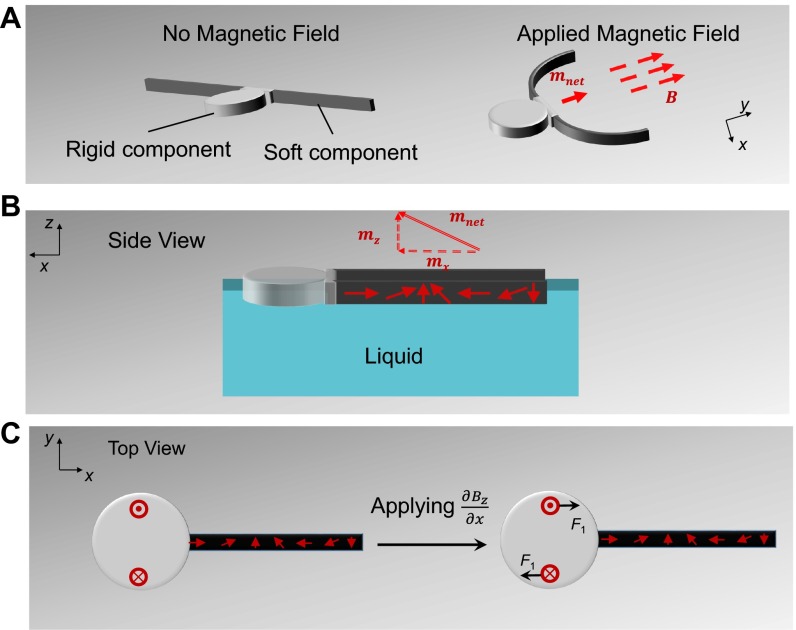
Fig. S3.

Strategies for steering an untethered programmable soft active device. Each coordinate frame represents the device’s body frame. (A) By designing the tentacles of the jellyfish-like robot to be symmetrical about its body frame’s y axis, we designed the net magnetization to always be parallel to its body frame’s y axis. By changing the direction of $\mathbf{B}\left(t\right)$, we aligned the orientation of the robot with the field. (B) The material was constrained on a water surface. The magnetic torque created by $m_z$ was counterbalanced by the surface tension of the water. The orientation of the material was controlled by applying a $\mathbf{B}\left(t\right)$ in the x–y plane, where the $m_x$ of the net magnetization would align with the applied $\mathbf{B}\left(t\right)$. (C) A rigid component with a programmed magnetization profile was added. By applying a spatial gradient, $\partial B_z/\partial x$, the rigid component experienced a coupled force, $F_1$, that allowed it to rotate about the z axis.

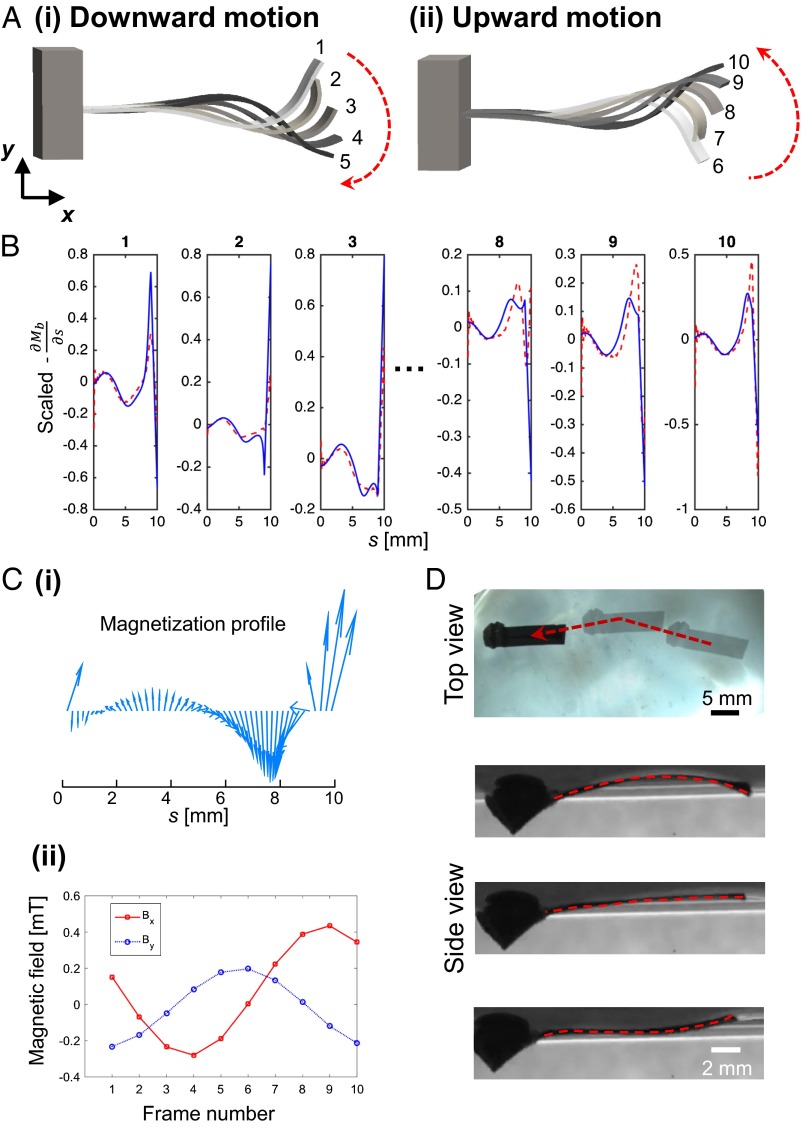
We had also programmed a spermatozoid-like undulating swimmer. To make this swimming gait more biomimetic than previous spermatozoid-like robots (22), we specified the gait to be a propagating traveling wave, with an amplitude that increases linearly from the fixed end to the free end (Fig. 3A). Despite the complexity of the gait, our programming method could obtain the necessary $\mathbf{m}\left(s\right)$ and actuating fields for the undulating swimmer (Fig. 3 B and C). After fabricating this swimmer, we experimentally show that it could use this gait to swim on an air–water interface (average speed, 11 mm/s; Fig. 3D and Movie S3).

Fig. 3.

Programming a spermatozoid-like undulating soft swimmer. (A) The desired undulation, which requires a traveling wave with increasing amplitude from the left tip to the right tip. The entire motion can be divided into two strokes: (i) downward motion and (ii) upward motion. The associated time frame for each shape is represented by a corresponding frame number. In the simulations, the time difference between each time frame is 0.1 s. (B) Optimization results for the desired first derivative of the bending moment to achieve the undulation. Each plot represents the desired first derivative of the bending moment of the beam for one time frame. The frame number is represented by the number at the top. The blue lines represent the desired first derivative of the bending moment, and the dotted red lines represent the obtained first derivative of the bending moment created by the magnetic actuation. The x axis for each frame corresponds to the length of the beam, which ranges from s = 0 to 10 mm. (C) The required (i) magnetization profile and (ii) magnetic field for the swimmer. This is the magnetization profile along the predeformed beam (see Fig. S6 for a more quantitative representation for the magnetization profile). Using the coordinate system in A as a reference, the variables $B_x$ and $B_y$ in the magnetic field plot represent the x-axis and y-axis components of the magnetic field, respectively. (D) Snapshots extracted from the movie of the undulating swimmer swimming on an air–water interface—top view and side view of the swimmer. Additional parameters for this device can be found in S9. Parameters for Each Case and Table S1.

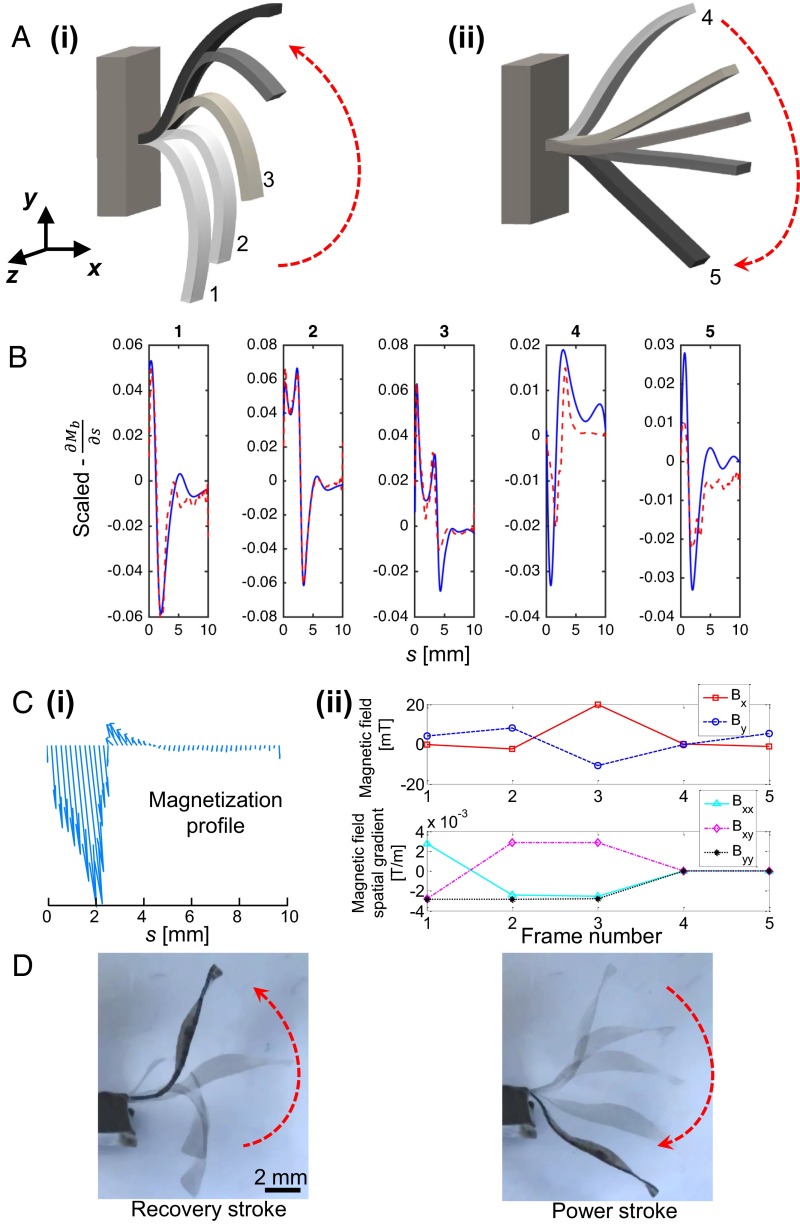
Finally, we created an artificial soft cilium that was able to approximate the complex beating pattern of a biological cilium (47). This beating pattern was divided into two strokes—the power and the recovery strokes (Fig. 4A). Due to the complexity of this motion, the optimization problem for obtaining $\mathbf{m}\left(s\right)$ and the actuating fields became highly nonconvex, containing many suboptimal solutions. The solution would be easily trapped and difficult to jump out from a suboptimal solution if we used only one optimization process to solve for the large number of design variables simultaneously (46). Hence, we used a multistep optimization approach that is similar to the previously reported ones in refs. 48 and 49 to divide the original optimization problem into two sequential optimization processes, allowing each process to solve for one subset of the design variables. As there are more design variables in the first optimization process than the second one (Fig. S4), we would have higher chances of obtaining a more accurate result for the more complicated optimization process if we solve it first. Therefore, our first optimization process was to determine the necessary $\mathbf{m}\left(s\right)$ and actuating fields for the more complex recovery stroke. The obtained $\mathbf{m}\left(s\right)$ was subsequently fed into a second optimization process that determined the required actuating fields for the simpler power stroke. Here, the power stroke was simpler than the recovery stroke because its desired first derivative of bending moment has fewer changes across the time frames, making it easier to use Eq. 7 to program them. The obtained results for the artificial cilium are shown in Fig. 4 B–D and Movie S4, and the key time-varying shapes that we used to closely mimic the complex beating pattern of a biological cilium were shown in Fig. 4A. Although other researchers have had some success in creating time-asymmetrical motions for their artificial cilia (50–53), our artificial cilium is the only one on a millimeter scale that can approximate the motions of a biological cilium.

Fig. 4.

Programming an artificial cilium. (A) Extracted 2D natural cilia motion as expressed in Cartesian coordinates. The motion pattern includes two strokes: (i) the recovery stroke and (ii) the power stroke. The key time frames used by the artificial cilium are associated with a corresponding frame number. The time difference between each time frame is 0.2 s. (B) Optimization results for the desired first derivative of the bending moment to achieve the cilium motion. Each plot represents the desired first derivative of the bending moment of the beam for one time frame. The frame number is represented by the number at the top of it. The blue lines represent the desired first derivative of the bending moment, and the dotted red lines represent the obtained first derivative of the bending moment created by the magnetic actuation. The x axis for each frame corresponds to the length of the beam, ranging from $s=$ 0 to 10 mm. The first three frames were given more weight during the optimization process because they were deemed to be more important. (C, i) The required magnetization profile and (ii) the magnetic field and its spatial gradients for the cilium (see Fig. S6 for a more quantitative representation for the magnetization profile). Using the coordinate system in A as a reference, the variables $B_x$ and $B_y$ in the magnetic field plot represent the x-axis and y-axis components of the magnetic field, respectively. The spatial gradients $B_{xx}$, $B_{xy}$, and $B_{yy}$ represent $\partial B_x/\partial x$, $\partial B_x/\partial y$, and $\partial B_y/\partial y$, respectively. (D) Snapshots extracted from the movie of the beating artificial cilium. Additional parameters for this device can be found in S9. Parameters for Each Case and Table S1.

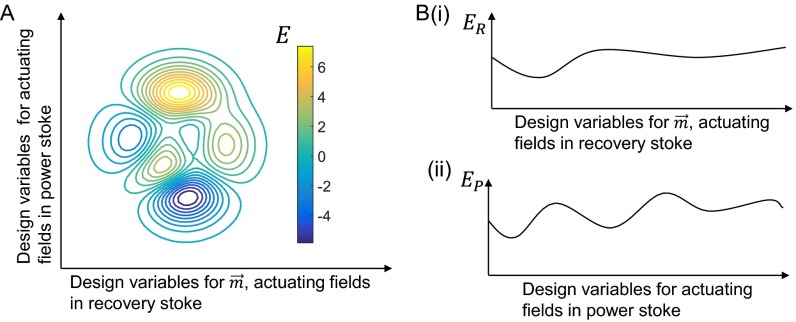
Fig. S4.

An illustration for the search space of the optimization problem for the artificial cilium. (A) The level set of the problem when there is only one optimization process. The x axis in this plot represents the design variables for $\mathbf{m}\left(s\right)$ and the actuating fields in the recovery stroke, whereas the y axis represents the design variables for the actuating fields in the power stroke. The isolines represent the contour of the fitness value quantified by E, where $E=E_R+E_P$. (B) Analysis for the search space of the problem when we use the two-step optimization approach. i shows the first optimization process where only the design variables for $\mathbf{m}\left(s\right)$ and the actuating fields in the recovery stroke are solved. The x axis in this plot represents these design variables, and the y axis represents $E_R$. ii shows the second optimization process where only the design variables for the actuating fields in the power stroke are solved. The x axis represents these design variables, and the y axis illustrates the generated function for $E_P$.

Discussion

Although the proposed programming methodology is promising, there are several limitations that need to be addressed in future studies. First, our method cannot produce all possible time-varying shapes when $\mathbf{m}\left(s\right)$ is time invariant and the actuating fields are position invariant as each of them can only be specified with a 1D Fourier series. This phenomenon can be explained from the magnetic actuation function in Eq. 7, which can be mathematically described as a function of six sets of 2D Fourier series. As all of the 2D Fourier coefficients in this function are created from the lower-dimensional 1D Fourier coefficients of $\mathbf{m}\left(s\right)$ and the actuating magnetic fields, many of these 2D Fourier coefficients become coupled with one another and cannot be arbitrarily specified. Thus, despite encompassing six sets of 2D Fourier series, the generated magnetic actuation can only represent a subset of 2D functions that are expressed in terms of s and t. This means that we can only program time-varying shapes whose first derivative of bending moment can be expressed in 2D functions, which are representable by the magnetic actuation function. Although a complete analysis to quantify the range of time-varying shapes achievable by our method is beyond the scope of this paper, we have provided a brief discussion on this topic in S4. Achievable Time-Varying Shapes. To better understand the range of achievable time-varying shapes, we will formulate a mathematical model to quantify this range in the future. As another future work, we will also increase the range of achievable shapes by developing more powerful electromagnets that can enable the actuating fields to become position variant (S6. Additional Discussion).

Second, because several metastable shapes may exist for a given control input, the programmable material may deform into an undesired shape. However, because the selected metastable shape is highly dependent on the previous shape, this limitation can be moderated by using a finer temporal resolution for the shape trajectories. This moderation reduces the deviation between the desired shape and the previous shape, making it easier to guide the material to deform into the desired shape.

Third, due to finite computational power, it is still an open challenge to obtain a global solution from highly nonconvex optimization problems, which have many design variables (46). As a result, we can only rely on numerical techniques such as the two-step optimization approach to moderate this challenge. Although this approach may allow us to obtain more accurate suboptimal solutions, it may also overconstrain the optimization problem unnecessarily and cause a reduction in the original search space (S5. Discussion for Two-Step Optimization Approach and Fig. S4). Therefore, we should only implement the two-step optimization approach when we cannot obtain an accurate solution with one optimization process. In view of this challenge, in the future we will also investigate new numerical techniques, allowing us to obtain more accurate solutions for a highly nonconvex optimization problem.

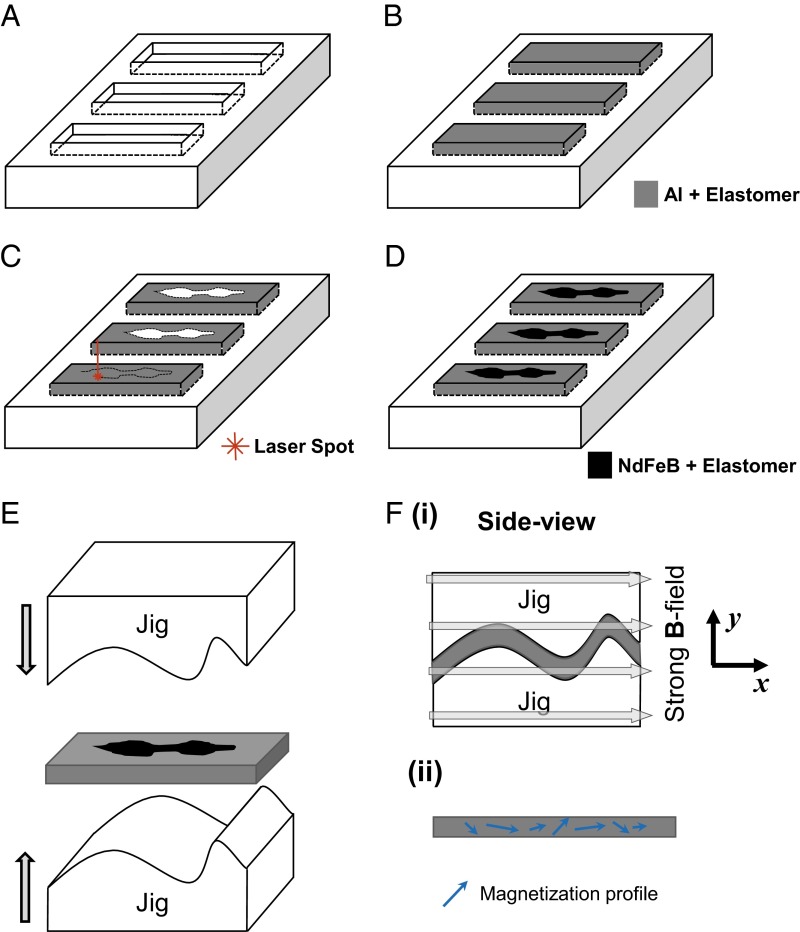
Fourth, our fabrication technique, the two-step molding process shown in Fig. 5 A–D, is only capable of tuning the amount of magnetic particles along the in-plane axis of the beams. Because we cannot tune the amount of magnetic particles along all axes of a structure, we are still unable to create an $\mathbf{m}$ that has a desirable nonuniform magnitude profile in 3D, preventing us from fabricating structures that can achieve specific 3D time-varying shapes. Furthermore, we could not program beams smaller than the millimeter-scale because it becomes difficult to manually sandwich such small-scale beams into the jigs during the magnetization process (Fig. 5F). We will explore new microfabrication processes that will allow us to create smaller-scale structures with desirable $\mathbf{m}$ that have 3D nonuniform magnitude profile.

Fig. 5.

The fabrication procedure to create a programmable magnetic soft composite beam: (A) a negative mold for the beam; (B) the passive component, Al plus Ecoflex, was poured into the mold in liquid form and allowed to cure; (C) based on the magnitude profile of $\mathbf{m}\left(s\right)$, a band of nonuniform width was cut out with a laser cutter; (D) the active component, NdFeB plus Ecoflex, was then poured and cured to replace the band; (E) the beam was bent into the jig profile; (F, i) the beam was magnetized with a strong B field ($\sim$ 1 T); (ii) the desired $\mathbf{m}\left(s\right)$ will be created after the beam was removed from the jig.

Fifth, although our proposed computational method is not restricted to creating miniature devices, we have yet to use it for macroscale devices. Nevertheless, the procedures for constructing such macroscale devices are discussed in S6. Additional Discussion, and the implementation for these procedures will be explored as a future work.

In summary, we have introduced a universal programming methodology that can enable scientists and engineers to magnetically program desired time-varying shapes for soft materials. The method was validated with a simple showcase, and we demonstrated its versatility by creating a reversible CMU logo, a jellyfish-like robot, a spermatozoid-like undulating swimmer, and an artificial cilium. Compared with other shape-programmable materials that may require minutes to induce a shape change (4, 8), our devices can transform into their desired shapes within seconds. We envision that this methodology may enable researchers to develop a wide range of novel soft programmable active surfaces and devices that can find broad applications in robotics, engineering, and biomedicine.

Materials and Methods

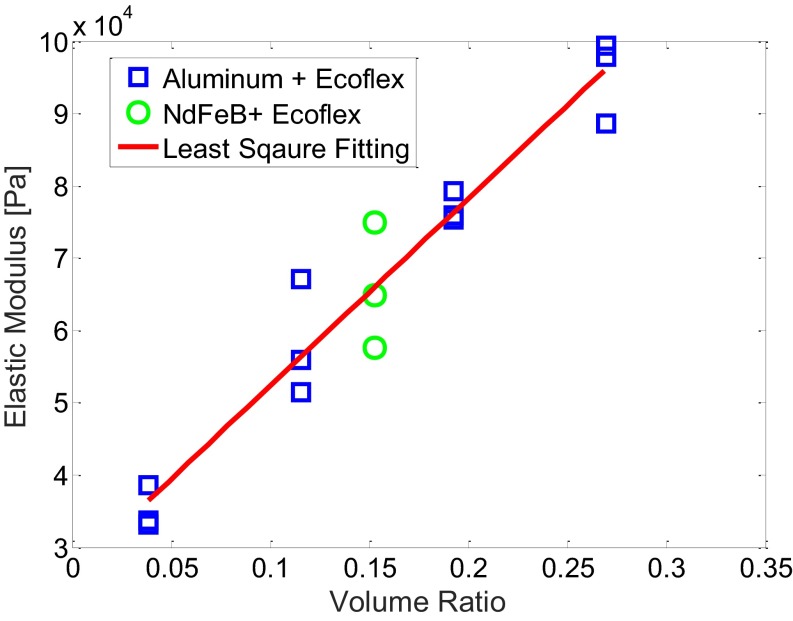
Here, we provide a detailed discussion for our fabrication technique. The required steps to create the desired magnetization profile for a programmable beam are summarized in Fig. 5. The programmable magnetic soft composite material consists of two components: a passive component and an active component that can be stimulated by magnetic excitation. The active component is created by embedding fine neodymium–iron–boron (NdFeB) particles that have an average size of 5 μm (MQFP; Magnequench) into a soft silicone rubber (Ecoflex 00-10; Smooth-on, Inc.). The volume ratio for the NdFeB particles and Ecoflex 00-10 is 0.15:1. The passive component is created by embedding aluminum (Al) powder with an average particle size of 5 μm into the same type of silicone rubber with the same volume ratio. The volume ratio is selected to ensure that the elastic modulus of the active and passive components are identical, allowing the composite to have a uniform elastic modulus. The relationship between the passive component’s volume ratio and its resultant elastic modulus was experimentally characterized (S7. Matching the Elastic Modulus Properties and Fig. S5).

Fig. S5.

Tensile test of the mixture of Ecoflex and aluminum with different volume ratios of the aluminum powder. The data for the mixture of Ecoflex and aluminum are represented as blue squares, and the data for the mixture of Ecoflex and NdFeB are represented as green circles. A linear model was fitted with the parameters shown in the figure.

To create a nonuniform $\mathbf{m}\left(s\right)$ that has a desired magnitude profile, the distribution between the passive and active components must be patterned. The locations that have a higher magnitude of magnetization will have more active components. To achieve this, a two-step micromolding process is adopted. First, a negative mold with the desired beam geometries is created by computer numerical control machining on an acrylic sheet (Fig. 5A). The passive component (in liquid form) is poured into the negative mold and is allowed to cure (Fig. 5B). Once the passive component is fully cured, a laser cutter is used to cut out a band with nonuniform width (Fig. 5C). The active component (in liquid form) is poured into the mold to replace the removed band (Fig. 5D). The two components form a composite of a uniform thickness once the active component is cured. Due to the nonuniform width of the band, the distribution of the active components can be patterned. This allows the beam to have an $\mathbf{m}\left(s\right)$ with a desired magnitude profile after the beam is magnetized. The desired orientation profile of $\mathbf{m}\left(s\right)$ is created by using laser-cut jigs to bend/fold the beam during the magnetization process (Fig. 5 E and Fi). Thus, by magnetizing the beam when it is sandwiched between the jigs, the desired orientation profile can be obtained after the applied magnetizing field and the jigs are removed (Fig. 5 F, ii). The NdFeB particles that are embedded within the active components will be saturated by the large uniform magnetizing field ($\sim 1$ T), creating the desired $\mathbf{m}\left(s\right)$ for the material.

S1. Boundary Conditions

To achieve the desired shapes, the boundary conditions of the beams must always be satisfied. Generally, there are two types of boundary conditions: the fixed and free ends of the beam (Fig. S2A). At the fixed ends, the desired vertical and rotational deflections must always be constrained to zero. Conversely, the bending moment at the free end is also constrained to zero because it is difficult to apply torques at the free ends. However, because not all time-varying shapes have a zero bending moment at their free end, we introduce a method to overcome this limitation.

Our proposed method is to physically add a small extension, $\mathrm{\Delta }L$, to the original length of the beam, $L_1$. Thus, the total length of the new beam becomes $\mathrm{\Delta }L+L_1=L$. The objective of this extension is to provide the necessary bending moment at the original free end of the beam while allowing the bending moment at the new tip to be zero. This is achieved by using a polynomial fitting curve to gradually reduce the desired bending moment at the original free end until it becomes zero at the new tip (Fig. S2B). We can determine the necessary magnetization profile for this extension by including it into the Fourier series representation of $\mathbf{m}\left(s\right)$. We have used this method to program the cosine function, jellyfish-like robot, and the spermatozoid-like undulating swimmer. It is not necessary to use this method for the artificial cilium because its desired motions have automatically satisfied the free-end boundary condition. Although the obtained time-varying shapes of the beam might have deviations with the desired prescribed deflection, this deviation can be kept small when the length of the extension is much smaller than the length of the original beam. Thus, in all of our designs, we have limited these extensions to be 10% of the beam’s original length.

S2. Programming Materials with 3D Time-Varying Shapes

Although we did not program materials with 3D time-varying shapes experimentally, we provide the theory and computational method here. Similar to the formulations for programming beams, we first specify the desired time-varying displacement fields along the x, y, and z axes of the material coordinates with the variables $\left(u,v,w\right)$, respectively. Based on these deflections, the time-varying deformation gradient tensor, $\mathbf{F}$, and strains can be computed. The resultant time-varying strains across the materials are given as follows:

$$\begin{array}{c}{\mathit{ϵ}}_{ij}=e_{ij}+\frac{1}{2}\left({\omega }_{ki}+e_{ki}\right)\left({\omega }_{kj}+e_{kj}\right),\\ \text{where}\hspace{0.17em}\hspace{0.17em}{e}_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right)\\ \text{and}\hspace{0.17em}\hspace{0.17em}{\omega }_{ij}=\frac{1}{2}\left(u_{i,j}-u_{j,i}\right).\end{array}$$ [S1]

The tensor, ${\mathit{ϵ}}_{ij}$, represents the Lagrangian strain tensor and the subscripts indicate the Cartesian directions, that is, $i,j,k=\left\{\mathrm{1,2,3}\right\}$. The above equations are written in index notation for convenience. The relationship between the strains and stresses within the materials can be expressed by the following:

$$\mathbf{S}=\mathbf{C}\mathit{ϵ},$$ [S2]

where $\mathbf{S}$ is the stress tensor in Lagrangian description, that is, the second Piola–Kirchhoff stress (second-PK stress), and $\mathbf{C}$ is a $9\times 9$ matrix where its coefficients can be determined by the material properties.

After we determine the stress distribution within the materials, we perform a quasistatic analysis. Because it is more desirable to perform the quasistatic analysis in Eulerian description, we convert the second-PK stress into the Cauchy stress in the Eulerian description as follows:

$$\mathit{\sigma }=J^{-1}\mathbf{F}\cdot \mathbf{S}\mathbf{F},$$ [S3]

where $J=\text{det}\left(\mathbf{F}\right)$. According to the theory for electromagnetic–elastic solids (54), the quasistatic equations can be written in index notation as follows:

$$\begin{array}{r}{f}_i=-{\sigma }_{kl,l},\\ {\tau }_i={\sigma }_{lk}-{\sigma }_{kl},\end{array}$$ [S4]

where ${\sigma }_{ij}$ is the component of the Cauchy stress tensor and $f_i$ and ${\tau }_i$ are the magnetic force and torque (per volume) in the ith direction, respectively. These magnetic forces and torques (per volume) are functions of $\mathbf{m}$ and the actuating fields:

$$\begin{array}{l}{\mathit{\tau }}_{\mathbf{m}}=\mathbf{m}\times \mathbf{B},\\ {\mathbf{f}}_m=\left(\mathbf{m}\cdot \nabla \right)\mathbf{B}.\end{array}$$ [S5]

Expressing the above equations in index notation gives the following:

$$\begin{array}{l}{f}_i=m_i{B}_{i,j},\\ {\tau }_i=B_k{m}_l-B_l{m}_k.\end{array}$$ [S6]

To account for the change in the magnetization profile after the material has deformed, we must map the magnetization profile from its initial undeformed state to its current deformed state. Because $\mathbf{m}$ is defined as the magnetization per unit volume, its magnitude varies similarly to the density of a body that undergoes a deformation. Thus, $\mathbf{m}$ can be defined as follows:

$$\mathbf{m}=\frac{\text{d}\mathbf{M}}{\text{d}V},$$ [S7]

where $\text{d}\mathbf{M}$ is magnetic moment within the volume of dV. When a deformation occurs, the magnetic moment changes its orientation, and the magnitude of its volume will also be changed:

$$\begin{array}{r}\text{d}\mathbf{M}\prime =\mathbf{R}\text{d}\mathbf{M}\\ \text{d}V\prime =J\text{d}V,\end{array}$$ [S8]

where $\mathbf{R}$ is the rotational component of $\mathbf{F}$, which can be found by the polar decomposition of $\mathbf{F}$. Therefore, the magnetization vector under deformation can be written as follows:

$$\mathbf{m}\prime =\frac{\text{d}\mathbf{M}\prime }{\text{d}V\prime }=\frac{\mathbf{R}}{J}\frac{\text{d}\mathbf{M}}{\text{d}V}=\frac{\mathbf{R}}{J}\mathbf{m}.$$ [S9]

This implies that the magnetic torques and forces in the deformed state can be expressed as ${\mathrm{\tau }\prime }_{\mathbf{m}}=\mathbf{m}\prime \times \mathbf{B}$ and ${\mathbf{f}\prime }_m=\left(\mathbf{m}\prime \cdot \nabla \right)\mathbf{B}$. By substituting these variables back into Eqs. S4 and S6, we obtain the equilibrium equations expressed explicitly with the magnetic torques and forces.

To have a universal approach to solve for these magnetic torques and forces, we will use Fourier series to represent the magnetization profile and magnetic fields again. Here, we specify the magnetization profile, $\mathbf{m}\left(x,y,z\right)$, to be a 3D vector where each of its component is represented by a 3D Fourier series expressed in terms of the material’s coordinates, that is, the x, y, and z axes of the material. Similarly, all of the components of the actuating fields, that is, $\mathbf{B}\left(t\right)$ and all of the five independent spatial gradients, will each be represented with a 1D Fourier series expressed in terms of t [see more details for the independent spatial gradients of $\mathbf{B}\left(t\right)$ in S8. Experimental Setup]. Mathematically, this means that $\mathbf{m}\left(x,y,z\right)$ and the actuating fields can be expressed as follows:

$$\mathbf{m}\left(x,y,z\right)=\left[\begin{array}{c}{m}_x\left(x,y,z\right)\\ m_y\left(x,y,z\right)\\ m_z\left(x,y,z\right)\end{array}\right],$$ [S10]

where

$$\begin{array}{l}{m}_x={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{1,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{2,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{3,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{4,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{5,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{6,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{7,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{a}_{8,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}},\\ m_y={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{1,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{2,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{3,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{4,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{5,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{6,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{7,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{b}_{8,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right),}}}\end{array}$$ [S11]

$$\begin{array}{l}{m}_z={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{1,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{2,ijk}\cos \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{3,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{4,ijk}\cos \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{5,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{6,ijk}\sin \left(i{\omega }_{x}x\right)\cos \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{7,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\cos \left(k{\omega }_{z}z\right)}}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m{\displaystyle \sum _{k=0}^g{c}_{8,ijk}\sin \left(i{\omega }_{x}x\right)\sin \left(j{\omega }_{y}y\right)\sin \left(k{\omega }_{z}z\right),}}}\end{array}$$ [S12]

$$\mathbf{B}\left(t\right)=\left[\begin{array}{c}{B}_x\left(t\right)\\ B_y\left(t\right)\\ B_z\left(t\right)\end{array}\right]=\left[\begin{array}{c}{\displaystyle {\sum }_{j=0}^m{\alpha }_j\cos \left(j{w}_{t}t\right)+{\beta }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\gamma }_j\cos \left(j{w}_{t}t\right)+{\eta }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\varphi }_j\cos \left(j{w}_{t}t\right)+{\chi }_j\sin \left(j{w}_{t}t\right)}\end{array}\right],$$

$${\mathbf{B}}_{\text{grad}}\left(t\right)=\left[\begin{array}{c}\frac{\partial B_x}{\partial x}\\ \frac{\partial B_x}{\partial y}\\ \frac{\partial B_y}{\partial y}\\ \frac{\partial B_z}{\partial x}\\ \frac{\partial B_z}{\partial y}\end{array}\right]=\left[\begin{array}{c}{\displaystyle {\sum }_{j=0}^m{\mathit{ϵ}}_j\cos \left(j{w}_{t}t\right)+{\delta }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\lambda }_j\cos \left(j{w}_{t}t\right)+{\mu }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\rho }_j\cos \left(j{w}_{t}t\right)+{\sigma }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\zeta }_j\cos \left(j{w}_{t}t\right)+{\kappa }_j\sin \left(j{w}_{t}t\right)}\\ {\displaystyle {\sum }_{j=0}^m{\upsilon }_j\text{cos}\left(j{w}_{t}t\right)+{\psi }_j\sin \left(j{w}_{t}t\right)}\end{array}\right].$$

The variables $a_{1,ijk}$ to $a_{8,ijk}$, $b_{1,ijk}$ to $b_{8,ijk}$, $c_{1,ijk}$ to $c_{8,ijk}$, ${\alpha }_j$, ${\beta }_j$, ${\gamma }_j$, ${\eta }_j$, ${\varphi }_j$, ${\chi }_j$, ${\mathit{ϵ}}_j$, ${\delta }_j$, ${\lambda }_j$, ${\mu }_j$, ${\rho }_j$, ${\sigma }_j$, ${\zeta }_j$, ${\kappa }_j$, ${\upsilon }_j$, and ${\psi }_j$ are the Fourier coefficients for their respective Fourier series. The angular frequencies, ${\omega }_x$, ${\omega }_y$, and ${\omega }_z$ are given as $2\pi /L_x$, $2\pi /L_y$, and $2\pi /L_z$, respectively. The variables $L_x$, $L_y$, and $L_z$ are the material’s maximum dimension along the x, y, and z axes, respectively. By substituting Eqs. S12, S11, S10, S9, and S6 into Eq. S4, we can express the six equilibrium equations in terms of these Fourier coefficients.

Similar to the approach presented in Computational Method, we determine the optimal Fourier coefficients via an optimization process. This can be achieved by dividing the motion into p time frames, and by discretizing the material’s spatial coordinates into q points. By substituting q different spatial coordinates of the material into the six equilibrium equations for every time frame, we can create 6p × q equations that are linearly dependent on the product of the Fourier coefficients:

$$\mathbf{K}\mathbf{u}={\mathbf{M}}_{\mathbf{b}}.$$ [S13]

The vectors $\mathbf{u}$ and ${\mathbf{M}}_{\mathbf{b}}$ represent the product of the Fourier coefficients and the desired stress tensor derivative across these six p × q equations, respectively. Subsequently, the optimal 3D Fourier coefficients in $\mathbf{m}\left(s\right)$, and the optimal 1D Fourier coefficients in $\mathbf{B}\left(t\right)$ and ${\mathbf{B}}_{\text{grad}}\left(t\right)$ can be solved by performing the optimization process shown in Eq. 10 from the main text. Once these coefficients are identified, the necessary $\mathbf{m}\left(x,y,z\right)$ and actuating fields can be generated.

S3. Steering Strategies

There are several strategies to steer untethered miniature devices magnetically. We introduce the first steering strategy by using the jellyfish-like robot as an example. To implement this strategy, we intentionally constrain the magnetization profile of the beams to be symmetrical around the y axis of the robot’s body frame (Fig. S3A). This allows the robot’s net magnetization to be always parallel to its body frame’s y axis. The net magnetization of the programmable material, ${\mathbf{m}}_{net}$, is given as follows:

$${\mathbf{m}}_{net}={\displaystyle {\int }_0^{L}A\mathbf{m}\left(s\right)ds}.$$ [S14]

Because the net magnetization of the robot always aligns with $\mathbf{B}\left(t\right)$, we can vary the directions of $\mathbf{B}\left(t\right)$ to steer the robot. Furthermore, because the required $\mathbf{B}\left(t\right)$ for changing the shape of the tentacles is always approximately in the same direction, we can control the tentacles’ shapes by adjusting the magnitude of $\mathbf{B}\left(t\right)$ after the robot achieves its desired orientation.

In addition to the first strategy, we present two other strategies that allow untethered programmable materials to steer in a plane while still achieving their desired shape transformations. The second strategy is to constrain certain motions of the programmable material so that it is easier to steer the device. The last strategy is to include a rigid component that can be used to control the device’s orientation.

The second strategy can be implemented by placing the material on a liquid interface in which the programmable material is constrained by the surface tension of the fluid. As an illustration, Fig. S3B shows the x–z plane of the programmable material’s body frame. Due to the surface tension of the fluid, the z-axis component of the net magnetization cannot create rigid-body torques that affect the orientation of the material. Thus, the alignment of the material on the liquid interface is solely dependent on the body frame’s x-axis component of the net magnetization. As a result, the robot’s orientation can be controlled by using an applied $\mathbf{B}\left(t\right)$ to align this x-axis component of the net magnetization. This strategy has been implemented to steer the undulating swimmer (Movie S3).

For the last steering strategy, we can control the orientation of the device by programming the magnetization profile of a rigid component. Multiple feasible magnetization profiles may exist, and an example is shown in Fig. S3C. In this case, although the net magnetization for the rigid component is zero, this component can still provide a rigid-body torque that can steer the material. By following the body frame assignment in Fig. S3C, a rigid-body torque around the z axis can be induced on the rigid component when the spatial gradient, $\partial B_z/\partial x$, is applied, allowing the material to steer in the x–y plane. Thus, by controlling the magnitude of the spatial gradient,$\partial B_z/\partial x$, it is possible to compensate for any z-axis torque that is induced by the programmable material. Although this spatial gradient will also induce a z-axis force for the x-axis component of $\mathbf{m}\left(s\right)$, the induced deflections by this force can be greatly reduced when the width of the beam is increased. Although this strategy has not been implemented in this work, we have demonstrated a similar concept in our previous work to steer an untethered miniature device (34, 55).

S4. Achievable Time-Varying Shapes

Although a complete analysis for determining the range of time-varying shapes achievable by our method is beyond the scope of this paper, we provide a brief discussion here. The proposed method cannot produce all possible time-varying shapes for small-scale materials because the materials have a time-invariant $\mathbf{m}$ and the actuating fields cannot be changed spatially. Eq. 7 in the main text suggests that there may not exist a feasible solution when a sequence of time-varying shapes requires a large change in their desired profile of $\left({\partial }^2\theta /\partial s^2\right)\left(s\right)$ across the time frames. Although such complicated time-varying shapes cannot be fully replicated, we can still approximate such motions by eliminating the shapes that have very different $\left({\partial }^2\theta /\partial s^2\right)\left(s\right)$ in the trajectory. This shape removal process may have to be done iteratively until our method can obtain a good solution. However, we believe that the minimum number of continuous shapes achievable by our proposed method should be two because we can pattern two axes of the magnetization profile independently, that is, the x- and y-axis components of $\mathbf{m}\left(s\right)$.

S5. Discussion for Two-Step Optimization Approach

Although the two-step optimization approach can be used as a technique to obtain a more accurate solution from a highly nonconvex optimization problem, it may also overconstrain the problem unnecessarily and cause a reduction in the original search space. As a result, the two-step approach should only be implemented when we cannot obtain an accurate solution with one optimization process.

To facilitate an in-depth discussion, we will use the optimization process for the artificial cilium as an example. If the original one-step optimization approach has been used, its level set can be illustrated with Fig. S4. In this level set, its design variables for $\mathbf{m}\left(s\right)$ and the actuating fields in the recovery strokes are shown along the x axis, whereas the y axis shows the design variables for the required actuating fields in the power strokes. The isolines in the level set show the contours of the fitness value, that is, the total error quantified by Eq. 10 in the main paper. This error, E, can be expressed as the sum of $E_r$ and $E_p$ where they represent the errors obtained from the recovery and power strokes, respectively. Because there are many design variables in this optimization process (i.e., 173 design variables), the solution will be easily trapped in a suboptimal solution for such a highly nonconvex optimization problem. Therefore, to reduce the complexity of this problem, we introduce a two-step optimization approach so that each process can solve for one subset of design variables.

When the two-step approach is implemented, the first optimization process can be represented by the plot in Fig. S4 B, i. The x axis for this plot represents the design variables for $\mathbf{m}\left(s\right)$ and the actuating fields in the recovery strokes, and the y axis represents $E_r$. Because this optimization does not include the design variables for the actuating fields in the power stroke, the dimensionality of this search space is much smaller than the original one-step optimization process. Therefore, it will be easier to jump out from a suboptimal solution compared with the original one-step optimization process. Once this optimization process has been completed, the necessary $\mathbf{m}\left(s\right)$ will be identified and it will be used as a constraint for the second optimization process. With this constraint, we will optimize the design variables for the actuating fields in the power stroke such that $E_p$ can be minimized (Fig. S4 B, ii). Once the optimal design variables in the second optimization process has been determined, we obtain the necessary actuating fields in the power stroke. Because the search space of the second optimization process is also much smaller than the original one-step optimization process, this process also has higher chances to jump out from a suboptimal solution. Because the two-step optimization approach has higher chances to jump out from a suboptimal solution compared with the original one-step approach, it is possible to use the two-step approach to obtain a more accurate solution.

Despite the benefits of the two-step optimization, its total search space is much smaller than the original one-step approach. This can be explained by the constrained relationship between $E_p$ and $\mathbf{m}\left(s\right)$. Because different $\mathbf{m}\left(s\right)$ can generate different functions of $E_p$, the selected $\mathbf{m}\left(s\right)$ may not produce the optimal $E_p$ function. In other words, although the selected $\mathbf{m}\left(s\right)$ may be optimal for the recovery stroke, it is still not necessarily the best for reducing the overall E. This implies that, although the two-step approach has simplified the original optimization problem, it may also overconstrain it. Thus, the obtained solution from the two-step approach may not be the global solution that contains the lowest $E=E_r+E_p$.

S6. Additional Discussion

Here, we discuss the possibility of extending the proposed approach to simultaneously determine the magnetization profiles for multiple beams and the effects when the actuating fields can be varied locally in space. We will also discuss how we can change the speed for the shape trajectory. Finally, we will give the mathematical expression for all of the 2D Fourier series listed in Eq. 7 in the main paper.

The programming method can determine the magnetization profiles for multiple beams simultaneously by using a corresponding set of Fourier series for each beam’s magnetization profile. For example, if there are r numbers of beams, there will be r sets of Fourier series. Thus, for each time frame, we can create $r\times q$ new equations by substituting different values of s across each beam into Eq. 7 in the main text. By assembling all of the equations across all time frames, there will be a total of $p\times r\times q$ equations. Using the optimization process shown in Eq. 10 in the main text, the optimal Fourier coefficients can be determined, thus generating the necessary magnetization profiles for all of the beams.

On the other hand, if $\mathbf{B}$ can be varied locally for l regions, there will be l number of independent $\mathbf{B}$ values, that is, there will be ${\mathbf{B}}_1,{\mathbf{B}}_2,\dots ,{\mathbf{B}}_l$. Each of these magnetic fields can then be represented by a Fourier series, that is, there are l sets of them. However, Eq. 7 in the main text will have to be slightly modified as we have to substitute the corresponding $\mathbf{B}$ in each region. Once this is done, the optimal Fourier coefficients can also be solved by Eq. 10 in the main text. The beam will be able to achieve a larger range of time-varying shapes when the actuating fields become position variant. Note that it is easier to create position-variant actuating fields when the materials are in macroscale. This is because a macroscale device will only require a small magnitude of magnetic field spatial gradients to achieve such actuating fields. The steps to program such macroscale devices are similar to programming microscale devices that have a position-variant $\mathbf{B}$.

Here, we also discuss how we can change the speed of the time-varying shapes. There is an upper speed limit for the programmable material to change its shape. This limit is dictated by either the speed of the electromagnetic coil system that generates the actuating fields or the fundamental natural frequency of the material. In our experiments, it is the speed of the electromagnets that limits our bandwidth to be 25 Hz. Based on this limitation, we have constrained the fastest component of the Fourier series representing $\mathbf{B}$ and ${\mathbf{B}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}}$ to 25 Hz. Reducing the speed for the shape change is, however, much simpler than increasing the speed as there is no bound for this speed reduction. Thus, for the jellyfish-like robot, we have reduced the speed of the recovery stroke to be approximately three times slower than its power stroke.

Finally, we will provide the mathematical representation of ${\mathrm{ℱ}}_2$ to ${\mathrm{ℱ}}_6$ here:

$$\begin{array}{r}{\mathrm{ℱ}}_2={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\alpha }_j+c_i{\gamma }_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\beta }_j+c_i{\eta }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\alpha }_j+d_i{\gamma }_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\beta }_j+d_i{\eta }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}},\end{array}$$ [S15]

$$\begin{array}{r}{\mathrm{ℱ}}_3={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\lambda }_j+c_i{\rho }_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\mu }_j+c_i{\sigma }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\lambda }_j+d_i{\rho }_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\mu }_j+d_i{\sigma }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}},\end{array}$$ [S16]

$$\begin{array}{r}{\mathrm{ℱ}}_4={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\rho }_j-c_i{\lambda }_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\sigma }_j-c_i{\mu }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\rho }_j-d_i{\lambda }_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\sigma }_j-d_i{\mu }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}},\end{array}$$ [S17]

$$\begin{array}{r}{\mathrm{ℱ}}_5={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\mathit{ϵ}}_j+c_i{\lambda }_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\delta }_j+c_i{\mu }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\mathit{ϵ}}_j+d_i{\lambda }_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\delta }_j+d_i{\mu }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}},\end{array}$$ [S18]

$$\begin{array}{r}{\mathrm{ℱ}}_6={\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\lambda }_j-c_i{\mathit{ϵ}}_j\right)\cos \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(a_i{\mu }_j-c_i{\delta }_j\right)\cos \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\lambda }_j-d_i{\mathit{ϵ}}_j\right)\sin \left(i{\omega }_{s}s\right)\cos \left(j{\omega }_{t}t\right)}}\\ +{\displaystyle \sum _{i=0}^n{\displaystyle \sum _{j=0}^m\left(b_i{\mu }_j-d_i{\delta }_j\right)\sin \left(i{\omega }_{s}s\right)\sin \left(j{\omega }_{t}t\right)}}.\end{array}$$ [S19]

S7. Matching the Elastic Modulus Properties

Because of the embedded metal particles, the elastic modulus of the composite materials is different from that of pure Ecoflex. The embedded aluminum and NdFeB powders were selected to have the same mean particles size of 5 μm. As the volume ratio of the embedded NdFeB powder to Ecoflex in the active component was predetermined, the active component’s elastic modulus was fixed. Therefore, the elastic modulus of the passive component, Ecoflex with embedded aluminum powder, was tuned by changing the volume ratio of the particles to Ecoflex. The elastic modulus of both the passive and active components were evaluated with a tensile testing machine (Instron 5943; Instron, Inc.). Each volume ratio was evaluated with three experiments, and a linear model was fitted to represent the relationship between the elastic modulus and the volume ratio. Based on the fitted model, the necessary volume ratio for the passive component’s elastic modulus to match the active components was determined (Fig. S5). The corresponding mass ratio was obtained by the following:

$$\text{mass}\hspace{0.17em}\text{ratio}=\frac{\text{density}\hspace{0.17em}\text{of}\hspace{0.17em}\text{particle}}{\text{density}\hspace{0.17em}\text{of}\hspace{0.17em}\text{Ecoflex}}\times \text{volume}\hspace{0.17em}\text{ratio}.$$ [S20]

S8. Experimental Setup

The magnetic field and its spatial gradients were generated by an electromagnetic coil system that has eight coils, as shown in Fig. S1. The coil system can be controlled to generate the desired magnetic field and its spatial gradient in the workspace with a uniformity above 95% across a $2\times 2\times 2$ cm³ volume. The mapping between each coil’s electrical current and the resulting actuating fields can be approximated in a linear equation:

$$\mathbf{A}\mathbf{I}=\left[\begin{array}{c}\mathbf{B}\\ {\mathbf{B}}_{\text{grad}}\end{array}\right].$$ [S21]

The vector $\mathbf{I}$ contains all of the coils’ electrical current, and the actuation matrix, $\mathbf{A}$, is used to correlate $\mathbf{I}$ with the actuating fields. The magnetic field can be expressed as $\mathbf{B}={\left[\begin{array}{ccc}{B}_x& B_y& B_z\end{array}\right]}^{\text{T}}$ in the global frames shown in the figures, and the spatial gradients of $\mathbf{B}$ are represented by ${\mathbf{B}}_{\text{grad}}$. Based on Gauss’s law, $\nabla \cdot \mathbf{B}=0$, and Ampère’s law dictates that $\nabla \times \mathbf{B}=\mathbf{0}$. Thus, there are only five independent components. Although there is more than one representation for ${\mathbf{B}}_{\text{grad}}$, we have selected the following representation for ${\mathbf{B}}_{\text{grad}}$:

$${\mathbf{B}}_{\text{grad}}={\left[\begin{array}{ccccc}\frac{\partial B_x}{\partial x}& \frac{\partial B_x}{\partial y}& \frac{\partial B_y}{\partial y}& \frac{\partial B_z}{\partial x}& \frac{\partial B_z}{\partial y}\end{array}\right]}^{\text{T}}.$$ [S22]

During the experiments, the time-varying shapes of the beam will be recorded by the camera.

S9. Parameters for Each Case

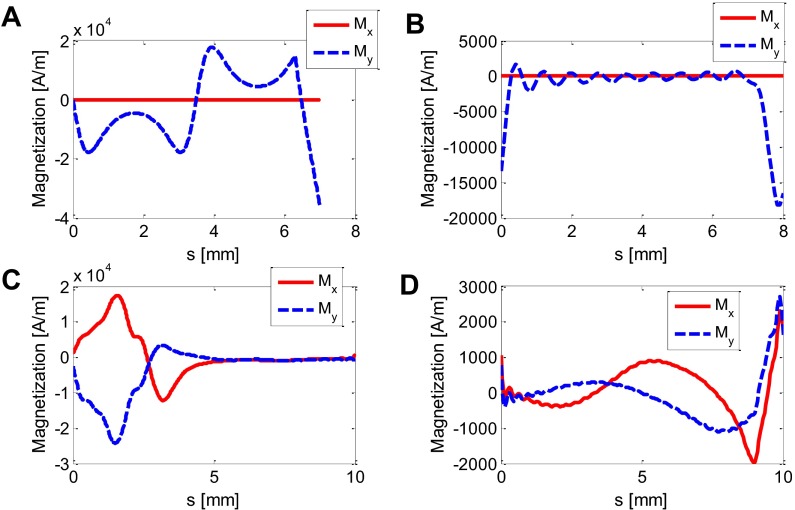
Here, we provide the parameters used for each experimental showcase, that is, the dimensions of the beams and the number of Fourier series coefficients, or n and m, respectively. The number of design variables for each optimization process will also be given. For the artificial cilium, because we have to optimize $\mathbf{m}\left(s\right)$, $\mathbf{B}\left(t\right)$, and ${\mathbf{B}}_{\text{grad}}\left(t\right)$, we require $2\left(2n+1\right)+5\left(2m+1\right)$ design variables. Because the motions for the jellyfish-like robot and the spermatozoid-like robot are relatively simple, we can constrain ${\mathbf{B}}_{\text{grad}}\left(t\right)$ to be a zero vector. Therefore, these two showcases only require $2\left(2n+1\right)+2\left(2m+1\right)$ design variables. Last, as we only need to pattern $m_y$ for the cosine shape showcase, the required number of design variables for this showcase is $2n+1$. These parameters are summarized in Table S1. The magnetization profile data for each case are summarized in Fig. S6.

Table S1.

Parameters for each experimental showcase

Showcase	Length, mm	Width, mm	Thickness, μm	m	n	Maximum strain energy, J	No. of design variables
Cosine	7	5	80	—	200	2.24e-8	401
Jellyfish-like robot	7	3	80	10	10	3.3e-9	84
Undulatory swimming robot	10	3	240	5	70	1.11e-10	304
Cilium	10	3	80	10	20	1.54e-8	173

Fig. S6.

Quantitative representation for the magnetization profiles for all of the showcases when they were undeformed. (A) Magnetization profile for the cosine showcase. (B) Magnetization profile for the jellyfish-like robot and reversible “CMU” logo. (C) Magnetization profile for the artificial cilium. (D) Magnetization profile for the spermatozoid-like undulating swimmer.