Effect of flow and peristaltic mixing on bacterial growth in a gut-like channel

Significance

The human colon is occupied by trillions of microbial cells. Recent sequencing studies have shown that many diseases lead to substantial changes in the composition of this gut microbiota and suggest a strong influence of composition on host physiology. However, not much is known about the underlying physiological factors shaping the gut microbiota. Here, we focus on the role of flow and mixing by colonic wall contractions. To grow in the proximal colon, microbes have to continuously overcome flow. Our in vitro study suggests that mixing helps to overcome flow, and controlled contractions by the colon strongly influence microbiota density and composition; flow and mixing are essential components toward developing a predictive understanding of the gut microbiota.

Abstract

The ecology of microbes in the gut has been shown to play important roles in the health of the host. To better understand microbial growth and population dynamics in the proximal colon, the primary region of bacterial growth in the gut, we built and applied a fluidic channel that we call the “minigut.” This is a channel with an array of membrane valves along its length, which allows mimicking active contractions of the colonic wall. Repeated contraction is shown to be crucial in maintaining a steady-state bacterial population in the device despite strong flow along the channel that would otherwise cause bacterial washout. Depending on the flow rate and the frequency of contractions, the bacterial density profile exhibits varying spatial dependencies. For a synthetic cross-feeding community, the species abundance ratio is also strongly affected by mixing and flow along the length of the device. Complex mixing dynamics due to contractions is described well by an effective diffusion term. Bacterial dynamics is captured by a simple reaction–diffusion model without adjustable parameters. Our results suggest that flow and mixing play a major role in shaping the microbiota of the colon.

The large intestine of vertebrates harbors vast amounts of bacteria. The importance of this gut microbiota to the health of the host has been a topic of intense recent interest. The composition and function of this complex microbial community have been shown to have a strong influence on host physiology and affect pathological conditions as diverse as cancer (1), inflammatory bowel diseases (2), intestinal infections (3), malaria (4), autism (5), and obesity (6). Many of the connections between the pathologies and microbiota have been found by using fecal samples as a proxy for the content of the gut, and much effort has been invested in characterizing the composition of the microbiota with sequencing of bacterial genomes in fecal samples (7, 8). It is also known that bacterial composition shows spatial variation along the human gut in healthy and diseased subjects (9–11).

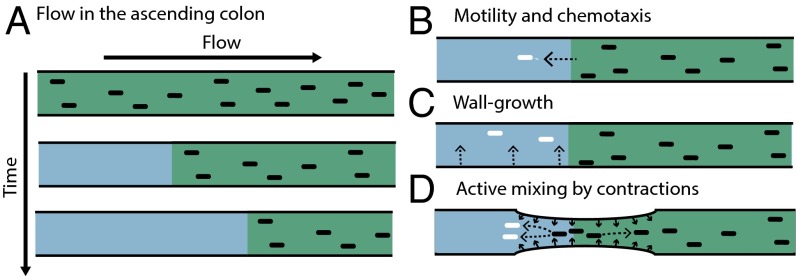
To better understand the spatiotemporal composition of the gut microbiota and how it is formed, it is important to analyze and understand the different physiological conditions and the resulting physical forces affecting bacterial growth dynamics in the colon and how these conditions change with time and space. One obvious feature of these dynamics is the movement of luminal content down the colon. In adult humans, this movement has a mean velocity of ∼20 µm/s in the proximal colon, the prime site of bacterial fermentation (see SI Appendix for velocity estimation). Importantly, the inflow to the colon from the small intestine has very low bacterial content (12, 13). Therefore, the movement down the colon alone can be expected to rapidly deplete bacterial density in the lumen of the proximal colon (even if the bacteria have high growth rates), a situation we refer to as “washout” (Fig. 1A). In the real colon, different factors might counteract this washout. One possibility would be active swimming of bacteria (Fig. 1B). However, whereas some bacteria in the colon may be motile (14), many abundant members of the gut microbiota do not carry genes for flagella [e.g., Bacteroides thetaiotaomicron, Bacteroides ovatus, Faecalibacterium prausnitzii (15)]. Correspondingly, flagellin, the main protein of flagella, is not strongly expressed in the colon (16) and flagellar activity might even be actively disrupted by the host (17). Furthermore, effective countering of the movement of the luminal content would require persistent swimming of the bacteria up the colon at a speed on the order of 20 µm/s, which is unrealistic. Another possible mechanism preventing washout would be replenishment of the lumen microbiota by bacteria shed from a bacterial reservoir adhering to the mucus layer and the epithelium on the colon walls (or “wall growth,” Fig. 1C) (18–20). However, for realistic bacterial growth rates, simple estimates indicate that a proper replenishment would require the number of wall-bound bacteria to be comparable to that of bacteria in the lumen, whereas the observed abundance of the wall-bound bacteria is several orders of magnitude lower (SI Appendix). Further, oxygen levels are still high in the mucus layer but very low in the lumen (21). Given that most bacteria in the lumen are strict anaerobes, they can hardly grow within the mucus layer(21, 22). Correspondingly, the composition of the bacterial community inhabiting the mucus layer is very different compared with that in the lumen (11, 21, 23, 24). Thus, whereas all these proposed mechanisms to maintain bacterial densities observed in the colonic lumen probably play a role, we argue that they are not sufficient, even if combined, to explain the high bacterial density observed.

Fig. 1.

Washout by flow and possible counteracting factors. (A) Flow alone leads to emptying of channel content over time. Additional factors are required to counteract this washout and help to maintain a stable bacterial density over time. Such factors may include: (B) active motility by bacteria to swim toward the nutrient source; (C) wall growth; and (D) peristaltic mixing, with backflow generated by contractions of colonic walls.

In this work, we investigate another mechanism which might be essential for preventing washout: contractions of the intestinal walls. For the human colon, these contractions include relatively frequent but uncorrelated contractions in the proximal colon as well as less frequent but more coordinated peristaltic movements along the whole colon (25). Importantly, these contractions can lead to a mixing of luminal content, here referred to as “peristaltic mixing.” Due to this mixing, some volume elements are displaced against the main flow direction (backflow), as illustrated in Fig. 1D. Simple simulation of the hydrodynamic flow indicated that local movement of the luminal content up the colon coupled with bacterial growth can prevent the washout and generate a steady state with a high-density bacterial population under large-scale movement of the luminal content down the colon (SI Appendix, Fig. S1).

There have been multiples studies of the gut microbiota using various in vitro setups and flow systems. Early studies have focused on the effect of chemical composition of the medium, for example using a three-stage chemostat setup (26). Over time, this approach has become increasingly advanced, with more robust cell seeding and automated control (27–29). To mix the medium and emulate the intestinal contractions, peristaltic contractions of the walls were used, but these setups can be viewed as chains of discrete compartments, without the possibility to study continuous spatial structure (30). A continuous flow system involving differential water and acid uptake from a flexible tube has also been developed (31); however, wall contraction and mixing were not implemented there. Peristaltic-like perturbations have also been used recently in microfluidic gut-on-chip devices (32–34); however, the perturbations studied were of small amplitudes, mainly designed to stretch and stimulate epithelial cells. To study the role of wall contractions and mixing for bacterial growth, we built and tested a laboratory model of the large intestine, the minigut. The minigut differs from the in vitro gut-like devices discussed above by emulating wall contractions with an array of flexible membrane valves evenly spread along the length of the channel. Longitudinal flow rate as well as the amplitude and timing of contractions of different valves are adjusted and controlled separately. We studied the dynamics of bacterial growth in the minigut device at different medium perfusion velocities with periodic contractions of the valves generating a peristalsis wave. Confocal microscopy was used to observe bacterial growth dynamics continuously over space and time. Several distinct regimes are observed: the washout regime (with near-zero bacterial density), the chemostat regime (with near-uniform density), and a third regime where the steady-state distribution of bacteria exhibited spatially varying density along the channel. We then characterized the dynamics of an engineered bacterial community of two cross-feeding strains in the minigut and observed distinct spatial dependence of bacterial composition. Our results establish that growth dynamics in the device can be effectively modeled by a reaction–diffusion system, with the complex mixing dynamics due to channel contractions described by a simple diffusion term. The model effectively captures the experimental results without freely adjustable parameters.

Results

Model and Analysis.

To study the role of flow and mixing on bacterial growth, we first develop a mathematical model. We consider growth occurring in a tube geometry of length $L$, with $x$ denoting the position along the tube. Nutrient (but not bacteria) enters the tube at $x=0$, and the culture (medium and bacteria) exits at $x=L$. The rate of flow is constant along the tube, denoted by $v$. Mixing generated by the contraction of the channel is modeled by an effective diffusion coefficient, $D$ (eddy diffusivity). A more detailed hydrodynamic model taking flow vortices and laminar flow profiles into account leads to similar predictions regarding growth and washout (SI Appendix, Fig. S1).

We explicitly model the dynamics of bacterial density $\rho (x,t)$ and nutrient concentration $n(x,t)$ over time $t$ with reaction–diffusion equations. With that, the model shares similarities with previous descriptions of growing populations under constant influence of convection (wind, water flow, etc.) (see, e.g., refs. 35 and 36). The equations for density and nutrients are given by

$$\frac{\partial \rho }{\partial t}=D\frac{{\partial }^2\rho }{\partial x^2}-v\cdot \frac{\partial \rho }{\partial x}+\lambda \left(n\right)\cdot \rho ,$$ [1]

$$\frac{\partial n}{\partial t}=D\frac{{\partial }^{2}n}{\partial x^2}-v\cdot \frac{\partial n}{\partial x}-\lambda \left(n\right)\cdot \rho /Y.$$ [2]

Here, flow is described by a convection term with flow velocity $v$. Bacterial growth follows Monod kinetics, given by a nutrient-dependent growth rate $\lambda \left(n\right)={\lambda }_0\cdot n/(K_M+n)$, with the Monod constant being $K_M$, and the maximum growth rate in the medium being ${\lambda }_0$ (37). The yield $Y$ gives the conversion factor between nutrient concentration and bacterial density. Boundary conditions ensure a constant inflow of nutrients with concentration $n_{in}$ at $x=0$, and a constant outflow at $x=L$ (SI Appendix).

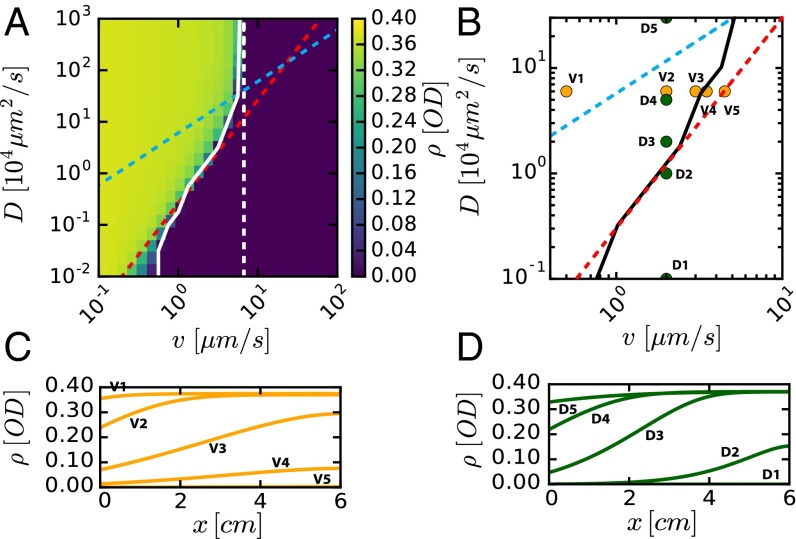
We explored the criterion for washout, i.e., the disappearance of a stable culture ($\rho \to 0$) in the long-time limit ($t\to \infty$), by solving Eqs. 1 and 2 numerically starting with a uniform initial bacteria density. The effect of flow and mixing was studied by varying $v$ and $D$, using growth and yield parameters that we measured (SI Appendix, Table S1). The results are shown in Fig. 2A for fixed $L$ and ${\lambda }_0$, by plotting the spatially averaged bacterial density ($\overline{\rho }$) obtained in the long-time limit for different $v$ and $D$. We see that high density is attained for low flow and strong mixing, whereas in the opposite limits of high flow or weak mixing, bacterial density vanishes, indicating washout.

Fig. 2.

Model predictions for bacterial densities when varying degree of mixing and flow. (A) The bacterial density averaged over the channel length predicted by the model is plotted against $\nu$ and $D$ values. Solid white line denotes boundary toward washout, where average density has reached zero (<0.1% of the maximum value). Dashed red line shows α = 1.8, dashed cyan line shows D/v = L. Chemostat washout condition v/(λL) ≥ 1 is denoted by the dashed white line. Steady-state spatial density profiles in C for fixed D = 2 10⁴ μm²/s and various values of v, and in D for fixed v = 2 μm/s and various values of D, as shown in B. The solid black line is the empirical phase boundary obtained from A. Growth rate and nutrient inflow concentration used are λ = 0.42 1/h and n_in = 2 mM, respectively.

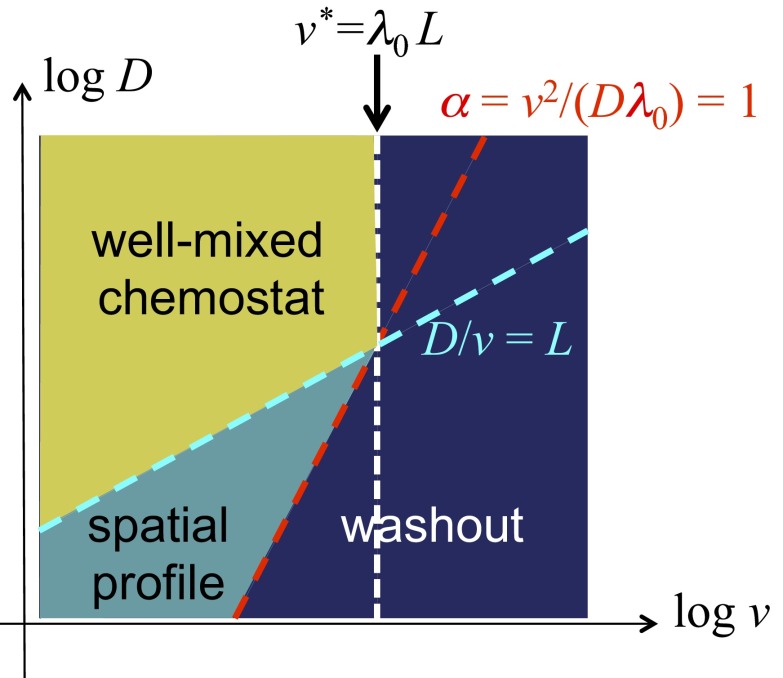
The nature of the parameter dependence can be understood qualitatively by a simple consideration (see Fig. 3 for more details). There are two important dimensionless parameters: the ratio of the diffusive mixing length, $\ell \equiv D/v$, to the channel length, $L$, i.e., $\ell /L$, and the ratio of local dilution rate, $v^2/D,$ to growth rate ${\lambda }_0$, i.e., $\alpha \equiv v^2/\left(D{\lambda }_0\right)$. The entire channel may be regarded as a well-mixed chemostat if $\ell /L\gtrsim 1$, i.e., above the dashed cyan line in Fig. 3. There, washout occurs if the flow rate exceeds a critical value $v^{\ast }={\lambda }_0\cdot L$ (dashed white line in Fig. 3). In the opposite regime, where $\ell /L\ll 1$ (below the dashed cyan line in Fig. 3), the channel is a chain of locally mixed regions (of lengths $\ell$). Spatially varying density profiles are expected in this case for $\alpha \lesssim 1$ (teal region in between the dashed red and cyan lines). Washout occurs to the right of the dashed red line.

Fig. 3.

Qualitative description of the behaviors of the reaction–diffusion model. The combined effect of flow and mixing defines a “diffusive mixing length” ℓ ≡ D/v. For length scale below ℓ, the culture is locally well mixed. If mixing is sufficiently strong such that ℓ becomes comparable to the length of the channel, i.e., ℓ ∼ L, then we may regard the entire channel as a well-mixed chemostat, with a “dilution rate” v/L. A chemostat can only sustain a stable culture below the chemostat washout condition (49), i.e., when the ratio of dilution and growth rates, α_L ≡ (v/L)/λ, is below 1. This translates to a critical flow velocity v* = λL above which washout occurs (dark-blue region). This condition is shown as the dashed white line, together with the dashed cyan line, ℓ = L, which indicates the boundary of the chemostat regime (region in yellow). For lower degrees of mixing where ℓ ≤ L (below the dashed cyan line), chemostat results do not apply. Here, the system consists of a number of locally well-mixed segments of length ℓ, and the characteristic ratio of dilution to growth becomes α ≡ (v/ℓ)/λ = v²/(Dλ) for each of these segments. We may expect α = 1 as an approximate criterion for washout in a long channel. This condition is shown as the dashed red line, above which washout occurs (dark blue). In between the cyan and red line (teal region), we expect a stable solution to exist in the channel. Solution in this regime is generally not expected to be spatially uniform, as it is no longer well mixed.

We compared this qualitative picture to the numerical solution of Eqs. 1 and 2. From the results shown in Fig. 2A, we defined a washout condition, the combination of $v$ and $D$ values where the average density drops to zero for long times; see the solid white line in Fig. 2A. This white line is reasonably well captured by the condition $\alpha =1.8$, shown as the dashed red line. Note that the phase boundary toward washout (white line) flattens for large $D$, as $v$ approaches the chemostat washout limit (dashed white line). The results obtained for different combinations of $L$ and ${\lambda }_0$ are shown in SI Appendix, Fig. S2. Convergence toward a steady state is shown in SI Appendix, Fig. S3.

We next show the spatial density profiles of the steady-state solution, $\rho (x,t\to \infty )$ for different flow and mixing rates (Fig. 2 C and D) with the different values of $v$ and $D$ used in the simulation indicated in Fig. 2B. In agreement with the qualitative picture presented in Fig. 3, the density profiles are essentially flat above the cyan line (i.e., for $\ell /L\gtrsim 1$); see conditions V1 and D5 in Fig. 2B. Washout is observed to the right of the red line ($\alpha \gtrsim 1$); see conditions V5 and D1 in Fig. 2B. In between the cyan and red lines, the profiles exhibit substantial spatial dependencies.

Experimental Setup.

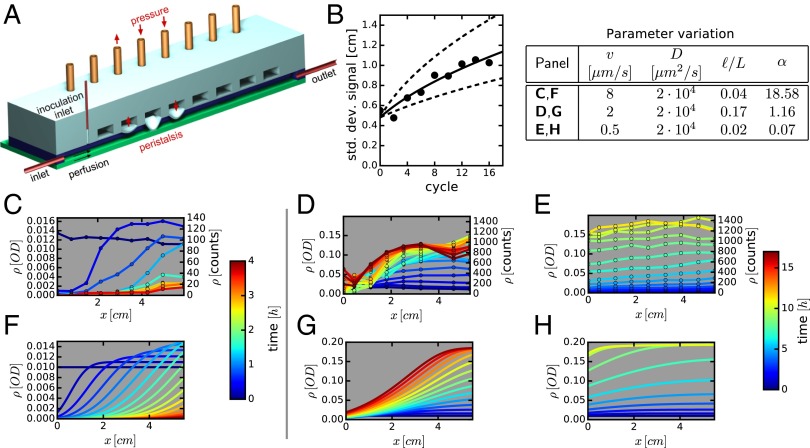
Intestinal flow and contractions are difficult to control or characterize in vivo. To test the predictions of the above model, we constructed a fluidic minigut device (Fig. 4A and SI Appendix, Fig. S4). In this device, bacterial growth occurs in a rectangular channel, 7 cm long with a 2 × 4-mm cross-section. Fresh medium containing nutrients is continuously supplied from one end of the channel, setting a mean flow velocity that can be changed from zero to over 50 μm/s. The ceiling of the channel is made of a silicone elastomer and has a regular array of eight individually addressable, pressure-actuated membrane valves (4-mm-wide valves with 7-mm period of the array) (38). The application of pressure to a valve leads to its contraction, emulating local contraction of intestinal walls (see the SI Appendix for a detailed technical description). The application of different levels of pressure to the valves at different times generates a broad range of spatial–temporal patterns of valve contraction and partial channel occlusion (from a minor reduction of the channel height all of the way to the ceiling touching the floor). As expected, the flow in the channel resulting from contraction of the valves led to efficient mixing along the channel, especially, when the ceiling touched the floor, resulting in major occlusion. The efficiency of mixing was characterized for different patterns of valve contraction that involved the actuation of each of the eight valves during each cycle of valve contraction (e.g., a peristaltic wave, valves actuated in a random order, etc.). To this end, a small blob of a fluorescent dye (or particles) was injected near the middle of the channel, and the spreading of the fluorescence intensity (proxy of dye concentration) along the channel was measured as a function of the number of cycles of valve contraction (SI Appendix, Fig. S5).

Fig. 4.

Effect of mixing and flow on bacterial growth. (A) Schematic of the minigut device with controlled “contractions” implemented by pressure-induced membrane deformations. (B) Mixing dynamics due to wall contraction is quantified by locally injecting fluorescent dye near the middle of the channel and measuring the spreading of the dye distribution along the channel with time. The width of the distribution is shown after different numbers of cycles of peristaltic contractions. The data are shown for a waiting time of 120 s between cycles, and it is fitted to diffusion-like spreading (solid line), with an effective diffusion constant of D = 2 · 10⁴ μm²/s; see SI Appendix, Fig. S5 for further details. (C–E) Cells from strain EQ403 grown in the device at different flow conditions. Bacterial densities measured at various times and locations are plotted. Each line is a snapshot of the density profile, with the time color-coded. (C) Flow-dominated regime with no cells in steady state (washout). (D) Intermediate regime with distinct spatial dependence of bacterial density. (E) Mixing-dominated regime with little spatial dependence. The flow and mixing parameters are indicated in the legend table. (F–H) Numerical simulations of the corresponding system using the reaction–diffusion model with only independently measured parameters; see Spatiotemporal Density Profiles in the Minigut. Experimentally measured cell counts are converted to optical density (OD) using a constant conversion factor (SI Appendix, Fig. S6). Relative errors in density are below 20%.

For periodic peristaltic waves and an aqueous solution of the fluorescent dye, the spreading, quantified as the SD of the spatial dye distribution along the channel, was well fitted by a square root of the number of cycles (SI Appendix, Fig. S5 A and B). Hence, the spreading was a diffusion-like process with an effective diffusion constant, $D$, set by the valve-generated hydrodynamic flow (known in fluid dynamics as the eddy diffusivity). At the shortest feasible period of the peristaltic wave (∼10 s), $D$ reached $\sim {10}^5\hspace{0.17em}{\mathrm{\mu }\text{m}}^2/\text{s}$, more than 3 orders of magnitude enhancement compared with the molecular diffusion of the fluorescent dye (SI Appendix, Fig. S5). Importantly, the value of D for an aqueous suspension of 2-µm fluorescent beads (similar in size to bacterial cells) was close to the value measured for the fluorescent dye (SI Appendix, Fig. S5 C and D), despite $\sim 100$× lower particle (molecular) diffusivity of the beads (0.2 vs. 25 µm²/s). This result suggests that flow-induced effective diffusivity $D$ is universally applicable to particles and molecules of all sizes (an expected outcome for $D$ significantly greater than the molecular diffusivity). Furthermore, when random patterns of valve contractions were applied instead of the regular peristaltic waves, the spreading of the fluorescent dye along the channel was substantially slower $(\sim 5$× reduced effective $D$; SI Appendix, Fig. S5 E and F). Last, we measured the spreading of the fluorescent dye when the carrier liquid had an ∼10× greater viscosity than water (SI Appendix, Fig. S5 G–J) and found $D$ to be $\sim 2$× lower than for the aqueous solution. (The reduction in $D$ was likely mostly caused by changes in the flow pattern rather than in the molecular diffusivity of the dye.) The tested range of viscosity agrees with direct observations in the gut (39). For most of the experiments with bacteria, we applied peristaltic waves with a period of 120 s and had a solution with viscosity 2× higher than water, resulting in an effective diffusion constant $D$ ∼ 2 · 10⁴ µm²/s (Fig. 4B). This diffusion constant is $\sim 20$× greater than the molecular diffusivity of small molecules and $\sim$10⁵ greater than the particle diffusivity of nonmotile Escherichia coli.

Spatiotemporal Density Profiles in the Minigut.

To study bacterial growth under the influence of flow and mixing and to test the predictions of the reaction–diffusion model, we grew fluorescently labeled E. coli cells (strain EQ403; see SI Appendix) in minimal medium in the device. Cells were first grown in batch culture to the midlog phase before transferring to the device. Flow of the medium was then turned on and mechanical contractions were applied at set amplitude and frequency for the duration of the experiment. At regular intervals, cell density was monitored along the device by counting cells in a fixed volume using a confocal microscope (SI Appendix, Fig. S6).

We characterized the spatiotemporal dynamics in the device for different combinations of mixing and flow conditions (SI Appendix, Fig. S7A). In agreement with the theoretical predictions, weak peristaltic mixing (low effective diffusivity) led to washout (blue symbols, SI Appendix, Fig. S7B; see also SI Appendix, Fig. S8A), whereas stronger mixing stabilized the culture (red symbols; SI Appendix, Fig. S7C). Conversely, for a given effective diffusivity, fast flow led to washout (orange symbols; SI Appendix, Fig. S7B) whereas reduced flow rate stabilized the culture (red and green symbols; SI Appendix, Fig. S7C). The full spatiotemporal dynamics was measured for a constant rate of cycles of membrane contractions (constant effective $D$) and varying flow rates, $v$ (Fig. 4 C–E) as well as for varying $D$ and constant $v$ (SI Appendix, Fig. S8 A and B). The drop in bacterial density over time for the fast flow (Fig. 4C) indicated washout that occurred despite mixing. At lower flow rates (Fig. 4 D and E), stable bacterial densities were obtained. The culture in Fig. 4E had a steady state with a weak spatial dependence, whereas the one in Fig. 4D exhibited a strong spatial dependence, with ∼4× higher density at the exit compared with the entrance.

To compare the experimental results to the predictions of our model (Figs. 2 and 3) qualitatively, we use the experimental values of $v$, $D$, and $\lambda$ to obtain the mixing length $\ell =D/v$ and the $\alpha$-parameter (Fig. 4 and SI Appendix, Fig. S7 A and B). For the conditions corresponding to Fig. 4E, we have $\ell \approx L$ and $\alpha \approx 0.1$, indicating that the entire channel can be regarded as a well-mixed chemostat, and hence little spatial dependence should be expected. For the conditions corresponding to Fig. 4D, $\ell \approx L$/6 and $\alpha \approx 1.2$, indicating that the system is in the regime where a strong spatial pattern is expected. For the conditions of Fig. 4C and SI Appendix, S8A, we have $\ell \ll L$ and $\alpha \gg 1$, corresponding to the washout regime.

For more quantitative comparisons, we simulated the reaction–diffusion model (Eqs. 1 and 2) using the same experimental values of $v$, $D$, and $\lambda$ (SI Appendix, Table S1 and Fig. S10 A and B). The spatiotemporal density profiles predicted by the model are shown below the corresponding data in Fig. 4 F–H, and SI Appendix, Fig. S8 C and D. The agreement between the predicted and observed density profiles is remarkable given the lack of any fitting parameters in the model. We note, however, that bacterial growth at the channel walls inevitably leads to deviations from model predictions. Moreover, there is a steady increase in the experimental noise due to increased scattering of light by cells growing on the walls and gas bubbles emerging on the walls, practically limiting the duration of experiments to ∼20 h.

The model also predicts that, at long times, the effect of small variations of $v$, $D$, and $\lambda$ on bacterial density distribution is strongest at conditions leading to nonuniform bacterial density along the channel, $\alpha \lesssim 1$ and $\ell <L$ (Fig. 4 D and G). We performed two more experiments at the same flow conditions as in Fig. 4D ($D=2\cdot {10}^4\hspace{0.17em}{\mathrm{\mu }\text{m}}^2\text{/s}$, $v=2\mathrm{\mu }\text{m/s}$), and the results (SI Appendix, Fig. S9) indicated general robustness of the experimental system and reproducibility of the growth dynamics. Similarity and slow evolution of the density distributions at long times were also consistent with the existence of a final stable distribution that the system converges to, according to the model.

Together with the direct characterization of mixing dynamics (SI Appendix, Fig. S5), our results establish that complex hydrodynamic mixing due to channel wall contractions is captured by the reaction–diffusion model and that regularly occurring wall contractions can effectively prevent washout. A combination of bacterial growth, flow, and mixing can generally lead to systematic variations in bacterial density along the minigut.

Effect of Spatial Coupling on Cross-Feeding.

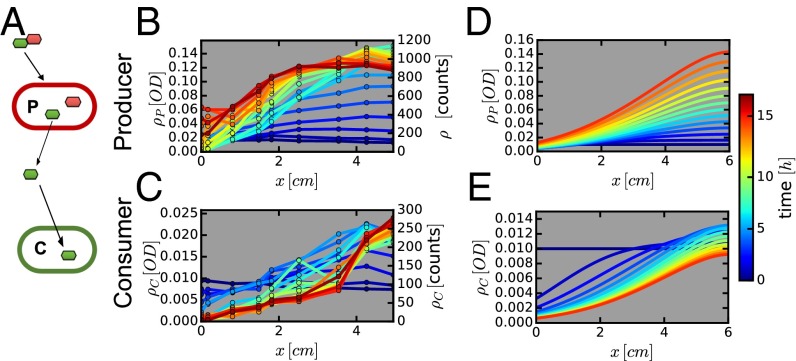
We next considered the effect of flow and mixing on interacting microbial populations. A common form of interaction among gut microbes is assumed to be cross-feeding (40). Examples include the breakdown of polysaccharides by Bacteriodetes and the utilization of the resulting monosaccharides by Bacteriodetes and other species including Firmicutes and Escherichia coli (see, e.g., ref. 41). Cross-feeding on many fermentation products has also been described, including the uptake of acetate and lactate (41), and hydrogen uptake by methanogens and sulfate reducing bacteria (42). To observe the possible effect of flow and peristaltic mixing on cross-feeding dynamics, we conducted experiments to investigate a simple mode of cross-feeding using two synthetically designed E. coli strains, as illustrated in Fig. 5A.

Fig. 5.

Two-strain cross-feeding ecology. (A) The Producer strain (EQ403) that breaks down lactose (disaccharide of galactose and glucose, shown as linked red and green hexagons), but is able to metabolize only glucose (red hexagon), releasing galactose (green hexagon). The Consumer strain (EQ386) only metabolizes galactose released by the producer. The density profiles for the producer and consumer are shown in B and C, respectively. Corresponding numerical solutions of the model are shown in D and E. Producers and consumers were initially uniformly distributed (OD₆₀₀ = 0.01) and lactose was the only carbon source provided. In both theoretical model and experiment, the parameters used correspond to the intermediate regime shown in Fig. 4C. Relative errors in experiments are below 20%.

For the Producer (P), we used strain EQ403, the properties of which were described above. This strain can break down lactose into glucose and galactose, but only metabolize glucose. As the Consumer (C), we constructed strain EQ386, which could not use lactose but could grow on glucose or galactose; see SI Appendix for strain details and SI Appendix, Fig. S10 for characterization. The two strains were labeled by mCherry and GFP, respectively, so that the abundance of each strain could be followed in the device over time using fluorescent microscopy.

The two strains were first grown together in lactose batch culture (SI Appendix, Fig. S10 C and D). Although the P strain grew faster initially, the two strains approached the same final density eventually because each strain could metabolize half of the nutrients (lactose). To study the result of flow and mixing, P and C were grown separately in batch cultures, in lactose and galactose minimal media, respectively. Exponentially growing cells were harvested, washed, and transferred together to the device, which is perfused with lactose minimal medium. Flow and mixing were set to the intermediate level described above (Fig. 4D), and cell count for each strain was monitored by microscopy as described above. The results are shown in Fig. 5 B and C. Because C is not expected to affect the growth of P, the density profile of P is very similar to that obtained previously when P was grown alone (compare Figs. 5B and 4D). The density profile of C (Fig. 5C) is clearly very different from that of P. The average density is much lower, and the overall change in density of C at the entrance (x = 0) and exit (x = 6 cm) is larger, and the rise in density is shifted toward the distal end. (The midpoint of density increase is at x = 1.5 cm for P and x = 3.5 cm for C.)

Two effects may likely account for the shifted density profile for C: (i) C is closer to washout due to its slower growth rate in galactose. (ii) Galactose accumulation increases along the proximal part of the device (due to the rise in P, Fig. 5B), so that C grows better toward the distal end. We examined bacterial growth for this cross-feeding system mathematically by expanding the reaction–diffusion model to two strains and two types of nutrients (lactose and galactose, assuming that glucose derived from lactose degradation is completely consumed by P), and including the differences in metabolism for the two strains (SI Appendix). Using previously determined physical parameters for the device and the measured growth properties of the two strains (SI Appendix, Table S1, Fig. S10 A and B), the model provides good predictions for the spatiotemporal bacterial and nutrient profiles with the bacterial profiles shown in Figs. 5 D and E. Nutrient profiles are shown in SI Appendix, Fig. S11. Model predictions for the density of C (Fig. 5E) capture the observed density profile remarkably well again, given the lack of any adjustable parameters. The predicted spatial profiles of nutrient concentrations (SI Appendix, Fig. S11) show that the availability of galactose is indeed distal-shifted. Thereby reduced growth makes it even harder for C to maintain in the channel. Compared with batch culture growth, flow limits strong cross-feeding to occur in the channel when mixing is limited and does not lead to a well-mixed situation.

Discussion

In this work, we developed a fluidic device, the minigut, to study bacterial growth in a gut-like system with controlled flow and wall contractions. The device allows the continuous observation of bacterial densities over time. The goal of this study was not to engineer a realistic model of the colon, but to evaluate the interplay between flow, mixing, and bacterial growth. Through mathematical modeling and experiments in the device, we demonstrated that the physical forces of flow and mixing could have a significant effect on bacterial growth and ecology: When combined with bacterial growth, recirculation flow generated by the channel wall contractions is sufficient to counter the washout effect that longitudinal flow along the channel exerts on the bacterial culture. Whereas strong and frequent wall contractions lead to homogeneous bacterial density and infrequent contractions do not prevent washout, contractions at an intermediate frequency create a stable distribution with bacterial density substantially increasing along the channel. In this regime, different locations along the channel become different niches with distinct steady states. When a second bacterial strain is introduced into the channel, cross-feeding of metabolites of the first strain, these niches become even more distinct, with large variations of the density of the second strain and of the ratio of densities of the two strains. At a quantitative level, our work shows that despite the complexity of hydrodynamic flow associated with the contraction of the channel wall, its effect on bacterial growth can be captured by an effective diffusion term (eddy diffusivity) in a reaction–diffusion model.

For adult humans, with 1.5 L/d of luminal fluid entering the colon (43), the average flow rate in the proximal colon is very high, $20\hspace{0.17em}\mathrm{\mu }\text{m/s}$ or even higher across the first 20 cm of the proximal colon (SI Appendix). The degree of physical mixing by colonic contractions has not been systematically characterized in vivo. However, uncoordinated but continuous mixing has been observed in the proximal large intestine (44). Further, observations with radiolabeled particles confirmed mixing in the proximal colon (45). Given the presence of strong flow and mixing, we expect the interplay of these two processes with bacterial growth to play an important role in maintaining a steady microbial population in the proximal large intestine. Some aspects of our model and the in vitro predictions could be tested in future animal experiments. Interventions in mice to change the transit times through the gut, a proxy for flow velocity, have been successfully implemented (46) and could be adapted to test our predictions.

The prospect of partial local mixing, together with other changes along the length of the proximal colon not considered in this work, including changes in the flow rate (due to water absorption) (47), the oxygen content (21), and pH profile (48), makes it likely that growth and abundance of primary strains from the main phyla Bacteriodetes and Firmicutes are also strongly position-dependent in the proximal colon. This would in turn trigger a domino effect that imposes spatial dependence on species that depend metabolically on these primary producers. Given that most bacterial growth in the gut is happening in the proximal large intestine, these effects can contribute substantially to the microbiota composition of feces.