Surfactant adsorption kinetics in microfluidics

Significance

Surfactant adsorption to interfaces is a dynamic process of relevance for foaming, emulsification, and detergency. Although the process has been described for centuries now, the rational measurement of adsorption and desorption constants, as well as the modeling of the binding mechanism, is still subject to many assumptions. The prevalence of transport through the bulk in classic measurements limits the reliability of the analysis. Microfluidics provides a means to achieve small sizes and significant droplet velocity to alleviate the limiting step of surfactant bulk transport. Adsorption kinetics are measured directly to make a link among droplet stabilization, ion exchange, and coalescence.

Abstract

Emulsions are metastable dispersions. Their lifetimes are directly related to the dynamics of surfactants. We design a microfluidic method to measure the kinetics of adsorption of surfactants to the droplet interface, a key process involved in foaming, emulsification, and droplet coarsening. The method is based on the pH decay in the droplet as a direct measurement of the adsorption of a carboxylic acid surfactant to the interface. From the kinetic measurement of the bulk equilibration of the pH, we fully determine the adsorption process of the surfactant. The small droplet size and the convection during the droplet flow ensure that the transport of surfactant through the bulk is not limiting the kinetics of adsorption. To validate our measurements, we show that the adsorption process determines the timescale required to stabilize droplets against coalescence, and we show that the interface should be covered at more than $90\mathrm{\%}$ to prevent coalescence. We therefore quantitatively link the process of adsorption/desorption, the stabilization of emulsions, and the kinetics of solute partitioning—here through ion exchange—unraveling the timescales governing these processes. Our method can be further generalized to other surfactants, including nonionic surfactants, by making use of fluorophore–surfactant interactions.

Surface active compounds are ubiquitous in our daily life, be it in living systems or in industrial and technological products (1–3). The compounds are used widely for the stabilization of foams and emulsions for food and cosmetic products, painting materials, and industrial coatings (3). Emulsions are nowadays also used in combination with microfluidic systems for applications in biotechnology (3–11). An emulsion is a dispersion of one liquid phase into another, stabilized by surfactants in a metastable state. The kinetic stabilization of emulsions occurs through several mechanisms, involving electrostatic or steric repulsion and the buildup of Marangoni stresses to improve the lifetime of emulsions against coalescence (12, 13). On the other hand, surfactants are involved in transport processes such as Ostwald ripening or solute transport, which mediates the chemical equilibration of the system (14–17): in general, all processes affecting the lifetime of emulsions (coalescence, rupture, exchange, and loss of molecules) are directly related to the physics and dynamics of the surfactant molecules at interfaces (3, 4, 6, 10, 11, 15, 16). The first analysis of surfactant layers dates back to the 18th century with Franklin’s experiments (1) and the first comprehensive studies on adsorption kinetics by Ward and Tordai (18) and Langmuir (19). From this point, a wide variety of models describe the adsorption dynamics, accounting for all kinds of molecular effects at interfaces (20–26). We expect two limiting cases: (i) the adsorption is limited by the bulk transport toward the interface, leading to a local equilibrium between the surfactant interfacial concentration and the bulk concentration in the vicinity of the interface at all times; and (ii) the adsorption is limited by the adsorption/desorption rate constants at the interface, and the bulk concentration is homogeneous at all time. If the bulk transport is a diffusive process, and if the adsorption is given by a Langmuir model, diffusion is always negligible below a critical radius $R^{\mathrm{\star }}=D/\left(k_{ads}{\mathrm{\Gamma }}_{\infty }\right)$, where D is the diffusion coefficient, $k_{ads}$ the adsorption rate, and ${\mathrm{\Gamma }}_{\infty }$ the maximal interfacial coverage (SI Text and Fig. S1). This cutoff radius $R^{\mathrm{\star }}$ was initially proposed by Jin et al. and is of the order of 50 μm for a series of classic surfactants (27). As a consequence, understanding the kinetics of surfactant in emulsification conditions is not possible using large-volume methods such as—among others—Wilhelmy tensiometry or even pendant droplet tensiometry. These methods are likely transport-limited unless adsorption barriers emerge. To make the adsorption the limiting process, the droplet size should thus be small. Even if the adsorption is not modeled by a Langmuir isotherm, the conclusion remains qualitatively valid. In the presence of convection, the timescale of transport is controlled by the Sherwood $Sh$ number, which compares the mass transfer with convection to the one in the purely diffusive regime (28). Thus, the effect of convection increases the cutoff radius by the Sherwood number $Sh$, leading to a new cutoff radius $R^{\prime \mathrm{\star }}=Sh\times R^{\mathrm{\star }}$. Molecular transport becomes negligible compared with adsorption kinetics for droplets even at larger dimensions. Such experiments using small sizes and convection have been performed by Alvarez et al. (25), showing the importance of reaching the kinetic regime to reliably extract adsorption constants. In our experiments, we consider here droplets moving in a microfluidic channel to increase the bulk transport by convection; we use droplet-based microfluidics to analyze the adsorption kinetics of a surfactant, overcoming the transport limitation. We use a perfluoropolyether (PFPE) with a carboxylic acid head group, soluble in the oil phase, as a model surfactant. We monitor the change of pH in the aqueous droplets produced on-chip as the surfactant adsorbs to the interface and releases its proton into the dispersed phase. From these experiments, we obtain a kinetic adsorption model, in a pure kinetic-limited adsorption regime. Another advantage of this technique is that the timescale of pH variation, which is used to obtain the adsorption rates, is much larger than the inverse of these adsorption rates. Equilibrium data are obtained independently and provide experimental values for the parameters required by the model. We finally address the issue of emulsion stability against coalescence (29): we compare the timescale of surfactant adsorption and the time above which droplets do not coalesce.

Fig. S1.

Scaling laws for the early time adsorption kinetics. The determination of the cutoff radius is shown. When the interfacial coverage is limited at an early stage by a diffusive process, a square root dependence with time is obtained for a flat interface. For a sphere, the power law has a 3/2 exponent. In the kinetic regime, a linear dependence is obtained for a Langmuir-type kinetics. The crossovers between the different regimes reveal that for sufficiently small droplets, the adsorption is never diffusion-limited.

SI Text

Diffusion vs. Adsorption.

We discuss here the crossover between different regimes of surfactant adsorption. We consider the limiting cases where the timescales is limited by diffusion, and when the adsorption is limited by a simple Langmuir adsorption model. A simple asymptotic analysis shows the relevant cutoffs (Fig. S1): for a sphere of radius R in the diffusion limited regime, the interfacial coverage $\mathrm{\Gamma }$ for very short timescales scales, like for a planar interface, as $\sqrt{D{C}^{2}t}$ (18, 26) and at larger timescales as ${\left(Dt\right)}^{3/2}C/R^2$ (with C being the surfactant concentration and D its diffusion coefficient and time t). Both regimes are separated by the cutoff timescale $R^2/D$. In contrast, in a simple Langmuir adsorption process, the kinetics are modeled by a first-order adsorption/desorption reaction. The coverage scales as $k_{ads}{\mathrm{\Gamma }}_{\infty }Ct$, with $k_{ads}$ being the adsorption constant and ${\mathrm{\Gamma }}_{\infty }$ the maximum interfacial coverage (Kinetics for a Langmuir Adsorption Process). Therefore, for a planar interface, a cutoff between both regimes is expected at a timescale of $D/\left(k_{ads}^2{\mathrm{\Gamma }}_{\infty }^2\right)$: at short times, diffusion is fast and the reaction of adsorption limits the kinetics. At longer times, diffusion becomes the limiting step. For a sphere, $D/\left(k_{ads}^2{\mathrm{\Gamma }}_{\infty }^2\right)$ should be compared with $R^2/D$. If $R^2/D<D/\left(k_{ads}^2{\mathrm{\Gamma }}_{\infty }^2\right)$, then diffusion is faster than adsorption. If the bulk transport is a diffusive process, and if the adsorption is given by a Langmuir model, diffusion is always negligible below a critical radius $R^{\mathrm{\star }}=D/\left(k_{ads}{\mathrm{\Gamma }}_{\infty }\right)$, where D is the diffusion coefficient, $k_{ads}$ the adsorption rate, and ${\mathrm{\Gamma }}_{\infty }$ the maximal interfacial coverage (Fig. S1).

Kinetics for a Langmuir Adsorption Process.

We assume here that the adsorption of the surfactant follows a standard Langmuir process. The rate of adsorption is proportional to the concentration of surfactant $C_0$ (at time $t=0$) in the bulk, the density of available sites at the interfaces $\left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right)$, and the adsorption constant $k_{ads}$. The desorption process is proportional to the density of occupied sites $\mathrm{\Gamma }$ and the desorption constant $k_{des}$.

$$\frac{d\mathrm{\Gamma }}{dt}=k_{ads}{C}_0\left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right)-k_{des}\mathrm{\Gamma }$$ [S1]

leads to an exponential relaxation of the interfacial coverage as $\mathrm{\Gamma }\left(t\right)={\mathrm{\Gamma }}_{eq}(1-\text{exp}\left(-t/\tau \right)$, with the timescale ${\tau }^{-1}=k_{ads}{C}_0+k_{des}$, the equilibrium interfacial coverage ${\mathrm{\Gamma }}_{eq}={\mathrm{\Gamma }}_{\infty }\kappa C_0/\left(1+\kappa C_0\right)$ and $\kappa =k_{ads}/k_{des}$. In this model, one proton is released into the bulk for each surfactant molecule adsorbing. At a short timescale, when the coverage is much smaller than the equilibrium coverage, mass conservation implies that $d\mathrm{\Gamma }/dt\times S=d\left[H^{+}\right]/dt\times V$, where S and V are, respectively, the surface and volume of the droplet. At longer times, the concentration of acidic surfactant in the oil decreases. Therefore, the full rate equation for the proton concentration in the droplet reads

$$\frac{V}{S}\frac{d\left[H^{+}\right]}{dt}=k_{ads}\left(C_0-\frac{1}{q}\left[H^{+}\right]\right)\times \left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right),$$ [S2]

where q is the volumetric ratio between the fluorous and the aqueous phase that accounts for dilution effects. If all ${\text{H}}^{+}$ are transferred from the oil to the water, the concentration in the water is simply $q{C}_0$. In the desorption process, the counter ion that leaves the droplet from the bulk is likely the most abundant positive ion. In our case, a ${\text{Na}}^{+}$ ion is transferred to the oil. Therefore, the rate equation for the ${\text{H}}^{+}$ in the droplet does not take into account the desorption process. Solving the equation of course requires the knowledge of $\mathrm{\Gamma }\left(t\right)$. However, when the timescales for surface adsorption and pH change are well-separated, one can assume that the interface is at equilibrium coverage ${\mathrm{\Gamma }}_{eq}$ at all times of pH change. Therefore, only the knowledge of ${\mathrm{\Gamma }}_{eq}$ is required to solve Eq. S2. In this case, the relaxation is again exponential and the timescale of pH change is simply

$${\tau }_{pH}=\frac{qR}{3k_{ads}\left({\mathrm{\Gamma }}_{\infty }-{\mathrm{\Gamma }}_{eq}\right)},$$ [S3]

with R being the radius of the droplets. Because we work above the CMC, $\left({\mathrm{\Gamma }}_{\infty }-{\mathrm{\Gamma }}_{eq}\right)$ is a constant and the initial velocity of the decay of the ${\text{H}}^{+}$ concentration ${d{\left[H\right]}^{+}/dt|}_{t=0}$ in the droplet is therefore (Eq. S2) expected to be linear with surfactant concentration.

Optical Setup.

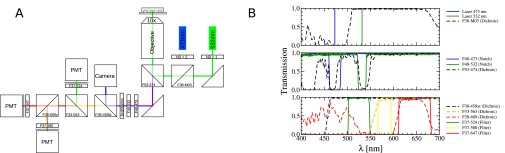
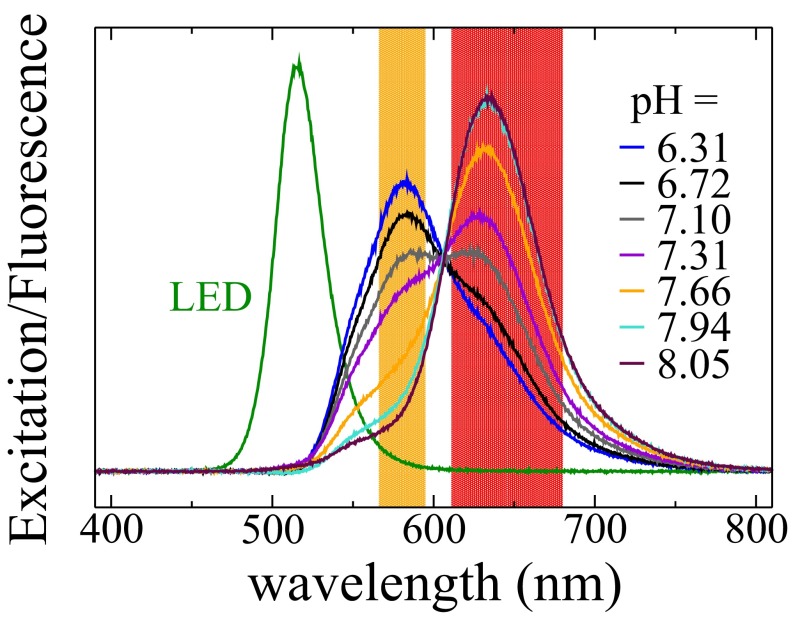
The optical setup is similar to that reported previously (38). In brief, it consists of the laser (Fig. S2) (532 nm with 25 mW, Cobolt Samba; the 473 nm is off in these experiments), which is directed through a neutral density filter ($ND=1$; Fig. S2; Thorlabs) and focused with an objective (10×; Olympus) into the microfluidic channels using dichroics (for specifications, see Fig. S2) (AHF Analysentechnik; optical accessories; Thorlabs). The microfluidic chip is mounted on a x-y-stage (Thorlabs). For focusing, we observe the droplets with a camera (Grashopper) using a blue LED (Olympus) from above. The LED is turned of for data acquisition of the fluorescence signal of the droplets. The dye in the droplets is excited by the 532-nm laser, and the fluorescent light is directed through several notches and filters and split with dichroics (AHF Analysentechnik) to be recorded by photomultipliers (PMTs) (H9656-20; Hamamatsu). The fluorescence at the two fluorescence maxima (around 647 nm and 580 nm) in an epifluorescence configuration. In this experiment, only the fluorescent signals (at a gain of 0.8) of the two PMTs around 580 nm and around 647 nm are recorded. We measure the droplet intensity at 647 nm ($I_{647}$) and 580 nm ($I_{580}$) and define the ratio of the fluorescence as the dimensionless number $I_{647}/I_{580}$. This ratio depends on the optical system but is independent of the total intensity. The data are transferred by a field programmable gate array board (cRIO; National Instruments) at 3 kHz using a program written in LabView (National Instruments).

Fig. S2.

(A) Fluorescence setup for the droplet-based microfluidic pH measurements with all optics: the microfluidic chip is mounted on an x-y stage. The 532-nm laser is focused into the channels through the microscope objective (×10), and the fluorescence is recorded in epifluorescence mode. (B) Optical properties of the dichroics, filters, notches, and lasers used in the setup.

Microfluidic Device Fabrication.

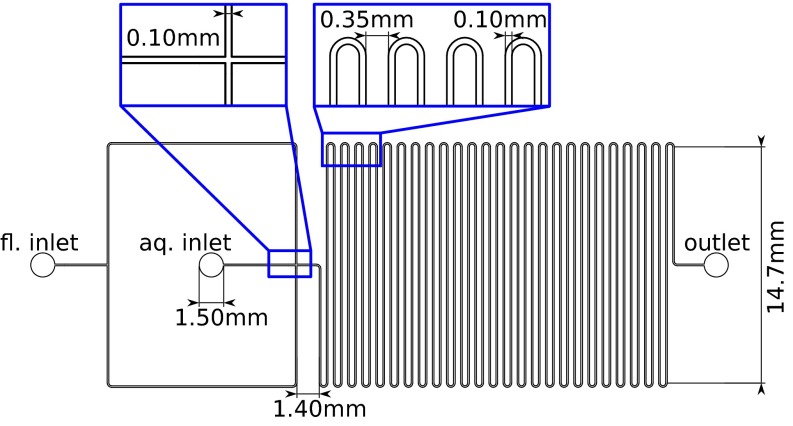
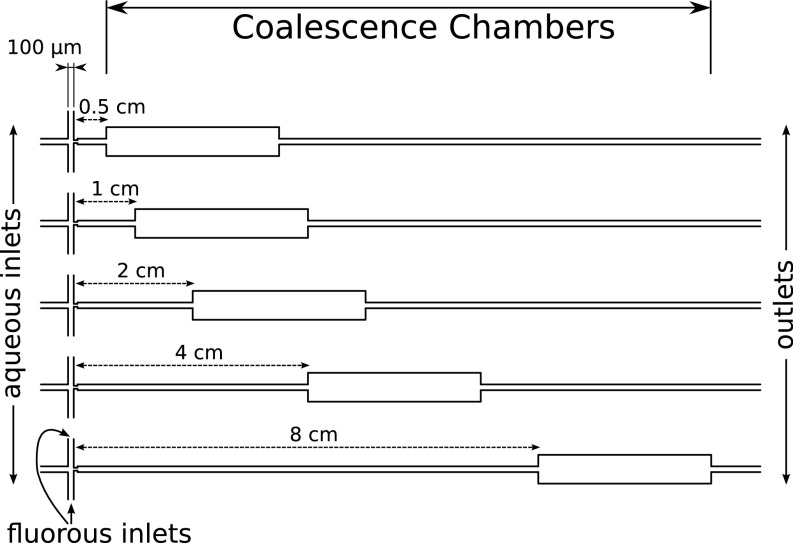
We manufacture microfluidic devices in PMMA and PDMS (Figs. S4 and S5). The PMMA microfluidic devices are used for the pH measurements and are milled with an end mill cutter for channels of 100 μm in diameter (Fig. S4), $\sim$ 80 μm in height. The channels are sealed to a second plate using hot embossing. UV-curable glue connects the inlets and the outlets to nanoports [coned, 10–32, polyether ether ketone (PEEK); Upchurch], which are attached to the syringes for device operation. The PMMA channels are hydrophobized by flowing a coating agent (Aquapel; PPG Industries) through the channels and subsequent drying with nitrogen. The design consists of a flow-focusing junction for droplet production and a long delay (75 cm in length). We chose PMMA as a material to sustain the pressure of the Poiseuille flow without deformations over the long length of the channel. The PDMS device for the coalescence experiments (Fig. S5) is produced using standard photo- and soft-lithography at a height of 40 μm (36, 37). The PDMS chips are hydrophobized by flowing a coating agent (Aquapel; PPG Industries) through the channels and subsequent drying with nitrogen. The design consists of a flow-focusing junction for droplet production and a coalescence chamber (29) at distances of 0.5 mm, 1 mm, 2 mm, 4 mm, or 8 mm from the production.

Fig. S4.

Design of the PMMA chip used for the experiment including the inlets for the two phases [fluorous (Left), aqueous phase (Center), and the outlet (Right)]. The channel height is 80 μm.

Fig. S5.

The design of the PDMS device for the coalescence experiments. The droplets are produced at the intersection of the aqueous and fluorous phase. Then, the droplets pass the coalescence chambers at different distances from the production and are collected at the outlets. The channel height is 40 μm, the channel diameter is 100 μm, and the width of the coalescence chamber is fivefold.

pH Calibration.

For the calibration of the experimental setup, we use 0.1 M HCl and 0.1 M NaOH (Sigma-Aldrich) to change the pH of the PBS solution to 5.46, 5.70, 5.84, 6.04, 6.31, 6.72, 7.10, 7.31, 7.66, 7.94, and 8.05, measured with a pH meter (Orion, Star A121; Thermo Scientific), pH electrode (pH-Einstabmesskette N64; SI Analytics), and Automatic Temperature Compensation Probe (8-pin stainless steel MD connector; Thermo Scientific). For the titration of the PBS solution, a titer of 1 mol of HCl (36.461 g of HCl; FIXANAL; Fluka Analytical) is diluted with Millipore water (Milli-Q Advantage A10; Merck Millipore) to obtain a solution of 0.1 M HCl. The error bars of the pH inside the droplets result from the extrema obtained from the calibration. In addition, we measure the fluorescence of the SNARF-1 solution for a series of pH (Fig. S7) on a home-built fluorescence bench (Ocean Optics spectrometer). We confirm that the ratio of fluorescence at 647 nm and 580 nm is pH-dependent. Because the exact ratio depends on the optical system used, the fluorescence measurement is performed on-chip with a surfactant solution at low concentration (0.02 mM) and an aqueous solutions with the different pH mentioned above.

Fig. S7.

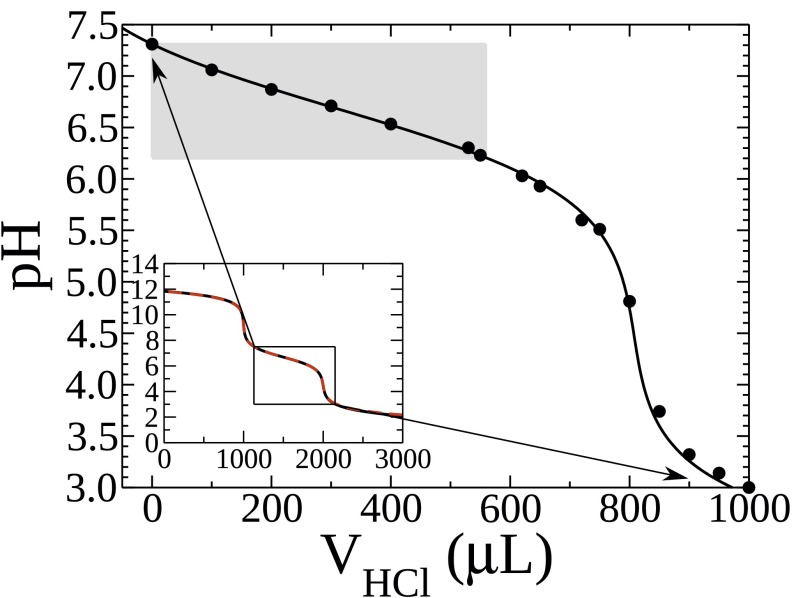
pH change with addition of HCl: titration (black circles) and calculation with (black line) and without (red line) dilution. The gray shaded area is accessible in our droplet-based microfluidic experiment.

Change of Proton Concentration with pH Change.

We titrate the phosphoric acid (0.1 M, $1\times$ PBS) solution with the titer of 0.1 M HCl (Fig. S7, black circles). Additionally, we calculate the change of pH (Fig. S7, black line) using the dissociation constants (pK_a) of the three equilibria of the triprotic phosphoric acid: 2.61, 7.21, and 12.62 at 25° C (40, 41). In an experiment, a titration is performed by adding a second solution. Thus, dilution of the original solution is inevitable. Within the droplet-based microfluidic experiment, though, the acid adsorbs to the interface and only protons are added into the aqueous solution. Therefore, no dilution takes place. Thus, we perform the calculation for the pH change as before, this time assuming that no dilution takes place (Fig. S7, red line) (40, 41). We then use these values (area accessible with our droplet-based microfluidic experiment: Fig. S7, gray shaded area) to calculate the amount of protons added to the droplets for the measured pH change (Fig. 1E).

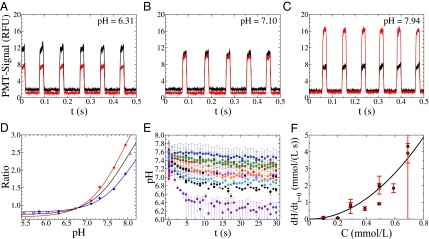
Fig. 1.

(A–C) Signal of the different photomultipliers at higher (647 nm, red line) and lower (580 nm, black line) wavelength for a pH of the aqueous phase of 6.31 (A), 7.10 (B), and 7.94 (C). (D) Calibration of the ratio of the fluorescent signals in relation to the pH of the original solution [repetitions (red and blue) and mean (black)]. (E) pH change with time for surfactant concentrations of 0.05 mM (blue), 0.10 mM (red), 0.20 mM (green), 0.29 mM (pink), 0.39 mM (orange), 0.49 mM (black), 0.59 mM (light blue), and 0.69 mM (purple). The error bars show the uncertainty due to the calibration of the ratio of the signals versus the pH. (F) Speed of the reaction at time 0 for the different concentrations of surfactant used. The error bars correspond to the uncertainty on the fitting parameter (SI Text and Fig. S8).

Fitting Procedures and Error Bars.

The data presented in Fig. 1F are obtained from the second-order kinetics fit of the data (Fig. 3). The initial slope is obtained as ${dH/dt|}_{t=0}=\mathrm{\Delta }{H}_{eq}/\tau$. (Note that fitting with a first-order kinetics also gives a quadratic dependence on C that, in this case, is not consistent with a first-order model, as discussed above.) To discriminate between the models, we compare the fits of the raw data using the exponential and the second-order fit (the example given here is dataset in Fig. 3H):

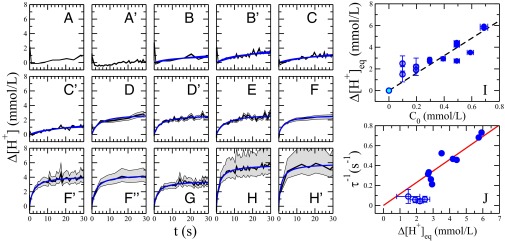
Fig. 3.

(A–H) Change of proton concentration inside the aqueous droplet with time using different concentrations of surfactant (carboxylic acid; Krytox) in the fluorous phase: 0.05 mM (A), 0.10 mM (B), 0.20 mM (C), 0.29 mM (D), 0.39 mM (E), 0.49 mM (F), 0.59 mM (G), and 0.69 mM (H), with ′ and ′′ representing repetitions of the same experimental condition. The black lines show the data calculated from the mean calibration curve with the gray shaded areas relating to the maximum and minimum calibration curves (Fig. 1D). (I) Fitted equilibrium change of proton concentrations ($\mathrm{\Delta }{\left[H^{+}\right]}_{eq}$; fitted values) for all concentrations of surfactant used. The light blue symbol is set to zero because no pH change takes place when no acidic surfactant is present. (J) Fitted ${\tau }^{-1}$ for all concentrations of surfactant. (I and J) The fitting of the data of the small concentrations (B and C) is less confident because the pH change is very small. Thus, the fitting value of $\mathrm{\Delta }{\left[H^{+}\right]}_{eq}$ is varied manually to obtain a range of fits.

First-order model:

$$f\left(t\right)=A\left(1-\text{exp}\left(-Bt\right)\right),$$ [S4]

where the fitting parameters are A and B. A is $\mathrm{\Delta }{\left[H\right]}_{eq}^{+}$, B is ${\tau }^{-1}$ and the initial slope is $AB$. Second-order model:

$$f\left(t\right)=A\frac{Bt}{1+Bt},$$ [S5]

where the fitting parameters are A and B. A is $\mathrm{\Delta }{\left[H\right]}_{eq}^{+}$, B is ${\tau }^{-1}$, and the initial slope is $AB$.

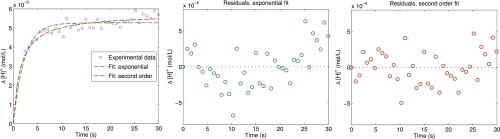
The fits of the data and the analysis of the residuals distribution are displayed in Fig. S8. The comparison of the residuals [i.e., the difference between the experimental data and the fit (Fig. 1F)] shows that the second-order model better models the results. The residuals of the exponential fit are correlated (for example, almost all of the points between 4 s and 16.5 s are negative), whereas the residuals are more random (and, in particular, the sign of two successive points is less correlated) for the second-order fit. This analysis shows that the second-order fit is better and confirms the self-consistency of the model. We have now plotted the data of Fig. 1F with error bars coming from the fitting procedure: the error bar in the measurement therefore comes from the reliability of the fit itself assessed using the bootstrapping method (42).

Fig. S8.

Exponential and second-order fits. (Left) Example of the dataset of Fig. 3H. (Center and Right) Residuals of the exponential fit (Center) and residuals of the second-order fit (Right). The data presented in Fig. 1F are obtained using a fitting procedure with a second-order model that is self-consistent and more reliably fits the data.

Molar Mass of Surfactant.

Methods.

MS is measured in the positive range ($m/z$ 600.00–4,000.00) using a LTQ XL mass spectrometer (Thermo Fisher). ESI is used in combination with an ion trap to determine the mean molar mass in profile mode. To compare the accuracy of the molar mass determination, we use NMR spectroscopy. We prepare a solution of 1:1 (wt/wt) of KrytoxFSL in the solvent Novec7500 containing 10% (wt/wt) chloroform-d₁ (99.8%, 5 × 1 mL; Deutero GmbH); 1D [¹H] NMR experiments are recorded at 25° C on a Bruker Avance 400-MHz spectrometer using 16,000 points and 256 scans with spectral widths of 4,006 Hz.

Results.

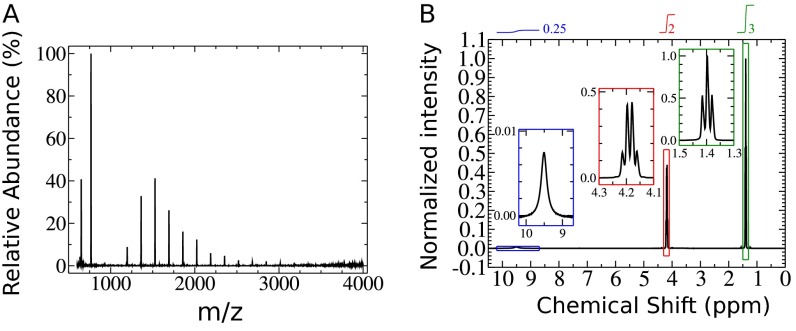
The molar mass is determined using ESI-MS and [¹H] NMR spectroscopy. Assuming, all of the peaks visible in the mass spectrum (Fig. S6A) contain a carboxylic end group, the molar mass of the KrytoxFSL is 1,634 g/mol. To confirm this observation, the [¹H] NMR spectrum is measured (Fig. S6B) to elucidate the structure and determine the relative amount of carboxylic acid groups. The proton of the carboxylic acid shows a singlet with a chemical shift δ of 9.5 ppm (43). On the other hand, the ethoxy group shows a triplet and a quartet with chemical shifts δ centered at 1.4 and 4.18, respectively. The singlet has an integral of $0.25\pm 0.01$ compared with the triplet and quartet with integrals of 3 and $2\pm 0.03$, respectively. Taking the molar mass of the solvent Novec7500 (414 g/mol) and the mass ratio of the two components into account, the determined molar mass is $\mathrm{1,659}\pm 67$ g/mol. Thus, the mean value of the determined molar mass by both methods (NMR and ESI) is 1,646 g/mol. The error in the determination of the molar mass is assumed to be 67 g/mol, referring to the error in the analysis of the NMR data.

Fig. S6.

Determination of the molar mass of the carboxylic acid Krytox used in all experiments. (A) ESI-MS spectrum of Krytox. (B) [¹H] NMR of a solution of 1:1 (wt/wt) of Krytox and Novec7500. To obtain the molar mass, the integrals of the triplet and the quartet from the ethoxy groups are related to the integral of the singlet from the carboxylic end group.

Coverage of the Interface.

To relate the adsorption constant $k_{ads}$ from the pH experiments to the coverage of the interface, and thus the coalescence data, we reuse Eq. 3:

$$\frac{1}{2}\frac{d\mathrm{\Gamma }}{dt}=k_{ads}{C}_0^2\left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right)-k_{des}\mathrm{\Gamma }.$$

Integration gives us

$$\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{\infty }}=\frac{k_{ads}{C}_0^2}{k_{ads}{C}_0^2+k_{des}}\cdot \left(1-e^{-2\left(k_{ads}{C}_0^2+k_{des}\right)\cdot t}\right).$$ [S6]

In the coalescence experiments, the flow velocity U and the distance from the production of the droplets L define the time $t=L/U$. Thus,

$$\frac{L}{U}{C}_0^2=-\frac{1}{2\cdot k_{ads}}\cdot \frac{{\mathrm{\Gamma }}_{eq}}{{\mathrm{\Gamma }}_{\infty }}\hspace{0.17em}\text{ln}\left(1-\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{eq}}\right).$$ [S7]

Above the CMC, we obtain

$$\frac{{\mathrm{\Gamma }}_{eq}}{{\mathrm{\Gamma }}_{\infty }}=\text{constant}\sim 1$$ [S8]

$$\frac{L}{U}{C}_0^2=-\frac{1}{2\cdot k_{ads}}\text{ln}\left(1-\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{eq}^{CMC}}\right),$$ [S9]

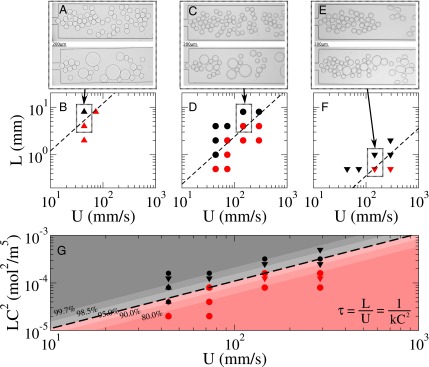
with the equilibrium coverage for the CMC, ${\mathrm{\Gamma }}_{eq}^{CMC}$. We obtain the value $L{C}_0^2/U$ (Eq. S9) from the coalescence experiments, which is the slope of the transition from unstable to stable droplets (Fig. 4). We obtain the iso-$\mathrm{\Gamma }$ lines displayed in Fig. 4 from Eq. S9.

Fig. 4.

Coalescence experiments at different distances from the production of droplets L and different speeds U. Stable (black) and unstable (red) droplets are produced at different concentration C of the surfactant [0.10 mM (B), 0.20 mM (D), and 0.49 mM (F); the droplets are stable if less than 1.5% of the droplets coalesce]. The corresponding images are shown in A, C, and E. Depending on the concentration of surfactant, the transition from stable to unstable interfaces takes place at different times t [dashed lines: $t=L/U=0.12$ s (B), $t=0.024$ s (D), and $t=0.0036$ s (F)]. (G) The data from B, D, and F scale linear with $L{C}^2=0.0011$ s mol²/m⁻⁶ × U (dashed line). The different symbols refer to the different concentrations (related to the symbols in B, D, and F). The coverage $\mathrm{\Gamma }/{\mathrm{\Gamma }}_{eq}^{CMC}$ of the interface for different values between 80.0% and 99.7% is represented by the lines of iso-$\mathrm{\Gamma }$ (Eq. 7).

Timescales of Adsorption.

The kinetics of adsorption are not described by a simple Langmuir isotherm but by a second-order reaction. Thus, we recalculate the cutoff radius between the kinetic-limited and the transport-limited adsorption by considering the two governing timescales, which describe the kinetics of adsorption of the first monolayer (i.e., the coalescence experiments) and the transport toward the interface (governed by convection).

First, we obtain the timescale for the transport at $t=0$, which is described using a typical height of the mass boundary layer $\delta =R/P{e}^{1/2}$. The Péclet number $Pe=d\times U/D$ is defined using the diameter of the droplet d (radius R), the speed of the droplet U, and the diffusion coefficient D. With the diameter of the droplets $d=70$ μm, a typical diffusion coefficient $D=5\times {10}^{-10}$ m²s⁻¹, and a typical speed of the droplets $U=100$ mm ${\text{s}}^{-1}$, a timescale for the transient regime (44)

$${\tau }_t=\frac{{\delta }^2}{D}=\frac{R}{2U}=175\hspace{0.17em}\mu \text{s}$$ [S10]

is obtained.

The initial variation of the coverage at the interface for a kinetic limited adsorption is

$$I_{kin}=\frac{d\mathrm{\Gamma }}{dt}={\frac{V}{S}\frac{d\left[{\text{H}}^{+}\right]}{dt}|}_{t=0}=2k_{ads}{C}_0^2{\mathrm{\Gamma }}_{\infty },$$ [S11]

which provides a timescale of

$${\tau }_{kin}=\frac{{\mathrm{\Gamma }}_{\infty }}{I_{kin}}=9\hspace{0.17em}\text{ms}$$ [S12]

using $k_{ads}=1.4\times {10}^3$ s⁻¹ m⁶ mol⁻², a typical concentration $C_0=0.2$ mM, and the maximum interfacial coverage ${\mathrm{\Gamma }}_{\infty }=8\times {10}^{-6}$ mol s⁻².

The process at very short times (at $t\sim 0$) is limited by the adsorption process. At times $t>0$, the interface is partially covered and a concentration gradient is established. Because convection is prevalent, the transport through the bulk is calculated using the Sherwood number $Sh$, the dimensions of the channel height $h=40$ μm, and the channel width $w=100$ μm (28). The Sherwood number depends on the geometry of the channels and the rigidity of the interface. Thus, applying the definition of Mikaelian et al. (28), we obtain only a rough estimate with values ranging from 47 to 87 with a mean of a $Sh=67$, which is used in the following. The initial change in the interfacial coverage for a transport limited regime is described by

$$I_{trans}=\frac{d\mathrm{\Gamma }}{dt}={\frac{V}{S}\frac{d\left[{\text{H}}^{+}\right]}{dt}|}_{t=0}=2ShD\frac{C}{R},$$ [S13]

with a timescale for the transport process of

$${\tau }_{trans}=\frac{{\mathrm{\Gamma }}_{\infty }}{I_{trans}}=21\hspace{0.17em}\text{ms}.$$ [S14]

At short times, the change in interfacial coverage due to a transfer limited adsorption scales linearly with surfactant concentration (Eq. S13), which is not in accordance with the experimental results (Fig. 1F). Additionally, the two timescales ${\tau }_{trans}$ and ${\tau }_{kin}$ are only valid at short times (right after the transient regime) and are of similar order of magnitude. Due to the kinetic limited adsorption depending on the square of the concentration and the coverage of the interface, the timescale of the adsorption process increases much faster than the timescale of the transport process. Desorption increases this effect. The calculation of all timescales underlies uncertainties in the variables $Sh$, $k_{ads}$, D, and ${\mathrm{\Gamma }}_{\infty }$ and can only be evaluated as a rough estimation. The calculated values for ${\tau }_{trans}$ are in any case much smaller than the timescales of the pH variation. Even in the coalescence experiments, we clearly see that the adsorption process is limited by the kinetics of adsorption of the surfactant to the interface.

Microfluidic Systems for pH Measurement.

Microfabrication.

The microfluidic channels are milled into a PMMA plate with a height of 2 mm, a length of 60 mm, and a width of 25 mm. The channels are milled with an end mill cutter for channels of 100 μm in diameter (Fig. S4). The height of the channels after milling is 99 $\pm$ 3 μm. The length of the delay line of the microfluidic channel is 75 cm. The PMMA plate, including the channel, and another PMMA plate with the same dimensions are mechanically cleaned and ultrasonic-cleaned (5 min) while being immersed in 2-propanol (ACS reagent, $99.5$%; Sigma-Aldrich). After this step, we clean the plates twice using a Plasmacleaner (using air at 0.45 millibars, 30 s, 70%; Diener electronic; Pico). We then combine the two parts using a temperature-controlled press (5 kN at $100\mathrm{°}$ C for 40 min) (45). For stress minimization, the PMMA is cooled down slowly ($\sim$1 h). After this step, the channel height is reduced to $\sim 80$ μm. The mean width of the channels is 95.6 $\pm$ 4.2 μm. We connect the inlets and the outlet of the PMMA chip using nanoports (coned, 10–32, PEEK; Upchurch) and UV-curable glue (35261; Loctite), which is treated with UV light (365 nm; Polylux-PT; Dreve) for 30 min. We hydrophobize the device with a coating agent ($3\times 15$ min; Aquapel; PPG Industries) before drying with nitrogen.

Device operation.

The two phases are injected into the device using syringes [Gastight Series 1000, Hamilton (VWR); pump: neMESYS 29:1 (Cetoni)], which we connect to the device using polytetrafluoroethylene (PTFE) tubing [o.d., 1.07 mm; i.d., 0.56 mm; Fisher Scientific) and fittings [short headless nut (F-333Nx) with ferrule (F-142N), nanotight sleeve fluorinated ethylene propylene (F-252x); o.d., 1.59 mm; i.d., 1.07 mm; Upchurch]. We set the flow rates to 7.5 μL/min and 1.5 μL/min for the fluorous and aqueous phases, respectively.

Microfluidic Systems for Coalescence Analysis.

Microfabrication.

We use microfluidic channels from PDMS. We design a microfluidic device with a flow-focusing junction and a coalescence chamber (29) at distances of 0.5 mm, 1 mm, 2 mm, 4 mm, and 8 mm from the production of the droplets (Fig. S5). The polymer mask is printed by Selba S.A. (resolution, 50,800 dots per inch). We replicate the microfluidic channels in PDMS using standard soft-lithography techniques from a mold using SU-8 (36, 37). We punch the inlets and outlet using a Harris Unicore biopsy punch (0.75-mm diameter) before we bond the PDMS to a microscopy glass slide using oxygen plasma oxidation (as above, once only). We hydrophobize the microfluidic channels using Aquapel ($1\times 15$ min). The Teflon tubing and syringe pumps used are described above.

Device operation.

For these coalescence experiments, we use varying total flow rates from 10.5 μL/min to 70 μL/min and a flow rate ratio of $q=q_{fl}/q_{aq}=6$, with $q_{fl}$ and $q_{aq}$ being the flow rates of the fluorous and aqueous phase, respectively. The coalescence events were monitored using a microscope (Olympus IX71) with an attached high speed camera (Phantom v411; Vision Research). For each of the flow rates and surfactant solutions at different concentrations, we manually define whether coalescence occurs. The droplets are stable if less than 1.5% of the droplets coalesce.

Experimental Results

We produce water-in-oil emulsions in microfluidics by dispersing a PBS solution into a continuous fluorous phase. A pH-sensitive fluorophore is used to measure the pH inside the droplets at different positions (and therefore time) inside the microfluidic channel using a fluorescence setup (SI Text and Fig. S2). The ratio of fluorescence intensities increases with increasing pH (Fig. 1 A–C SI Text and Fig. S3), and the pH measurement is sensitive and reliable in the range between 6.2 and 7.8 (Fig. 1D) (30). We determine the change in pH with time (corresponding to the position on the chip) inside the aqueous droplets (with a radius $R\sim$ 80 μm) for the different concentrations of surfactants used (Fig. 1E). The error bars are related to the uncertainty of the calibrations, but each calibration curve shows the same trend (Fig. 1D). Because we consider only differences in pH, the errors become less crucial. At low surfactant concentration ($C=0.05$ mmol/L), the pH remains constant in time. For larger concentrations—here up to 0.69 mmol/L—the pH decreases by more than 1 unit with a typical timescale of the order of 1 s. Qualitatively, this variation of pH corresponds to the transfer of protons from the fluorous phase toward the aqueous phase (SI Text). Increasing the surfactant concentration in the fluorous phase has two effects: the pH decreases to a smaller equilibrium value, and the timescale of the process is shorter.

Fig. S3.

In bulk, the dye SNARF-1, diluted inside PBS solutions with different pH values, is excited with a green LED, and the fluorescence of the solutions is measured (see color coding). The orange and red shaded areas show the wavelengths reaching the two photomultipliers.

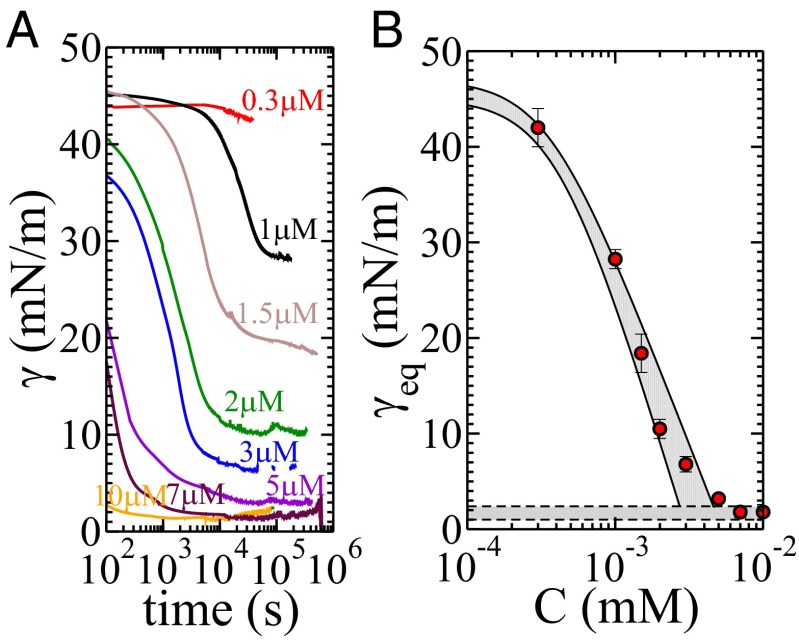
The equilibrium pH is a function of the surfactant concentration: we can conclude that the proton transfer is not limited by the adsorption of the first monolayer to the interface. To determine the surfactant coverage, we measure the critical micellar concentration (CMC). We perform surface-tension measurements using a Wilhelmy plate tensiometer for several surfactant concentrations; the results are displayed in Fig. 2B. Indeed, all pH measurements are obtained above the CMC: the equilibrium coverage is constant for all considered concentrations. Therefore, the additional exchange of protons occurs while the interface is at equilibrium coverage, through the desorption of the surfactant and the subsequent adsorption of other surfactant molecules. The surfactant desorption involves the extraction of a counter ion from the aqueous phase to guarantee electroneutrality. Considering the typical ion concentrations in the droplets, the extraction of the ${\text{Na}}^{+}$ ions is the most likely event. The overall process can therefore be modeled as

$$\begin{array}{c}{\text{KryCOOH}}_{\text{fl}}\rightleftharpoons {\text{KryCOO}}_{\text{int}}^{\mathrm{-}}+{\text{H}}_{\text{aq}}^{+}\\ {\text{Na}}_{\text{aq}}^{+}+{\text{KryCOO}}_{\text{int}}^{-}\rightleftharpoons {\text{KryCOONa}}_{\text{fl}},\end{array}$$

where $fl$ refers to the oil phase, $aq$ to the aqueous phase, and $int$ to the interface. This model relies on the assumption that the dissociation of the carboxylic acid and the diffusion of the protons (31) inside the aqueous phase are instantaneous compared with the adsorption of the surfactant.

Fig. 2.

(A) Surface tension data with time for different concentrations. (B) Equilibrium surface tension for all concentrations fitting Eq. 6: ${\gamma }_0$ = 46 $\pm$ 1 mN/m; ${\mathrm{\Gamma }}_{\infty }$ = 8.0 $\pm$ 1.0 μmol/m²; κ = 7 $\pm$ 1 $\times$ 10⁶ m⁶/mol²; CMC = 4 $\pm$ 1 μM; ${\mathrm{\Gamma }}_{eq}^{CMC}=$ 7.9 μmol/m².

Failure of the Langmuir Adsorption Model.

We now quantitatively analyze the reaction rate, the equilibrium of the reaction and the order of the reaction. The initial reaction rate is not a linear relationship with surfactant concentration (Fig. 1F). For a Langmuir process of adsorption on a droplet of radius R, we relate the rate of adsorption to the rate of pH change through the surfactant mass conservation at the interface, leading to (SI Text):

$$\frac{V}{S}\frac{d\left[H^{+}\right]}{dt}=k_{ads}\left(C_0-\frac{1}{q}\left[H^{+}\right]\right)\times \left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right),$$ [1]

where V and S are the volume and surface area of the droplet, respectively, $C_0$ is the initial concentration of the surfactant, and q is the volumetric ratio between the fluorous and the aqueous phase that accounts for dilution effects: were all ${\text{H}}^{+}$ transferred from the oil to the water, the concentration in the water would simply be $q{C}_0$. When the timescales for surface adsorption and pH change are well-separated, the relaxation of the pH in the droplet is exponential and the initial velocity ${d\left[H^{+}\right]/dt|}_{t=0}$ in the droplet is expected to be linear in surfactant concentration (Eq. 1 and SI Text). Experimentally, we find a square dependence of the initial rate, indicating that the adsorption process does not follow a simple Langmuir process (Fig. 1F). The dependence of the initial reaction rate with the concentration requires the modeling of adsorption with a second-order reaction. At this stage, the microscopic details leading to this isotherm remain elusive.

Construction of the Second-Order Adsorption Model.

We construct a consistent model for the adsorption process and for the pH variation based on our experimental results. We propose a rate equation where the rate of proton transfer is proportional to the square of the surfactant concentration:

$$\frac{1}{2}\frac{V}{S}\frac{d\left[H^{+}\right]}{dt}=k_{ads}{\left(C_0-\frac{1}{q}\left[H^{+}\right]\right)}^2\times \left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right).$$ [2]

For consistency in the model, and because there is no physical reason to assume that the ${\text{H}}^{+}$ transfer is independent of the adsorption of surfactant, the straightforward model for adsorption with the adsorption and desorption constant, $k_{ads}$ and $k_{des}$, respectively, is

$$\frac{1}{2}\frac{d\mathrm{\Gamma }}{dt}=k_{ads}{C}_0^2\times \left({\mathrm{\Gamma }}_{\infty }-\mathrm{\Gamma }\right)-k_{des}\mathrm{\Gamma }.$$ [3]

Using the assumption that we have a separation of timescales between the adsorption process and the pH change in the droplet, the interface is quickly reaching equilibrium (denoted as eq), whereas the pH is changing slowly. Therefore, as previously, the pH change occurs for $\mathrm{\Gamma }={\mathrm{\Gamma }}_{eq}$. Eq. 2 is therefore a second-order kinetic law leading to the ${\text{H}}^{+}$ variation as

$$\begin{array}{l}\frac{\mathrm{\Delta }\left[H^{+}\right]}{\mathrm{\Delta }{\left[H^{+}\right]}_{eq}}=\frac{t/{\tau }_{pH}}{1+t/{\tau }_{pH}}\\ \text{with}\hspace{0.17em}\hspace{0.17em}{\tau }_{pH}=\frac{qR}{6k_{ads}{C}_0\left({\mathrm{\Gamma }}_{\infty }-{\mathrm{\Gamma }}_{eq}\right)}.\end{array}$$ [4]

To quantitatively check the validity of our model, we have fitted all experimental data with Eq. 4 using $\mathrm{\Delta }{\left[H^{+}\right]}_{eq}$ and ${\tau }_{pH}$ as fitting parameters (Fig. 3 A–H). First, we find that the equilibrium value $\mathrm{\Delta }{\left[H^{+}\right]}_{eq}$ scales linearly with the concentration of surfactant (Fig. 3I). This result implies the full transfer of protons from the oil to the droplet, while the interface is at equilibrium. Second, we find that the timescale τ of the process scales as $1/C_0$, as expected for a second-order process (Fig. 3J). Combining these results, we recover that the initial speed of the reaction scales as $C_0^2$. In principle, for a full transfer of protons from the oil to the droplet, we expect $\mathrm{\Delta }{\left[H^{+}\right]}_{eq}=q{C}_0$, where q is the ratio of the oil-to-water volume fractions. Experimentally, we find that this ratio is ∼8, whereas we impose a ratio of flow rates of 5. The error might come from the difficulty to determine accurately the concentration of the carboxylic acid polymer (SI Text). However, the experimental data are in good quantitative agreement with our model.

Bulk Equilibrium Data.

The measurement of ${\tau }_{pH}$ as a function of $C_0$ provides a means to determine $k_{ads}$, provided that both quantities ${\mathrm{\Gamma }}_{\infty }$ and ${\mathrm{\Gamma }}_{eq}$ are known. These two quantities are equilibrium quantities and are measurable using standard characterization techniques (Fig. 2). Using the standard Gibbs isotherm, these measurements provide the values of ${\mathrm{\Gamma }}_{eq}\left(C\right),{\mathrm{\Gamma }}_{\infty }$ and, in addition, the CMC, above which the interfacial coverage stays constant. Based on our model, we fit the experimental data with a second-order model of the form

$${\mathrm{\Gamma }}_{eq}={\mathrm{\Gamma }}_{\infty }\frac{\kappa C^2}{1+\kappa C^2}$$ [5]

$${\gamma }_{eq}={\gamma }_0+\frac{RT{\mathrm{\Gamma }}_{\infty }}{2}\text{ln}\left(1+\kappa C^2\right).$$ [6]

We here obtain ${\mathrm{\Gamma }}_{\infty }$ = 8.0 $\pm$ 1.0 μmol/m², κ = 7 $\pm$ 1 $\times$ 10⁶ m⁶ mol⁻², and a CMC of $C_{CMC}$ = 4 $\pm$ 1 mmol/m³. These values lead to the determination of $k_{ads}$ = (1.4 $\pm$ 1) $\times$ 10³ s⁻¹ m⁶ mol⁻². We note that the value of ${\mathrm{\Gamma }}_{\infty }$ corresponds to a value obtained for small head groups, compatible with our molecule and other data from the literature for fluorinated surfactants (32). It should be noted that we used our model for consistency. However, a standard Langmuir isotherm would provide the same value for ${\mathrm{\Gamma }}_{\infty }$ and also shows that—contrary to our microfluidic method—equilibrium measurements do not provide a means to discriminate possible isotherm models. Our experiments provide a measurement of the adsorption constants, provided that the equilibrium is independently determined through standard measurements. The same isotherm model is used to describe the equilibrium and the kinetics of pH change in the droplet, which enables the straightforward use of the equilibrium constants in the microfluidic experiments in a consistent manner.

Impact on Coalescence.

In the previous sections, we have measured the adsorption rate using pH measurement on timescales of a several seconds. One of the conclusions is that the timescale of the adsorption of the first monolayer of surfactant is fast, of the order of 10 ms. In the following, we compare this timescale and the timescale required to stabilize an emulsion against coalescence. These measurements of coalescence are obtained during the very early kinetics $(t<200$ ms), which is consistent with the timescale of the adsorption of the first monolayer. The quantitative results are discussed in the following. For these experiments, we use the same fluorous and aqueous phases as above, to determine the transition between stable and unstable emulsions in flow, based on our previous analysis (29). Several chips were produced in which droplets flow without contact in a channel of length L. In these chips, we vary the surfactant concentration and the droplet speed U to change the incubation time of the droplets ($t=L/U$) with a radius $R\sim$ 35 μm. The critical parameter that controls the separation between stable and unstable emulsions is the parameter $L{C}^2$ (29). Here, this parameter is proportional to the speed of the droplet U (Fig. 4). Therefore, the coalescence experiments lead to the definition of a timescale for the stabilization of the interface of the form: $\tau =1/\left(k{C}^2\right)$, where $k\sim$ 909 s⁻¹ m⁶ mol⁻². We can reuse the rate equation for $\mathrm{\Gamma }$ (Eq. 3) to compare the stabilization time of the interface during microfluidic emulsification to the adsorption process. Rewriting Eq. 3, the parameter $L{C}_0^2/U$ is expressed above the CMC as a function of the adsorption rate constant $k_{ads}$, the equilibrium interfacial coverage at the CMC ${\mathrm{\Gamma }}_{eq}^{CMC}$ and ${\mathrm{\Gamma }}_{\infty }$ (Fig. 2 and SI Text):

$$\frac{L}{U}{C}_0^2\approx -\frac{1}{2\cdot k_{ads}}\text{ln}\left(1-\frac{\mathrm{\Gamma }}{{\mathrm{\Gamma }}_{eq}^{CMC}}\right).$$ [7]

We can now determine $\mathrm{\Gamma }$ from the parameter $L{C}^2/U$. Fig. 4G shows the lines of iso-$\mathrm{\Gamma }$ superimposed to the coalescence data: the stabilization of the emulsion occurs when the coverage of the interface is close to its equilibrium coverage (in the range of 90–95%).

Discussion

The values extracted from the pH measurement on-chip provide a quantitative description of the kinetics of stabilization and of transfer across the interface in a unified picture. The value of $k_{ads}$ is obtained from the pH measurements for a process occurring at a timescale of several seconds. The value is, however, directly usable to predict the short-time kinetics of surfactant adsorption in coalescence experiments, where the timescale is now one to two orders of magnitude smaller (of order tens of milliseconds). This comparison implied that the coverage stabilizing emulsions in microchannels is close to the equilibrium coverage. Because all of our experiments were performed above the CMC of the surfactant, these results are consistent with the experimental observations that emulsions in microfluidics are hardly stabilized with surfactant concentrations below the CMC (i.e., for equilibrium coverages much smaller than 90%). The experiments show that the adsorption of the first monolayer of surfactant as well as the change of pH are limited by the second-order adsorption kinetics. Thus, the mass transport occurs at a smaller timescale. The timescale for the transport of the surfactant to a clean interface is of the order of tens of milliseconds using an $Sh$ of 47–87 (SI Text) (28). The calculated timescales of mass transfer and adsorption are of the same order of magnitude. These theoretical timescales give only a rough estimate as a result of uncertainties in the diffusion coefficient as well as the adsorption coefficient. The experiments however are fully consistent with a kinetic-limited model. The practical consequence for emulsification in microfluidics is that although channels can be designed to give enough time for the surfactant to adsorb at the interface, the chemical binding to the interface is the key parameter determining the emulsion stabilization timescale.

An important consequence of our analysis is that we also model the kinetics of equilibration of the chemical potential across the interface (33–35). The transfer of protons toward the aqueous droplet is balanced by the extraction of a counter ion from the droplet to the oil. We have shown recently that no barrier to partitioning could be measured at the timescale of about 45 s (17): the timescale for the establishment of the chemical equilibrium across the interface is therefore smaller. Here we show that the equilibrium is reached in a couple of seconds at most ($\sim$5 s; Fig. 1), for a process involving the full transfer of the ions from one phase to the other. We can now quantify the rate of extraction of ions. According to Eq. 3, if we consider the transport of the counter ion ${\text{Na}}^{+}$ from the droplet toward the oil at steady state, the timescale of the process will simply be the same as the pH-variation timescale. Therefore, we can expect equilibration of positively charged ions to occur as fast as a couple of seconds. This timescale could be considered as a limit for small organic molecule, as observed in previous experiments (17), and this effect has to be taken into consideration when optimizing surfactant formulations. Finally, our method is currently limited to the analysis of carboxylic acid surfactants. However, the transport of organic molecules by surfactant molecules could in principle be used to generalize the method to obtain a universal method of adsorption/desorption constants using an appropriate choice of the pair surfactant/fluorescent dye.

Conclusion

We have designed a microfluidic method to measure the dynamics of adsorption of surfactants to the droplet interface based on droplet pH. With this method, the adsorption kinetics is measured directly, because the transport in the bulk is fast due to the small size of the droplet and the convection associated with the droplet motion in a microchannel. The adsorption process—modeled as a second-order Langmuir process—determines the timescale of the bulk equilibration of the pH. With our results, we make a quantitative link between the process of adsorption/desorption and the kinetics of partitioning, which are two problems of relevance in emulsification. These processes can indeed be described within the same framework. In brief, for our surfactant, for all processes occurring at timescales larger than 1 s, we can safely assume that phase partitioning across the interface is established at all times. In contrast, for processes shorter than 1 s, the dynamics of the chemical equilibration has to be considered. In the general case, the timescale of chemical equilibration is controlled by the ratio of a typical dimension, the radius of the droplet R, and a typical speed $k_{ads}C\left({\mathrm{\Gamma }}_{\infty }-{\mathrm{\Gamma }}_{eq}\right)$. In our experiments, the timescale is at least one to two orders of magnitude larger than the kinetics of equilibration of the surfactant layer itself, of order ${\left(k_{ads}{C}^2+k_{des}\right)}^{-1}.$ This latter timescale corresponds to the time required to cover 90% of the interface, thereby preventing droplet coalescence.

Materials and Methods

Microfluidic Device Fabrication.

We manufacture microfluidic devices in poly(methyl methacrylate) (PMMA) and polydimethylsiloxane (PDMS) (SI Text and Figs. S4 and S5). The PMMA microfluidic devices are used for the pH measurements. The PDMS device for the coalescence experiments (Fig. S5) is produced using standard photo- and soft-lithography (36, 37).

Device Operation.

Liquids are injected into the channels through glass syringes (Hamilton) connected to the chips via tubings. The syringes are actuated by syringe pumps (Nemesys; Cetoni) at constant speed. For the pH-change experiments, the flow rates are fixed to 7.5 μL/min and 1.5 μL/min for the oil phase and aqueous phase, respectively. For the coalescence experiments, the total flow rates are varied from 10.5 μL/min to 70 μL/min with a flow rate ratio of $q=q_{fl}/q_{aq}=6$, where $q_{fl}$ and $q_{aq}$ are the flow rates of the fluorous and aqueous phase, respectively. In all cases, the droplets are produced in the dripping regime. The experiments are performed at room temperature (23 $\pm$ 1 °C).

Emulsification System.

We produce water-in-oil emulsions using an aqueous dispersed phase and a fluorous continuous phase. The aqueous phase consists of a buffer solution (9.5 mM PBS, 0.146 M sodium chloride, pH $\sim$ 7.3; Sigma-Aldrich) with the pH-sensitive dye SNARF-1 (30) (Life Technologies) at 10 μM. The continuous phase contains the fluorous solvent [3-ethoxyperfluoro(2-methylhexane); Novec7500; 3M] and the acidic surfactant (PFPE with a carboxylic head group; KrytoxFSL; DuPont) with varying concentrations of 0.01 mM, 0.02 mM, 0.03 mM, 0.05 mM, 0.10 mM, 0.20 mM, 0.29 mM, 0.39 mM, 0.49 mM, 0.59 mM, 0.69 mM, and 2.0 mM. The mean molar mass of KrytoxFSL is 1,646 g/mol $\pm$ 67 g/mol, as determined using electrospray ionization MS (ESI-MS) and [¹H] NMR spectroscopy (Fig. S6).

On-Chip Fluorescence Measurement and Data Processing.

We use a laser-induced fluorescence setup as adapted from Baret et al. (38) to determine the pH inside the droplets. Details on the optical system are provided in Fig. S2.

pH Calibration.

We use solutions of PBS with known pH values of 5.46, 5.70, 5.84, 6.04, 6.31, 6.72, 7.10, 7.31, 7.66, 7.94, and 8.05. The titration curve of the PBS solution is measured using a standard pH meter (Orion, Star121; Thermo Scientific) (SI Text and Fig. S7). The variations in the calibrations are averaged over two runs, which determines the error bar in the calibration. The calibration is performed where the droplets have reached this terminal velocity (9.8 mm $\widehat{=}$ 0.5 s after production) (39). We use the same flow rates for all experiments to avoid bias (39).

On-Chip Time-Dependent pH Measurements.

The kinetics of the pH change in droplet is measured by recording the ratio of droplet fluorescence $I_{647}/I_{580}$ at positions along the channel corresponding to different times given by the channels cross-section and the total flow rates.

Equilibrium Surface-Tension Measurement.

Time-dependent surface tensions are measured at the oil–water interface using a Wilhelmy plate configuration (Wilhelmy plate platinum; wetted length, 39.24 mm; KSV-Nima LL, KN-ISR-2 Langmuir Trough; LOT-QuantumDesign). For all concentrations, the experiments are equilibrated over several hours at 25 °C. For the smallest concentration ($C=$ 0.3 μM), no equilibrium could be reached over 11 days.