Energy-efficient neural network chips approach human recognition capabilities

The dream to create novel computing hardware that captures aspects of brain computation has occupied the minds of researchers for over 50 y. Driving goals are to carry both the astounding energy efficiency of computations in neural networks of the brain and their learning capability into future generations of electronic hardware. A realization of this dream has now come one step closer, as reported by Esser et al. (1). The authors demonstrate that a very energy-efficient implementation of an artificial neural network (i.e., of a circuit that shares properties with networks of neurons in the brain) achieves almost the same performance as humans as shown on eight benchmark datasets for recognizing images and sounds. It had previously been shown that somewhat different types of deep artificial neural networks can do this, but these required power-hungry computing hardware, such as graphics processing units (2).

A characteristic feature of artificial neural networks is that they cannot be programmed in terms of instructions and variables, the way a traditional computer can. Rather, their computations are determined by a large set of numbers (parameters) that loosely correspond to the strengths (weights) of synapses between neurons in the brain and the excitabilities (biases) of neurons (see the parameters “w” and “b” in Fig. 1). Because these numbers have little meaning for humans, especially not in a large neural network, they are produced through an optimization algorithm that adjusts them in an iterative process. This process aims at minimizing the errors for a concrete computational task, such as classifying visual objects in natural scenes. The architectures and neuron models of artificial neural networks are usually chosen to maximize the performance of particular learning algorithms for particular tasks, and not to make the artificial neural network more similar to biological networks of neurons.

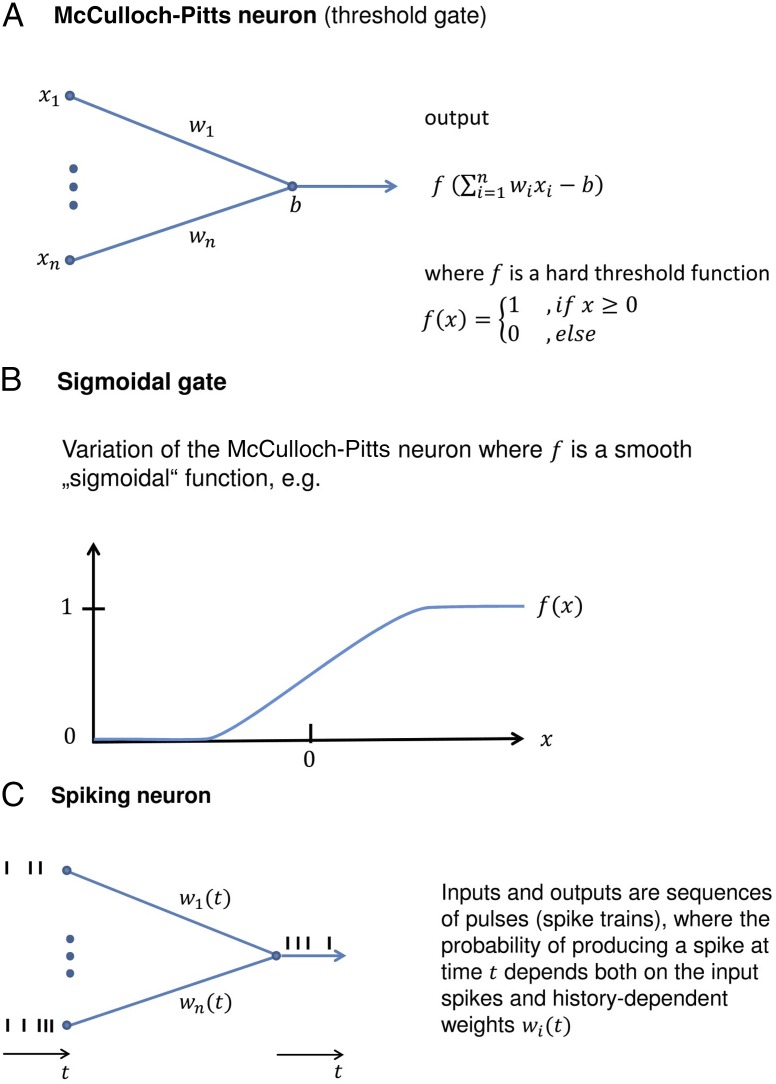
Fig. 1.

Neuron models for artificial and biological neural networks. (A) The oldest neuron model in artificial neural networks and computer science. It can be implemented very efficiently in hardware and is used for the results of Esser et al. (1). (B) The most common neuron model for applications of backprop in artificial neural networks. (C) A spiking neuron model, which reflects more aspects of neurons in the brain.

The first neural network models, proposed by McCulloch and Pitts (3), were actually designed to capture essential aspects of neural computation in the brain. The underlying neuron model (Fig. 1A) is today referred to as a McCulloch–Pitts neuron or threshold gate. However, it turned out to be difficult to design learning algorithms for networks consisting of several layers of such neurons. This difficulty was caused by the jump of the activation function f between binary outputs 0 and 1. Therefore, this neuron model was replaced in the 1980s (4) by a sigmoidal neuron model with analog outputs (Fig. 1B), where the activation function f interpolates in a smooth differentiable manner between 0 and 1. The simplest and still most commonly used learning algorithm for this type of neural network is a gradient-descent optimization, which minimizes the errors of the network outputs for a given task. If the activation function of each neuron is differentiable, one can also compute via the chain rule for neurons that do not directly produce a network output, how their parameters should be changed to reduce the errors at the network output. The resulting layerwise application of the chain rule, starting at the output neurons and moving back toward the input layer, is the famous “backprop” (backward propagation of errors) learning algorithm. The transition of the neuron model from A to B in Fig. 1 is actually also meaningful from the perspective of modeling biological neurons. These neurons emit sequences of pulses [called action potentials or spikes (Fig. 1C)], which they send via axons and synaptic connections to other neurons. Because each spike is an all-or-none event, it shares some features with the binary output of a McCulloch–Pitts neuron. But neurons in the brain tend to emit spikes in an unreliable manner. The probability of producing a spike at a given time depends, in standard models for a biological neuron, on its synaptic inputs in a smooth manner.

Most approaches for emulating neurons in energy-efficient hardware have favored neuron models with discrete outputs, such as the McCulloch–Pitts neuron (Fig. 1A) or the spiking neuron (Fig. 1C). Both of these neurons can be emulated on the TrueNorth chip of IBM (5). The breakthrough reported in Esser et al. (1) arose from the discovery that the parameters of networks of McCulloch–Pitts neurons can also be determined through a variation of the backprop algorithm, despite the nondifferentiability. This discovery came on the shoulders of a better understanding of backprop and its variations. One important aspect of all learning algorithms is that it does not pay to fit their parameters too well to a given set of training examples (i.e., target input/output pairs for the network). This becomes understandable if one takes into account that one does not want the neural network to perform well just on a fixed set of training examples, but also on similar but new examples. For example in an application to visual object classification, one wants the learning algorithm to force the neural network to extract classification rules that also work for new images, rather than allow it to implement rote learning for the classification of images in the training set. This generalization capability is enhanced if one forces the network to compress the information that it receives through the training examples. One very successful type of information compression is characteristic for convolutional neural networks, which form an important subclass of artificial neural networks. There, one forces subsets of neurons to use the same parameters. This works especially well for tasks such as visual processing, where it makes sense to apply the same feature extraction to all patches of an image. The implementation of convolutional neural networks on the TrueNorth chip requires additional clever methods for dealing with the limited fan-in of its neurons, and for the conversion of multivalued sensory inputs to bits.

The learning algorithm of Esser et al. (1), which was independently discovered by Courbariaux and Bengio (6), applies another information compression trick proposed by Courbariaux et al. (7) and Esser et al. (8): after all iterations of the backprop algorithm are completed, one rounds the values of weights to just two or three values. Obviously, binary or ternary weights can be stored more efficiently on a chip than analog weights. The resulting loss in computational precision is balanced to some extent by enhanced generalization capability through this additional information compression. However, to make the backprop algorithm work one needs to store and update somewhere else precise analog weights during the iterative error reduction via gradient descent. Therefore, the learning process itself cannot be carried out on the chip in the approach of Esser et al. (1). Another clever trick from Courbariaux et al. (7) and Esser et al. (8) is used to make the results of this external backprop algorithm applicable to the McCulloch–Pitts neurons on the chip, despite the nondifferentiability of their activation function f: one replaces the true derivative of f, which has a singularity at 0, by the derivative of a virtual smooth activation function. The resulting learning process for large and deep networks of McCulloch–Pitts neurons works so well that Esser et al. (1) achieve close to state-of-the art performance on several difficult benchmark datasets for classifying visual or auditory inputs. In addition, the implementation on the TrueNorth chip is so energy-efficient that it can also be installed in mobile devices.

Apart from its obvious commercial significance, this achievement also throws new light on an old problem in the theory of computational complexity, more precisely on the computational power of threshold circuits, which is the common name for feedforward networks of McCulloch–Pitts neurons in theoretical computer science. When one started a few decades ago to analyze the computational power of different idealized circuit models for parallel computation, one realized that the inclusion of threshold gates—rather than just gates that compute AND, OR of arbitrarily many bits in one step—substantially increases their computational power. This finding provided a first hint that the summation of thousands of input pulses on the membrane of a biological neuron is a really powerful computation step. In fact, it has already turned out to be quite difficult to prove for a concrete function that it cannot be computed by polynomial size-threshold circuits of depth 2 with binary weights (9), and it is currently still conceivable that depth 3 circuits of this type can even solve problems that are complete for nondeterministic polynomial time (i.e., NP-complete). The results of Esser et al. (1) provide new evidence that the computational power of threshold circuits is in fact very large. In addition, their learning algorithm for threshold circuits provides the first principled way to approximately “program” threshold circuits for specific computational tasks. An interesting open question is whether one can reduce the fairly large depth of the resulting threshold circuits for concrete tasks similarly, as has been demonstrated for other types of deep neural networks (10).

The results of Esser et al. (1) also raise another scientific question: To what extent do artificial neural network models that can be efficiently implemented in current hardware capture computing and learning principles of networks of neurons in the brain? The TrueNorth chip can also be configured to emulate networks of a simple type of spiking neuron model that emits pulses in continuous time (Fig. 1C). However, at this point we do not have powerful learning algorithms for networks of spiking neurons, nor do we know which features of a spiking neuron enable brain-like computation and learning. The spike output of simple spiking neuron models depends deterministically on their synaptic input, whereas biological neurons behave like stochastic computing units. In addition, biological synapses and neurons should be thought of as temporal filters, whose current output does not only depend on their current input, but also on the recent history of their inputs. Furthermore the brain uses many genetically and physiologically different types of neurons and synapses that have more specialized filtering and plasticity properties. Synaptic connections between them form networks whose architecture differs in essential aspects from that of common deep artificial neural networks. These facts suggest that the organization of computations in networks of neurons in the brain is quite different from that in most types of currently considered artificial neural network models (11).

One important functional property of brain networks is that they can learn in an online manner, where new categories or training examples can be introduced at later stages of a learning process, without requiring a repetition of the whole learning process and a reproduction of previously used training examples. A learning algorithm like that in Esser et al. (1) cannot do that. However, many online learning methods have been developed in machine learning. Hence, online learning capability is a challenging but still feasible next goal for neuromorphic hardware. One possible implementation approach is to add a plasticity processor in a hybrid neuromorphic system (12).

The backprop algorithm is a supervised learning algorithm, where a teacher (supervisor) needs to provide for each training example the desired network output. This is needed to compute the error of the network output: that is, the difference between the desired and actual output. However, such extensive help from an internal teacher is likely to be quite rare in the brain. After all, if some neurons in the brain “know” already the target output for a computational task, the resulting learning process amounts to duplication of a capability, rather than to its emergence. Exceptions are specific types of learning tasks, such as the prediction of subsequent sensory stimuli. There the environment provides the required teacher, simply in the form of the actual subsequent sensory stimuli. A teacher is also available in the brain for predicting sensory input from one sensory modality in terms of inputs from other sensory modalities. But, for many types of tasks, the brain has to engage different types of learning methods that do not require a teacher, such as unsupervised and reward-based learning (13). These other learning methods will also become essential if one wants to enable larger and more versatile neuromorphic systems to acquire brain-like functional capabilities. We really would like to enable them to learn from observations and play, and to carry learned knowledge to new tasks.