Theory of prokaryotic genome evolution

Significance

Bacteria and archaea have small genomes with tightly packed protein-coding genes. Typically, this genome architecture is explained by “genome streamlining” (minimization) under selection for high replication rate. We developed a mathematical model of microbial evolution and tested it against extensive data from multiple genome comparisons to identify the key evolutionary forces. The results indicate that genome evolution is not governed by streamlining but rather, reflects the balance between the benefit of additional genes that diminishes with the genome size and the intrinsic preference for DNA deletion over acquisition. These results explain the observation that, in an apparent contradiction with the population genetic theory, microbes with large genomes reach higher abundance and are subject to stronger selection than small “streamlined” genomes.

Abstract

Bacteria and archaea typically possess small genomes that are tightly packed with protein-coding genes. The compactness of prokaryotic genomes is commonly perceived as evidence of adaptive genome streamlining caused by strong purifying selection in large microbial populations. In such populations, even the small cost incurred by nonfunctional DNA because of extra energy and time expenditure is thought to be sufficient for this extra genetic material to be eliminated by selection. However, contrary to the predictions of this model, there exists a consistent, positive correlation between the strength of selection at the protein sequence level, measured as the ratio of nonsynonymous to synonymous substitution rates, and microbial genome size. Here, by fitting the genome size distributions in multiple groups of prokaryotes to predictions of mathematical models of population evolution, we show that only models in which acquisition of additional genes is, on average, slightly beneficial yield a good fit to genomic data. These results suggest that the number of genes in prokaryotic genomes reflects the equilibrium between the benefit of additional genes that diminishes as the genome grows and deletion bias (i.e., the rate of deletion of genetic material being slightly greater than the rate of acquisition). Thus, new genes acquired by microbial genomes, on average, appear to be adaptive. The tight spacing of protein-coding genes likely results from a combination of the deletion bias and purifying selection that efficiently eliminates nonfunctional, noncoding sequences.

The majority of bacterial and archaeal genomes are small, at least compared with the genomes of multicellular and many unicellular eukaryotes (1, 2). Also, with the exception of deteriorating genomes of some parasitic bacteria, the prokaryotic genomes are highly compact, with densely packed protein-coding genes and a low fraction of noncoding sequences (3). The small genome size is thought to be selected for fast replication, whereas the high gene density additionally facilitates coregulation of gene expression via the operon organization (4, 5). Across the full range of cellular life forms, a significant positive correlation has been shown to exist between genome size and $N_{e}u$, where $N_e$ is the effective population size, and $u$ is the mutation rate per nucleotide (6–9). Accordingly, a simple and appealing population genetic theory has been developed, under which selection strength controls genome size and complexity (6, 9). Prokaryotes, with the exception of some parasites, have large effective population sizes on the order of ${10}^9$ or even higher, which implies strong selection enabling prokaryotes to maintain compact genomes (10). Under this strong selection regime, even short nonfunctional sequences incur cost that is “visible” to selection, conceivably through a combination of increasing energy expenditure and reducing the replication rate, and are efficiently weeded out (11). In eukaryotes, at least the multicellular forms, the effective population size is substantially (by orders of magnitude) smaller, and consequently, selection is not strong enough to eliminate superfluous genetic material, which results in “bloated” genomes but also provides the raw material for the evolution of complex features (6–8). It is often assumed, implicitly or explicitly, that any extra genetic material arising from duplication or acquisition is, on average, slightly deleterious for the host, because the new DNA does not perform any immediately beneficial function but incurs the cost right from the beginning. This theory, which is steeped in the well-established principles of population genetics, provides a simple, unified framework for understanding evolution of genomic complexity without invoking widespread adaptation. This nonadaptive theory can be reasonably assumed as the null hypothesis of genome evolution, the predictions of which have to be falsified to claim adaptive phenomena (8, 12).

The population genetic theory clearly predicts an inverse correlation between the strength of selection at different levels and genome size: small genomes are predicted to be subject to stronger selection than large genomes (9). However, when protein sequence-level selection was measured for multiple groups of closely related bacteria using the ratio of the nonsynonymous to synonymous substitution rates (dN/dS) as a proxy, the opposite effect, namely a significant negative correlation between dN/dS and genome size, was observed, indicating that larger prokaryotic genomes typically evolve under a stronger selection than small ones (13).

Here, we sought to further investigate the evolutionary factors that control genome evolution in prokaryotes. We reproduced the negative correlation between dN/dS and genome size on an expanded genome collection and then, developed a mathematical model of genome evolution by gene gain and loss in prokaryotic populations. By fitting the distribution of genome sizes predicted by the model to the empirical distribution for many groups of prokaryotes, we found that a good fit between theory and the data could be obtained only for models that included a positive mean fitness contribution of the gained genes countered by a deletion bias. These results imply that, at the level of gene gain and loss, selection for genome compactness does not play a major role in determining the genome size in prokaryotes. Rather, the relatively small number of genes in prokaryotes is explained by the diminishing return associated with the acquisition of new genes as the genome grows combined with the intrinsic deletion bias.

Results

Protein-Level Selection and Microbial Genome Size: Model Prediction and Genomic Data.

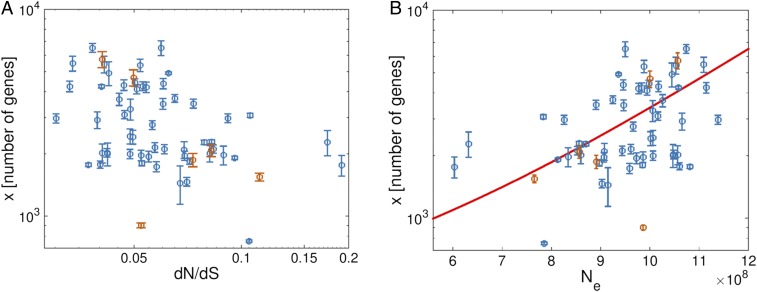
It has been shown previously that, in prokaryotes, genome size is negatively and significantly correlated with dN/dS, suggestive of a stronger protein-level selection in larger genomes (13). For the purpose of this work, we reproduced these findings on a substantially expanded set of groups of closely related bacterial and archaeal genomes compiled in the latest version of the Alignable Tight Genomic Cluster (ATGC) database (14) (Fig. 1). Specifically, genome size (measured by the number of genes) and dN/dS values are correlated with Spearman’s rank correlation coefficient $\rho =-$0.397. These findings imply that, in addition to local influences of different environments and lifestyles, there are underlying universal components of gene gain and loss probabilities with respect to genome size that are common across all microbes.

Fig. 1.

Genome size and selection in prokaryotes. Mean observed genome sizes (number of genes) are plotted against (A) the selection strength and (B) the estimated effective population size for each ATGC. Error bars correspond to 1 SD. ATGCs with more than 20 species are indicated in orange. The mean genome size, calculated using the mathematical model, is indicated in B by a solid red line. The model was applied with a constant selection coefficient, the gain and loss rates of Eq. 11, and optimized parameters shown in Table 1.

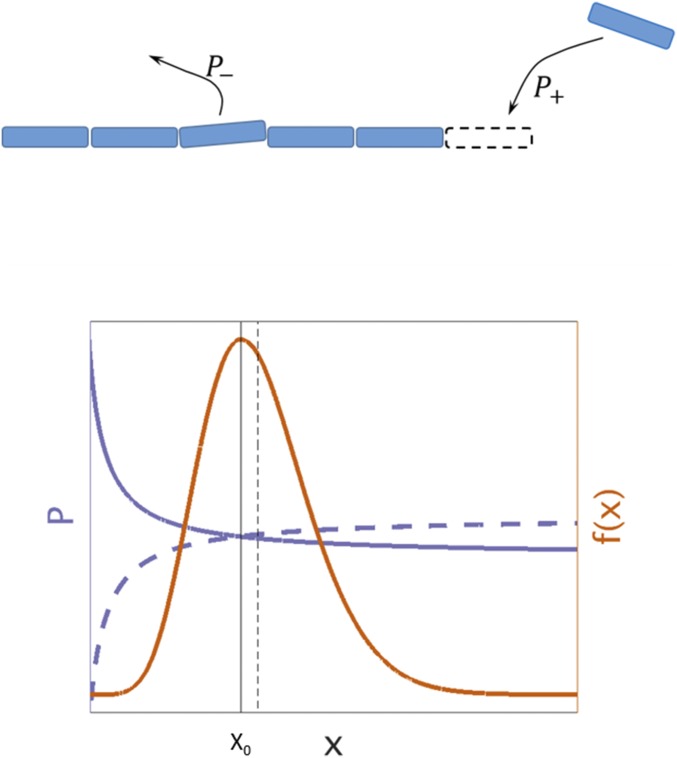
To quantitatively analyze the relations between selection strength and genome size, a mathematical model was implemented using the Moran process framework (15). In the model, a genome is represented as a collection of $x$ genes, and the variation in genome size is attributed to stochastic gain and loss of genes (Fig. 2). New genes are assumed to be acquired at rate $\alpha$, which in principle, depends on $x$ and accounts for the probability that the acquired genetic material is inserted in a nondeleterious locus and expressed. Genes can be acquired by either horizontal gene transfer (in the model, assumed to draw genes from an infinite pool) or duplication, and $\alpha$ represents a weighted average over all possible evolutionary processes that lead to gene gain. Reconstructions of genome evolution performed on the ATGCs indicate that the contribution of horizontal gene transfer by far exceeds that of duplication (14). To model gene loss, the deleted gene is picked from the genome at random with the deletion rate $\beta$, which analogous to $\alpha$, in principle, depends on $x$. Acquisitions and deletions of genetic material are either fixed or eliminated stochastically, with a fixation probability that depends on the selection coefficient $s$, which is a function of genome size as well $s=s\left(x\right)$. Specifically, $s\left(x\right)$ denotes the mean selective advantage of an individual with $x+1$ genes over an individual with $x$ genes. Conveniently, selection coefficients associated with gene acquisition and gene deletion are related as (Methods)

$$s_{deletion}=-s_{acquisition}.$$ [1]

The fixation probability $F$ can be approximated by

$$F\left(x\right)\approx \frac{s\left(x\right)}{1-e^{-N_{e}s\left(x\right)}},$$ [2]

where $N_e$ is the effective population size (16). The effective population size is estimated for each prokaryotic group from the dN/dS ratio (Methods). Fixed acquisition and deletion events, hereinafter “gene gain” and “gene loss,” respectively, occur with probabilities given by the multiplication of the event rate and the fixation probability:

$$P_{+}\left(x\right)=\alpha \left(x\right)\mathrm{\cdot }\frac{s\left(x\right)}{1-e^{-N_{e}s\left(x\right)}}$$ [3]

and

$$P_{-}\left(x\right)=\beta \left(x\right)\mathrm{\cdot }\frac{s\left(x\right)\mathrm{\cdot }{e}^{-N_{e}s\left(x\right)}}{1-e^{-N_{e}s\left(x\right)}},$$ [4]

where Eq. 2 is used together with the relation of Eq. 1.

Fig. 2.

The model of genome evolution. (Upper) Illustration of the mathematical model of genome size evolution. The number of genes changes stochastically via gene gains and losses, which occur with probabilities $P_{+}$ and $P_{-}$, respectively. (Lower) Gene gain (solid purple curve) and loss (dashed purple curve) probabilities. Gain and loss probabilities are equal at $x_0$, indicated by a vertical solid line. For values of $x$ smaller than $x_0$, the gain probability is larger than the loss probability, and therefore, the extremum of the steady-state genome size distribution (orange curve) at $x_0$ is a maximum. The distribution is moderately skewed, and the mean value of $x$, indicated by a vertical dashed line, is close to the value of $x_0$ (indicated by the solid vertical line).

Gain and loss probabilities govern the stochastic genome size dynamics, with the intuitive relation (derivation is given in Methods)

$$\dot{x}=P_{+}\left(x\right)-P_{-}\left(x\right),$$ [5]

meaning that, at each time step, there is a probability $P_{+}$ that one gene is gained and a probability $P_{-}$ that one gene is lost, where time is measured in fixation time units (a unit is the time that it takes, on average, for an acquired gene to be fixed in the population) rather than generations. Because of the stochastic fluctuations, genome sizes form a distribution. If, for a certain genome size value $x_0$, the gain and loss probabilities are equal, there is a steady-state genome size distribution with an extremum point at $x_0$ as illustrated in Fig. 2 and SI Appendix, Fig. S1. The extremum point depends on the deletion–acquisition rates ratio $r\left(x\right)$,

$$r\left(x\right)=\frac{\beta \left(x\right)}{\alpha \left(x\right)},$$ [6]

and the equality of gain and loss probabilities implies

$$s\left(x_0\right)=\frac{lnr\left(x_0\right)}{N_e}.$$ [7]

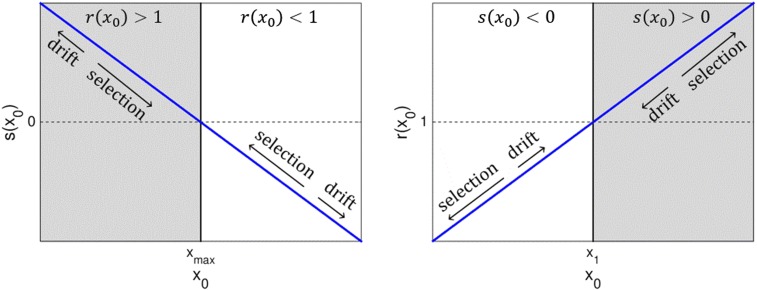
As reflected in the above equation (and intuitively), steady state is possible only when the more frequent event, gene acquisition or gene deletion, is counterselected at genome size $x_0$ (Fig. 3). For example, positive $s\left(x_0\right)$ implies selective advantage for larger genomes. In this case, steady state is possible only when deletion rates are higher than acquisition rates [i.e., $r\left(x_0\right)>1$]. Formally, the sign of $s\left(x_0\right)$ in Eq. 7 is determined by the sign of $lnr\left(x_0\right)$. In the special case of acquisition and deletion rates being equal at $x_0$, $s\left(x_0\right)=0$, which implies that either there is no selection with respect to genome size or the fitness function has an extremum at $x_0$ (Eq. 16). The genome size distribution extremum point at $x_0$ is a maximum only if an additional condition is satisfied: for $x<x_0$, gain and loss probabilities must satisfy $P_{+}>P_{-}$ (SI Appendix, Fig. S1). This condition is met when

$$P_{+}^{\prime }\left(x_0\right)<P_{-}^{\prime }\left(x_0\right).$$ [8]

The case where $x_0$ is a minimum of the steady-state genome size distribution is biologically irrelevant, corresponding to genome sizes tending toward either zero or infinity (SI Appendix, Fig. S1).

Fig. 3.

Different regimes for the selection and the gain/loss rates ratio (Eq. 7). In the shaded area, the genome size steady state is achieved for $s\left(x_0\right)>0$, and accordingly, $r\left(x_0\right)>1$. In this regime, gene loss is selected against but occurs at higher rates than gene acquisition and therefore, denoted drift. Genome sizes $x_{max}$ and $x_1$ (shown by vertical lines) denote values for which $s\left(x_0\right)=0$ and $r\left(x_0\right)=1$, respectively. These values are not necessarily the same, and the resulting value of $x_0$ depends on the functional forms of $s\left(x\right)$ and $r\left(x\right)$, which are shown as straight blue lines for convenience.

For the calculation of the steady-state distribution of genome size, it is useful to present the population model of the genome size evolution as a random walk, where the probability of a step up is $P_{+}$, and the probability of a step down is $P_{-}$. The equation for the genome size distribution (Methods) has a steady-state solution:

$$f\left(x\right)\propto {\left[P_{+}\left(x\right)+P_{-}\left(x\right)\right]}^{-1}{e}^{2\int \frac{P_{+}\left(x\right)-P_{-}\left(x\right)}{P_{+}\left(x\right)+P_{-}\left(x\right)}dx}.$$ [9]

If $\alpha$ depends on $x$, $f\left(x\right)$ depends on the functional forms of both $\alpha \left(x\right)$ and $\beta \left(x\right)$ and unlike the equation for $x_0$ (Eq. 7), cannot be written using $r\left(x\right)$ only. The genome size distribution allows one to compare different functional forms for $P_{\pm }\left(x\right)$ in terms of compatibility with observed genome sizes under the assumption that, whatever the gene gain and loss probabilities might be, they are similar in all prokaryotes. Specifically, maximizing the log likelihood of the data given a specific model allows optimization of model parameters and comparison of different cases (details are in Methods). To account for the most general case, where both the selection coefficient and the acquisition–deletion rates ratio vary with genome size, $s$ is taken as linear in $x$, and $r$ is taken as a power law:

$$s\left(x\right)=a+b\mathrm{\cdot }x$$ [10]

and

$$r\left(x\right)=r\prime \mathrm{\cdot }{x}^{\lambda }.$$ [11]

These functional forms were chosen to minimize the number of optimized parameters. The linear selection coefficient can be regarded as a first-order expansion, and the power law functional form for $r\left(x\right)$ was chosen, because it includes two extreme cases, those with constant and linear rates ratio, as well as all intermediates. The selection coefficient sign is not assumed a priori but is an outcome of the fitting process. Furthermore, it is in principle possible that the selection coefficient sign will be different in different ATGCs because of their different typical genome sizes.

Even for $s\left(x\right)$ and $r\left(x\right)$, which are approximated by low-order functions, maximizing the log likelihood requires fitting five parameters (Methods), and therefore, in principle, it is not evident that the resulting fit corresponds to a global maximum of the log likelihood rather than a local peak. We, therefore, performed the fitting with different starting points in parameter space chosen as explained in Methods. In brief, Eq. 7 is used to estimate the mean genome size for different effective population sizes, and parameters are optimized, such that goodness of fit $R^2$ with respect to the mean genome sizes of the ATGCs and effective population sizes is maximized. This procedure resulted in five different sets of parameters (SI Appendix, Table S1) that were then used as starting points for additional optimization by log-likelihood maximization (Methods). Three of five starting points converged to similar values (SI Appendix, Table S2), whereas the remaining two converged to local maxima associated with significantly lower likelihood. In all optimized sets of parameters (from both stages), the selection coefficient is positive for all ATGCs, indicating that additional genes are, on average, beneficial as expected given the positive correlation between genome size and effective population size (SI Appendix, Fig. S2).

In all three log-likelihood optimized parameter sets, the selection coefficient is strictly positive for all ATGCs and weakly depends on $x$. Formally, the variation of the fixation probability with genome size is an order of magnitude smaller than the variation of acquisition and deletion rates with genome size (Methods). Accordingly, additional fittings were performed using constant selection coefficient (namely, independent of the genome size). In this case, the log-likelihood optimization always converged to the same set of parameters, with $s\approx 6\times {10}^{-12}$ and $r$ values between $1.0034$ and $1.0072$, corresponding to smallest and largest genomes, respectively (fitted parameters are summarized in SI Appendix, Table S4). This value of $s$ implies $x_0\mathrm{\cdot }s\mathrm{\cdot }{N}_e\mathrm{\sim }1$ (i.e., the “resolution of selection” is on the order of a single gene). Notably, the dependence of $r$ on $x$ is weak. The mean steady-state genome size is a function of effective population size for this fit (Fig. 1).

For complementarity, fitting with constant $r$ together with an $x$-dependent selection coefficient was performed as well (SI Appendix), allowing inference of the selection landscape beyond the first-order expansion for a constant acquisition–deletion rates ratio. In this case, the best fit is achieved for positive and saturating selection landscape, indicating that, on average, additional genes are beneficial but that the benefit decreases with the growth of the genome size.

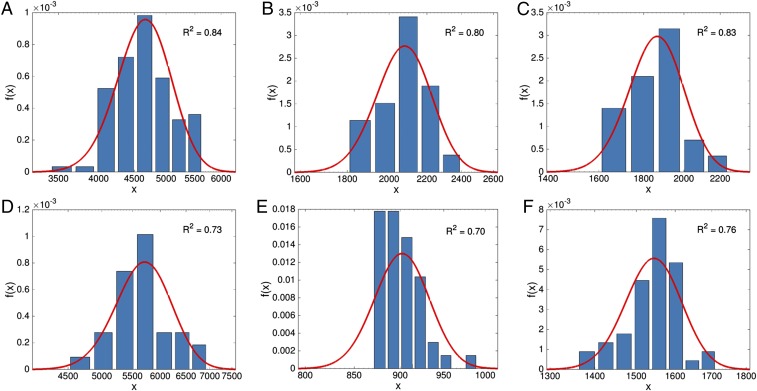
As an approximation for nonuniversal, ATGC-specific factors that affect the genome size, optimization of the gene acquisition and deletion rates was performed separately for each ATGC. The selection coefficient was taken to be the same for all ATGCs and set to the value obtained in the global fitting at the previous stage. For each ATGC, $r\prime$ and $\lambda$ were optimized, where the fitting of 120 parameters (compared with 5 parameters at the previous stage) is justified by the Akaike Information Criterion (AIC) (Table 1). The fitted values of $r^{\text{'}}$ and $\lambda$ are shown in SI Appendix, Fig. S3, and the resulting genome size distributions for ATGCs with 20 or more species are shown in Fig. 4.

Table 1.

Parameter values, log likelihood, and AIC for the selection landscape and deletion–acquisition rates ratio of Eqs. 10 and 11

Selection landscape	No. of parameters	Parameters values	LL	AIC
Linear $s$ and power law $r$ (Eqs. 10 and 11)	5	$a=6\times {10}^{-12}$	$-6.04\times {10}^3$	$1.21\times {10}^4$
		$b=2\times {10}^{-16}$
		$r\prime =0.99$
		$\lambda =2\times {10}^{-3}$
		${\lambda }_{+}=7\times {10}^{-4}$
Power law $r$ (Eq. 11) and constant $s$	4	$s=6\times {10}^{-12}$	$-6.02\times {10}^3$	$1.21\times {10}^4$
		$r\prime =0.99$
		$\lambda =1.7\times {10}^{-3}$
		${\lambda }_{+}=1\times {10}^{-3}$
Power law $r$ (Eq. 11) and constant $s$ individual ATGC fit	120	$s=6\times {10}^{-12}$	$-4.55\times {10}^3$	$9.34\times {10}^3$
		${\lambda }_{+}=1\times {10}^{-2}$
		$\lambda$ and $r\prime$ are shown in SI Appendix, Fig. S3
SI Appendix, Eq. S1 with constant $r$	2	$\gamma =2.92$	$-6.21\times {10}^3$	$1.24\times {10}^4$
		$r=1.0006$

The selection landscape of SI Appendix, Eq. S1 with constant deletion–acquisition rates ratio is also shown for comparison. Log-likelihood (LL) calculation details are given in Methods.

Fig. 4.

Comparison of the model predictions with the empirical genome size distributions. The observed genome size distributions are shown by bars for six ATGCs that consist of 20 species or more each. Genome size distributions predicted by the population evolution model are shown by red lines using the selection landscape and deletion–acquisition rate of Eqs. 10 and 11 and optimized $r^{\text{'}}$ and $\lambda$ parameter values for each ATGC separately (optimized values are shown in SI Appendix, Fig. S3). The goodness of fit $R^2$ is indicated for each ATGC. The ATGCs are as follows (the numbers of genomes for each ATGC are indicated in parentheses): (A) ATGC0001 (109), (B) ATGC0003 (22), (C) ATGC0004 (22), (D) ATGC0014 (31), (E) ATGC0021 (45), and (F) ATGC0050 (51). All ATGC genomes are listed in Dataset S1.

Evolution of Distinct Functional Classes of Genes.

In our model, the gene acquisition and deletion rates, $\alpha \left(x\right)$ and $\beta \left(x\right)$, respectively, are general characteristics of the organism that do not depend on the content of the acquired or lost genetic material. In contrast, the selection coefficient inferred above represents a local average with respect to the gene content of the organism and the available genetic material in the assumed infinite gene pool. The model can be extended to account for different classes of genes that evolve under distinct selection landscapes. Specifically, the number of class $i$ genes, $x_i$, is determined by the stochastic equation (Methods)

$${\dot{x}}_i=k_i\mathrm{\cdot }\alpha \left(x\right)\mathrm{\cdot }{F}_{+}\left(s_i\left(x_i\right)\right)-\frac{x_i}{x}\mathrm{\cdot }\beta \left(x\right)\mathrm{\cdot }{F}_{-}\left(s_i\left(x_i\right)\right),$$ [12]

where $x$ is the total number of genes, $k_i$ is the probability of gain of a class $i$ gene, and the selection landscape $s_i$ is assumed to be a function of $x_i$ only. The width of the steady-state distribution is determined primarily by the linear term $x_i/x$ in the loss probability. To further test the model consistency with the empirical data, steady-state distributions were calculated for subsets of genes. The subsets were chosen based on the functional classes of genes as classified in the COG (Clusters of Orthologous Genes) database (17, 18). The selection landscape and $k_i$ were optimized for the best log-likelihood fit of the distribution predicted by the model to the genomic data (SI Appendix, Table S5). The distributions were calculated using the values of $\alpha \left(x\right)$ and $\beta \left(x\right)$ that were obtained by fitting the distributions for complete gene sets (Table 1). The mean value of $x_i$ can be approximated by the equilibrium value $x_i^0$, for which the gain and loss probabilities are equal (analogous to $x_0$ for the complete genomes as described above):

$$x_i^0{e}^{-N_e{s}_i\left(x_i^0\right)}=k_i\frac{x}{r\left(x\right)}.$$ [13]

This expression can be regarded as a generalization of previously reported scaling laws for different functional classes of genes with the genome size (19–21), where the ATGC-specific effective population sizes are taken into account (the full implications of this extension of the scaling analysis will be discussed elsewhere). Comparison of the empirical data and the model predictions for the number of genes in most of the functional classes shows a good fit between the model predictions and the genomic data (SI Appendix, Figs. S4 A and B and S5 A and B). For the translation system components and the genes involved in energy transformation, the log-likelihood values were $-\mathrm{3,334}$ and $-\mathrm{6,115}$, respectively, compared with the −6,022 value for complete genomes. Thus, notably, the genes for translation system components, the most conserved, universal functional class (22), are described by the model much better than a random subset of genes.

Finally, analogous to the whole-genome fitting procedure, to account for ATGC-specific effects, model distributions were further optimized by fitting ATGC-specific $k_i$ values. The resulting distributions for most of the functional classes showed good fits between the model and the genomic data as illustrated in SI Appendix, Fig. S6 A and B for the translation system components and genes involved in energy transformation of the largest ATGC001 (complete results are in SI Appendix, Figs. S7–S10). However, two classes of genes, namely the components of the “mobilome,” such as prophage genes and transposons, as well as the singletons (genes with no detectable orthologs within the given ATGC), dramatically deviate from model predictions (SI Appendix, Figs. S6 C and D, S9, and S10). For these gene classes, the observed distributions are significantly wider than those predicted by the model, regardless of the model parameters or the selection landscape. Accordingly, the log-likelihood values reflect the disagreement and are $-\mathrm{18,870}$ and $-\mathrm{49,384}$ for mobilome and singletons, respectively. Such a poor fit effectively indicates that these classes of genes evolve under evolutionary regimes qualitatively different from that of the rest of the genomes. Many of the mobilome components, in particular transposons, are prone to active duplication within the genome and therefore, cannot be described with the gene gain rate inferred for the complete gene sets. The singletons dramatically differ from the evolutionarily conserved genes shared by multiple microbes with respect to the tempo and mode of evolution. Most of the singletons encode small proteins and evolve fast, suggesting that they are associated with little (if any) benefit (23, 24). Thus, the key result of this analysis, namely the positive sign of the mean selection coefficient, does not apply to the singletons.

Discussion

The notion of strong purifying selection that favors small genomes (or more precisely, a small number of genes) in prokaryotes (10) seemed incompatible with the observed significant positive correlation between the genome sizes of bacteria and archaea and the inferred selection strength on the protein level reflected in the dN/dS ratio (13) (this work). These observations indicate that, on average, the larger the genome of a bacterium or an archaeon, the stronger selection under which the protein-coding genes evolve. This apparent discrepancy between the comparative genomic observations and the predictions of the population genetic theory motivated us to further investigate the selection regimes of microbial genomes. To this end, we compared the predictions of a mathematical model of genome evolution with the genome size distributions in 60 clusters of closely related bacteria and archaea.

To infer the selection landscape with regard to the genome size, the effective population size was estimated for each ATGC using the dN/dS ratio and assuming the same selection coefficient $s_c$ for the core genes in all ATGCs. This assumption is reasonable, because 51–56 core genes used for the dN/dS calculation are nearly universal and encode central biological functions, such as translation, that are functionally highly similar across the entire bacterial domain of cellular life (22). Small variations in $s_c$ across the different ATGCs might slightly affect the inferred gain and loss probabilities through the changes in the estimated effective population size associated with each ATGC. However, to affect our conclusions, namely that additional genes are, on average, beneficial, the variations in $s_c$ between ATGCs would have to be dramatic, such that the correlation between the genome size and the dN/dS ratio (Fig. 1A) would be abolished or reversed.

Inference of gain and loss probabilities requires estimation of three terms, namely gene gain and loss rates and the selection landscape. In principle, all three values depend on the genome size, such that it is impossible to infer all terms without assumptions on the functional forms of the respective dependencies. However, it has to be emphasized that our conclusions do not depend on specific modeling assumptions and hold as long as $s\left(x\right)$ and $r\left(x\right)$ are monotonic functions for typical prokaryotic genome sizes. The steady-state genome size distribution reflects the selection–drift balance: acquisition of new genes is, on average, beneficial, albeit with a small estimated selection coefficient (Table 1), and balanced by a deletion rate that is slightly greater than the acquisition rate. Under this regime, the selection on the gain or loss of an individual gene is weak, allowing substantial variation in genome size, but sufficient to produce the correlation between N_e and genome size. The fitted values of the deletion–acquisition rates ratio are very close to, albeit greater than unity. This slight but consistent excess of gene loss over gain is likely to reflect the deletion bias that has been identified as an intrinsic feature of genome evolution in both bacteria and eukaryotes (25–27).

Extension of the model to account for subsets of genes allowed additional validation of the model consistency and assessment of the selection affecting any class of genes. In particular, we analyzed genes that are associated with specific cellular functions as classified in the COG database (17, 18) under the assumption that functionally similar genes evolve under similar selection landscapes. We obtained good fits to the model for all functional classes, indicating that the conclusion on the typical beneficial effect of gene acquisition applies to functionally diverse classes of genes. However, there were two notable exceptions to this consistency, namely the mobilome and the singletons. The distributions of the sizes of these classes in all ATGCs are much wider than predicted by the model, and the parameters could not be optimized to obtain a good fit. These observations imply that the evolutionary regimes of the mobilome and the singletons qualitatively differ from the genes in the other functional classes that possess “normal” cellular functions. There are indications of the nature of these differences. Many components of the mobilome, such as transposons, propagate within a genome, so that the dynamics of this class is dominated by duplication rather than gain from an external gene pool. The singletons are fast evolving genes that, on average, do not confer any benefit on the organism. Indeed, in a separate recent analysis of microbial genome evolution models, we have shown that the replacement rate of the singletons is effectively infinite compared with the replacement rates of the rest of the genes (28).

The model analysis described here was performed assuming a steady state with respect to the genome size, and two points have to be addressed in this regard. Each ATGC consists of phylogenetically close genomes (29) that cannot be considered independent samples from the genome size distribution without additional substantiation. We, therefore, verified that, for each ATGC, the divergence between the genomes, defined in this case as the number of gains and losses, was greater than the genome size distribution width, ensuring that a sufficient number of evolutionary events occurred so that the genomes represent an independent set of samples from the size distribution. A low bound for the number of gene gain and loss events that occurred since the divergence of individual genomes can be estimated from the number of singletons divided by the probability of the acquisition of such genes. The required number of gains and loss events for sufficient sampling of the distribution can be estimated from the SD of all genome sizes in an ATGC. The estimated numbers of gain events are greater than the SDs for all ATGCs (SI Appendix, Fig. S11), indicating that the genome size distribution was sampled sufficiently.

In our previous work, a comprehensive analysis of gain and loss events was performed for the same groups of microbial genomes (ATGCs) that were analyzed here (14). The gene loss to gain ratios obtained through a maximum likelihood reconstruction of genome evolution formed a broad distribution, with the mean value of about two. The evolution models analyzed here (Eqs. 10 and 11) yield a skewed distribution of genome sizes, which implies a distribution of loss/gain ratios with the mean slightly greater than unity. The distributions and parameters fitted here cannot explain such a large difference between the model predictions and inferences from genome comparison. Thus, it seems likely that, most of the time, the majority of the genomes are somewhat smaller than the long-term equilibrium size. A biologically plausible scenario is that prokaryotes are exposed to beneficial genetic material only for short periods of time, resulting in brief intervals of fast growth followed by slow genome shrinking (30). Steady state is possible under this scenario as well but only as the average over multiple cycles of gain and loss, which probably occur on a timescale much longer than the scale of the ATGC evolution. The strict steady-state analysis presented here can be regarded as a coarse-grained description of more complex evolutionary scenarios; however, our key finding, that acquired genes are, on average, beneficial, is expected to hold also for higher-order analyses.

The results of this analysis indicate that elimination of genes under the pressure of purifying selection is not the dominant factor of microbial evolution. On the contrary, acquisition of genes by microbes seems to be largely an adaptive process, although the positive selection that governs the genome dynamics, on average, is likely to be weak. This conclusion by no means contradicts the population genetic theory as such (9) but is incompatible with the assumption that newly acquired (and fixed in the population) genes are, on average, neutral. In other words, all of the estimates of the cost of the genetic material (11) can be valid in themselves, but the positive selection coefficient that is, on average, associated with new genes offsets these costs. Given that new genes are, on average, beneficial, microbes with larger $N_e$ values that evolve under strong purifying selection typically accrue a greater number of genes than microbes with smaller populations. This reasoning explains the negative correlation between dN/dS and the number of genes (Fig. 1) that, at first glance, seemed paradoxical and to contradict the theory. Conceivably, the evolution of genuinely neutral, noncoding sequences is governed by the cost combined with the deletion bias, resulting in the purge of such sequences predicted by the theory and hence, the “wall to wall” architecture of the prokaryotic genomes (3).

To summarize, the analysis described here presents the formal theory of the evolution of prokaryotic gene content. Perhaps unexpectedly, comparison of the theory predictions with the genomic data shows that gene gain by prokaryotes, leading to genome growth, is largely an adaptive process, with the exception of “nonfunctional” gene classes, the mobilome and the singletons. From the biological standpoint, it seems plausible that the apparent beneficial effect of gene gain is a combined result of the capture of metabolic enzymes that can expand the biochemical capacity of microbes (31), regulators and signaling proteins that enhance regulatory circuits (32), and defense genes (33). However, much more research is required to reconstruct the full functional landscape of microbial evolution.

Methods

Prokaryotic Genome Size Data and Nonsynonymous to Synonymous Nucleotide Substitution Ratio.

Genomes of 707 prokaryotic species grouped into 60 ATGCs (14, 29) were analyzed. In addition to the number of genes ($x)$, selection forces acting on the protein level were inferred for each ATGC. Nonsynonymous to synonymous nucleotide substitution ratio ($dN/dS$) was evaluated for each pair of species that belongs to the same ATGC using concatenated sequences of all core genes. The indicated $dN/dS$ value for each ATGC is the median across all species pairs in the ATGC. Based on the COG database annotations (17, 18), singleton genes were identified and counted for each species. The effective population size was estimated for each ATGC from the calculated $dN/dS$ value as explained in the following section.

Inference of Effective Population Size.

Synonymous mutations are assumed to be neutral and, therefore, fixed at a rate $1/N_e$. Together with the fixation probability given by Eq. 2, for nonsynonymous mutations, we have (34)

$$\frac{dN}{dS}\approx \frac{N_e{s}_c}{1-e^{-N_e{s}_c}},$$ [14]

where $s_c$ denotes the selection coefficient acting on the core genes for which the $dN/dS$ values are calculated. It is assumed that $s_c$ is similar for all ATGCs and that the variation in $N_e$ within an ATGC is significantly smaller than the differences in $N_e$ between different ATGCs. The value of $s_c$ is set, such that the effective population size for Escherichia coli is ${10}^9$, and Eq. 14 allows estimation of effective population size for each ATGC.

Selection Function Symmetry with Respect to Gene Acquisition and Deletion.

The relation given by Eq. 1 is derived as follows. Noting by $s$ the selection advantage of gene acquisition, the reproduction rate for genome size $x$ is $1$, and for genome size $x+1$, it is, therefore, $1+s$. For gene deletion, the reproduction rate is $1$ for genome size of $x+1$, and for consistency, the reproduction rate for genome size $x$ is given by $1-s$, corresponding to selection advantage of $–s$ for gene deletion.

Selection and Fitness Relations.

The selection coefficient $s$ is related to the fitness $\varphi$ by

$$s_{ab}\mathrm{=}\frac{{\mathit{\varphi }}_a}{{\mathit{\varphi }}_b}\mathrm{-}1$$ [15]

when considering the selective advantage of individual $a$ over individual $b$ (16, 35). For the inference of the selection coefficient that is associated with gene acquisition at genome size $x$, it is useful to assign genome sizes of $x+1$ and $x$ to individuals $a$ and $b$, respectively. The selection coefficient–fitness relation is, therefore,

$$s\left(x\right)=\frac{\varphi \left(x+1\right)-\varphi \left(x\right)}{\varphi \left(x\right)}\approx {\partial }_{x}ln\varphi \left(x\right).$$ [16]

Mean Genome Size Dynamics.

For uniform population invaded by mutation that is associated with fitness ${\varphi }_1$, the population fitness dynamics is given by

$$\dot{\mathit{\varphi }}\mathrm{=}{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}\text{d}{\mathit{\varphi }}_1\left({\mathit{\varphi }}_1\mathrm{-}\mathit{\varphi }\right)\mathcal{P}\left({\mathit{\varphi }}_1\right)F\left(\mathit{\varphi },{\mathit{\varphi }}_1\right),}$$ [17]

where $\mathcal{P}\left({\varphi }_1\right)$ is mutations probability density, $F\left(\varphi ,{\varphi }_1\right)$ is the fixation probability, and time is measured in fixation time units (rather than in Moran generations) (36). Eq. 17 is general, the only assumption being that the mutation rate is low enough, such that the weak mutation limit condition is satisfied. However, for the model analysis, it is more practical to derive the equation for genome size dynamics rather than the fitness. The integral over ${\varphi }_1$ is a sum for all possible mutations and contains two terms corresponding to gene acquisition and gene deletion. Accordingly, $\mathcal{P}\left({\varphi }_1\right)$ is given by gene acquisition and deletion rates:

$$\mathcal{P}\left({\varphi }_1^{+}\right)=\alpha \left(x\right)$$ [18]

and

$$\mathcal{P}\left({\varphi }_1^{-}\right)=\beta \left(x\right),$$ [19]

where the + and − superscripts indicate acquisition and deletion events, respectively. The fitness derivative with respect to the number of genes can be approximated as

$${\varphi }^{\text{'}}=\frac{\mathrm{\Delta }\varphi }{\mathrm{\Delta }x}\approx \frac{{\varphi }_1^{+}-\varphi }{1},$$ [20]

such that ${\varphi }_1^{\pm }-\varphi =\pm {\varphi }^{\text{'}}$. The fitness time derivative can be calculated using the chain rule:

$$\dot{\mathit{\varphi }}\mathrm{=}\mathit{\varphi }\prime \dot{x}$$ [21]

and

$$P_{\pm }=\mathcal{P}\left({\varphi }_1^{\pm }\right)F_{\pm }.$$ [22]

Substituting Eqs. 18, 19, 20, 21, and 22 to Eq. 17, we get Eq. 5 for genome size dynamics.

Steady-State Genome Size Distribution.

The genome size distribution satisfies the difference equation

$$f\left(x,t+\mathrm{\Delta }t\right)=f\left(x,t\right)\left(1-P_{+}\left(x\right)-P_{-}\left(x\right)\right)+f\left(x-\mathrm{\Delta }\text{x},t\right)\hspace{0.17em}{P}_{+}\left(x-\mathrm{\Delta }\text{x}\right)+f\left(x+\mathrm{\Delta }\text{x},t\right)\hspace{0.17em}{P}_{-}\left(x+\mathrm{\Delta }\text{x}\right).$$ [23]

This equation can be approximated by a second-order differential equation (37). The left-hand side is expanded to first order in $\mathrm{\Delta }t$, and the right-hand size is expanded to second order in $\mathrm{\Delta }x$, giving the following expression:

$$\dot{f}\approx -\frac{\mathrm{\Delta }x}{\mathrm{\Delta }\text{t}}{\partial }_x\left[\left(P_{+}-P_{-}\right)f\right]+\frac{{\left(\mathrm{\Delta }x\right)}^2}{\mathrm{\Delta }\text{t}}\frac{1}{2}{\partial }_x^2\left[\left(P_{+}+P_{-}\right)f\right],$$ [24]

where in the weak mutation limit, $\mathrm{\Delta }x=1$ for $\mathrm{\Delta }t=1$ in fixation time units. For the steady-state distribution, $\dot{f}=0$. The resulting differential equation has a solution in the form of Eq. 9.

Optimization of the Goodness of Fit $R^2$ for Mean Genome Size Vs. Effective Population Size Dependency.

To search the parameter space more efficiently during the log-likelihood optimization, a preliminary optimization stage was implemented. Eq. 7 determines the relation between $x_0$ and $N_e$. For given $s\left(x\right)$ and $r\left(x\right)$, the genome size dependence on effective population size can be compared with the dependence observed in ATGCs, where mean genome size is taken as an approximation for $x_0$. This approximation does not introduce large errors for modestly skewed genome size distributions (SI Appendix, Fig. S12), and ATGCs genome size distributions are only slightly skewed (Fig. 4). Specifically, it is possible to optimize the selection and deletion–acquisition rates ratio parameters (Eqs. 10 and 11) to maximize the goodness of fit $R^2$. At the next stage, the parameters that gave the highest $R^2$ values are used as starting points for the log-likelihood optimization. Note that the log-likelihood scheme requires one additional parameter: the genome size distribution depends in principle on $\alpha \left(x\right)$ and $\beta \left(x\right)$, whereas in Eq. 7, only the ratio $r\left(x\right)$ appears. These values are given for the deletion–acquisition rates ratio of Eq. 11 by $\alpha \left(x\right)=x^{{\lambda }_{+}}$ and $\beta \left(x\right)=r\prime \mathrm{\cdot }{x}^{{\lambda }_{-}}$, where $\lambda ={\lambda }_{-}-{\lambda }_{+}$. The selection landscape and deletion–acquisition rates ratio of Eqs. 10 and 11 require optimization of five parameters: $a$, $b$, $r\prime$, ${\lambda }_{+}$, and ${\lambda }_{-}$.

Maximum Likelihood Optimization.

The log likelihood (LL) of the model given the data is estimated as

$$LL={\displaystyle \sum }_{i}lnf\left(x_i\right),$$ [25]

where $x_i$ is the observed genome size in ATGC species, and $f\left(x\right)$ is the predicted steady-state distributions of Eq. 9. Specifically, for the log-likelihood estimation of a model, the parameters were optimized to maximize the log-likelihood $LL\left(\overrightarrow{Z}\right)$:

$$LL\left(\overrightarrow{Z}\right)={\displaystyle \sum }_{i}lnf\left(x_i;N_e^i,\overrightarrow{Z}\right),$$ [26]

where the sum is over all 707 species, $\overrightarrow{Z}$ components are all optimized parameters, and $N_e^i$ is the effective population size corresponding to the ATGC that contains species $i$. For the constant fitness coefficient, individual fitting of $r\prime$ and $\lambda$ was performed separately for each ATGC, forming a set of 60 $\left\{\overrightarrow{Z}\right\}=\left\{r\prime ,\lambda \right\}$ pairs. The log likelihood was calculated as follows:

$$LL\left(\left\{\overrightarrow{Z}\right\}\right)={\displaystyle \sum }_i{\displaystyle \sum }_{j\in ATG{C}_i}lnf\left(x_j;N_e^j,{\left\{\overrightarrow{Z}\right\}}_i\right),$$ [27]

where the inner sum is over all species that belong to ATGC $i$, and the outer sum is over all ATGCs.

Gain and Loss Probabilities Genome Size Dependent.

The gene gain (loss) probability depends on genome size through the selection coefficient and the acquisition (deletion) rate. The variation in gain and loss probability $\mathrm{\Delta }{P}_{\pm }$ for genome size variation $\mathrm{\Delta }x$ is given by

$$\mathrm{\Delta }{P}_{+}=F_{+}\mathrm{\cdot }{\partial }_x\alpha \mathrm{\cdot }\mathrm{\Delta }x+\alpha \mathrm{\cdot }{\partial }_x{F}_{+}\mathrm{\cdot }\mathrm{\Delta }x$$ [28]

and

$$\mathrm{\Delta }{P}_{-}=F_{-}\mathrm{\cdot }{\partial }_x\beta \mathrm{\cdot }\mathrm{\Delta }x+\beta \mathrm{\cdot }{\partial }_x{F}_{-}\mathrm{\cdot }\mathrm{\Delta }x,$$ [29]

where all quantities are calculated using the mean ATGCs genome size and effective population size. If, say, the second term in the above equations is significantly smaller than the first term, the variation in $P_{+}$ and $P_{-}$ with genome size is mainly caused by the variation in $\alpha$ and $\beta$, whereas $s$ can be taken as constant with respect to $x$.

For parameters fitted using linear selection landscape and summarized in SI Appendix, Table S2, the terms involving the derivatives of $F_{+}$ and $F_{-}$ are order of magnitude smaller than the $\alpha$ and $\beta$ derivative terms.

The Model with Two Types of Genes.

The model can be extended to account for distinct classes of genes evolving under different selection landscapes. For two classes, the numbers of genes in each class, $x_1$ and $x_2$, are governed by two coupled stochastic equations:

$${\dot{x}}_1=k_1\mathrm{\cdot }\alpha \left(x_1+x_2\right)\mathrm{\cdot }{F}_{+}\left(s_1\left(x_1\right)\right)-\frac{x_1}{x_1+x_2}\mathrm{\cdot }\beta \left(x_1+x_2\right)\mathrm{\cdot }{F}_{-}\left(s_1\left(x_1\right)\right)$$ [30]

and

$${\dot{x}}_2=k_2\mathrm{\cdot }\alpha \left(x_1+x_2\right)\mathrm{\cdot }{F}_{+}\left(s_2\left(x_2\right)\right)-\frac{x_2}{x_1+x_2}\mathrm{\cdot }\beta \left(x_1+x_2\right)\mathrm{\cdot }{F}_{-}\left(s_2\left(x_2\right)\right),$$ [31]

where the interpretation is as follows. The probability to acquire a gene of class $i$ is $k_i$ and is a property of the gene pool. In addition, the associated selection landscape $s_i$ is assumed to be a function of $x_i$ only. The loss rate for class $i$ is given by the product of $\beta$, which is defined per genome, and the fraction of type $i$ genes. The derivation of Eqs. 30 and 31 follows the same steps as for the complete genome. The integral of Eq. 17 in this case is a sum with four terms, namely, acquisition or deletion of either class $1$ or class $2$ genes. The fitness time derivative includes two terms:

$$\dot{\mathit{\varphi }}\mathrm{=}{\dot{x}}_1{\mathrm{\partial }}_1\mathit{\varphi }\mathrm{+}{\dot{x}}_2{\mathrm{\partial }}_2\mathit{\varphi },$$ [32]

where ${\partial }_i$ stands for differentiation with respect to $x_i$. The last stage in the derivation is to split terms associated with $x_1$ or $x_2$ dynamics into two separate equations. This operation is possible, because the number of genes in each class is determined exclusively by gene gain and loss events: there is no process in the model that allows switching the gene type.

To calculate the steady-state distribution for a subset of genes, $x_1$ is set to the subset size, and $x_2$ represents the remaining genes. In this case, we have $x_1\ll x_2$, and accordingly, $x_1+x_2\approx x_2\approx x$; therefore, Eq. 30 is decoupled from Eq. 31.