Abstract
The particle size distribution (PSD) is a critical aspect of the oceanic ecosystem. Local variability in the PSD can be indicative of shifts in microbial community structure and reveal patterns in cell growth and loss. The PSD also plays a central role in particle export by influencing settling speed. Satellite‐based models of primary productivity (PP) often rely on aspects of photophysiology that are directly related to community size structure. In an effort to better understand how variability in particle size relates to PP in an oligotrophic ecosystem, we collected laser diffraction‐based depth profiles of the PSD and pigment‐based classifications of phytoplankton functional types (PFTs) on an approximately monthly basis at the Hawaii Ocean Time‐series Station ALOHA, in the North Pacific subtropical gyre. We found a relatively stable PSD in the upper water column. However, clear seasonality is apparent in the vertical distribution of distinct particle size classes. Neither laser diffraction‐based estimations of relative particle size nor pigment‐based PFTs was found to be significantly related to the rate of 14C‐based PP in the light‐saturated upper euphotic zone. This finding indicates that satellite retrievals of particle size, based on particle scattering or ocean color would not improve parameterizations of present‐day bio‐optical PP models for this region. However, at depths of 100–125 m where irradiance exerts strong control on PP, we do observe a significant linear relationship between PP and the estimated carbon content of 2–20 μm particles.
Keywords: particle size, phytoplankton, productivity, North Pacific, laser diffraction
Key Points:
Particle size is not correlated to productivity in the surface mixed layer of Station ALOHA
Seasonal changes in the vertical distribution of particle size classes are apparent
The carbon content of 2–20 μm particles is positively related to productivity rates at the DCM
1. Introduction
In an elegant text on the scattering of light by marine particles, Jonasz and Fournier [2011] state that “one could argue that seawater is nothing else but suspended particles, whose sizes range from molecules through fish and whales.” Undeniably, seawater carries a rich load of particles including colloids (0.001–1 μm), organisms of various morphologies (autotrophs and heterotrophs, 0.001–1000 μm), viruses, detrital material (nanometer–millimeter), and multicellular organisms (>100 μm). The size distribution of these particles follows a classic pattern—the concentration of particles rapidly decreases with increasing particle size [Jerlov, 1976; Sheldon et al., 1972]. In effect, this tells us that the larger the particle is, the rarer it is. From a biological perspective, changes in the particle size distribution largely reflect the time‐variant growth and loss of organisms of various sizes: for example as a result of the seasonal succession from smaller dinoflagellates to larger diatoms in the coastal ocean [Smayda and Trainer, 2010], as episodic blooms of large nitrogen‐fixing organisms (e.g., Trichodesmium spp.) and diatom‐diazotroph associations occur in the open ocean, [Letelier and Karl, 1996; Scharek et al., 1999] or as a result of size‐selective protist grazing on small bacterioplankton [Epstein and Shiaris, 1992; Hagström et al., 1986].
Planktonic organisms, including both heterotrophs and autotrophs, contribute substantially to total oceanic particle loads and are the dominant particulate component in the scattering and absorption of light in the surface waters of the ocean [Field et al., 1998; Jonasz and Fournier, 2011; Stramski et al., 2001]. Phytoplankton, the autotrophic fraction of the plankton residing in the euphotic zone, contribute roughly half of the net photosynthetic carbon fixation on the planet. The cell sizes of individual phytoplankton, which can range from roughly 0.5 to 1000 μm, impact surface area to volume ratios and hence nutrient use efficiency as well as the chlorophyll‐specific absorption of light and the quantum efficiency of photosynthesis [Bricaud et al., 2004; Sathyendranath et al., 1987]. Each of these size‐specific differences can lead to variation in community photosynthetic rates. Accordingly, a relatively nascent effort is being made to evaluate the extent to which the relative size distribution of phytoplankton communities drives observed variability in the rate of net primary productivity (NPP, see review by Nair et al. [2008]) and ultimately export [e.g., Guidi et al., 2009]. The implicit but often unstated assumption is that larger cells lead to higher growth rates and enhanced productivity [Chisholm, 1992; Schlesinger et al., 1981]. These relationships are readily apparent when looking across large gradients in particle loads and productivity, for example, from upwelling regimes to the oligotrophic gyres, but are less clear within regimes or within taxa [Chisholm, 1992; Marañón et al., 2001].
Derivations of community structure and hence particle size structure are increasingly being seen as a means of potentially constraining variability in productivity, as they reflect snapshots of phytoplankton species composition or phytoplankton functional types [Claustre et al., 2005; Kostadinov et al., 2010; Uitz et al., 2008]. An example of how shifts in phytoplankton community structure (and the PSD) relate to NPP in oligotrophic regions is found in the work of Ondrusek et al. [2001]. These authors developed a primary production model in the subtropical North Pacific Ocean using in situ measurements of chlorophyll, the quantum yield of photosynthesis, and chlorophyll‐specific absorption coefficients. Although the model captured the mean productivity of this system, it was only able to account for 50% of the variability in measured production rates. The authors concluded that “understanding community shifts from small prokaryote dominated systems to large eukaryote dominated systems appears to be one of the key elements to improving the performance” of bio‐optical models in the open ocean [Ondrusek et al., 2001]. Similarly, Li et al. [2011] report that while less abundant, “larger” phytoplankton (>2 μm) in the North Pacific subtropical gyre (NPSG) appear more efficient at carbon fixation than smaller‐celled organisms. The authors then hypothesize that shifts in community structure toward these “larger” cells would lead to enhanced productivity in this system. Contrarily, increased abundance of small cells has also been linked to variability in NPP in other oligotrophic regions. Lomas et al. [2010] report coherence between an enigmatic increase of the cyanobacterium Synechococcus between 1996 and 2007 and enhanced NPP in the Sargasso Sea of the North Atlantic. The authors hypothesized that this increase was due to the ability of Synechococcus to enhance growth rates and accumulate biomass in response to nanomolar pulses of nitrate. This finding indicates that shifts in photosynthetic or nutrient use efficiency may be more important to variability in NPP than particle size alone [Chisholm, 1992]. Several studies also report poor relationships between paired measurements of relative particle size and primary productivity [Hayward and Venrick, 1982; Marañón et al., 2003; Marañón et al., 2007; Marañón et al., 2001]. Marañón et al. [2003] in particular conclude that the lack of a relationship between changes in chlorophyll size‐fractions and NPP in the oligotrophic Atlantic imply that “microbial communities in oligotrophic regimes respond to environmental forcing with significant changes in primary productivity that are not associated with trophic shifts.” Taken together, it is not clear whether the available data from oligotrophic ocean regimes fully support a reliable relationship between either the PSD or PFTs and NPP. Positive enhancements in productivity may be more closely related to efficiency of energy capture or uncoupling of growth and loss terms rather than changes in community structure.
These conflicting conclusions regarding the role of phytoplankton community composition as a driver of primary productivity are potentially limited by methodological constraints inherent to measurement of both production rates [see Peterson, 1980 for known biases in the 14C tracer method] and estimations of community composition. For example, an increase in one class of cells (e.g., Synechococcus) does not necessarily imply a shift in the mean PSD. Additionally, physical filtration‐based size‐fractionation may have artifacts (e.g., absorption of dissolved organics onto filters, membrane clogging, inefficient trapping of cells, or cell breakage) (as examples see Gasol and Moran [1999]; Sørensen et al. [2013]). There are a number of other approaches to the characterization of phytoplankton community structure that may prove useful in further elucidating potential linkages between PSD and NPP, albeit none are without disadvantage. For instance, several studies [Bricaud et al., 2004; Kostadinov et al., 2010; Uitz et al., 2008; Vidussi et al., 2001] have used high‐performance liquid chromatography (HPLC) of diagnostic pigments to estimate the relative proportions of phytoplankton functional types: picophytoplankton (0.2–2.0 μm), nanophytoplankton (2–20 μm), and microphytoplankton (>20 μm). These groupings are based on taxonomical classifications of Sieburth et al. [1978]. The primary advantage of this approach is that pigmented particles reflect a diverse consortium of living phytoplankton with no influence from heterotrophic or detrital material. Disadvantages are that filtration is required, diagnostic pigments may be shared by various phytoplankton groups, pigment concentrations per cell may vary with light history and exposure, and size classes are somewhat arbitrary given the known size continuum of phytoplankton classes [Marañón et al., 2007]. Nonetheless, Bricaud et al. [2004] report that the relative proportions of these pigment‐based classes are tightly linked to variation in the chlorophyll‐specific absorption coefficient (a*, m2 mg chlorophyll a −1) and the efficiency of light absorption. Given that the general formulation of many bio‐optical models for the estimation of marine primary productivity relies on a*, this finding has direct implications for the role of community structure on NPP, albeit the relationship between pigment based PFTs and NPP has not been thoroughly explored in open ocean regimes.
A second approach to measure the PSD is via laser diffraction, where a laser beam illuminates a sample volume containing particles and an inversion of the volume scattering function at small forward angles is performed to retrieve the in situ particle size distribution [Agrawal et al., 1991]. A commercial in situ laser diffractometer (LISST‐100X, Laser In Situ Scatterometer/Transmissometer, Sequoia Scientific Inc., hereafter simply LISST) has been utilized in both oceanic and lake environments to study particle dynamics [Barone et al., 2015; Gartner et al., 2001; Mikkelsen and Pejrup, 2001; Serra et al., 2001]. The principle of operation is straightforward: a collimated laser beam is projected through a sample volume having a 5 cm path length. The angular scattering distribution between 0.1° and 20° at 670 nm is measured at a silicon detector with 32 log‐spaced rings and the scattering signal is inverted assuming some particle shape [Agrawal et al., 1991; Agrawal et al., 2008]. There is no mechanical aperture, so forward scattering at each angle is collected simultaneously and the size distribution of particles within 1.25 and 250 μm (equivalent spherical diameter, ESD) is rapidly assessed in a high‐throughput fashion (1 Hz). The LISST has been rigorously tested in the laboratory with suspensions of beads, phytoplankton cultures, and various irregularly shaped particles (e.g., sieved sediments) [Agrawal et al., 2008; Karp‐Boss et al., 2007]. In side‐by‐side tests, LISST estimations of the particle size distribution, volume concentration, and mean particle size agree well with results from the Coulter counter [Reynolds et al., 2010], microscopy [Groundwater et al., 2012], and a digital camera (silhouette photography with a LED flash) [Mikkelsen et al., 2005]. The primary disadvantages of laser diffraction are that retrieval of the PSD requires knowledge of a static inversion function which may not adequately reflect the population, individual particles are not analyzed directly, and the method cannot discriminate between living and particulate detrital material.
In order to improve our understanding of the relationship between particle size and NPP in the oligotrophic NPSG, we have investigated particle and productivity dynamics in a region that has been sampled by the Hawaii Ocean Time‐series (HOT) program at roughly monthly intervals since 1988 [Karl and Lukas, 1996]. The location of sampling is 100 km north of Oahu, Hawaii at Station ALOHA (A Long‐Term Oligotrophic Habitat Assessment; 22° 45'N, 158° 00'W), in approximately 4750 m of water. This region was chosen because of the rich biogeochemical data available and as a representative of oligotrophic ocean regimes. Additionally, key transitions in phytoplankton community structure and NPP are known to occur in this region, including those at episodic to seasonal scales [Li et al., 2011; Winn et al., 1995]. Picoplankton taxa constitute a dominant component of the plankton assemblage throughout the year [Campbell and Vaulot, 1993]; however, stochastic blooms of chain‐forming diatoms and/or colonial diazotrophic cyanobacteria are frequently superimposed over the picoplanktonic assemblage during the late summer and early autumn months [Dore et al., 2008; Fong et al., 2008; Scharek et al., 1999; White et al., 2007]. Such seasonal shifts in plankton often accompany transitions in the upper ocean physical forcing [Claustre et al., 2005; Kostadinov et al., 2010; Uitz et al., 2008]. This documented variability in the size and taxonomic composition of the phytoplankton community represents a promising starting point for our effort to explore the relationship between changes in the phytoplankton community and primary productivity.
2. Methods
To evaluate shifts in phytoplankton communities, we use a combination of pigment‐based approximations of phytoplankton functional types and laser diffraction‐based particle size distributions. Time‐variant shifts in these independent metrics are compared to rate determinations of primary productivity. HPLC data and in situ measurements of 14C‐based primary productivity at Station ALOHA are available for December 1988 to December 2012; LISST measurements of the PSD are available from September 2009 to April 2014.
2.1. Discrete Samples and Methods
As a part of the HOT program core measurement set, seawater is collected and filtered onto 25 mm diameter glass fiber filters (Whatman GF/F) for pigment analysis by HPLC. Samples are analyzed via protocols outlined in Bidigare et al. [2005]. In this work, we used HPLC data to estimate the relative contributions of specific phytoplankton functional types (PFTs) according to the method described in Bricaud et al. [2004] and Uitz et al. [2008]. In short, relative proportions (%) of picophytoplankton, nanophytoplankton, and microphytoplankton are estimated using diagnostic pigments associated with taxonomic groups of marine photoautotrophs in case 1 waters. The pigments used, their abbreviations, and their taxonomic associations are noted in Table 1. The fraction of total chlorophyll a contained in each size class is calculated as shown in equations (1)–(4); the coefficients used represent the global ratio of each respective pigment to total chlorophyll a [Uitz et al., 2006].
| (1) |
| (2) |
| (3) |
| (4) |
Table 1.
Diagnostic Pigments, Representative Algal Classes for Station ALOHA, and General Size Bins From the Algorithms by Bricaud et al. [2004] and Uitz et al. [2008]a
| Diagnostic Pigment | Algal Class | Grouping |
|---|---|---|
| Zeaxanthin | Primarily cyanobacteria | Pico |
| Chlorophyll b | Prochlorococcus | Pico |
| Alloxanthin | Cryptophyceae | Nano |
| 19'‐butanoyloxyfucoxanthin (19'BF) | Haptophyceae and Pelagophyceae | Nano |
| 19'‐hexanoyloxyfucoxanthin (19'HF) | Primarily Haptophyceae | Nano |
| Fucoxanthin | Primarily Bacillariophyceae (diatoms) | Micro |
| Peridinin | Dinophyceae | Micro |
We do not assume strict delineation of size between the classes of picoplankton (“pico”), nanoplankton (“nano”), or microplankton (“micro”); however, we do assume that these pigments correspond to distinct phytoplankton functional types defined by the corresponding algal classes.
When applying these formulations for Station ALOHA, the following must be considered: (1) peridinin concentrations are uniformly low (<7 ng L−1) at this location such that calculations of the fraction of microplankton are largely driven by fucoxanthin levels (0–70 ng L−1 range) and hence diatoms; (2) while there are Chl b containing eukaryotes (e.g., chlorophytes and prasinophytes), Chl b at Station ALOHA is primarily derived from Prochlorococcus spp. [Andersen et al., 1996]; (3) alloxanthin concentrations are rarely detectable at Station ALOHA and so nanoplankton calculations are driven by biomarkers for pelagophytes and prymnesiophytes, and (4) the size classes are rough approximations; in fact this approach groups picoeukaryotes into the nanophytoplankton and small diatoms (<20 μm) as microphytoplankton. For this reason, we do not assume strict size classes for PFTs even though the prefixes (e.g., “pico”) used here do imply size. Data have been compared to in situ 14C‐based measurements of dawn to dusk primary productivity rates available for this same time period; methods for the deployment and processing of the HOT 14C array are described in Letelier et al. [1996].
2.2. LISST Deployment
The LISST was deployed on a bio‐optical package approximately 1.5 m3 in size. The instrument was mounted horizontally with open water flow through the optical path and lowered at a constant descent rate of 10 m min−1 to a depth of ∼200 m using the ship's winch. The package was deployed on an approximately monthly basis between September 2009 and April 2014 for a total of 42 cruises; 2–3 night casts were performed during each cruise. In the present work, data were only used from (1) downcasts so that the instrument was seeing undisturbed water and (2) profiles collected at night in order to avoid light contamination that would otherwise lead to erroneous concentrations of particles in the smallest size bins [Andrews et al., 2011]. From these casts, only data from depths below 20 m and above 175 m were considered. The rationale for the last criterion is to avoid the potential influence of entrained air bubbles [Zhang et al., 2002] on the slope of the PSD in surface waters (<20 m) and to exclude depths well below the 1% surface light level (95–130 m) [Letelier et al., 2004] where net photosynthetic carbon assimilation is minimal. Selection of a 20 m threshold for bubble injection is also guided by the observation that wind speeds at Station ALOHA (<12 m s−1, Woods Hole/HOT mooring meteorological data, http://www.soest.hawaii.edu/whots/) correspond to a bubble penetration depth of <15 m [Vagle et al., 2010]. These considerations (avoidance of ambient light and contamination of the scattering signal by bubbles) are absolutely necessary for proper interpretation of LISST data in oceanic settings [also see Barone et al., 2015].
2.3. LISST Description, Processing Methods, and Rationale
Before the light scattering distribution measured by the LISST is inverted to obtain the particulate volume distribution, the signal must be corrected for background scattering due to pure water and any imperfections of the optics that would cause instrument drift (referred to as the “zscat” by the manufacturer). In the oligotrophic waters at Station ALOHA, we found that the mean LISST raw scattering signal in deep water (∼200 m, raw counts = 32 ± 5 over 32 rings and 42 cruises) was equivalent to our on‐deck background measurements using deionized, reverse osmosis water from the ship's system (raw counts = 34 ± 5). The p values of a two‐sample t test ranged from 0.2 to 0.9; deep water and clean water backgrounds were not significantly different. For consistency, we used the mean of the deepest 2 m of the water column profile as our background (maximal depths of downcast ranged from 176 to 230 m); maximal depths achieved were a function of current speed and the extent to which the optical package descended vertically. While these backgrounds represent the lower detection limit of the LISST, they are not particle‐free; the concentration of particulate carbon at 200 m at Station ALOHA is ∼0.7 μmol L−1. After correction of the raw scattering signal for this background, we verified that the scattering signal in the upper 20–150 m was significantly greater than the background values (∼200 m). In >85% of the samples collected, the scattering signal recorded between 20 and 150 m was significantly greater (n = 56 night profiles over 42 cruises; one‐tailed t test p < 0.05) than deep water blanks for rings 12–32 (corresponding to equivalent spherical diameters (ESD) of 1.25–40 μm). The percent of retrievals significantly greater than deep water blanks was lowest (∼20%) at smaller ring detectors (e.g., at rings 1–6 which correspond to ESD > 100 μm, data not shown). This detection limit is similar to that cited by Barone et al. [2015]. In this same region, using identical deployment procedures and processing routines for data collected in July–September 2013, they found that the signal measured for rings 12–32 was significantly higher than the deep water background signal (202–204 m) for >90% of values in the upper 20–150 m. Thus it is this size (1.25–40 μm) and depth range (20–150 m) where the LISST provides the most reliable signal in our region of study; particles greater than ∼110 μm are not generally above detection limits.
Sequoia Scientific provides two kernel matrices for the scattering inversion. The standard kernel is calculated using Mie theory as a composite of several indices of refraction, and is designed to produce accurate inversion results over a broad range of particle types (ranging from organic to inorganic). Sequoia also provides an empirically derived “randomly shaped” matrix that was developed from light scattering measurements of sieved mineral grains [Agrawal et al., 2008]. The random shape matrix was developed to address artifacts that were observed in data collected on populations of natural particles, where a spurious increase in the small size bins was observed [Agrawal et al., 2008; Mikkelsen and Pejrup, 2001]. We tested both of the inversion kernels provided by Sequoia Scientific as well as a kernel matrix recommended for phytoplankton assemblages by Andrews et al. [2010], where the index of refraction (n) is assumed to be a constant value of 1.17. After the inversion, the data are corrected for the difference in laser power between the factory calibration and the in situ data and an instrument‐specific correction factor is applied to obtain the calibrated particle volume concentration, in units of volume particles per volume of water. Average particle volume distributions were then computed at 2 m intervals for each downcast. A 2 m bin size encompasses on average 240 LISST scans and corresponds to a scanned volume of 0.4 L. All data processing was done in MATLAB using manufacturer‐supplied code for the background scattering correction (getscat.m), the scattering inversion (invert.p using 15 iterations), and the laser power and concentration corrections (vdcorr.m).
The shape of the PSD is commonly described by the exponent (also known as the PSD slope or Junge slope) of a power‐law fit to the relationship between particle number concentration and diameter, the so‐called power‐law model. The general form of this model is
| (5) |
where N(D) is the particle concentration at a given diameter (units of particles L−1 μm−1), N0 is the differential particle concentration at D0, D0 is a reference diameter, and ξ is the exponent of the distribution. In this work, the PSD slope was estimated from the change to particle concentration normalized by the width of each size bin. For purposes of comparison to other studies [e.g., Buonassissi and Dierssen, 2010; Kostadinov et al., 2012; Reynolds et al., 2010], we have applied a linear least squares fit to log‐transformed data; the size range was restricted to 2.63–109.24 μm (median diameters); the reference diameter, D 0 was 2.63 μm, the smallest size bin used in our fit. The rationale for restriction of the size range is to improve the fit of the power law parameterization, and avoid the largest and smallest bins which are subject to the greatest instrument and/or data processing artifacts, for example, scattering at density gradients [Buonassissi and Dierssen, 2010; Kostadinov et al., 2012; Styles, 2006]. As Barone et al. [2015] discuss, the PSD slope should be interpreted with caution given that (1) there is a somewhat arbitrary need to exclude outer and inner rings which are most sensitive to errors and contamination from the PSD fit, and (2) the common means for fitting these spectra are biased [Clauset et al., 2009]; for example, nonlinear fitting procedures are statistically preferable to the near universal utilization of linear regression of log‐normalized data that pervade the LISST‐specific literature.
While the fit parameters are shown, there is no a priori reason to assume that the PSD at Station ALOHA follows a power law. Accordingly, we examined the normalized bias of the PSD to assess differences in the shape of the PSD produced by the inversion kernel. The normalized bias (NB) is simply a description of how the PSD deviates from a modeled (or predicted) PSD, in this case the power‐fit to the PSD data. NB (%) is calculated as follows:
| (6) |
where P(Di) is the predicted particle concentration at a given diameter Di, and O(Di) is the observed particle concentration at the same diameter. We estimated the median NB at each 2 m depth bin with all available profiles in the data set. Figure 1 shows the particulate spectra and the NB for all tested inversions. The shape of the PSD generated using the random inversion shows larger deviations from a power law than the spherical inversion, particularly for small particles (<3 μm). The inversion matrix suggested by Andrews et al. [2010] generated significantly lower particle concentrations, particularly above 40 μm.
Figure 1.
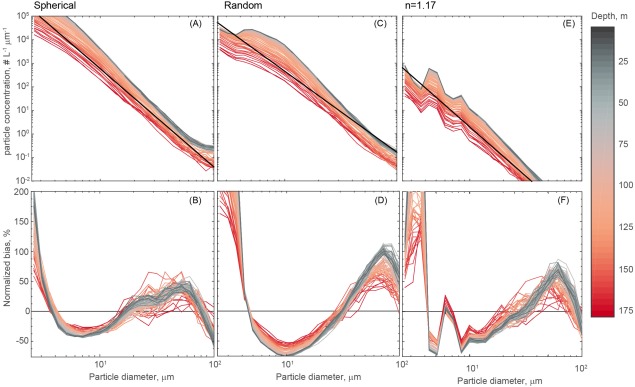
The mean PSD derived from a spherical inversion (a), random inversion (c) and n = 1.17 (e). Data are binned to 2 m depth bins, and each sample represents the median of all available LISST profiles at that depth. The black line indicates the mean power law fit. The normalized bias of a power law fit is shown for the spherical (b), random (d) and n = 1.17 (f) inversions as a function of size (x‐axis) and depth (color scale).
As a means of describing changes in the PSD over depth and time, we also used a weighted average particle size, Davg (units of μm), shown in Slade et al. [2011] as
| (7) |
where, A(Di) is the areal size distribution in suspended cross‐sectional area per volume (m2 m−3) for each LISST size class i, with mean diameter Di. The areal size distribution is calculated from the volume size distribution (μL L−1) by assuming spherical geometry: . The use of areal size distribution in the calculation of Davg makes intuitive sense because cross‐sectional area is what the LISST actually detects. It is important to note that, unlike the PSD slope, the average particle size estimate makes no assumptions about the shape of the PSD.
To simplify the description of size spectra, we have adopted a version of the particle classification scheme proposed by Sieburth et al. [1978] for the separation of planktonic organisms in picoplankton (0.2–2 μm), nanoplankton (2–20 μm), and microplankton (20–200 μm). We calculate the binned particle volume in the effective size ranges of 1.25–2.05 μm (the smallest size bin the LISST is capable of resolving), 2.05–20.86 μm, and 20.86–109.25 μm (the upper limit is restricted to avoid scattering artifacts introduced by density gradients) [Styles, 2006] and to reflect our finding that particles > ∼ 100 μm are often not detectable. These classes are referred to as 1.25–2 μm, 2–20 μm, and 20–100 μm, respectively. Clearly, this operational definition excludes a large fraction of picoplankton (<1.25 μm) and larger aggregates or organisms that fall out of this size range. Nonetheless, trends in a component of picoeukaryote populations (nominally 0.2–3.0 μm in diameter) [Worden and Not, 2008], diatoms (∼2–200 μm) [Hasle, 1996], nanophytoplankton such as prymnesiophytes >5 μm [Venrick, 1982], and detrital material (1.25–100 μm) should be captured by this approach.
Finally, to transform particle abundance (N(D)) into particulate carbon concentrations, we used the relationship derived by Menden‐Deuer and Lessard [2000] for non‐diatom protistan plankton. This transformation was developed using cultures of cyanobacteria, dinoflagellates, and prymnesiophytes and is expressed as follows:
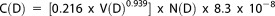 |
(8) |
where C is carbon concentration (μmol C L−1), V is the volume in μm3 of a spherical particle at a given median ring diameter (D), N(D) is the particle abundance in cells L−1, here not normalized to the bin‐width and the scaling factor (8.3 × 10−8) converts from pg C to μmol C. Just as we have done for particle volume, we have binned carbon content into three classes: 1.25–2 μm, 2–20 μm, and 20–100 μm, respectively. We define the total particle carbon (TPC in μmol L−1) as the sum of the carbon concentration in the 1.25–109.25 μm range. LISST‐derived TPC does not include contributions from heterotrophic and photosynthetic bacteria less than ∼1.25 μm nor is it impacted by dissolved organic carbon absorption onto glass fiber filters measurements [see Moran et al., 1999]. Nevertheless, Barone et al. [2015] report that the sum of flow cytometrically derived bacterial carbon and LISST‐TPC accounted for 76% ± 9% of measured PC between 25 and 75 m and 51% ±14% at 125 m at Station ALOHA. For this reason, we consider LISST TPC to be a reasonable approximation for living and detrital particles between 1.25 and 100 μm.
3. Results and Discussion
3.1. Diagnostic Pigments and Productivity
We have applied equations (1), (2), (3), (4) to HPLC data collected in the upper 125 m of the water column at Station ALOHA and analyzed results from two ecologically relevant depth bins: (1) the upper 45 m which generally encompasses the surface mixed layer and is considered light‐saturated (e.g., light levels are above half‐saturation irradiances (EK) for photosynthesis and NPP is largely independent of photosynthetically active radiation at 14C incubation depths (PARz), see Li et al. [2011]); and (2) 100–125 m encompassing the two standard sampling depths nearest the deep chlorophyll maxima which ranged between ∼100 and 140 m over the study period. Notably, this deeper bin is light‐limited (PARz < EK) and NPP should be a linear function of light levels [Letelier et al., 2004; Li et al., 2011]. The seasonal cycle of the relative proportions of pico, nano, and microphytoplankton in these depth bins are shown in Figure 2. Picophytoplankton consistently account for greater than 50% of the total chlorophyll with maxima in the summer‐fall months and the largest observed seasonal amplitude (6–7%, Figure 2a) whereas microphytoplankton contributions peak in spring to summer months and show a more damped seasonal amplitude (2–3%, Figure 2c). These trends are similar in surface and deep strata. Nanophytoplankton seasonal cycles show opposing trends when these depth strata are compared; maxima occur in spring in the surface and fall at depth with an amplitude of ∼5% in both strata (Figure 2b). Essentially, the euphotic zone of Station ALOHA is a regime dominated by picophytoplankton, with changes in the relative abundance of larger cells (or at least pigments diagnostic of these cells) being more subtle.
Figure 2.
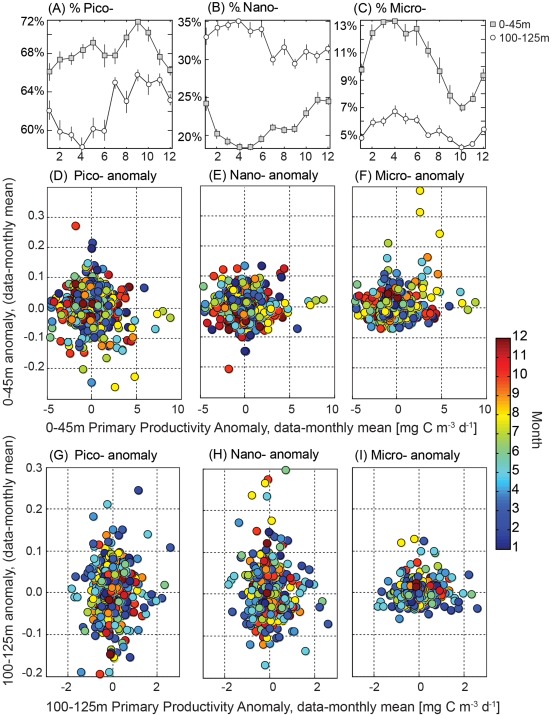
(a–c) Monthly mean (±standard error) contributions of picophytoplankton, nanophytoplankton, and microphytoplankton to chlorophyll a as determined by the HPLC‐based algorithm (see equation (1)–(4)) for samples collected within the upper 45 m (circles, including standard sampling depths of 5, 25, and 45 m) and for samples collected between 100 and 125 (squares) over the period of 1988–2013. Anomaly (fraction—monthly mean for each standard sampling depth) of the relative contributions of picophytoplankton, nanophytoplankton, and microphytoplankton relative to paired measures of net in situ primary productivity in the upper 45 m (d–f) and 100–125 m, (g–i) also corrected to remove the monthly climatological mean. Colors correspond to sampling month. No significant statistical relationships were found between the HPLC‐based size composition and primary productivity (t test, p > 0.05).
Given that the inherent maximal growth rates of diatoms [Geider et al., 1986] (which are presumed to compose the pigment based microphytoplankton pool) are generally thought to exceed those of the predominant picophytoplankton in this system (Prochlorococcus and Synechococcus) [Chisholm, 1992], we might expect enhanced NPP when this class comprises a larger fraction of the standing stock. We do not however find any relationships between absolute rates of NPP and HPLC size fractions (data not shown). To reduce the impact of the seasonal cycle of solar irradiance on pigment concentrations, particularly in the deeper depth bin, we have also examined the relative change in HPLC size fractions and NPP by subtracting the climatological monthly mean from all data (Figure 2). The variability for any one class is on the order of ±10%, with larger anomalies in pico and nanophytoplankton fractions at depth than in the surface (Figure 2). There are no statistically significant relationships between HPLC‐based particle size classes and primary productivity or anomalies thereof (two‐tailed t tests, p ≫ 0.05). The largest anomalies in productivity (> 5 mg C m−3 d−1 in surface and > 2 mg C m−3 d−1 at depth) are in fact associated with “normal” HPLC‐based PFTs (Figure 2); however, episodic increases in microphytoplankton are apparent in spring and summer months in the upper 45 m.
To the extent that these pigment ratios represent changes in taxonomic groups rather than physiology, our findings suggest the following: (1) there are clear and stable seasonal cycles in the relative contributions of pico, nano, and microphytoplankton to total chlorophyll, and (2) increases in microplankton are episodically associated with but not necessary for elevated primary productivity in the upper water column at Station ALOHA during the spring‐summer time frame. These analyses suggest that shifts in community structure, from small to large or vice versa, do not drive variability in NPP in this regime. If this is the case, then retrieval of phytoplankton functional types from present‐day ocean color remote sensing [e.g., Silio‐Calzada et al., 2008; Uitz et al., 2009] may be of limited utility in oligotrophic regimes.
A final point about the relationship between pigments and productivity in the surface ocean of the NPSG: photoadaptation is in fact readily apparent in this region. In the upper euphotic zone, absolute concentrations of chlorophyll peak in low‐light winter months and decline in high‐light summer months as cells adjust to ambient light and nutrient conditions [Letelier et al., 1993; Westberry et al., 2008; Winn et al., 1995]. This seasonality (Figure 3) opposes the cycle of primary productivity which is highest in summer and lowest in winter [Karl et al., 2012; Letelier et al., 1996]. Accordingly there is no relationship between either total chlorophyll a or weighted diagnostic pigments (equation (4)) and NPP in the light‐replete upper 45 m at Station ALOHA. Alternately, at the base of the euphotic zone where productivity is tightly regulated by light [Letelier et al., 2004; Li et al., 2011], the monthly climatology of HPLC chlorophyll is significantly related to NPP (linear regression, R2 = 0.72, p < 0.05, Figure 3). So while the surface ocean shows pigment and light independent variability in NPP, the base of the euphotic zone in this region exhibits coherent shifts in NPP and total chlorophyll but not specific PFT fractions. Again though, these conclusions are subject to light‐dependent shifts in absolute and relative pigment concentrations. We next explore relationships between NPP, mean particle size, and carbon‐based particle size classes which are not subject to the effects of photoadaptation.
Figure 3.
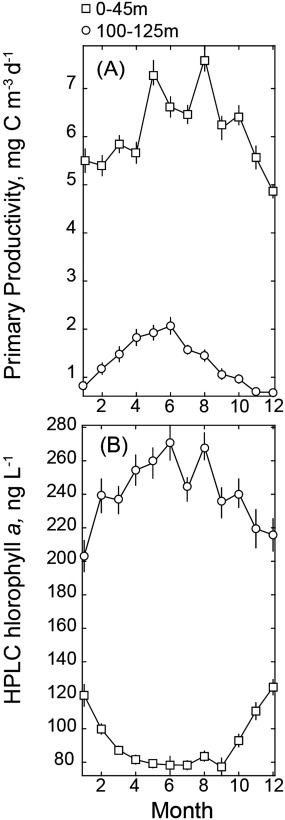
Seasonal cycle of monthly mean (±standard error) NPP (a) and HPLC chlorophyll a (b) for samples collected within the upper 45 m (circles, including standard sampling depths of 5, 25, and 45 m) and for samples collected between 100 and 125 (squares) over the period of 1988–2013.
3.2. Initial Characterization of the Particle Size Distribution at Station ALOHA
Given that laser diffraction is not routinely applied in oligotrophic settings, first we characterized and examined the shape and fit of the PSD for Station ALOHA. The approximation of particle size from forward scatter relies on mathematical inversion of the observed scattering signal and certain assumptions about particle shape and refractive index. Without explicit knowledge of the bulk suspended particle properties, these assumptions cannot be verified [Graham et al., 2012]. Moreover, there are multiple scenarios that may lead to divergence of in situ particle size distributions from a power function (the Junge distribution); these include largely monospecific blooms, flocculation/aggregation, and instrument artifacts [Chami et al., 2006]. We have processed raw LISST data in MATLAB using three kernel matrices (spherical, random, and assuming a refractive index of 1.17) and found that the default composite sphere kernel provides a better fit to a Junge‐type distribution (Figure 1) and more reasonable particle concentrations (Table 2). The n = 1.17 kernel matrix generated lower particle concentrations across all size bins, whereas the random inversion provided similar spectra to the spherical inversion, albeit the predicted concentrations of <5 μm particles was lower by an order of magnitude (Figure 1). We then compare the predicted particle concentrations from these three inversions to the mean concentration of flow cytometry derived abundances of eukaryotes at Station ALOHA at discrete depths (25 and 125 m, Table 2). Notably, these cells include pico‐ and nanoeukaryotes and span cell diameters of approximately 0.2–20.0 μm [Pasulka et al., 2013]. This comparison shows that both the random and n=1.17 retrievals of particle abundance (∑1.25–109 μm) underestimate eukaryotes abundances and therefore must also underestimate total phytoplankton concentrations. Similarly, the estimated particulate carbon concentrations for both the random and n=1.17 inversions are markedly lower than the spherical inversion. Last, we note that the shape of the n=1.17 inversion spectra is unique and not easily explained by a power law (Figure 1). The random and spherical inversions do however produce highly similar temporal and vertical patterns (data not shown). For these reasons, we have elected to perform all calculations of particle concentrations, volume, and carbon using the spherical inversion; this selection also allows us to more readily compare our results to those of other studies.
Table 2.
The Median ± Standard Deviation of the Total Particle Abundance (1.25–100 μm), Total Particle Volume (TPV), and Total Particle Carbon (TPC) at 25 m and 125 m Calculated Using the Spherical, Random, and n = 1.17 Inversion Matrices for All LISST Casts (n = 56)a
| Inversion | Particle Abundance (# L−1) | TPV (μL L− 1) | TPC (μmol C L−1) | Eukaryotic Phytoplankton (# L−1) | Particulate Carbon (μmol C L−1) |
|---|---|---|---|---|---|
| 25m | 1.1 × 106 ± 3.7 × 105 | 2.3 ± 0.5 | |||
| Spherical | 1.3 × 106 ± 3.6 × 105 | 0.065 ± 0.033 | 0.82 ± 0.37 | ||
| Random | 2.0 × 105 ± 7.9 × 104 | 0.052 ± 0.035 | 0.59 ± 0.44 | ||
| n = 1.17 | 1.9 × 103 ± 3.2 × 104 | 1.8 × 10−4 ± 1.3 × 10−4 | 0.002 ± 0.001 | ||
| 125m | 9.1 × 105 ± 3.1 × 105 | 1.3 ± 0.3 | |||
| Spherical | 1.3 × 106 ± 6.3 × 105 | 0.032 ± 0.017 | 0.41 ± 0.18 | ||
| Random | 1.7 × 105 ± 8.6 × 104 | 0.024 ± 0.016 | 0.27 ± 0.16 | ||
| n = 1.17 | 1.4 × 103 ± 0.6 × 103 | 8.6 × 10−5 ± 5.3 × 10−5 | 0.001 ± 0.001 |
For reference, we report the climatological average ± standard deviation of the abundance of eukaryotic phytoplankton, which is a fraction of the total particle abundance and particulate carbon for September 2009 to December 2013, the period of data available which overlap LISST deployments.
Evaluation of power model fits to the log of the particle size distributions also justify using the spherical inversion. The mean slope of the PSD (Figure 4d, Table 3) is well within the range typically observed in oceanic waters, mostly from 3.8 to 4.5 [Reynolds et al., 2010; Stemmann et al., 2008] and R2 of the model fit were above 0.97 (p < 0.01) on average (Table 2). Nevertheless, all tested kernels did show consistent divergence from the idealized power law at specific size bins (Figure 1). For the spherical inversion, a power law overestimates the volume of <2 μm particles and particles in the 20–80 μm size range and underestimates particle concentration in the 2–20 μm particle size range. The shape of the NB is similar for the random inversion; however, the magnitudes of deviations are larger. Given that these deviations tend to occur over consistent size ranges, they likely reflect real aspects of the bulk community size structure in our study area. Alternatively, as noted above, the shape of the n = 1.17 inversion showed the largest underestimations of small, <5 μm particles. In sum, these analyses indicate that while a power law is a good statistical approximation of the PSD at Station ALOHA, systematic departures are apparent in distinct size classes. It must also be acknowledged that these slopes are influenced by small, out of range particles (<1.25 μm) which are known to contribute to the smallest LISST size bins [Andrews et al., 2011]. For this reason and as a consequence of known biases using log‐log fits, these values should only be used for general comparisons of the PSD. In that regard, both Davg (which makes no assumption about the shape of the PSD) and the exponent of the power law suggest a rather stable vertical distribution of mean particle size at Station ALOHA (Figure 4 and Table 3). Moderate increases in mean Davg (Figure 4) are apparent in the upper 45 m in spring (February–May) and these increases extend to the lower euphotic zone in fall (September–October); these increases are not statistically significant due to high variability in Davg (t test, p > 0.7).
Figure 4.
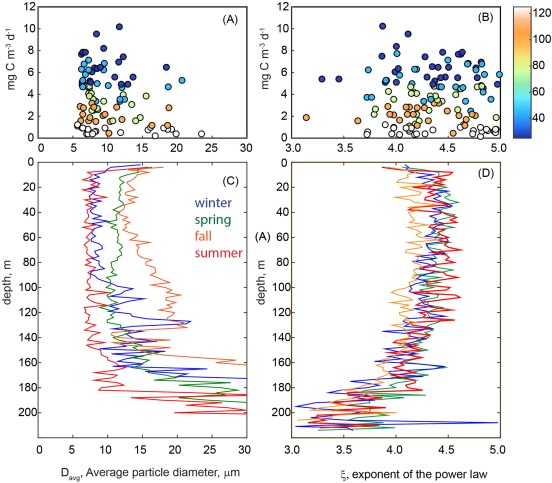
Relationship between NPP measured between 25–125m, (mg m−3 d−1) and (a) the average particle diameter (Davg) and (b) the absolute value of exponent of a power law fit (ξ) of the particle size distribution. Colors correspond to sampling depth. The mean depth profile of Davg and ξ for winter (November–January, blue), spring (February–May, green), summer (June–August, red), and fall (September–October, orange) and shown in Figures 4c and 4d, respectively. While shown, values at less than 20 m are not considered due to the potential influence of bubbles (<20 m). In the 20–175 m strata, the mean ± the standard deviation for ξ was 4.2 ± 0.7, whereas the Davg was 13.5 ± 5.7 μm (n = 63 casts binned to 2 m resolution for a period spanning September 2009 to April 2014). Larger values of ξ indicate greater contributions by small particles; smaller values of ξ indicate greater contributions by large particles.
Table 3.
The Median and Standard Deviation (SD) of Two Descriptors of the Particle Size Distribution at Station ALOHA Standard Sampling Depths (Between 20 and 175 m), Average Particle Size and PSD Slopea
| Depth (m) | Davg (μm) median | Davg (μm) SD | PSD slope, ξ median | PSD slope, ξ SD | R2 of PSD Fit |
|---|---|---|---|---|---|
| 25 | 10.69 | 5.17 | 4.48 | 0.91 | 0.99 |
| 45 | 9.67 | 6.67 | 4.49 | 0.70 | 0.99 |
| 75 | 9.75 | 5.14 | 4.39 | 0.65 | 0.99 |
| 100 | 10.52 | 12.96 | 4.36 | 0.82 | 0.99 |
| 125 | 10.35 | 7.66 | 4.32 | 0.67 | 0.98 |
| 150 | 11.56 | 16.71 | 4.26 | 1.44 | 0.98 |
| 175 | 20.21 | 26.67 | 3.86 | 2.04 | 0.97 |
Data used are mean and SD within ± 2 m of the sampling depths shown.
3.3. Temporal Variability of Particle Size Classes and Mean Particle Size
Laser scatterometry allows for much higher vertical and temporal resolution sampling than can be offered by any discrete bottle‐based measurements (e.g., HPLC) and permits an assessment of the temporal variability of the abundance and volume of particle size classes as well as the relative contributions of size classes to total particle volume. To investigate variability of particle size at Station ALOHA, we first examined changes in particle volume and carbon content over time and then assessed shifts in the average weighted particle diameter (Davg). As described above, particle volume estimated via the LISST was grouped into size bins of roughly 1.25–2 μm, 2–20 μm, and 20–100 μm. Particles in the 1.25–2 μm size range generally exhibit maxima at depths of 100–140 m with only rare increases within the upper ocean (September 2009 and June 2011, Figures 5a and 6a). Conversely, 2–20 μm particles were maximal in the upper water column, typically within the mixed layer (Figures 5b and 6b) with a shape similar to the depth dependence of NPP (Figure 6c). No persistent depth profile was apparent for particles in the 20–100 μm size class (Figure 5c). There is also apparent seasonality to these particle distributions, specifically for the 1.25–2.0 μm size class which exhibits progressively deeper maximum depths when grouped by season (Figure 6a). From shallow to deep, the centers of the seasonal depth maxima (Figure 6a, calculated as the depth of the maximum value within 90–130m) are as follows: winter (November–January, 102 m, n = 16), spring (February–May, 104 m, n = 13), summer (June–August, 106 m, n = 15), and fall (September–October, 122 m, n = 12). Seasonal differences in 1.25–2.0 μm volume concentrations are less apparent in the surface mixed layer where only fall profiles differ from other seasons; volume concentrations are < 1 × 10−3 for fall and ≥ 1 × 10−3 in all other seasons (Figure 6a). For the 2.0–20 μm size class, volume concentrations in the upper 45 m are lowest in winter, increase in spring and reach maxima in summer and fall (Figure 6b). At depths typical of the DCM (100–125m), the lowest 2.0–20 μm volume concentrations are observed in winter and the highest in spring, with summer and fall values falling in between.
Figure 5.

Contour plots of particle volume in the following size classes: (a) 1.25–2.0 μm, (b) 2.0–20 μm, and (c) 20–100 μm as measured at approximately monthly intervals between September 2009 and April 2014. Breaks in coverage are a result of gaps in instrument availability or cruise scheduling.
Figure 6.
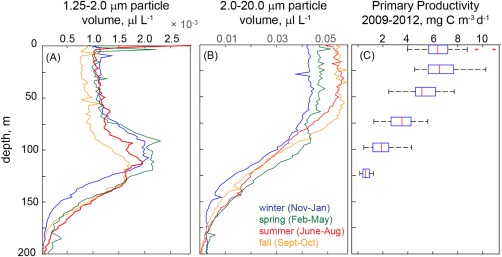
Mean particle volume normalized to the maximum particle volume for each profile in two size classes: (a) 1.25–2 μm and (b) 2–20 μm. Profiles are shown as the mean for each season (months noted in the legend). Note that the x‐axis limits differ. The depth profile of primary productivity measured at HOT standard sampling depths (5, 25, 75, 100, and 125 m) is shown in panel C, where the central mark of each box is the median, the edges of the boxes are the 25th and 75th percentile and whiskers extend to the 95th percentile. Outliers are plotted as crosses.
While not comparable to trends seen in HPLC‐based size fractions, we find that LISST‐based particle size classes do show moderate seasonality in surface waters, particularly for the 2.0–20 μm size class which increase from winter through summer/fall. Notably, within this size class, particles with an ESD of ∼5 μm are the most significant contributors to particle volume and carbon content (Figure 7). We cannot determine the identity of these 5 μm particles; however, this size range is consistent with small eukaryotic nanoplankton [DuRand et al., 2001]. Differences between HPLC and LISST‐based seasonality may be a result of contributions of detrital material to LISST‐based particle loads or a consequence of the impact of photoacclimation, for example, changes in pigment per cell, on HPLC PFTs, rather than cell concentrations.
Figure 7.
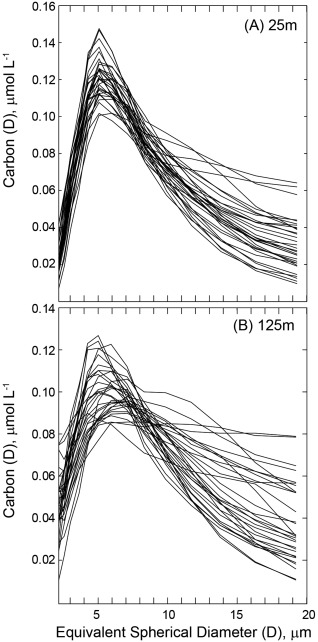
Spectra of the carbon content of particles of equivalent spherical diameter [Carbon (D)] of 2–20 μm for (a) 25 m and (b) 125 m. At both depth horizons, a peak in carbon content is found at 5 μm; however, the peak is broader at 125 m.
We also observed shifts in the mean particle diameter (Figure 8). In the surface mixed layer (25 m), Davg ranged from ∼5 to 20 μm with episodic increases in September 2009, 2012, and in spring and winter months of 2013 (Figure 8a). At the depth horizon of 125 m, typically at or near the chlorophyll maximum at this site, Davg was more variable, ranging from 5 to 30 μm with values regularly exceeding ∼15 μm nearly every fall/winter. These metrics indicate a relatively stable particle size in surface waters at Station ALOHA punctuated by episodic increases in particle diameter with a more regular increase in particle size at depth (100–125m) in fall/winter months.
Figure 8.
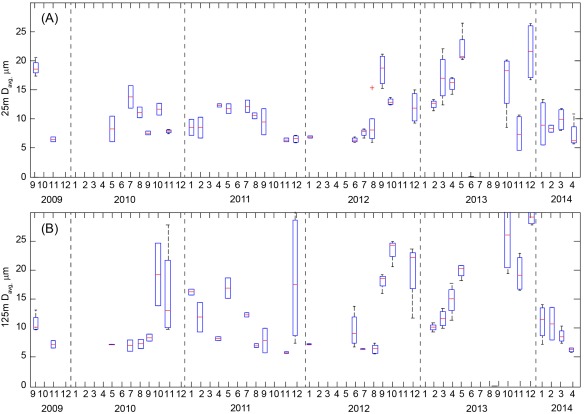
Box and whisker plot of weighted mean particle diameter (Davg) at the depth horizon of (a) 25 ± 2 m and (b) 125 ± 2 m. The climatological median ± one standard deviation was 10.3 ± 4.7 μm at 25 m and 10.9 ± 7.3 at 125 m. In both plots, the central mark of each box is the median, the edges of the boxes are the 25th and 75th percentile and whiskers extend to the 95th percentile. Outliers are plotted as crosses. Data are derived from 2 to 3 nighttime casts per cruise.
Last, we have investigated the relationship between LISST‐based size fractions and net primary production. We find no relationship between Davg or the PSD slope and NPP rates (Figures 4a and 4B). This indicates that changes in NPP are not impacted by the relative mean particle size. We can also ask whether we see increased NPP as a result of alteration in the concentration of individual particle size classes. In this case, we find that the estimated volume and carbon content of particles within the 2–20 μm fraction shows a positive relationship to NPP (Figure 9b) only in the lower euphotic zone (discrete depths of 100 and 125 m; Model 2 linear regression, R2 = 0.25 and 0.12, respectively, p < 0.05, n = 23). This relationship is even stronger when both depths are considered (R2 = 0.41, slope = 0.37 d−1, Figure 9b). At the other standard depths, there was no significant relationship between LISST‐derived carbon content and primary productivity. To further investigate this finding, we have also examined the relationship between NPP and particulate carbon (PC) as determined by high‐temperature combustion via the HOT program. Again, we find a linear relationship with PC and NPP at the base of the euphotic zone (Model 2 regression for 100 and 125 m, R2 = 0.41, slope = 0.13 d−1, Figure 9d). The vertical profiles of PC and NPP are similar in shape (see Figure 6c for NPP) at Station ALOHA, which would lead one to expect some relationship between PC (a proxy for biomass) and PP when the full euphotic zone is considered, albeit not necessarily at a single depth. Together these data indicate that increases in the 2–20 μm fraction may contribute to growth and biomass accumulation (carbon and chlorophyll‐based, see Figures 3 and 9) at the base of the euphotic zone. In general, increases in 2–20 μm carbon and productivity at depth occur in summer‐fall months, consistent with the timing of deepening or shoaling of the 1% light level [see Letelier et al. 2004]. In summary, our findings indicate that neither mean particle size nor shifts in the carbon content of any of the three particle size fractions considered in this study are associated with enhanced productivity in the surface ocean of the NPSG. However, in the lower euphotic zone seasonal increases in the proportion of the 2–20 μm size fraction appears to coincide with enhanced NPP, notably during periods when the 1% light level crosses the 100 m depth horizon. This increase in the carbon content in 2–20 μm particles does not correspond to significant changes in Davg or the PSD slope, suggesting that shifts in one component of the community may not alter the mean character of the particulate pool.
Figure 9.
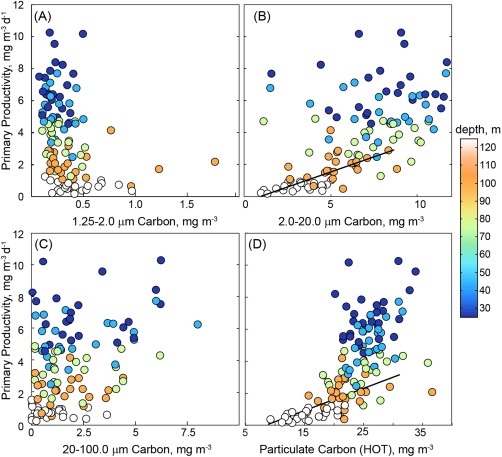
Relationship between the rate of NPP measured in 12 h in situ incubations at Station ALOHA between September 2009 and December 2012 and the carbon content of particles in the following size classes: (a) 1.25–2.0 μm, (b) 2.0–2 0 μm, (c) 20–100 μm as well as (d) particulate carbon collected by HOT program. LISST data are the mean of values measured within ±2m of the depth of NPP incubations. Colors correspond to depth. Total particulate carbon and particles in the 2–20 μm range show a positive relationship to measured productivity rates, however this relationship is only linearly significant at 100 and 125 m depth horizons (Type II linear regression shown in Figure 9b: slope = 0.36 d−1, R2 = 0.41; Type II linear regression shown in Figure 9d: slope = 0.13 d−1, R2 = 0.43).
Subtle changes in particle size classes may translate into significant export production without measurable increases in bulk chlorophyll or NPP. Because the annual mean of new production in this oligotrophic region is approximately 6% of NPP [Karl et al., 2012], even small increases in large cells (e.g., the 2–4% seasonal change in diatom markers indicated by HPLC, Figure 2 or the <5 mg m−3 change in 2–20 μm carbon estimated by the LISST at the 100–125 m depth horizon, Figure 9) may drive pulses of organic matter export into the aphotic zone. Diatoms in particular are known to contribute disproportionally to the particulate flux observed in deep sediment traps [Scharek et al., 1999]. Intriguingly, Karl et al. [2012] report annually recurring, elevated fluxes of particulate carbon and nitrogen in 2800–4000 m sediment traps between 15 July and 15 August. This pulse is not detected in the shallow traps (150 m) presumably due to differences in trapping efficiency between deep and shallow traps as well as the selective remineralization of particles with depth [Karl et al., 2012]; hence we have not made an attempt to correlate the PSD to shallow export fluxes. If this increase in carbon content and NPP also leads to a proportional increase in carbon flux, then the base of the euphotic zone may serve as a source of organic material for the annual recurrent summer export pulse. This hypothesis would require knowledge of the PSD of sediment trap material, which we are currently lacking at Station ALOHA [albeit this relationship has been studied elsewhere, e.g., Durkin et al., 2015; Guidi et al., 2008]. Future studies pairing measurements of the PSD and size‐fractionated productivity with sediment traps would be a step toward better understanding the relative contributions of various size classes to net community production and export in this region.
4. Conclusions
In order to better understand how phytoplankton community structure and particle size impact productivity in the open ocean, we have compared pigment‐based PFTs and laser diffraction‐based estimates of particle size classes to parallel measures of 14C‐based primary productivity conducted by the HOT program. The conclusion we reach is similar to the assessment of Chisholm [1992]: “the simplicity of the general relationships serve as a stable backdrop against which the exceptions can shine.” Particle size and productivity do not seem to covary in the upper euphotic zone at Station ALOHA; albeit there are exceptions at the base of the euphotic zone where light levels exert strong control on NPP.
In the upper 45 m, there are clear and stable seasonal cycles in HPLC pigments diagnostic for pico, nano, and microphytoplankton; however, these cycles are not significantly correlated to productivity, in either an absolute or relative sense (Figure 2). The chlorophyll content of the three HPLC‐based size fractions and the monthly anomaly thereof show no statistically significant relationship to rates of primary production. Particle volume and carbon content for particles 1.25–110 μm similarly show no relationship to productivity in surface waters (Figure 9). So while there is temporal variation in PFTs and PSDs (Figures 2, 6, and 8), these shifts do not help explain the variability in upper euphotic zone productivity in the NPSG. This lack of correlation may reflect methodological bias. For example, HPLC‐based classifications only approximate changes in phytoplankton community structure; relative proportions of diagnostic pigments are impacted by photoacclimation as well as biomass changes. Laser diffraction only detects a fraction of the true PSD, particles smaller than ∼1.25 μm are poorly detected although it is these very particles that are responsible for ∼50% of productivity in this region [Williams et al., 2008] and particles >100 μm are rare enough to be at the detection limit of the LISST. Of course the 14C tracer method also comes with biases, e.g., bottle effects, 14C DOC excretion and re‐uptake and dark 14C uptake [Peterson, 1980]. These biases may obscure relationships between particle size and productivity. Alternately, a more resonant hypothesis is that the variability in productivity in the upper 45 m of Station ALOHA is driven by size‐independent shifts in phytoplankton physiology. A number of studies have noted the role of short‐lived upwelling and mixing events as well as the passage of mesoscale eddies that result in nutrient injections to surface waters that can fuel net growth [Calil et al., 2011; Letelier et al., 2000]. Transient nutrient injections can potentially lead to changes in the efficiency of light absorption, or the quantum yield of photosynthesis without affecting community structure and hence particle size [Finkel et al., 2004; Geider et al., 1986]. So while changes in particle size may reflect shifts in community structure they do not necessarily imply shifts in net productivity in the stratified surface waters of the NPSG. Further investigation of the variability of chlorophyll‐specific absorption or the quantum yield of photosynthesis in this system is warranted to constrain the variability of PP rates in the surface mixed layer at Station ALOHA.
At the base of the euphotic zone, we find a significant relationship between chlorophyll a (Figure 3), and carbon content (which is a function of particle volume, equation (7)) in particles with an equivalent spherical diameter between 2 and 20 μm and parallel measures of PP at depths of 100 and 125 m (Figure 9b). This increase does not correspond to an increase in mean descriptors of the PSD: Davg or the PSD slope (Figure 4). So it seems that while one fraction of the particulate spectrum increases, compensatory changes in other fractions preserve the mean character of the PSD. We believe this increase in 2–20 μm particulate matter reflects a real increase in phytoplankton that can partially explain the increases in summer‐fall NPP at these depths. The 1% light level at Station ALOHA varies seasonally by ∼30 m [Letelier et al., 2004] from ∼120 m depth during summer to ∼90 m depth during winter. NPP rates at the deepest standard sampling depths measured by the HOT program (100 and 125 m) closely follow light levels; rates are highest in summer when light penetrates further in the water column allowing summer deepening of the nitracline [Letelier et al., 2004]. During these summer periods, we observe an increase in the volume and carbon content of relatively large cells (2–20 μm); particles of ∼5 μm diameter drive this signal. We hypothesize that the deepening of isolumes and the subsequent utilization of nitrate allows for increase in the abundance of eukaryotes or small diatoms that would be detected in this size range. Notably, while the HPLC pigment‐based approach does not show this same relationship between discrete PFTs and NPP, the seasonal cycle of total chlorophyll at 100–125 is positively related to NPP. In summary, while we cannot rule out factors such as an increase in detrital particles or an accumulation of sinking particles at depth in summer, the seasonal deepening of isolumes and increased nitrate availability appear to fuel net growth and biomass accumulation at the base of the euphotic zone. This study in effect reveals a water column partitioned into a light‐independent surface mixed layer where changes in phytoplankton physiology drive variability in NPP and a light‐dependent region at the base of the euphotic zone where 2–20 μm particles may contribute to observed increases in phytoplankton biomass that drive enhanced NPP.
Acknowledgments
This work was funded by the NASA New Investigator Program (NNX10AQ81G, A.W.) and an Alfred P. Sloan Foundation Research Fellowship (A.W.). Additional support was provided by the NSF to the HOT program (current grant OCE 1260164 to M.J.C.), C‐MORE (EF0424599 to D.M.K.), the Gordon and Betty Moore Foundation (to D.M.K.), and the Simons Foundation (D.M.K., M.J.C., and A.W.). The authors are very grateful to Wayne H. Slade for many helpful and enjoyable discussions regarding data processing methods. We are ever indebted to the tenacious and committed staff of the HOT program for their significant efforts in the careful deployment of optical instrumentation, specifically we acknowledge Lance Fujieki, Blake Watkins, and Dan Sadler for their efforts at sea. All LISST data are available on the HOT website (http://hahana.soest.hawaii.edu/hot/hot-dogs/) and code for additional data processing is available upon request to the corresponding author (awhite@coas.oregonstate.edu).
White, A. E. , Letelier R. M., Whitmire A. L., Barone B., Bidigare R. R., Church M. J., and Karl D. M. (2015), Phenology of particle size distributions and primary productivity in the North Pacific subtropical gyre (Station ALOHA), J. Geophys. Res. Oceans, 120, 7381–7399, doi:10.1002/2015JC010897.
References
- Agrawal, Y. , McCave I., and Riley J. (1991), Laser diffraction size analysis, in Principles, Methods, and Application of Particle Size Analysis, edited by James P. M. Syvitski, pp. 119–129, Cambridge University Press, N. Y. [Google Scholar]
- Agrawal, Y. , Whitmire A., Mikkelsen O. A., and Pottsmith H. (2008), Light scattering by random shaped particles and consequences on measuring suspended sediments by laser diffraction, J. Geophys. Res., 113, C04023, doi:10.1029/2007JC004403. [Google Scholar]
- Andersen, R. A. , Bidigare R. R., and Latasa M. (1996), A comparison of HPLC pigment signatures and electron microscopic observations for oligotrophic waters of the North Atlantic and Pacific Oceans, Deep Sea Res., Part II, 43(2), 517–537. [Google Scholar]
- Andrews, S. , Nover D., and Schladow S. (2010), Using laser diffraction data to obtain accurate particle size distributions: The role of particle composition, Limnol. Oceanogr., 8, 507–526. [Google Scholar]
- Andrews, S. , Nover D., Reardon K., Reuter J., and Schladow S. (2011), Limitations of laser diffraction for measuring fine particles in oligotrophic systems: Pitfalls and potential solutions, Water Resour. Res., 47, W05523, doi:10.1029/2010WR009837. [Google Scholar]
- Barone, B. , Bidigare R. R., Church M. J., Karl D. M., Letelier R. M., and White A. E. (2015), Particle distributions and dynamics in the euphotic zone of the North Pacific Subtropical Gyre, J. Geophys. Res. Oceans, 120, 3229–3247, doi:10.1002/2015JC010774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bidigare, R. R. , Van Heukelem L., and Trees C. C. (2005), Analysis of algal pigments by high‐performance liquid chromatography, in Algal Culturing Techniques, pp. 327–345, Academic, N. Y. [Google Scholar]
- Bricaud, A. , Claustre H., Ras J., and Oubelkheir K. (2004), Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations, J. Geophys. Res., 109, C11010, doi:10.1029/2004JC002419. [Google Scholar]
- Buonassissi, C. , and Dierssen H. (2010), A regional comparison of particle size distributions and the power law approximation in oceanic and estuarine surface waters, J. Geophys. Res., 115, C10028, doi:10.1029/2010JC006256. [Google Scholar]
- Calil, P. H. , Doney S. C., Yumimoto K., Eguchi K., and Takemura T. (2011), Episodic upwelling and dust deposition as bloom triggers in low‐nutrient, low‐chlorophyll regions, J. Geophys. Res., 116, C06030 , doi:10.1029/2010JC006704. [Google Scholar]
- Campbell, L. , and Vaulot D. (1993), Photosynthetic picoplankton community structure in the subtropical North Pacific Ocean near Hawaii (station ALOHA), Deep Sea Res. Part I, 40(10), 2043–2060. [Google Scholar]
- Chami, M. , Shybanov E. B., Khomenko G. A., Lee M. E.‐G., Martynov O. V., and Korotaev G. K. (2006), Spectral variation of the volume scattering function measured over the full range of scattering angles in a coastal environment, Appl. Opt., 45(15), 3605–3619. [DOI] [PubMed] [Google Scholar]
- Chisholm, S. W. (1992), Phytoplankton size, in Primary Productivity and Biogeochemical Cycles in the Sea, edited by P. G. Falkowski and A. D. Woodhead, pp. 213–237, Springer, N. Y. [Google Scholar]
- Clauset, A. , Shalizi C. R., and Newman M. E. (2009), Power‐law distributions in empirical data, SIAM Rev., 51(4), 661–703. [Google Scholar]
- Claustre, H. , Babin M., Merien D., Ras J., Prieur L., Dallot S., Prasil O., Dousova H., and Moutin T. (2005), Toward a taxon‐specific parameterization of bio‐optical models of primary production: A case study in the North Atlantic, J. Geophys. Res., 110, C07S12 , doi:10.1029/2004JC002634. [Google Scholar]
- Dore, J. E. , Letelier R. M., Church M. J., Lukas R., and Karl D. M. (2008), Summer phytoplankton blooms in the oligotrophic North Pacific Subtropical Gyre: Historical perspective and recent observations, Prog. Oceanogr., 76(1), 2–38. [Google Scholar]
- DuRand, M. D. , Olson R. J., and Chisholm S. W. (2001), Phytoplankton population dynamics at the Bermuda Atlantic Time‐series station in the Sargasso Sea, Deep Sea Res. Part II, 48(8), 1983–2003. [Google Scholar]
- Durkin, C. A. , Estapa M. L., and Buesseler K. O. (2015), Observations of carbon export by small sinking particles in the upper mesopelagic, Mar. Chem., 175, 72–81. [Google Scholar]
- Epstein, S. S. , and Shiaris M. P. (1992), Size‐selective grazing of coastal bacterioplankton by natural assemblages of pigmented flagellates, colorless flagellates, and ciliates, Microb. Ecol., 23(3), 211–225. [DOI] [PubMed] [Google Scholar]
- Field, C. B. , Behrenfeld M. J., Randerson J. T., and Falkowski P. (1998), Primary production of the biosphere: Integrating terrestrial and oceanic components, Science, 281(5374), 237–240. [DOI] [PubMed] [Google Scholar]
- Finkel, Z. V. , Irwin A. J., and Schofield O. (2004), Resource limitation alters the 3/4 size scaling of metabolic rates in phytoplankton, Mar. Ecol. Prog. Ser., 273, 269–279. [Google Scholar]
- Fong, A. , Karl D., Lukas R., Letelier R., Zehr J., and Church M. (2008), Nitrogen fixation in an anticyclonic eddy in the oligotrophic North Pacific Ocean, ISME J., 2(6), 663–676. [DOI] [PubMed] [Google Scholar]
- Gartner, J. W. , Cheng R. T., Wang P.‐F., and Richter K. (2001), Laboratory and field evaluations of the LISST‐100 instrument for suspended particle size determinations, Mar. Geol., 175(1), 199–219. [Google Scholar]
- Gasol, J. M. , and Moran X. A. (1999), Effects of filtration on bacterial activity and picoplankton community structure as assessed by flow cytometry, Aquat. Microb. Ecol., 16(3), 251–264. [Google Scholar]
- Geider, R. , Platt T., and Raven J. A. (1986), Size dependence of growth and photosynthesis in diatoms: A synthesis, Mar. Ecol. Prog. Ser, 30, 93–104. [Google Scholar]
- Graham, G. , Davies E., Nimmo‐Smith W., Bowers D., and Braithwaite K. (2012), Interpreting LISST‐100X measurements of particles with complex shape using digital in‐line holography, J. Geophys. Res., 117, C05034 , doi:10.1029/2011JC007613. [Google Scholar]
- Groundwater, H. , Twardowski M. S., Dierssen H. M., Sciandra A., and Freeman S. A. (2012), Determining size distributions and composition of particles suspended in water: A new SEM‐EDS protocol with validation and comparison to other methods, J. Atmos. Oceanic Technol., 29(3), 433–449. [Google Scholar]
- Guidi, L. , Jackson G. A., Stemmann L., Miquel J. C., Picheral M., and Gorsky G. (2008), Relationship between particle size distribution and flux in the mesopelagic zone, Deep Sea Res. Part I, 55(10), 1364–1374. [Google Scholar]
- Guidi, L. , Stemmann L., Jackson G. A., Ibanez F., Claustre H., Legendre L., Picheral M., and Gorskya G. (2009), Effects of phytoplankton community on production, size, and export of large aggregates: A World‐Ocean analysis, Limnol. Oceanogr., 54(6), 1951–1963. [Google Scholar]
- Hagström, Å. , Andersson A., and Larsson U. (1986), Size‐selective grazing by a microflagellate on pelagic bacteria, Mar. Ecol. Prog. Ser., 33, 51–57. [Google Scholar]
- Hasle, G. R. (1996), Marine diatoms, in Identifying Marine Diatoms and Dinoflagellates, edited by C. R. Tomas, pp. 5–385, Academic Press Inc., San Diego, Calif. [Google Scholar]
- Hayward, T. , and Venrick E. (1982), Relation between surface chlorophyll, integrated chlorophyll and integrated primary production, Mar. Biol., 69(3), 247–252. [Google Scholar]
- Jerlov, N. G. (1976), Marine Optics, Elsevier, Amsterdam, Netherlands. [Google Scholar]
- Jonasz, M. , and Fournier G. (2011), Light Scattering by Particles in Water: Theoretical and Experimental Foundations: Theoretical and Experimental Foundations, Academic press, Amsterdam, Netherlands. [Google Scholar]
- Karl, D. M. , and Lukas R. (1996), The Hawaii Ocean Time‐series (HOT) program: Background, rationale and field implementation, Deep Sea Res., Part II, 43(2), 129–156. [Google Scholar]
- Karl, D. M. , Church M. J., Dore J. E., Letelier R. M., and Mahaffey C. (2012), Predictable and efficient carbon sequestration in the North Pacific Ocean supported by symbiotic nitrogen fixation, Proc. Natl. Acad. Sci. U. S. A., 109(6), 1842–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karp‐Boss, L. , Azevedo L., and Boss E. (2007), LISST‐100 measurements of phytoplankton size distribution: Evaluation of the effects of cell shape, Limnol. Oceanogr. Methods, 5, 396–406. [Google Scholar]
- Kostadinov, T. , Siegel D., and Maritorena S. (2010), Global variability of phytoplankton functional types from space: Assessment via the particle size distribution, Biogeosci. Discuss., 7(3), 4295–4340. [Google Scholar]
- Kostadinov, T. , Siegel D. A., Maritorena S., and Guillocheau N. (2012), Optical assessment of particle size and composition in the Santa Barbara Channel, California, Appl. Opt., 51(16), 3171–3189. [DOI] [PubMed] [Google Scholar]
- Letelier, R. M. , and Karl D. M. (1996), Role of Trichodesmium spp. in the productivity of the subtropical North Pacific Ocean, Mar. Ecol. Prog. Ser., 133, 263–273. [Google Scholar]
- Letelier, R. M. , Bidigare R. R., Hebel D. V., Ondrusek M., Winn C., and Karl D. M. (1993), Temporal variability of phytoplankton community structure based on pigment analysis, Limnol. Oceanogr., 38(7), 1420–1437. [Google Scholar]
- Letelier, R. M. , Dore J., Winn C., and Karl D. (1996), Seasonal and interannual variations in photosynthetic carbon assimilation at Station ALOHA, Deep Sea Res. Part II, 43(2), 467–490. [Google Scholar]
- Letelier, R. M. , Karl D. M., Abbott M. R., Flament P., Freilich M., Lukas R., and Strub T. (2000), Role of late winter mesoscale events in the biogeochemical variability of the upper water column of the North Pacific Subtropical Gyre, J. Geophys. Res., 105(C12), 28,723–28,739. [Google Scholar]
- Letelier, R. M. , Karl D. M., Abbott M. R., and Bidigare R. R. (2004), Light driven seasonal patterns of chlorophyll and nitrate in the lower euphotic zone of the North Pacific Subtropical Gyre, Limnol. Oceanogr, 49, 508–519. [Google Scholar]
- Li, B. , Karl D. M., Letelier R. M., and Church M. J. (2011), Size‐dependent photosynthetic variability in the North Pacific Subtropical Gyre, Mar. Ecol. Prog. Ser., 440, 27–40. [Google Scholar]
- Lomas, M. , Steinberg D., Dickey T., Carlson C., Nelson N., Condon R., and Bates N. (2010), Increased ocean carbon export in the Sargasso Sea linked to climate variability is countered by its enhanced mesopelagic attenuation, Biogeosciences, 7(1), 57–70. [Google Scholar]
- Marañón, E. , Holligan P. M., Barciela R., González N., Mouriño B., Pazó M. J., and Varela M. (2001), Patterns of phytoplankton size structure and productivity in contrasting open‐ocean environments, Mar. Ecol. Prog. Ser., 216(216), 43–56. [Google Scholar]
- Marañón, E. , Behrenfeld M. J., González N., Mouriño B., and Zubkov M. V. (2003), High variability of primary production in oligotrophic waters of the Atlantic Ocean: Uncoupling from phytoplankton biomass and size structure, Mar. Ecol. Prog. Ser., 257(1), 1–11. [Google Scholar]
- Marañón, E. , Cermeno P., Rodríguez J., Zubkov M. V., and Harris R. P. (2007), Scaling of phytoplankton photosynthesis and cell size in the ocean, Limnol. Oceanogr., 52(5), 2190–2198. [Google Scholar]
- Menden‐Deuer, S. , and Lessard E. J. (2000), Carbon to volume relationships for dinoflagellates, diatoms, and other protist plankton, Limnol. Oceanogr., 45(3), 569–579. [Google Scholar]
- Mikkelsen, O. , and Pejrup M. (2001), The use of a LISST‐100 laser particle sizer for in‐situ estimates of floc size, density and settling velocity, Geo Mar. Lett., 20(4), 187–195. [Google Scholar]
- Mikkelsen, O. , Hill P. S., Milligan T. G., and Chant R. J. (2005), In situ particle size distributions and volume concentrations from a LISST‐100 laser particle sizer and a digital floc camera, Cont. Shelf Res., 25(16), 1959–1978. [Google Scholar]
- Moran, S. , Charette M., Pike S., and Wicklund C. (1999), Differences in seawater particulate organic carbon concentration in samples collected using small‐and large‐volume methods: The importance of DOC adsorption to the filter blank, Mar. Chem., 67(1), 33–42. [Google Scholar]
- Nair, A. , Sathyendranath S., Platt T., Morales J., Stuart V., Forget M.‐H., Devred E., and Bouman H. (2008), Remote sensing of phytoplankton functional types, Remote Sens. Environ., 112(8), 3366–3375. [Google Scholar]
- Ondrusek, M. E. , Bidigare R. R., Waters K., and Karl D. M. (2001), A predictive model for estimating rates of primary production in the subtropical North Pacific Ocean, Deep Sea Res., Part II, 48(8), 1837–1863. [Google Scholar]
- Pasulka, A. L. , Landry M. R., Taniguchi D. A., Taylor A. G., and Church M. J. (2013), Temporal dynamics of phytoplankton and heterotrophic protists at station ALOHA, Deep Sea Res., Part II, 93, 44–57. [Google Scholar]
- Peterson, B. J. (1980), Aquatic primary productivity and the 14C‐CO2 method: A history of the productivity problem, Annu. Rev. Ecol. Syst., 11, 359–385. [Google Scholar]
- Reynolds, R. , Stramski D., Wright V., and Woźniak S. (2010), Measurements and characterization of particle size distributions in coastal waters, J. Geophys. Res., 115, C08024, doi:10.1029/2009JC005930. [Google Scholar]
- Sathyendranath, S. , Lazzara L., and Prieur L. (1987), Variations in the spectral values of specific absorption of phytoplankton, Limnol. Oceanogr., 32(2), 403–415. [Google Scholar]
- Scharek, R. , Tupas L., and Karl D. M. (1999), Diatom fluxes to the deep sea in the oligotrophic North Pacific gyre at Station ALOHA, Mar. Ecol. Prog. Ser., 182, 55–67. [Google Scholar]
- Schlesinger, D. , Molot L., and Shuter B. (1981), Specific growth rates of freshwater algae in relation to cell size and light intensity, Can. J. Fish. Aquat. Sci., 38(9), 1052–1058. [Google Scholar]
- Serra, T. , Colomer J., Cristina X. P., Vila X., Arellano J. B., and Casamitjana X. (2001), Evaluation of laser in situ scattering instrument for measuring concentration of phytoplankton, purple sulfur bacteria, and suspended inorganic sediments in lakes, J. Environ. Eng., 127(11), 1023–1030. [Google Scholar]
- Sheldon, R. , Prakash A., and Sutcliffe W. (1972), The size distribution of particles in the ocean, Limnol. Oceanogr, 17(3), 327–340. [Google Scholar]
- Sieburth, J. , Smetacek V., and Lenz J. (1978), Pelagic ecosystem structure: Heterotrophic compartments of the plankton and their relationship to plankton size fractions, Limnol. Oceanogr, 23(6), 1256–1263. [Google Scholar]
- Silio‐Calzada, A. , Bricaud A., Uitz J., and Gentili B. (2008), Estimation of new primary production in the Benguela upwelling area, using ENVISAT satellite data and a model dependent on the phytoplankton community size structure, J. Geophys. Res., 113, C11023, doi:10.1029/2007JC004588. [Google Scholar]
- Slade, W. H. , Boss E., and Russo C. (2011), Effects of particle aggregation and disaggregation on their inherent optical properties, Opt. Express, 19(9), 7945–7959. [DOI] [PubMed] [Google Scholar]
- Smayda, T. , and Trainer V. (2010), Dinoflagellate blooms in upwelling systems: Seeding, variability, and contrasts with diatom bloom behaviour, Prog. Oceanogr., 85(1), 92–107. [Google Scholar]
- Sørensen, N. , Daugbjerg N., and Richardson K. (2013), Choice of pore size can introduce artefacts when filtering picoeukaryotes for molecular biodiversity studies, Microb. Ecol., 65(4), 964–968. [DOI] [PubMed] [Google Scholar]
- Stemmann, L. , Eloire D., Sciandra A., Jackson G., Guidi L., Picheral M., and Gorsky G. (2008), Volume distribution for particles between 3.5 to 2000 μm in the upper 200 m region of the South Pacific Gyre, Biogeosciences, 5(2), 299–310. [Google Scholar]
- Stramski, D. , Bricaud A., and Morel A. (2001), Modeling the inherent optical properties of the ocean based on the detailed composition of the planktonic community, Appl. Opt., 40(18), 2929–2945. [DOI] [PubMed] [Google Scholar]
- Styles, R. (2006), Laboratory evaluation of the LISST in a stratified fluid, Mar. Geol., 227(1), 151–162. [Google Scholar]
- Uitz, J. , Claustre H., Morel A., and Hooker S. B. (2006), Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll, J. Geophys. Res., 111, C08005, doi:10.1029/2005JC003207. [Google Scholar]
- Uitz, J. , Claustre H., Griffiths F. B., Ras J., Garcia N., and Sandroni V. (2009), A phytoplankton class‐specific primary production model applied to the Kerguelen Islands region (Southern Ocean), Deep Sea Res. Part I, 56(4), 541–560. [Google Scholar]
- Uitz, J. , Huot Y., Bruyant F., Babin M., and Claustre H. (2008), Relating phytoplankton photophysiological properties to community structure on large scales, Limnol. Oceanogr., 53(2), 614–630. [Google Scholar]
- Vagle, S. , McNeil C., and Steiner N. (2010), Upper ocean bubble measurements from the NE Pacific and estimates of their role in air‐sea gas transfer of the weakly soluble gases nitrogen and oxygen, J. Geophys. Res., 115, C12054, doi:10.1029/2009JC005990. [Google Scholar]
- Venrick, E. (1982), Phytoplankton in an oligotrophic ocean: Observations and questions, Ecol. Monogr., 52, 129–154. [Google Scholar]
- Vidussi, F. , Claustre H., Manca B. B., Luchetta A., and Marty J. C. (2001), Phytoplankton pigment distribution in relation to upper thermocline circulation in the eastern Mediterranean Sea during winter, J, Geophys, Res, 106(C9), 19,939–19,956. [Google Scholar]
- Westberry, T. , Behrenfeld M., Siegel D., and Boss E. (2008), Carbon‐based primary productivity modeling with vertically resolved photoacclimation, Global Biogeochem. Cycles, 22, GB2024, doi:10.1029/2007GB003078. [Google Scholar]
- White, A. E. , Spitz Y. H., and Letelier R. M. (2007), What factors are driving summer phytoplankton blooms in the North Pacific Subtropical Gyre, J. Geophys. Res., 112, C12006, doi:10.1029/2007JC004129. [Google Scholar]
- Williams, P. J. l. B. , Thomas D. N., and Reynolds C. S. (2008), Phytoplankton Productivity: Carbon Assimilation in Marine and Freshwater Ecosystems, John Wiley, Malden, Mass. [Google Scholar]
- Winn, C. D. , Campbell L., Christian J. R., Letelier R. M., Hebel D. V., Dore J. E., Fujieki L., and Karl D. M. (1995), Seasonal variability in the phytoplankton community of the North Pacific Subtropical Gyre, Global Biogeochem. Cycles, 9(4), 605–620. [Google Scholar]
- Worden, A. Z. , and Not F. (2008), Ecology and diversity of picoeukaryotes, Microbial Ecology of the Oceans, 2nd ed, pp. 159–205. [Google Scholar]
- Zhang, X. , Lewis M., Lee M., Johnson B., and Korotaev G. (2002), The volume scattering function of natural bubble populations, Limnol. Oceanogr., 47(5), 1273–1282. [Google Scholar]


