Abstract
This paper proposes a joint model for longitudinal binary and count outcomes. We apply the model to a unique longitudinal study of teen driving where risky driving behavior and the occurrence of crashes or near crashes are measured prospectively over the first 18 months of licensure. Of scientific interest is relating the two processes and predicting crash and near crash outcomes. We propose a two-state mixed hidden Markov model whereby the hidden state characterizes the mean for the joint longitudinal crash/near crash outcomes and elevated g-force events which are a proxy for risky driving. Heterogeneity is introduced in both the conditional model for the count outcomes and the hidden process using a shared random effect. An estimation procedure is presented using the forward–backward algorithm along with adaptive Gaussian quadrature to perform numerical integration. The estimation procedure readily yields hidden state probabilities as well as providing for a broad class of predictors.
Keywords: Adaptive quadrature, hidden Markov model, joint model, random effects
1. Introduction
The Naturalistic Teenage Driving Study (NTDS), sponsored by the National Institute of Child Health and Human Development (NICHD), was conducted to evaluate the effects of experience on teen driving performance under various driving conditions. It is the first naturalistic study of teenage driving and has given numerous insights to the risky driving behavior of newly licensed teens that includes evidence that risky driving does not decline with experience as discussed by Simons-Morton et al. (2011). During the study 42 newly licensed drivers were followed over the first 18 months after obtaining a license. The participants were paid for their participation, and there were no dropouts. Driving took place primarily in southern Virginia among small cities and rural areas. For each trip, various kinematic measures were captured. A lateral accelerometer recorded driver steering control by measuring g-forces the automobile experiences. These recordings provide two kinematic measures: lateral acceleration and lateral deceleration. A longitudinal accelerometer captured driving behavior along a straight path and records accelerations or decelerations. Another measure for steering control is the vehicle’s yaw rate, which is the angular deviation of the vehicle’s longitudinal axis from the direction of the automobile’s path. Each of these kinematic measures was recorded as count data as they crossed specified thresholds that represent normal driving behavior. Crash and near crash outcomes were recorded in two ways. First, the driver of each vehicle had the ability to self report these events. Second, video cameras provided front and rear views from the car during each trip. Trained technicians analyzed each trip the driver took using the video and determination of crash/near crash events made. Table 1 shows the aggregate data for the driving study. More information on the study can be found at http://www.vtti.vt.edu. Our interests are the prediction of crash and near crash events from longitudinal risky driving behavior. Crash or near crash outcomes are our binary outcome of interest, while excessive g-force events are our proxy for risky driving. It is likely that crash/near crash outcomes are best described by some unobserved or latent quality like inherent driving ability. Previously, Jackson et al. (2013) analyzed the driving data using a latent construct where the previously observed kinematic measures describe the hidden state and the hidden state describes the CNC outcome. Our approach here characterizes the joint distribution of crash/near crash and kinematic outcomes using a mixed hidden Markov model where both outcomes contribute to the calculation of the hidden state probabilities.
Table 1.
Kinematic measures and correlation with CNCs, naturalistic teenage driving study,* correlation computed between the CNC and elevated g-force event rates
| Category | Gravitation force | Frequency | % Total events | Correlation with CNCs* |
|---|---|---|---|---|
| Rapid starts | > 0.35 | 8747 | 39.6 | 0.28 |
| Hard stops | ≤ −0.45 | 4228 | 19.1 | 0.76 |
| Hard left turns | ≤ −0.05 | 4563 | 20.6 | 0.53 |
| Hard right turns | ≥ 0.05 | 3185 | 14.4 | 0.62 |
| Yaw | 6° in 3 seconds | 1367 | 6.2 | 0.46 |
| Total | 22,090 | 100 | 0.60 |
There is a previous literature on mixed hidden Markov models. Discrete-time mixed Markov latent class models are introduced by Langeheine and van de Pol (1994). A general framework for implementing random effects in the hidden Markov model is discussed by Altman (2007). In this work, the author presented a general framework for a mixed hidden Markov model with a single outcome. The mixed hidden Markov model presented by Altman unifies existing hidden Markov models for multiple processes, which provides several advantages. The modeling of multiple processes simultaneously permits the estimation of population-level effects as well as allowing great flexibility in modeling the correlation structure because they relax the assumption that observations are independent given the hidden states. There are a variety of methods available for estimation of parameters in mixed hidden Markov models. Altman (2007) performed estimation by evaluating the likelihood as a product of matrices and performing numerical integration via Gaussian quadrature. A quasi-Newton method is used for maximum likelihood estimation. Bartolucci and Pennoni (2007) extend the latent class model for the analysis of capture-recapture data, which takes into account the effect of past capture outcomes on future capture events. Their model allows for heterogeneity among subjects using multiple classes in the latent state. Scott (2002) introduces Bayesian methods for hidden Markov models which was used as a framework to analyze alcoholism treatment trial data [Shirley et al. (2010)]. Bartolucci, Lupparelli and Montanari (2009) use a fixed effects model to evaluate the performance of nursing homes using a hidden Markov model with time-varying covariates in the hidden process. Maruotti (2011) discusses mixed hidden Markov models and their estimation using the expectation–maximization algorithm and leveraging the forward and backward probabilities given by the forward–backward algorithm and partitioning the complete-data-log-likelihood into sub-problems. Maruotti and Rocci (2012) proposed a mixed non-homogeneous hidden Markov model for a categorical data.
We present a model that extends the work of Altman (2007) in several ways. First, we allow the hidden state to jointly model longitudinal binary and count data, which in the context of the driving study represent crash/near crash events and kinematic events, respectively. We also introduce an alternative method to evaluate the likelihood by first using the forward–backward algorithm [Baum et al. (1970)] followed by performing integration using adaptive Gaussian quadrature. Implementation of the forward–backward algorithm allows for easy recovery of the posterior hidden state probabilities, while the use of adaptive Gaussian quadrature alleviates bias of parameter estimates in the hidden process [Altman (2007)]. Understanding the nature of the hidden state at different time points was of particular interest to us in our application to teenage driving, and our estimation procedure yields an efficient way to evaluate the posterior probability of state occupancy.
In this paper we first introduce a joint model for crash/near crash outcomes and kinematic events which allows the mean of each these to change according to a two-state Markov chain. We introduce heterogeneity in the hidden process as well as the conditional model for the kinematic events via a shared random effect. We then discuss an estimation procedure whereby the likelihood is maximized directly and estimation of the hidden states is readily available by incorporating the forward–backward algorithm [Baum et al. (1970)] in evaluating individual likelihoods. We apply our model to the NTDS data and show that these driving kinematic data and CNC events are closely tied via the latent state. We use our model results to form a predictor for future CNC events based on previously observed kinematic data.
2. Methods
Here we present the joint model for longitudinal binary and count outcomes using two hidden states as well as the estimation procedure for model parameters.
2.1. The model
Let bi = (bi1, bi2, …, bini) be an unobserved binary random vector whose elements follow a two-state Markov chain (state “0” represents a good driving state and state “1” represents a poor driving state) with unknown transition probabilities p01, p10 and initial probability distribution r0. We model the crash/near crash outcome Yij, where i represents an individual and j the month since licensure, using the logistic regression model shown in (1):
| (1) |
where the log(mij) is an offset to account for the miles driven during a particular month. Treatment of the CNC outcome as binary is not problematic since more than 98% of the monthly observations had one or fewer CNCs observed. Although the log link is ideal for count data, it is a reasonable correction for the miles driven for the logit link when the risk of a crash is low. An alternative parameterization would be to include the miles driven as a covariate in the model. The parameter α1 assesses the odds-ratio of a crash or near crash event when in the poor versus good driving state; this odds ratio is simply eα1, while α2 reflects unaccounted for covariates beyond the hidden state. The Xij are the sum of the observed elevated g-force count data and this model incorporates heterogeneity among subjects introducing the random effect in the mean structure shown in (2):
| (2) |
where ui is the random effect with Gaussian distribution and tj reflects the month of observation since licensure for a particular individual (note that these observations are equally spaced and tj was not statistically significant when included in the CNC process, hence its omission in this part of the model). Here the parameter β3 in (2), along with the variance of the random effect distribution, accounts for any variation not explained by the other terms included in the model and induces a correlation between outcomes. Next, we assume that is a Markov chain and that bij |ui is independent of bit|ui for j ≠ t. The transition probabilities for the Markov chain must lie between 0 and 1, and the sum of transitioning from one state to either state must be 1. Hence, the transition probabilities are modeled as
| (3) |
where the parameter δ* in (3) characterizes the degree of correlation between transition probabilities among individuals. Two different types of correlations are described by δ. If δ* < 0, then this implies individuals have a tendency to remain in either state. If δ* > 0, then this implies some individuals exhibit a tendency to transition more between states than others. This approach to describe the transitions in similar to that presented by Albert and Follmann (2007). Introducing random effects in this manner is of great benefit computationally, however, there is a downside risk in that this implementation assumes the processes are highly correlated. This is especially important for the hidden process where if the correlation between transition probabilities is not very strong, biased estimates will result. We present these findings in our simulation section.
2.2. Estimation
Letting Ψ represent all parameters included in the model discussed above, the likelihood for the joint model is
| (4) |
where the summation associated with b represents all possible state sequences for an individual and the initial state probabilities are given by {ri0} and may include a subject-specific random effect. In (4) we assume the crash/near crash and kinematic event data are conditionally independent. We also assume the {ui} are independent and identically distributed and the observations for any driver are independent given the random effect ui and the sequence of hidden states. Given these assumptions, the likelihood given in (4) simplifies to a product of one-dimensional integrals shown in (5):
| (5) |
The different roles the random effects perform in this joint model are of particular interest. The purpose of the inclusion of the random effect in the conditional model for the kinematic data {(xi|(bi|ui))} provides a relaxation of the assumption that the observations for an individual are conditionally independent given the hidden states {bi} as well as accounting for overdispersion for the kinematic event data. The inclusion of the random effect in the transition probabilities allows the transition probabilities to vary across individuals, inducing a correlation between transition probabilities that induces a relationship between the kinematic events and CNC processes. Further, the random effect provides a departure from the assumption that the transition process follows aMarkov chain. One could formulate a reduced model that includes a random effect only in the hidden process, in the hidden process and one or both observed processes, or only in observed processes.
Several possibilities exist for maximizing the likelihood given by (5). Two common approaches are the Monte Carlo expectation maximization algorithm introduced by Wei and Tanner (1990) and the simulated maximum likelihood methods discussed by McCulloch (1997). In Section 2.3, we propose a different method for parameter estimation that does not rely on Monte Carlo methods which are difficult to implement and monitor for convergence. Our method utilizes the forward–backward algorithm to evaluate the individual likelihoods conditional on the random effect. As we will show, incorporation of this algorithm provides a simpler means of computing the posterior probability of the hidden state at any time point than MCEM. Further, this method provides a straightforward approach for likelihood and variance evaluation. This approach has the added benefit of producing the estimated variance–covariance matrix for parameter estimates as determined by the inverse of the observed information matrix.
2.3. Maximizing the likelihood using an implementation of the forward–backward algorithm
In maximizing the likelihood given by (5), our approach first evaluates the portion of the likelihood described by the observed data given the random effect and hidden states shown here:
| (6) |
using the forward–backward algorithm and subsequent numerical integration over the random effect via adaptive Gaussian quadrature. We then use a quasi-Newton method to maximize this result. The alteration of the forward–backward algorithm to accommodate joint outcomes is described as follows. Here, let the vectors with realized values (yik, …, yij)′ and with realized values (xik, …, xij)′. Decompose the joint probability for an individual as follows:
| (7) |
where aim(j) and zim(j) are referred to as the forward and backward quantities, respectively, and are
The aim(j) and zim(j) are computed recursively in j by using the following:
and
For any individual, the likelihood conditional on the random effect may be expressed as a function of the forward probabilities, so for a two-state Markov chain the conditional likelihood for an individual is
| (8) |
where ai0(ni|Ψ,ui) and ai1(ni|Ψ,ui) are the forward probabilities for subject i associated with states 0 and 1, respectively, evaluated at the last observation of the subject’s observation sequence ni. The marginal likelihood for an individual can now be found by integrating with respect to the random effect
| (9) |
and the complete likelihood can be expressed as a product of individual likelihoods.
2.4. Numerical integration
Adaptive Gaussian quadrature can be used to integrate (9). This technique is essential to obtaining accurate parameter estimates, as the integrand is sharply “peaked” at different values depending on the observed measurements of the individual. Applying the results described in Liu and Pierce (1994) to the joint hidden Markov model, numerical integration of (9) is achieved by considering the distribution of the random effects to be N(0, θ2). The procedure for obtaining maximum likelihood estimates for model parameters are shown in Table 2.
Table 2.
Procedure for obtaining maximum likelihood estimates for the joint mixed hidden Markov model
| (1) | Select initial parameter estimates p0. |
| (2) | Compute the set of adaptive quadrature points for each individual qi given the current parameter estimates pm. |
| (3) | Maximize the likelihood obtained using the forward–backward algorithm and adap- tive quadrature via qi ∈ Q using the quasi-Newton method. |
| (4) | Update parameter estimates p(m+1). |
| (5) | Repeats steps (2)–(4) until parameters converge. |
2.5. Estimation of posterior hidden state probabilities
The forward–backward implementation in evaluating the likelihood is not only efficient (the number of operations to compute the likelihood conditional on the random effect is of linear order as the observation sequence increases), but it also provides a mechanism for recovering information about the hidden states. By leveraging the forward and backward probabilities, we can compute the hidden posterior state probabilities {b̂ij}:
| (10) |
since
equation (10) can be expressed as
| (11) |
Evaluation of (11) is accomplished via adaptive Gaussian quadrature as outlined in the earlier section and the quantities of interest in (11) are readily available after running the forward–backward algorithm.
Using a shared random effect is also attractive in that it is computationally more efficient than incorporating separate random effects for the count outcome and transition probabilities. Generally speaking, once the number of random effects exceeds three or four (depending on the type of quadrature being used and the number of nodes included for each integration), direct maximization is no longer a computationally efficient method and Monte Carlo expectation maximization (MCEM) is an appealing alternative approach. In accounting for heterogeneity with a single random effect, we eliminate the need for MCEM.
3. Simulation of the mixed model
We performed a simulation to investigate the performance of parameter estimation using the proposed approach. Under the shared random effect parameterization, we use the model in (12) for the simulation
| (12) |
where ui ~ N(0, eλ).
The simulations were conducted with 20 observations on 60 subjects. Using a 1.86-GHz Intel Core 2 Duo processor, the fitting of the shared model took less than 3 minutes on average. The simulation results (1000 simulations) are shown in Table 3. Parameter estimates obtained using adaptive Gaussian quadrature with five and eleven points, respectively, are presented along with true parameter value (θ) and mean , the sample standard deviation for the parameter estimates θ̂sd, and the average asymptotic standard errors σθ̂. In performing the estimation using five quadrature points, parameter estimation was quite accurate with the exception of the coefficient of the random effect δ* in the 0–1 transition with an average estimated value of 2.15 compared to the actual value of 2.0. Other parameters display very little bias. The bias for δ* virtually disappears when performing the integration via adaptive Gaussian quadrature using ten points where the average estimated value was δ* = 2.02. These results were unchanged when evaluating for possible effects due to the total number of subjects or observations (varying n and I). Additionally, the average asymptotic standard errors agree quite closely to the sample standard deviations for all model parameters. Similar results hold for the case where random effects are only included in the hidden process. We used different starting values to examine the sensitivity of estimation to initial values, and our proposed algorithm was insensitive to the selection of these values. Simulation results provide support that the complexity of the model does not inhibit parameter estimation, rendering discovery of heterogeneity in the observed and hidden processes as a nice byproduct for the model.
Table 3.
Parameter estimates for mixed hidden Markov model 1000 simulations (60 individuals, 20 observations) using Q = 5 and Q = 11 quadrature points
| Q = 5 | Q = 11 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | θ | θ̂sd | σθ̂ | θ̂sd | σθ̂ | ||||
| α0 | −1.0 | −1.01 | 0.12 | 0.12 | −1.01 | 0.11 | 0.11 | ||
| α1 | 2.0 | 2.03 | 0.18 | 0.19 | 2.03 | 0.18 | 0.17 | ||
| α2 | 1.5 | 1.52 | 0.41 | 0.42 | 1.51 | 0.42 | 0.44 | ||
| β0 | −1.0 | −1.01 | 0.10 | 0.10 | −1.00 | 0.09 | 0.06 | ||
| β1 | 2.0 | 2.01 | 0.12 | 0.09 | 2.02 | 0.11 | 0.09 | ||
| β2 | 0.25 | 0.255 | 0.06 | 0.07 | 0.251 | 0.06 | 0.04 | ||
| γ01 | −0.62 | −0.61 | 0.19 | 0.18 | −0.62 | 0.19 | 0.17 | ||
| γ10 | 0.4 | 0.42 | 0.34 | 0.32 | 0.42 | 0.30 | 0.30 | ||
| λ | 0.0 | −0.03 | 0.16 | 0.15 | −0.03 | 0.16 | 0.16 | ||
| δ* | 2.00 | 2.15 | 0.45 | 0.41 | 2.02 | 0.43 | 0.42 | ||
| δ1 | 1.00 | 1.08 | 0.22 | 0.21 | 1.02 | 0.20 | 0.21 | ||
| δ2 | 3.00 | 2.97 | 0.41 | 0.43 | 2.97 | 0.44 | 0.42 | ||
| πi1 | −0.8 | −0.82 | 0.06 | 0.05 | −0.81 | 0.05 | 0.05 | ||
While performance of the estimation procedure for the mixed hidden Markov model in (12) was quite good, this model formulation assumes near perfect correlation between the random effects. To examine the robustness of the estimation procedure to this assumption, we evaluated model performance in the case where there are correlated random effects in the hidden process. For this case, data was simulated for the transition probabilities using (13):
| (13) |
where (u1,u2) follow a bivariate normal distribution BVN(0, Σ). Our model was then fit to the simulated data using the parameterization in (14):
| (14) |
The results for this simulation are shown in Table 4. For moderate departures from perfect correlation, biased estimates result in the hidden process. Thus, we recommend first considering correlated random effects in the hidden process before use of the shared random effects model. In the case of our application, the transition process exhibited very high correlation, so we proceed in the analysis with our estimation procedure. Details for estimation using bivariate adaptive Gaussian quadrature are shown in the supplementary material [Jackson, Albert and Zhang (2015)].
Table 4.
Parameter estimates for the hidden process when the true underlying random effects distribution is correlated. 1000 simulations (60 individuals, 20 observations)
| Parameter | True value | ρ = 1 | ρ = 0.95 | ρ = 0.9 | ρ = 0.8 | ρ = 0.7 | ρ = 0.6 |
|---|---|---|---|---|---|---|---|
| γ10 | −0.62 | −0.620 | −0.628 | −0.640 | −0.67 | −0.69 | −0.72 |
| γ01 | 0.4 | 0.401 | −0.399 | 0.398 | 0.32 | 0.28 | 0.26 |
| δ | 2.0 | 2.00 | 2.11 | 2.28 | 2.44 | 2.61 | 2.68 |
4. Results
The two-state mixed hidden Markov model presented in the previous sections was applied to the NTDS data. Table 5 displays the parameter estimates and associated standard errors. The initial probability distribution for the hidden states was common to all individuals in the study and modeled using logit(r1) = π1 and the random effects distribution was N(0, eλ). Several models were compared based on the relative goodness-of-fit measure, AIC. Model excursions included evaluating the suitability of a three-state hidden Markov model without random effects (AIC = 3563.06) (model shown in the supplementary material [Jackson, Albert and Zhang (2015)]), the two-state model without random effects (AIC = 3548.97), and the two-state model with random effects (AIC = 3492.73).
Table 5.
Parameter estimates for the mixed hidden Markov model as applied to the NTDS data
| Parameters | Estimate | Std Err |
|---|---|---|
| α0 | −7.48 | 0.14 |
| α1 | 1.49 | 0.25 |
| α2 | 0.03 | 0.02 |
| β0 | −5.97 | 0.13 |
| β1 | 1.31 | 0.06 |
| β2 | 0.007 | 0.004 |
| β3 | 1.10 | 0.04 |
| λ | −0.18 | 0.33 |
| δ* | 1.25 | 0.32 |
| γ10 | −2.13 | 0.35 |
| γ01 | −3.47 | 0.28 |
| δ1 | 1.75 | 0.24 |
| δ2 | −2.17 | 0.53 |
| π1 | −0.83 | 0.28 |
The fixed effects model provided initial parameter estimates for most model parameters while multiple starting values for λ were used in conjunction with a grid search over parameters β3 and δ* to determine these initial values. The number of quadrature points implemented at each iteration was increased until the likelihood showed no substantial change. As illustrated in the simulation study, there were eleven points used in the adaptive quadrature routine. Standard error estimates were obtained using a numerical approximation to the Hessian using the {nlm} package in R. The coefficients of the hidden states α1 and β1 are both significantly greater than zero, indicating that drivers operating in a poor driving state (bij = 1) are more likely to have a crash/near crash event and, correspondingly, a highly number of kinematic events. While the variance component of the random effect is somewhat small, the dispersion parameter β3 is highly significant, indicating the data are overdispersed. Interestingly, heterogeneity is not exhibited in the CNC outcome as the coefficient for the random effect α2 is insignificant, providing support to the notion that the hidden state is capturing unobserved quantities in a meaningful way. There is evidence of heterogeneity across individuals in their propensity to change between states as indicated by λ and δ*. In the case of the NTDS data, δ* > 0 indicates a positive correlation between the transition probabilities, meaning that some individuals are prone to changing more often between states than others. Co-efficients in the hidden process, δ1 and δ2, illustrate that transition between states depends on previous CNC outcomes. A prior crash was associated with an increased probability of transitioning from the good driving state to the poor one (δ1 = 1.75) and a decreased probability of transitioning from the poor to the good driving state (δ2 = 2.17). Since the shared random effect, which assumes a perfect correlation between the random components, may not be robust to a more flexible random effects structure, we also fit the model using correlated random effects in the hidden process (see simulation results). For a variety of starting values, the correlation coefficient estimates were near 1 (0.998 or greater), giving us confidence in using the shared random effect approach.
An interpretation of parameter estimates given in Table 5 is subject-specific and depends on a driver’s exposure for a given month. If we consider a subject driving the average mileage for all subjects (358.1 miles), parameter estimates indicate that the risk of a crash/near crash outcome increases from 0.16 to 0.47 when in the poor driving state, bij = 1. Correspondingly, this “average” subject would also expect to experience 2.43 more kinematic events on average when in the poor driving state. For the typical teenager, the likelihood of moving out of the poor driving state decreases from 10.6% to 1.3% when experiencing a CNC event in the previous month. Similarly, the likelihood of moving out of the good driving state increases from 3.01% to 15.2% when experiencing a CNC event in the previous month.
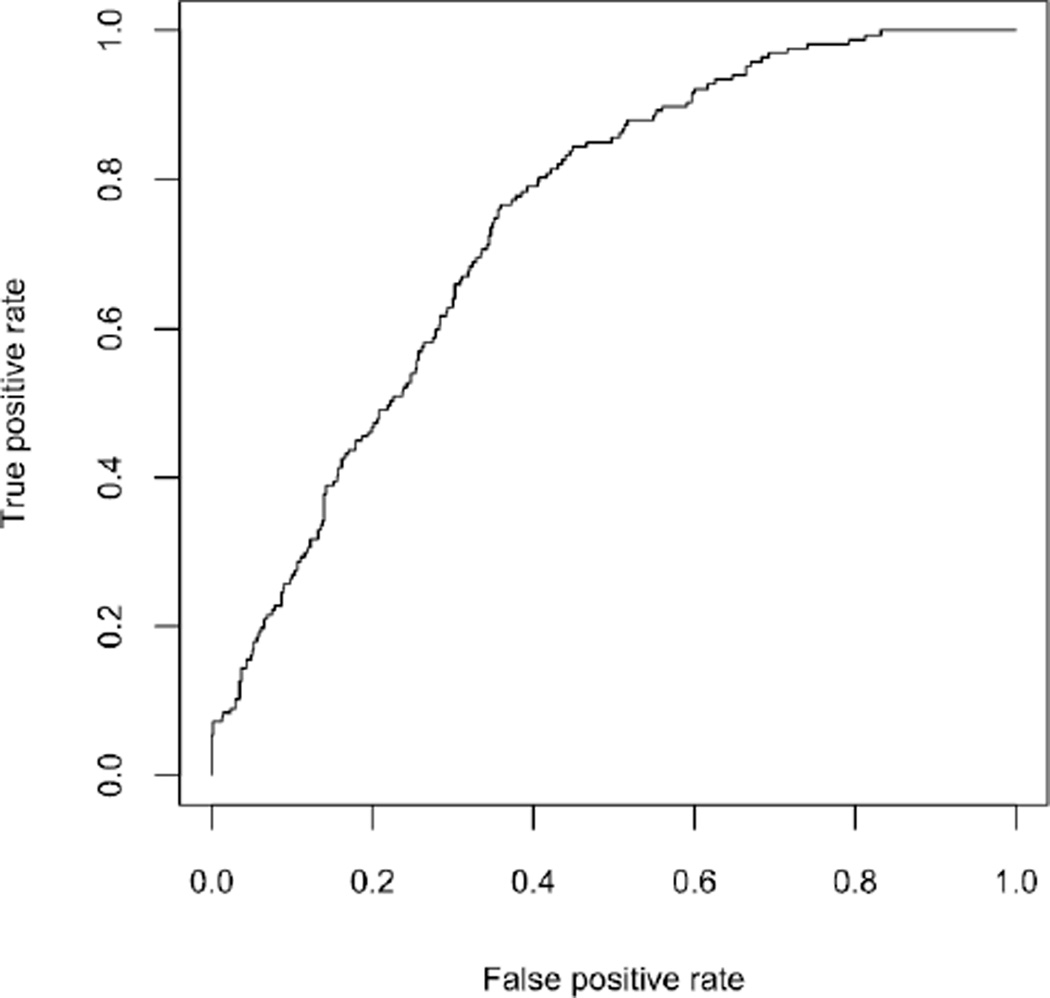
A receiver operating characteristic (ROC) curve was constructed to determine the predictive capability of our model by plotting the true positive rate versus the false positive rate for different cutoff values. The ROC curve based on the “one-step ahead” predictions [observed outcome given all previous kinematic observations Pr(Yij = 1|yi1, …, yi,j−1,xi1, …,xi,j−1)] is shown in Figure 1. An attractive feature of our model is that it allows for the development of a predictor based on prior kinematic events. We constructed this ROC curve using a cross-validation approach whereby one driver was removed from the data set, model parameters were then determined using the remaining data and these results were then used to predict the removed driver’s crash/near crash outcomes. The predictive accuracy of this model was moderately high with an area under the curve of 0.74. Although the goodness of fit was best for the two-state mixed hidden Markov model, area under the curve for the other models was nearly identical.
Fig. 1.
ROC curve for the mixed hidden Markov model based one “one-step ahead” predictions (area under the curve = 0.74).
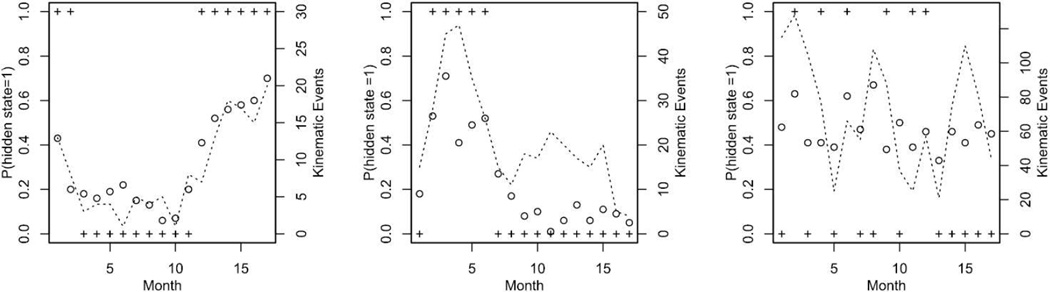
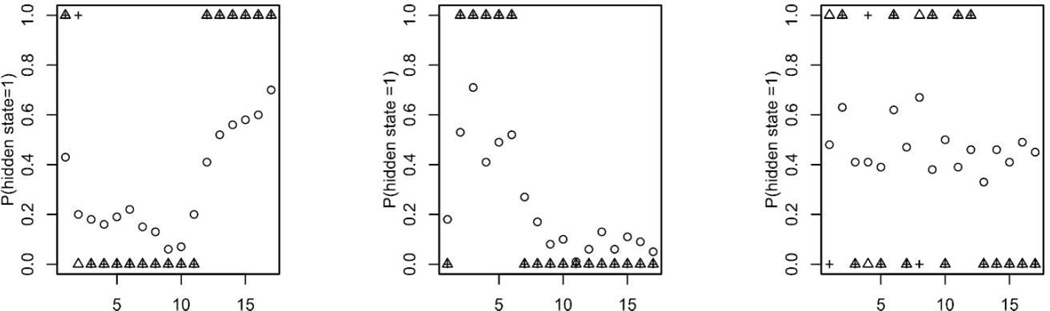
A sample of three drivers and their corresponding hidden state probability Eui|yi,xi{E(bij|yi,xi,ui)} along with their crash/near crash outcomes and total number of kinematic events is shown in Figure 2. It is evident how the total kinematic measures influence the predicted value of the hidden state and work particularly well for cases where driving is “consistent” over relatively short time periods (i.e., low variation in kinematic measures for a given time period). In cases where the driving kinematics exhibit a great deal of variability, the model does not perform as well in predicting crash/near crash outcomes as indicated by the rightmost panel in Figure 2. As a comparison, we show the results of global decoding of the most likely hidden state sequence using the Viterbi algorithm in Figure 3 for the same three drivers. Hidden state classification is similar whether using global or local decoding for the left two panels in Figure 3, which is indicative of most drivers in the study, while there are differences in the case of the rightmost panel likely due to the greater variability in these data.
Fig. 2.
Predicted value of the hidden state given the observed data for three drivers. The (○) indicates the probability of being in state 1 (poor driving), (+) indicates a crash/near crash event and the dotted line indicates the composite kinematic measure.
Fig. 3.
Comparison of local and global decoding of the hidden states and CNC outcomes. The (○) indicates the probability of being in state 1 (poor driving), (+) indicates a CNC event and the (Δ) indicates the hidden state occupation using the Viterbi algorithm.
5. Discussion
In this paper we presented a mixed hidden Markov model for joint longitudinal binary and count outcomes introducing a shared random effect in the conditional model for the count outcomes and the model for the hidden process. An estimation procedure incorporating the forward–backward algorithm with adaptive Gaussian quadrature for numerical integration is used for parameter estimation. A welcome by-product of the forward–backward algorithm is the hidden state probabilities for an individual during any time period. The shared random effect eliminates the need for more costly numerical methods in approximating the likelihood, such as higher dimensional Gaussian quadrature or through Monte Carlo EM.
The model was applied to the NTDS data and proved to be a good predictor of crash and near crash outcomes. Our estimation procedure also provides a means of quantifying teenage driving risk. Using the hidden state probabilities which represent the probability of being in a poor driving state given the observed crash/near crash and kinematic outcomes, we can analyze the data in a richer way than standard summary statistics. Additionally, our approach allows for a broader class of predictors whereby the investigator may make predictions based on observations that go as far into the past as warranted.
There are limitations to our approach. The shared random effect proposes a rather strong modeling assumption in order to take advantage of an appealing reduction in computational complexity. Using more general correlated random effects approaches is an alternative, but others have found that identification of the correlation parameter is difficult [Smith and Moffatt (1999) and Alfò, Maruotti and Trovato (2011)]. Formal testing for heterogeneity in these models is also a challenging problem [Altman (2008)].
There is also a potential issue of having treated the miles driven during a particular month (mij) as exogenous. For some crashes, it is possible that previous CNC outcomes (yi,j−1) may affect the miles driven in the following month and our model does not capture this dynamic. As with any study, greater clarity in the information obtained for each trip might yield more valuable insights. Metrics such as the type of road, road conditions and trip purpose, while potentially useful, were not available for this analysis.
There are extensions to the model that may be useful. The model can address more than two outcomes. We summarize the kinematic events at a given time as the sum across multiple types. This approach could be extended to incorporate multiple correlated processes corresponding to each kinematic type. Depending on the situation, the additional flexibility and potential benefits of such an extension may be worth the increased computational cost.
Acknowledgments
We thank the Center for Information Technology, National Institutes of Health, for providing access to the high-performance computational capabilities of the Biowulf cluster computing system. We also thank Bruce Simons-Morton for discussions related to this work. Inquiries about the study data may be sent to P. S. Albert at albertp@mail.nih.gov.
Supported by the Intramural Research program of the National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development.
Footnotes
SUPPLEMENTARY MATERIAL
Adaptive quadrature for the three-state mixed hidden Markov model (DOI: 10.1214/14-AOAS765SUPP; .pdf).We provide details on the adaptive quadrature routine for the MHMM with bivariate normal random effects in the hidden process, as well as expressions for the three-state hidden Markov model.
Contributor Information
John C. Jackson, Email: john.jackson@usma.edu.
Paul S. Albert, Email: albertp@mail.nih.gov.
REFERENCES
- Albert PS, Follmann DA. Random effects and latent processes approaches for analyzing binary longitudinal data with missingness: A comparison of approaches using opiate clinical trial data. Stat. Methods Med. Res. 2007;16:417–439. doi: 10.1177/0962280206075308. [DOI] [PubMed] [Google Scholar]
- Alfò M, Maruotti A, Trovato G. A finite mixture model for multivariate counts under endogenous selectivity. Stat. Comput. 2011;21:185–202. [Google Scholar]
- Altman RM. Mixed hidden Markov models: An extension of the hidden Markov model to the longitudinal data setting. J. Amer. Statist. Assoc. 2007;102:201–210. [Google Scholar]
- Altman RM. A variance component test for mixed hidden Markov models. Statist. Probab. Lett. 2008;78:1885–1893. [Google Scholar]
- Bartolucci F, Lupparelli M, Montanari GE. Latent Markov model for longitudinal binary data: An application to the performance evaluation of nursing homes. Ann. Appl. Stat. 2009;3:611–636. [Google Scholar]
- Bartolucci F, Pennoni F. A class of latent Markov models for capture-recapture data allowing for time, heterogeneity, and behavior effects. Biometrics. 2007;63:568–578. doi: 10.1111/j.1541-0420.2006.00702.x. [DOI] [PubMed] [Google Scholar]
- Baum LE, Petrie T, Soules G, Weiss N. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Statist. 1970;41:164–171. [Google Scholar]
- Jackson J, Albert P, Zhang Z. Supplement to “A two-state mixed hidden Markov model for risky teenage driving behavior. 2015 doi: 10.1214/14-AOAS765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson JC, Albert PS, Zhang Z, Simons-Morton B. Ordinal latent variable models and their application in the study of newly licensed teenage drivers. J. R. Stat. Soc. Ser. C. Appl. Stat. 2013;62:435–450. doi: 10.1111/j.1467-9876.2012.01065.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langeheine R, van de Pol F. Discrete-time mixed Markov latent class models. In: Dale A, Davies RB, editors. Analyzing Social and Political Change: A Casebook of Methods. London: Sage; 1994. [Google Scholar]
- Liu Q, Pierce DA. A note on Gauss–Hermite quadrature. Biometrika. 1994;81:624–629. [Google Scholar]
- Maruotti A. Mixed hidden Markov models for longitudinal data: An overview. International Statistical Review. 2011;79:427–454. [Google Scholar]
- Maruotti A, Rocci R. A mixed non-homogeneous hidden Markov model for categorical data, with application to alcohol consumption. Stat. Med. 2012;31:871–886. doi: 10.1002/sim.4478. [DOI] [PubMed] [Google Scholar]
- McCulloch CE. Maximum likelihood algorithms for generalized linear mixed models. J. Amer. Statist. Assoc. 1997;92:162–170. [Google Scholar]
- Scott SL. Bayesian methods for hidden Markov models: Recursive computing in the 21st century. J. Amer. Statist. Assoc. 2002;97:337–351. [Google Scholar]
- Shirley KE, Small DS, Lynch KG, Maisto SA, Oslin DW. Hidden Markov models for alcoholism treatment trial data. Ann. Appl. Stat. 2010;4:366–395. [Google Scholar]
- Simons-Morton BG, Ouimet MC, Zhang Z, Klauer SE, Lee SE, Wang J, Albert PS, Dingus TA. Crash and risky driving in- volvement among novice adolescent drivers and their parents. Am. J. Public Health. 2011;101:2362–2367. doi: 10.2105/AJPH.2011.300248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MD, Moffatt PG. Fisher’s information on the correlation coefficient in bivariate logistic models. Aust. N. Z. J. Stat. 1999;41:315–330. [Google Scholar]
- Wei GCG, Tanner MA. A Monte Carlo implementation of the EM algorithm and the poor man’s data augmentation algorithms. J. Amer. Statist. Assoc. 1990;85:699–704. [Google Scholar]