Monte Carlo based approach to the LS-NaI 4πβ-γ anticoincidence extrapolation and uncertainty

Abstract

The 4πβ-γ anticoincidence method is used for the primary standardization of β−, β+, electron capture (EC), α, and mixed-mode radionuclides. Efficiency extrapolation using one or more γ ray coincidence gates is typically carried out by a low-order polynomial fit. The approach presented here is to use a Geant4-based Monte Carlo simulation of the detector system to analyze the efficiency extrapolation. New code was developed to account for detector resolution, direct γ ray interaction with the PMT, and implementation of experimental β-decay shape factors. The simulation was tuned to ⁵⁷Co and ⁶⁰Co data, then tested with ^99mTc data, and used in measurements of ¹⁸F, ¹²⁹I, and ¹²⁴I. The analysis method described here offers a more realistic activity value and uncertainty than those indicated from a least-squares fit alone.

1. Introduction

The method of 4πβ-γ coincidence counting (Campion, 1959) continues to be adapted to a growing number of radionuclides. Two recent reviews cover the developments in the method (Bobin, 2007) and measurement uncertainties (Fitzgerald et al., 2015). One of the outstanding challenges mentioned by that latter paper, in an example on ¹⁷⁷Lu decay, involves finding the uncertainty in an efficiency extrapolation intercept. A function that appears linear within the scatter of the data, may in fact be slightly non-linear. Since the veracity of the intercept value and uncertainty are predicated on the actual linearity of the data, such an underlying discord between the model and the data would indicate that the intercept uncertainty is actually larger than what is given by the least-squares fit procedure.

In fact, linear or polynomial functions are not necessarily adequate for extrapolating efficiency curves, and are especially suspect when the beta detector is sensitive to more than one type of radiation (Bobin, 2007, Section 3.2). Monte Carlo models of the detection system and radiation transport through the detectors have been used to analyze efficiency extrapolations (Dias et al., 2006) and perform sensitivity tests (Simpson et al., 2012; Miyahara et al., 1986). Here we present a Monte Carlo simulation of an anticoincidence system at NIST and develop methodology to assess the true activity and uncertainty using the model and the data.

2. Experimental Apparatus and Method

The NIST live-timed anticoincidence counting (LTAC) system has been described previously (Fitzgerald and Schultz, 2008; Lucas, 1998). The details pertinent to modelling will be discussed here. The basic design is a single photomultiplier-tube (PMT) liquid scintillation (LS) detector, sitting inside a NaI(Tl), “NaI”, well detector. The LS source consists of a disposable hemispherical glass vial of approximate diameter 3 cm, which is filled with 3 mL to 5 mL of LS cocktail into which a radioactive solution is added by pycnometer. The vial is then sealed by filling the neck with epoxy. The underside of the filled vial is coated with about 0.5 mL of optical grease, and then placed firmly on top of the PMT (Burle² 8575). Finally the NaI detector is lowered on to the PMT assembly, with an o-ring seal between the NaI flange and the can that holds the PMT.

The NaI detector housing has an outer diameter of 13 cm, a well diameter of 6.4 cm and a well depth of 7.7 cm. The geometric efficiency of the NaI detector is about 0.75.

The system is used only in anti-coincidence mode. Presently there are two data acquisition paths, which are usually operated in parallel. The first is an analog processing chain using a 4-channel (usually 1 beta, 3 gamma) anti-coincidence unit with adjustable extending dead-time and a 10 MHz clock. The second system is list-mode acquisition consisting of a Caen DT5724 digitizer (100 MHz, 14-bit ADC with pulse-height analysis) operated using in-house acquisition and analysis software written in Labview. The triggering threshold for each channel was set to be above the noise level. If the voltage in a channel rises above the trigger threshold, then list-mode data (time, energy) are recorded for that channel. Then the γ-ray energy windows and β-channel lower level discriminator are set during offline analysis. During normal operation, the results from the analog and digital systems agree to less than 0.05 %. Extending dead-times are set between 50 µs and 100 µs such that no afterpulses can be observed.

The anti-coincidence methodology is essentially the same as the coincidence methodology. Here we introduce the basic notation used in this paper. All count rates are considered to be estimates of the true values, and thus have been corrected for background, decay, and dead-time. To avoid PMT noise in the LS detector, the lowest lower-level threshold used in an extrapolation was always chosen to be above the single photoelectron peak, such that the background rate was below 8 s⁻¹. For a given lower-level threshold in the LS or “beta” detector, the count rate is N_LS. In the NaI detector, the ratio of anti-coincident γ rays to total γ rays is called Y, which is a measure of the LS inefficiency for decays corresponding to those γ rays. Pairs of N_LS and Y data are acquired for various thresholds and extrapolated to Y = 0, where the intercept is (in the simple β-γ case) a measure of the activity, N₀. In general, the extrapolation equation is,

$$N_{\text{LS}}=N_0{f}^{-1}(1-kY),$$ (1)

where k is a factor that depends on the various LS and NaI efficiencies, and is generally a function of the LS threshold³. For the simplest decay schemes, the correction factor f = 1, and k is considered to be a constant, which results in a linear extrapolation. In multi-dimensional coincidence, multiple NaI gates are set, and the extrapolation is in multiple variables, Y_i. In that case, we can define a single effective inefficiency parameter,

$$Y_{\text{eff}}=\sum a_i{Y}_i,$$ (2)

to substitute for Y in Equation 1. For more complicated β decay, for example decay with a β branch to the daughter ground state, the extrapolation would be non-linear, possibly quadratic. In some cases, it can be linearized by finding the appropriate a_i values (Baerg, 1973; Grigorescu, 1973). For electron capture (EC), or mixed modes of decay, the extrapolation equation would be more complicated and f would need to be applied to the intercept to obtain N₀.

3. Monte Carlo Model

A Monte Carlo simulation of the apparatus was designed using Geant4 (Agostinelli et al., 2003). We will first describe a few modifications that were made to the Geant4 libraries themselves (3.1), then describe the user code (3.2).

3.1 Geant4

Geant4 consists of a collection of C++ libraries that can be used to simulate detector geometries, radioactive decay, radiation transport and secondary particle creation (e.g. Auger electrons, atomic relaxation). Furthermore, the code contains a framework for simulating an experiment, randomizing stochastic processes, and processing data. Small changes were made to a few parts of the G4processes.dll library for the present work.

First, in the code G4BetaDecayCorrections.cc, the atomic number was changed from “abs(Z)” to “Z”, such that positron decay spectrum would have the proper shape. Also, the screening correction was changed to be a constant at low energies, instead of suddenly ceasing, which had caused a step in the low-energy beta spectra. Both of these modifications were communicated to the Geant team, who implemented similar changes to later updates of Geant, starting with version 4.9.6.

Also, the capability was added to input custom beta-decay shape factors. This was done by modifying G4BetaDecayType.hh and G4BetaDecayCorrections.cc (and .hh). In this way, an experimental beta shape factor can be added to the existing nuclear data files.

A modification was made to the G4EmSaturation.cc code, which calculates LS ionization quenching. Originally, the code applied a single-step approximation to Birks’ integral. This was modified to use the Legrand96 integration method in Geant, for higher accuracy.

The final change made to the Geant4 package was to update the atomic and nuclear data for each nuclide used, as needed.

3.2 User Code

The Monte Carlo simulation of the NIST LTAC system was built from Geant4 and called “LTAC1”. The geometry was based on the measured dimensions and approximated using cylinders. The model parameters were then tuned using experimental data form a variety of radionuclides. The aluminum housing of the NaI detector, LS PMT, glass LS vial, lead shield, and the room air were all included in the simulation, to account for scattering. For the NaI detector, the energy resolution was approximated with random Gaussian noise parameterized as a quadratic function of energy based on data from ⁶⁰Co, ^99mTc, ²⁴¹Am γ rays as well as X rays from ¹³¹I.

For the LS detector, ionization quenching and resolution were considered to be essential, since the efficiency extrapolation is typically carried out over the low-energy portion of the LS spectrum. Therefore, a more detailed detection model was used for LS than for NaI, as follows. A particle slowing down in the LS cocktail changes energy from E₀ to E_f during a step, which leads to the creation of N_opt optical photons. That N_opt value is drawn randomly from a Poisson distribution with a mean value $(\overline{N_{\text{opt}}})$ equal to Birks’ integral (Birks, 1951),

$$\overline{N_{\text{opt}}}={\int }_{E_f}^{E_o}\frac{S}{1+kB\eta (E)}dE,$$ (3)

where the product kB is Birks’ constant (about 0.08 mm/MeV) , η(E) is the stopping power, and S is the scintillation yield (about 4000 to 5000 optical photons / MeV). Note that kB and S are the two tuning parameter for the simulation, set for each batch of LS sources. The other gain parameters that follow remain fixed.

The optical photons created through scintillation are then tracked through the detector, and the number of photoelectrons produced by the photocathode is taken to be a random binomial draw from the number of optical photons that hit the photocathode with probability equal to the cathode efficiency (ε_cath ≈ 0.22, and depends on wavelength). Those photoelectrons are multiplied by two dynode gains, each implemented by Poisson draws. Finally, Gaussian noise is applied, for two reasons. The first reason is that the experimental spectra at low energies do not show discrete photoelectron peaks above the first photoelectron peak, but rather a smooth spectrum. Second, at high energies (above about 200 keV), the experimental energy resolution is higher than that expected from the statistics of the above processes alone. It was found that adding Gaussian noise with standard deviation of about 8 % matched the experimental spectra in both these aspects.

For convenience, the final number of electrons, N_e, at the anode is scaled to an effective LS energy,

$$E_{\text{LS}}=\frac{N_{\mathrm{e}}}{S\overline{{\epsilon }_{\text{geo}}}{\epsilon }_{\text{cath}}{\epsilon }_{\text{dyn}1}{\epsilon }_{\text{dyn}2}}.$$ (4)

The mean geometric efficiency for the optical photons, $\overline{{\epsilon }_{\text{geo}}}$, was determined by running the simulation for 500 keV electrons and calculating the average number of cathode hits per optical photon. This geometric efficiency (about 0.50) is much larger than the solid angle subtended by the photocathode, due mainly to reflections at the liquid-air interface at the top of the LS cocktail and the glass-air interface on the sides of the glass vial. Note that an additional limit is placed on the maximum length (5 cm) of an optical photon track, thereby eliminating long tracks when, for instance, a photon is trapped inside the glass, totally-internally reflecting.

Tracking the multitude of optical photons per decay takes considerable computation time (4 hours for 1·10⁶ decays of ⁵⁷Co). For quicker runs, a simplification was implemented in which optical photon tracking was turned off. That is, optical photons were created as above, counted as N_opt, then destroyed without tracking. In that case, the number of photoelectrons at the cathode was approximated by a binomial draw from N_opt with probability equal to the geometric efficiency, ε_geo(Z), for the height, z, in the LS cocktail at which the energy deposition occurred. The additional dispersion caused by the height effect (Mann and Taylor, 1980) is therefore maintained, while the simulation runs 10 times faster, with nearly the same result.

This model automatically accounts for the LS scintillation efficiency to γ rays, atomic x rays, and bremsstrahlung, since those photons interact with the LS cocktail to create electrons, which then induce scintillation.

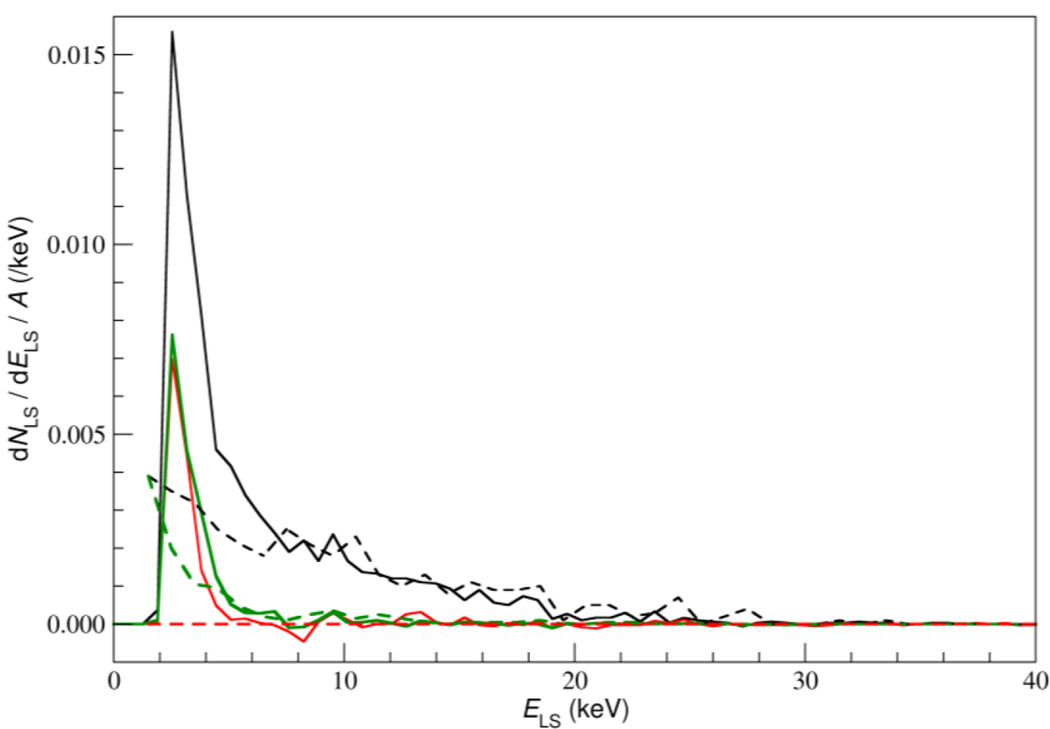
Cherenkov production was also included in the model within the LS cocktail, glass vial, and glass faceplate of the PMT. This effect accounts for the PMT response to γ rays, via scattered electrons. Our implementation was informed by, though somewhat simpler than, that of Thiam et al. (2010), in that optical properties in Geant4 were defined for the LS cocktail, LS vial and PMT faceplate. For all LS cocktails, an index of refraction of 1.34 was used and scintillation efficiency was peaked around 400 nm, following the manufacturer’s response curve. For the pyrex glass face, the refractive index was 1.48 at 400 nm. To implement the wavelength dependence of the photocathode, the absorption length parameters in the glass were set absorb (thus, stop tracking before they hit the photocathode) 100% of optical photons for wavelengths above 600 nm and below 300 nm, with a curve based on the manufacturer’s efficiency data. The method was verified for the PMT faceplate by covering the PMT with a black plastic sheet and recording spectra from ⁶⁰Co, ⁵⁷Co, and ⁶⁸Ge/⁶⁸Ga, as shown in Figure 1. Agreement was found between the simulation and experimental data above E_LS ≈ 5 keV, which is already below the lowest threshold used. However, the experimental ⁶⁰Co spectrum showed enhanced single-photoelectron emission, which could be due to γ-ray interaction with the photocathode or electrodes, but would not affect our coincidence measurements. Note, there was no leakage of β particles or LS light from the LS hemisphere through the black plastic to the PMT. This was determined by checking for coincidence between the ⁶⁰Co sum-peak (2.5 MeV) in the NaI detector and the LS signal. No coincidences were observed, indicating that when both γ-rays were accounted for in the NaI detector, there was no signal in the LS PMT. Similar leakage checks were performed for ⁶⁸Ge/⁶⁸Ga and ⁵⁷Co, with the same null result.

Figure 1.

Absolute efficiency per decay of the LS PMT obtained by wrapping the PMT in black plastic before placing the LS source on top. Experimental (solid lines) and simulated (dashed lines) LS spectra for ⁵⁷Co (red, lowest response), ⁶⁸Ge/⁶⁸Ga (green), and ⁶⁰Co (black, highest response). The response is presumably due to γ-rays interacting in the PMT window. No β-particle nor LS-light leakage occurred, as explained in the text.

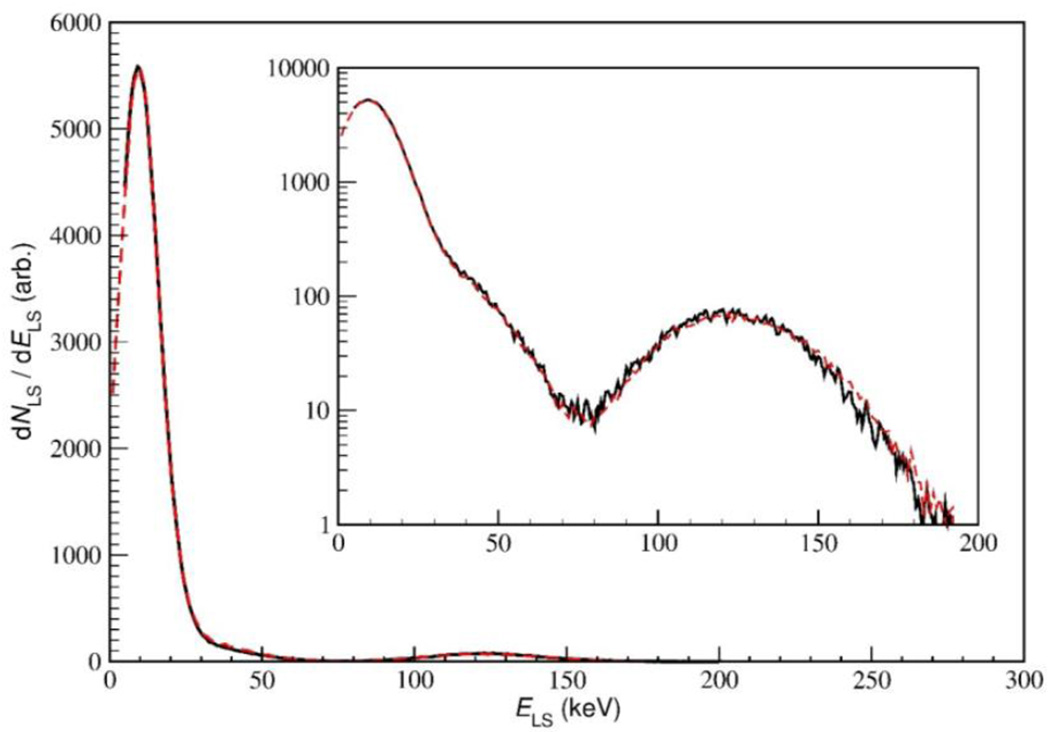
The output from the complete LS model is shown in Figure 2 for ⁵⁷Co, which features low-energy electron and X-ray emission with considerable summing. After tuning the model parameters (S = 5,500/MeV, kB = 0.07 mm/MeV) for this LS source (3 mL of Ultima Gold AB, 0.3 mL of water and 0.05 g of ⁵⁷Co solution), the simulated spectral shape matches the experimental data.

Figure 2.

Experimental (solid black line) and simulated (dashed red line) LS spectra for ⁵⁷Co. Inset is same data, on a log scale.

4. Applications

The simulation has been applied to activity measurements for various radionuclides. The general procedure is to input necessary nuclear data, run the simulation in the same conditions as the experiment, check that the spectra agree qualitatively, and then perform efficiency extrapolations on both the data and the simulation. The simulation can be run to high precision to look for trends in the residuals, and the intercept of the simulation extrapolation $(\widetilde{N_0})$ can be compared to the number of decays in the simulation (Ã). Then, a correction factor, f, can be applied to the experimental intercept, to reveal the activity,

$$f=\frac{\tilde{A}}{\widetilde{N_0}}.$$ (5)

Alternatively, the simulated data can be scaled to the experimental data, using only one scale parameter, instead of extrapolating. (For linear data, that scaling is equivalent to using the simulated slope in the extrapolation.) Furthermore, the simulation can be run for tests of sensitivity to NaI gates, model parameters, and the presence of radioactive impurities mixed in with the source.

4.1 ^99mTc

Measurement of ^99mTc activity by coincidence counting is challenging due to the fact that most of the LS events stem from 2 keV conversion electrons (DDEP, 2015). The problem is typically approached using proportional-counter-based coincidence (Goodier and Williams, 1966) by making sources from drops of technetium pertechnetate dried under hydrogen sulfide (NCRP, 1985) on thin polymer films. The source preparation is difficult due to the volatility of technetium and the fragility of the thin films. Thus, LS is an attractive alternative. However, the LS efficiency is also low, with the maximum LS efficiency used in the extrapolation per ^99mTc decay was about 15 %.

Given the above challenges, ^99mTc is a good test of the Monte Carlo simulation. As part of a recent ⁹⁹Mo standardization, three ^99mTc LS vials were made, each containing 0.15 g of a slightly acidic ^99mTc solution in 3 mL of Ultima Gold AB. The solution was prepared to match that from an earlier study, and contained 85 µg/g of Na₂MoO₄ and 53 µg/g of NaCl dissolved in 0.3 mol/L HNO₃. The three ^99mTc sources and a blank were measured in the LTAC system. The main goal of the work was to obtain spectra. However, here we analyze the ^99mTc LTAC data using both a linear extrapolation and by scaling the simulation extrapolation to the data. The ^99mTc activity was also determined to ± 0.5 % using an ionization chamber that had recently been calibrated using a proportional-counter coincidence system (Michotte and Fitzgerald, 2010). Here we use that as the “known” value of the activity, A, to test our simulation.

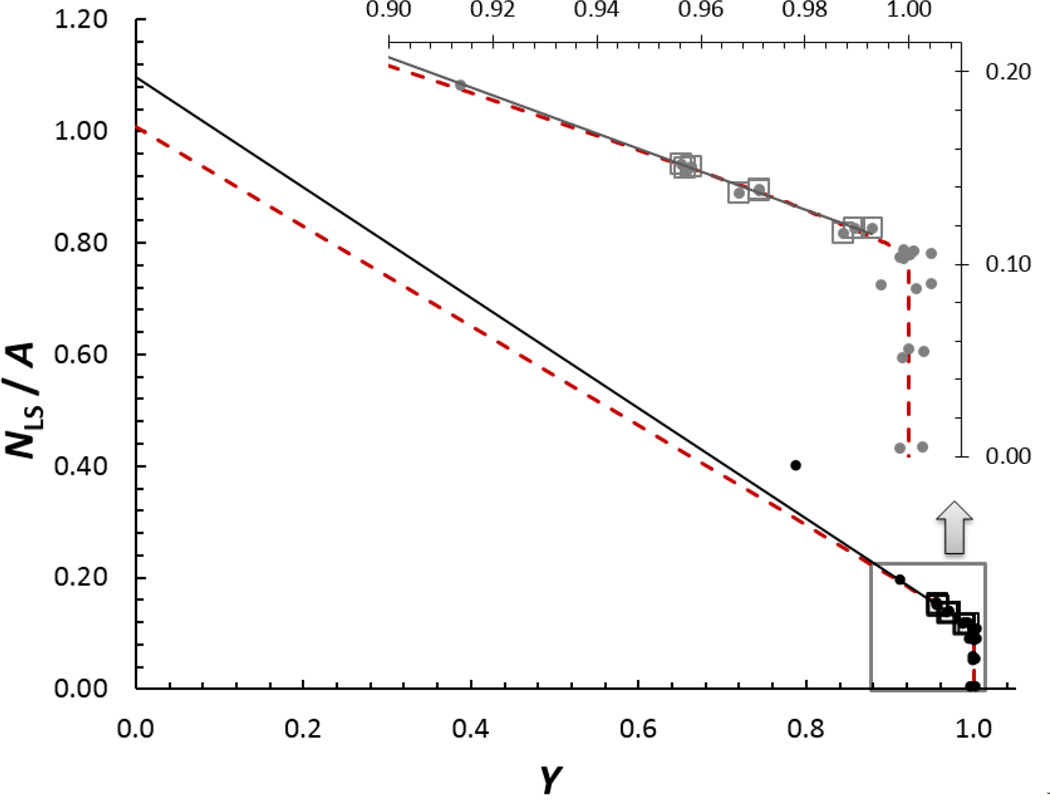
The NaI gate was set around the 140 keV γ ray and the resulting efficiency extrapolation is shown in Figure 3. A linear fit to the data resulted in an intercept relative to the known activity of N₀/A = (1.10 ± 0.06). Additionally, the Monte Carlo scaling method was used by scaling the Monte Carlo extrapolation curve to match the experimental data. Essentially this uses the Monte Carlo slope and only leaves the intercept as a free parameter. The Monte Carlo scaling resulted in a more accurate and precise value of N₀/A = (1.009 ± 0.007). Here, the uncertainties for both methods are standard deviations in the intercepts from the least-squares analyses. No trends are visible in either set of residuals. If the simulation data is extrapolated over the same domain, it gives $\widetilde{N_0}/\tilde{A}=(1.080\pm 0.06)$. So using Equation 5 to correct the intercept would yield N₀/A = (1.02 ± 0.06). Comparing this result to the (1.009 ± 0.007) value above shows that the scaling method produced a more accurate and precise result. The scaling method was useful in this case because the data used in the extrapolation covered so little range in efficiency, that the slope was not well-defined by the data.

Figure 3.

Efficiency extrapolation for ^99mTc, relative to the activity (A) determined previously. The data in squares were used for a linear extrapolation (solid line) and for scaling Monte Carlo simulation (dashed line). The inset shows fit region in detail. The point at Y ≈ 0.8 corresponds to a LS lower-level threshold in the single-photoelectron peak of the PMT, with high background (30 s⁻¹), so was ignored. The point at Y ≈ 0.9 was just above the noise threshold, but was ignored out of prudence, since systematic tests of the noise were not carried out at the time.

With the simulation, high-precision sensitivity tests were carried out by varying S, kB, the γ-ray gate, and nuclear data. The total uncertainty in the final activity from these effects would be 1.9 %, due mostly to the atomic and nuclear data (DDEP, 2015). Varying S from 4000/MeV to 3700/MeV changed the result by 0.03 %, changing kB from 0.075 mm/MeV to 0.06 mm/MeV changed the result by < 0.01 %.

4.2 ¹⁸F

The usual method for standardizing ¹⁸F activity is to measure the ¹⁸F positron emission rate, and then divide by the positron branching ratio (Fitzgerald et al., 2014; Schrader et al., 2007). In that case, one must exclude any electron capture decay events, which produce electrons of about 0.5 keV, by, for instance, limiting the LS threshold to be above the single-photoelectron peak. This methodology was checked using the Monte Carlo by running the simulation with and then without the electron capture branch present. No effect was seen on the LS rate and the extrapolation intercept decreased by 0.2(2) %.

An extrapolation of the Monte Carlo simulated data resulted in an intercept that was a factor of 1.0001 (1) higher than the β⁺ branching ratio, thus if a correction factor, f, was to be applied to the experimental intercept, it would be the reciprocal of the intercept, or 0.9999. The ratio of the slope to intercept from the Monte Carlo was −0.989 (3) and for the experimental data this was −0.996 (5), in agreement within the combined uncertainty. The experimental uncertainty was the standard deviation of the mean for 24 repeated measurements on two sources, and the Monte Carlo uncertainty was only that from the least-squares fit.

4.3 ¹²⁹I

LS-based 4πβ-γ anticoincidence counting of ¹²⁹I is complicated by the similar energies of the betas (151 keV), which decay to the 40 keV state of ¹²⁹Xe, and the electrons, X rays and γ rays emitted by the relaxation of the ¹²⁹Xe excited state (DDEP, 2015). Even an efficiency extrapolation constrained to start below 40 keV would still have contribution from the conversion electrons, a situation that would lead to a non-linear extrapolation.

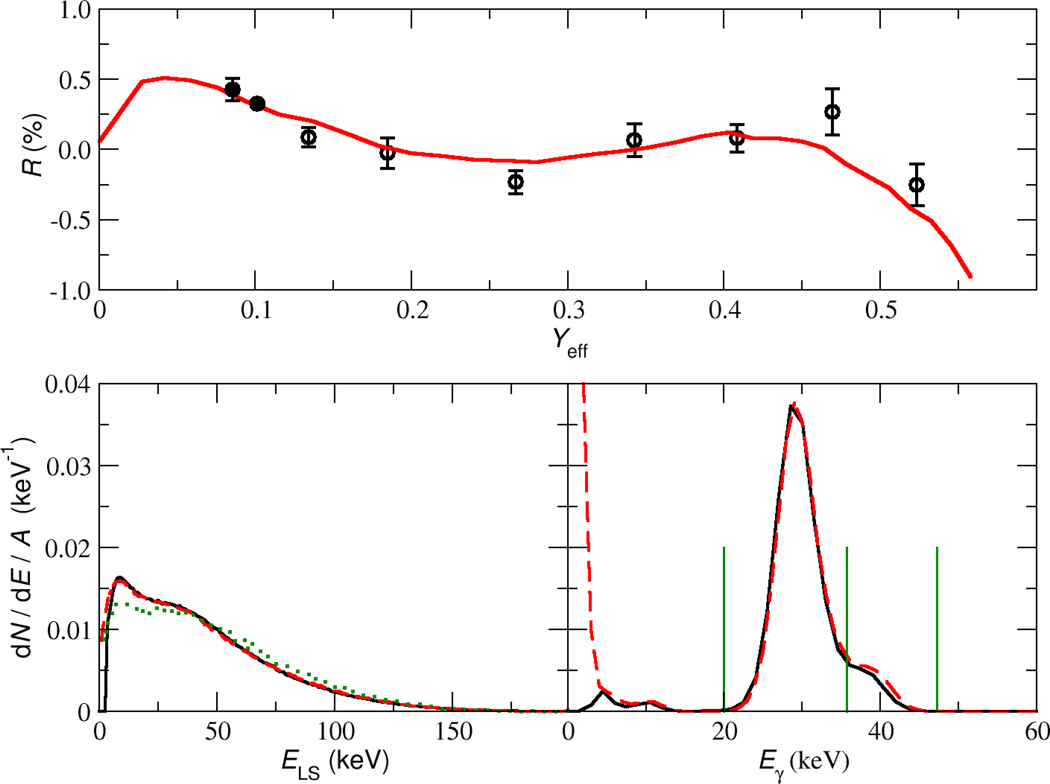
This problem was approached using the simulation. The measured and simulated spectra and extrapolation residuals are shown in Figure 4. Recent measurements were made at NIST by various LS-based methods. The LS hemispheres consisted of 4 mL of Hionic Fluor and 0.25 g of a weakly-basic ¹²⁹I solution. The Monte Carlo model yield was tuned to match the experimental data using S = 3,600/MeV. For the anticoincidence measurements, two NaI gates were used, with gate 1 corresponding mostly to K X-ray events and gate 2 having a large contribution from the 40-keV γ-rays, as well as K X-rays. An effective inefficiency (found by simulation) to yield the true intercept for a quadratic extrapolation was Y_eff = 0.74 Y₁ + 0.26 Y₂. Nonetheless, the residuals show an obvious trend, as can be seen in the top panel of Figure 4. Thus, the least-squares uncertainty of the intercept does not represent the true uncertainty.

Figure 4.

[bottom] Experimental ¹²⁹I spectra (black solid lines) as well as Monte Carlo simulations (red dashed lines) for LS [left] and NaI [right]. The dotted LS spectrum ignores the shape factor (der Mateosian, 1954). The vertical green lines delineate gates 1 and 2, from left to right. [top] Residuals (R) from a quadratic fit, where uncertainty bars are standard deviations for 3 sources. The fit domain spanned only the open circles. Monte Carlo residuals are shown by the solid red line.

Using Y_eff in the simulation resulted in a correction factor of f = 0.9982. The standard deviation of intercept values resulting from 7 Y_eff weighting choices, made by changing the a_i parameters in Equation 2, corrected each time by the respective f, was 0.4 %, which was the main source of uncertainty in the massic activity.

The value of this approach is evident if we imagine a worse case with a longer extrapolation. If we ignore the high-efficiency data in the experiment, resulting in a limited extrapolation domain of 0.35 < Y_eff < 0.55, a linear or quadratic extrapolation intercept would be +7% or −4% from the original (short extrapolation) value. Likewise if we use that same restricted extrapolation domain of the Monte Carlo simulated data, the simulated intercepts would similarly be +6 % and −3.9 % different from the original value. Thus, if we correct the experimental intercepts by f (Equation 5), the recovered activities would only change by +1.0 % or −0.1 % for the long linear and quadratic extrapolations. Thus, the simulation improves the accuracy of long efficiency extrapolations.

4.4 ¹²⁴I

Anticoincidence counting of electron capture nuclides suffers the fate that even a truly linear extrapolation will not generally reveal the actual activity, due to the differing K/L/M capture ratios between the capture branches that produce γ rays, and those that do not (Funck and Nylandstedt Larsen, 1983). Derivation of the correction factor is complicated by the atomic cascades following the EC, and have been simulated previously for some radionuclides (Chauvenet et al., 1987).

The measurement of ¹²⁴I is further complicated by the mixture of β⁺ with the EC branches and the coincidence summing of various γ rays, X rays, and annihilation radiation in the NaI and in the LS spectra. The simulation proves useful for deriving the correction factor and uncertainty to the extrapolation intercept. Even in proportional-counter coincidence, the fit residuals have shown non-random trends (Woods et al., 1992). Thus, ¹²⁴I is an extreme test-case for the simulation method.

We set three NaI gates, G1 around the 603-keV peak from the first-excited state to the ground state, G2 around the 511-keV annihilation peak, and G3 from 1325 keV to 1690 keV corresponding to higher-level γ rays (and sum peaks) (DDEP, 2015). A linear fit was found by 3-dimensional extrapolation to be Y_eff = 0.40 Y₁ − 0.01 Y₂ + 0.61 Y₃. Introducing Y_eff into the simulation model resulted in an intercept of 0.993. Therefore, the intercept of the data was corrected by f = 1/0.993 to yield the activity. To obtain an uncertainty, 5 other Y_eff values that roughly fit the data (such that we judge that the standard deviation of the 5 resulting intercepts represent the standard uncertainty). The resulting 5 intercepts for the experimental data and model scaled similarly, such that the standard deviation of the corrected intercept values was 0.5 %. The standard deviation of the intercepts for 5 measurements on 3 sources was 0.8 %, the high value due to the long extrapolation (Y_eff > 0.56), which amplifies small variability in the data. Varying S and kB within a range that yielded reasonable fits to the data produced standard deviations in the intercept of 0.6 % and 0.8 % respectively, indicating that the simulation is sensitive to model parameters for this challenging nuclide.

Finally, the simulation was valuable for calculating the effect due to possible ¹²⁵I and ¹²³I impurities in the solution. Adding a 1.0 % ¹²⁵I impurity raised the apparent activity by 1.3 %, whereas adding a 1.0 % ¹²³I impurity only raised the apparent activity by 0.27 %. Thus, the effect of impurities on coincidence counting of ¹²⁴I depends strongly on the decay scheme of the impurity.

5. Conclusion

The Geant4-based Monte Carlo simulation matches well the qualities of the LS and NaI spectra and of the efficiency extrapolation curves for the trials described here. The biggest challenge encountered was ¹²⁴I, due to its mixed modes of decay and low LS efficiency. In that case the model parameters and secondary effects like γ-ray interaction within the PMT become more important.

Further development of the simulation is possible for those secondary effects, for more-detailed modelling of the scintillation process, and in tuning the model to each individual source, instead of by batch, for low-efficiency cases.