An efficient protocol for obtaining accurate hydration free energies using quantum chemistry and reweighting from molecular dynamics simulations

Graphical abstract

1. Introduction

The accurate determination of hydration free energy (HFE) is of paramount importance to the fields of chemistry, biophysics and rational drug design. HFE, the free energy required to transfer a molecule from the gas phase to an aqueous solution at the limit of infinite dilution, in turn affects other properties critical to the drug design process. Properties such as: solubility, distribution, protomeric state, ligand binding and diffusion, are all affected by a ligand’s hydrophilicity and therefore its HFE. One of the key goals for computational chemistry is the accurate prediction of HFE values.

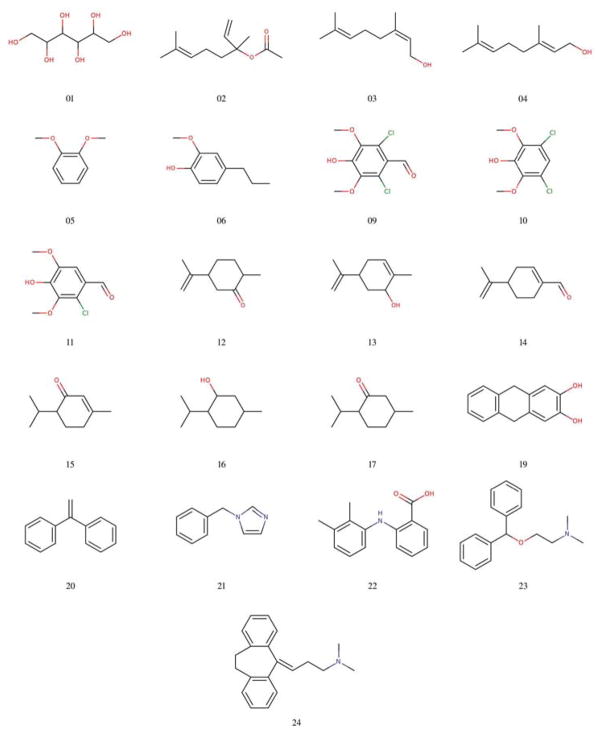
Accurate HFE determination is also of critical importance to computational chemistry method development, as it serves as an evaluation tool for a diverse set of theoretical methods from force field parameters, sampling methods, free energy protocols and even quantum chemistry techniques. The statistical assessment of modeling of proteins and ligands (SAMPL) challenge Nicholls et al. [2008]; Guthrie [2009]; Marenich et al. [2009a]; Geballe et al. [2010]; Klimovich and Mobley [2010]; Klamt and Diedenhofen [2010]; Ribeiro et al. [2010]; Muddana et al. [2012]; König and Brooks [2011]; Gallicchio and Levy [2012]; Lawrenz et al. [2012]; Mobley et al. [2011]; Geballe and Guthrie [2012]; Beckstein and Iorga [2011]; Reinisch et al. [2012]; Kehoe et al. [2011]; Guthrie [2014]; Mobley et al. [2014]; König et al. [2014a]; Mikulskis et al. [2014] has emerged as a venue for computational chemists to evaluate the efficacy of their methods with respect to blinded, high quality, curated experimental data. In the SAMPL4 challenge, we predicted HFE values (1 M fixed-concentration standard-state) for the 21 molecules in the blind portion of the small molecule challenge (Figure 2), where the non-Boltzmann Bennett (NBB) free energy method König et al. [2014a]; König and Boresch [2011]; König et al. [2014b] was used in combination with molecular mechanics (MM) and quantum mechanics (QM) to make HFE predictions.

Figure 2.

The 21 molecules from the blind portion of the SAMPL4 hydration free energy challenge.

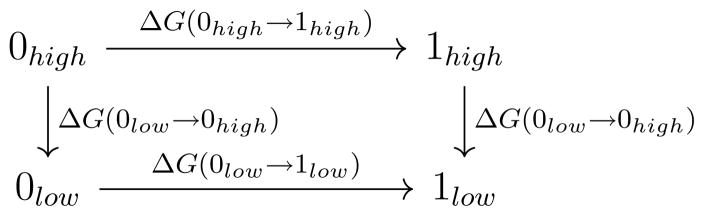
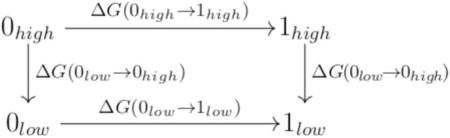
NBB is a free energy method for calculating the free energy difference between two expensive (QM) potential energy surfaces (PES) based on sampling from two cheaper (MM) PES. König and Boresch [2011]; König et al. [2014a,b] This is achieved by reweighting the data obtained from the cheaper PES to the more expensive PES. The convergence of the NBB calculations relies on the capability of Bennett’s acceptance ratio method Bennett [1976] to determine many complex free energy differences in just one step (Figure 1). Gao and Xia [1992]; Gao et al. [1993]; Gao and Freindorf [1997]; Vaidehi et al. [1992]; Luzhkov and Warshel [1992]; Wesolowski and Warshel [1994]; König et al. [2009] It is advantageous to use NBB to connect QM surfaces based on MM, because it allows one to harness the advantages of both methods in a computationally efficient manner. The calculation of free energy differences involves accurately computing potential energy differences over an ensemble of configurations from the states of interest. MM methods can quickly sample the potential energy surface, but may have difficulty accurately modeling solute–solvent interactions. Conversely, QM methods are very accurate, but their relative expense precludes them from generating ensembles for all but the smallest of gas phase systems. NBB allows for the combination of these methods’ complementary strengths. The accurate QM Hamiltonian can address weaknesses of the assumptions inherent in a fixed charge MM force field, or weaknesses in the parameterization itself, which frequently occurs in difficult to parameterize drug-like molecules. Conversely, the sampling from the MM trajectories captures the conformational entropy and anharmonic effects, which is often not technically feasible with QM calculations alone.

Figure 1.

The thermodynamic cycle used for indirect free energy calculations in this work.

While coupling QM and MM methods together using NBB is enticing in principle, the results of our submissions to SAMPL4 using this approach were mixed. Computing HFE values using QM/MM B3LYP/6-31G(d)/TIP3P coupled to MM using the CHARMM general force field (CGENFF) Vanommeslaeghe et al. [2010, 2012] and TIP3P yielded root mean square deviations from experiment (RMSD) of 1.6 kcal·mol⁻¹, our best submission. However, by making a different choice of solvent, including the use of implicit solvent, choosing a different QM method, or even using purely MM or QM approaches, statistically different results may be obtained. König et al. [2014a] Because the “parametric space” encompassed by the choice of density functional, basis set and solvent model is large, in the current work we exhaustively explore the results’ dependence upon these choices. We will choose an effective QM method, by using the HFE of the SAMPL4 data set as our objective. Since we will focus on the efficiency and accuracy of the calculations, we make extensive use of implicit solvation methods. In the end, we provide an accurate and efficient QM-NBB protocol to obtain results that are consistently more accurate than either pure QM or MM calculations alone.

2. Methods

2.1. Free Energy Methods

The most basic method to estimate the free energy difference, ΔG^i→j, between a sampled state i and an unsampled state j is the Zwanzig equation, Zwanzig [1954] it is also known as thermodynamic perturbation. This free energy difference is obtained via the following:

$$\mathrm{\Delta }{G}^{i\to j}=-{\beta }^{-1}ln{\langle exp[-\beta (U_j-U_i)]\rangle }_i.$$ (1)

Here β⁻¹ is the thermodynamic temperature (k_BT), U_i is the potential energy of a configuration drawn from state i using the Hamiltonian of state i, and the angle brackets imply an ensemble average over state i. This approach Zwanzig [1954] can, in principle, be used to obtain a free energy value for a QM PES, using an ensemble generated using a much cheaper MM force field. Such free energy differences can be used to correct for errors that may arise from a classical force field representation in molecular dynamics (MD), without the need to run prohibitively expensive ab initio molecular dynamics. The applicability of this approach is limited by the overlap between QM and MM potential energy surfaces, and the size of the system of interest, because of this, alternative free energy schemes may be preferable. Dybeck et al. [2016]; Jia et al. [2016]; Ryde and Söderhjelm [2016]; König and Brooks [2015]; Cave-Ayland et al. [2014]; Sampson et al. [2015]; Rodinger and Pomès [2005]; Heimdal and Ryde [2012]; Mikulskis et al. [2014]; Genheden et al. [2015]; Olsson et al. [2016]; Hudson et al. [2015a,b]; Beierlein et al. [2011]; Fox et al. [2013]

Improving upon the Zwanzig equation, Bennett Bennett [1976] showed that the minimum variance estimate of the free energy difference between two states, using configurations drawn from both states, is calculated by

$$\mathrm{\Delta }{G}^{i\to j}=-{\beta }^{-1}ln\left(\frac{{\langle f(\beta [U_i-U_j+C])\rangle }_j}{{\langle f(\beta [U_j-U_i+C])\rangle }_i}\right)+C$$ (2)

where f is the Fermi function

$$f(x)=\frac{1}{1+exp(x)}$$ (3)

and C is a constant. An iterative procedure is applied, such that the ratio in eq. 2 approaches unity. This estimator is known as Bennett’s Acceptance Ratio (BAR), and it is very commonly applied to studying free energy changes in chemical processes. When considering the free energy differences between more than two states, such as in a chain of states during an alchemical transformation process, the multistate BAR (MBAR) estimator should also be considered. Shirts and Chodera [2008] One disadvantage of the BAR method, is that it requires configurations to be drawn from both states i and j. When working with QM based methods, direct sampling is computationally too demanding.

Using the NBB estimator, similarly to Zwanzig, we can estimate the free energy of an unsampled state i by using configurations drawn from a sampled state i′. This is accomplished by biasing the sampled states i′ and j′ using the potential energy difference between i and i′ as follows

$$V_i^{\mathrm{b}}=U_{i^{\prime }}-U_i.$$ (4)

The correct ensemble averages in the unsampled states i and j are then recovered from the biased states by applying Torrie and Valleau’s relationship Torrie and Valleau [1977] to calculate the unbiased ensemble average, 〈X〉_i, from configurations taken from a biased state i′.

$${\langle X\rangle }_i=\frac{{\langle Xexp(\beta V_i^{\mathrm{b}})\rangle }_{i^{\prime }}}{{\langle exp(\beta V_i^{\mathrm{b}})\rangle }_{i^{\prime }}}$$ (5)

Combining eq. 2 and eq. 5 yields the NBB equation, which allows us to estimate the free energy difference between two unsampled states i and j.

$$\mathrm{\Delta }{G}^{i\to j}=-{\beta }^{-1}ln\left(\frac{{\langle f(\beta [U_i-U_j+C])exp(\beta V_j^{\mathrm{b}})\rangle }_{j^{\prime }}{\langle exp(\beta V_i^{\mathrm{b}})\rangle }_{i^{\prime }}}{{\langle f(\beta [U_j-U_i-C])exp(\beta V_i^{\mathrm{b}})\rangle }_{i^{\prime }}{\langle exp(\beta V_j^{\mathrm{b}})\rangle }_{j^{\prime }}}\right)+C$$ (6)

2.2. MD Simulation

All MD simulations were carried out using the PERT module within the CHARMM simulation package. Brooks et al. [2009, 1983] CGENFF parameters Vanommeslaeghe et al. [2010, 2012] along with the TIP3P water model Jorgensen et al. [1983]; Neria et al. [1996] were used to generate all ensembles. All trajectories used a 1 fs timestep and were thermostated to 300 K, no constraints were used. MD simulations in the gas phase were performed without non-bonded cutoffs, using a Langevin integrator with a friction coefficient of 5 ps⁻¹ on all atoms. These simulations were 50 ns long, with coordinates saved every 1000 steps for later post-processing. The aqueous phase was modeled by 1492 TIP3P water molecules filling a truncated octahedron box inscribed in a 38.60 Å cube. Long range electrostatics were represented using smooth particle mesh Ewald summation, Darden et al. [1993]; Essmann et al. [1995] while Lennard-Jones interactions were continuously switched off between 10 and 12 Å. A Nosé-Hoover thermostat Hoover [1985] maintained the canonical ensemble. Soft-core potentials Beutler et al. [1994]; Zacharias et al. [1994] were used to avoid the so-called “van der Waals endpoint problem”. Aqueous phase simulations were 1 ns long and coordinates were saved every 20 steps for later post-processing. All simulations were repeated in triplicate with different random seeds, to obtain a simple estimate the statistical uncertainty. Condensed phase simulations were initially equilibrated using a Langevin piston barostat for 0.1 ns and further equilibrated for 0.1 ns in the canonical ensemble. This approach neglected the work contribution, which is expected to be very small for these systems, to expedite the MD calculations.

HFE from classical simulations were calculated by turning off all non-bonded solute interactions, both in the gas and aqueous phases. This alchemical mutation was carried out in five steps. In step 1, the charges on the gas phase solute were decremented to zero over six states (λ = 0.00, 0.05, 0.15, 0.40, 0.80 and 1.00). We refer to this process as “uncharging”. In step 2, we decremented the Lennard-Jones interactions in the gas phase over seven states (λ = 0.00, 0.15, 0.35, 0.65, 0.80, 0.90 and 1.00). We refer to this process as “vanishing”. In step 3, we transfer the non-interacting ligand, A^(n,Ø), from the gas to the aqueous phase. The free energy of this process is equivalent to zero. Step 4 negates the vanishing process in the aqueous phase, this required thirteen states (λ = 0.00, 0.05, 0.10, 0.20, …, 0.90, 0.95 and 1.00). Finally, step 5 negates the uncharging process in the aqueous phase, this required twelve more states (λ = 0.00, 0.05, 0.10, 0.20, …, 0.90 and 1.00). Thus, in total, the MM HFE was calculated in five steps,

$${\mathrm{A}}_{\text{gas}}^{(+,\text{LJ})}\stackrel{\mathrm{\Delta }{G}_1}{\to }{\mathrm{A}}_{\text{gas}}^{(\mathrm{n},\text{LJ})}\stackrel{\mathrm{\Delta }{G}_2}{\to }{\mathrm{A}}_{\text{gas}}^{(\mathrm{n},\varnothing )}\stackrel{\mathrm{\Delta }{G}_3}{\to }{\mathrm{A}}_{\text{aq}}^{(\mathrm{n},\varnothing )}\stackrel{\mathrm{\Delta }{G}_4}{\to }{\mathrm{A}}_{\text{aq}}^{(\mathrm{n},\text{LJ})}\stackrel{\mathrm{\Delta }{G}_5}{\to }{\mathrm{A}}_{\text{aq}}^{(+,\text{LJ})},$$ (7)

where + denotes the fully-charged states, and n denotes uncharged states.

To enhance sampling, Hamiltonian Replica Exchange Sugita and Okamoto [1999]; Sugita et al. [2000] was used to periodically exchange structures between neighboring λ-states. Because all of these λ-states are already necessary to estimate the HFE using a purely MM Hamiltonian, or using a hybrid QM/MM approach, multiplexing the alchemical states together via replica exchange provides accelerated convergence, for marginal cost. Exchanges were attempted every 1000 steps. In the gas phase, the average acceptance rate of attempted exchanges was 43%, while in the aqueous phase, it was 24%.

2.3. QM Optimization

All QM calculations in this work were performed using Gaussian 09. Frisch et al. [2009] Pure QM HFE were calculated using either a “vertical” or “adiabatic” protocol. In the vertical scheme, geometry optimizations were performed exclusively in the gas phase, and then a single point energy calculation (SPC) was performed on that static geometry in the aqueous phase, as modeled by an implicit solvent. In the adiabatic scheme, geometry optimizations are carried out in both the gas and aqueous phases. Next, the Hessian matrices are computed for both phases, and these are used to compute the thermal corrections (to 298.15 K) for each molecule in the harmonic limit. Finally, a SPC was optionally computed on the static geometries using a larger (triple-ζ) basis set, in both phases, to attempt to further improve the computed HFE, and to explore the efficacy of triple-ζ basis sets. All QM optimizations were performed with “Tight” wave function and geometry convergence criteria. For DFT calculations, “UltraFine” numerical quadrature was used as required for the M06-2X functional, and also such that fair comparisons could be made across all selected methodologies. To mimic the effects of bulk aqueous solvent, both the default implicit solvent in Gaussian 09 (keyword “SCRF=IEFPCM”) Scalmani and Frisch [2010] and the SMD Marenich et al. [2009b]; Ribeiro et al. [2010]; Marenich et al. [2009a] implicit solvent (keyword “SCRF=SMD”) models were used. An extensive range of QM methods (M06-2X, Zhao and Truhlar [2007, 2008] B3LYP, Becke [1993] PBE0, Adamo and Barone [1999] OLYP, Handy and Cohen [2001]; Hoe et al. [2001]; Lee et al. [1988]; Miehlich et al. [1989] BLYP, Lee et al. [1988]; Miehlich et al. [1989] M06-L, Zhao and Truhlar [2006] Hartree-FockRoothaan [1951] and MP2 Head-Gordon et al. [1988]) and basis sets (6-31G(d), Ditchfield [1971] 6-31+G(d), Hariharan and Pople [1974] DZP, ²Dunning [1970] def2-SV(P)Weigend and Ahlrichs [2005] and cc-pVDZ Dunning [1989]) were used throughout this benchmarking study.

2.4. pK_a Calculation

While a majority (17 of 21) of the molecules in the SAMPL4 blind set are electrostatically neutral at pH = 7.4, four molecules (21, 22, 23 and 24) were believed to possibly have contributions from non-neutral states at equilibrium. To account for this, and mitigate its effect upon our results and guidance, we estimated the pK_a values for these molecules using adiabatic QM solvation calculations. The M06-2X/6-31+G(d) method was used for these calculations in a manner consistent with the QM optimization protocol as described above. An additional SPC at the M06-2X/6-311++G(d,p) level was also carried out.

A detailed description of the nuances of the computational estimation of pK_a values is beyond the scope of this work, the reader is directed to the recent review literature. Seybold and Shields [2015]; Casasnovas et al. [2014] Briefly, the objective is to compute the free energy of deprotonating a ligand, AH⁺, in the aqueous phase. This quantity, ΔG_aq, can then be readily converted into a pK_a using eq. 9, where R = k_B/N_A is the usual gas constant. The relative populations of the various protomers, and hence the free energy of relaxing the protomer constraint, is obtained by application of the Henderson-Hasselbalch equation at pH = 7.4.

$${\text{AH}}_{\text{aq}}^{+}\stackrel{\mathrm{\Delta }{G}_{\text{aq}}}{\to }{\mathrm{A}}_{\text{aq}}+{\mathrm{H}}_{\text{aq}}^{+}$$ (8)

$$\mathrm{\Delta }{G}_{\text{aq}}=ln(10)RT\mathrm{p}{K}_{\mathrm{a}}$$ (9)

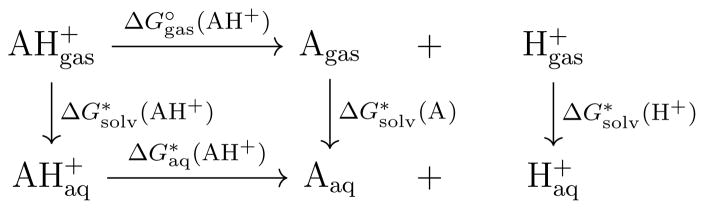
In the absolute scheme, calculation of ΔG_aq is accomplished with the standard thermodynamic cycle, shown in Figure 3. Values for $G({\text{AH}}_{\text{aq}}^{+})$ and G(A_aq) are obtained directly from the QM calculations. The value of $G({\mathrm{H}}_{\text{gas}}^{+})$ is analytic, while ΔG_solv(H⁺) is experimentally determined. Tissandier et al. [1998] A final factor of RT ln(24.46) is also included to account for change of standard state from 1 atm·L⁻¹, denoted “∘”, in the gas phase to 1 mol·L⁻¹, denoted “*”, in the aqueous phase. Physically, this term corresponds to the loss of entropy when compressing an ideal gas from 1 atm to 24.46 atm (1 M), this is approximately 1.89 kcal·mol⁻¹ at 298.15 K. This scheme is generally robust, but is often imprecise. Errors from the solvation of charged ligands and uncertainties associated with the experimental value of hydrating a free proton (ΔG_solv(H⁺) = −265.9 kcal·mol⁻¹), Tissandier et al. [1998] are thought to be the main culprits.

Figure 3.

The thermodynamic cycle used for absolute pK_a calculations in this work.

2.5. QM/MM- and QM-NBB Calculations

When calculating the HFE using NBB between a hybrid QM/MM surface and a classical MM surface (QM/MM-NBB), we use the “indirect” scheme (Figure 1) for computing the free energy difference between two states, as pioneered by Gao and co-workers and Warshel and co-workers, Gao and Xia [1992]; Gao et al. [1993]; Gao and Freindorf [1997]; Vaidehi et al. [1992]; Luzhkov and Warshel [1992]; Wesolowski and Warshel [1994] and combine it with the NBB free energy estimator. That is, to vastly reduce computational costs, instead of performing NBB between every pair of adjacent intermediate λ states, we only connect the QM/MM surface to the MM surface at the endpoints, i.e. from λ₀ → λ₁ and from λ_K−1 → λ_K, where λ₀ and λ_K correspond to the physical states of interest. This is necessary from a practical perspective, because the full “direct” NBB calculation for all K intermediate states, with N configurations drawn from each state, would require KN expensive QM/MM energy evaluations, a prohibitively expensive endeavor. Furthermore, the direct approach does not necessarily increase accuracy, since the convergence of the free energy method strongly depends on the overlap between MM and QM. Dybeck et al. [2016]; Jia et al. [2016] Instead, the indirect NBB approach only requires only 4N QM/MM energy evaluations, while the free energy difference between the remaining interior λ_k states (where k ∈ {1, …, K − 1}) are treated using the MM potential with the standard BAR approach. Provided sufficient overlap exists in the two NBB calculations, the direct and indirect approaches yield equivalent results, because free energy is a state function.

When estimating the HFE using NBB combined with pure QM and an implicit solvent, the BAR calculation on the interior λ states may be avoided completely. This is because the solvent water molecules are now removed, and sufficient overlap exists, with NBB biasing, to connect λ₀ → λ_K directly. In this case, 4N QM calculations are still required, and the NBB equation simplifies to the following.

$$V_i^{\mathrm{b}}=U_{i,\text{MM}}-U_{i,\text{QM}}$$ (10)

$$\mathrm{\Delta }{G}_{\text{QM}}^{\text{gas}\to \text{aq}}={\beta }^{-1}ln\left(\frac{{\langle f(\beta [U_{\text{gas},\text{QM}}-U_{\text{aq},\text{QM}}+C])exp(\beta V_{\text{aq}}^{\mathrm{b}})\rangle }_{\text{aq},\text{MM}}{\langle exp(\beta V_{\text{gas}}^{\mathrm{b}})\rangle }_{\text{gas},\text{MM}}}{{\langle f(\beta [U_{\text{aq},\text{QM}}-U_{\text{gas},\text{QM}}-C])exp(\beta V_{\text{gas}}^{\mathrm{b}})\rangle }_{\text{gas},\text{MM}}{\langle exp(\beta V_{\text{aq}}^{\mathrm{b}})\rangle }_{\text{aq},\text{MM}}}\right)+C$$ (11)

QM/MM-NBB calculations use DFT to model the solute and TIP3P to model the solvent explicitly. These calculations were performed using Q-Chem Shao et al. [2006] as implemented by the Q-Chem/CHARMM interface. Woodcock III et al. [2007] The implicit solvent QM calculations were performed using Gaussian 09. The solvent was modeled implicitly using SMD. To speed up the QM calculations, coarser integration grids and looser wave function convergence criteria were used than for the analogous QM optimized calculations. This increased performance ca. five-fold and incurred a loss of < 0.005 kcal·mol⁻¹ precision.

3. Results & Discussion

3.1. QM Optimization

To efficiently gauge basis set and DFT functional effects upon the QM-NBB calculations of HFE, we first calculated the HFE using several standard QM protocols as described above. These benchmarking calculations allowed us to efficiently try different protocols for the SAMPL4 test set, Guthrie [2014] and ultimately guided our choice of functional, basis set and solvation method for the expensive QM-NBB calculations.

Table 1 shows the RMSD of our adiabatic HFE calculations with harmonic frequency corrections applied using the SMD implicit solvent. This HFE protocol produced consistently strong results across all choices of functional and basis set (average RMSD of 1.95 kcal·mol⁻¹). Using a vertical HFE protocol (Table 8) also provided very strong results (average RMSD 1.82 kcal·mol⁻¹) for the SAMPL4 data set, and for a significantly reduced cost relative to the adiabatic HFE calculations. For small, rigid molecules, which tend to dominate the SAMPL4 blind set, the assumption implicit in using the vertical protocol – namely that the geometric reorganization free energy is small relative to the solvation free energy – are generally valid, however in general, when dealing with larger and more flexible ligands, the solute might undergo significant reorganization as it moves from gas phase to aqueous phase, and the adiabatic protocol may yield better results.

Table 1.

RMSD between HFE determined using QM optimization and experiment. These calculations used the SMD implicit solvent model with fully optimized structures in both the gas and aqueous phases. Thermal corrections to 298.15 K were applied in the harmonic limit. Free energies reported in kcal·mol⁻¹.

	6-31G(d)	DZP	def2-SV(P)	6-31+G(d)	cc-pVDZ
M06-2X	1.41	1.92	1.54	2.05	1.47
B3LYP	1.81	1.29	2.38	1.78	2.47
PBE0	1.39	1.36	1.83	1.77	1.98
OLYP	1.91	1.22	2.60	1.53	2.65
BLYP	2.39	1.21	2.97	1.79	3.02
M06-L	1.47	1.29	2.23	1.75	2.30
HF	2.27	2.32	1.92	2.92	1.57
MP2	1.74	1.40	2.48	2.29	2.42

Including a triple-ζ SPC (Table 9), along with harmonic corrections and the SMD solvent, gives a marginal improvement overall, RMSD 1.75 kcal·mol⁻¹. Unfortunately this improvement not uniformly distributed, as 15 of the 40 methods tested experience worse performance with a triple-ζ basis than with a double-ζ basis. The most expensive hybrid functionals, especially M06-2X, gain the most benefit from larger basis sets, while the performance of the affordable pure functionals suffers tremendously. This result is especially disappointing, as the three top performing methods (OLYP/DZP, BLYP/DZP and M06-L/DZP), all have significantly worse results with the analogous TZ2P basis set. These three methods also all provide predictions which are of equal quality to the very best triple-ζ predictions, with the notable exception of the MP2/6-311++G(3df,3pd) results, which are too expensive to consider for QM-NBB, and are provided for comparison purposes only. While disappointing, these results are consistent with the well established literature demonstrating the irregular convergence behavior of certain density functionals, Wang and Wilson [2004, 2005]; Wang et al. [2005] especially pure functionals, such as BLYP and OLYP. Because of the computationally expensive nature of these triple-ζ basis set corrections, and their inconsistent performance, we chose not to pursue them further in this work, and cannot recommend them in general for the SMD implicit solvent model. The IEFPCM implicit solvent, the Gaussian 09 default, generally gave very poor results. For example, adiabatic frequency corrected IEFPCM calculations (Table 7) resulted in average RMSD of 2.94 kcal·mol⁻¹, so we cannot recommend this approach either. Finally, while the SMD implicit solvent was parameterized using the M05-2X/6-31G(d) method, Zhao et al. [2006] our results demonstrate its broad compatibility with many combinations of functional and basis set, beyond those with which it was initially conceived.

If we attempt to account for the presence of non-neutral equilibrium structures via pK_a calculations, we can further reduce our RMSD values. Using the protocol for absolute pK_a calculations described in the methods section, we predict 21 has a pK_b of 8.74, 22 has a pK_a of 5.71, 23 has a pK_b of 6.30 and 24 has a pK_b of 5.69. From these equilibrium constants, we can readily calculate the free energy correction from the reference neutral molecule, upon which the QM calculations were performed, to the equilibrium conditions at pH = 7.4. Combining these pK_a corrections with the adiabatic protocol (Table 10) decreases the average RMSD from 1.95 kcal·mol⁻¹ to 1.82 kcal·mol⁻¹. Combining them with the vertical protocol (Table 11), yields more dramatic improvement, reducing the average from 1.82 kcal·mol⁻¹ to 1.57 kcal·mol⁻¹.

Based upon this analysis, we chose six QM methods to use in our implicit solvent QM-NBB protocol. Five methods were chosen overall, two of these methods (OLYP/DZP and BLYP/DZP) were chosen because of their strong performance in our QM optimization benchmarking studies using the adiabatic HFE scheme (Table 1), and the remaining three (M06-2X/6-31G(d), B3LYP/6-31G(d) and PBE0/6-31G(d)) because of their ubiquity within the field of quantum chemistry. The sixth method, BLYP/def2-SV(P), was chosen because of its poor performance in our benchmarking studies, and it will serve as a negative control in our QM-NBB calculations, and subsequent analysis.

For our six QM methods, we present fine grained results for each molecule the test set. The RMSD is repeated from the previous tables for convenience, as well as three additional non-parametric statistical estimators: the Theil–Sen estimator (T-S), Theil [1950] the Kendall rank correlation coefficient (τ) Kendall [1938] and the median signed deviation from experiment (MdnSD). These non-parametric estimators may be more robust than their parametric counterparts, especially for data with outliers. For example, if we calculate the standard Pearson’s R correlation coefficient for the six QM methods presented in Table 2, we obtain values between 0.94 and 0.96, implying nearly perfect linear correlation between our predicted values and experiment. However, if we discard the predictions for molecule 1, which are significantly more hydrophilic than the rest of the members of data set, our correlation values drop significantly into the range of 0.62 – 0.74, with the BLYP/def2-SV(P) data now responsible for the, significantly, worst correlation. The Kendall’s τ rank correlation metric properly discriminates between the predictions with good and bad correlation a priori. Similarly, the Theil–Sen estimator is able to robustly capture the slope of the linear fit between the QM optimized predictions and the experimental data. Finally, the median signed error is used to gauge the extent to which certain methods systematically underpredict (+) or overpredict (−) hydrophilicity. With these non-parametric estimators, we are able to robustly account for the disproportionate effect of molecules such as 1, which are significant outliers to the rest of the set, or molecules such as 21–24, where we are either ignoring, or imperfectly modeling significantly challenging chemical phenomena, such as deprotonation.

Table 2.

HFE predictions for six selected QM levels of theory using the adiabatic solvation scheme. Three non-parametric estimators have been applied to the QM data, to mitigate the effects of strong outliers, such as 1. Free energies reported in kcal·mol⁻¹.

Molecule	M06-2X/ 6-31G(d)	OLYP/ DZP	B3LYP/ 6-31G(d)	PBE0/ 6-31G(d)	BLYP/ DZP	BLYP/ def2-SV(P)	Expt.
1	−25.73	−23.97	−24.95	−25.30	−24.14	−21.22	−23.62 ± 0.3
2	−3.02	−2.97	−2.18	−3.02	−2.63	−0.47	−2.49 ± 0.9
3	−5.88	−5.71	−4.21	−5.48	−5.56	−2.75	−4.78 ± 0.3
4	−4.98	−5.45	−4.43	−5.42	−4.76	−2.65	−4.45 ± 0.2
5	−4.54	−4.42	−3.87	−4.22	−6.16	−2.47	−5.33 ± 0.1
6	−7.40	−7.29	−6.85	−7.13	−6.73	−5.22	−5.26 ± 0.2
9	−7.61	−6.45	−7.13	−6.75	−7.33	−4.94	−8.24 ± 0.8
10	−6.33	−4.75	−4.83	−4.88	−4.85	−3.12	−6.24 ± 0.4
11	−7.28	−6.63	−6.49	−6.52	−7.00	−5.05	−7.78 ± 0.8
12	−3.61	−4.69	−3.47	−4.16	−4.49	−2.69	−4.44 ± 0.2
13	−5.12	−5.20	−4.53	−4.75	−4.93	−3.11	−5.03 ± 0.4
14	−3.46	−4.14	−2.79	−3.26	−4.21	−1.57	−4.09 ± 0.2
15	−4.27	−5.30	−4.18	−4.58	−5.14	−3.24	−4.51 ± 0.1
16	−3.85	−3.41	−3.14	−3.66	−3.26	−2.03	−3.20 ± 0.3
17	−3.31	−3.59	−2.96	−3.48	−3.57	−1.89	−2.53 ± 0.3
19	−3.26	−3.71	−2.19	−3.55	−3.18	−1.01	−3.78 ± 0.1
20	−1.89	−2.13	−0.77	−2.07	−1.73	0.63	−2.78 ± 0.1
21	−7.10	−8.54	−6.15	−8.50	−7.11	−5.96	−7.63 ± 0.1
22	−6.30	−6.40	−4.72	−5.96	−6.19	−3.55	−6.78 ± 0.1
23	−4.98	−6.04	−4.28	−5.23	−5.78	−2.10	−9.34 ± 0.6
24	−4.77	−5.58	−3.56	−5.19	−4.71	−1.86	−7.43 ± 0.6
RMSD	1.41	1.22	1.81	1.39	1.21	2.97
T-S	0.90	0.79	0.84	0.73	0.85	0.78
τ	0.70	0.70	0.68	0.69	0.72	0.56
MdnSD	0.48	−0.17	1.11	0.28	−0.05	2.40

3.2. Implicit Solvent QM-NBB

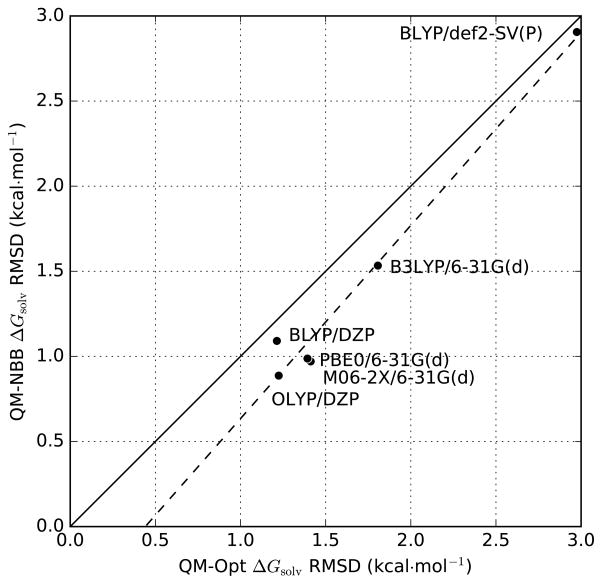
The application of the NBB free energy estimator to QM potential energy calculations with implicit solvent consistently yields higher quality HFE predictions. For all six QM methods tested, the QM-NBB protocol reduces the RMSD of the predicted HFE with respect to experiment (Table 3). Figure 4 shows the consistency of the RMSD reduction by using MM trajectories for sampling. Helpfully, the RMSD reduction is greater for QM methods that were already most effective for the QM optimization calculations. Even the extremely poorly performing BLYP/def2-SV(P) method enjoys a marginal decrease in RMSD. Our other statistical estimators also indicate an improvement in the quality of our predictions, as the Theil–Sen estimator indicates the slope of our predictions approaches unity. More significant, is the consistent improvement in the rank ordering coefficient, τ. This shows that QM-NBB might be an effective method for ranking the affinity of ligands relative to each other, an important property for the potential application of this method in the field of drug discovery. The median signed error is largely unchanged, and still relatively small for the better performing QM methods. Our best QM-NBB HFE predictions were calculated using the OLYP/DZP method. With a RMSD of 0.89 kcal·mol⁻¹, this is the most accurate set of HFE predictions on the SAMPL4 blind data set to be found in the literature. This is very advantageous result from an efficiency perspective, as OLYP is a pure functional, and does not have a kinetic energy density term, nor a Hartree–Fock exchange. This makes it much cheaper to use than other accurate functionals, such as M06-2X.

Table 3.

Detailed results for our QM-NBB calculations with the SMD solvent. Free energies reported in kcal·mol⁻¹.

Molecule	M06-2X/ 6-31G(d)	OLYP/ DZP	B3LYP/ 6-31G(d)	PBE0/ 6-31G(d)	BLYP/ DZP	BLYP/ def2-SV(P)	Expt.
1	−21.56 ± 0.2	−21.23 ± 1.2	−20.74 ± 0.6	−21.05 ± 0.5	−19.96 ± 0.9	−17.60 ± 0.2	−23.62 ± 0.3
2	−2.20 ± 0.4	−2.56 ± 0.1	−1.67 ± 0.2	−2.34 ± 0.3	−2.51 ± 0.2	−0.40 ± 0.1	−2.49 ± 0.9
3	−4.58 ± 0.0	−4.84 ± 0.3	−3.91 ± 0.2	−4.64 ± 0.2	−4.73 ± 0.1	−2.61 ± 0.2	−4.78 ± 0.3
4	−4.84 ± 0.2	−4.79 ± 0.2	−3.99 ± 0.2	−4.77 ± 0.2	−4.66 ± 0.1	−2.57 ± 0.1	−4.45 ± 0.2
5	−3.57 ± 0.5	−4.23 ± 0.2	−3.02 ± 0.3	−3.69 ± 0.5	−4.35 ± 0.0	−2.16 ± 0.1	−5.33 ± 0.1
6	−4.83 ± 0.6	−4.83 ± 0.2	−4.03 ± 0.5	−4.76 ± 0.6	−4.66 ± 0.1	−2.73 ± 0.1	−5.26 ± 0.2
9	−8.00 ± 0.4	−7.48 ± 0.5	−7.61 ± 0.2	−7.65 ± 0.2	−7.87 ± 0.7	−5.97 ± 0.5	−8.24 ± 0.8
10	−5.86 ± 0.3	−4.88 ± 0.5	−5.05 ± 0.2	−5.32 ± 0.2	−5.06 ± 0.4	−3.70 ± 0.5	−6.24 ± 0.4
11	−6.81 ± 0.4	−6.57 ± 0.4	−6.36 ± 0.4	−6.49 ± 0.2	−6.84 ± 0.4	−5.13 ± 0.5	−7.78 ± 0.8
12	−3.53 ± 0.3	−4.29 ± 0.3	−3.26 ± 0.2	−3.70 ± 0.4	−4.39 ± 0.2	−2.36 ± 0.3	−4.44 ± 0.2
13	−4.69 ± 0.2	−4.68 ± 0.1	−4.01 ± 0.2	−4.65 ± 0.2	−4.50 ± 0.1	−2.65 ± 0.1	−5.03 ± 0.4
14	−3.24 ± 0.2	−4.14 ± 0.2	−3.11 ± 0.2	−3.53 ± 0.3	−4.16 ± 0.3	−1.97 ± 0.3	−4.09 ± 0.2
15	−3.80 ± 0.2	−4.46 ± 0.2	−3.74 ± 0.3	−4.13 ± 0.2	−4.56 ± 0.3	−2.84 ± 0.3	−4.51 ± 0.1
16	−3.33 ± 0.1	−3.23 ± 0.1	−2.94 ± 0.1	−3.28 ± 0.1	−3.25 ± 0.1	−1.83 ± 0.1	−3.20 ± 0.3
17	−2.83 ± 0.4	−3.29 ± 0.4	−2.64 ± 0.3	−3.02 ± 0.5	−3.06 ± 0.2	−1.61 ± 0.2	−2.53 ± 0.3
19	−3.24 ± 0.1	−3.68 ± 0.0	−2.26 ± 0.0	−3.50 ± 0.1	−3.21 ± 0.0	−1.08 ± 0.0	−3.78 ± 0.1
20	−1.79 ± 0.0	−2.02 ± 0.1	−0.78 ± 0.1	−2.01 ± 0.0	−1.62 ± 0.2	0.66 ± 0.1	−2.78 ± 0.1
21	−8.94 ± 0.2	−9.07 ± 0.2	−8.05 ± 0.1	−9.03 ± 0.2	−8.71 ± 0.3	−6.48 ± 0.2	−7.63 ± 0.1
22	−7.20 ± 0.3	−6.91 ± 0.3	−6.07 ± 0.4	−7.06 ± 0.3	−6.59 ± 0.3	−4.37 ± 0.5	−6.78 ± 0.1
23	−7.75 ± 0.3	−8.23 ± 0.2	−6.37 ± 0.2	−7.93 ± 0.3	−7.79 ± 0.3	−4.14 ± 0.3	−9.34 ± 0.6
24	−5.74 ± 0.2	−6.56 ± 0.1	−4.45 ± 0.2	−6.08 ± 0.1	−6.03 ± 0.2	−2.95 ± 0.2	−7.43 ± 0.6
RMSD	0.97 ± 0.1	0.89 ± 0.2	1.53 ± 0.1	0.99 ± 0.1	1.09 ± 0.2	2.91 ± 0.1
T-S	0.93	0.85	0.90	0.87	0.83	0.81
τ	0.80	0.83	0.82	0.84	0.81	0.80
MdnSD	0.43	0.15	1.02	0.50	0.37	2.38

Figure 4.

Comparison of RMSD of different QM protocols based on pure QM optimized structures (abscissa) and MM trajectories that we analyzed with QM-NBB (ordinate). The use of MM trajectories consistently improves the results by accounting for conformational entropy.

While the QM-NBB protocol is consistently more effective than the analogous QM-optimization protocol, this gain in accuracy is expensive. In the present work, each HFE prediction from QM-NBB required 40,000 primitive QM single point energy calculations. While these QM calculations are embarrassingly parallel, and efforts to optimize the configurational sampling rate could reduce the number of QM energy evaluations, Rosta and Hummer [2009] a large quantity of raw QM data is required by the QM-NBB estimator. The associated expense of generating this QM data is significantly greater than for the QM-optimization protocol, underscoring the need for thorough methodological benchmarking.

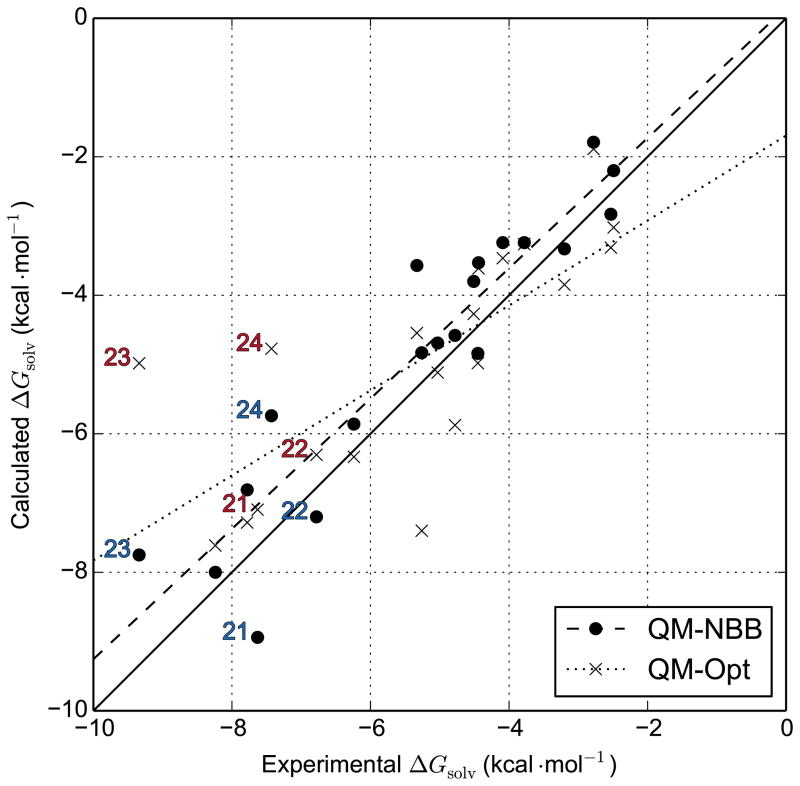
As Figure 5 illustrates, QM-NBB with M06-2X/6-31G(d) effectively reduces the extent of the worst outliers that we encounter in the analogous QM optimization calculations. This is likely a direct consequence of the “ensemble” nature of the QM-NBB calculations. Unlike in the case of QM optimizations, where one conformation dominates the calculation, the NBB approach allows for ensemble averaging, benefiting our predictions in two ways. First, this effect may be partially due to the fact that with QM optimizations, a bad initial guess of the geometry can get trapped in a local energy minimum and yield poor results. QM-NBB calculations use an ensemble average, and poor initial conditions can be compensated in the equilibration and production stages of the MM simulations. Second, the QM-NBB calculations should also outperform QM optimizations in cases where the potential energy surface of a ligand is broad and shallow, or multiple low-lying energy minima are present. In this case, QM optimizations will dramatically over emphasize the global minimum structure, while the QM-NBB calculations will correctly draw from a much more balanced set of conformational states, and properly balance the relative contributions of entropy and enthalpy. This effect, and QM-NBB’s outperformance of QM optimizations, should be more pronounced for larger, floppier molecules. We observe exactly this in M06-2X/6-31G(d) calculations, where QM-NBB calculations dramatically shift the predictions of some of the largest molecules (21, 22, 23 and 24). This effect can also be thought of as including non-harmonic conformational entropy from the ligand. Typical QM schemes only account for the contribution of entropy from the region of phase space immediately surrounding the global minimum structure via the simple harmonic oscillator approximation.

Figure 5.

Comparison of QM-NBB data against QM-Opt data for the M06-2X/6-31G(d) level of theory. Molecule 1 has been omitted from the figure and from the best fit line, because of its disproportionate influence. The titratable molecules 21, 22, 23 and 24 are explicitly labeled in red (QM-optimization) and blue (QM-NBB).

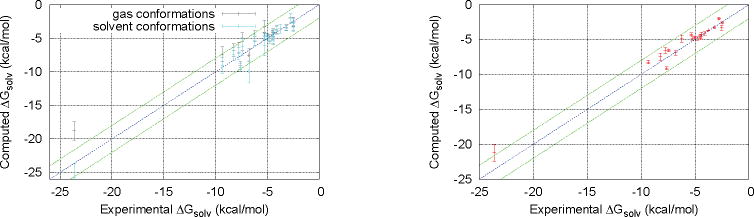
Another aspect that is partially neglected by the vertical or adiabatic HFE schemes is the balance of the conformational preferences in the gas phase versus the aqueous phase. In the gas phase, the solute can stabilize itself by forming intramolecular hydrogen bonds, which is known as the “self-solvation” effect. Roseman [1988]; König and Boresch [2009]; König et al. [2013] While the formation of intramolecular hydrogen bonds is also possible in the aqueous phase, it is competing with the formation of intermolecular hydrogen bonds to the solvent. This effect alone demands that a single conformational structure cannot possibly be representative of the entire hydration process.

The effect of the conformational preferences in gas phase and solution is illustrated on the left side of Fig. 6. The plot shows the distributions of the vertical hydration free energies of different conformations sampled by MM in both gas phase (gray) and in aqueous solution (turquoise). The error bars indicate the mean and standard deviations of more than 10,000 conformations drawn from each trajectory and analyzed with OLYP/DZP/SMD. A striking feature is that the gas phase conformations tend to underestimate the solvent affinity, while the conformations in aqueous solution tend to overestimate the solvent affinity. Correspondingly, the gas phase conformations would lead to an RMSD of 1.5 kcal·mol⁻¹, while the solvent phase conformations would lead to and RMSD of 1.1 kcal·mol⁻¹. By combining the data from both phases according to their appropriate weights, QM-NBB leads to an RMSD of 0.9 kcal·mol⁻¹ (right side of Fig. 6).

Figure 6.

Comparison of the underlying implicit solvent free energies for conformations in the gas phase (gray) and in aqueous phase (turquoise) on the left side with the resulting QM-NBB results (red) on the right side. All data is based on the OLYP/DZP QM method with the SMD implicit solvent.

Unfortunately, combining the QM-NBB calculations with the same pK_a corrections that were effective with the QM optimized calculations significantly increases the RMSD with respect to experiment for most of the effective QM methods (the negative control benefits marginally). This might be due to the fact that the pK_a corrections themselves were drawn from a single QM optimized structure, and thus our pK_a calculations suffer from many of the same limitations and drawbacks that we have discussed above. It is also important to note that the very same molecules that are likely to exhibit significant contributions from non-neutral states under equilibrium conditions, are also the same large, floppy molecules where QM-NBB predictions diverge the most from the single conformer QM optimized predictions. Furthermore, the artifacts associated with the overrepresentation of a particular conformer are exacerbated even more, due to the presence of a large net charge on the ligand. To properly treat these effects, the pK_a corrections for the QM-NBB predictions should be repeated with a NBB protocol for molecules 21 – 24. Finally, while obvious, it is important to mention the difficulty in drawing strong conclusions from such a small set, four in the SAMPL4 data set (4 molecules with protonizable groups).

3.3. Explicit Solvent QM/MM-NBB

Among our various submissions to SAMPL4 challenge, König et al. [2014a] our explicit solvent B3LYP/6-31(d)/TIP3P calculations enjoyed the lowest RMSD with respect to experiment (RMSD = 1.6±0.6 kcal·mol⁻¹). To follow up on this work, we were interested in exploring alternative QM methods. Due to the extremely expensive nature of these QM/MM-NBB calculations, and our initial benchmarking calculations using QM optimizations, we chose the M06-2X/6-31G(d)/TIP3P method, believing it produced the most consistently high quality HFE predictions. Unfortunately the predictions using the more expensive M06-2X functional are remarkably similar to those from our SAMPL4 submission, and show consistency even with predictions for specific individual molecules from the SAMPL4 set. In addition to having a relatively high RMSD (1.54 kcal·mol⁻¹), the rank correlation is also poor (τ = 0.59), being effectively equivalent to that from our negative control calculations using the BLYP/def2-SV(P) method with SMD implicit solvent.

This QM/MM-NBB result is consistent, yet better than one obtained in a recent study based on the same set of molecules and using the same QM/MM method with the MESS-E (multiple-environment single-system with Fock matrix extrapolation) method (RMSD = 2.18 kcal·mol⁻¹). König et al. [2016] This approach approximates a full QM/MM calculation by approximating the effect of the classical solvent molecules as a perturbation to the gas phase wave function, instead of treating it in a fully self consistent manner. This requires constraining both the solute and solvent molecules to rigid bodies, however it increases the speed of the QM/MM energy calculations by several orders of magnitude relative to the regular procedure. Since the MESS approach uses rigid solute molecules, but allows for solvent relaxation, the improvement of our calculations by RMSD of ca. 0.6 kcal·mol⁻¹ with respect to experiment in comparison with MESS indicates that solute entropy contributes significantly to the HFE. Such contributions become highly relevant when attempting to reach “chemical accuracy” of 1 kcal·mol⁻¹.

It is also interesting to observe that our HFE predictions from QM/MM-NBB are also significantly too hydrophilic (MdnSD = −0.65 kcal·mol⁻¹). It might be related to the amount of Hartree–Fock exchange in the hybrid functionals as discussed in Reference 96. This may also be due to the prepolarized nature of the TIP3P explicit solvent, which exaggerates the partial charges to better mimic bulk water properties. Furthermore, because TIP3P uses point charges, instead of a more physically accurate delocalized charge distribution, the solvent molecules may over polarize the QM wave function at short range in the interfacial region. This result is consistent with other QM/MM explicit solvent HFE studies. König et al. [2016]; Shaw et al. [2010] Water models that explicitly account for polarization and charge-penetration effects may mitigate these issues, and studying their effectiveness will be the subject of followup work.

4. Conclusions

In this work we computed hydration free energies for 21 molecules in the blind SAMPL4 data set to determine an effective choice of QM method to use in combination with the QM-NBB free energy protocol. Our initial benchmarking calculations were carried out using standard QM optimization protocols, indicating that several well known (M06-2X/6-31G(d) and PBE0/6-31G(d)) and less well known (OLYP/DZP and BLYP/DZP) QM methods might produce superior results when used in conjunction with the NBB free energy method than the corresponding pure QM method. This same benchmarking work indicated that calculations using an additional single point triple-ζ basis correction did not significantly outperform calculations without the SPC, and that the SMD implicit solvent significantly outperforms the IEFPCM implicit solvent. While pK_a corrections seemed to improve the results of the QM optimization calculations with respect to experiment, this was not the case with the QM-NBB calculations. This is a disappointing result, as we expect significant contributions from non-neutral states for molecules 22, 23 and 24. However given the relative lack of data on titratable molecules present in this data set, it is difficult to draw a strong conclusion from this result. The QM/MM-NBB calculations carried out using the popular M06-2X/6-31G(d) method produced results that were inferior to those from the same method with the SMD implicit solvent. Overall, the QM-NBB method with SMD implicit solvent produced HFE predictions that correlated very strongly with those from QM optimizations. These QM-NBB HFE predictions were found to have smaller RMSD values with respect to experiment for all six QM methods tested. Our best overall results (RMSD = 0.89 kcal·mol⁻¹) were produced using the QM-NBB free energy estimator in combination with the OLYP/DZP QM method with the SMD implicit solvent, and are the best known results in the literature for the blind SAMPL4 data set. We have applied this QM method together with the NBB free energy estimator in the recently completed SAMPL5 distribution coefficient challenge, Rustenburg et al. [2016] and strongly endorse it for making HFE predictions. We have shown that the QM-NBB method with SMD implicit solvent, while more expensive than typical QM optimization calculations, consistently improves the quality of hydration free energy predictions by including configurational entropy that is impossible to account for using standard QM techniques. The NBB method with implicit SMD solvent can be used as a drop in replacement for standard QM techniques in situations where highly accurate hydration free energy predictions are of paramount importance.

Table 4.

Detailed results for our QM-NBB calculations with the SMD solvent with pK_a corrections included. Free energies reported in kcal·mol⁻¹.

Molecule	M06-2X/ 6-31G(d)	OLYP/ DZP	B3LYP/ 6-31G(d)	PBE0/ 6-31G(d)	BLYP/ DZP	BLYP/ def2-SV(P)	Expt.
21	−8.95 ± 0.2	−9.08 ± 0.2	−8.06 ± 0.1	−9.04 ± 0.2	−8.72 ± 0.3	−6.49 ± 0.2	−7.63 ± 0.1
22	−11.82 ± 0.3	−11.53 ± 0.3	−10.69 ± 0.4	−11.68 ± 0.3	−11.21 ± 0.3	−8.99 ± 0.5	−6.78 ± 0.1
23	−9.05 ± 0.3	−9.53 ± 0.2	−7.67 ± 0.2	−9.23 ± 0.3	−9.09 ± 0.3	−5.44 ± 0.3	−9.34 ± 0.6
24	−8.35 ± 0.2	−9.17 ± 0.1	−7.06 ± 0.2	−8.69 ± 0.1	−8.64 ± 0.2	−5.56 ± 0.2	−7.43 ± 0.6
RMSD	1.39 ± 0.1	1.38 ± 0.1	1.53 ± 0.1	1.42 ± 0.1	1.41 ± 0.1	2.65 ± 0.1
T-S	1.00	0.88	0.93	0.90	0.89	0.83
τ	0.77	0.77	0.77	0.78	0.75	0.76
MdnSD	0.34	0.05	0.98	0.38	0.05	2.17

Table 5.

Detailed results for our QM/MM-NBB calculations using M06-2X/6-31G(d) with TIP3P solvent, with and without pK_a corrections applied. Free energies reported in kcal·mol⁻¹

	without pKa corrections	with pKa corrections	Expt.
1	−22.05 ± 0.7		−23.62 ± 0.3
2	−3.87 ± 1.0		−2.49 ± 0.9
3	−5.83 ± 0.3		−4.78 ± 0.3
4	−5.69 ± 0.8		−4.45 ± 0.2
5	−5.69 ± 0.4		−5.33 ± 0.1
6	−5.22 ± 0.3		−5.26 ± 0.2
9	−10.00 ± 1.3		−8.24 ± 0.8
10	−6.89 ± 0.8		−6.24 ± 0.4
11	−7.88 ± 0.9		−7.78 ± 0.8
12	−4.64 ± 0.3		−4.44 ± 0.2
13	−6.00 ± 0.5		−5.03 ± 0.4
14	−5.54 ± 0.3		−4.09 ± 0.2
15	−6.38 ± 0.3		−4.51 ± 0.1
16	−4.44 ± 0.3		−3.20 ± 0.3
17	−4.87 ± 0.6		−2.53 ± 0.3
19	−4.43 ± 0.6		−3.78 ± 0.1
20	−2.61 ± 0.1		−2.78 ± 0.1
21	−9.31 ± 0.4	−9.31 ± 0.4	−7.63 ± 0.1
22	−3.87 ± 2.1	−6.18 ± 2.1	−6.78 ± 0.1
23	−6.12 ± 1.0	−6.77 ± 1.0	−9.34 ± 0.6
24	−5.56 ± 0.7	−6.87 ± 0.7	−7.43 ± 0.6
RMSD	1.54 ± 0.3	1.29 ± 0.2
T-S	0.81	0.86
τ	0.59	0.72
MdnSD	−0.65	−1.05