Statistical Methods for Testing Genetic Pleiotropy

Abstract

Genetic pleiotropy is when a single gene influences more than one trait. Detecting pleiotropy and understanding its causes can improve the biological understanding of a gene in multiple ways, yet current multivariate methods to evaluate pleiotropy test the null hypothesis that none of the traits are associated with a variant; departures from the null could be driven by just one associated trait. A formal test of pleiotropy should assume a null hypothesis that one or no traits are associated with a genetic variant. For the special case of two traits, one can construct this null hypothesis based on the intersection-union (IU) test, which rejects the null hypothesis only if the null hypotheses of no association for both traits are rejected. To allow for more than two traits, we developed a new likelihood-ratio test for pleiotropy. We then extended the testing framework to a sequential approach to test the null hypothesis that $k+1$ traits are associated, given that the null of k traits are associated was rejected. This provides a formal testing framework to determine the number of traits associated with a genetic variant, while accounting for correlations among the traits. By simulations, we illustrate the type I error rate and power of our new methods; describe how they are influenced by sample size, the number of traits, and the trait correlations; and apply the new methods to multivariate immune phenotypes in response to smallpox vaccination. Our new approach provides a quantitative assessment of pleiotropy, enhancing current analytic practice.

GENETIC pleiotropy is when a single gene influences more than one trait. Detecting pleiotropy, and understanding its causes, can improve the biological understanding of a gene in multiple ways: (1) There is potential to expand understanding of the medical impact of a gene, such as in phenome-wide association studies (Denny et al. 2013); (2) the pharmacologic genetic target could affect multiple traits or diseases, allowing a drug developed for a disease to be repurposed for other diseases or suggesting that a toxicity should be monitored for multiple traits; and (3) joint analysis of multiple traits can increase accuracy of phenotype prediction (Maier et al. 2015). Yet, understanding pleiotropy can be challenging. A gene can be associated with more than one trait for many reasons, such as when a single genetic variant directly influences multiple traits or when different variants within a gene influence different traits. Alternatively, the association of a gene with some of the traits can be indirect, such as when a gene directly influences a trait, and that trait directly influences a second trait; the gene and the second trait are indirectly associated. The association of a gene with multiple traits can also result from spurious associations. One cause of spurious association is when subjects with more than one disease symptom are more likely ascertained for a study than if they had only one symptom—called Berkson’s bias (Berkson 1946). A second cause is misclassification between two similar traits, a common problem for some psychiatric conditions. A third cause is when a genetic marker is in linkage disequilibrium with each of two causal loci (Gianola et al. 2015). These types of biases, and a thorough review of pleiotropy with numerous examples, are nicely summarized elsewhere (Solovieff et al. 2013). Despite the great deal of attention given to pleiotropy, most statistical tests do not formally test pleiotropy. Rather, they test the null hypothesis that no trait is associated with a variant; rejecting this null could be due to just one associated trait, not a situation of pleiotropy. The aim of this report is to provide a formal statistical method to assess pleiotropy to infer the number of traits associated with a variant.

Statistical methods to evaluate pleiotropy have been developed from different angles, ranging from comparison of univariate marginal associations of a genetic variant with multiple traits, to multivariate analyses with simultaneous regression of all traits on a genetic variant, to reversed regression of a genetic variant on all traits. A brief survey of statistical methods for pleiotropy is provided here, with more details provided elsewhere (Schriner 2012; Yang and Wang 2012; Solovieff et al. 2013; Zhang et al. 2014). Univariate analyses are often based on comparison of variant-specific P-values across multiple traits. Although simple and feasible for meta-analyses, this approach ignores correlation among the traits and is based on post hoc analyses. More formal meta-analysis methods aggregate P-values to test whether any traits are associated with a variant, yet a significant association could be driven by just one trait. A slightly more sophisticated approach, also based on summary P-values, tests whether the distribution of P-values differs from the null distribution of no associations beyond those already detected (Cotsapas et al. 2011). Descriptions of additional univariate methods are given elsewhere (Solovieff et al. 2013).

Multivariate methods have been popular for quantitative traits. Although different statistical methods have been proposed, some of them result in the same statistical tests. The following three approaches to analyze quantitative traits result in the same F-statistic to test whether any of the traits are associated with a genetic variant: (1) simultaneous regression of all traits on a single variant [for example, using the statistical software R function lm(Y ∼ g), where Y is a matrix of traits and g a vector for a single genetic variant coded as 0, 1, 2 for the dose of the minor allele], (2) regression of the minor allele dose on all traits (lm(g ∼ Y)), and (3) canonical correlation of Y with g [using either plink.multivariate (Ferreira and Purcell 2009) or R code given in Appendix A]. The regression of the dose of the minor allele on all traits is a convenient approach, particularly if some of the traits are binary. A slightly different approach is to account for the categorical nature of the dose of the minor allele: Instead of using linear regression, use ordinal logistic regression of the dose on the traits [R MultiPhen package (O’Reilly et al. 2012)]. An advantage of this approach is that it allows for binary traits, unlike most methods that assume traits are quantitative with a multivariate normal distribution. However, score tests for generalized linear models, based on estimating equations, have been developed as a way to simultaneously test multiple traits, some of which could be binary (Xu and Pan 2015). An approach somewhat between univariate and multivariate is based on reducing the dimension of the multiple traits by principal components (PC) and using a reduced set of PCs as either the dependent or the independent variables in regression. A comparison of univariate and multivariate approaches found that multivariate methods based on multivariate normality {e.g., canonical correlation, linear regression of traits on minor allele dose, reverse regression, MultiPhen, and Bayes methods [BIMBAM (Stephens 2013) and SNPTEST (Marchini et al. 2007)]} all had similar power and were generally more powerful than univariate methods (Galesloot et al. 2014).

The power advantage of multivariate over univariate methods occurs when the direction of the residual correlation is opposite from that of the genetic correlation induced by the causal variant (Liu et al. 2009; Galesloot et al. 2014). In addition to the methods discussed above, a few new approaches have been proposed, but have not yet been compared with others. An interesting approach is to scale the different traits by their standard deviation and then assume that the effect of a single-nucleotide polymorphism (SNP) is constant across all traits to construct a test of association with 1 d.f.—so-called “scaled marginal models” (Roy et al. 2003; Schifano et al. 2013). Finally, an approach based on kernel machine regression extended the sequential kernel association test (Wu et al. 2010) to multiple traits, providing a simultaneous test of multiple traits with multiple genetic variants in a genomic region (Maity et al. 2012).

A limitation of all current approaches is that they test whether any traits are associated with a genetic variant, and small P-values could be driven by the association of the genetic variant with a single trait. Hence, post hoc analyses are required to interpret the possibility of pleiotropy. This can be quite challenging when scaling up to a large number of genetic variants. Another significant challenge is to distinguish direct from indirect associations. When there is evidence that a secondary trait is associated with a genetic marker, and one wishes to distinguish whether the same genetic marker has a direct effect on a primary trait vs. an indirect effect, with the secondary trait acting as a mediator between the genetic marker and the primary trait, ideas from causal modeling have proved useful. For example, disentangling direct from indirect effects can be achieved by regressing the primary trait on the secondary trait, the genetic marker, and all other covariates shared between the primary and secondary traits. Results from this regression can be used to construct an adjusted primary trait that can then be used in subsequent analyses (Vansteelandt et al. 2009). Another approach is based on Bayesian methods to partition associations into unassociated, indirect, and direct associations. However, it is difficult to accurately classify the type of causal association, particularly when residual correlations are large (e.g., it is difficult to discriminate between direct and indirect effects) (Stephens 2013).

The above methods are used to test whether a single genetic variant is associated with multiple traits. When scaling up to genome-wide data, it has been useful to use all the genetic markers to estimate the marker-predicted heritability of a trait. This has recently been extended to multiple traits to estimate pleiotropy as the genetic correlation of multiple traits. Mixed models are used to partition the phenotype correlations into genetic correlation (i.e., correlation of polygenic total genetic values) and environmental correlation (Korte et al. 2012; Lee et al. 2012; Zhou and Stephens 2014; Furlotte and Eskin 2015). Although this approach does not evaluate whether particular SNPs or particular genomic regions are the cause for phenotype correlations, it has the potential to guide design of studies that focus on pleiotropy. For example, the correlation of two phenotypes can be partitioned as $r_{\mathrm{P}}=h_1{h}_2{r}_{\mathrm{g}}+e_1{e}_2{r}_{\mathrm{e}},$ where $h_i^2$ is the heritability of trait i, $e_i^2=1-h_i^2,$ $r_{\mathrm{g}}$ is the genetic correlation, and $r_{\mathrm{e}}$ is the environmental correlation (Falconer and Mackay 1996, p. 314). Heritability in the narrow sense is the percentage of the variance of the trait explained by additive genetic factors. This illustrates that if both traits have low heritability, the phenotype correlation is primarily due to environmental correlation (and nonadditive genetic effects that are missed by $r_{\mathrm{g}}$), implying that large sample sizes would be needed to test pleiotropy when there are small genetic effects.

We have emphasized that current methods to evaluate pleiotropy do not perform a formal test of the null hypothesis of no pleiotropy. For the special case of two traits, one can construct a null hypothesis of no pleiotropy based on the intersection-union (IU) test (Silvapulle and Sen 2004). Consider the regression equation ${\mathit{y}}_{\mathit{j}}={\beta }_{o,j}+{\beta }_{1,j}\mathit{g}+{\mathit{e}}_{\mathit{j}},$ where ${\mathit{y}}_{\mathit{j}}$ is the vector of values for the jth trait, ${\beta }_{o,j}$ is the intercept, ${\beta }_{1,i}$ is the slope association parameter of interest, $\mathit{g}$ is the vector of doses for the minor allele, and ${\mathit{e}}_{\mathit{j}}$ is a vector of residuals. The union null hypothesis is ${\mathrm{H}}_0:{\beta }_{\mathrm{1,1}}=0\text{ or }{\beta }_{\mathrm{1,2}}=0,$ and the intersection alternative hypothesis is ${\mathrm{H}}_1:{\beta }_{\mathrm{1,1}}\ne 0\text{ and }{\beta }_{\mathrm{1,2}}\ne 0.$ Testing each ${\beta }_{1,i}$ at a desired type I error, say $\alpha =0.05,$ the null is rejected only if both tests reject. There is no need to correct for multiple testing, because the type I error rate is not inflated by this procedure. But this approach can be conservative, particularly if the two tests are uncorrelated. The IU test can be extended to $p>2$ traits, but rejection of the null would occur only when all $p$ tests are significant at the specified $\alpha .$ For our situation, we wish to reject the null if at least two of the p tests reject. One approach would be to apply the IU test to each pair of traits and reject the null if at least one of the IU tests rejects. But this would entail many pairs of tests, and for this situation one would need to correct for testing multiple pairs. Bonferroni correction would lead to an overly conservative test.

Because of current limitations, we developed a likelihood-ratio test for testing the null hypothesis of no pleiotropy—the null hypothesis that one or no traits are associated with a genetic variant vs. the alternative hypothesis that two or more traits are associated. We then extended the testing framework to test the null hypothesis that k or fewer traits are associated vs. the alternative hypothesis that more than k traits are associated ($k=\mathrm{0,1},\mathrm{...}p-1$). By this generalization, we propose sequential testing to test the null hypothesis that $k+1$ traits are associated, given that the null hypothesis of k traits are associated was rejected. This sequential approach provides a refined approach to evaluate how many traits, and which traits, are associated with a genetic variant, accounting for correlation among the traits and possibly adjusting for covariates that could differ across the traits.

Methods

Likelihood-ratio test of pleiotropy: null of one or fewer traits

Suppose that p traits are measured on each of n subjects. Let ${{\mathit{y}}^{\prime }}_{\mathit{j}}=\left(y_{j1},\mathrm{...},y_{jn}\right)$ denote the vector of measures on the jth trait for n subjects. Assume that each trait is modeled by linear regression, denoted

$${\mathit{y}}_{\mathit{j}}=\mathit{x}{\mathit{\beta }}_{\mathit{j}}+{\mathit{\epsilon }}_{\mathit{j}},$$

where $\mathit{x}$ is the dose of the minor allele for n subjects. Also assume that all ${\mathit{y}}_{\mathit{j}}$ and $\mathit{x}$ are centered, so intercepts can be ignored. For simplicity of presentation, we ignore adjusting covariates, but our methods are general and allow for trait-specific covariates. By stacking vectors, we can express the model as $\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{\epsilon },$ where ${\mathit{y}}^{\prime }=\left({{\mathit{y}}^{\prime }}_{\mathbf{1}},\mathrm{...},{{\mathit{y}}^{\prime }}_{\mathit{p}}\right),$ $\mathit{X}=\mathrm{diag}\left(\mathit{x}\right),$ ${\mathit{\beta }}^{\prime }=\left({{\beta }^{\prime }}_1,\mathrm{...},{{\beta }^{\prime }}_p\right),$ and ${\mathit{\epsilon }}^{\prime }=\left({{\mathit{\epsilon }}^{\prime }}_{\mathbf{1}},\mathrm{...},{{\mathit{\epsilon }}^{\prime }}_{\mathit{p}}\right).$ The error term $\mathit{\epsilon }\sim N\left(0,\mathbf{\Omega }\right),$ where $\mathbf{\Omega }=\mathbf{\Sigma }\otimes \mathit{I},$ I is an $n\times n$ identity matrix, $\otimes$ is the Kronecker product, and the $p\times p$ matrix $\mathbf{\Sigma }$ is the covariance matrix for the within-subject covariances of the errors. Under this model, the log-likelihood function of $\left(\mathit{\beta }\mathrm{,}\mathbf{\Sigma }\right)$ is given by

$$l_n\left(\mathit{\beta },\mathbf{\Sigma }\right)=-\frac{n}{2}\log \left|\mathbf{\Sigma }\right|-\frac{1}{2}{\left(\mathit{y}-\mathit{X}\mathit{\beta }\right)}^{\prime }\left({\mathbf{\Sigma }}^{-1}\otimes \mathit{I}\right)\left(\mathit{y}-\mathit{X}\mathit{\beta }\right)\mathrm{.}$$

Suppose that the covariance $\mathbf{\Sigma }$ is known; otherwise, we can obtain a consistent estimate by maximum-likelihood estimation. For example, we can estimate $\mathit{\beta }$ by using methods from seemingly unrelated regression, an approach called feasible generalized least squares. Separate ordinary linear regression for each trait can be used to obtain residuals to estimate $\widehat{\mathbf{\Sigma }},$ and then this is used in the generalized least-squares (GLS) solution,

$$\widehat{\mathit{\beta }}={\left[{\mathit{X}}^{\prime }\left({\widehat{\mathbf{\Sigma }}}^{-1}\otimes \mathit{I}\right)\mathit{X}\right]}^{-1}{\mathit{X}}^{\prime }\left({\widehat{\mathbf{\Sigma }}}^{-1}\otimes \mathit{I}\right)\mathit{y}.$$

Note that the feasible generalized least squares is asymptotically equivalent to maximum-likelihood estimation (MLE). There are two special cases when separate ordinary regressions and GLS result in the same solution: (1) when $\mathbf{\Sigma }$ is a diagonal matrix and (2) when the regressors in ${\mathit{X}}_j$ are the same for all traits. Hence, for the case where each trait is regressed on the same x, without additional adjusting covariates, separate ordinary least-squares regression and GLS give the same results. The covariance matrix of the residuals then provides a consistent estimate of $\mathbf{\Sigma }.$ Then, the Cholesky decompositon of $\mathbf{\Omega }$ is $\mathbf{\Omega }={\mathbf{\Omega }}^{1/2}{\mathbf{\Omega }}^{1/2},$ where ${\mathbf{\Omega }}^{1/2}={\mathbf{\Sigma }}^{1/2}\otimes \mathit{I}$ and ${\mathbf{\Omega }}^{-1/2}={\mathbf{\Sigma }}^{-1/2}\otimes \mathit{I}.$ We then decorrelate the data by $\tilde{\mathit{y}}={\mathbf{\Omega }}^{-1/2}\mathit{y}$ and $\tilde{\mathit{X}}={\mathbf{\Omega }}^{-1/2}\mathit{X},$ to transform the model to $\tilde{\mathit{y}}=\tilde{\mathit{X}}\mathit{\beta }+\tilde{\mathit{\epsilon }}\mathrm{,}$ where $\tilde{\mathit{\epsilon }}={\mathbf{\Omega }}^{-1/2}\mathit{\epsilon }\mathrm{\sim }N\left(\mathrm{0,}{\mathit{I}}_{np}\right),$ which has log-likelihood $l_n\left(\mathit{\beta }\right)=-\left(1/2\right){(\tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta })}^{\prime }\left(\tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta }\right)\mathrm{.}$ Based on this log likelihood, we derived the likelihood-ratio test (LRT) to test the null hypothesis of no pleiotropy: One or no traits are associated with a genetic variant. Below we outline how to compute the LRT and provide details of the derivations in Appendix B.

The null hypothesis of no pleiotropy can be expressed as

$${\mathrm{H}}_0:\hspace{0.5em}\text{Of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{parameters}\hspace{0.17em}{\beta }_{1,}\mathrm{...},{\beta }_p,\hspace{0.17em}\text{there}\hspace{0.17em}\text{exists}\hspace{0.17em}\text{at}\hspace{0.17em}\text{most}\hspace{0.17em}\text{one}\hspace{0.17em}\text{that}\hspace{0.17em}\text{is}\hspace{0.17em}\text{nonzero}\hspace{0.17em}\leftrightarrow {\mathrm{H}}_1:\hspace{0.5em}\text{otherwise}\mathrm{.}$$

The null hypothesis is equivalent to testing whether one of the following $p+1$ tests holds,

$${\mathrm{H}}_{k0}:\hspace{0.5em}{\beta }_k\ne \mathrm{0,}{\beta }_j=0\left(j\ne k\right),$$

for $k=0,\dots \mathrm{,}p.$ Note that ${\mathrm{H}}_{00}$ represents all ${\beta }_k=0$ $\left(k=1,\dots \mathrm{,}p\right),$ while for $k>0,$ ${\mathrm{H}}_{k0}$ allows ${\beta }_k\ne 0$ while all other ${\beta }_j=0\left(j\ne k\right).$ To represent these p + 1 hypotheses, we use ${\mathrm{H}}_{k0}:{\mathit{V}}_{\mathit{k}}\mathit{\beta }=0.$ Let ${\mathit{V}}_{\mathbf{0}}$ be a matrix such that ${\mathrm{H}}_{00}:{\mathit{V}}_{\mathbf{0}}\mathit{\beta }=0$ tests whether all ${\beta }_j=0.$ This is the usual multivariate test. In this case, ${\mathit{V}}_{\mathbf{0}}$ is the identity matrix of dimension $p.$ To construct ${\mathit{V}}_{\mathit{k}}$ $\left(k>0\right),$ create an identity matrix of dimension $p$ and then remove the kth row. This results in ${\mathit{V}}_{\mathit{k}}\mathit{\beta }={({\beta }_1,\mathrm{...},{\beta }_{k-1},{\beta }_{k+1}{\beta }_p)}^{\prime }.$ Then, the null hypothesis is equivalent to

$${\mathrm{H}}_0:\hspace{0.5em}\text{There}\hspace{0.5em}\text{exists}\hspace{0.5em}\text{one}\hspace{0.5em}\text{of}\hspace{0.5em}{\mathrm{H}}_{k0}:{\mathit{V}}_{\mathit{k}}\mathit{\beta }=0,\hspace{0.5em}\text{for}\hspace{0.17em}k=\mathrm{0,}\dots \mathrm{,}p\mathrm{.}$$

To construct the LRT, center $\mathit{y}$ and $\mathit{x}$ about their means, use ordinary least squares to estimate $\mathit{\beta },$ use the residuals to estimate $\mathbf{\Sigma },$ and then use $\mathbf{\Sigma }$ to decorrelate $\mathit{y}$ and $\mathit{X}$ according to $\tilde{\mathit{y}}={\mathbf{\Omega }}^{-1/2}\mathit{y}\mathrm{,}\tilde{\mathit{X}}={\mathbf{\Omega }}^{-1/2}\mathit{X},$ where ${\mathbf{\Omega }}^{-1/2}={\mathbf{\Sigma }}^{-1/2}\otimes \mathit{I}.$ Then, for each $k=0,\dots \mathrm{,}p,$ compute

$$t_k=\widetilde{{\mathit{y}}^{\prime }}\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}_k{\left[{\mathit{V}}_k{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{{\mathit{V}}^{\prime }}_k\right]}^{-1}{\mathit{V}}_k{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}.$$

An alternative way to express $t_k$ is $t_k={\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}-\tilde{\mathit{X}}{\mathit{\beta }}_{{\mathit{V}}_{\mathit{k}}}\Vert }^2,$ the squared $l_2$ norm between the fitted values based on the ordinary least-squares estimates, ${\mathit{\beta }}_{\mathit{n}},$ and the fitted values based on the constrained estimates, ${\mathit{\beta }}_{{\mathit{V}}_k}$ (see Appendix B).

As shown in Appendix B, the LRT is

$$T=\underset{k=0,\dots \mathrm{,}p}{{\displaystyle \min }}{t}_k\mathrm{.}$$

Because $t_j$ is based on the sum of squared differences of the fitted values between the unconstrained and constrained models, for a correctly specified constrained model, $t_j$ has a ${\chi }^2$ distribution. But the distribution of $T$ is more complicated. The statistic $T$ has two different asymptotic distributions depending on when $\mathit{\beta }$ = 0 or not. When $\mathit{\beta }=0,$ the asymptotic distribution of each $t_j$ is a ${\chi }^2$ distribution, yet the distribution of the minimum of them, $T,$ is unknown. Alternatively, when $\mathit{\beta }=0,$ we can use the commonly used ${\chi }^2$ test for the null hypothesis that all ${\beta }_j=0.$ This motivates us to do the test by two stages. The first stage is to just test ${\mathrm{H}}_{00}:\hspace{0.17em}\mathit{\beta }=0,$ using the statistic $t_0\mathrm{\sim }{\chi }_p^2$ as the test statistic, so we reject ${\mathrm{H}}_{00}$ if $t_0>{\chi }_p^2\left(\alpha \right),$ where ${\chi }_p^2\left(\alpha \right)$ is the $1-\alpha$ quantile of the ${\chi }^2$ distribution with $p$ d.f. If ${\mathrm{H}}_{00}$ cannot be rejected, then the ${\mathrm{H}}_0$ of no pleiotropy cannot be rejected. If ${\mathrm{H}}_{00}$ is rejected, we turn to the second stage to test the null hypothesis that one ${\mathrm{H}}_{k0}$ holds for $k=1,\dots \mathrm{,}p.$ For this we ignore $t_0$ and use the test statistic

$$T_1=\underset{k=1,\dots \mathrm{,}p}{{\displaystyle \min }}{t}_k\mathrm{.}$$

Since $T_1\mathrm{\sim }{\chi }_{p-1}^2,$ we reject the null hypothesis that only one ${\mathrm{H}}_{k0}$ holds for $k=1,\dots \mathrm{,}p$ if $T_1>{\chi }_{p-1}^2\left(\alpha \right).$ Then, the null hypothesis ${\mathrm{H}}_0$ of no pleiotropy is rejected only if both ${\mathrm{H}}_{00}$ is rejected and the null hypothesis that only one ${\mathrm{H}}_{k0}$ holds is rejected $\left(k=1,\dots \mathrm{,}p\right).$

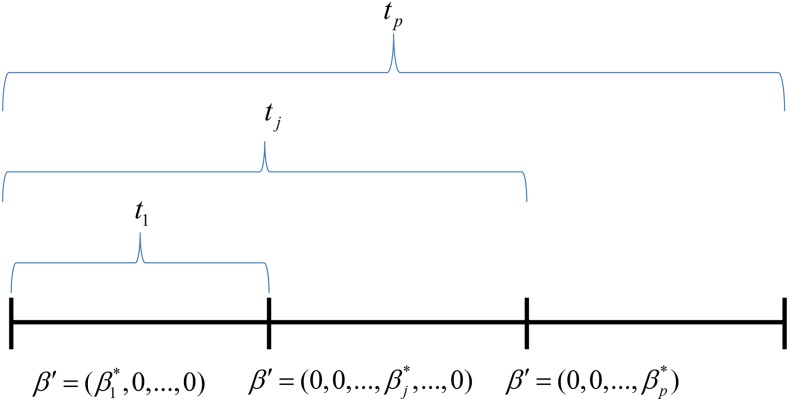
To provide intuition why $T_1$ has a large sample ${\chi }^2$ distribution with (p − 1) d.f. when only one ${\beta }_j$ differs from zero, while all others equal zero, we present an example in Figure 1. In this example ${\beta }_1\ne 0$ and ${\beta }_j=0\left(j\ne 1\right).$ As shown in Appendix B (Corollary 1), the distribution of $t_j$ for a correctly specified model is ${\chi }_{p-1}^2.$ In contrast, the incorrect models result in arbitrarily large values of $t_j$ (see Corollary 2 in Appendix B). This means that $t_1$ will be minimum and $T=t_1\sim {\chi }_{p-1}^2.$

Figure 1 .

Example to illustrate why the pleiotropy LRT has an approximate ${\chi }_{p-1}^2$ distribution when only one ${\beta }_j$ differs from zero. For this example, ${\beta }_1\ne 0$ and ${\beta }_j=0\left(j\ne i\right).$ Then, $t_1$ will be the minimum because it measures the sum of squared differences of the fitted values for the unconstrained ordinary least-squares model and the constrained model, which in this case is correctly specified. Because all other $t_j\left(j\ne 1\right)$ represent misspecified models, their values can become arbitrarily large as n increases. Hence, the correctly specified model will have the smallest values of $t_j.$ And the distribution of $t_j$ for a correctly specified model is ${\chi }_{p-1}^2.$

General likelihood-ratio sequential testing: null of K associated traits

The above sequential approach is based on testing the null hypothesis ${\mathrm{H}}_{00}:\mathit{\beta }=0,$ and then if this rejects, to turn to the second stage to test the null hypothesis that only one ${\mathrm{H}}_{k0}:{\beta }_k\ne 0,{\beta }_j=0\left(j\ne k\right)$ holds for $k=1,\dots \mathrm{,}p.$ The advantage of this approach is that if ${\mathrm{H}}_{00}$ is rejected and the null hypothesis that only one ${\mathrm{H}}_{k0}$ holds is accepted, we can conclude that there is only one nonzero $\beta .$ But if the null hypothesis that only one ${\mathrm{H}}_{k0}$ holds is rejected, we cannot make a firm conclusion about the number of traits associated with a genetic variant. To provide a more rigorous testing framework, we extended our approach to sequentially test the null hypothesis that a specified number of $\beta$’s are nonzero. So, if the null hypothesis that k $\beta$’s are nonzero is rejected, but the null hypothesis that $k+1$ $\beta$’s are nonzero is accepted, we can conclude there are $k+1$ traits associated with a genetic variant. Furthermore, because the sequential testing is based on a likelihood-ratio framework, evaluating all possible combinations of nonzero $\beta$’s, the combination that fails to reject the null hypothesis provides evidence of which traits are associated with the genetic variant. The details of the statistical procedures of this general sequential testing method are provided in Appendix B, as well as a proof that the type I error is controlled. In summary, this general sequential procedure provides a formal way to determine not only they number of traits associated with a genetic variant, but also which traits are associated.

Simulations

To evaluate the adequacy of the ${\chi }^2$ distribution for the LRT, we performed simulations. For the pleiotropy null, we performed two sets of simulations. The first one assumed that all ${\beta }_j=0,$ the usual null for multivariate data. The second one fixed ${\beta }_1=1$ and all other ${\beta }_j=0$ $\left(j=2,\mathrm{...},p\right).$ The value of ${\beta }_1=1$ was chosen because the power for detecting this marginal effect size was very large for our setup. We assumed three different sample sizes, $n=100,500,1000,$ and two different values of $p=4,10.$ The small sample size of $n=100$ was used to evaluate the adequacy of our asymptotic derivations for small samples. The variance of the errors was assumed to be 1, and the covariance was assumed to be either a constant $\rho$ for all pairs of traits (i.e., exchangeable correlation structure) or a range of covariances. For the range of covariances, we randomly chose covariances from a specified range, assuming a uniform distribution of the covariances. With a specified covariance structure, we simulated the random errors from either a multivariate normal distribution or a multivariate t distribution with 3 d.f., to evaluate the impact of heavy-tailed distributions. For all simulations, a single SNP was simulated, assuming a minor allele frequency of 0.2.

To evaluate the power of our proposed LRT for pleiotropy, we simulated 10 traits from a multivariate normal distribution with variances of 1 and equal covariances among the traits, set at $\rho =0.2,0.5,\text{ or }0.8,$ for a total of n = 500 subjects. The number of traits associated with the SNP ranged over two, three, or five. The marginal effect of a trait was set at $\beta =\mathrm{0.25.}$ This effect size explains 2% of the variation of a trait, and there is 90% power to detect a marginal effect of this size, using nominal $\alpha =\mathrm{0.05.}$ We also set the marginal effect to $\beta =0.2,$ which corresponds to an explained 1.2% of the variation of a trait, and there is 70% power to detect a marginal effect of this size. All simulations were repeated 1000 times.

Data application

Our newly developed LRT for pleiotropy was applied to a data set that has 10 immunologic phenotypes measured in response to primary smallpox vaccination. These phenotypes included measures of humoral immunity (neutralizing antibody titer) and cellular immunity [two separate IFNγ ELISPOT assays and cytokine secretion upon viral stimulation as measured by ELISA (IL-1β, IL-2, IL-6, IL-12p40, IFNα, IFNγ, TNFα)]. All 645 subjects included in the presented analyses were of Caucasian ancestry. All subjects provided informed consent for use of their samples and this study was approved by the Mayo Clinic Institutional Review Board. A genome-wide association of the 10 phenotypes was performed, with each phenotype adjusted for relevant covariates (i.e., P-value <0.10 for association of a covariate with the phenotype, including eigenvectors to adjust for potential population stratification). Details of the study can be found in prior published reports (Kennedy et al. 2012a,b; Ovsyannikova et al. 2012a,b, 2013, 2014).

Data availability

Software implementing the proposed tests for pleiotropy for quantitative traits is available as an R package called “pleio” in the Comprehensive R Archive Network (https://cran.r-project.org/web/packages/pleio/index.html).

Results

Simulation results

The type I error rates based on simulations are presented in Table 1, Table 2, Table 3, Table 4, Table 5, and Table 6. For all simulations, we show results from the two-stage test (using $t_0$ for stage 1 and $T_1=\min \left\{t_k;k=1,\mathrm{...},p\right\}$ for stage 2), but in all cases, the results from the two-stage test were identical to those from the compound pleiotropy test $T=\min \left\{t_k;k=0,\mathrm{...},p\right\}.$. The results for when only one ${\beta }_j$ differs from zero (Table 1, Table 2, and Table 5) illustrate that the LRT can have inflated type I error rates for small sample sizes $\left(n=100\right),$ with more extreme inflation as p increased from 4 to 10. In contrast, for moderate to large sample sizes $\left(n=500,1000\right),$ the type I error rates were close to the nominal level, with only an occasional slight inflation. The inflated type I error rate for small sample sizes seems to be caused by the need to estimate the covariance matrix of the residuals. When we simulated errors that were independent and used the identity matrix for the residual correlations, the simulated type I error rates were very close to the nominal rates for all sample sizes. In contrast, when all ${\beta }_j$ were zero (Table 3, Table 4, and Table 6), the LRT has conservative type I error rates. This, however, is not of concern, because controlling the type I error rate when only one ${\beta }_j$ differs from zero is the major error that should be controlled when testing pleiotropy. These results were consistent for different amounts and patterns of residual correlations and for multivariate normal and multivariate t distributions.

Table 1 .

Empirical type I error rate for common correlation structure when ${\beta }_1=1$ and all other ${\beta }_j=0$ $\left(j\ne 1\right),$ based on multivariate normal distribution

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0.2	0.072	0.020
		0.5	0.070	0.016
		0.8	0.066	0.014
	10	0.2	0.105	0.036
		0.5	0.092	0.032
		0.8	0.094	0.029
500	4	0.2	0.056	0.017
		0.5	0.058	0.011
		0.8	0.058	0.009
	10	0.2	0.061	0.010
		0.5	0.056	0.011
		0.8	0.068	0.019
1000	4	0.2	0.052	0.012
		0.5	0.058	0.008
		0.8	0.051	0.010
	10	0.2	0.057	0.012
		0.5	0.052	0.010
		0.8	0.046	0.007

Underlined values are for when empirical type I error exceeds the upper 95% C.I.

Table 2 .

Empirical type I error rate for random correlation structure when ${\beta }_1=1$ and all other ${\beta }_j=0$ $\left(j\ne 1\right),$ based on multivariate normal distribution

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0–0.2	0.066	0.011
		0.2–0.5	0.065	0.013
		0.5–0.8	0.055	0.011
	10	0–0.2	0.077	0.018
		0.2–0.5	0.106	0.029
		0.5–0.8	0.112	0.039
500	4	0–0.2	0.065	0.007
		0.2–0.5	0.049	0.015
		0.5–0.8	0.047	0.008
	10	0–0.2	0.049	0.011
		0.2–0.5	0.067	0.016
		0.5–0.8	0.053	0.012
1000	4	0–0.2	0.042	0.007
		0.2–0.5	0.055	0.009
		0.5–0.8	0.043	0.009
	10	0–0.2	0.072	0.012
		0.2–0.5	0.056	0.012
		0.5–0.8	0.056	0.011

Underlined values are for when empirical type I error exceeds the upper 95% C.I.

Table 3 .

Empirical type I error rate for common correlation structure when all ${\beta }_j=0,$ based on multivariate normal distribution

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0.2	0.005	0.002
		0.5	0.006	0.001
		0.8	0.009	0.002
	10	0.2	0.015	0
		0.5	0.011	0
		0.8	0.014	0.003
500	4	0.2	0.003	0
		0.5	0.005	0.001
		0.8	0.011	0.001
	10	0.2	0.005	0.001
		0.5	0.003	0.001
		0.8	0.009	0.001
1000	4	0.2	0.005	0
		0.5	0.008	0
		0.8	0.004	0.001
	10	0.2	0.011	0.002
		0.5	0.012	0
		0.8	0.009	0.002

Table 4 .

Empirical type I error rate for random correlation structure when all ${\beta }_j=0,$ based on multivariate normal distribution

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0–0.2	0.005	0
		0.2–0.5	0.012	0.001
		0.5–0.8	0.014	0.001
	10	0–0.2	0.018	0.002
		0.2–0.5	0.01	0.002
		0.5–0.8	0.029	0.004
500	4	0–0.2	0.004	0
		0.2–0.5	0.009	0
		0.5–0.8	0.007	0.001
	10	0–0.2	0.009	0
		0.2–0.5	0.009	0.001
		0.5–0.8	0.019	0.005
1000	4	0–0.2	0.006	0.001
		0.2–0.5	0.006	0
		0.5–0.8	0.004	0
	10	0–0.2	0.01	0.002
		0.2–0.5	0.01	0
		0.5–0.8	0.01	0

Table 5 .

Empirical type I error rate when ${\beta }_1=1$ and all other ${\beta }_j=0$ $\left(j\ne 1\right),$ based on multivariate t distribution with 3 d.f., with common correlation structure

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0.2	0.042	0.011
		0.5	0.067	0.019
		0.8	0.057	0.015
	10	0.2	0.088	0.018
		0.5	0.104	0.028
		0.8	0.094	0.030
500	4	0.2	0.059	0.011
		0.5	0.038	0.007
		0.8	0.043	0.009
	10	0.2	0.041	0.016
		0.5	0.059	0.021
		0.8	0.050	0.010
1000	4	0.2	0.052	0.006
		0.5	0.047	0.006
		0.8	0.054	0.009
	10	0.2	0.054	0.010
		0.5	0.058	0.015
		0.8	0.055	0.016

Underlined values are for when empirical type I error exceeds the upper 95% C.I.

Table 6 .

Empirical type I error rate when all ${\beta }_j=0,$ based on multivariate t distribution with 3 d.f., with common correlation structure

Sample size	No. traits	Trait correlation	Nominal type I error rate
			0.05	0.01
100	4	0.2	0.009	0
		0.5	0.007	0
		0.8	0.011	0.002
	10	0.2	0.015	0.001
		0.5	0.015	0.002
		0.8	0.013	0.003
500	4	0.2	0.003	0
		0.5	0.005	0
		0.8	0.005	0
	10	0.2	0.009	0.001
		0.5	0.008	0
		0.8	0.008	0.001
1000	4	0.2	0.004	0.001
		0.5	0.009	0.001
		0.8	0.007	0.001
	10	0.2	0.011	0.001
		0.5	0.002	0
		0.8	0.011	0.001

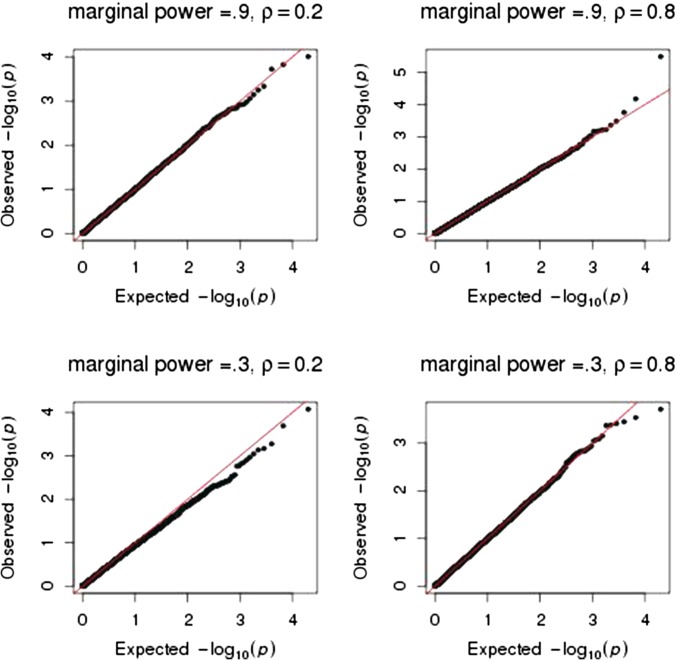
To further evaluate the adequacy of our asymptotic approximations for large samples, we performed 10,000 simulations for 1000 subjects and four traits that had a common correlation structure. All but one $\beta$ was zero; the nonzero $\beta$ was chosen such that there was either 90% or 30% power to detect its marginal effect using $\alpha =\mathrm{0.001.}$ This scenario reflects modern large-scale genomic studies that use more stringent significance thresholds. The quantile–quantile plots in Figure 2 show that the asymptotic ${\chi }^2$ distribution to test pleiotropy provides adequate P-values over the entire range of P-values for when the marginal effect of one $\beta$ is small (power of 30%) or large (power of 90%) and for when the correlation of the traits is small $\left(\rho =0.2\right)$ or large $\left(\rho =0.8\right).$

Figure 2 .

Quantile–quantile plots of P-values to test the null hypothesis of no pleiotropy. Sample size was 1000 with four equally correlated traits $\left(\rho =0.2\text{ or }0.8\right).$ All but one $\beta$ was zero; the nonzero $\beta$ was chosen such that there was either 30% or 90% power to detect its marginal effect using $\alpha =\mathrm{0.001.}$ A total of 10,000 simulations were performed.

The simulation-based power is illustrated in Table 7 and Table 8. The general patterns show that the power to detect two or more associated traits increases with the number of truly associated traits, the effect size of each trait, and larger residual correlations among the traits.

Table 7 .

Power to detect pleiotropy when associated traits have $\beta =0.25$ (explain 2% trait variation; power = 90% for marginal effect)

No. associated traits $\left(\beta =0.25\right)$	Trait correlation	Nominal type I error rate
		0.05	0.01
2	0.2	0.503	0.237
	0.5	0.801	0.581
	0.8	0.971	0.900
3	0.2	0.859	0.677
	0.5	0.956	0.858
	0.8	0.999	0.998
5	0.2	0.980	0.928
	0.5	0.999	0.985
	0.8	1.000	1.000

Shown is a multivariate normal distribution with equal correlation structure, for a sample size of 500 subjects and minor allele frequency of genetic variant set to 0.20.

Table 8 .

Power to detect pleiotropy when associated traits have $\beta =0.2$ (explain 1.2% trait variation; power = 70% for marginal effect)

No. associated traits $\left(\beta =0.2\right)$	Trait correlation	Nominal type I error rate
		0.05	0.01
2	0.2	0.220	0.069
	0.5	0.393	0.165
	0.8	0.964	0.850
3	0.2	0.494	0.255
	0.5	0.715	0.478
	0.8	1.000	0.991
5	0.2	0.842	0.636
	0.5	0.907	0.750
	0.8	1.000	1.000

Shown is a multivariate normal distribution with equal correlation structure, for a sample size of 500 subjects and minor allele frequency of genetic variant set to 0.20.

To provide insights into the properties of our proposed sequential testing of multiple traits, we simulated six traits with a common correlation structure such that three of the traits were associated with a genetic variant (i.e., three true nonzero $\beta$’s). The effect sizes of the associated traits were chosen to have marginal power of 0.3, 0.7, or 0.9 for a sample size of 1000 subjects. These marginal effect sizes correspond to 0.2%, 0.6%, and 1.0% explained variation of the marginal trait. A total of 1000 simulations were performed. The results are presented in Table 9. The frequency of accepting the null hypothesis that all $\beta$’s = 0 (e.g., no $\beta$’s selected to be associated with the genetic variant) ranged from 0.646 for when power was 0.3 to 0.015 when power was 0.9—not surprising that greater power resulted in greater frequency of selecting at least one $\beta$ to be nonzero. Table 9 also presents the frequency for which the three true nonzero $\beta$’s were selected, conditional on at least one of the six $\beta$’s was selected. For weak marginal power (e.g., power of 0.3), the frequency of selecting all three nonzero $\beta$’s was small (0.034–0.213, depending on the trait correlation). Yet the frequency of selecting at least one of the three nonzero $\beta$’s was reasonable (0.747–0.862). The frequency of correctly selecting all three nonzero $\beta$’s increased as either marginal power increased or trait correlation increased. For example, for marginal power of 0.7, the frequency of selecting all three nonzero $\beta$’s was 0.179 for weak correlation ($\rho$ = 0.2), and was 0.851 for strong correlation ($\rho$ = 0.8). For marginal power of 0.9, the frequency of selecting all three nonzero $\beta$’s was 0.472 for weak correlation ($\rho$ = 0.2), and was 0.956 for strong correlation ($\rho$ = 0.8). In contrast to selecting true nonzero $\beta$’s, we also present in Table 9 the frequency of wrongly selecting $\beta$’s that are truly zero. Not surprisingly, when marginal power is weak (power of 0.3), if at least one $\beta$ is selected, there is a significant chance of wrongly selecting a true-zero $\beta$ (e.g., frequency of 0.209 when $\rho$ = 0.2). This type of error decreased as the marginal power for traits increased and the trait correlation increased. For example, when power was 0.9 and trait correlation was $\rho$ = 0.8, the frequency of selecting one true-zero $\beta$ was 0.034, approaching the nominal type I error rate of 0.05. Table 9 illustrates that although there is a chance of wrongly selecting one true-zero $\beta ,$ the frequency of selecting more than one true-zero $\beta$ was small.

Table 9 .

Properties of sequential testing for six traits: proportions out of 1000 simulations with no $\beta$’s selected, proportions according to the number of true nonzero $\beta$’s selected, and proportions according to the number of zero $\beta$’s falsely selected

Marginal power	$\beta$	Explained variation (%)	Trait correlation	Probability no $\beta$’s selected	No. true $\beta$’s selected				No. $\beta$’s falsely selected
					0	1	2	3	0	1	2	3
0.3	0.081	0.2	0.2	0.646	0.138	0.644	0.184	0.034	0.782	0.209	0.008	0.000
			0.5	0.830	0.235	0.471	0.229	0.065	0.694	0.247	0.053	0.006
			0.8	0.850	0.253	0.267	0.267	0.213	0.693	0.127	0.140	0.040
0.7	0.139	0.6	0.2	0.128	0.048	0.361	0.412	0.179	0.867	0.119	0.011	0.002
			0.5	0.169	0.113	0.178	0.337	0.372	0.792	0.140	0.057	0.012
			0.8	0.169	0.105	0.011	0.034	0.851	0.864	0.024	0.019	0.093
0.9	0.180	1.0	0.2	0.014	0.007	0.109	0.413	0.472	0.923	0.071	0.005	0.001
			0.5	0.015	0.030	0.028	0.172	0.770	0.920	0.048	0.017	0.015
			0.8	0.015	0.043	0.001	0.000	0.956	0.918	0.034	0.005	0.044

Marginal power is for detecting the effect of a single trait in a sample size of 1000 subjects $\left(\alpha =0.05\right),$ and the corresponding $\beta$ and trait explained variation are provided.

Data application results

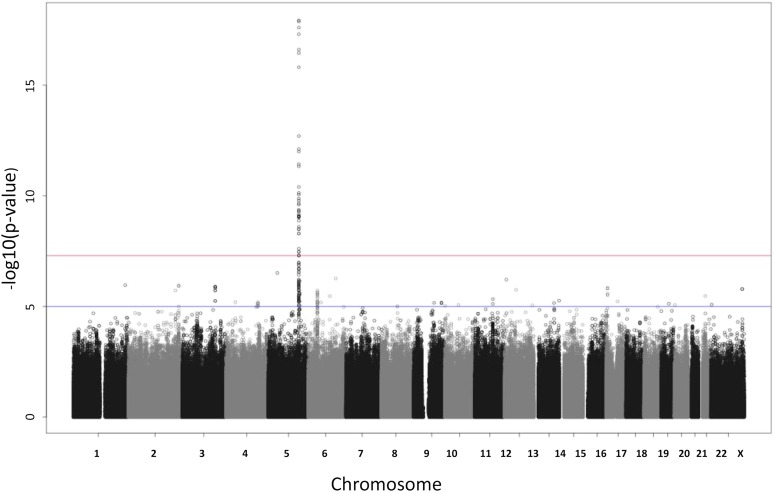
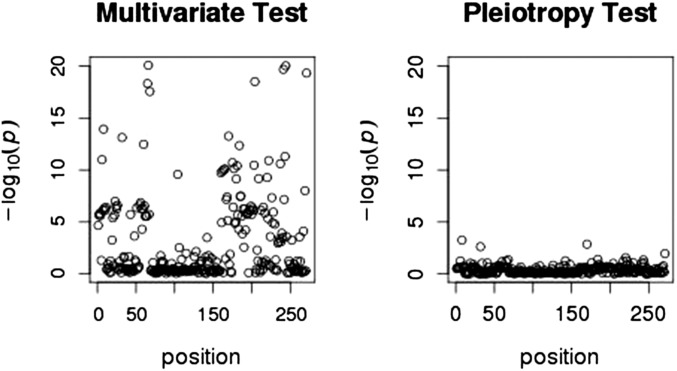
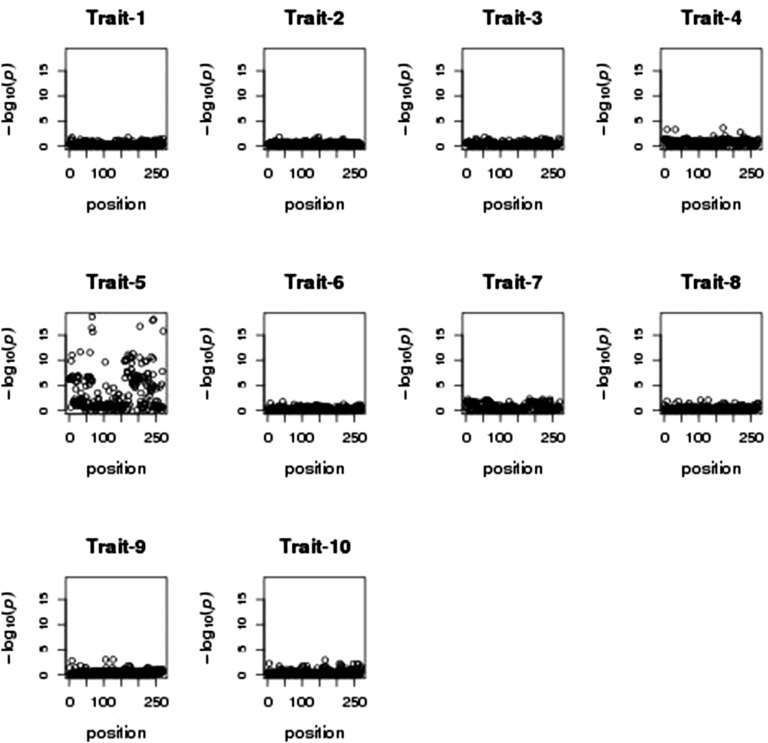
Based on the traditional multivariate regression of all 10 traits on each SNP, we found a strong association of at least one of the traits with SNPs in a region on chromosome 5 (see Figure 3). Figure 4 illustrates the traditional multivariate test $\left(t_0\right)$ in a small region of chromosome 5 (left panel) and the LRT of pleiotropy in the same region (right panel). The test for pleiotropy provides strong evidence that the signal of association was driven by a single phenotype. This is confirmed qualitatively in Figure 5, which shows the individual marginal trait associations for the chromosome 5 region. Although the individual marginal associations in Figure 5 give the visual impression that only one trait is strongly associated with the chromosome 5 SNPs, the LRT of pleiotropy provides a formal statistical test that accounts for the correlations among the traits.

Figure 3 .

Manhattan plot of the multivariate regression of 10 traits on each SNP, using statistic $t_0,$ to test whether any of the traits are associated with an SNP. The upper red horizontal line corresponds to a P-value of $5\times {10}^{-8}$ and the lower blue line to a P-value of ${10}^{-5}.$

Figure 4 .

Zoomed-in region of chromosome 5, comparing the traditional multivariate regression of 10 traits on each SNP (left) with the pleiotropy LRT for the same traits and region (right).

Figure 5 .

Zoomed-in region of chromosome 5 for each of the univariate regression results for the 10 traits. Trait 5 is the only trait showing strong associations with SNPs in this region of chromosome 5.

Discussion

Genetic pleiotropy has been of scientific interest since the time of Gregor Mendel, as he described different traits in peas controlled by genes, such as pea coat color and texture, color of flowers, and whether there were axial spots. In current research, understanding pleiotropy can aid the understanding of complex biological mechanisms of genes (as shown in our vaccine response data), as well as aid the development of pharmacologic and vaccine targets. Yet the statistical methods to assess pleiotropy have resorted to ad hoc comparison of univariate statistical tests or multivariate methods that test the null hypothesis of no trait associations. Because a formal statistical test of pleiotropy was lacking, we developed a novel LRT statistic. The statistic is easy to compute, based on well-known linear regression methods for quantitative traits. Our simulations show that the LRT closely follows a ${\chi }^2$ distribution when only one trait is associated with a genetic variant and that the LRT tends to be conservative when no traits are associated. We proposed a sequential testing procedure, where the null hypothesis of no associated traits could be tested first (using standard multivariate regression methods) and, if significant, be followed by a test of whether only one trait is associated. If the test of only one associated trait rejects, we proposed sequential testing the null of j associated traits (j = 2, …, p − 1), until the sequential test fails to reject the null hypothesis. This approach provides a way to assess the number of traits associated with a genetic variant, accounting for the correlations among the traits. A limitation of our approach, and most other methods for associations of genetic variants with multiple traits, is that it has limited power when an allele is rare. An alternative approach is to compare the similarity of multiple traits with the similarity of rare-variant genotypes across a genetic region, for pairs of subjects (Broadaway et al. 2016). The benefit of this approach is balanced with the limitation of not knowing which genotypes are associated with which traits. Our proposed sequential testing might provide a worthy follow-up procedure if some variants are not too rare.

Although our proposed methods assumed the subjects are independent, it is straightforward to extend our approach to pedigree data. To do so, the variance matrix of residuals for independent subjects, $V\left(\mathit{\epsilon }\right)=\left(\mathbf{\Sigma }\otimes \mathit{I}\right),$ would be replaced with $V\left(\mathit{\epsilon }\right)=\left(\mathbf{\Sigma }\otimes \mathit{K}\right).$ The matrix K contains diagonal elements $K_{ii}=1+h_i,$ where $h_i$ is the inbreeding coefficient for subject i, and off-diagonal elements $K_{ij}=2{\varphi }_{ij}.$ The parameter ${\varphi }_{ij}$ is the kinship coefficient between individuals i and j, the probability that a randomly chosen allele at a given locus from individual i is identical by descent to a randomly chosen allele from individual j, conditional on their ancestral relationship. For subjects from different pedigrees, ${\varphi }_{ij}=0,$ so K can be structured as a block-diagonal matrix, with diagonal block ${\mathit{K}}_{\mathit{i}}$ for the ith pedigree. With this adjustment, our methods can be used for pedigree data or for data with population structure where matrix K is an estimate of genetic relationships (Schaid et al. 2013).

Application of our new approach to a study of immune phenotypes in response to smallpox vaccination strongly suggests that only 1 of 10 correlated traits is statistically associated with SNPs in a region on chromosome 5. The benefit of this type of analysis is that it provides strong guidance on follow-up functional studies for genome-wide association studies with multiple traits. In our case, it allowed investigators to focus on the single immunologic trait truly associated with the chromosome 5 SNPs, rather than conducting labor-intensive, expensive, and time-consuming experiments on unrelated immune response traits.

We recognize that our proposed LRT depends on the assumption that residuals have a multivariate normal distribution. Our simulations with a multivariate t distribution (3 d.f.) suggest that the LRT is robust to heavy-tailed distributions. To ensure robustness with the traditional multivariate regression, it is common practice to transform the data to have at least normally distributed marginal distributions, such as use of normal quantile transformation. This is a reasonable approach for our proposed LRT.

A limitation of our method is that each of the traits is assumed to be quantitative. If all traits are binary, or if there is a mixture of quantitative and binary traits, then the dependence of the LRT on an assumed likelihood would need to be reconsidered. One approach is to consider a general multivariate exponential family of models (Prentice and Zhao 1991; Zhao et al. 1992; Sammel et al. 1997). Another approach would be to consider the reverse regression of an SNP dose on all traits, like the ordinal logistic MultiPhen approach of O’Reilly et al. (2012), yet develop an LRT for pleiotropy whereby one of the $\beta$’s is allowed to be unconstrained under the null. An alternative approach that we are developing is based on generalized linear models and generalized estimating equations. The theoretical underpinnings of these alternate approaches, and their computational challenges, are topics of future research.

Appendix A

R code to compute F-statistic for canonical correlation of matrix Y with vector x.

library(CCA)

cc.fit <- cc(Y,x)

cc.fstat <- function(cc.fit){

rho <- cc.fit$cor

lambda <- 1 - rho^2

dimx <- max(dim(cc.fit$xcoef))

dimy <- max(dim(cc.fit$ycoef))

k <- max(c(dimx, dimy))

n <- nrow(Y)

fstat <- ((1-lambda)/lambda) * ((n-k-1)/k)

pval <- 1-pf(fstat, k, n-k-1, ncp=0)

return(list(fstat=fstat, pval=pval))

}

Appendix B: Hypothesis Tests for Linear Model

Notation and model

Based on the regression model described in the main text, suppose that p traits are measured on each of n subjects, with ${{\mathit{y}}^{\prime }}_{\mathit{j}}=\left(y_{j1},\mathrm{...},y_{jn}\right)$ the vector of measures on the jth trait for n subjects, and stack the vectors as ${\mathit{y}}^{\prime }=\left({{\mathit{y}}^{\prime }}_{\mathbf{1}},\mathrm{...},{{\mathit{y}}^{\prime }}_{\mathit{p}}\right).$ Let $\mathit{X}=\mathrm{diag}\left(\mathit{x}\right),$ where x is a vector of length n. We assume that y and x are centered on their means. We can express the model as $\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{\epsilon },$ where ${\mathit{\epsilon }}^{\prime }=\left({{\mathit{\epsilon }}^{\prime }}_1,\mathrm{...},{{\mathit{\epsilon }}^{\prime }}_{\mathit{p}}\right).$ The error term $\mathit{\epsilon }\mathrm{\sim }N\left(\mathrm{0,}\mathbf{\Omega }\right),$ where $\mathbf{\Omega }=\mathbf{\Sigma }\otimes \mathit{I}$ and the $p\times p$ matrix $\mathbf{\Sigma }$ is the covariance matrix for the within-subject covariances of the errors. Then, the Cholesky decompositon of $\mathbf{\Omega }$ is $\mathbf{\Omega }={\mathbf{\Omega }}^{1/2}{\mathbf{\Omega }}^{1/2},$ where ${\mathbf{\Omega }}^{1/2}={\mathbf{\Sigma }}^{1/2}\otimes \mathit{I}$ and ${\mathbf{\Omega }}^{-1/2}={\mathbf{\Sigma }}^{-1/2}\otimes \mathit{I}.$ Using $\tilde{\mathit{y}}={\mathbf{\Omega }}^{-1/2}\mathit{y}\mathrm{,}\tilde{\mathit{X}}={\mathbf{\Omega }}^{-1/2}\mathit{X},$ the model can transform to independent standard normal random variables, $\tilde{\mathit{y}}=\tilde{\mathit{X}}\mathit{\beta }+\tilde{\mathit{\epsilon }}\mathrm{,}$ where $\tilde{\mathit{\epsilon }}={\mathbf{\Sigma }}^{-1/2}\mathit{\epsilon }\mathrm{\sim }N\left(\mathrm{0,}{\mathit{I}}_{np}\right),$ and with log likelihood $l_n\left(\mathit{\beta }\right)=-\left(1/2\right){\left(\tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta }\right)}^{\prime }(\tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta })\mathrm{.}$

Theorem 1. Let $V$ be a $k\times p$ matrix of rank $k$ $\left(k\le p\right).$ Then the minimizer of ${\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta }\Vert }^2$ under the constraint $\mathit{V}\mathit{\beta }=0$ is

$${\mathit{\beta }}_{\mathit{V}}={\mathit{\beta }}_{\mathit{n}}-{\mathit{\beta }}_{\mathit{V}}^{\ast }\mathrm{,}$$

where ${\mathit{\beta }}_n={\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}$ is the ordinary least-squares (OLS) estimate and

$${\mathit{\beta }}_V^{\ast }={\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}.$$

Furthermore,

$${\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}\Vert }^2={\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2+{\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2\mathrm{.}$$ (B1)

Proof. Denote ${\mathit{\beta }}^{\ast }={\mathit{\beta }}_{\mathit{n}}-\mathit{\beta }.$ Note that

$$\begin{array}{c}{\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}\mathit{\beta }\Vert }^2=\hspace{0.17em}{\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}+\tilde{\mathit{X}}\left({\mathit{\beta }}_{\mathit{n}}-\mathit{\beta }\right)\Vert }^2\\ ={\Vert \tilde{\mathit{y}}-\mathit{X}{\mathit{\beta }}_{\mathit{n}}\Vert }^2+{\mathit{\beta }}^{\prime }\ast {\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\mathit{\beta }\ast +\hspace{0.17em}2{\left(\tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\right)}^{\prime }\tilde{\mathit{X}}\mathit{\beta }\ast \\ ={\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2+{\mathit{\beta }}^{\prime }\ast {\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\mathit{\beta }\ast .\end{array}$$

The last above step results from $2{\left(\tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\right)}^{\prime }\tilde{\mathit{X}}\mathit{\beta }\ast =0,$ because $\tilde{\mathit{y}}\tilde{\mathit{X}}={{\mathit{\beta }}^{\prime }}_{\mathit{n}}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}.$

Under the constraint $\mathit{V}\mathit{\beta }=0,$ $\mathit{V}\mathit{\beta }\ast =\mathit{V}{\mathit{\beta }}_{\mathit{n}}.$ Applying the Lagrange multiplier method, we minimize

$$Q\left({\mathit{\beta }}^{\ast }\mathrm{,}\lambda \right)={\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2+{\mathit{\beta }}^{\ast }{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}{\mathit{\beta }}^{\ast }+\hspace{0.17em}2\lambda \left(\mathit{V}{\mathit{\beta }}^{\ast }-\mathit{V}{\mathit{\beta }}_{\mathit{n}}\right).$$

By taking the derivative of $Q$ with respect to $\mathit{\beta }$ and $\lambda ,$ we obtain the solution ${\mathit{\beta }}_{\mathit{V}}^{\ast }={\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}$ and the estimate of $\mathit{\beta }$ is ${\mathit{\beta }}_{\mathit{V}}={\mathit{\beta }}_{\mathit{n}}-{\mathit{\beta }}_{\mathit{V}}^{\ast }.$

Therefore, we have

$${\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}\Vert }^2={\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2+{\mathit{\beta }}_{\mathit{V}}^{\ast }\prime {\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\mathrm{.}$$

This completes the Proof.

Remark. Equation B1 illustrates that the residual sums of squares (ssq) for the constrained model $\left({\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}\Vert }^2\right)$ are partitioned into two parts: (1) the ssq for the OLS fit $\left({\Vert \tilde{\mathit{y}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2\right)$ and (2) the sum of squared differences of the fitted values for the OLS model and the constrained model $\left({\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2={\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}\Vert }^2\right).$

Corollary 1. Under the null hypothesis, $V\beta =0,$

$${\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2={\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}{\Vert \mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{\epsilon }}\Vert }^2\mathrm{\sim }{\chi }_k^2\mathrm{.}$$

Proof.

$${\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2={\Vert \tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}\Vert }^2=\widetilde{{\mathit{y}}^{\prime }}\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\times {\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}=\widetilde{{\mathit{y}}^{\prime }}\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}=\widetilde{{\mathit{\epsilon }}^{\prime }}\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{\epsilon }}.$$

The substitution of $\tilde{\mathit{y}}$ with $\tilde{\mathit{\epsilon }}$ in the last step of the above Proof can be made because by the assumed linear model, $\tilde{\mathit{y}}=\tilde{\mathit{X}}\beta +\tilde{\mathit{\epsilon }},$ we find that

$$\begin{array}{c}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{y}}=\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\left(\tilde{\mathit{X}}\mathit{\beta }+\tilde{\mathit{\epsilon }}\right)\\ =\mathit{V}\mathit{\beta }+\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{\epsilon }}\\ =\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{\epsilon }}.\end{array}$$

The last step above results because $\mathit{V}\mathit{\beta }=0$ under the null hypothesis.

It is easy to verify that the matrix ${\mathit{P}}_{\mathit{V}}=\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }$is idempotent and is of rank $k$ if the rank of $\mathit{V}$ is of rank $k.$ Because $\tilde{\mathit{\epsilon }}=\mathrm{\sim }N\left(\mathrm{0,}{\mathit{I}}_{\mathit{n}\mathit{p}}\right)$ and ${\mathit{P}}_{\mathit{V}}$ is idempotent, $\widetilde{{\mathit{\epsilon }}^{\prime }}{\mathit{P}}_{\mathit{V}}\tilde{\mathit{\epsilon }}\mathrm{\sim }{\chi }_k^2,$ completing the Proof.

Corollary 2. If $\mathit{V}{\mathit{\beta }}_{\mathbf{0}}\ne 0,$ then

$${\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2=O\left(n\right)\to \infty \mathrm{.}$$

Proof. It follows from the Proof of Corollary 1 that ${\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2=\widetilde{{\mathit{y}}^{\prime }}{\mathit{P}}_{\mathit{V}}\tilde{\mathit{y}}.$ By the linear model, we have

$$\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert =\widetilde{{\mathit{y}}^{\prime }}{\mathit{P}}_{\mathit{V}}\tilde{\mathit{y}}={{\mathit{\beta }}^{\prime }}_{\mathbf{0}}{\tilde{\mathit{X}}}^{\prime }{\mathit{P}}_{\mathit{V}}\tilde{\mathit{X}}{\mathit{\beta }}_{\mathbf{0}}+{\mathit{\epsilon }}^{\prime }{\mathit{P}}_{\mathit{V}}\mathit{\epsilon }+\mathbf{2}{{\mathit{\beta }}^{\prime }}_{\mathbf{0}}{\tilde{\mathit{X}}}^{\prime }{\mathit{P}}_{\mathit{V}}\mathit{\epsilon }.$$

It is clear that ${\mathit{\epsilon }}^{\prime }{\mathit{P}}_{\mathit{V}}\mathit{\epsilon }\mathrm{\sim }{\chi }_k^2=O_p\left(1\right)$ and ${{\mathit{\beta }}^{\prime }}_{\mathbf{0}}{\tilde{\mathit{X}}}^{\prime }{\mathit{P}}_{\mathit{V}}\mathit{\epsilon }=O_p\left(n^{1/2}\right).$ In addition, ${{\mathit{\beta }}^{\prime }}_{\mathbf{0}}{\tilde{\mathit{X}}}^{\prime }{\mathit{P}}_{\mathit{V}}\tilde{\mathit{X}}{\mathit{\beta }}_{\mathbf{0}}={\left(\mathit{V}{\mathit{\beta }}_{\mathbf{0}}\right)}^{\prime }{\left[\mathit{V}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}\mathit{\beta }=n{\left(\mathit{V}{\mathit{\beta }}_{\mathbf{0}}\right)}^{\prime }{\left[\mathit{V}{\left(n^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}^{-1}\mathit{V}\mathit{\beta }=O\left(n\right)$ since $\mathit{V}{\left(n^{-1}{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\to \mathit{V}{\left(E{\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }=O\left(1\right)$ in probability. Combining all three facts yields Corollary 2.

Hypothesis tests

Now we consider the null hypothesis of no pleiotropy:

$${\mathrm{H}}_0:\text{ Of the parameters }{\beta }_{1,}\mathrm{...},{\beta }_p,\text{ there exists at most one that is nonzero}\leftrightarrow {\mathrm{H}}_1:\text{otherwise}\mathrm{.}$$

The null hypothesis is equivalent to testing whether one of the following $p+1$ tests holds:

$${\mathrm{H}}_{k0}:{\beta }_k\ne \mathrm{0,}{\beta }_j=0\left(j\ne k\right),$$

for $k=0,\dots \mathrm{,}p.$ Note that ${\mathrm{H}}_{00}$ represents all ${\beta }_k=0$ $\left(k=1,\dots \mathrm{,}p\right),$ while for $k>0,$ ${\mathrm{H}}_{k0}$ allows ${\beta }_k\ne 0$ while all other ${\beta }_j=0\hspace{0.5em}\left(j\ne k\right).$

To represent these $p+1$ hypotheses, we use ${\mathrm{H}}_{k0}:{\mathit{V}}_{\mathit{k}}\mathit{\beta }=0.$ Let ${\mathit{V}}_{\mathbf{0}}$ be a matrix such that ${\mathrm{H}}_{00}:{\mathit{V}}_{\mathbf{0}}\mathit{\beta }=0$ tests whether all ${\beta }_j=0.$ In this case, ${\mathit{V}}_{\mathbf{0}}$ is the identity matrix of dimension $p.$ To construct ${\mathit{V}}_{\mathit{k}}$ $\left(k>0\right),$ create an identity matrix of dimension $p$ and then remove the kth row. This results in ${\mathit{V}}_{\mathit{k}}\mathit{\beta }={\left({\beta }_1,\mathrm{...},{\beta }_{k-1},{\beta }_{k+1}{\beta }_p\right)}^{\prime }.$ Then, the null hypothesis is equivalent to

$${\mathrm{H}}_0:\hspace{0.5em}\text{there}\hspace{0.5em}\text{exists}\hspace{0.5em}\text{one}\hspace{0.5em}\text{of}\hspace{0.5em}{\mathrm{H}}_{k0}:\hspace{0.5em}{\mathit{V}}_{\mathit{k}}\mathit{\beta }=0,\hspace{0.5em}\text{for}\hspace{0.5em}k=0,\dots \mathrm{,}p\mathrm{.}$$

For $k=0,1,\dots \mathrm{,}p,$ set $t_k=\widetilde{{\mathit{y}}^{\prime }}{\mathit{P}}_{{\mathit{V}}_{\mathit{k}}}\tilde{\mathit{y}}.$ Then it follows from Theorem 1 that

$$t_k={\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{{\mathit{V}}_{\mathit{k}}}\Vert }^2-{\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}\Vert }^2\mathrm{,}$$

where ${\mathit{\beta }}_{{\mathit{V}}_{\mathit{k}}}$ is the least-squares estimate under the constraint ${\mathit{V}}_{\mathit{k}}\mathit{\beta }=0$ and

$${\mathit{P}}_{{\mathit{V}}_{\mathit{k}}}=\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{{\mathit{V}}^{\prime }}_{\mathit{k}}{\left[{\mathit{V}}_{\mathit{k}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{{\mathit{V}}^{\prime }}_{\mathit{k}}\right]}^{-1}{\mathit{V}}_{\mathit{k}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\mathrm{.}$$

Then we have the following corollary.

Corollary 3. The LRT, $-2$ × log of ratio of likelihoods, is given by

$$T=\underset{k=0,\dots \mathrm{,}p}{{\displaystyle \min }}{t}_k\mathrm{.}$$

If ${\mathrm{H}}_{00}$ holds, then

$$t_k={\mathit{\epsilon }}^{\prime }{\mathit{P}}_{{\mathit{V}}_{\mathit{k}}}\mathit{\epsilon }\mathrm{,}$$

and $t_0\mathrm{\sim }{\chi }_p^2\mathrm{,}{t}_k\mathrm{\sim }{\chi }_{p-1}^2$ for $k=1,\dots \mathrm{,}p.$

If only one ${\mathrm{H}}_{k0}$ $\left(k>0\right)$ holds, then

$$T\mathrm{\sim }{\chi }_{p-1}^2\mathrm{.}$$

From Corollary 3, we can see that the test statistic $T$ has two different asymptotic distributions when $\mathit{\beta }$ = 0 or not. When $\mathit{\beta }=0,$ the asymptotic distribution of $T$ is unknown. Alternatively, when $\mathit{\beta }=0,$ we can use the commonly used ${\chi }_p^2$ test for the null hypothesis that all ${\beta }_j=0.$ This motivates us to do the test by two stages. The first stage is just test ${\mathrm{H}}_{00}:$ $\mathit{\beta }=0,$ using the statistic $t_0\mathrm{\sim }{\chi }_p^2$ as the test statistic, so we reject ${\mathrm{H}}_{00}$ if $t_0>{\chi }_p^2\left(\alpha \right),$ where ${\chi }_p^2\left(\alpha \right)$ is the $1-\alpha$ quantile of a ${\chi }^2$ distribution with p d.f. If ${\mathrm{H}}_{00}$ cannot be rejected, then ${\mathrm{H}}_0$ cannot be rejected. If ${\mathrm{H}}_{00}$ is rejected, we turn to the second stage to test the null hypothesis that one ${\mathrm{H}}_{k0}$ holds for $k=1,\dots \mathrm{,}p.$ Then we can use the test statistic $T_1={\min }_{k=1,\dots \mathrm{,}p}{t}_k\mathrm{.}$ Since $T_1\mathrm{\sim }{\chi }_{p-1}^2,$ we reject the null hypothesis that one ${\mathrm{H}}_{k0}$ holds for $k=1,\dots \mathrm{,}p$ if $T_1>{\chi }_{p-1}^2\left(\alpha \right).$ Then, the null hypothesis ${\mathrm{H}}_0$ is rejected only if both ${\mathrm{H}}_{00}$ is rejected and the null hypothesis that one ${\mathrm{H}}_{k0}$ holds is rejected $\left(k=1,\dots \mathrm{,}p\right).$ Since both tests are conducted at type I error rate of $\alpha ,$ and this is based on the principal of the IU test (Silvapulle and Sen 2004), the type I error rate for rejecting ${\mathrm{H}}_0$ is no more than $\alpha .$

Remark. If $p$ is too large, it might be beneficial to ignore the $t_0$ and directly use $T_1\mathrm{\sim }{\chi }_{p-1}^2$ to construct the rejection region.

Sequential test of nonzero betas

The above solutions can be easily extended to test the following null hypothesis:

$${\mathrm{H}}_0:\text{There}\hspace{0.5em}\text{exist}\hspace{0.5em}\text{at}\hspace{0.5em}\text{most}\hspace{0.5em}K\hspace{0.5em}\text{nonzero}\hspace{0.5em}\text{components}\hspace{0.5em}\text{of}\hspace{0.5em}\mathit{\beta }\leftrightarrow {\mathrm{H}}_1: \hspace{0.17em}\text{otherwise} \mathrm{.}$$

With appropriately defined $\mathit{V}$ matrices (there are $C_K^p$ matrices), the LRT reduces to

$$T=\underset{k=1,\dots \mathrm{,}{C}_K^p}{{\displaystyle \min }}{\Vert {\mathit{P}}_{{\mathit{V}}_{\mathit{k}}}\tilde{\mathit{y}}\Vert }^2\mathrm{,}$$

where ${\mathit{P}}_{{\mathit{V}}_{\mathit{k}}}=\tilde{\mathit{X}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{{\mathit{V}}^{\prime }}_{\mathit{k}}{\left[{\mathit{V}}_{\mathit{k}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\mathit{V}}^{\prime }\right]}_{\mathit{k}}^{-1}{\mathit{V}}_{\mathit{k}}{\left({\tilde{\mathit{X}}}^{\prime }\tilde{\mathit{X}}\right)}^{-1}{\tilde{\mathit{X}}}^{\prime }\mathrm{.}$

In the above, ${\mathit{V}}_{\mathit{k}}$ is a $\left(p-K\right)\times p$ matrix. For example, if for indexes $1\le i_1<\cdots <i_K\le p,$ we test

$${\beta }_{i_1}\ne \hspace{0.5em}\mathrm{0,}\dots \mathrm{,}{\beta }_{i_K}\ne \hspace{0.5em}0\hspace{1em}\text{and}\hspace{1em}{\beta }_j=0,j\ne \hspace{0.5em}{i}_1\mathrm{,}\dots \mathrm{,}{i}_K\mathrm{,}$$

then we can constitute the corresponding matrix ${\mathit{V}}_{i_1\mathrm{,}\dots \mathrm{,}{i}_K}$ as follows: (i) Constitute a $p\times p$ identity matrix and (ii) delete the rows for indexes $i_1,\dots ,i_K.$

Then we can use the following multistage test:

• i. First test ${\mathrm{H}}_{00}:$ $\mathit{\beta }=0.$ Reject if $t_0>{\chi }_p^2\left(\alpha \right).$ If reject, go to the next stage; otherwise stop and conclude ${\mathrm{H}}_{00}$ is true.

• ii. For $s=1,\dots \mathrm{,}K-1,$ test ${\mathrm{H}}_{s0}:$ there are only $s$ components of $\mathit{\beta }$ ≠ 0. Reject ${\mathrm{H}}_{s0}$ if $T_s>{\chi }_{p-s}^2\left(\alpha \right),$ where $T_s={\min }_{1\le i_1<\cdots <i_s\le p}\widetilde{{\mathit{y}}^{\prime }}{\mathit{P}}_{{\mathit{V}}_{{\mathit{i}}_{\mathbf{1}}\mathrm{,}\dots \mathrm{,}{\mathit{i}}_{\mathit{s}}}}\tilde{\mathit{y}}\mathrm{.}$ The indexes range over the $C_s^p$ choices. If reject, continue testing by incrementing s by 1. If fail to reject ${\mathrm{H}}_{s0},$ stop testing and conclude there are s traits associated with x.

The type I error rate of this sequential testing is no greater than the nominal $\alpha$ level. To understand this, suppose there are $K$ nonzero $\beta$’s, and define the type I error as concluding there are $>K$ nonzero $\beta$’s. Note that the test statistic $T_s$ at each stage is based on the minimum of statistics, where each statistic is based on ${\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}^{\ast }\Vert }^2={\Vert \tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{n}}-\tilde{\mathit{X}}{\mathit{\beta }}_{\mathit{V}}\Vert }^2,$ a measure of distance between fitted values based on the unconstrained OLS model and the constrained model determined by V. If one of the constrained models is correct, then by Corollaries 1 and 2, $T_s\sim {\chi }^2.$ If, however, none of the constrained models are correct, $T_s=O\left(n\right)\to \infty .$ This means that at testing stage $j<K,$ the probability of rejecting the null hypothesis at stage j depends on the power to detect the misspecified models, which approach 1 as n increases. With this background, we can formally evaluate the type I error rate. Define $r_j$ as an indicator of whether the null hypothesis is rejected at stage j. The probability of a type I error is the probability of rejecting the sequential stage testing up to and including stage K. This joint probability can be expressed as

$$P\left(r_0,r_1,r_2,\mathrm{...},r_K\right)=P\left(r_0\right)P\left(r_1|r_0\right)P\left(r_2|r_0,r_1\right)\mathrm{...}P\left(r_K|r_0,r_1,\mathrm{...},r_{K-1}\right).$$ (B2)

The last term in expression (B2) represents the probability of rejecting the null hypothesis when the null hypothesis is true, so one of the constrained models is correct. The test statistic at stage K follows a ${\chi }_{p-K}^2$ distribution, so $P\left(r_K|r_0,r_1,\mathrm{...},r_{K-1}\right)=\alpha .$ All other terms in (B2) approach 1 as n increases, because all stages$j<K$ represent misspecified models. This proves that the type I error rate is no greater than the specified $\alpha$ level.