Abstract
Two broad paradigms exist for inferring the ratio of nonsynonymous to synonymous substitution rates, from coding sequences: (i) a one-rate approach, where is represented with a single parameter, or (ii) a two-rate approach, where and are estimated separately. The performances of these two approaches have been well studied in the specific context of proper model specification, i.e., when the inference model matches the simulation model. By contrast, the relative performances of one-rate vs. two-rate parameterizations when applied to data generated according to a different mechanism remain unclear. Here, we compare the relative merits of one-rate and two-rate approaches in the specific context of model misspecification by simulating alignments with mutation–selection models rather than with -based models. We find that one-rate frameworks generally infer more accurate point estimates, even when varies among sites. In other words, modeling variation may substantially reduce accuracy of point estimates. These results appear to depend on the selective constraint operating at a given site. For sites under strong purifying selection (), one-rate and two-rate models show comparable performances. However, one-rate models significantly outperform two-rate models for sites under moderate-to-weak purifying selection. We attribute this distinction to the fact that, for these more quickly evolving sites, a given substitution is more likely to be nonsynonymous than synonymous. The data will therefore be relatively enriched for nonsynonymous changes, and modeling contributes excessive noise to estimates. We additionally find that high levels of divergence among sequences, rather than the number of sequences in the alignment, are more critical for obtaining precise point estimates.
Keywords: dN/dS, mutation–selection models, evolutionary rate, sequence simulation, molecular evolution
A variety of computational approaches have been developed to infer selection pressure from protein-coding sequences in a phylogenetically aware context. Among the most commonly used methods are those that compute the evolutionary rate ratio which represents the ratio of nonsynonymous to synonymous substitution rates. Beginning in the mid-1990s, this value has been calculated using maximum-likelihood (ML) approaches (Goldman and Yang 1994; Muse and Gaut 1994), and since then, a wide variety of inference frameworks have been developed to infer at individual sites in protein-coding sequences (Nielsen and Yang 1998; Yang et al. 2000; Yang and Nielsen 2002; Yang and Swanson 2002; Kosakovsky Pond and Frost 2005; Kosakovsky Pond and Muse 2005; Lemey et al. 2012; Murrell et al. 2012b, 2013).
Typically, the performance of evolutionary models is examined using simulation-based approaches wherein sequences are simulated according to the model being examined, and inferences are subsequently performed on the simulated data. This approach ensures that simulated and inferred parameters correspond. Although useful, this strategy fundamentally assumes that the data being analyzed were generated by the same mechanism that the inference model used, and hence the model has been correctly specified. Crucially, this scenario does not apply to the analysis of natural sequence data. Indeed, real genomes evolve according to a variety of interacting evolutionary forces, not according to a phylogenetic model of sequence evolution. As such, it remains unclear how well evolutionary models perform when they are applied to sequence data that have been technically misspecified, i.e., where the data do not conform to the inference model’s assumptions. Indeed, ML-based inference methods are guaranteed to converge upon the true parameter value when the model is properly specified (provided there are sufficient data), but there is no such guarantee when the data violate critical model assumptions and/or when the model is misspecified (White 1982; Yang 2006).
We therefore seek to we extend our understanding of -based inference model performance by studying how well these models infer site-specific point estimates when the model is mathematically misspecified. To this end, we simulate sequences not under a -based model, but instead using the mutation–selection (MutSel) modeling framework. Unlike -based models, MutSel models are based on population genetics principles and describe the site-specific evolutionary process as a dynamic interplay between mutational and selective forces (Halpern and Bruno 1998; Yang and Nielsen 2008). Therefore, many regard MutSel models as more mechanistically representative of real coding-sequence evolution than -based models, which are primarily phenomenological in nature (Thorne et al. 2007, 2012; Holder et al. 2008; Rodrigue et al. 2010; Tamuri et al. 2012; Liberles et al. 2013). For this reason, MutSel-based simulation approaches have been used to study the behavior of phylogenetic and evolutionary rate inferences (Holder et al. 2008; McCandlish et al. 2013; dos Reis 2015; Spielman and Wilke 2015b).
Recently, we introduced a mathematical framework that allows us to accurately calculate a ratio directly from the parameters of a MutSel model (Spielman and Wilke 2015b). This framework gives rise to a robust benchmarking strategy through which we can simulate sequences using a MutSel model, infer on the simulated sequences using established approaches, and then compare the inferred to the expected given by the parameters of the MutSel model. We have previously successfully used such an approach to identify biases in inference approaches for whole-gene evolutionary rates (Spielman and Wilke 2015b). Here, we employ this approach to evaluate the performance of site-specific -based inference approaches.
Because the models used for inference are mathematically misspecified to the data, we can expect inferences to feature statistical biases, which in turn illuminate how these models might behave in more complex scenarios. Several important distinctions between and MutSel models contribute to the model misspecification examined here. Most importantly, while models assume that all nonsynonymous substitutions occur at the same rate, MutSel models assume different rates for each type of nonsynonymous substitution and similarly for synonymous substitutions in certain contexts. This distinction gives rise to a key difference in model assumptions. In particular, because the parameter is a rate constant, models implicitly assume that substitutions are Poisson distributed in time. By contrast, in the MutSel model, is not a rate constant, and thus substitutions will be overdispersed relative to a Poisson process.
Two primary questions motivate the present study: (i) How accurate are various inference frameworks for point estimation? And (ii) under what conditions does capture the long-term evolutionary dynamics of site-specific coding-sequence evolution? For the first question, we focus our efforts on distinguishing performance between two inference paradigms: one-rate and two-rate models. One-rate models parameterize with a single parameter for effectively fixing at all sites, whereas two-rate models use separate parameters for and at each site. Some studies have suggested that the two-rate paradigm leads to more robust positive-selection inference (Kosakovsky Pond and Muse 2005; Murrell et al. 2013), whereas others have suggested that the extra parameter may actually confound positive selection inference (Yang et al. 2005; Wolf et al. 2009). Here, we do not benchmark positive-selection inference, but we instead ask how this parameterization affects point estimation in the context of model misspecification. We therefore must emphasize that this study applies primarily to sequences evolving under equilibrium conditions and not necessarily to sequences evolving under shifting selection pressures.
The second question arises naturally from our use of MutSel models, which describe the equilibrium site-specific codon fitness values. As a consequence, any calculated from MutSel model parameters represents, by definition, the steady-state (Spielman and Wilke 2015b). Since is an inherently time-sensitive measurement (Rocha et al. 2006; Kryazhimskiy and Plotkin 2008; Wolf et al. 2009; Mugal et al. 2014; Meyer et al. 2015), it is not necessarily true that measured from a given data set will reflect the equilibrium value. Therefore, our approach additionally enables us to identify the conditions under which site-specific ratios are expected to reflect long-term, rather than transient, evolutionary dynamics.
Materials and Methods
Derivation of MutSel simulation parameters
We simulated heterogeneous alignments, such that each site evolved according to a distinct distribution of codon fitnesses, according to the Halpern and Bruno (1998) (HB98) MutSel model using Pyvolve (Spielman and Wilke 2015a). The HB98 rate matrix is given by
| (1) |
where is the site-invariant mutation rate, where is the focal nucleotide before mutation and the focal nucleotide after mutation during the substitution from codon i to j. is the fixation probability from codon i to j at site k and is defined as
| (2) |
where is the scaled selection coefficient from codon i to j at site k (Halpern and Bruno 1998). Thus, this model is specified using a nucleotide-level mutation model ( parameters) and codon-level fitness values ( parameters).
We simulated four sets of alignments, all of which assumed a Hasegawa et al. (1985) (HKY85) mutation model with the transition–transversion bias parameter κ set to 4. Two alignment sets assumed equal nucleotide frequencies ( for ), and the other two alignment sets assumed unequal nucleotide frequencies (arbitrarily set to ), to incorporate underlying nucleotide compositional bias. We refer to these parameterizations, respectively, as and For each mutational parameterization, we simulated an alignment set where all synonymous codons shared the same fitness value (no codon bias) and an alignment set where synonymous codons differed in fitnesses (codon bias). The and simulations without codon bias used the same sets of fitness parameters, and similarly the and simulations with codon bias used the same sets of fitness parameters.
Following previous work showing that site-specific amino acid frequencies in natural protein alignments tend to follow a Boltzmann distribution (Porto et al. 2004; Ramsey et al. 2011), we simulated 100 site-specific amino acid frequency distributions from a Boltzmann distribution:
| (3) |
Here, is the state frequency of amino acid a, a and b index amino acids from 0 to 19, and the parameter λ increases with evolutionary rate (Ramsey et al. 2011). For each frequency distribution, we sampled a value for λ from a uniform distribution and we selected a random ranking for all amino acids. These frequency calculations formed the basis of our derivation of fitness values used in all simulations.
Importantly, when a symmetric nucleotide mutation model is assumed (e.g., ), codon fitness values can be calculated directly as the logarithm of codon equilibrium frequency values (Sella and Hirsh 2005). Therefore, we directly computed codon fitness values from the derived frequency values, under the assumption that synonymous codons shared the same fitness. These fitness parameters were employed for both and simulations without codon bias.
To derive fitness parameters for simulations with codon bias, we randomly selected a preferred codon for each amino acid. We assigned a state frequency of where γ was drawn from a uniform distribution to the preferred codon, and we assigned the remaining frequency evenly to all remaining synonymous codons. In this way, the overall amino acid state frequency was unchanged, but its synonymous codons occurred with differing frequencies. Note that a single parameter γ was selected for each frequency distribution (i.e., each resulting alignment position) and not for each set of synonymous codons. Again, fitness distributions were directly computed from these resulting codon frequencies for use in both and simulations with codon bias.
Unlike the simulations, the simulations did not contain symmetric mutation rates. Therefore, we obtained stationary codon frequencies for the simulations, for use in calculations, numerically as the dominant eigenvector of each MutSel model’s matrix, which was constructed from mutation rates and codon fitness values. In this way, all stationary codon frequency distributions incorporated, by definition, information regarding both codon-level fitness and nucleotide-level mutation.
We simulated heterogeneous alignments across an array of balanced phylogenies, containing 128, 256, 512, 1024, or 2048 sequences. For each number of taxa, we simulated sequences with varying degrees of divergence, with all branch lengths equal to 0.0025, 0.01, 0.04, 0.16, or 0.64. Throughout, we use N to refer to a given simulation’s number of taxa and B to refer a given simulation’s branch length. We simulated 50 alignment replicates for each combination of N and B. We additionally simulated alignments, using only the parameterizations, along five different empirical phylogenies (Table 1), again with 50 replicates each. For these simulations, we directly used the original empirical branch lengths.
Table 1. Empirical phylogenies.
| Data set | Na | Tree length | Mean branch length (± SD) | Source |
|---|---|---|---|---|
| amineb | 3039 | 440.861 | 0.073 ± 0.149 | Spielman et al. (2015) |
| Camelidc | 212 | 15.428 | 0.037 ± 0.049 | Kosakovsky Pond and Muse (2005); Murrell et al. (2012a, 2013) |
| vertrhod | 38 | 12.815 | 0.183 ± 0.159 | Murrell et al. (2012a, 2013) |
| h3e | 3854 | 5.951 | 0.0005 ± 0.001 | Meyer and Wilke (2015) |
| hivrtf | 383 | 5.642 | 0.007 ± 0.01 | Murrell et al. (2012a) |
Number of taxa.
Vertebrate biogenic amine receptors.
Llama and dromedary partial heavy-chain antibody sequences.
Vertebrate rhodopsin.
Influenza strain H3N2 hemagglutinin.
HIV-1 reverse transcriptase.
inference
For each simulated codon frequency distribution, we computed according to the method outlined in Spielman and Wilke (2015b). For each simulated alignment, we inferred site-specific values with the HyPhy software v2.2 (Kosakovsky Pond et al. 2005), using several approaches: fixed-effects likelihood (FEL) (Kosakovsky Pond and Frost 2005), fast unconstrained Bayesian approximation (FUBAR) (Murrell et al. 2013), and single ancestral counting (SLAC) (Kosakovsky Pond and Frost 2005). We specified the Muse and Gaut (1994) MG94 × HKY85 (Kosakovsky Pond and Frost 2005) rate matrix with F1 × 4 codon frequencies, which has been shown to reduce bias in estimation (Spielman and Wilke 2015b). We provide customized HyPhy batchfiles, which enforce the F1 × 4 codon frequency specification, in the Github repository: https://github.com/sjspielman/dnds_1rate_2rate.
For both FEL and FUBAR, we inferred with both a one-rate model, in which is represented by a single parameter, and a two-rate model, in which and are modeled by separate parameters (Kosakovsky Pond and Frost 2005). For the one-rate FUBAR inferences, we specified 100 grid points to account for the reduced grid dimensionality caused by ignoring variation, and we specified the default 20 × 20 grid for two-rate FUBAR inferences (Murrell et al. 2013). We left all other settings as their default values. Similarly, for SLAC inference, we calculated in two ways. As SLAC enumerates and on a site-specific basis, there exist two ways to calculate site-wise : can be considered site specific, or values can be globally averaged, and this mean can be used to normalize all site-specific estimates. The former calculations effectively correspond to a two-rate model (SLAC2), and the latter calculations correspond to a one-rate model (SLAC1). We conducted all inferences using the true tree along which we simulated each alignment.
As in Kosakovsky Pond and Frost (2005), we excluded all unreliable inferences when correlating inferred and true values. Specifically, we excluded FEL estimates where and the P-value indicating whether the estimate differed significantly from 1 was also equal to 1. Such estimates represent uninformative sites where no mutation has occurred (Meyer et al. 2015). In addition, we excluded SLAC2 estimates if the number of synonymous mutations counted was 0, and hence the resulting was undefined. Finally, we excluded all FEL and FUBAR inferences for which the algorithm did not converge as uninformative.
Statistical analysis
Statistics were conducted in the R statistical programming language. Linear modeling was conducted using the R package lme4 (Bates et al. 2012). We inferred effect magnitudes and significance, which we corrected for multiple testing, using the glht() function in the R package multcomp (Hothorn et al. 2008). In particular, we built mixed-effects linear models in the lme4 package with the general code lmer(X method + (1|replicate) + (1|N:B)), where X is either the Pearson correlation between inferred and true or the root-mean-square deviation (RMSD) of the inferred from the true RMSD is calculated as where is the true parameter value and θ is the estimated value. Note that, for all mixed-effects linear models, we excluded simulations under the branch length condition.
Data availability
All code and results are freely available from the Github repository: https://github.com/sjspielman/dnds_1rate_2rate.
Results
Approach
We simulated fully heterogeneous alignments under the HB98 MutSel model (Halpern and Bruno 1998), using the simulation software Pyvolve (Spielman and Wilke 2015a). Our simulation strategy is described in detail in Materials and Methods. Briefly, MutSel models are parameterized with a nucleotide-level mutation model and a distribution of codon fitness values. All simulations employed the HKY85 mutation model (Hasegawa et al. 1985) with the transition–transversion bias parameter We simulated data under four primary conditions: specifying either equal or unequal nucleotide frequencies in the HKY85 model and specifying no codon bias or codon bias for the codon fitness values. Simulations without codon bias assumed that all synonymous codons had the same fitness, and simulations with codon bias assumed that synonymous codons differed in fitness values. We refer to simulations with equal nucleotide frequencies as and to simulations with unequal nucleotide frequencies as
Each simulated alignment contained 100 sites, and simulations were conducted along balanced phylogenies with the number of sequences N set as 128, 256, 512, 1024, or 2048 and with branch lengths B set as 0.0025, 0.01, 0.04, 0.16, or 0.64. For each of the 25 possible combinations of parameters N and B, we simulated 50 replicate alignments. Importantly, the site-specific evolutionary models were the same within each simulation set, making inferences across N and B conditions directly comparable. We note that the extremely high divergence level in simulations does not represent real sequence data, but these simulations do allow us to study inference method performance under the limiting condition of (approximately) infinite time.
We inferred site-specific for each simulated alignment, using three approaches: FEL (Kosakovsky Pond and Frost 2005), SLAC (Kosakovsky Pond and Frost 2005), and FUBAR (Murrell et al. 2013). Each of these methods employs a somewhat different approach when computing site-specific values. FEL fits a unique model to each alignment site (Kosakovsky Pond and Frost 2005), SLAC directly counts nonsynonymous and synonymous changes along the phylogeny where ancestral states are inferred with maximum likelihood (Kosakovsky Pond and Frost 2005), and FUBAR employs a Bayesian approach to determine ratios according to a prespecified grid of rates (Murrell et al. 2013).
For each inference method, we inferred at each site in both a two-rate context (separate and parameters per site) and a one-rate context (a single parameter per site). Although SLAC, as a counting-based method, always enumerates both and on a per-site basis, one can derive an effectively one-rate SLAC by normalizing each site-wise estimate by the mean of all site-wise estimates. We refer to one-rate inferences with these methods as FEL1, FUBAR1, and SLAC1 and similarly to two-rate inferences as FEL2, FUBAR2, and SLAC2, respectively. Throughout, we use method to refer to distinct algorithmic approaches (FEL, FUBAR, and SLAC), and we use model to refer to a one-rate or a two-rate parameterization. We use either framework or approach to more generally discuss one-rate vs. two rate methods.
We performed all inference using the HyPhy batch language (Kosakovsky Pond et al. 2005). Note that we did not consider the popular random-effects likelihood methods introduced by Yang et al. (2000) (e.g., M3, M5, and M8) because these methods are used predominantly in a one-rate context. Available two-rate extensions to this framework are computationally burdensome and cannot model the amount of rate heterogeneity required to calculate per-site rates (Kosakovsky Pond and Muse 2005). Finally, we computed true values from the MutSel parameters, using the approach described in Spielman and Wilke (2015b).
Modeling synonymous rate variation may reduce inference accuracy
After inferring site-wise for all simulated alignments, we quantified performance for all inference frameworks, using several metrics, primarily the Pearson correlation between true and inferred Importantly, our simulation strategy necessitates a somewhat different interpretation of results than would more traditional simulation approaches. The true ratios calculated from the MutSel parameterizations used during simulation correspond to the expected at steady state, i.e., the signature of natural selection at evolutionary equilibrium. We can expect to recover this true value only if the simulated data reflect the stationarity condition. When either the simulated divergence or the number of sequences analyzed is low, it not necessarily possible to capture the true equilibrium distribution of codons. Therefore, we considered the most accurate inference frameworks as those that produced the highest correlations within a given choice of N and B.
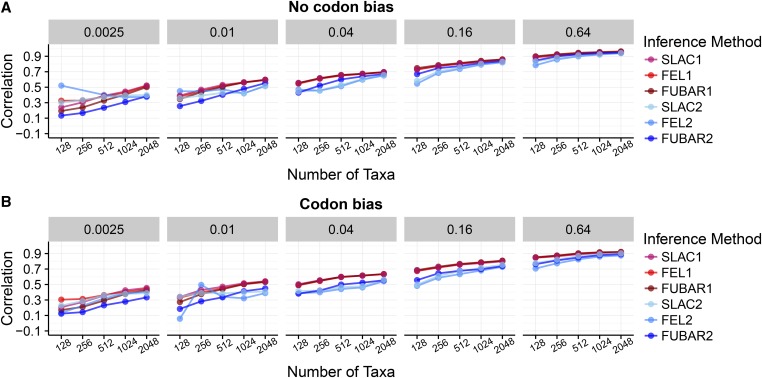
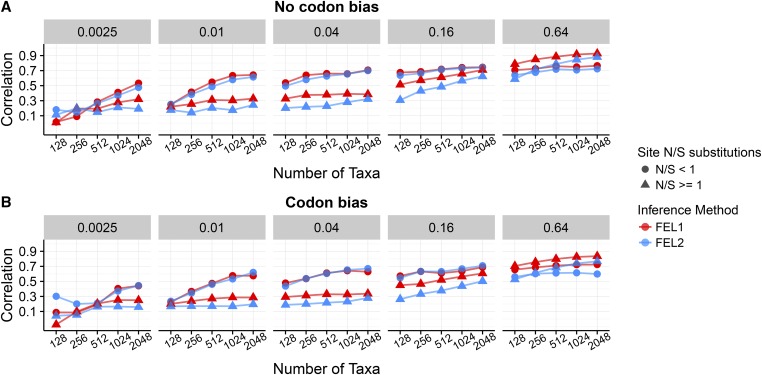
In Figure 1, we show resulting Pearson correlation coefficients, averaged across all 50 replicates, between inferred and true for each inference framework, specifically for simulations. Results for simulations showed virtually identical correlations ( ANOVA; Supplemental Material, Figure S1). In the absence of codon bias, at all sites. As such, we expected that one-rate inference frameworks would outperform two-rate inference frameworks. We indeed found that one-rate inference frameworks showed the highest correlations when there was no synonymous selection (Figure 1A), in particular at low-to-intermediate divergence levels (). As the sequences became more diverged, and hence more informative, two-rate frameworks increasingly performed as well as one-rate frameworks did. Even so, two-rate frameworks almost never outperformed one-rate frameworks.
Figure 1.
Pearson correlation coefficients between true and inferred across inference approaches and N-B conditions, for simulations. (A) Correlations for alignments simulated without codon bias. (B) Correlations for alignments simulated with codon bias. The label above each panel indicates the branch lengths B of the balanced phylogeny along which sequences were simulated, and the x-axes indicate the number of sequences N. Each point represents the correlation coefficient averaged across 50 replicates. Figure S1 shows corresponding simulations. Note that certain FEL2 points (at and for codon bias simulations) are not present because FEL2 generally failed to converge under these conditions.
In the presence of codon bias, both and varied at each site, and therefore we expected that two-rate frameworks would be more well suited for these simulations. Surprisingly, however, one-rate frameworks still outperformed two-rate frameworks across N and B conditions, in spite of the pervasive site-wise variation across sites (Figure 1B and Figure S1). Moreover, correlation differences between one-rate and two-rate frameworks were more pronounced for simulations with codon bias than for simulations without codon bias. In other words, two-rate frameworks performed worse on data simulated with codon bias than they did on data simulated without codon bias.
To complement our correlation analysis, we calculated several additional metrics to quantify accuracy: (i) RMSD of the inferred from the true (Figure S2), (ii) estimator bias for each inference framework (Figure S3), and (iii) variance in residuals for a simple linear model regressing inferred on true (Figure S4). These metrics displayed the same general trends as did correlation analysis: One-rate frameworks were generally more accurate and precise (lower RMSD, lower estimator bias, and lower residual variance) than were two-rate frameworks, and these overarching trends were more pronounced for simulations with codon bias (all ANOVA). As divergence increased, each metric dropped substantially for both one- and two-rate frameworks, with error and/or bias for one-rate frameworks dissipating more quickly than for two-rate frameworks. These patterns were consistent between the and simulations for estimator bias and residual variance (both ANOVA), although displayed marginally smaller RMSD values compared to ( with an average difference of ANOVA). Thus, inference was robust to the presence of nucleotide compositional bias.
Rate parameterization affects estimation more strongly than does inference method
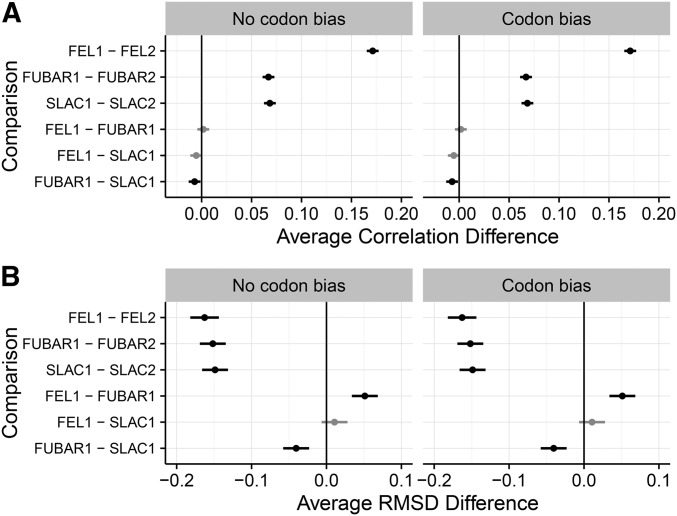
We next quantified performance differences among inference frameworks more rigorously, using linear models. For each simulation set, we built mixed-effects linear models with either Pearson correlation or RMSD as the response, inference approach as a fixed effect, and replicate as well as interaction between N and B as random effects. We performed multiple-comparisons tests, with corrected P-values, to ascertain the relative performances across inference approaches.
Linear model analysis confirmed prior observations that each one-rate method significantly outperformed its respective two-rate counterpart (Figure 2 for simulations and Figure S5 for simulations). In addition, correlations differences among one-rate methods were not statistically significant for any inferences performed on simulations (Figure 2A). For simulations, SLAC1 yielded significantly higher correlations than did FUBAR1, although the effect magnitude size was minimal, with a mean difference of (Figure S5A).
Figure 2.
Pairwise comparisons of correlation strength, RMSD, and variance in residual across methods, determined through multiple-comparisons tests, for simulations. (A) Results for multiple-comparison tests of correlation strength. (B) Results for multiple-comparison tests of RMSD. Points indicate the estimated average difference between measurements for the respective inference approaches, and lines indicate 95% confidence intervals. Solid lines indicate that the performance difference between methods differed significantly from 0 (all ). Shaded lines indicate that the difference was not statically significant (). All P-values were corrected for multiple testing. Corresponding multiple-comparison results for simulations are in Figure S5.
For both and simulations, that one-rate methods yielded less error in point estimates than did two-rate methods (Figure 2B and Figure S5B). Unlike results from linear models with correlation as the response, however, RMSD analysis showed some more substantial differences among one-rate methods. Overall, SLAC1 and FEL1 performed comparably, but FUBAR1 showed lower RMSD than both SLAC1 and FEL1, albeit with a very small effect magnitude. This result persisted across all simulation conditions. Together, these findings suggest the number of parameters used to model mattered more than did the specific inference method chosen.
We next examined whether linear modeling results, specifically those comparing correlation strength between methods, were driven by particular simulation conditions. We directly compared correlations between one-rate and two-rate inferences, for each method (FEL, SLAC, and FUBAR) across N and B conditions, specifically for simulations. These comparisons indicated that improvement of one-rate over two-rate parameterizations was largely driven by results for intermediate divergence levels (Figure S6). For example, under FEL inference, the greatest improvement of FEL1 over FEL2 occurred where and
Data contain insufficient information for precise site-wise estimation
We next sought to determine why one-rate frameworks outperformed two-rate frameworks. Given the broad similarity among inference methods and simulation sets, we considered only FEL inferences on simulations for these analyses.
To begin, we confirmed that simulations with codon bias indeed led to variation in the data by comparing distributions of inferred with FEL2, between simulations with and without codon bias. If our implementation of codon bias indeed produced variation, the inferred distributions from codon bias simulations should contain more variation compared to the inferred distributions for simulations without codon bias, whose inferences should be concentrated at Indeed, distributions for codon bias simulations displayed substantially more variation than did distributions for simulations without codon bias (Figure S7).
We next compared the optimized branch lengths inferred by HyPhy during rate estimation to those used for simulation. Because branch length parameters influence estimation, it is possible that biases in these parameters could influence the resulting rate inferences. Importantly, we should not expect branch lengths used for a MutSel simulation to match precisely those optimized under a -based model, due to differences in model assumptions, although branch lengths should be consistently inferred across simulation conditions. Across simulations, we found no significant difference among distributions of optimized branch lengths, for a given set of simulations using the same branch length B (Figure S8). Therefore, differences in branch length optimization did not seem to affect inferences.
We proceeded to compare directly the inferred values across simulation conditions, for a single representative replicate (Figure S9, A and B). The relationship between one-rate and two-rate estimates featured considerable noise, across all simulation conditions. To determine the source of this noise, we confirmed that estimates between one-rate and two-rate models were comparable. We examined individual estimates between FEL1 and FEL2, again for a single replicate. Aside from low-information conditions (e.g., and/or ), estimates were virtually identical between FEL1 and FEL2, for simulations both with and without codon bias (Figure S9, C and D). This result demonstrated that the added parameter in two-rate inference methods did not affect estimation, but rather it contributed substantial noise to the final estimate.
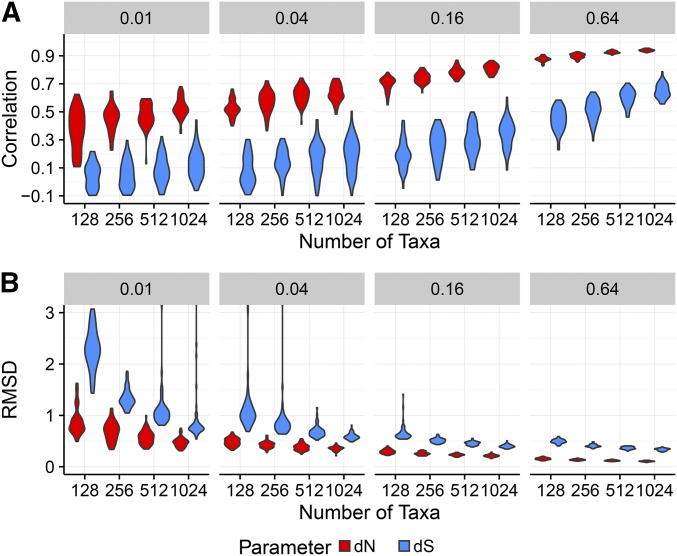
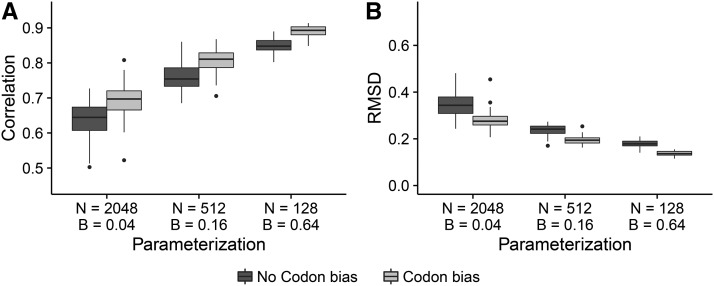
Finally, we assessed how well FEL2 estimated relative to specifically for simulations with codon bias, in which variation exists. We found that FEL2 consistently estimated more precisely than measured using both correlations and RMSD (Figure 3). Although accuracy for both and estimation increased as either B or N increased, estimates universally displayed higher correlations and lower RMSD than did estimates. As such, it appeared that was simply statistically more difficult to estimate than was
Figure 3.
estimates are more precise than are estimates. Results are shown for a subset of conditions for simulations with codon bias, inferred with FEL2. (A) Violin plots of Pearson correlations between inferred and true and values. (B) Violin plots of RMSD of inferred from true and values. Outlying points beyond the y-axis ranges have been removed for visualization.
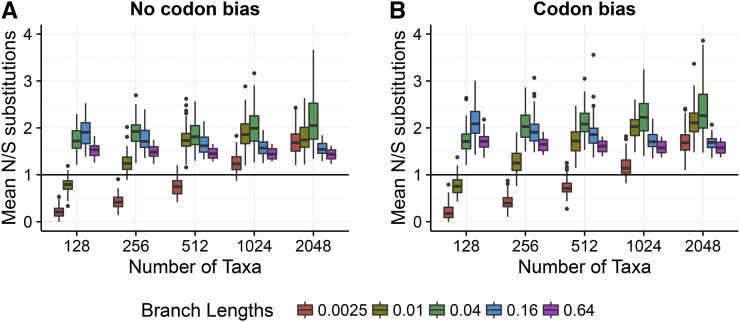
We hypothesized that this result was a direct consequence of the relative amount of information in the alignments for nonsynonymous vs. synonymous changes. Using the simulated ancestral sequences within each simulated alignment, we directly counted the number of nonsynonymous and synonymous changes that had occurred across the phylogeny. We observed that nonsynonymous changes occurred roughly twice as frequently over the course of a simulation than did synonymous changes (Figure 4). This result was fully compatible with the notion that statistical estimation of was more challenging than that of because of sample size: Alignments contained nearly double the amount of information contributing to than to As a consequence, estimation was less precise and noisier across simulation conditions, ultimately explaining why two-rate frameworks yielded less precise estimates compared to one-rate frameworks.
Figure 4.
Ratio of the number of nonsynonymous to synonymous changes that occurred during simulations, counted directly from simulated ancestral sequences. Each boxplot represents, across 50 replicates, the per-alignment ratio of the number of nonsynonymous changes to synonymous changes averaged across sites. Results shown here are from simulations.
One-rate frameworks outperform two-rate frameworks primarily at weakly constrained sites
All previous analyses compared inferences across alignment replicates. Yet each alignment featured an array of selective constraints, with each site evolving with a different underlying Whether the heterogeneous selective constraints across sites influenced our previous results was not immediately clear. For example, according to the structure of the genetic code, 74% of all possible single-nucleotide changes are nonsynonymous, and the remaining 26% are synonymous. Therefore, a neutrally evolving site, where both nonsynonymous and synonymous changes are equally likely to go to fixation, should experience approximately three times more nonsynonymous than synonymous substitutions. By contrast, sites under stringent selection pressure will tolerate few amino acids, and thus these sites may feature more synonymous than nonsynonymous changes. Noting this distinction, we next examined whether one-rate or two-rate frameworks performed differently, depending on a given site’s evolutionary constraint.
We therefore reanalyzed our simulations, specifically under FEL1 and FEL2 inference, while considering sites to be in one of two categories: having a relative enrichment for synonymous substitutions or having a relative enrichment for nonsynonymous substitutions (Figure 5). Across simulation conditions, FEL1 and FEL2 models yielded virtually identical correlations at sites enriched for synonymous substitutions (linear model, ). By contrast, FEL1 consistently outperformed FEL2 when sites contained more nonsynonymous than synonymous substitutions, with an average correlation increase of (linear model, ). The condition did not adhere to this general pattern and consistently favored one-rate frameworks, likely due to difficulty in estimating due to mutational saturation at such high divergences. Together, these results show that one-rate frameworks offered the most improvement, relative to two-rate frameworks, when sites had experienced more nonsynonymous changes. On the other hand, when the data were enriched for synonymous changes, one-rate and two-rate frameworks provided comparable estimates.
Figure 5.
Mean Pearson correlations between inferred and true specifically for simulations analyzed with FEL1 and FEL2. Sites that have experienced relatively more synonymous changes are represented with circles, and sites that have experienced relatively more nonsynonymous changes are represented with triangles.
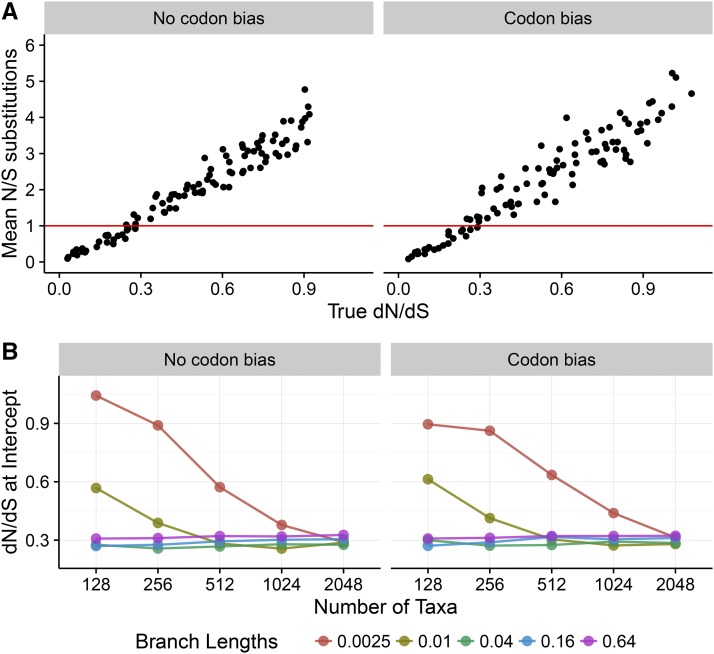
To ascertain more broadly at which sites a one-rate inference framework may be preferred, we examined the relationship between substitution counts and true across simulations (Figure 6). Figure 6A shows the relationship between true and the mean ratio of nonsynonymous to synonymous substitution counts, along the simulated phylogeny, specifically for and In Figure 6A, points below the line represent sites with, on average, a relative enrichment for synonymous compared to nonsynonymous changes, and similarly points above the line represent sites with an average enrichment for nonsynonymous compared to synonymous changes. We found that sites under stronger selective constraint indeed featured relatively more nonsynonymous changes, and sites under weaker constraint featured relatively more synonymous changes.
Figure 6.
Relationship between true and the ratio of the number of nonsynonymous to synonymous changes that occurred during simulations, counted directly from simulated ancestral sequences. Results are shown for simulations. (A) Regression of the ratio of nonsynonymous to synonymous substitution counts specifically for the and simulation. (B) True across simulation conditions, where sites transition from being enriched for synonymous changes to being enriched for nonsynonymous changes.
To generalize across all simulation conditions, we calculated the true where, on average, sites transitioned from having more synonymous to more nonsynonymous changes (Figure 6B). In general, sites became enriched for nonsynonymous substitutions at However, the transition point was substantially larger for simulation conditions with low levels of divergence, likely because substitutions did not have sufficient time to accumulate. Taken together, these results reveal that one-rate frameworks may offer the most improvement over two-rate frameworks when i.e., when sites are under moderate-to-weak purifying selection. By contrast, one-rate and two-rate frameworks showed minimal, if any, differences when applied to sites subject to strong purifying selection ().
Divergence is more important than is the number of sequences for identifying long-term evolutionary constraint
We additionally observed that inference accuracy increased as both the number of sequences N and the branch lengths B (divergence) grew (Figure 1, Figure S1, Figure S2, Figure S3, and Figure S4), suggesting that large and/or highly informative data sets are necessary for the inferred to capture the actions of natural selection at evolutionary equilibrium. However, it was not immediately clear whether N, B, or some combination of these conditions drove this trend. Therefore, we next assessed the relative importance of N and B on estimating the equilibrium rate ratio.
We calculated the tree length for each N and B parameterization, specifically for simulations. Note that, in the context of our mutation–selection simulations, the tree length indicates the expected number of substitutions per site across the entire tree, relative to the number of neutral substitutions (Tamuri et al. 2012; Spielman and Wilke 2015a). If N and B served roughly equal roles in terms of providing information, then any combination of N and B corresponding to the same tree length should have produced similar correlations. We did not, however, observe this trend; instead, all else being equal, B had a significantly greater influence than did N on the resulting correlations. For example, as shown in Figure 7, we compared correlations and RMSD from FEL1 for three combinations of N and B conditions that all yielded virtually the same tree lengths (162–164). Simulations with lower N and higher B resulted in far more accurate estimates, even though all simulations in Figure 7 experienced the same average number of substitutions. This increase was highly significant; for data simulated without codon bias, correlations increased an average of ∼28%, from to , and similarly RMSD decreased an average of ∼50% (both linear model). For data simulated with codon bias, correlations increased an average of ∼33%, from to and RMSD decreased an average of ∼52% (both linear model). Therefore, the relative importance of divergence over number of taxa held for simulations with and without codon bias alike.
Figure 7.
The amount of divergence is more important than the number of sequences for obtaining the equilibrium value. Boxplots represent either (A) correlation or (B) RMSD across the 50 respective simulation replicates. Results shown correspond to simulations inferred with FEL1. From left to right, tree lengths are 163.76, 163.52, and 162.56.
Simulations along empirical phylogenies recapitulate observed trends
While the balanced-tree simulations described above provided a useful framework for examining overarching patterns in inference-framework behaviors, they did not necessarily reflect the properties of empirical data sets. We therefore assessed how applicable our results were to real data analysis by simulating an additional set of alignments along five empirical phylogenies (Table 1). Importantly, we considered the original empirical branch lengths for this analysis, so these phylogenies featured a range of number of taxa and divergence levels representative of empirical studies. We simulated alignments using the MutSel parameterizations, with both no codon bias and codon bias. We simulated 50 replicate alignments for each phylogeny and parameterization, and for efficiency we inferred using only FUBAR1 and FUBAR2.
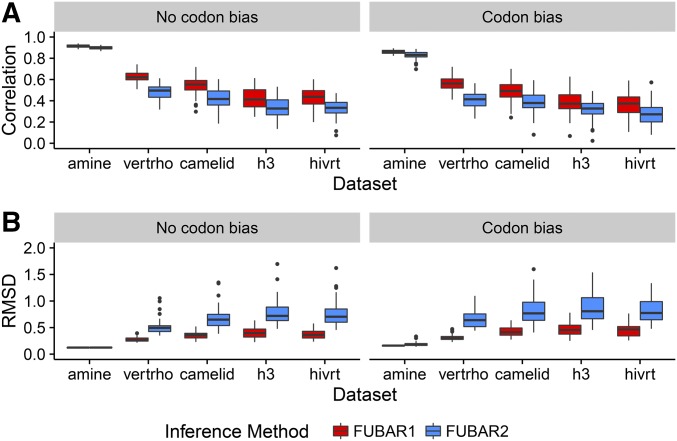
We identified the same general trends in these empirical simulations as we observed for simulations along balanced trees: FUBAR1 estimated more precisely than did FUBAR2, and phylogenies with higher divergence levels yielded more accurate estimates (Figure 8). Furthermore, FUBAR2 estimated more accurately than (Figure S10), again reflecting the relative difficulty in estimating compared to Importantly, most empirical phylogenies showed mean correlations with true of with the key exception of the biogenic amine receptor phylogeny (“amine”), whose extremely high number of taxa and divergence yield exceptionally high correlations with both FUBAR1 and FUBAR2. Therefore, we found that under more realistic conditions, estimated will correlate with the equilibrium ratio with only moderate strength.
Figure 8.
Inference results for simulations performed along empirical phylogenies (Table 1). (A) Pearson correlations between inferred and true values. (B) RMSD of inferred from true values.
In addition, results for simulations along the empirical phylogenies supported our findings regarding the relative importance of divergence vs. number of taxa, in particular through the juxtaposition of results for camelid and vertebrate rhodopsin (“vertrho”) simulations. These phylogenies showed similar tree lengths, but the camelid tree length was driven by the number of sequences, and the vertebrate rhodopsin tree length was driven by its larger branch lengths (Table 1). Correlations and RMSD revealed a far higher inference accuracy for the vertebrate rhodopsin simulations than for the camelid simulations. On average, vertebrate rhodopsin correlations were 0.08 higher than were camelid correlations, and vertebrate rhodopsin RMSD was 0.1 lower than was camelid RMSD (both linear model). These metrics were consistent between simulations with and without codon bias (both linear model test for interaction effect of presence of codon bias). Therefore, even for data simulated along empirical phylogenies, sequence divergence proved more important than did the number of taxa for accurately estimating the equilibrium rate ratio.
Discussion
In this study, we have examined the relative accuracy of one-rate and two-rate site-specific inference approaches. Importantly, we performed these analyses in the specific context of point estimation in the presence of model misspecification. We have found that one-rate inference models usually yielded more accurate inferences than did two-rate models, across a variety of inference algorithms. More specifically, we provide evidence that one-rate models may improve upon two-rate models predominantly for sites subject to moderate-to-weak purifying selection. By contrast, one-rate and two-rate models infer point estimates with comparable accuracy when sites are under stronger purifying selection. These results hold for sequences both without codon bias (synonymous codons are equally fit) and with codon bias (synonymous codons differ in fitness), suggesting that two-rate models are not necessarily more reliable than are one-rate models even when variation exists. We attribute these results to the relative amounts of information present in the data used for estimating and parameters. When relatively more information is available to estimate the parameter becomes overly influenced by noise and hence reduces accuracy in estimates.
Our study provides novel insight into how inference frameworks behave specifically when they are misspecified to the data. Indeed, real genomes do not evolve according to a model, and thus virtually all applications of models will be misspecified to some degree. Although it is certainly true that mutation–selection models also do not precisely capture real sequence evolution, this simulation framework provides a starting place to uncover model properties and limitations in an explicitly misspecified context.
We have demonstrated that two-rate frameworks do not necessarily accomplish their intended goal of modeling synonymous rate variation. Logically, one would presume that, when differs among sites, estimating separately across sites would produce more accurate estimates than would fixing to a constant value. Indeed, an assumed presence of synonymous substitution-rate variation is the very justification for using a two-rate model (Kosakovsky Pond and Muse 2005). However, if the data do not contain sufficient information for inferring then two-rate parameterizations may suffer from excessive amounts of noise, and hence in certain circumstances, one-rate models may be preferable.
Our use of MutSel models for simulations raises several important caveats that directly affect how to interpret our results. As described, our results are contingent on the fact that our simulation model did not match our inference model, and hence the inference model was mathematically misspecified. In other words, we ask how -based models perform in estimating a parameter that the MutSel model does not explicitly contain, although it can be calculated from the MutSel parameters. As a consequence, certain biases arise during inference. For example, comparable performance of SLAC, an approximate counting-based method, with FEL and FUBAR, both of which employ more rigorous statistical procedures, may be directly attributed to model misspecification. Indeed, previous studies using data simulated under the inference model have suggested that SLAC may be a biased estimator when correctly specified, particularly at high divergences (Kosakovsky Pond and Frost 2005). Therefore, it is certainly possible that a two-rate framework would outperform a one-rate framework if the model were correctly specified. Indeed, previous studies have shown that two-rate models perform well for data simulated with explicit and constant parameters (Kosakovsky Pond and Frost 2005; Kosakovsky Pond and Muse 2005; Murrell et al. 2012b, 2013).
Second, the substitution process under a MutSel models is not necessarily temporally homogeneous, whereas in -based models, substitutions are Poisson distributed over time. As a consequence, sequence divergence will have a strong effect on inference accuracy for data generated in a MutSel framework. Indeed, can be calculated only based on the substitutions that have occurred in the sequence data examined. If, for example, sequences were not highly diverged, then estimates will be biased based on which substitutions have had an opportunity to occur. Conversely, for data simulated under a framework, which particular substitutions had a chance to occur will matter far less, as all nonsynonymous changes occur at the same rate. Because the temporal inhomogeneity of the MutSel process does not match the corresponding homogeneity of the -based model process, our observed correlations between inferred and true (Figure 1) were generally lower than they would have been if sequences were simulated with a -based model.
Third, because MutSel models can correspond only to sites evolving under an evolutionary equilibrium [i.e., under either purifying selection or neutral evolution where (Spielman and Wilke 2015b)], our results do not immediately apply to contexts where sequences do not evolve under equilibrium or for the specific application of positive-selection inference (). For example, inference is perhaps most commonly used to study sequences evolving along a changing fitness landscape, as would be the case for viral and/or pathogen evolution (Delport et al. 2008; Murrell et al. 2012a; Demogines et al. 2013; Meyer et al. 2015; Meyer and Wilke 2015) By contrast, the MutSel model used here assumes that the fitness landscape is static across the phylogeny. As such, our results may or may not have any bearing on parameterizations used for positive-selection inference.
Finally, our codon bias simulations assumed that variation was driven by selection on synonymous codons. In other circumstances, synonymous rate variation might emerge when a given gene contains mutational hotspots, e.g., regions with a strongly elevated nucleotide mutation rate. In such circumstances, it is possible that a two-rate model would outperform a one-rate model if the variation in mutational processes were sufficiently large (Kosakovsky Pond and Frost 2005).
Our results build on the well-documented time dependency of the metric, a phenomenon studied primarily in the context of polymorphic data (Rocha et al. 2006; Kryazhimskiy and Plotkin 2008; Wolf et al. 2009; Mugal et al. 2014; Meyer et al. 2015). Our results extend these findings and indicate that this time dependency is more general and pertains also to circumstances where the data contain only fixed differences. This finding makes intuitive sense: As divergence increases, sites will be more likely to visit the full range of selectively tolerated states, at which time the long-term evolutionary constraints will become apparent. It is therefore likely that most measurements will be biased by time to some degree, even if all differences are fixed and not polymorphic. Our results suggest that this bias can be ameliorated by focusing data set collection to include fewer, more divergent sequences rather than as many sequences as one can obtain. Increasing the number of taxa in a given analysis may be beneficial only if the new sequences are substantially diverged from the existing sequences. These findings should also inform studies that seek to relate site-specific protein evolutionary rate (i.e., ) to structural properties, such as relative-solvent accessibility or weighted contact number (Echave et al. 2016). Our findings predict that more diverged data sets should provide more meaningful information about long-term evolutionary constraints, which structural quantities reflect.
Acknowledgments
Computational resources were provided by the University of Texas at Austin’s Center for Computational Biology and Bioinformatics and the Stampede cluster at the Texas Advanced Computing Center. We thank Julian Echave for insightful discussion and helpful feedback. This work was supported in part by National Institutes of Health (NIH) grant F31 GM113622-01 (to S.J.S.), NIH grant R01 GM088344 (to C.O.W.), Army Research Office grant W911NF-12-1-0390 (to C.O.W.), Defense Threat Reduction Agency grant HDTRA1-12-C-0007 (to C.O.W.), and National Science Foundation Cooperative Agreement no. DBI-0939454 (BEACON Center) (to C.O.W.).
Footnotes
Communicating editor: E. A. Stone
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.185264/-/DC1.
Literature Cited
- Bates, D., M. Maechler, and B. Bolker, 2012 lme4: Linear Mixed-Effects Models Using S4 Classes (R package version 0.999999-0).
- Delport W., Scheffler K., Seoighe C., 2008. Frequent toggling between alternative amino acids is driven by selection in HIV-1. PLoS Pathog. 4: e1000242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demogines A., Abraham J., Choe H., Farzan M., Sawyer S. L., 2013. Dual host-virus arms races shape an essential housekeeping protein. PLoS Biol. 11: e1001571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- dos Reis M., 2015. How to calculate the non-synonymous to synonymous rate ratio of protein-coding genes under the Fisher-Wright mutation-selection framework. Biol. Lett. 11: 20141031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echave J., Spielman S. J., Wilke C. O., 2016. Causes of evolutionary rate variation among protein sites. Nat. Rev. Genet. 17: 109–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman N., Yang Z., 1994. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 11: 725–736. [DOI] [PubMed] [Google Scholar]
- Halpern A. L., Bruno W. J., 1998. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol. Biol. Evol. 15: 910–917. [DOI] [PubMed] [Google Scholar]
- Hasegawa M., Kishino H., Yano T., 1985. Dating the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22: 160–174. [DOI] [PubMed] [Google Scholar]
- Holder M., Zwickl D., Dessimoz C., 2008. Evaluating the robustness of phylogenetic methods to among-site variability in substitution processes. Philos. Trans. R. Soc. B 363: 4013–4021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hothorn T., Bretz F., Westfall P., 2008. Simultaneous inference in general parametric models. Biom. J. 50: 346–363. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Frost S. W. D., 2005. Not so different after all: a comparison of methods for detecting amino acid sites under selection. Mol. Biol. Evol. 22: 1208–1222. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Muse S. V., 2005. Site-to-site variation of synonymous substitution rates. Mol. Biol. Evol. 22: 2375–2385. [DOI] [PubMed] [Google Scholar]
- Kosakovsky Pond S. L., Frost S. W. D., Muse S. V., 2005. HyPhy: hypothesis testing using phylogenetics. Bioinformatics 21: 676–679. [DOI] [PubMed] [Google Scholar]
- Kryazhimskiy S., Plotkin J. B., 2008. The population genetics of dN/dS. PLoS Genet. 4: e1000304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Minin V. N., Bielejec F., Kosakovsky Pond S. L., Suchard M. A., 2012. A counting renaissance: combining stochastic mapping and empirical Bayes to quickly detect amino acid sites under positive selection. Bioinformatics 28: 3248–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberles D. A., Teufel A., Liu L., Stadler T., 2013. On the need for mechanistic models in computational genomics and metagenomics. Genome Biol. Evol. 5: 2008–2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCandlish D. M., Rajon E., Shah P., Ding Y., Plotkin J. B., 2013. The role of epistasis in protein evolution. Nature 497: E1–E2. [DOI] [PubMed] [Google Scholar]
- Meyer A. G., Wilke C. O., 2015. Geometric constraints dominate the antigenic evolution of influenza H3N2 hemagglutinin. PLoS Pathog. 11: e1004940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer A. G., Spielman S. J., Bedford T., Wilke C. O., 2015. Time dependence of evolutionary metrics during the 2009 pandemic influenza virus outbreak. Virus Evol. 1: vev006–vev010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mugal C. F., Wolf J. B. W., Kaj I., 2014. Why time matters: codon evolution and the temporal dynamics of dN/dS. Mol. Biol. Evol. 31: 212–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell B., de Oliveira T., Seebregts C., Kosakovsky Pond S. L., Scheffler K. et al, 2012a Modeling HIV-1 drug resistance as episodic directional selection. PLoS Comput. Biol. 8: e1002507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell B., Wertheim J. O., Moola S., Weighill T., Scheffler K., et al. , 2012b Detecting individual sites subject to episodic diversifying selection. PLoS Genet. 8: e1002764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell B., Moola S., Mabona A., Weighill T., Scheward D., et al. , 2013. FUBAR: a Fast, Unconstrained Bayesian AppRoximation for inferring selection. Mol. Biol. Evol. 30: 1196–1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muse S. V., Gaut B. S., 1994. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol. Biol. Evol. 11: 715–724. [DOI] [PubMed] [Google Scholar]
- Nielsen R., Yang Z., 1998. Likelihood models for detecting positive selected amino acid sites and applications to the HIV-1 envelope gene. Genetics 148: 929–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porto M., Roman H. E., Vendruscolo M., Bastolla U., 2004. Prediction of site-specific amino acid distributions and limits of divergent evolutionary changes in protein sequences. Mol. Biol. Evol. 22: 630–638. [DOI] [PubMed] [Google Scholar]
- Ramsey D. C., Scherrer M. P., Zhou T., Wilke C. O., 2011. The relationship between relative solvent accessibility and evolutionary rate in protein evolution. Genetics 188: 479–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocha E. P. C., Maynard Smith J., Hurst L. D., Holden M. T. G., Cooper J. E., et al. , 2006. Comparisons of dN/dS are time dependent for closely related bacterial genomes. J. Theor. Biol. 239: 226–235. [DOI] [PubMed] [Google Scholar]
- Rodrigue N., Philippe H., Lartillot N., 2010. Mutation-selection models of coding sequence evolution with site-heterogeneous amino acid fitness profiles. Proc. Natl. Acad. Sci. USA 107: 4629–4634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella G., Hirsh A. E., 2005. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA 102: 9541–9546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spielman S. J., Wilke C. O., 2015a Pyvolve: a flexible python module for simulating sequences along phylogenies. PLoS One 10: e0139047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spielman S. J., Wilke C. O., 2015b The relationship between and scaled selection coefficients. Mol. Biol. Evol. 32: 1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spielman S. J., Kumar K., Wilke C. O., 2015. Comprehensive, structurally-informed alignment and phylogeny of vertebrate biogenic amine receptors. PeerJ 3: e773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamuri A. U., dos Reis M., Goldstein R. A., 2012. Estimating the distribution of selection coefficients from phylogenetic data using sitewise mutation-selection models. Genetics 190: 1101–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne J. L., Choi S. C., Yu J., Higgs P. G., Kishino H., 2007. Population genetics without intraspecific data. Mol. Biol. Evol. 24: 1667–1677. [DOI] [PubMed] [Google Scholar]
- Thorne J. L., Lartillot N., Rodrigue N., Choi S. C., 2012. Codon models as vehicles for reconciling population genetics with inter-specific data, pp. 97–110 in Codon Evolution: Mechanisms and Models, edited by Cannarozzi G., Schneider A. Oxford University Press, New York. [Google Scholar]
- White H., 1982. Maximum likelihood estimation of misspecified models. Econometrica 50: 1–25. [Google Scholar]
- Wolf J. B. W., Kunstner A., Nam K., Jakobsson M., Ellegren H., 2009. Nonlinear dynamics of nonsynonymous and synonymous substitution rates affects inference of selection. Genome Biol. Evol. 1: 308–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, Z., 2006 Computational Molecular Evolution. Oxford University Press, London/New York/Oxford. [Google Scholar]
- Yang Z., Nielsen R., 2002. Codon-substitution models for detecting molecular adaptation at individual sites along specific lineages. Mol. Biol. Evol. 19: 908–917. [DOI] [PubMed] [Google Scholar]
- Yang Z., Nielsen R., 2008. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol. Biol. Evol. 25: 568–579. [DOI] [PubMed] [Google Scholar]
- Yang Z., Swanson W. J., 2002. Codon-substitution models to detect adaptive evolution that account for heterogeneous selective pressures among site classes. Mol. Biol. Evol. 19: 49–57. [DOI] [PubMed] [Google Scholar]
- Yang Z., Wong W. S. W., Nielsen R., 2005. Bayes Empirical Bayes inference of amino acid sites under positive selection. Mol. Biol. Evol. 22: 1107–1118. [DOI] [PubMed] [Google Scholar]
- Yang Z. H., Nielsen R., Goldman N., Pedersen A. M. K., 2000. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics 155: 431–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All code and results are freely available from the Github repository: https://github.com/sjspielman/dnds_1rate_2rate.