Ultrashort Echo Time Magnetization Transfer (UTE-MT) Imaging and Modeling: Magic Angle Independent Biomarkers of Tissue Properties

Abstract

Magnetic resonance (MR) imaging biomarkers such as T₂, T₂* and T_1rho have been widely used, but are confounded by the magic angle effect. The purpose of this study is to investigate the use of the two-dimensional ultrashort echo time magnetization transfer (UTE-MT) sequence for potential magic angle independent MR biomarkers. Magnetization transfer was investigated in cadaveric Achilles tendon samples using the UTE-MT sequence at five MT powers and five frequency offsets ranging from 2–50 kHz. The protocol was applied at 5 sample orientations ranging from 0–90° relative to the B₀ field. The results were analyzed with a two-pool quantitative MT model. Multiple TE data was also acquired and mono-exponential T₂* was calculated for each orientation. Macromolecular proton fractions and exchange rates derived from UTE-MT modeling did not appreciably change between the various orientations whereas the T₂* relaxation time demonstrated up to a 6-fold increase from 0° to 55°. The UTE-MT technique with two-pool modeling shows promise as a clinically compatible technique that is resistant to the magic angle effect. This method provides information on the macromolecular proton pool that cannot be directly obtained by other methods, including regular UTE techniques.

Graphical abstract

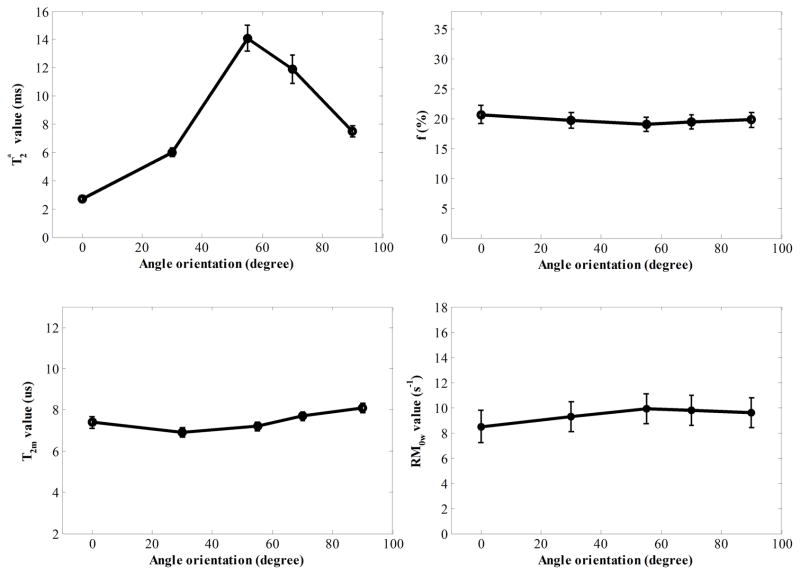
Graphes of T₂* values derived by fitting multiple-TE data and macromolecular proton fractions (f), T₂ value of macromolecular proton (T_2m) and exchange rate from macromolecular proton to water proton (RM_0w) derived from two-pool MT modeling with five angle orientations between fiber direction F⃗ and B⃗₀. Fitting errors of these parameters were shown by error bars.

Introduction

Over the past several decades, extensive research has been performed on the use of magnetic resonance (MR) imaging biomarkers for the evaluation of musculoskeletal tissue integrity, particularly focused on early osteoarthritis (1). T₂ and T₂* are among the most widely studied and both have been linked to alterations in the macromolecular structure of cartilage. Although nearly all commercial vendors now have standard packages that include measurements of transverse relaxation times, their routine clinical use remains limited. This is largely due to the uncertainty in the interpretation of values generated with these quantitative techniques, and a principal confounding factor is the so-called magic angle effect.

The magic angle effect is caused by changes in dipole-dipole interactions, which are minimized when tissue fiber orientation approaches 54.7° relative to the main magnetic field (2). The large orientational dependence of T₂ relaxation time in anisotropic, collagen-rich tissues has been known for more than half a century (2,3). With regards to hyaline articular cartilage, the magic angle effect is pronounced in the regions of greatest anisotropy, such as the superficial layer. For instance, studies have shown that both the T₂ and T₂* values of the superficial layer of femoral condyle cartilage obtained on clinical systems can vary by nearly 10 ms depending on the sampled location in young, asymptomatic adult volunteers (4,5). Considering that the values in these studies for the superficial layer ranged from ~45–55 ms for T₂ and ~20–50 ms for T₂*, these spatial variations account for a significant proportion of the total measurement (4,5). Furthermore, when the amount of variability in these reference values are compared with those obtained from histologically evaluated cartilage specimens, where mean differences in T₂ and T₂* of normal versus degenerated cartilage specimens also ranges from ~5–10 ms (6), it is clear that the magic angle effects rival the expected relaxation changes related to biochemical alteration and tissue compromise. In fact, previous authors have estimated that approximately 60% of the depth-wise variation of T₂ in human cartilage is accounted for by changes in collagen anisotropy (7). Studies that have investigated T_1rho using traditional, continuous wave spin-lock pulses in cartilage have found similar results, whereby dipolar interaction is the dominant relaxation mechanism and therefore measurements are exquisitely sensitive to the magic angle effect (8).

Magnetization transfer (MT) imaging is an indirect technique that has been used to provide information on proton pools with extremely fast transverse relaxation (9). In a two-pool MT model, contrast is based on interactions between macromolecular and water protons. Specifically, saturation pulses transmitted at a radiofrequency off the main water proton frequency will preferentially affect the macromolecular proton pool. The saturated macromolecular protons will subsequently transfer magnetization to the water proton pool and imaging of the decreased water proton signal will provide information on these interactions when compared with an unsaturated image. MT measures have shown promise as MR biomarkers in longer T2 structures such as cartilage, including sensitivity to changes in macromolecules (10). MT has also been shown to have much less orientational dependence compared with T₂ relaxation measurements (11). While MT can be used to indirectly study macromolecular proton pools, conventional acquisition methods are limited with regards to acquiring adequate signal from tissues with short mean transverse relaxation times.

In recent years, ultrashort echo time (UTE) sequences have been used to study tissues or tissue components with short transverse relaxation times, which result in little or no signal when imaged using conventional MR sequences. Tendon is one such tissue, where the highly anisotropic structure of collagen and relatively low hydration results in short mean transverse relaxation times. The magic angle effect has a proportionally larger impact on these highly anisotropic tissues and authors have shown a 37-fold increase in T₂, 10-fold increase in UTE-T₂*, and 7-fold increase in UTE-T_1rho with tendon specimen orientation from 0° to 55° relative to the main magnetic field (12–15). Use of the UTE sequence shows promise in that it allows for signal detection and quantification of otherwise “invisible” tendon when imaged using clinical MR sequences (16). However, the need for the development and validation of less magic angle dependent MR biomarkers for short T₂ tissues is clear. The purpose of our study is to investigate the use of the two-dimensional UTE magnetization transfer (UTE-MT) sequence with two-pool modeling for the potential magic angle independent assessment of tissue properties.

Materials and methods

Sample Preparation and Imaging Parameters

Human Achilles tendon samples dissected from four fresh cadaveric ankle specimens were harvested for this study. Data were acquired with a 2D UTE-MT sequence on a clinical 3T Signa TwinSpeed scanner (GE Healthcare Technologies, Milwaukee, WI) with a maximum gradient strength of 40 mT/m and a maximum slew rate of 150 mT/m/ms. A home-built birdcage coil (~2 cm in diameter) was used for signal excitation and reception. The UTE-MT sequence employed a short non-selective hard pulse (duration = 16μs) excitation followed by 2D radial ramp sampling with a minimal nominal TE of 8μs. The MT preparation is consisted of a Fermi shaped radiofrequency (RF) pulse (duration = 8 ms, bandwidth is 160Hz) followed by a gradient crusher. The area ratio of the MT pulse to a rectangular pulse with the same duration and peak amplitude is 0.59. The UTE-MT imaging protocol included: TR = 50 ms, TE = 8 μs, Flip angle = 5°, FOV = 5 × 5 cm², matrix = 256 × 256; one MT pulse per TR, five MT powers (300°, 600°, 900°, 1200° and 1500°) and five MT frequency offsets (2, 5, 10, 20 and 50 kHz), with a total of 25 different MT datasets and the total scan time was 17.5min. The peak B₁ value of MT pulse in 1500° is 20.7uT. The same protocol was applied to each tendon sample five times, with the sample oriented 0°, 30°, 55°, 70° and 90° relative to the B₀ field. Multiple TE data was also acquired with these five angle orientations for mono-exponential fitting to determine T₂* value of the water component. The protocol for multiple-TE data acquisition was identical with the UTE-MT protocol except that a non-MT pulse was used and TEs were 0.008, 2, 4, 8, 12, 16, 20 ms with a total scan time of 4.9min.

Pre-measurement of T₁ values is necessary for MT modeling. A multiple-TR UTE protocol was employed for T₁ measurement, whose sequence parameters were the same with the MT modeling protocol except that a no MT pulse was used, image flip angle = 25°, and TRs were 25, 50, 100, 200, 400, 600 ms. The total scan time for T₁ measurement was 9.2min. Previous work has shown that T₁ is resistant to the magic angle effect (11), and therefore the multiple-TR sequence was only performed with angle orientation = 55° for each sample. Thus, total scan time for MT modeling including the T₁ measurement and MT sequences are 26.7min.

Image and Data Analysis

Two-pool UTE-MT modeling was performed on the datasets as previously described by Ramani et al (17). Ramani et al introduced a simple method by treating the MT pulse as a rectangular continuous wave (CW) signal with the same mean saturating power as the experimentally used shaped pulse in each repetition time, the so-called continuous wave power equivalent (CWPE) approximation. ^W_CWPE is the angular frequency of precession induced by the off-resonance MT pulse and is a measure of the amplitude of the B₁ field, as represented by:

$$w_{\text{CWPE}}=\frac{{\theta }_{\text{sat}}\pi }{p_{1}180°}\sqrt{\frac{p_2}{{\tau }_{\mathit{sat}}TR}},$$ [1]

where θ_sat is the flip-angle of MT pulse. p₁ is the ratio of the area of the MT pulse to a rectangular pulse with the same duration and peak amplitude and p₂ is the ratio of the square of the MT pulse area to the square of the area of the same rectangular pulse. τ_sat; is the duration of the MT pulse, and TR is the time interval between adjacent two MT pulses. The acquired data with a variety of saturation powers and off-resonance frequencies Δf were fitted by the Ramani model where the signal intensity S is given by:

$$S=g{M}_{0w}\frac{R_{1m}\left[\frac{R{M}_{0w}f}{R_{1w}(1-f)}\right]+R_{\mathit{RFm}}+R_{1m}+R{M}_{0w}}{\left[\frac{R{M}_{0w}f}{R_{1w}(1-f)}\right](R_{1m}+R_{\mathit{RFm}})+\left(1+{\left[\frac{w_{\text{CWPE}}}{2\pi \mathrm{\Delta }f}\right]}^2\left[\frac{1}{R_{1w}{T}_{2w}}+\right]\right)(R_{\mathit{RFm}}+R_{1m}+R{M}_{0w})}$$ [2]

where g is a amplitude scaling factor of the acquired data including the item of exp(−TE/T₂*). f is the macromolecular proton fraction, i.e. $f=\frac{M_{0m}}{M_{0m}+M_{0w}}$. M_0m and M_0w are the fully relaxed magnetization of macromolecular pool and water pool respectively. R_1m and R_1w are the longitudinal rate constants, respectively. R is the first-order magnetization exchange rate constant between the two pools. R_RFm is the loss rate of longitudinal magnetization of macromolecular pool due to the RF saturation of the MT pulse. It is related to the absorption lineshape G(2πΔf) of the spins in the macromolecular pool and is given by:

$$R_{\mathit{RFm}}=\mathrm{\pi }{w}_{\text{CWPE}}^2\mathrm{G}(2\mathrm{\pi }\mathrm{\Delta }\mathrm{f}).$$ [3]

Since the protons in the macromolecular pool do not experience the motional narrowing that the protons in the free pool experience, they cannot be characterized by the Lorentzian lineshape function that results from the Bloch formalism. Super-Lorentzian lineshapes have been reported to be good representations for the macromolecular pool in Achilles tendon (18). The super-Lorentzian expression is as follows:

$$G(2\mathrm{\pi }\mathrm{\Delta }\mathrm{f})=\underset{0}{\overset{\pi /2}{\int }}d\theta \mathit{sin}\theta \sqrt{\frac{2}{3}}\frac{T_{2m}}{\mid 3{\mathit{cos}}^2\theta -1\mid }exp(-2{[\frac{2\pi \mathrm{\Delta }f{T}_{2m}}{\mid 3{\mathit{cos}}^2\theta -1\mid }]}^2),$$ [4]

where θ is the angle orientation between the axis of molecular orientation and the B₀.

Then, if the apparent longitudinal relaxation rate R_1obs (= 1/T₁), which can be measured by a conventional T₁ measurement sequence such as multiple-TR UTE protocol mentioned above, is known, R_1wis determined by (17,18):

$$R_{1\mathrm{w}}=\frac{R_{1\text{obs}}}{1+\frac{\frac{R{M}_{0w}f}{R_{1w}(1-f)}(R_{1m}-R_{1\text{obs}})}{(R_{1m}-R_{1\text{obs}})+R{M}_{0w}}}.$$ [5]

Since the quantitative MT experiments are largely insensitive to R_1m (i.e. the relaxation rate of the macromolecular pool), R_1m has been fixed arbitrarily to be 1s⁻¹(17–19). Above all, acquired MT data can be fitted to Eq. [2] with the information of Eq. [1] and Eq. [3] to Eq. [6]. Thus, the parameters including f, RM_0w and T_2m can be determined by this fitting procedure. RM_0w is the proton exchange rate from macromolecular to water. The residual of fitting was represented by $\text{Residual}=\sqrt{\frac{{\sum }_i{(S_{i,\mathit{fit}}-S_i)}^2}{{\sum }_i{S}_i^2}}$, where, S_i, S_i,fit(i=1,…,N, N is the total number of data points in one MT datasets) are the experimental and fitted data points.

The analysis algorithm was written in Matlab (The MathWorks Inc., Natick, MA, USA) and was executed offline on the DICOM images obtained by the protocols described above. A Levenberg-Marquardt algorithm was employed for the nonlinear least-squares fitting in both MT modeling and multiple-TE mono-exponential fitting. The program allowed placement of region of interests (ROIs) on the first UTE image of the series, which were then copied onto each of the subsequent images. The mean intensity within each of the ROIs was used for both two-pool modeling and multiple-TE mono-exponential fitting.

Results

Figure 1 shows UTE-MT images of a cadaveric human Achilles tendon sample acquired at five angular orientations (i.e. 0°, 30°, 55°, 70°, 90°) between fiber direction and the B₀ field. Using the UTE sequence, high signal intensity is obtained from the Achilles tendon all images at all angular orientations, facilitating MT modeling as conventional clinical sequences show near zero signal, thereby limiting MT modeling. The image intensity increased with higher off-resonance frequencies due to reduced saturation of macromolecular spins. Signal intensity varied depending on orientation and the greatest signal was observed for the Achilles tendon when the fibers were oriented near the magic angle of 55°. T₂* also was significantly increased near the magic angle due to the minimization of dipole-dipole interaction.

Figure 1.

Localizers and MT images of five angle orientations (i.e. 0°, 30°, 55°, 70°, 90°) between fiber direction F⃗ and main field B⃗₀. The localizer sequence was the conventional GRE sequence with TE/TR=3.2/8.6ms. The first columns are the images of localizers and the direction of both F⃗ and B⃗₀ are represented by white arrows. The blue dashed lines are the imaging planes. The second to fourth columns are the corresponding MT images with off-resonance frenquencies of 50, 20 and 5KHz and a flip angle of 1200°. Each row of MT images with the same angle orientation are normlized by themselves.

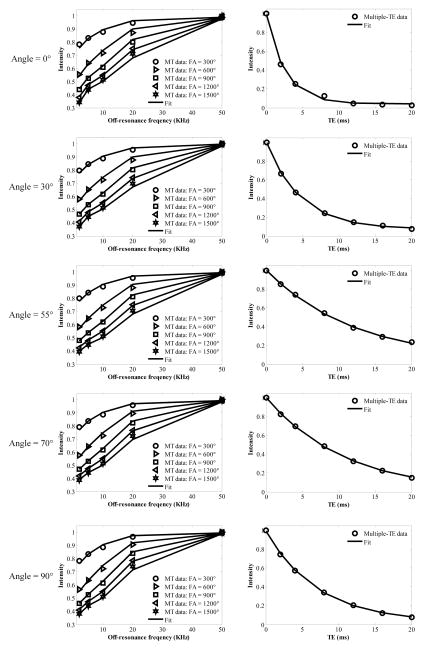
Figure 2 shows the results of both UTE-MT modeling and multiple-TE T₂* fitting. The measured T₁ value of this sample was 698ms. The two-pool UTE-MT modeling provides excellent fitting (all Residuals were less than 2.1%) of signal changes over five MT power (i.e. 300°, 600°, 900°, 1200° and 1500°) and five off-resonance frequencies (i.e. 2, 5, 10, 20, 50 KHz). Furthermore, the UTE-MT modeling performed well for all five angular orientations (i.e. 0°, 30°, 55°, 70° and 90°), thereby allowing direct comparison of values at each orientation. Excellent T₂* fitting was also achieved for all five angular orientations, allowing quantitative comparison of the angular dependence of UTE-MT modeling and T₂* relaxation time.

Figure 2.

Graphs of fitting results of both MT modeling (first column) and multiple-TE data (second column). The results of five angle orientations between fiber direction F⃗and B⃗₀ are shown in the first to fifth rows, respectively.

Figure 3 shows the relationship of UTE-MT modeling parameters and T₂* relaxation time with respect to angular orientation in a representative cadaveric human Achilles tendon sample. As can be seen, T_2w* shows a strong magic angle behavior, with ~6 times increase from 2.5 ms when the sample was oriented parallel to the B₀ field, to 14.8 ms when the sample was oriented 55° relative to the B₀ field. Meanwhile, the UTE-MT modeling parameters, including macromolecular proton fractions (f), T₂ value of macromolecular proton (T_2m) and exchange rate from macromolecular proton to water proton (RM_0w) derived from MT modeling, all show minimal angular dependence with less than 10% variation. These results suggest that the f, T_2m and RM_0w can be used as magic angle insensitive biomarkers of the Achilles tendon.

Figure 3.

Graphes of T₂* values derived by fitting multiple-TE data and macromolecular proton fractions (f), T₂ value of macromolecular proton (T_2m) and exchange rate from macromolecular proton to water proton (RM_0w) derived from two-pool MT modeling with five angle orientations between fiber direction F⃗ and B⃗₀. Fitting errors of these parameters were shown by error bars.

Table 1 shows the mean and coefficient of variation (CV) values of f, T_2m, RM_0w and T₂* across five angle orientations between fiber direction F⃗ and B⃗₀ of four cadaveric human Achilles tendon samples. CV is a statistical measure defined as the dispersion of data points in a data series around the mean. It is calculated as follows: (standard deviation) / (mean value). The small CV values of f, T_2m and RM_0w in all the four samples show magic angle independent results from MT modeling. In contrast, the relatively large CV values of T₂* show its magic angle sensitivity.

Table 1.

Mean and coefficient of variation (CV) values of f, T_2m, and RM_0w derived by two-pool MT modeling and T₂* derived by multiple-TE data fitting across five angle orientations (i.e. 0°, 30°, 55°, 70°, 90°) between fiber direction F⃗ and B⃗₀ of four Achilles tendons.

Sample	f (%)	T2m (us)	RM0w (s−1)	T2*(ms)
1	19.8±3.0%	7.5±6.7%	9.4±6.4%	8.4±54.8%
2	19.9±3.0%	7.6±7.9%	16.7±6.6%	5.9±69.5%
3	19.6±3.1%	7.2±6.9%	10.6±7.5%	5.6±66.1%
4	20.0±1.5%	7.6±9.2%	9.2±2.2%	6.1±75.4%

Discussion

In this study, we have shown that UTE-MT modeling can be performed on data acquired on a clinical 3T scanner and provides parameters that are resistant to the magic angle effect, such as macromolecular proton fractions and exchange rates between water and macromolecular protons. This contrasts with the exquisitely magic-angle sensitive mono-exponential UTE-T₂* relaxation times, which demonstrated up to a 6-fold increase from 0° to 55° in our tendon specimens, a finding similar to previously published results (13,14).

Henkelman et al were among the first to show that MT demonstrated no orientation dependence (11). Their experiments were performed on a variety of tissues, including tendon and cartilage, and the classic two-pool MT model introduced by the same group was used for fitting (11,19). However, their sequence and model utilized a long continuous MT RF pulse to drive the two-pool system to the steady state and was employed on an NMR spectrometer. This method may not be possible with clinical MR imaging hardware systems due to very large specific absorption rates (SAR). To accomplish MT imaging on a conventional clinical scanner, Ramani et al employed a continuous wave power equivalent method for pulsed wave saturation and were able to fit a number of parameters such as the T₂ values of both water (T_2w) and macromolecular protons (T_2m), macromolecular proton fractions (f), proton exchange rates from macromolecular to water (RM_0w) pools (17). Using the UTE-MT technique and Ramani model on a clinical 1.5T system, Hodgson et al found a bound proton fraction of 21.0 ± 1.2% versus 16.4% in the Achilles tendons of eight volunteers and a psoriatic arthritis patient, respectively (p < 0.05) (18). The bound proton fractions in our specimens (19–21%) are comparable to those reported in healthy volunteers (18) and is in keeping with the high collagen content of the Achilles tendon, which has been reported at 22% of the total tendon wet weight (20).

In recent years, a number of potential clinically compatible, magic angle resistant MR biomarkers have been proposed. This includes T_1rho using an adiabatic spin-lock RF pulse (21,22), UTE-T₂* bi-component fractions (23,24), and diffusion weighted imaging (25). Our results confirm that UTE-MT also yields magic-angle independent measurements. Compared with the other techniques, a unique advantage of the UTE-MT sequence is that information on the macromolecular protons can be obtained. This proton pool typically demonstrates extremely rapid T₂ relaxation and cannot be directly obtained by other clinically compatible methods, including UTE or zero echo time (ZTE) techniques. The combination of UTE-MT modeling measurements with UTE-T₂* bi-component fractions would be of interest to provide information on all proton pools, including macromolecular protons, bound water, and free water. This along with correlation with physical and biomechanical measurements will be investigated in future work.

In this study, we used a home-built birdcage coil (~2 cm in diameter) for signal transmission and receiving, which has excellent transmission efficiency. The SAR values were very low, but cannot be compared with the in vivo condition. In particular, SAR values can be quite different with different body parts and transmission coils despite similar protocols. For example, to image a human leg in vivo, the SAR value of the UTE-MT protocol with a MT power of 1400° and TR = 100 ms is close to the SAR limitation.

Our study has a number of limitations. First, we had a small sample size without histologic correlation. In severely degenerated tendons, collagen fibers are disrupted, collagen content decreases, and water increases. In this setting, the degree of magic angle effect on T₂ times may decrease slightly, but would still be expected to be present. Second, the imaging parameters used in this study are prohibitively long for clinical translation (i.e. 26.7min for one slice). We have tried MT modeling with as few as ten datasets and the results were comparable to those obtained using all 25 datasets. Alternatively, an optimal data acquisition scheme using the theory of Cramer-Rao lower bounds (CRLB) to select MT powers and frequency offsets for MT modeling can be employed to reduce scan time (26). Furthermore, the scan time of the T₁ measurement sequence can also be decreased by reducing the number of TR or TR values. Overall, there is ample opportunity to reduce scan time for clinical use, although the limits of reducing datasets remain to be fully studied. In particular, with reduced datasets, the fitting can be more sensitive to noise or image artifacts caused by off-resonance or motion. Third, although the image flip angle used in this study was very small (i.e. 5°), a bias was still introduced into the Ramani MT model due to T₁ weighting and on-resonance saturation. In addition, the relatively small saturation pulse duty cycle of the UTE-MT protocol may lead to substantial underestimation of the exchange rate between macromolecular and water pools, creating inaccuracy in the measurement of T_2w. Alternative models that consider the excitation pulse and repetition time are less sensitive to T₁ weighting (27).

In conclusion, UTE-MT modeling provides information on tissue properties, such as the macromolecular proton fraction and exchange rates between water and macromolecular protons, and is much less sensitive to the magic angle effect compared with mono-exponential T₂* values of the water protons. UTE-MT modeling can be applied to both short and long T₂ tissues such as the Achilles tendon, ligaments, menisci, bone, calcified cartilage and superficial layers of cartilage, and may be potentially be useful for disease identification, monitoring disease progression, and assessing response to therapy.

Abbreviations used

MR

magnetic resonance

UTE

Ultrashort echo time

RF

radiofrequency

UTE-MT

UTE magnetization transfer

CW

continuous wave

CWPE

continuous wave power equivalent

ROIs

region of interests

CV

coefficient of variation

SAR

specific absorption rates

ZTE

zero echo time

CRLB

Cramer-Rao lower bounds