A theoretical analysis of chemical exchange saturation transfer echo planar imaging (CEST-EPI) steady state solution and the CEST sensitivity efficiency-based optimization approach

Abstract

Chemical exchange saturation transfer (CEST) MRI is sensitive to dilute labile protons and microenvironmental properties, augmenting routine relaxation-based MRI. Recent development of quantitative CEST (qCEST) analysis such as omega plot and RF-power based ratiometric calculation have extended our ability to elucidate the underlying CEST system beyond the simplistic apparent CEST measurement. CEST MRI strongly varies with experimental factors, including the RF irradiation level and duration as well as repetition time and flip angle. In addition, CEST MRI effect is typically small, and experimental optimization strategies have to be carefully evaluated in order to enhance the CEST imaging sensitivity. Although routine CEST MRI has been optimized largely based on maximizing the magnitude of the CEST effect, the CEST signal-to-noise (SNR) efficiency provides a more suitable optimization index, particularly when the scan time is constrained. Herein, we derived an analytical solution of the CEST effect that takes into account of key experimental parameters including repetition time, imaging flip angle and RF irradiation level, and solved its SNR efficiency. The solution expedites CEST imaging sensitivity calculation, substantially faster than Bloch-McConnell equations-based numerical simulation approach. In addition, the analytical solution-based SNR formula enables the exhaustive optimization of CEST MRI, which simultaneously predict multiple optimal parameters such as repetition time, flip angle and RF saturation level based on the chemical shift and exchange rate. The sensitivity efficiency-based optimization approach could simplify and guide imaging of CEST agents, including glycogen, glucose, creatine, gamma-aminobutyric acid and glutamate.

1. INTRODUCTION

Chemical exchange saturation transfer (CEST) MRI is sensitive to the chemical exchange process between labile protons and bulk water signal, providing a contrast mechanism for imaging dilute CEST agents and microenvironment properties such as pH and temperature (1–5). Indeed, CEST-weighted MRI has found substantial interest in molecular imaging as well as in vivo applications such as acute stroke (6–15), tumor (16–24) and epilepsy imaging (25). Whereas the CEST MRI measurement varies with experimental factors, particularly the RF irradiation level and duration, such dependence has been harnessed as a novel approach for quantitative CEST (qCEST) analysis including omega plot and RF-power based ratiometric calculation (26–33). It is necessary to point out that the development of qCEST analysis allows simultaneous determination of the CEST agent concentration and exchange rate with minimal a priori information, advancing the CEST MRI as a novel molecular imaging approach (34–37).

Despite the substantial sensitivity advantage of CEST imaging over MR spectroscopy, the CEST MRI effect is typically small due to the relatively low concentration and/or moderate exchange rate, requiring meticulous optimization (38–45). It has been shown that the apparent CEST MRI measurement strongly varies with the RF irradiation level (B₁) and duration. Recent studies have also shown that the CEST effect depends on experimental factors such as repetition time (TR) and flip angle (FA), which need to be taken into account for proper optimization (46). Although CEST optimization strategies have been largely based on maximization of the CEST effect, the CEST signal-to-noise (SNR) per unit time (efficiency)-based optimization approach ensures the maximal CEST MRI sensitivity, particularly important when the total scan time is constrained (47,48). Because the fully relaxed magnetization state under an extremely long repetition time is rarely used, we here derived a steady state analytical solution for the CEST MRI effect, and solved its SNR efficiency as a function of experimental variables including TR and FA. We confirmed that the analytical solution provides accurate quantification of the CEST MRI effect, in good agreement with Bloch-McConnell equations-based numerical simulation. In addition, the use of analytical solution accelerates SNR efficiency computation, enabling the exhaustive optimization approach to simultaneously optimize multiple parameters, which could simplify and guide experimental optimization.

2. THEORY

2.1. Quantitative solution of CEST MRI effect

For the representative CEST echo planar imaging (EPI) sequence with a continuous wave (CW) RF saturation (Fig. 1), the control scan signal without RF irradiation can be shown to be (49)

${\mathrm{S}}_0\left(\mathrm{TR},\mathrm{FA}\right)=\frac{1-{\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}}\cdot \sin (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{TE}/{\mathrm{T}}_{2\mathrm{w}}^{\ast }}$ (1)

where TR is the repetition time, TE is the echo time, T_1w and T^*_2w are the bulk water longitudinal and apparent transverse relaxation time, respectively, and FA is the image excitation flip angle. For the irradiated scans, the steady state signal (please see appendix 1) can be solved as (36,50–52)

$${\mathrm{S}}_{\mathrm{Sat}}\left({\mathrm{R}}_{1\mathrm{\rho }},\mathrm{TR},\mathrm{FA},\mathrm{Ts},{\mathrm{B}}_1\right)=\frac{\left(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\right)\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{Ts}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{Ts}}\right)}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{Ts}}}\cdot \sin (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{T}\mathrm{E}/{\mathrm{T}}_{2\mathrm{w}}^{\ast }}$$ (2)

Note that we assumed short EPI readout time (i.e., TR=Tr+Ts, where Tr and Ts are the relaxation recovery and saturation times, respectively.) We have ${\mathrm{R}}_{1\mathrm{\rho }}={\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }+\left({\mathrm{R}}_{2\mathrm{w}}+\frac{{\mathrm{f}}_{\mathrm{s}}\cdot {\mathrm{k}}_{\mathrm{s}\mathrm{w}}\cdot \mathrm{\alpha }}{{\left({\mathrm{\omega }}_1/{\mathrm{\delta }}_{\mathrm{s}}\right)}^2+{\left({\mathrm{k}}_{\mathrm{s}\mathrm{w}}/{\mathrm{\delta }}_{\mathrm{s}}\right)}^2}\right){\sin }^2\mathrm{\theta }$, where R_1,2w are the bulk water longitudinal and transverse relaxation rates, δ_s is the labile proton offset, and α is the saturation coefficient $\mathrm{\alpha }=\frac{{\mathrm{\omega }}_1^2}{\mathrm{p}\cdot \mathrm{q}+{\mathrm{\omega }}_1^2}$, in which $\mathrm{p}={\mathrm{r}}_{2\mathrm{s}}-\frac{{\mathrm{k}}_{\mathrm{s}\mathrm{w}}{\mathrm{k}}_{\mathrm{w}\mathrm{s}}}{{\mathrm{r}}_{2\mathrm{w}}}$, $\mathrm{q}={\mathrm{r}}_{1\mathrm{s}}-\frac{{\mathrm{k}}_{\mathrm{s}\mathrm{w}}{\mathrm{k}}_{\mathrm{w}\mathrm{s}}}{{\mathrm{r}}_{1\mathrm{w}}}$, k_ws = f_s·k_sw, r_1w,s;2w,s =R_1w,s;2w,s +k_ws,sw;2w,s. In addition, we have $\mathrm{\theta }={\tan }^{-1}\left({\mathrm{\omega }}_1/\mathrm{\Delta }\mathrm{\omega }\right)$, where ω₁ and Δω are the RF irradiation level and offset, f_s and k_sw are the labile proton ratio and exchange rate, and R_1s,2s are their longitudinal and transverse relaxation rates, respectively. The CEST MRI signal is given as (please see appendix 1)

$$\frac{{\mathrm{S}}_{\mathrm{sat}}\left({\mathrm{R}}_{1\mathrm{\rho }},\mathrm{TR},\mathrm{FA},\mathrm{Ts},{\mathrm{B}}_1\right)}{{\mathrm{S}}_0\left(\mathrm{TR},\mathrm{FA}\right)}=\frac{\frac{\left(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\right)\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{Ts}}\right)}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{Ts}}}}{\left(1-{\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}\right)/\left(1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}\right)}$$ (3)

Fig. 1.

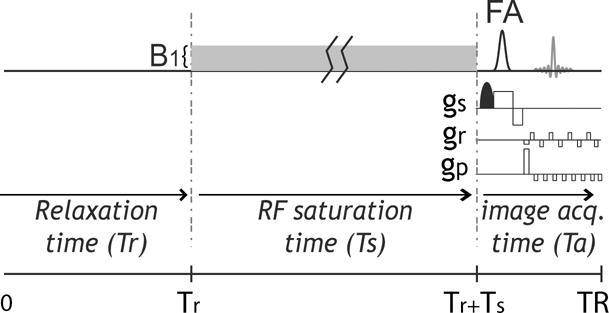
Illustration of CEST EPI pulse sequence that includes relaxation delay, RF saturation time (Ts) under an RF field denoted by B₁. Because the EPI duration is substantially shorter than typical Tr and Ts, which are on the order of T_1w, the repetition time is approximately equal to the sum of Tr and Ts.

2.2. Quantitative CEST indices

The routinely used CEST asymmetry ratio (CESTR) is given as $\mathrm{CESTR}=\frac{{\mathrm{S}}_{\mathrm{ref}}-{\mathrm{S}}_{\mathrm{lab}}}{{\mathrm{S}}_0}$, where S_ref and S_lab are scans with RF saturation applied at the labile proton frequency and reference offset, respectively, and S₀ is the control scan without RF saturation. Note that CESTR is complex, being a function of labile proton concentration, exchange rate and chemical shift as well as relaxation times and experimental factors such as TR, FA, Ts and B₁. It is necessary to point out that the inverse CEST asymmetry ratio, being $\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}=\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{lab}}}-\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}$ is related to the conventional CESTR, being $\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}=\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{lab}}\cdot {\mathrm{S}}_{\mathrm{ref}}}\right)\cdot \mathrm{CESTR}$ (53).

2.3. CEST SNR and CNR efficiency

It has been shown that the SNR for the routine CEST analysis (CESTR) is given by (46)

$${\mathrm{SNR}}_{\mathrm{CESTR}}\left({\mathrm{f}}_{\mathrm{s}},{\mathrm{k}}_{\mathrm{s}\mathrm{w}},\mathrm{TR},\mathrm{FA},\mathrm{Ts},{\mathrm{B}}_1\right)\approx \frac{\mathrm{CESTR}}{\sqrt{2+\mathrm{CEST}{\mathrm{R}}^2}}\cdot {\mathrm{SNR}}_{{\mathrm{S}}_0\left(\mathrm{TR},\mathrm{FA}\right)}$$ (4.a)

where ${\mathrm{SNR}}_{{\mathrm{S}}_0}$ is SNR of the control image, which depends on TR and FA. The SNR for CESTR_ind can be shown to be (please see appendix 2)

$${\mathrm{SNR}}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}\left({\mathrm{f}}_{\mathrm{s}},{\mathrm{k}}_{\mathrm{s}\mathrm{w}},\mathrm{TR},\mathrm{FA},\mathrm{Ts},{\mathrm{B}}_1\right)=\frac{\mathrm{CESTR}}{\sqrt{2+\mathrm{CEST}{\mathrm{R}}^2\cdot \left(1+{\left(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}+\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{lab}}}\right)}^2\right)}}\cdot {\mathrm{SNR}}_{{\mathrm{S}}_0\left(\mathrm{TR},\mathrm{FA}\right)}$$ (4.b)

For small CEST effect, we have CESTR²<<1, and the SNR for CESTR and CESTR_ind are approximately equal. The SNR per unit time (SNR efficiency) can be calculated from the SNR with normalization by the square root of the total scan time (i.e. ${\mathrm{SNR}}_{\mathrm{put}}=\mathrm{SNR}/\sqrt{\text{scan time}}$). Notably, the relative SNR (rSNR) is calculated by normalizing the CEST SNR by the SNR of the thermal equilibrium signal to have a uniform reference.

$$\mathrm{r}\mathrm{SNR}=\frac{{\mathrm{SNR}}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}\left({\mathrm{f}}_{\mathrm{s}},{\mathrm{k}}_{\mathrm{s}\mathrm{w}},\mathrm{TR},\mathrm{FA},\mathrm{Ts},{\mathrm{B}}_1\right)}{{\mathrm{SNR}}_{{\mathrm{S}}_0\left(\mathrm{TR}=\mathrm{\infty },\mathrm{FA}=\mathrm{\pi }/2\right)}}$$ (5)

The CEST effect CNR can be derived following the error propagation theorem. For the routine CESTR calculation, we have (please see appendix 3)

$$\mathrm{CNR}=\frac{\left|\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{a}},\mathrm{p}{\mathrm{H}}_{\mathrm{a}}\dots \right)-\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{b}},\mathrm{p}{\mathrm{H}}_{\mathrm{b}}\dots \right)\right|}{\sqrt{\begin{array}{l}{\left(\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{a}},\mathrm{p}{\mathrm{H}}_{\mathrm{a}}\dots \right)\cdot {\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{b}},\mathrm{p}{\mathrm{H}}_{\mathrm{b}}\dots \right)}\right)}^2\\ +{\left(\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{b}},\mathrm{p}{\mathrm{H}}_{\mathrm{b}}\dots \right)\cdot {\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{a}},\mathrm{p}{\mathrm{H}}_{\mathrm{a}}\dots \right)}\right)}^2\end{array}}}\cdot {\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{a}},\mathrm{p}{\mathrm{H}}_{\mathrm{a}}\dots \right)}\cdot {\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{f}}_{\mathrm{b}},\mathrm{p}{\mathrm{H}}_{\mathrm{b}}\dots \right)}$$ (6)

where subscripts a and b denote different labile proton ratios and/or exchange rates. This shows that the CNR can be derived based on the SNR and CEST effects calculated from the analytical solution. Similarly, the CNR efficiency can be calculated from the CNR with normalization by the square root of the scan time. Note that Eq. 6 is general and can be applied to alternative CEST indices.

3. RESULTS and DISCUSSION

Fig. 1 illustrates a CEST gradient echo EPI sequence with a continuous wave (CW) RF irradiation. Because the typical EPI echo time is negligible compared to TR and saturation time, TR is approximately equal to the sum of the relaxation recovery duration and saturation time (i.e., TR ≈ Tr+Ts). The RF duty cycle is given by Ts/TR, which we set to 50% for typical RF amplifier performance. The steady state CEST solution was derived following the spin locking theorem (50,54) and relaxation recovery (Please see the appendix 1).

Fig. 2 tests the accuracy of the analytical CEST solution (Eq. 3) against the Bloch-McConnell equations-based numerical simulation, assuming representative parameters of T_1w=2s, T_1s=1s, T_2w=100ms and T_2s=15ms. We assumed a typical labile proton ratio and exchange rate of 1:1000 and 100 s⁻¹ at a representative chemical shift of 2 ppm at 4.7 Tesla. Fig. 2a shows three Z-spectra from −3 to 3 ppm for representative TRs of 1, 2 and 5 times of T_1w. For simplicity, we assumed a FA of 90°. Note that the normalized signal intensity decreases with TR due to inadequate relaxation recovery. Fig. 2b shows that CESTR estimated from the steady state non-equilibrium solution. Notably, CESTR decreases at short TR due to reduced saturation duration. Fig. 2c compares rSNR efficiency (rSNR) calculated from the analytical solution with that simulated from Bloch-McConnell equations. Briefly, we used the randn function in Matlab to generate normally distributed pseudorandom numbers, which were superimposed on simulated control, reference and label signals, and calculated the CESTR. The noise superimposition was repeated for 8,192 times to estimate SNR. Admittedly, it took 35 s to numerically solve the SNR (Dell Precision T7400, 8 GB RAM, Dual Processers E5420) while the computation time was less than 0.01 s using the analytical solution, equivalent to an acceleration factor of over 3,500. This advantage enables the practical use of the exhaustive optimization strategy for designing CEST MRI experiment. Fig. 2d shows three Z-spectra for representative flip angles of 30, 60 and 90°, assuming a typical TR of twice T_1w. The analytical solution and numerical simulation are in good agreement. The apparent CEST effect decreases with FA (Fig. 2e), consistent with prior findings (46). Fig. 2f shows that rSNR efficiency peaks at an FA of approximately 75°. Note that the optimal FA for maximal CEST imaging rSNR is different from that of the Ernst angle, being 82° for TR=2*T_1w.

Fig. 2.

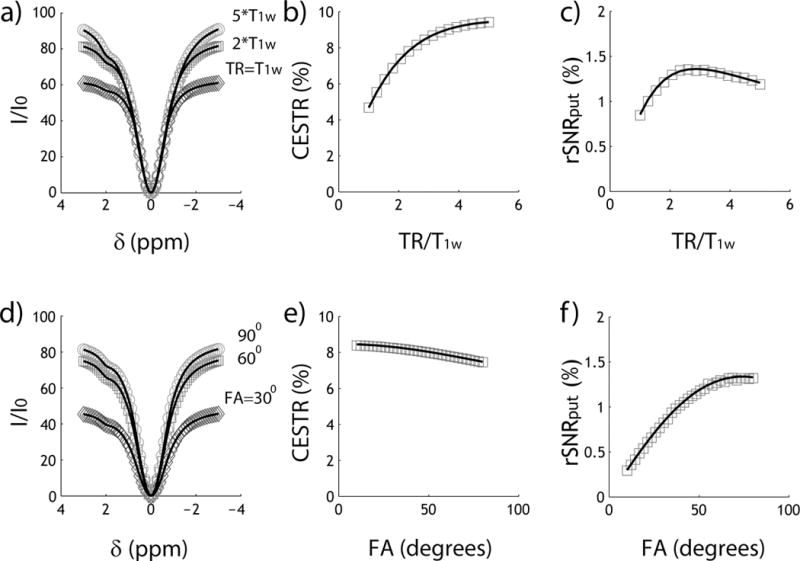
Evaluation of the steady state CEST analytical solution. Markers are data points simulated from Bloch-McConnell quations while lines are from the analytical solution. a) Z-spectra for three representative TR of 1, 2 and 5 times of T_1w. b) CESTR as a function of TR. c) CEST rSNR efficiency as a function of TR. d) Z-spectra for three representative FA of 30, 60 and 90°. e) CESTR as a function of FA. f) CEST rSNR efficiency as a function of FA.

Fig. 3 compares CESTR and CESTR_ind effects and their sensitivity. We assumed a relatively optimal TR of 4 s (i.e. ~ 2*T_1w) and FA of 75° (Fig. 2). Fig. 3a shows that CESTR_ind is consistently higher than CESTR, particularly at strong B₁ level. This is because CESTR_ind is not sensitive to the direct RF spillover effect. interestingly, Fig. 3b shows that the SNR efficiency for routine CESTR analysis is approximately equal to but marginally higher than that of CESTR_ind. This is consistent with Eq. 4b, which shows that for small CEST effect, CESTR and CESTR_ind analyses provide approximately the same CEST imaging sensitivity.

Fig. 3.

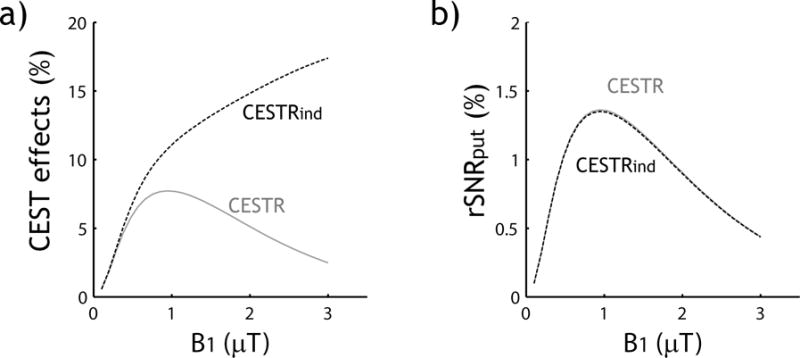
Comparison of the magnitude of CEST effect and their sensitivity measured by CESTR and CESTR_ind. a) Routine CEST asymmetry analysis (CESTR) and the direct RF-saturation compensated inverse CEST asymmetry (CESTR_ind) as a function of B₁. b) SNR efficiency of CESTR and CESTR_ind as a function of B₁.

Fig. 4 demonstrates the steady state solution-based exhaustive optimization strategy. Fig. 4a shows the peak rSNR efficiency as a function of exchange rate and labile proton chemical shift under simultaneously optimized TR, B₁ and FA. Because the effective longitudinal relaxation rate for label scan (i.e., ${\mathrm{R}}_{1\mathrm{\rho }}^{+}$) increases with the exchange rate, the optimal TR (TR_opt) decreases at high exchange rate (Fig. 4b). Interestingly, TR_opt decreases at small chemical shift, likely because a moderate TR results in a relative enhancement of the apparent concentration of labile protons as the labile proton signal typically relaxes faster than bulk water. Fig. 4c shows the optimal B₁ increases with both the exchange rate and chemical shift, as expected. Fig. 4d shows that the optimal FA decreases at small chemical shift and high exchange rate, likely due to the decreased optimal TR under such conditions. It has been shown that under the conditions of near bulk water resonance and large B₁ field, there could be an oscillatory signal due to the residual transverse magnetization (52). Because the typical saturation duration is significantly longer than transverse relaxation time in the rotating frame (i.e., T_2ρ), the oscillatory signal should be small, warranting Eq. 2. Because of its advantage to simultaneously optimize TR, FA and B₁, Fig. 5a shows that exhaustive optimization strategy identifies peak SNR efficiency substantially higher than that assuming the thermal equilibrium state (i.e., TR=5*T_1w). This is because CEST MRI experimental variables have relatively complex interdependence, and exhaustive optimization approach faithfully optimize multiple variables concurrently. Indeed, the optimal B₁ level determined from the exhaustive optimization strategy is substantially higher than the routine prediction based on long TR solution (Fig. 5b). We further applied the CEST sensitivity efficiency-based optimization strategy and predicted optimal TR, FA and B₁ for a number of representative CEST agents at 4.7 T, including Gly(55), Glc(50), Cr(56), GABA(55), Glu(16) and ensemble amides(6), based on their exchange rates and chemical shifts (Table 1).

Fig. 4.

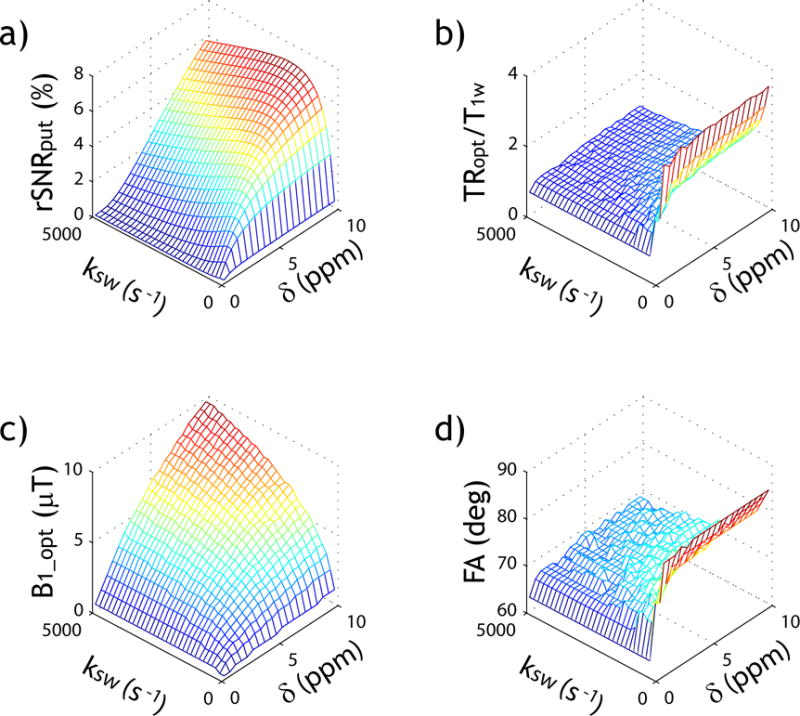
Evaluation of the exhaustive optimization strategy of CEST MRI. a) Peak SNR efficiency as a function of labile proton exchange rate and chemical shift. b) Optimal TR normalized by T_1w as a function of labile proton exchange rate and chemical shift. c) Optimal B₁ as a function of labile proton exchange rate and chemical shift and d) Optimal FA as a function of labile proton exchange rate and chemical shift.

Fig. 5.

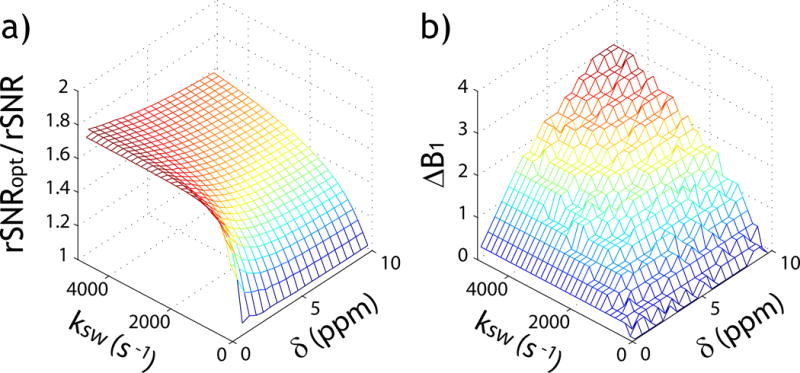
Demonstration of the advantage of the exhaustive optimization strategy. a) Ratio of peak SNR efficiency from the exhaustive optimization strategy (TR, FA and B₁ optimization) over that assuming a long TR. b) The optimal B₁ difference between the exhaustive optimization strategy and routine optimization approach assuming a long TR.

Table 1.

Suggested experimental parameters from SNR efficiency-based optimization algorithm for representative metabolites at 4.7 T.

	δs (ppm)	Ksw (s−1)	TRopt/T1w	FAopt (deg)	B1_opt (μT)
Glc	~ 1.1	~ 4680 (pH=7.4, Rm Temp)	0.9	67	2.0
Gly	~ 1.2	~ 600 (pH=7.4, 25°C)	1.3	72	1.5
Cr	1.9	~1,190 (pH=7.0, 37°C)	1.2	71	2.3
GABA	2.8	~800 (pH=5.6, 25°C)	1.6	75	2.5
Glu	3.0	~5,500 (pH=7.0,37°C)	0.9	68	4.3
Amides	~ 3.5	~30 (pH=7.0, 37°C)	3.4	85	0.8

Our study derived the steady state non-thermal equilibrium CEST solution and its sensitivity efficiency. The substantial acceleration in computation speed over the conventional Bloch-McConnell numerical approach enables prediction of optimal values for multiple parameters, which could simply and guide CEST MRI experimental optimization (57−60). It complements the conventional optimization strategy that assumes the thermal equilibrium state, which is rarely implemented experimentally. By incorporating experimental factors such as TR and FA into the solution, our work is promising to improve the accuracy of qCEST analysis (36). Although our study here investigates only continuous wave (CW)-CEST MRI with GE EPI readout, the results may be generalized to several other commonly-used image sequences. For example, adding a flip-back RF pulse after the readout in spin echo EPI resets the Z-magnetization similar to GE EPI readout, provided that there is negligible spin relaxation during the echo time (i.e., TE<<T_1w), and therefore, the formulas derived in our study are applicable. For the case of rapid acquisition with relaxation enhancement (RARE) readout, if no Z-magnetization is recycled to the next scan, the spin relaxes towards its equilibrium state from null, similar to the spin evolution for a GE EPI readout with a 90 degree excitation pulse. It is necessary to point out that the formula can also be extended to include the contribution from magnetization transfer (MT) and/or multiple exchangeable sites by modifying the relaxation rate term (40). However, MT properties varies a lot in different tissues from blood, brain to kidney (61). Because the complexity of the SNR calculation increases exponentially with the number of dimensions, it is suggested to first determine non-adjustable parameters such as relaxation, magnetic field strength and MT and treat them as fixed variables in order to expedite the sensitivity efficiency-based optimization prediction.

Our study here showed that the inverse CEST asymmetry provides nearly identical SNR as the routine asymmetry analysis, despite the difference in their magnitudes. This finding helps to clarify the advantage and limitation of different means of CEST quantification. The derivation of SNR and CNR efficiency can be extended to alternative means of qCEST analysis. For example, SNR of the recently proposed RF power-based ratiometric analysis (i.e., PRCESTR and PRICESTR) can be directly estimated from the SNR of CESTR and CESTR_ind (please see appendix 3). Worth noting is that the analytical solution also allows the constrained optimization. For instance, the specific absorption rate (SAR) limit can be included in the SNR efficiency optimization computation by restricting the magnitude and duration of RF saturation ( $\mathrm{SAR}\propto {\displaystyle {\int }_0^{\mathrm{Ts}}{\mathrm{B}}_1^2\mathrm{dt}/\mathrm{TR}}$) while searching for the optimal experimental conditions under the constraint. Our work here only investigated the CW RF irradiation scheme. For labile protons undergoing slow chemical exchange, it has been shown that the pulsed RF irradiation provides similar CEST effect as CW irradiation (62,63). In addition, the recent derivation of an approximated solution for pulsed CEST MRI effect (64) may be incorporated to the sensitivity solution to further refine optimization of pulsed CEST MRI scheme.

4. CONCLUSIONS

Our study derives the steady state non-thermal equilibrium analytical solution of CEST imaging, SNR and CNR efficiency, providing an expeditious and quantitative description of the CEST MRI sensitivity. The solution elucidates the effects of key scan parameters on CEST MRI measurements, thereby facilitating the use of exhaustive optimization strategy to simultaneously optimize multiple parameters and enhance the sensitivity of CEST MRI.

5. MATERIALS AND METHODS

The CEST MRI effect was simulated using Bloch-McConnell equations of a typical 2-pool exchange model in MATLAB (Mathworks, Natick MA), assuming representative bulk water T_1w and T_2w of 2 s and 100 ms, and T_1s and T_2s of 1 s and 15 ms, respectively (65). To test the accuracy of the non-equilibrium steady state analytical solution, we simulated a typical labile proton ratio and exchange rate of 1:1000 and 100 s⁻¹ for a representative chemical shift of 2 ppm at 4.7 Tesla. The SNR was calculated using Eq. 4a and compared with numerically simulated SNR from Bloch-McConnell equations, as described previously (46). To evaluate the optimal experimental conditions for CEST MRI, we calculated multi-dimensional SNR efficiency for each set of TR, FA and B₁, with TR from 0.5 to 10 s with intervals of 0.1 s, FA from 60° to 90° with intervals of 1°, and B₁ from 0 to 10 μT with intervals of 0.25 μT, respectively. In addition, we investigated broad ranges of exchange rate and chemical shift from 25 and to 5500 s⁻¹ with intervals of 87 s⁻¹, and from 0.5 to 10 ppm with intervals of 0.25 ppm, respectively.

Appendix

1) Steady state non-thermal equilibrium CEST effect solution

The control signal without RF saturation can be shown to be

$${\mathrm{S}}_0\left(\mathrm{TR}\right)=\frac{1-{\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{TR}/{\mathrm{T}}_{1\mathrm{w}}}}\cdot \sin (\mathrm{FA})$$ (A1.1)

For the saturated scan, the Z-magnetization at the beginning of the sequence (t=0) after the previous saturation is given by

$${\mathrm{I}}_{\mathrm{sat}}(0)={\mathrm{I}}_{\mathrm{sat}}(\mathrm{TR})\cdot \cos (\mathrm{FA})$$ (A1.2a)

The Z-magnetization evolves towards its equilibrium state following standard relaxation recovery, and we have

$${\mathrm{I}}_{\text{sat}}(\mathrm{Tr})={\mathrm{I}}_{\text{sat}}(\mathrm{TR})·\cos (\mathrm{FA})·{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}+(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}})$$ (A1.2b)

The spin signal evolution following the RF saturation can be described by the spin locking theorem, and we have

$$\begin{array}{l}{\mathrm{I}}_{\mathrm{sat}}(\mathrm{TR})={\mathrm{I}}_{\mathrm{sat}}(\mathrm{Tr})\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}\right)\\ =\left({\mathrm{I}}_{\mathrm{sat}}(\mathrm{TR})\cdot \cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}+\left(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\right)\right)\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}\right)\end{array}$$ (A1.2c)

The steady state signal can be solved as

$${\mathrm{I}}_{\mathrm{sat}}(\mathrm{TR})=\frac{\left(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\right)\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}\right)}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}}$$ (A1.3)

Hence, the detectable signal is the sine projection of magnetization I_sat(TR).

$$\begin{array}{l}{\mathrm{S}}_{\mathrm{sat}}\left(\mathrm{TR}\right)={\mathrm{I}}_{\mathrm{sat}}(\mathrm{TR})\cdot \sin (\mathrm{FA})\\ =\frac{\left(1-{\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\right)\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}+\frac{{\mathrm{R}}_{1\mathrm{w}}{\cos }^2\mathrm{\theta }}{{\mathrm{R}}_{1\mathrm{\rho }}}\cdot \left(1-{\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}\right)}{1-\cos (\mathrm{FA})\cdot {\mathrm{e}}^{-\mathrm{Tr}/{\mathrm{T}}_{1\mathrm{w}}}\cdot {\mathrm{e}}^{-{\mathrm{R}}_{1\mathrm{\rho }}\cdot \mathrm{T}\mathrm{S}}}\cdot \sin (\mathrm{FA})\end{array}$$ (A1.4)

The CESTR and CESTR_ind can be calculated as $\mathrm{CESTR}=\frac{{\mathrm{S}}_{\mathrm{ref}}-{\mathrm{S}}_{\mathrm{lab}}}{{\mathrm{S}}_0}$ and $\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}=\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{lab}}}-\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}$, respectively.

2) CEST MRI SNR derivation

1. For routine CESTR, its standard deviation can be obtained as

   $$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{CESTR}}^2={\left(\frac{\partial \mathrm{CESTR}}{\partial {\mathrm{S}}_{\mathrm{ref}}}\right)}^2{\mathrm{\sigma }}_{\mathrm{ref}}^2+{\left(\frac{\partial \mathrm{CESTR}}{\partial {\mathrm{S}}_{\mathrm{lab}}}\right)}^2{\mathrm{\sigma }}_{\mathrm{label}}^2+{\left(\frac{\partial \mathrm{CESTR}}{\partial {\mathrm{S}}_0}\right)}^2{\mathrm{\sigma }}_0^2\\ =\frac{{\mathrm{\sigma }}_{\mathrm{ref}}^2}{{\mathrm{S}}_0^2}+\frac{{\mathrm{\sigma }}_{\mathrm{label}}^2}{{\mathrm{S}}_0^2}+{\left(\frac{{\mathrm{S}}_{\mathrm{ref}}-{\mathrm{S}}_{\mathrm{label}}}{{\mathrm{S}}_0^2}\right)}^2{\mathrm{\sigma }}_0^2\\ =\left(2+\mathrm{CEST}{\mathrm{R}}^2\right)\frac{{\mathrm{\sigma }}^2}{{\mathrm{S}}_0^2}\end{array}$$ (A2.1)

   If the noise level remains stable and dominated by the thermal noise, the noise terms can be treated as the same for all images. The SNR for the routine CESTR can be shown to be

   $${\mathrm{SNR}}_{\mathrm{CESTR}}=\frac{\mathrm{CESTR}}{{\mathrm{\sigma }}_{\mathrm{CESTR}}}=\frac{\mathrm{CESTR}}{\sqrt{2+\mathrm{CEST}{\mathrm{R}}^2}}\cdot {\mathrm{SNR}}_{{\mathrm{S}}_0(\mathrm{TR},\mathrm{FA})}$$ (A2.2)
2. For the inverse CEST asymmetry of CESTR_ind, we have

   $$\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}=\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{lab}}}-\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}=\mathrm{CESTR}\cdot \left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}\cdot {\mathrm{S}}_{\mathrm{label}}}\right)$$ (A2.3)

   The standard deviation of CESTR_ind can be obtained as

   $$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}^2\approx {\left(\frac{\partial \mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\partial {\mathrm{S}}_{\mathrm{ref}}}\right)}^2{\mathrm{\sigma }}_{\mathrm{ref}}^2+{\left(\frac{\partial \mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\partial {\mathrm{S}}_{\mathrm{label}}}\right)}^2{\mathrm{\sigma }}_{\mathrm{label}}^2+{\left(\frac{\partial \mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\partial {\mathrm{S}}_0}\right)}^2{\mathrm{\sigma }}_0^2\\ =\left[{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}^2}\right)}^2+{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{label}}^2}\right)}^2+{(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{label}}}-\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}})}^2\right]\frac{{\mathrm{\sigma }}_0^2}{{\mathrm{S}}_0^2}\end{array}$$ (A2.4)

   Its SNR can be shown to be

   $$\begin{array}{l}{\mathrm{SNR}}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}=\frac{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\sqrt{\frac{1}{{\mathrm{S}}_0^2}\left[{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}^2}\right)}^2+{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{label}}^2}\right)}^2\right]{\mathrm{\sigma }}^2+\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}^2\frac{{\mathrm{\sigma }}^2}{{\mathrm{S}}_0^2}}}\\ =\frac{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\sqrt{\frac{1}{{\mathrm{S}}_0^2}\left[2\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}^2}\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{label}}^2}+{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}^2}-\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{label}}^2}\right)}^2\right]{\mathrm{\sigma }}^2+\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}^2\frac{{\mathrm{\sigma }}^2}{{\mathrm{S}}_0^2}}}\end{array}$$ (A2.5)

   This can be simplified as

   $$\begin{array}{l}{\mathrm{SNR}}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}=\frac{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\sqrt{\left[2\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}^2}\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{label}}^2}+{\left(\left(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}-\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{label}}}\right)\left(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}+\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{label}}}\right)\right)}^2\right]+\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}^2}}{\mathrm{SNR}}_{{\mathrm{S}}_0(\mathrm{TR},\mathrm{FA})}\\ =\frac{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}{\sqrt{\left[2{\left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}{\mathrm{S}}_{\mathrm{label}}}\right)}^2+{\left(\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}\left(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}+\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{label}}}\right)\right)}^2\right]+\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}^2}}{\mathrm{SNR}}_{{\mathrm{S}}_0(\mathrm{TR},\mathrm{FA})}\end{array}$$ (A2.6)

   Because $\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}=\mathrm{CESTR}\cdot \left(\frac{{\mathrm{S}}_0^2}{{\mathrm{S}}_{\mathrm{ref}}\cdot {\mathrm{S}}_{\mathrm{label}}}\right)$, the ${\mathrm{SNR}}_{{\mathrm{CESTR}}_{\mathrm{ind}}}$ can be further expressed as

   $${\mathrm{SNR}}_{\mathrm{CEST}{\mathrm{R}}_{\mathrm{ind}}}=\frac{\mathrm{CEST}{\mathrm{R}}^2}{\sqrt{2+\mathrm{CEST}{\mathrm{R}}^2\cdot \left(1+{\left(\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{ref}}}+\frac{{\mathrm{S}}_0}{{\mathrm{S}}_{\mathrm{label}}}\right)}^2\right)}}{\mathrm{SNR}}_{{\mathrm{S}}_0(\mathrm{TR},\mathrm{FA})}$$ (A2.7)

   For small CEST effect (i.e., CESTR²<<1), we have ${\mathrm{SNR}}_{{\mathrm{CESTR}}_{\mathrm{ind}}}\approx {\mathrm{SNR}}_{\mathrm{CESTR}}$.
3. For the RF-power based ratiometric analysis (i.e., $\mathrm{PRCESTR}=\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)/\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)$), we have

   $$\begin{array}{l}{\mathrm{\sigma }}_{\mathrm{PRCESTR}}^2\approx {\left(\frac{\partial \mathrm{PRCESTR}}{\partial \mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}\right)}^2{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2+{\left(\frac{\partial \mathrm{PRCESTR}}{\partial \mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}\right)}^2{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2\\ =\frac{1}{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{b}}\right)}{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2+\frac{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{a}}\right)}{\mathrm{CEST}{\mathrm{R}}^4\left({\mathrm{B}}_{1\mathrm{b}}\right)}{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2\\ =\frac{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{a}}\right)}{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{b}}\right)}\left(\frac{1}{\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2}+\frac{1}{\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2}\right)\end{array}$$ (A2.8)

   Hence its SNR can be shown to be

   $$\begin{array}{l}{\mathrm{SNR}}_{\mathrm{PRCESTR}}=\frac{\frac{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}}{\sqrt{\frac{1}{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{b}}\right)}{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2+\frac{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{a}}\right)}{\mathrm{CEST}{\mathrm{R}}^4\left({\mathrm{B}}_{1\mathrm{b}}\right)}{\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2}}\\ =\frac{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)\cdot \mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}{\sqrt{\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{b}}\right)\cdot {\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2+\mathrm{CEST}{\mathrm{R}}^2\left({\mathrm{B}}_{1\mathrm{a}}\right)\cdot {\mathrm{\sigma }}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2}}\\ ==\frac{{\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}\cdot {\mathrm{SNR}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}}{\sqrt{\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{a}}\right)}^2+\mathrm{S}\mathrm{N}{\mathrm{R}}_{\mathrm{CESTR}\left({\mathrm{B}}_{1\mathrm{b}}\right)}^2}}\end{array}$$ (A2.9)

   The same formula is applicable to RF-power based ratiometric analysis of inverse CEST asymmetry (PRICESTR).

3) CEST MRI CNR derivation

The relationship between CNR and SNR of any two signals can be generally described as the following. We denote the contrast as $\mathrm{C}=\mathrm{S}(\mathrm{a})-\mathrm{S}(\mathrm{b})$, where S(a) and S(b) represent two CEST effects. We have

$${\mathrm{\sigma }}_{\mathrm{C}}^2\approx {\left(\frac{\partial \mathrm{C}}{\partial \mathrm{S}(\mathrm{a})}\right)}^2{\mathrm{\sigma }}_{\mathrm{S}(\mathrm{a})}^2+{\left(\frac{\partial \mathrm{C}}{\partial \mathrm{S}(\mathrm{b})}\right)}^2{\mathrm{\sigma }}_{\mathrm{s}(\mathrm{b})}^2={\mathrm{\sigma }}_{\mathrm{S}(\mathrm{a})}^2+{\mathrm{\sigma }}_{\mathrm{S}(\mathrm{b})}^2$$ (A3.1)

The CNR can be shown to be

$$\begin{array}{l}\mathrm{CNR}=\frac{\left|\mathrm{S}(\mathrm{a})-\mathrm{S}(\mathrm{b})\right|}{\sqrt{{\mathrm{\sigma }}_{\mathrm{S}(\mathrm{a})}^2+{\mathrm{\sigma }}_{\mathrm{S}(\mathrm{b})}^2}}=\frac{\left|\mathrm{S}(\mathrm{a})-\mathrm{S}(\mathrm{b})\right|}{\sqrt{{\left(\frac{\mathrm{S}(\mathrm{a})}{{\mathrm{SNR}}_{\mathrm{S}(\mathrm{a})}}\right)}^2+{\left(\frac{\mathrm{S}(\mathrm{b})}{{\mathrm{SNR}}_{\mathrm{S}(\mathrm{b})}}\right)}^2}}\\ =\frac{\left|\mathrm{S}(\mathrm{a})-\mathrm{S}(\mathrm{b})\right|}{\sqrt{{\left(\mathrm{S}(\mathrm{a})\cdot {\mathrm{SNR}}_{\mathrm{S}(\mathrm{b})}\right)}^2+{\left(\mathrm{S}(\mathrm{b})\cdot {\mathrm{SNR}}_{\mathrm{S}(\mathrm{a})}\right)}^2}}{\mathrm{SNR}}_{\mathrm{S}(\mathrm{a})}\cdot {\mathrm{SNR}}_{\mathrm{S}(\mathrm{b})}\end{array}$$ (A3.2)