Abstract
The vertebral arteries (VAs) are anatomically divided into four segments (V1–V4), which cumulatively transport blood flow through neck and ultimately form the posterior circulation of the brain. The vital physiological function of these conduit vessels depends on their geometry, composition and mechanical properties, all of which may vary among the defined arterial segments. Despite their significant role in blood circulation and susceptibility to injury, few studies have focused on characterizing the mechanical properties of VAs, and none have investigated the potential for segmental variation that could arise due to distinct perivascular environments. In this study, we compare the passive mechanical response of the central, juxtaposed arterial segments of porcine VAs (V2 and V3) via inflation-extension mechanical testing. Obtained experimental data and histological measures of arterial wall composition were used to adjust parameters of structure-motivated constitutive models that quantify the passive mechanical properties of each arterial segment and enable prediction of wall stress distributions under physiologic loads and boundary conditions. Our findings reveal significant segmental differences in the arterial wall geometry and structure. Nevertheless, similar wall stress distributions are predicted in these neighboring arterial segments if calculations account for their specific perivascular environments. These findings allow speculation that segmental differences in wall structure and geometry are a consequence of a previously introduced principle of optimal operation of arteries, which ensures effective bearing of physiological load and a favorable mechanical environment for mechanosensitive vascular smooth muscle cells.
Keywords: Arterial mechanics, Elasticity, Vertebral artery, Continuum mechanics, Structure-motivated constitutive model
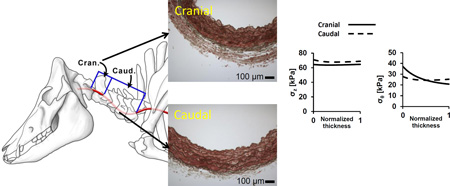
Graphical Abstract
The diverse perivascular environments along the vertebral arteries induce structural and geometrical variations that promote uniform wall stress distributions under physiological conditions and thus support the principle of optimal mechanical operation in conduit blood vessels.
INTRODUCTION
The vertebral artery (VA) is a conduit vessel that directs blood flow cranially through the neck, and is anatomically divided into four arterial segments along its course (V1–V4). The first arterial segment (V1) extends from its origin at the subclavian artery to the C6 transverse process. The second arterial segment (V2) comprises the intraosseous course from the C6 to C2 vertebrae through the transverse foramina. The third arterial segment (V3) takes an extraosseous course from the C2 transverse process until entry into the dura mater at the foramen magnum. And finally, the fourth arterial segment (V4) is the intradural portion from the foramen magnum until the two VAs merge to form the basilar artery. Essentially, V1 is at the transition from the thorax to the neck, V2 and V3 course through the neck (and are therefore the most vulnerable to trauma) and V4 is the final portion of the artery within the skull before it merges to form the basilar artery [1, 2].
In the event of a blunt cervical spine trauma, arterial injury occurs in 30% of patients, with the most injury sustained by the vertebral and carotid arteries. Injuries to the VA present as dissections, pseudoaneurysms, and arterial occlusions [3, 4]. Studies show that 18% of injuries involve the V1 arterial segment, 67% involve the V2 (intraosseous) arterial segment, 31% involve V3 arterial segment, and 6% the V4 arterial segment [5]. All VA injuries can lead to a delayed onset of vascular occlusion, with potentially devastating consequences that include posterior cerebral bleeding or irreversible ischemic tissue damage [6]. For example, in the cases where delayed presentation of vertebrobasilar ischemia from posterior circulation occurs, reported mortality rates range from 75% to 86% [7].
Treatment modalities for VA injuries include antiplatelet and anticoagulation therapies, open surgical repair, and endovascular approaches [5]. In the cases of enlarging pseudoaneurysms or symptomatic dissections, endovascular stent therapy is the most common intervention with consistent and acceptable clinical outcomes [8]. Additional endovascular interventions including microcatheters, balloons, glues, and coils have shown utility and promise in a subset of injuries and disease states [9–11]. Given the rates and varied clinical outcomes of these injuries and the established interplay between most interventional modalities and the mechanical behavior of the compromised vessels, there is a clear need to characterize the mechanical properties of VAs [8, 10, 12].
Comprehensive mechanical characterization of the VAs likely requires arterial segment-specific characterization of vessel wall geometry, composition, and mechanical properties. The V2 and V3 arterial segments are of particularly high clinical relevance, as they are implicated in an overwhelming majority of VA injuries (over 90%) following blunt cervical trauma [5]. Moreover, the transition from the V2 to V3 arterial segment is anatomically coupled with a distinct change in the perivascular environment. That is, the V2 arterial segment is embedded within the bone (intraosseous) and thus possibly subjected to restricted deformation while the V3 arterial segment exists outside the bone (extraosseous). We posit that understanding and differentiating the arterial segmental mechanical behavior of the VA can provide guidelines to evaluate predisposing factors for delayed and sudden occurrence of complications in high grade injuries and design site-specific protocols for endovascular interventions.
Among the numerous biomechanical investigations devoted to conduit blood vessels, only a few deal with VAs [12–16]. While these studies provide useful information that describes the vessel mechanical response, they do not enable development of a constitutive formulation of the mechanical properties of the vessel wall. This is an important distinction, as a constitutive material model is required to calculate the local stress environment of mechanosensitive vascular cells and fully understand the mechanical implications of both vascular injury and clinical intervention. Moreover, segmental differences in the mechanical properties of the VA could be used to discriminate among distinct modes of injury and disease etiologies. The objectives of this study are two-fold. First, an integrated experimental-theoretical approach was applied to quantify the passive mechanical response of the porcine V2 and V3 arterial segments. Obtained data were then processed to yield a structure-motivated constitutive model of the arterial tissue and enable segmental comparisons in wall geometry, composition, and mechanical properties. Second, a comparative analysis of the stress distribution across the arterial wall was performed between these arterial segments, and the results obtained were interpreted in the framework of a previously elaborated principle of optimal mechanical operation [17].
MATERIALS AND METHODS
Vessel isolation
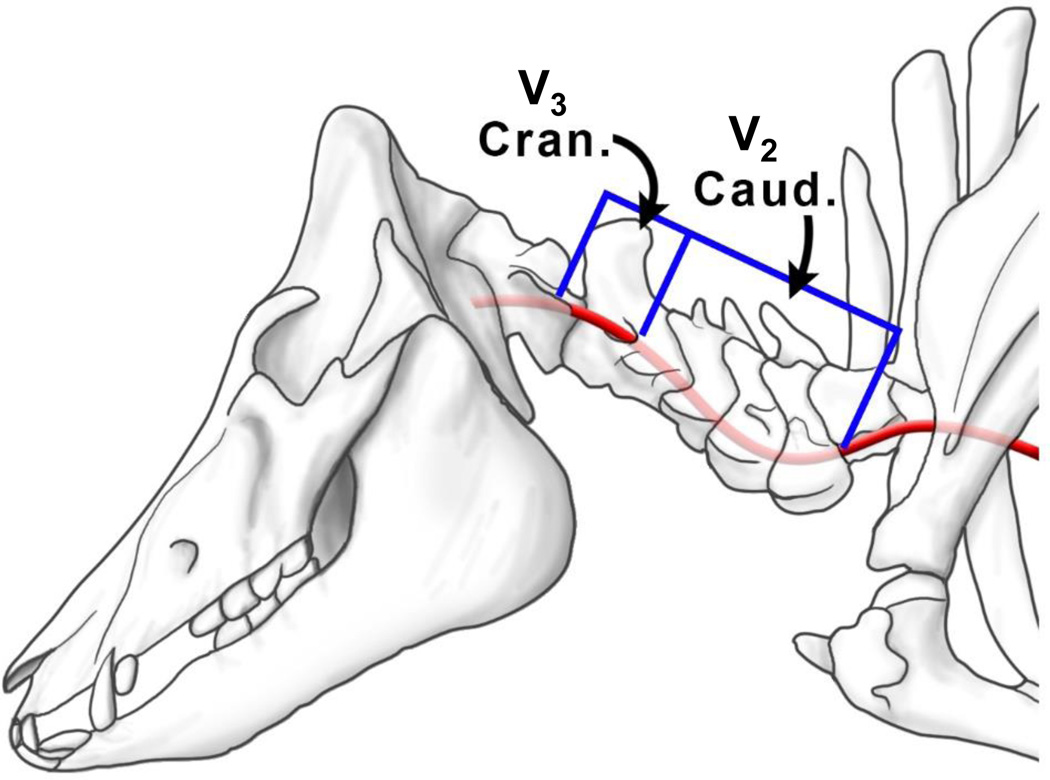
Whole porcine spines were purchased from a local slaughterhouse immediately after sacrifice of adult animals (8–12 month old, 75–125 lbs, male American Yorkshire Pigs), cooled on ice, and transported immediately to the laboratory. The transverse canal was approached both ventrolaterally and from the vertebral canal using an autopsy saw (Stryker Model 810) to cut within 3–5 mm of the canal. The transverse canal was fully accessed using chisels, bone cutters, and rongeurs. The vessels were then removed using scissors and scalpels to dissect minor arteries and connective tissue. Care was taken to neither nick the VA nor stretch it beyond its anatomical length. The experimental sample set includes 5 caudal VAs embedded in the bone from C2 – C6 (V2 arterial segment) and 5 cranial VAs (V3 arterial segment) (Fig. 1). Excised vessels were rinsed and submerged in phosphate buffer solution and cooled in ice until the initiation of mechanical testing. No more than three hours passed from the time of animal sacrifice to the initiation of mechanical testing.
Figure 1.
Schematic of the caudal (V2 arterial segment) and cranial (V3 arterial segment) portions of the porcine vertebral artery.
Zero-stress configuration
The zero-stress configuration of each vessel was obtained by introducing a radial cut into a ring-shape sample (1 mm thick), and was considered to be a circular sector. The zero-stress configuration was quantified by measuring the inner and outer arc lengths (Li and Lo) and the thickness (H) of the idealized sector via analytical microscopy (Image-Pro 6.0).
The opening angle (Φ) and cross-sectional area (A) of the sector were then calculated as [18]:
| (1) |
Mechanical testing
The sample was cannulated via sterile suture and mounted within a chambered mechanical testing system (Bose BioDynamic 5270, Eden Prairie, MN) configured for an inflation-extension test. The sample was submerged in and perfused with continuously aerated (95% O2 + 5% CO2) Krebs-Henseleit solution at 37°C and pH of 7.4. The passive mechanical response was assessed under a fully relaxed smooth muscle cell state, which was induced by flushing the circulating medium with a 10−5 M sodium nitroprusside solution and allowing 15 minutes for acclimation [19]. To initiate mechanical testing, each sample was mechanically preconditioned via repeated inflation (internal pressure of 20–200 mmHg) at an intermediate degree of axial stretch (axial stretch ratio of 1.3). The in-vivo axial stretch ratio of each vessel was estimated using a series of inflation-extension tests in which the sample was inflated (internal pressure of 20–200 mmHg) at constant axial stretch ratios between 1.1 and 1.5. The in-vivo axial stretch ratio was taken to be the axial stretch ratio under which the axial force remained approximately constant during the inflation-deflation process [20, 21]. Samples were then maintained at the identified in-vivo axial stretch ratio and once again mechanically preconditioned with five pressurization cycles (20–200 mmHg) to obtain an elastic pressure-diameter response. Immediately following preconditioning, samples were subjected to quasi-static inflation (20–200 mmHg) at the in-vivo axial stretch ratio. The preconditioning/testing procedure was then repeated at two additional axial stretch ratios, which correspond to 110% and 120% of the in-vivo value. The test procedure was repeated three times for each sample, and the average axial force (F), luminal pressure (P), and deformed outer diameter (do) were recorded for each experimental state via automated system software (Wintest) and an external camera integrated via LabView (National Instruments).
Histological quantification
The area fractions of total collagen, elastin, and smooth muscle were determined following a previously described semi-quantitative image thresholding protocol [22]. Briefly, ring samples from the middle section of each vessel were fixed in 4% paraformaldehyde, embedded in paraffin wax, and cut via microtome to yield transverse sections (5 µm thick) for histological analysis. Slides were stained using a combination of Verhoeff’s elastic and Masson’s trichrome stain [23]. Images were obtained using a Nikon E600 microscope with CCD camera. The numbers of red, blue, and black pixels in each image were quantified using ImageJ software (NIH) to estimate the mass fractions of smooth muscle, collagen, and elastin, respectively. All slides were stained in the same batch; unstained pixels were not included in the analysis; and, threshold values were fixed to maintain consistency. Black pixels were quantified using a bandpass filter from brightness 0–101. Blue pixels were quantified using a bandpass filter from brightness 101–255 and hue 18–198. Red pixels were quantified using a bandpass filter from brightness 101–255 and band-stop filter from 18–198. The area fractions of other wall constituents (e.g., ground substance) were neglected.
Geometry of intraosseous canal
In order to characterize the osteological constraints on the VAs, short and long axis measurements of the nominally elliptical transverse foramina of three pig necks from the same supplier were taken using Neiko Electronic Digital Calipers. Measurements from the C2 – C6 vertebrae were taken on both the left and right transverse foramina. Although there were notable anomalies within even this small sample (i.e., incomplete foramina that would more appropriately be classified as “notches”, and incidences of evidently bifurcated VAs resulting in split transverse foramina), only VA samples that conform to typical morphology were selected for mechanical testing, and thus these anomalous osteological morphologies were likewise excluded.
Constitutive framework
Following well-elaborated methodology, the strain and stress analysis of an arterial wall is based on a semi-inverse method of determining the loads required to realize a prescribed finite deformation. Under the considered loading conditions, the VA is assumed to undergo an axisymmetric, finite elastic deformation, which is characterized by the right Cauchy-Green strain tensor,
| (2) |
where λ is the stretch and subscript r, θ, or z indicates the radial, circumferential, or axial direction; R and r are the radial coordinates of an arbitrary point within the arterial wall before and after deformation; L and l are the length of the arterial segment before and after deformation. Due to material incompressibility, detC = 1, which yields
| (3) |
where ro is the deformed outer radius of the vessel. The values of ro and λz completely describe the deformation of the vessel regardless of the tissue mechanical properties. For the case of axisymmetric deformation, the constitutive stress–strain relations of arterial tissue are derived from a strain energy density function (SEF), which is a function of the principle stretches. Taking into account material incompressibility, the explicit dependence of the SEF on the radial stretch λr can be eliminated, and the constitutive equations that relate the stretches to the components of the Cauchy stress in the circumferential, σθ, and the axial, σz, directions are
| (4) |
where is the SEF and σr is the radial stress [24]. After integrating the differential equations of equilibrium and accounting for the fact that the artery is subjected to an internal pressure, i.e. σr (r = ri) = −P, then
| (5) |
Using the condition that the outer surface is traction-free, i.e. σr (r = ro) = 0, and integrating the axial stress over the arterial cross-section, it follows that the value of applied internal pressure P and axial force F required to realize the prescribed deformation are
| (6) |
The obtained solution can be used in two aspects. First, via appropriate processing of the data obtained from a set of biaxial experiments on tubular arterial specimens, the solution for the finite inflation and extension of a thick-walled tube given above can be used to identify the mechanical properties of the arterial tissue. After motivated selection of the analytical form of the SEF, material constants can be determined from the condition
| (7) |
where the superscript E and T refer to the experimentally recorded and theoretically calculated values of the pressure and axial force corresponding to a set of N experimental states; subscript n indicates a particular experimental state; w1 and w2 are weighting coefficients, such that w1 + w2 = 1.
A second use of the obtained solution is that given the vessel geometry in the stress-free state, the SEF, and the value of the applied pressure and axial stretch in a deformed state, then the stretch and stress distribution across the wall can be calculated via Eqs. (2)–(6). Moreover, this solution enables calculation of linearized measures of the vessel mechanical response around a specified deformed state, such as pressure-radius modulus (called also Peterson's modulus) Ep given by the expression
| (8) |
where Δr0 is the small increase in deformed outer radius due to a small increase in pressure ΔP [20]. Or similarly, the compliance (C), calculated as:
| (9) |
where is the mid-wall radius and Δrm the difference in mid-wall radii at two pressures. ΔP is the difference in those two pressures and r̄m is the mid-wall radius at the mean value of those pressures
Consider the particular case when the radial deformation (inflation) of the vessel is restricted above certain value of the internal pressure P*. Thus
| (10) |
where is limiting value of the deformed outer radius. This kinematic constraint canbe realized when the vessel is inserted into a rigid tube with an internal radius equal to .
In this case for pressures above P* the components of the circumferential and axial Cauchy stresses are calculated again from Eq. (4), but the radial stress is
| (11) |
The outer surface is no longer traction free. Inserting r = ro into Eq.(11) yields the radial stress at the outer surface . A comparison between the corresponding expression for and the expression for P* in Eq. (10) yields .
Statistical analysis
Mean values of stress-free dimensions, wall structure, loaded dimensions, and descriptors of structural/wall mechanics for VA segments (V2 and V3) were compared using unpaired, two-tailed t-tests. Differences in mean values were considered significant when p < 0.05.
RESULTS
Zero-stress configurations of the V2 and V3 arterial segments
The zero-stress wall thickness of the V2 and V3 arterial segments significantly differ, with an average wall thickness that is approximately 55% greater in the latter arterial segment. Other geometrical descriptors of the zero-stress configuration (opening angle, inner arc length, and outer arc length) were not statistically different between the arterial segments, although in general values were greater in the V3 arterial segment (Table 1).
Table 1.
Geometrical parameters of the stress-free and loaded configurations of the V2 and V3 arterial segments, as well as structural mechanical properties.
| V2 (n=5) | V3 (n=5) | |
|---|---|---|
| Stress-free dimensions | ||
| Inner arc-length(Li) [mm] | 5.23 (0.54) | 5.24 (0.97) |
| Outer arc-length(Lo) [mm] | 7.26 (0.58) | 8.09 (0.85) |
| Opening angle(OA) [◦] | 53.77 (16.07) | 66.67 (17.09) |
| Thickness(H) [mm] | 0.47 (0.09) | 0.74 (0.11)* |
| Wall structure | ||
| Medial thickness(HM) [mm] | 0.41 (0.08) | 0.51 (0.15) |
| Adventitial thickness(HA) [mm] | 0.05 (0.01) | 0.23 (0.05)* |
| HM/HA | 8.14 (2.46) | 2.56 (1.39)* |
| Loaded dimensions (P=100 mmHg, λz=λin-vivo) | ||
| In vivo axial stretch(λin-vivo) | 1.23 (0.12) | 1.32 (0.24) |
| Inner diameter (di) [mm] | 2.00 (0.29) | 1.94 (0.52) |
| Outer diameter(do) [mm] | 2.65 (0.37) | 2.97 (0.61) |
| Wall thickness(h) [mm] | 0.33 (0.05) | 0.52 (0.09)* |
| Structural mechanics (P=100 mmHg, λz=λin-vivo) | ||
| Peterson’s modulus [kPa] | 253.61 (118.91) | 214.47 (112.27) |
| Compliance [Mpa−1] | 6.96 (2.85) | 7.89 (4.23) |
Arterial wall composition and microstructural organization
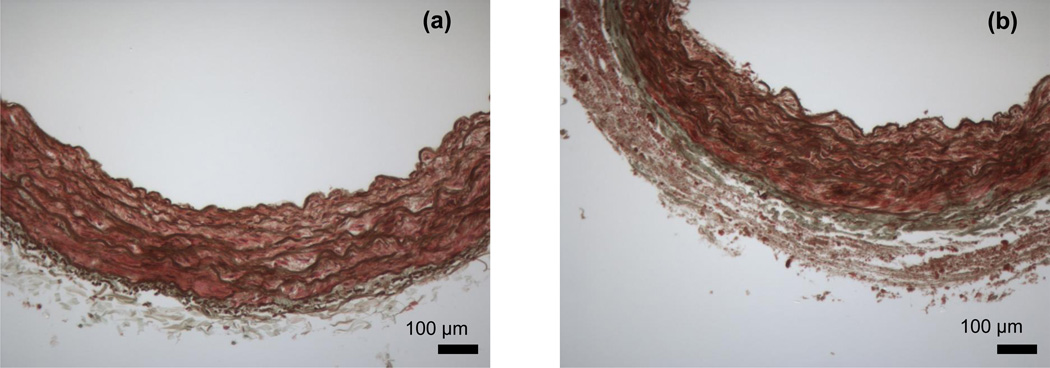
Circumferentially-oriented elastic lamellae were observed within the media of both the V2 and V3 arterial segments, a feature consistent with the microstructure of other conduit vessels [26–28]. The area fractions of elastin, collagen, and vascular smooth muscle were determined through histological image thresholding and were found to be nearly identical in the V2 and V3 arterial segments (Table 1). Representative cross-sections can be found in Figs. 2a and 2b. Quantitative microscopy was used to determine the mean thickness of the media and adventitia of each arterial segment, with a significantly thicker adventitial layer observed in the V3 arterial segment (Table 1).
Figure 2.
Representative histological images of Verhoeff-Masson’s stained cross-sections for (a) V2 and (b) V3 arterial segments of the porcine vertebral artery.
Intraosseous canal dimensions
The intraosseous canal formed by the C2–C6 vertebrae exhibited an ellipsoid cross-sectional geometry, and thus is well-characterized by long- and short-axis measurements. The average dimensions in these vertebrae were: were 5.62 ± 1.21 mm (long-axis) and 3.41 ± 0.65 mm. Moreover, densely packed fibrous tissue was also present in the intraosseous canal, although the amount and geometry of this tissue notably varied along the length of the canal.
Experimentally recorded mechanical response
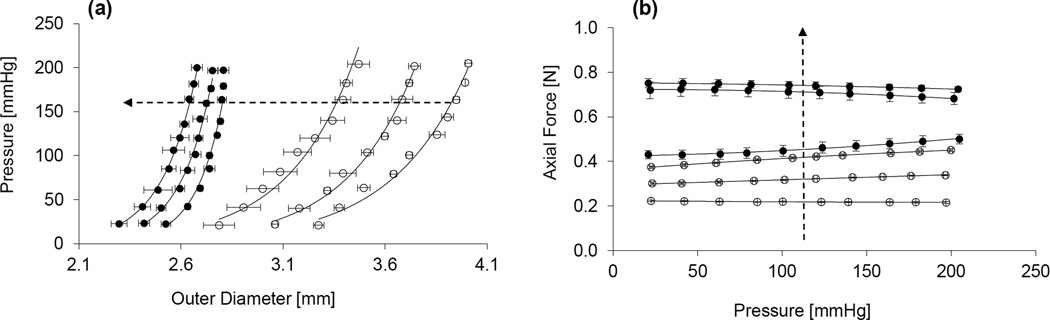
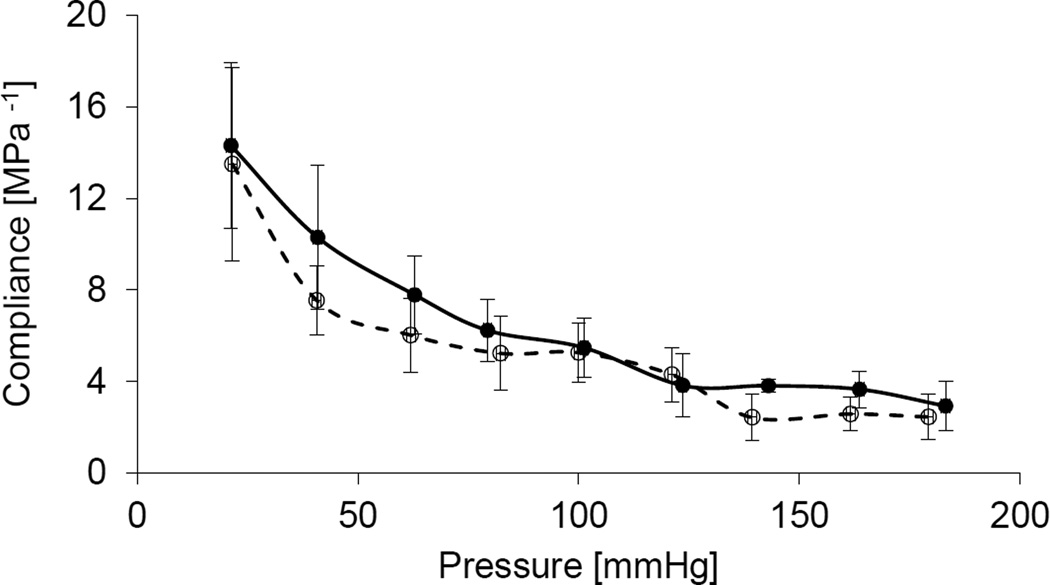
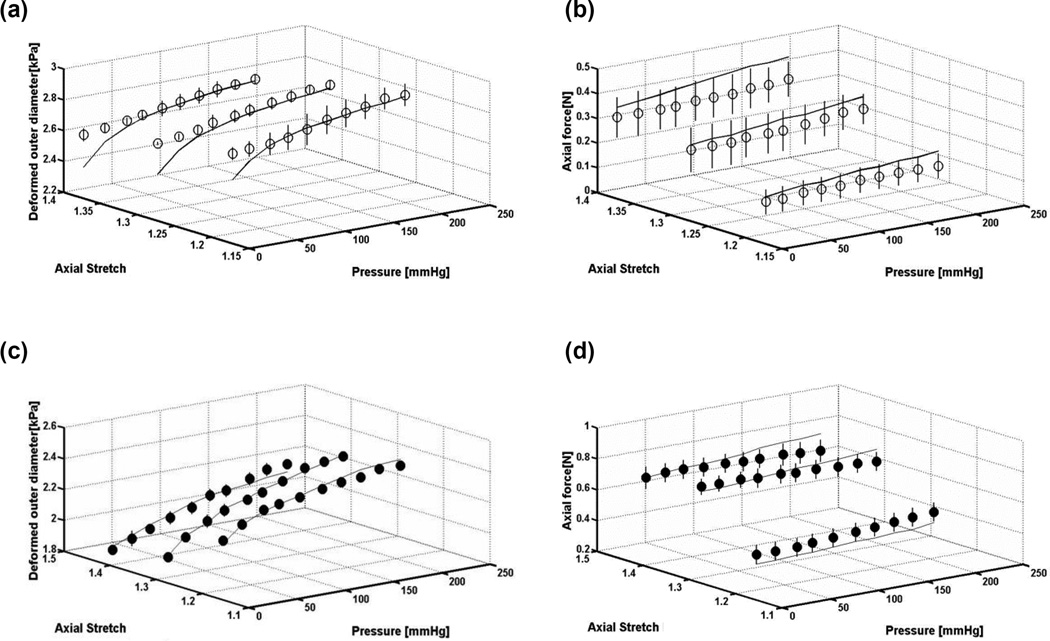
The passive mechanical responses of the porcine VAs were assessed via quasi-static inflation-extension tests, generating bi-axial data in terms of the pressure – deformed outer diameter and axial force – pressure relationships at multiple axial stretches. A typical nonlinear pressure-deformed diameter was observed in both arterial segments at all levels of fixed axial stretch, characterized by a steepening of the curves at higher pressures (Fig. 3a). The axial force – pressure relationships show that axial force increases with axial stretch over the examined pressure range, with the V3 arterial segment exhibiting uniformly higher axial forces at all loading states (Fig. 3b). Peterson’s modulus (Ep) and compliance (C) were calculated for each vessel at physiologic loading conditions (P = 100 mmHg, λz = λin, vivo), with no statistical differences observed between the V2 and V3 arterial segments (Table 1). Moreover, the similarity in arterial segmental compliance was persistent over the examined range of pressures (Fig. 4).
Figure 3.
Representative (a) pressure – outer diameter and (b) axial force – pressure relationships of the V2 (empty circles) and V3 (solid circles) segments of the porcine vertebral artery at multiple axial stretches. Dotted arrow indicates direction of increasing axial stretches, which are 100%, 110% and 120% of the in-vivo value. Error bars represent the standard deviation of three repeat measurements.
Figure 4.
Compliance – pressure relationships at the in-vivo axial stretch of V2 (empty circles) and V3 (solid circles) segments of the porcine vertebral artery. Error bars represent the standard deviation of three repeat measurements.
Constitutive model parameter adjustment
We used a four fiber, structure-motivated constitutive model of the arterial wall proposed in [25], with the form
| (12) |
where φe and φc are the area fractions of elastin and collagen determined via a semi-quantitative microscopy, respectively, and total collagen content is assumed to be equally distributed among the four collagen fiber families (represented by the second term on the right-hand side of Eq. 12). Therefore in this structure-motivated model, the first and second terms on the right-hand side of Eq. 12 reflect the contribution of elastin and collagen to load-bearing, respectively. is the first invariant of the right Cauchy-Green strain tensor. b, bk1, and bk2 are material constants, with subscript k denoting a family of collagen fibers oriented at a mean angle of αk with respect to the longitudinal vessel axis. The four collagen fiber families considered are orientated axially (α=0°), circumferentially (α=90°), or helically (two symmetric families, with α = +/− the helical angle determined via parameter adjustment) within the arterial wall with respect to the longitudinal direction. Therefore, is the stretch of each family of collagen fibers due to deformation.
Given the recorded mechanical data and zero-stress configuration for each sample, the material parameters for the proposed constitutive model were adjusted through minimizing the objective function which reflects the agreement between experimental measurements and theoretical predictions (Eq. 7). For each sample, the ranges over which parameter values were sought were identical, with limiting values based on the physical meaning of each parameter as well as on previous studies [28, 29]. Multiple iterations of functional minimization were performed to ensure that the obtained parameter values were insensitive to the initial guesses within the prescribed ranges. No statistically significant differences were found between the adjusted material parameters of the V2 and V3 arterial segments, and a high degree of variance was found among parameter values within each group (Table 2). Such a high degree of variation in parameter values among samples of a given vessel type is typical for nonlinear models of arterial tissue [28, 29]
Table 2.
Material parameters and area fractions of elastin, smooth muscle, and collagen for structure-motivated models of the V2 and V3 arterial segments. Material parameters (b, b11, b12, b21, b22, b31, b32, b41, b42, and α) were adjusted for best-fit of model predictions with experimental data, while area fractions were based on semi-quantitative histology on arterial samples. Note: It is accepted that the contribution of smooth muscle to to passive response of arterial tissue is negligible; therefore the area fraction of smooth muscle (φsm) was not utilized in the developed model and is included here only for completeness.
| b [kPa] | b11 [kPa] |
b12 | b21 [kPa] |
b22 | b31 and b41 [kPa] |
b32 and b42 |
Helical angle α [±°] |
Error | φe [%] |
φsm [%] |
φc [%] |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V2 | ||||||||||||
| 1 | 20.87 | 4.83 | 2.44 | 1518.12 | 0.20 | 372.39 | 7.00 | 58.41 | 0.57 | 32.40 | 51.80 | 8.28 |
| 2 | 80.55 | 3426.88 | 0.20 | 709.34 | 0.28 | 179.42 | 3.17 | 37.40 | 0.41 | 20.59 | 65.60 | 9.83 |
| 3 | 33.73 | 184.23 | 8.00 | 1139.02 | 0.20 | 473.74 | 2.74 | 52.49 | 0.74 | 24.56 | 63.11 | 16.76 |
| 4 | 116.59 | 16.86 | 7.98 | 3232.84 | 0.21 | 174.20 | 6.58 | 58.57 | 0.87 | 21.28 | 67.97 | 9.08 |
| 5 | 1.52 | 1476.95 | 0.20 | 291.84 | 1.48 | 460.63 | 1.87 | 41.35 | 0.55 | 29.48 | 65.65 | 4.56 |
| MEAN | 50.55 | 1021.95 | 3.76 | 1378.23 | 0.47 | 332.07 | 4.27 | 49.64 | 0.63 | 25.66 | 62.82 | 9.70 |
| SD | 46.98 | 1477.40 | 3.96 | 1134.02 | 0.56 | 147.01 | 2.35 | 9.79 | 0.18 | 5.15 | 6.40 | 4.43 |
| V3 | ||||||||||||
| 1 | 62.82 | 474.84 | 0.53 | 3.81 | 1.88 | 20.04 | 2.37 | 32.20 | 0.29 | 21.48 | 64.24 | 10.48 |
| 2 | 3.91 | 8.53 | 4.21 | 2324.42 | 0.20 | 847.40 | 0.86 | 51.37 | 1.53 | 32.01 | 54.19 | 11.47 |
| 3 | 20.95 | 180.34 | 0.20 | 577.32 | 3.35 | 186.44 | 5.35 | 30.21 | 0.73 | 40.70 | 50.34 | 7.41 |
| 4 | 0.48 | 272.76 | 7.66 | 493.76 | 0.32 | 610.86 | 4.81 | 50.55 | 0.65 | 22.85 | 61.74 | 9.30 |
| 5 | 412.35 | 7.07 | 0.20 | 23.92 | 0.20 | 3.53 | 7.00 | 57.72 | 1.78 | 9.92 | 76.43 | 11.32 |
| MEAN | 100.107.41 188.71 | 2.56 | 684.65 | 1.19 | 333.65 | 4.08 | 44.41 | 0.99 | 25.39 | 61.39 | 9.99 | |
| SD | 176.301.48 196.51 | 3.32 | 953.53 | 1.40 | 377.42 | 2.45 | 12.39 | 0.63 | 11.61 | 10.11 | 1.68 | |
Model predictions
Model predictions for the pressure – deformed outer diameter and axial force – pressure relationships of both the V2 and V3 arterial segments agree well with experimental data (Fig. 5). Consistently acceptable agreement between theoretical predictions and experimental data across all samples (R >0.91) indicates the proposed structure-motivated constitutive formulation is an adequate model for VA mechanics.
Figure 5.
Representative pressure – deformed outer diameter and pressure-axial force relationships for (a,b) V2 and (c,d) V3 arterial segments at multiple axial stretches, with comparison of model predictions (solid line) to experimentally recorded measurements (open circles). Error bars represent the standard deviation of three repeat measurements.
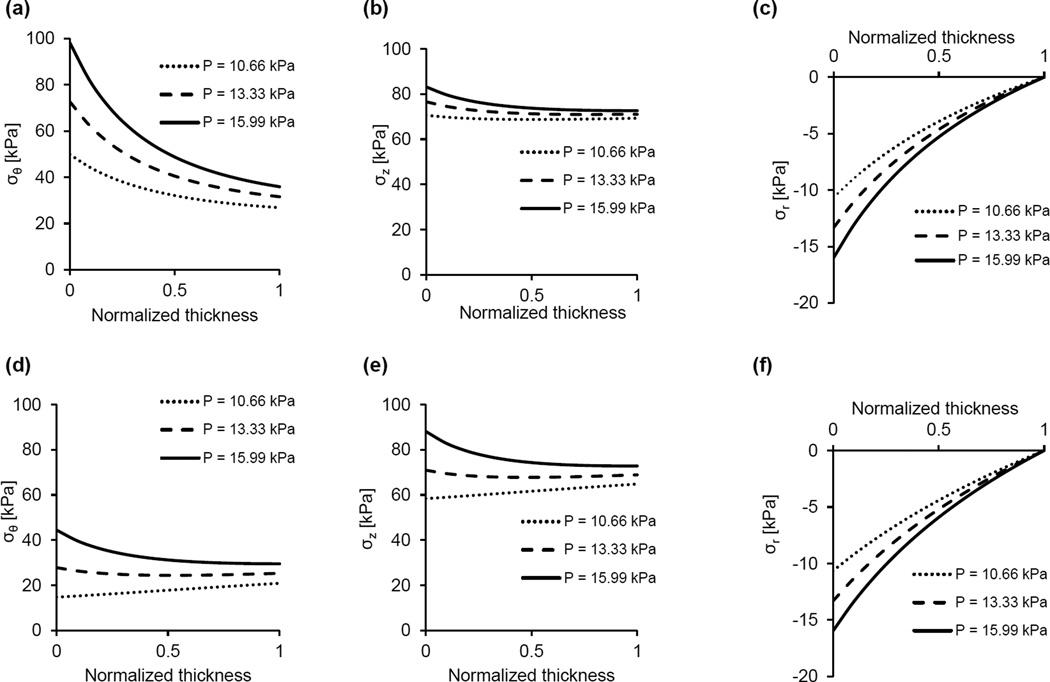
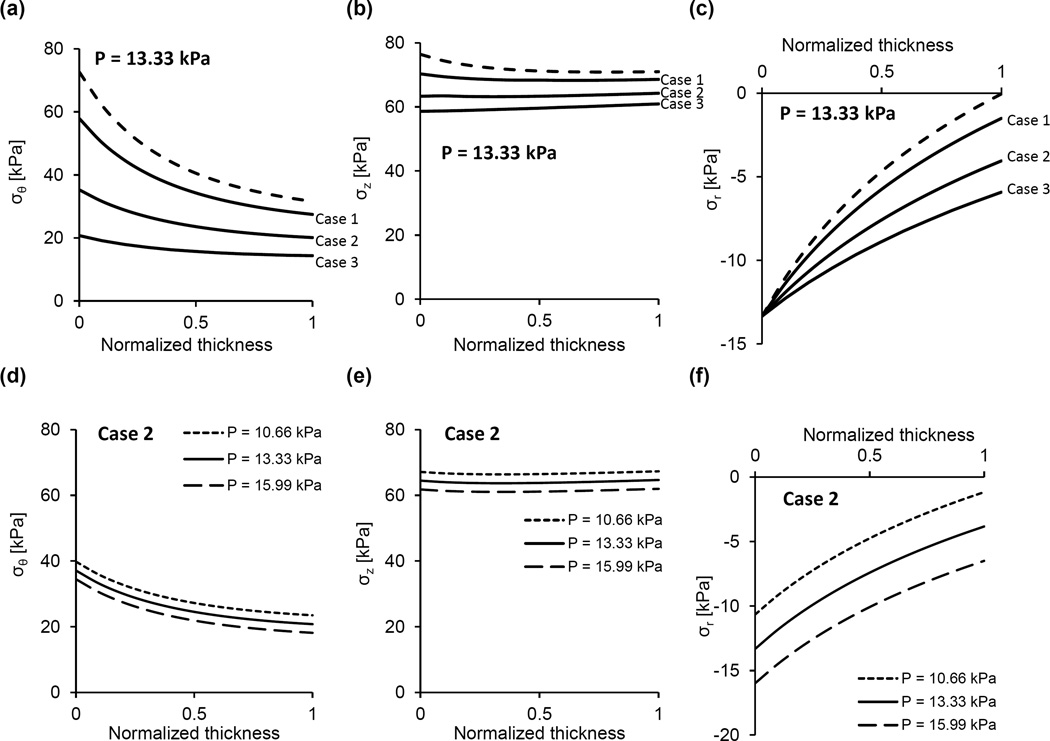
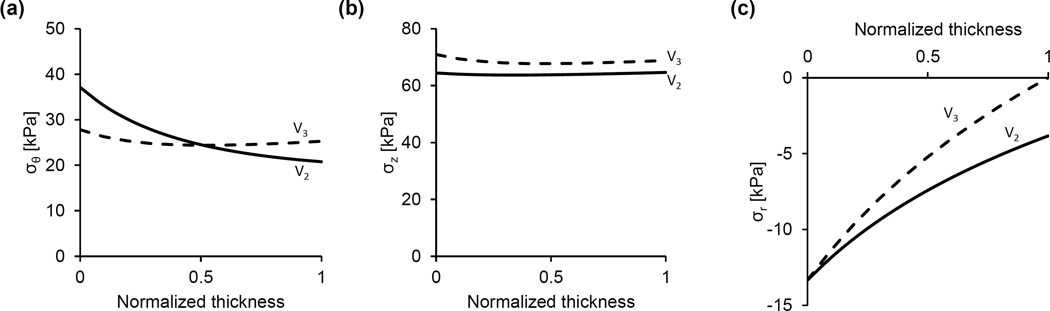
The constitutive model was used to calculate the stress distributions across the arterial wall at in-vivo axial stretch and various pressures and/or degrees of radial restriction. We first calculated the distributions of the radial, circumferential, and axial stresses when no radial restriction is imposed on the arterial segments and pressure varies over the physiologic range (Fig. 6). Because this might be not the case for the V2 arterial segment in-vivo, we then calculated the stress distributions when its radial deformation is restricted (Fig. 7). The upper panels (Figs. 7a–7c) show the stress distributions at fixed internal pressure (13.33 kPa) and variable degrees of radial restriction. In this representative example, if the radial deformation is unrestricted the deformed outer radius is 1.40 mm and the stress distributions are given by the dashed line in these figures. When kept at the in-vivo axial stretch and subject to no internal pressure, the deformed outer radius of this sample is 1.18 mm. Variable geometrical constraints were imposed such that the deformed outer radius cannot exceed values of 1.39 mm, 1.37 mm and 1.35 mm, corresponding to a 4.6%, 13.6% and 22.7% decrease in maximal radial displacement, respectively, when compared to the unrestricted case. The lower panels (Figs. 7d–7f) show the stress distributions at fixed radial restriction (maximal deformed outer radius of 1.37 mm) and under variable pressures. Finally, Fig. 8 shows the stress distributions in the case of geometrical restriction (maximal deformed outer radius of 1.381 mm) such that the mid-wall circumferential stresses in V2 and V3 arterial segments are equal.
Figure 6.
Representative predictions of the circumferential, axial, and radial stress distributions across the arterial wall at the in-vivo axial stretch under various pressures for the V2 (a–c) and V3 (d–f) arterial segments. In all cases (a–f), radial deformation is unrestricted.
Figure 7.
Representative predictions of the (a) circumferential, (b) axial, and (c) radial stress distributions across the arterial wall of the V2 arterial segment at the in-vivo axial stretch and pressure of 13.33 kPa. The dashed line represents unrestricted radial deformation, where the deformed outer radius ro is 1.40 mm. Conversely, cases 1–3 indicate different degrees of restriction on the radial deformation characterized by a maximal deformed outer radius (ro*) and the lumen pressure at which this limiting radius is realized (P*). Specifically, for case 1, ro*= 1.39 mm and P* = 11.83 kPa; for case 2, ro*= 1.37 mm and P* = 9.28 kPa; and for case 3, ro*= 1.35 mm and P* = 7.42 kPa. (d–f) Stress distributions across the wall of the V2 arterial segment at fixed radial restriction (maximal deformed outer radius of 1.37 mm) under various pressures.
Figure 8.
Representative predictions of the (a) circumferential, (b) axial, and (c) radial stress distributions across the arterial wall of the V2 and V3 arterial segments at the in-vivo axial stretch and pressure of 13.33 kPa. In the case of the V2 arterial segment, a restriction on the deformed outer radius was imposed and tuned such that the mid-wall circumferential stresses of the V2 and V3 arterial segments are equal. In this case, the maximal deformed outer radius, ro*, of the V2 arterial segment is 1.381 mm (the unrestricted deformed outer radius under the applied loads is ro is 1.40 mm).
DISCUSSION
The aim of this study was to quantify the passive mechanical response of the central segments (V2 and V3) of the porcine vertebral artery (VA) and develop structure-motivated constitutive models to facilitate arterial segment comparisons in terms of wall mechanical properties and stresses. The passive mechanical response of the each sample was recorded as internal pressure-deformed outer diameter and axial force-internal pressure relationships at various degrees of axial stretch that span the in-vivo value. Structure-motivated constitutive models that incorporate compositional information on the arterial wall were adjusted via numerical algorithms that seek the best fit between experimental data and theoretical predictions. The models were used to calculate the circumferential wall stress distribution in each arterial segment under prescribed loading and boundary conditions, as well as calculate values of Peterson’s modulus and compliance at physiological loads. While quantitative results obtained in porcine VAs may not reflect human VAs, we expect that the observed effect of the perivascular environment on VA structure and mechanics will be retained among species.
The mechanical response of the VAs is qualitatively similar to that of other conduit vessels, as both arterial segments exhibit a steepening of the pressure-deformed diameter curves at higher pressures and an independence of axial force on pressure when fixed at the in-vivo axial stretch (Fig. 5). Also similar to most conduit vessels, the V3 arterial segment manifests nearly uniform distributions of circumferential and axial stress across the wall thickness, (Fig. 6d and 6e), a feature that is due to the residual strains present in the traction free configuration [25, 26]. The magnitude of the opening angle in this vessel, which is an indicator for the existence of residual strains, is similar to values reported for porcine carotid and primary renal arteries [27, 28].
If the V2 arterial segment is considered unrestricted, the circumferential stresses are higher than those in the V3 arterial segment (Fig. 6a vs. Fig. 6b). Moreover, with no restriction and under physiological loading, the V2 arterial segment stress distribution is not homogenous despite the existence of residual strains. While these model predictions refer to the experimental mode of unrestricted inflation, they are not representative of the deformation experienced by this artery in the living organism. The V2 artery is surrounded by bone and enclosed perivascular tissue that likely impose restrictions on the inflation of the vessel when the pressure exceeds a certain value. Unfortunately, it was not possible to measure both the dimensions of V2 artery in the state of zero-stress and the dimensions of the intraosseous canal with intact, densely packed fibrous tissue in which the artery is embedded. The effect of plausible restriction on the radial displacement was simulated by prescribing the maximal value of deformed outer radius. As expected, under physiological pressure when the radial displacement of the outer arterial surface is reduced compared to displacement in the unconfined case, the circumferential and axial stress magnitudes and their gradients across the thickness significantly diminish (Figs. 7a and 7b). The spatial variation of the compressive radial stress is also altered, and at the outer surface represents the reactive traction of a rigid boundary. An interesting result is the effect of restricted radial deformation on the circumferential and axial stresses over a range of physiological pressures (Fig. 7d, e). These stresses decrease as the pressure increases, while the gradients virtually do not change. This result is due to the fact that as the pressure is increased the stresses produced by deformation remain constant and, in accordance with Eq. (11), the contribution of radial stress due to material incompressibility is a slightly increasing compressive stress.
It was tempting to identify the geometrical restriction on the V2 arterial segment for which the circumferential stress is close to stress of the V3 arterial segment when subject to physiological loading (Fig. 8). This allows us to speculate that the geometry and the tissue properties of the two neighboring arterial segments change in the manner to keep the stress fields very close despite the difference in their perivascular environment. This conclusion is in line with the central premise of our previous findings that the zero-stress state geometry and mass fractions of the basic structural constituents of aortic tissue meet a principle of optimal mechanical operation that ensures effective bearing of the physiological load and a favorable mechanical environment for mechanosensitive vascular smooth muscle cells [17]. A supportive finding to this speculation is the pronounced differences in wall structure and thickness between the arterial segments, where the comparatively low V2 arterial segment wall thickness is due primarily to nearly absent adventitial layer (Table 1). The major role of adventitia is to prevent overstretching of the vessel under high pressures. We posit that in the V2 arterial segment, the surrounding bone and enclosed perivascular tissue prevent the possibility of vessel over-inflation, thus satisfying a primary physiological role of the adventitial layer and rendering it functionally redundant.
The Peterson's moduli of V2 and V3 arterial segments have similar values under pressure of 100 mmHg and in-vivo axial stretch when radial deformation is considered to be unrestricted (Table 1). However, we speculate a possible effect of radial restriction (of the V2 arterial segment) in the living organism would be that small variations in pressure around 100 mmHg would virtually not affect the deformed radius and thus Peterson's modulus tends to infinity. This means that the V2 arterial segment behaves as a rigid tube clamped to the adjacent, deformable V1 and V3 arterial segments. Arterial hemodynamics would not be disturbed, however, because the length of the propagating pulse wave is much longer than the length of the V2 arterial segment.
There are several study limitations that should be considered in the interpretation of the obtained results. Firstly, the proposed one-layered model was used under the assumption of tissue homogeneity in the radial direction. However, there are obvious structural and compositional differences between the media and adventitia, and these layers likely possess different residual strains. In this case, the development of two-layer constitutive models would provide a more accurate characterization of VA wall mechanics. Secondly, a four fiber family approximation was used to capture the variation of collagen fiber orientation in the arterial wall, whereas it has been shown that fibers are dispersed over a wide range of orientations and thus better modeled with a continuous distribution function [30]. More thorough histological studies, such as multiphoton microscopy, can be used to characterize the distribution of fiber orientations along the VA and identify increasingly accurate segment-specific material models. Thirdly, the considerable content of smooth muscle in the VA (Table 2) indicates that an active mechanical component may significantly modulate the overall in-vivo mechanical behavior of this vessel. Therefore, comprehensive mechanical characterization of the VA requires additional studies that quantify the active mechanical response to various mechanical and chemical stimuli. Fourthly, sample-specific quantification of intraosseous canal dimensions was not performed; instead, representative canal dimensions were acquired and used to motivate parametric studies that examined the effect of different degrees of geometrical (radial) constraint on VA mechanics. Sample-specific registration with intraosseous canal dimensions may enable greater correlation between geometrical constraints and structural/mechanical properties of the VAs. And finally, while we focused on the V2 and V3 arterial segments for the purpose of studying the effects of distinct perivascular environments on vascular tissue structure and mechanics, future studies that consider the presently excluded segments (V1 and V4) are required for comprehensive characterization of the VAs.
CONCLUSION
To our knowledge, this study is the first to characterize the passive mechanical properties of the second and third arterial segments of the porcine VAs. Segment-specific passive mechanical properties were quantified through bi-axial mechanical testing coupled with structure-motivated constitutive modeling, enabling assessment of the local mechanical environment within the arterial wall. We observed significant differences in wall structure and geometry between the intraosseous V2 arterial segment and the extraosseous V3 arterial segment, and speculate that these differences are driven by diverse perivascular environments. Indeed, accounting for segment-specific perivascular environments leads to a similarity in wall stress distribution along the VA, and thus allows speculation that structural and geometrical differences are in agreement with a previously introduced principle of optimal operation of arteries. Quantifying the passive mechanical response of VAs is a necessary step to understand normal and aberrant mechanical performance, and may provide guidelines for improving the surgical inventions in this vital region of the circulatory system.
Statement of Significance.
Among the numerous biomechanical investigations devoted to conduit blood vessels, only a few deal with vertebral arteries. While these studies provide useful information that describes the vessel mechanical response, they do not enable identification of a constitutive formulation of the mechanical properties of the vessel wall. This is an important distinction, as a constitutive material model is required to calculate the local stress environment of mechanosensitive vascular cells and fully understand the mechanical implications of both vascular injury and clinical intervention. Moreover, segmental differences in the mechanical properties of the vertebral arteries could be used to discriminate among distinct modes of injury and disease etiologies.
Acknowledgments
This research was supported by the NIH INBRE Grant for South Carolina (P20GM103499). We would also like to thank T. Antonelli and C. Leischner for help during the vessel dissection.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Ulm AJ, Quiroga M, Russo A, Russo VM, Graziano F, Velasquez A, Albanese E. Normal anatomical variations of the V3 arterial segment of the vertebral artery: surgical implications: Laboratory investigation. J Neurosurg: Spine. 2010;13(4):451–460. doi: 10.3171/2010.4.SPINE09824. [DOI] [PubMed] [Google Scholar]
- 2.Humphrey JD. Cardiovascular solid mechanics: cells, tissues, and organs. New York: Springer; 2002. p. 757. xvi. [Google Scholar]
- 3.Edwards NM, Fabian TC, Claridge JA, Timmons SD, Fischer PE, Croce MA. Antithrombotic therapy and endovascular stents are effective treatment for blunt carotid injuries: results from long term follow up. J Am Coll Surg. 2007;204(5):1007–1013. doi: 10.1016/j.jamcollsurg.2006.12.041. discussion 1014–5. [DOI] [PubMed] [Google Scholar]
- 4.Miller PR, Fabian TC, Croce MA, Cagiannos C, Williams JS, Vang M, Qaisi WG, Felker RE, Timmons SD. Prospective screening for blunt cerebrovascular injuries: analysis of diagnostic modalities and outcomes. Ann Surg. 2002;236(3):386–393. doi: 10.1097/01.SLA.0000027174.01008.A0. discussion 393–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alterman DM, Heidel RE, Daley BJ, Grandas OH, Steven SL, Goldman MH, Freeman MB. Contemporary outcomes of vertebral artery injury. J VascSurg. 2013;57(3):741–746. doi: 10.1016/j.jvs.2012.09.006. discussion 746. [DOI] [PubMed] [Google Scholar]
- 6.Biffl WL, Cothren CC, Moore EE, Kozar R, Cocanour C, Davis JW, Mclntyre RC, Jr, West MA, Moore FA. Western Trauma Association critical decisions in trauma: screening for and treatment of blunt cerebrovascular injuries. J Trauma. 2009;67(6):1150–1153. doi: 10.1097/TA.0b013e3181c1c1d6. [DOI] [PubMed] [Google Scholar]
- 7.Biffl WL, Moore EE, Elliott JP, Ray C, Offner PJ, Franciose RJ, Brega KE, Burch JM. The devastating potential of blunt vertebral arterial injuries. Ann Surg. 2000;231(5):672–681. doi: 10.1097/00000658-200005000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pham MH, Rahme RJ, Arnaout O, Hurley MC, Bernstein RA, Batjer HH, Bendok BR. Endovascular stenting of extracranial carotid and vertebral artery dissections: a systematic review of the literature. Neurosurgery. 2011;68(4):856–866. doi: 10.1227/NEU.0b013e318209ce03. discussion 866. [DOI] [PubMed] [Google Scholar]
- 9.Mei Q, Sui M, Xiao W, Sun Z, Bai R, Huang C, Hou L. Individualized endovascular treatment of high-grade traumatic vertebral artery injury. ActaNeurochir. 2014;156(9):1781–1788. doi: 10.1007/s00701-014-2074-0. [DOI] [PubMed] [Google Scholar]
- 10.Waldman DL, Barquist E, Poynton FG, Numaguchi Y. Stent graft of a traumatic vertebral artery injury: case report. J Trauma. 1998;44(6):1094–1097. doi: 10.1097/00005373-199806000-00027. [DOI] [PubMed] [Google Scholar]
- 11.Lee YJ, Ahn JY, Han IB, Chung YS, Hong CK, Joo JY. Therapeutic endovascular treatments for traumatic vertebral artery injuries. J. Trauma Acute Care Surg. 2007;62(4):886–891. doi: 10.1097/01.ta.0000209398.07973.60. [DOI] [PubMed] [Google Scholar]
- 12.Ho H, Mithraratne K, Schmid H, Sands G, Hunter P. Computer simulation of vertebral artery occlusion in endovascular procedures. International journal of computer assisted radiology and surgery. 2010;5(1):29–37. doi: 10.1007/s11548-009-0379-x. [DOI] [PubMed] [Google Scholar]
- 13.Symons BP, Leonard T, Herzog W. Internal forces sustained by the vertebral artery during spinal manipulative therapy. Journal of Manipulative & Physiological Therapeutics. 2002;25(8):504–510. doi: 10.1067/mmt.2002.127076. [DOI] [PubMed] [Google Scholar]
- 14.Berczi V, Toth P, Kovach AG, Monos E. Biomechanical properties of canine vertebral and internal carotid arteries. Acta Physiologica Hungarica. 1989;75(2):133–145. [PubMed] [Google Scholar]
- 15.Hayashi K, Handa H, Nagasawa S, Okumura A, Moritake K. Stiffness and elastic behavior of human intracranial and extracranial arteries. J Biomech. 1980;13(2):175–184. doi: 10.1016/0021-9290(80)90191-8. [DOI] [PubMed] [Google Scholar]
- 16.Nagasawa S, Handa H, Okumura A, Naruo Y, Okamoto S, Moritake K, Hayashi K. Mechanical properties of human cerebral arteries: part 2. Vasospasm. Surg. Neurol. 1980;14(285):0. [PubMed] [Google Scholar]
- 17.Rachev A, Greenwald S, Shazly T. Are geometrical and structural variations along the length of the aorta governed by a principle of"optimal mechanical operation? J Biomech Eng.; 2013;135(8):81006. doi: 10.1115/1.4024664. [DOI] [PubMed] [Google Scholar]
- 18.Rachev A, Stergiopulos N, Meister JJ. Theoretical study of dynamics of arterial wall remodeling in response to changes in blood pressure. J Biomech. 1996 May;29(5):635–642. doi: 10.1016/0021-9290(95)00108-5. [DOI] [PubMed] [Google Scholar]
- 19.Zhou B, Rachev A, Shazly T. The biaxial active mechanical properties of the porcine primary renal artery. J Mech Behav Biomed Mater. 2015;48:28–37. doi: 10.1016/j.jmbbm.2015.04.004. [DOI] [PubMed] [Google Scholar]
- 20.Dobrin PB. Biaxial anisotropy of dog carotid artery: estimation of circumferential elastic modulus. J Biomech. 1986;19(5):351–358. doi: 10.1016/0021-9290(86)90011-4. [DOI] [PubMed] [Google Scholar]
- 21.Takamizawa K, Hayashi K. Strain energy density function and uniform strain hypothesis for arterial mechanics. J Biomech. 1987;20(1):7–17. doi: 10.1016/0021-9290(87)90262-4. [DOI] [PubMed] [Google Scholar]
- 22.Prim DA, Zhou B, Hartstone-Rose A, Uline MJ, Shazly T, Eberth JF. A mechanical argument for the differential performance of coronary artery grafts. J Mech Behav Biomed Mater. 2015;54:93–105. doi: 10.1016/j.jmbbm.2015.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.O'Connor WN, Valle S. A combination Verhoeff's elastic and Masson's trichrome stain for routine histology. Stain Technol. 1982;57(4):207–210. doi: 10.3109/10520298209066710. [DOI] [PubMed] [Google Scholar]
- 24.Rachev A. Remodeling of Arteries in Response to Changes in their Mechanical Environment. In: Holzapfel G, Ogden R, editors. Biomechanics of Soft Tissue in Cardiovascular Systems, CISM-P, Courses and Lectures, Course and Lecture No. 441. New York: Springer; 2003. pp. 100–161. [Google Scholar]
- 25.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast. 2000;61(1–3):1–48. [Google Scholar]
- 26.Liu SQ, Fung YC. Zero-stress states of arteries. J Biomech Eng. 1988;110(1):82–84. doi: 10.1115/1.3108410. [DOI] [PubMed] [Google Scholar]
- 27.Garcia A, Pena E, Laborda A, Lostate F, De Gregorio MA, Doblare M, Martinez MA. Experimental study and constitutive modelling of the passive mechanical properties of the porcine carotid artery and its relation to histological analysis: Implications in animal cardiovascular device trials. Med Eng Phys. 2011;33(6):665–676. doi: 10.1016/j.medengphy.2011.01.016. [DOI] [PubMed] [Google Scholar]
- 28.Zhou B, Wolf L, Rachev A, Shazly T. A structure-motivated model of the passive mechanical response of the primary porcine renal artery. J Mech Med Biol. 2013 [Google Scholar]
- 29.Wagner HP, Humphrey JD. Differential Passive and Active Biaxial Mechanical Behaviors of Muscular and Elastic Arteries: Basilar Versus Common Carotid. J Biomech Eng. 2011;133(5):1–10. doi: 10.1115/1.4003873. [DOI] [PubMed] [Google Scholar]
- 30.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc., Interface. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]