Community trait overdispersion due to trophic interactions: concerns for assembly process inference

Abstract

The expected link between competitive exclusion and community trait overdispersion has been used to infer competition in local communities, and trait clustering has been interpreted as habitat filtering. Such community assembly process inference has received criticism for ignoring trophic interactions, as competition and trophic interactions might create similar trait patterns. While other theoretical studies have generally demonstrated the importance of predation for coexistence, ours provides the first quantitative demonstration of such effects on assembly process inference, using a trait-based ecological model to simulate the assembly of a competitive primary consumer community with and without the influence of trophic interactions. We quantified and contrasted trait dispersion/clustering of the competitive communities with the absence and presence of secondary consumers. Trophic interactions most often decreased trait clustering (i.e. increased dispersion) in the competitive communities due to evenly distributed invasions of secondary consumers and subsequent competitor extinctions over trait space. Furthermore, effects of trophic interactions were somewhat dependent on model parameters and clustering metric. These effects create considerable problems for process inference from trait distributions; one potential solution is to use more process-based and inclusive models in inference.

1. Introduction

Understanding the link between patterns such as diversity, trait distribution and species relatedness, and the assembly processes that underlie them, is a fundamental goal of community ecology [1]. Such an understanding facilitates general expectations for how processes can structure a local community, and underpin statistical methods of inferring processes from community patterns [2–8]. One method involves quantifying community clustering (species having similar niches) or overdispersion (species having dissimilar niches) to infer habitat filtering and competition [2]. Such methods have been used on a wide range of natural communities of different organisms [5] but their limitations are debated (e.g. [7]). Methods based on trait clustering/dispersion often focus on habitat filtering and competition as the major structuring processes. The potential effects of trophic interactions, such as herbivory and predation, are commonly ignored [3,7].

It is somewhat surprising that this bias in focus towards competition and habitat filtering in process inference techniques exists given the wealth of theory and empirical research showing the importance of trophic interactions for species coexistence and richness [9–12]. Indeed, predatory and competitive interactions are equally able to limit or promote coexistence [13]. Several influential papers discuss this limitation and its potential implications. Cavender-Bares et al. [4] identify the strength of the trophic interactions and the degree of consumer specialization as two essential variables that dictate community structure. They also argue that competitive communities that are affected by strong consumption from higher trophic levels should show signals of such trophic interactions in community patterns such as trait distributions. If the strength of trophic consumption is correlated with environmental factors (e.g. [14]), it may amplify habitat filtering and thus increase clustering. Strong trophic consumer specialization has on the other hand been suggested to decrease clustering in consumer communities [4]. Although plausible, these suggestions, based on intuitive reasoning, have to our knowledge not been formally tested within the scope of current process inference tools. Furthermore, Vamosi et al. [5] conclude that trophic level effects may be dependent on the type and properties of the predators present and thus also call for more formal investigations.

The aim of this study is to conduct such an investigation of the effect of herbivory/predation (referred to as trophic consumption from now on) on competitive community structure. We focus on two general questions: (i) can correct inference be done by interpreting competitive community clustering as a signal of habitat filtering or competitive exclusion, in the presence of trophic consumption? (ii) If trophic consumption affects competitive community structure, is such an effect consistent across parameter space driving clustering [14], overdispersion [4] or a combination of the two? We used a trait-based population dynamic model to simulate the assembly of a theoretical competitive community with different degrees of habitat filtering and strength of competition. We measured clustering in trait distributions and use these as reference points against which to evaluate the effect of trophic consumption. We tested three a priori predictions. (i) Habitat filtering and competition cause trait clustering and overdispersion, respectively, in the competitive communities (this is a baseline prediction). (ii) Invasions of specialized trophic consumers into a competitive community can punctuate the lower level community trait distribution and thus cause decreased trait clustering (greater trait dispersion). (iii) Strong trophic consumption at extremes of the competitive community trait distribution will increase trait clustering.

2. Material and methods

(a). Model overview

We assume a regional species pool of top consumers (figure 1a) and a pool of competitive consumers (figure 1b) from which a local community is assembled. We refer to the species in the competitive communities as competitive consumer species from now on, because they compete via consumption of shared resources. Each competitive consumer in the species pool is defined by a resource utilization trait (v) that ultimately determines the type of resources it can use. Such a trait could, for example, be body size, a trait that has been shown to affect resource consumption [15–21]. We assume that the competitive consumer community is assembled in a spatially distinct and homogeneous habitat (referred to as an island from now on to avoid confusion with the term habitat filtering) through colonization from the species pool (figure 1b). The island contains a number of explicit resources (figure 1c) with trait (u), in the same trait dimension as the resource utilization trait of the competitive consumers. Similar to well-established precedents in classic studies (e.g. [22–24]), the match between the competitive consumer and resource traits dictates the consumption rate and ultimately fitness. A similar modeling framework was also used in recent models of trophic interactions (e.g. [25–27]). Small differences between v and u result in high consumption rates, a perfect match renders the highest consumption rate. Consumption rate declines symmetrically with increased trait mismatch according to a kernel that defines the organism niche width. We illustrate niche widths as black and grey lines in figure 1.

Figure 1.

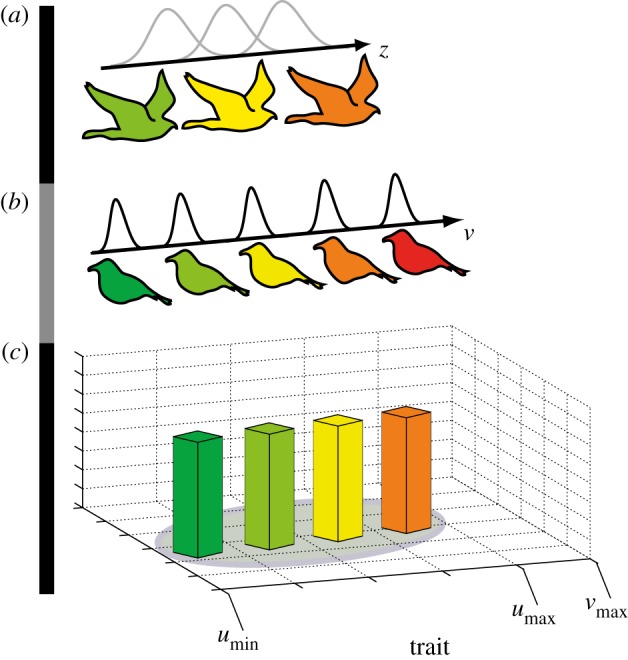
Model illustration. A species pool of top consumers (a) with some trait z (e.g. birds of prey with body size z) and a pool of competitive consumers (b) with trait v (e.g. granivorous birds with beak size v) are allowed to invade an island (c) with resources defined by trait u (e.g. seeds with size u), here u_min = v_min. The three trophic levels are distributed on the same trait dimension (e.g. size) here illustrated by color. The invasion fitness of a focal consumer or competitor is a function of its trait matching to its resources, the traits of its competitors on the same trophic level and their niche widths (black and grey niche kernels). If the resource's trait distribution on the island only ranges over a small proportion of the species pool trait distribution (if |u_{max_pool} − v_{max_island}| is large), the competitive community will be habitat filtered. If the niche width of the competitors is high (high variance of black niche kernels), competition strength will be high in the system. The competitive community structure was used as a reference point for the effect of invading trophic consumers (a) with different efficiency and niche width (variance of grey niche kernels).

As an explanatory example, and illustrated in figure 1, the resource distribution is analogous to seeds of different sizes. The resource specialization trait is analogous to the beak size for a granivorous bird that consumes seeds (or the size of grain preferred based on its beak size). The invasion fitness of a competitive consumer on the island will be a function of the match between its utilization trait and the traits of available resources, its niche width, the niche width and traits of its competitors, and the number of competing consumers in the community. Competition between consumers acts via the depletion of the resource, and consumers with similar resource utilization trait values will compete more than consumers with less similar trait values.

Similar to the utilization trait (v) and resource trait (u) mapping explained above and given an assumption of correlation between beak size and body size in the competitive consumers, trophic interactions between the competitive consumer community and the highest trophic level are dictated by the match between v and, for example, body size of the trophic consumer z (figure 1). This accords with empirical results showing that each consumer tends to consume organisms from lower trophic levels within a size range that is related to its own size [15–21]. This is also the way several other models have been formulated [25–27]. We assume that a focal trophic consumer will catch competitive consumers at some maximum rate when z and v match. We also assume that this rate declines with mismatch according to a symmetric niche kernel. The width of this kernel is referred to as the trophic consumer niche width and we illustrate this as grey kernels in figure 1. The fitness of a focal trophic consumer species is, therefore, a function of its specialization trait and niche width, the specialization traits and abundance of the competitive consumers, and the abundances, traits and niche widths of other trophic consumers in the community. Using the same analogy as above, this part of the model can be viewed as birds of prey that have a size preference in its prey, in this example being a granivorous bird.

(b). Population dynamics

We use a version of the discrete time Lotka–Volterra model of coupled dynamics of resources, competitive consumers and trophic consumers:

2.1

;

2.2

;

2.3

;where R_t, N_t and P_t are the resource, competitive consumer and trophic consumer population sizes, respectively, at time t [28]. Each equation defines the dynamics of a single population or species and the parameter K denotes the resource carrying capacity, c is the conversion factor from one trophic level to the next, a is the attack rate and m is the mortality. These parameters are assumed to be the same for all species interactions and subscripts denote if the parameter is associated with the competitive consumer (con) or the trophic consumer (pred).

The community is described by dynamic vectors R, N and P representing species' abundance for the three trophic levels, and by static vectors u, v and z representing the species traits (see also [29]). Each element R, N and P corresponds to elements in u, v and z, respectively. The density of a particular resource i at time step t + 1 generalized to a multi species system is defined as

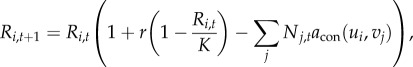2.4

;where attack rate a_con is the trait-dependent Gaussian function [30]:

2.5

;where b_con and σ_con denote maximum attack rate and competitive consumer niche width, respectively. Here, we also assume that b_con and σ_con are the same for every species interaction and that the total consumption on resource i is obtained through the sum of the consumption over all j competitive consumers (equation (2.4)).

The competitive consumer population j at time step t + 1 is a function of resource availability, mortality, gain through consumption and loss to predation:

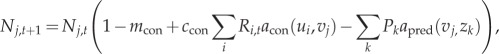2.6

;where attack rate for the trophic consumers on the competitive consumer (last term in equation (2.6)) is defined as

2.7

;The total gain is the summed gain from consuming each available resource i and the total loss is the sum of the predation over all trophic consumers k.

Finally, the trophic consumer population dynamics are given by loss to mortality and gain from consumption

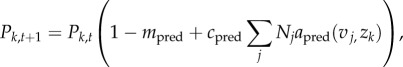2.8

;where the total predation by trophic consumer k (last term in equation (2.8)) is defined as the sum of predation on all competitive consumers j.

(i). Invasion fitness

The per capita growth (fitness) for the competitive consumers and trophic consumers is formulated as functions f₁, f₂ and f₃ in the general formulation (equations (2.1)–(2.3)). The fitness of an invader when rare (invasion fitness) indicates if an invading species can invade an established community and reach positive population equilibrium. Following Ripa et al. [29] and in line with equations (2.4)–(2.8), we generalize these functions to fitness functions that describe the fitness of any given trait (u, v or z) for any given condition defined by R, N and P (community richness and abundance) and u, v and z (trait distributions). We generate one fitness function for each resource (G_1,i), and one each for competitive consumers (G₂) and trophic consumers (G₃) as

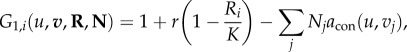2.9

;

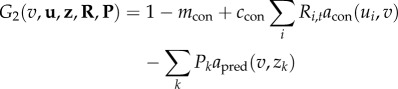2.10

;

2.11

;where again the attack rate functions a_con(u_i, v_j) and a_pred(v_j, z_k) are defined as in equations (2.5) and (2.7). Note that N and P are not included in G₂ and G₃, respectively. This is due to the lack of explicit intraspecific density dependence in competitive consumers and trophic consumers. Such regulation is instead mediated through the consumption on the lower trophic levels and shared consumers at higher levels. From equations (2.9)–(2.11), we formulate the general model that describes the per capita growth rate of any population in the community given any trait and population density as

2.12

;

2.13

;

2.14

;

(c). Simulation procedure and data analysis

The simulation and analysis involved three steps. (i) The competitive consumer species pool and island resources were defined. (ii) A local competitive consumer community was assembled until none of the species in the pool had positive invasion fitness; then the trait distribution was quantified. (iii) One or several trophic consumers were introduced to the island and the effect on the competitive consumer trait distribution was quantified.

(i). Competitive consumer community assembly

We first defined the competitive consumer species pool as 500 distinct (in terms of traits) species randomly and uniformly distributed in trait space between v_min = 0 and v_max = 50. These were the species from which the island competitive consumer community (defined by v and N) was assembled. Note that v_min, v_max and the number of species in the pool were chosen to produce diverse enough communities to analyse community structure, yet simple enough to give reasonable computational tractability. To check for robustness of our results, we also ran simulations with 100 distinct species in the species pool, giving identical qualitative results.

Second, we defined the island as a number of resources (defined by u) evenly distributed with a distance 1 in trait space, partially overlapping with the consumer species pool trait distribution. The distance in trait space between resources was chosen to result in rich communities and this value should be interpreted in relation to other parameters such as competitor consumer niche width which we vary. Different resource widths on the island, measured in per cent overlap in trait space between the consumer species pool and the resource distribution defined as 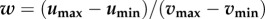and ranging from 25 to 100%, were tested among simulations. This percentage dictates the degree of habitat filtering and also the number of resources available on the island. For the 100% scenario, all competitive consumers in the species pool have suitable resources in the island and could potentially invade (low degree of habitat filtering), whereas for the 25% scenario a small proportion could invade (high habitat filtering).

We also simulated the assembly of competitive consumers under different degrees of competition. This was determined by the niche width (σ_con) of the competitive consumer species (see equation (2.5)). A narrow niche width denotes specialization on a small range of resources. This will lead to low competition between competitive consumers with a given trait difference compared with consumers with a wide niche width and the same trait difference. Niche width was varied among simulations between σ_con = 0.01 and σ_con = 2.4. Other parameters that determine the consumer properties which are not directly related to competition, such as r = 1, K = 300, b_con = 0.005, m_con = 0.1 and c_con = 0.15, were kept constant (electronic supplementary material, table S1). These constants were also chosen to produce diverse enough communities to analyse community structure, yet simple enough to give reasonable computational tractability. All initial population sizes in simulations, irrespective of the population being a competitor or a predator, were set to one individual.

For each of the competitive consumer niche widths and resource widths on the island, we assembled the competitive consumer community by random and sequential invasion. A consumer species was picked randomly from the pool, and its fitness computed according to equation (2.10). Note that, at this stage of the assembly process, there were no trophic consumers in the island and the vectors z and P were thus empty (for the first invader all resources were at their carrying capacity). If invasion fitness (G₂) was more than 1 we introduced the competitive consumer to the island and simulated the post invasion equilibrium population sizes R* and N* using equations (2.12) and (2.13) and by iterating through time (electronic supplementary material, appendix 1, figure S1). The next potential consumer was then selected and its fitness calculated using R*. This procedure was conducted repeatedly until no more species in the species pool had positive invasion fitness (electronic supplementary material, appendix 1, figure S2a). Simulations were replicated 50 times each with randomly chosen resource trait values and a stochastic invasion process. All results below are mean values over replicates.

(ii). Trophic consumer invasion

The invasion procedure of trophic consumers to the island was done in a way that was conceptually similar to the assembly of the competitive consumer trophic level. First, the fitness landscape was computed, using equation (2.11), for all trophic consumer traits ranging from v_min − 5 to v_max + 5. For the first predator, the fitness landscape was calculated at the consumer-only equilibrium. For subsequent predators, it was calculated for the equilibria with previous predators present. A random trophic consumer with positive fitness was then allowed to invade according to one of three invasion algorithms. (i) Random invasion uniformly distributed over the whole range of trait space. (ii) Random invasion into the centre of the competitive consumer trait space. This was done by not allowing a predator to invade a range of 5* σ_pred at each end of consumer trait space (results not shown). (iii) Random invasion into the periphery of the competitive consumer trait space, here defined as the range 5* σ_pred at the ends of trait space.

The realized invasion success of a predator and its effect on the full community and the fitness landscapes were computed through simulation of the population dynamics until equilibrium was reached (electronic supplementary material, appendix 1, figure S2) using equations (2.12)–(2.14). The invasion procedure above was iterated until 1, 2, 3, 4 or 5 (depending on our analysis) trophic consumers coexisted in the community or until no more trophic consumers had positive invasion fitness. The simulation was repeated each with a stochastic top consumer invasion process until we had 50 replicates of each community. Competitor species were not allowed to invade at this point. The results below are mean values over replicates.

(iii). Community structure analysis

We evaluated the trophic consumer(s) effect on three response variables: (i) the competitive consumer community structure defined as the degree of trait clustering, (ii) the number of competitive consumers that went extinct and (iii) the change in the competitive consumer fitness landscape measured as the change in the area under kernel that describes the fitness landscape that was more than 1 (positive invasion fitness). This was done for different trophic consumer community complexity ranging from one to five trophic consumers.

In line with Webb et al. [2,31] and Harmon-Threatt & Ackerly [32], we computed the community structure, as mean trait distance (MTD) and mean nearest trait distance (MNTD), for each of the assembled competitive consumer communities (including the four reference communities). MTD calculates the mean trait distance separating all species in a community, while MNTD calculates the mean distance, in trait space, between the species and their nearest neighbour. To assess if a community is clustered or overdispersed, MTD and MNTD are compared to MTD and MNTD values in randomly assembled null model communities, respectively. The calculations are identical for both metrics thus we only provide the formula for MTD below. MTD of a focal community, here referred to as MTD_foc, was compared to the mean MTD of 1000 randomly assembled null model communities (MTD_rand) with the same richness as the focal community. The difference between MTD_foc and MTD_rand was standardized by the standard deviation of the random communities (MTD_sd):

2.15

;where C denotes the degree of community clustering (in a general sense, here either based on MTD or MNTD values) of the competitive community. The effect of trophic consumers on clustering was computed as C_{without_trophic_consumers}−C_{with_trophic_consumer}. We also recorded the number of competitive consumer extinctions and analysed the effect that predation had on further invasions from the species pool of competitive consumers. The effect on consumer invasion was computed as the change in the integral of the consumer fitness landscape that was above fitness = 1 (compare fitness landscapes in the electronic supplementary material, appendix 1, figures S2a and S2b). If this integral increased as a function of trophic consumer invasion this implies that the trophic interactions facilitate invasion of consumer species.

3. Results

Four competitive consumer communities, from parts of our analysed consumer niche width and habitat filtering parameter space, were chosen for analysis of the effect of trophic consumption. Two exhibited clustered (underdispersed) trait distributions, with the resource width on the island (w) (also dictating habitat filtering) parameter set to 25% and the competitor niche width parameter set to 0.5 or 2. Two exhibited overdispersed trait distributions with niche width set to 0.5 or 2 and w set to 100%. The invasion procedure was done both with specialist and generalist trophic consumers (σ_pred ranging from 0.1 to 2.4) and with different consumption efficiency (c_pred ranging from 0.01 to 0.28). Other parameters that determine the trophic consumer properties m_pred = 0.1 and c_pred = 0.15 were kept constant (electronic supplementary material, table S1). Competitive consumer species richness and trait clustering behaved as expected in the absence of trophic consumers. Low habitat filtering (high w values) and narrow competitive consumer niches allowed for high local species richness (figure 2a). Low habitat filtering also tended to give low (close to zero) or overdispersed (negative) trait clustering (figure 2b). In general, clustering decreased with increased consumer niche width both during scenarios of low (detected by MTD) and high (detected by MNTD) habitat filtering (figure 2b).

Figure 2.

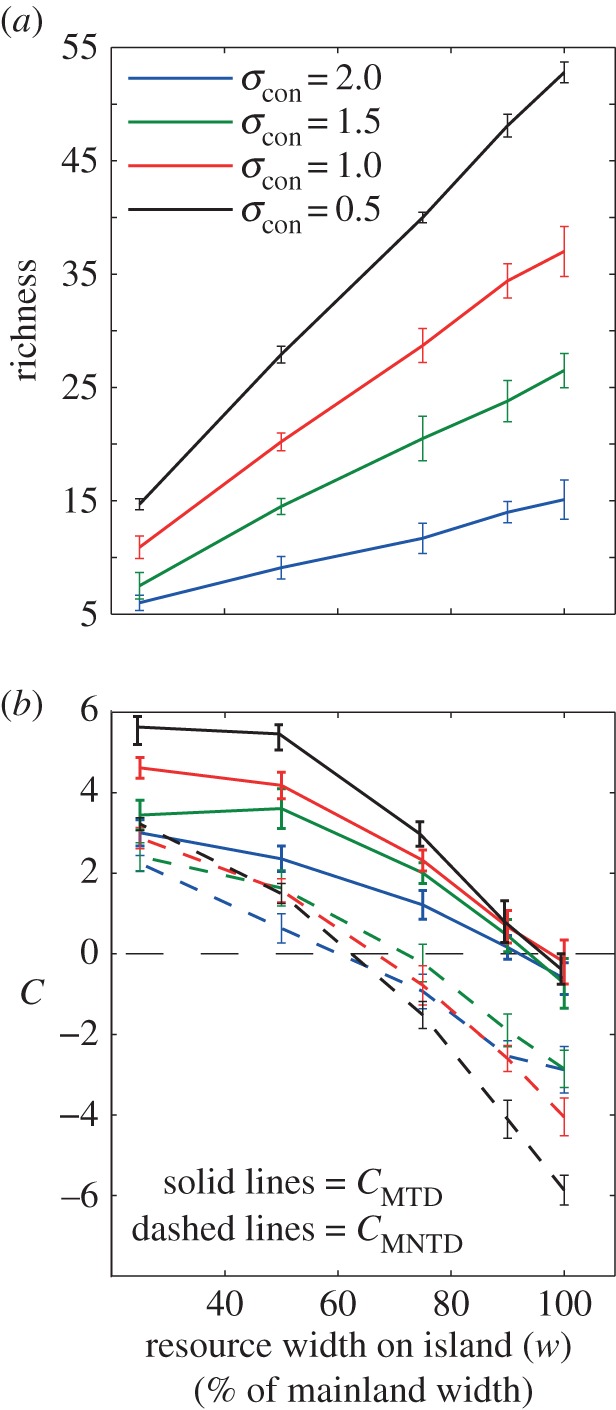
Mean (lines) and standard deviation (error bars) of consumer community richness (a) and trait clustering (C) based on MTD and MNTD (b) as a function of the overlap between resource width in trait space on the island and the trait distribution of competitor species. For the w = 100% scenario, all competitive consumers in the species pool have suitable resources in the island and could potentially invade (low degree of habitat filtering) while for the 25% scenario a small proportion could invade (high habitat filtering). Lines denote four levels of consumer niche width. Positive and negative clustering values indicate clustering and overdispersion, respectively. All results are based on 50 replicated simulations. Constant parameter values in our model that generated these results: r = 1, K = 300, b_con = 0.005, m_con = 0.1 and c_con = 0.15.

Surprisingly, diversity and the degree of clustering decreased for extremely low values of niche width (see a fine-grained parameter space representation of our results, electronic supplementary material, appendix 1, figure S3). Such low degree of clustering in competitive communities only was particularly evident in simulations where the species pool had few species (electronic supplementary material, appendix 1, S3d). This unexpected decrease in clustering with decreased niche width can be explained by the invasion fitness, which is a function of trait matching and niche width. When niche width of the consumers becomes smaller than the average distance in trait space between island resources, consumers that have trait values that happen to fall in between resources will have low fitness and may not be able to invade.

Trophic consumer invasion most often decreased trait clustering (figures 3 and 4), though some increases were observed for invasion of a single trophic consumer with large niche width, in particular, when the reference competitive communities were overdispersed (see a fine-grained parameter space representation of our results, electronic supplementary material, appendix 1, figures S4–S7). The most drastic decreases in community clustering occurred when the reference competitive community was clustered (as in figure 4), and the trophic consumer was more generalist (cf. figures 3 and 4). These results were also mostly robust across community clustering metrics as our analyses based on MTD and MNTD show similar results (electronic supplementary material, figures S4 and S5). The only clear discrepancy that we found between MTD and MNTD results was an increase in MNTD, while MTD decreased as a result of predation, when the reference community was overdispersed (figure 5).

Figure 3.

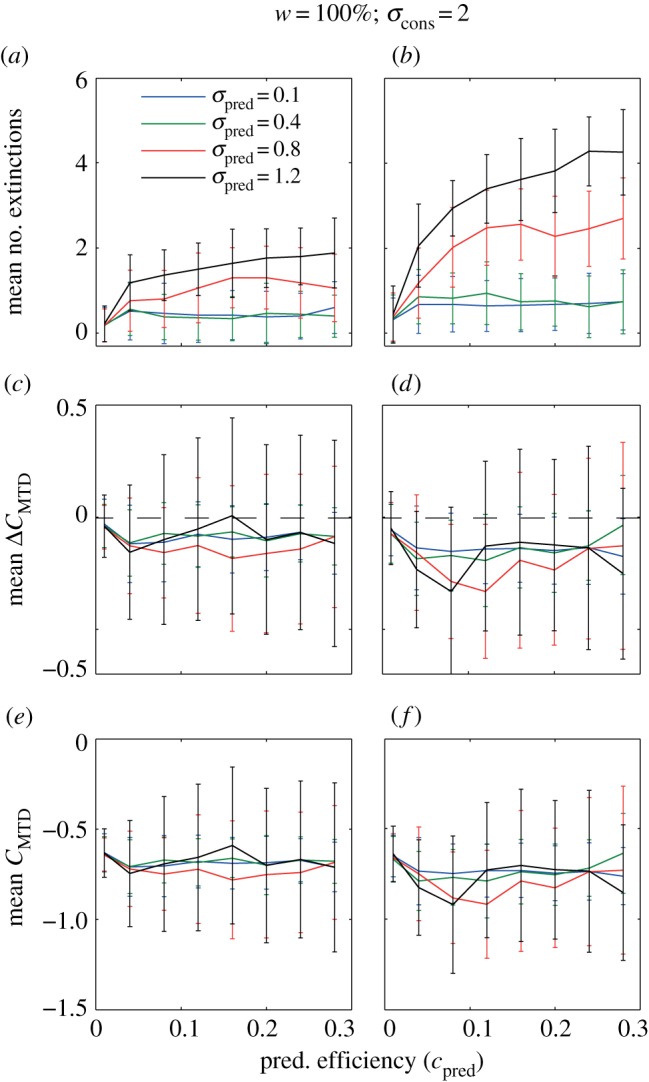
The effect of one (a,c,e) and three (b,d,f) trophic consumers on the number of extinctions (a,b), change in community trait clustering C (c,d) and community clustering C after predator invasion (e,f). All C-values are based on MTD. Here the reference competitive consumer community has a low degree of clustering (see the electronic supplementary material, appendix 1, figure S3, resource width on the island = 100% and consumer niche width = 2). Lines and error bars represent the mean and standard deviation for 50 replicated simulations. A fine-grained parameter space resolution of these results also including invasions of one to five predators is in electronic supplementary material, appendix 1, figure S4. Positive and negative clustering values indicate clustering and overdispersion, respectively. Constant parameter values in our model that generated these results: r = 1, K = 300, b_con = 0.005, m_con = 0.1, c_con = 0.15 m_pred = 0.1 and c_pred = 0.15.

Figure 4.

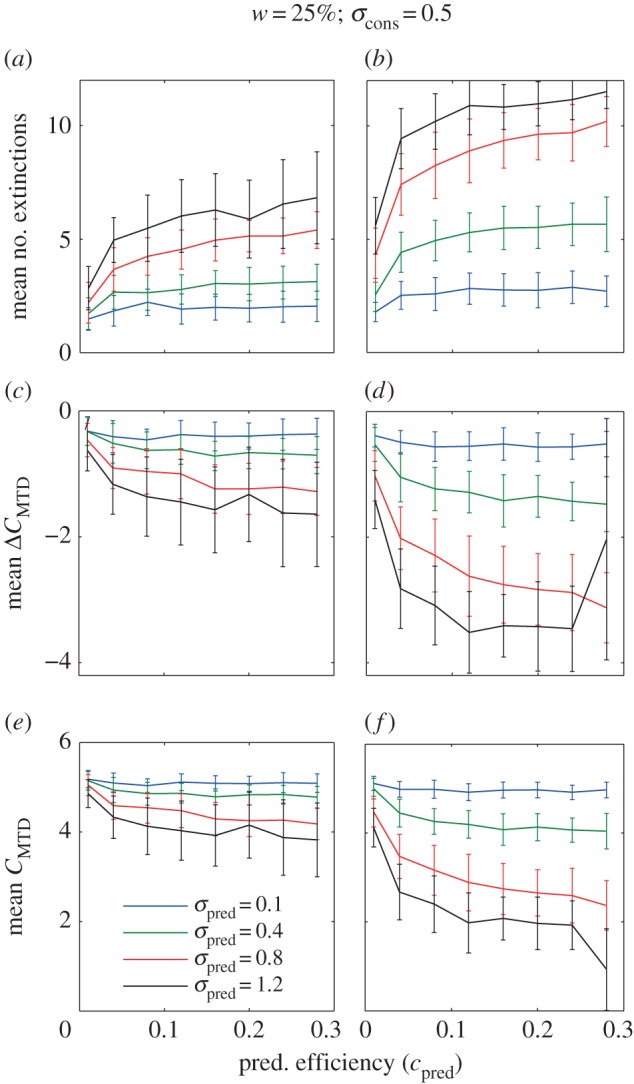
The effect of one and three (columns) trophic consumers on the number of extinctions (row 1), change in community trait clustering C (row 2) and community clustering C after predator invasion (row 3). All C-values are based on MTD. Here the reference consumer community has a high degree of clustering (see the electronic supplementary material, appendix 1, figure S3, resource width on the island = 25% and consumer niche width = 0.5). Lines and error bars represent the mean and standard deviation for 50 replicated simulations. A fine-grained parameter space resolution of these results also including invasions of one to five predators are in the electronic supplementary material, appendix 1, figure S5. Positive and negative clustering values indicate clustering and overdispersion, respectively. Constant parameter values in our model that generated these results: r = 1, K = 300, b_con = 0.005, m_con = 0.1, c_con = 0.15 m_pred = 0.1 and c_pred = 0.15.

Figure 5.

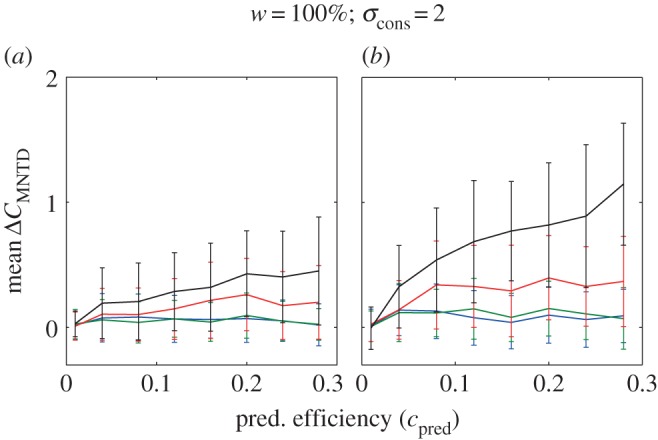
The effect of one (a) and three (b) trophic consumes on the change in MNTD community clustering C after predator invasion. Here the reference competitive consumer community has a low degree of clustering (see the electronic supplementary material, appendix 1, figure S3, resource width on the island = 100% and consumer niche width = 2). Lines and error bars represent the mean and standard deviation for 50 replicated simulations. A fine-grained parameter space resolution of these results also including invasions of one to five predators are in electronic supplementary material, appendix 1, figure S4. Constant parameter values in our model that generated these results: r = 1, K = 300, b_con = 0.005, m_con = 0.1, c_con = 0.15 m_pred = 0.1 and c_pred = 0.15.

The cause of the change in community structure is the fact that invasion of trophic consumers caused extinctions in the competitive consumer trophic level. The number of extinctions was positively related to trophic consumer niche width, efficiency and the number of trophic consumers (figures 3 and 4). As trophic consumers invaded, the fitness landscape changed such that competitive consumers that could not invade in the reference community could get positive invasion fitness (see fitness landscapes in electronic supplementary material, appendix 1, figures S2a and S2b).

Our results were largely similar, showing a decrease in competitor community clustering as a result of predator invasion both for the overdispersed (figure 3) and clustered (figure 4) reference consumer communities, and the results were robust to the way the species pool was defined and to the invasion scenario. Even in simulations in which trophic consumer invasions were restricted to the peripheral parts of competitive consumer trait space, which potentially could give a clustering effect, invasion caused decreased clustering both in the clustered (electronic supplementary material, appendix 1, figure S8) and less clustered (electronic supplementary material, appendix 1, figure S9) reference communities.

4. Discussion

Process inference methods based on analysis of trait distributions have been criticized due to, for example, scale dependence and exclusion of important processes such as trophic interactions and evolution (reviewed in e.g. [3–8,33]). The exclusion of trophic interactions causes particular concern as few competitive communities are unaffected by trophic interactions. Trophic interactions have been shown to structure natural communities [4,5,9] and patterns that can be observed in nature can have multiple explanations [1]. This creates risk of misinterpreting signals when one or few assembly processes are considered in the inference procedure. While other theoretical studies have generally demonstrated the importance of predation for coexistence (e.g. [13]), ours provide a quantitative demonstration of such effects on assembly process inference. In our results, trophic consumption generally decreased the clustering of the competitive communities, though for some parameter values for the MNTD-based metric, trophic consumption increased clustering. These effects of trophic consumption on clustering and their dependence on parameter values and clustering metric combine to limit inference of processes from trait distributions.

We show that different processes, such as trophic interactions and competition, can give similar community patterns in the form of low community clustering (i.e. overdispersion). Predators that invade a competitive community can cause extinctions and the probability of such extinctions increases with predator efficiency, predator niche width and the number of predators that invade. When trophic consumption decreased the clustering of the competitive communities, this was via evenly distributed extinctions of competitive consumers across trait space. This even distribution of extinctions was due to two phenomena. First, the trophic consumers tended to invade evenly over the competitive community due to competition between them. This is shown in electronic supplementary material, appendix 1, figure S2b, where the fitness peaks of the trophic consumers are more or less evenly distributed in trait space. This result is in line with results showing that coexistence between species in a particular trophic level decreases with increasing niche overlap [13]. Although Chesson & Kuang [13] did not use a trait-based approach, our results are comparable as a narrow niche width facilitates coexistence between similar species, both trophic consumers and competitors. Second, invasion by trophic consumers led to changed consumer abundances, which in turn led to indirect density-dependent (among competitive consumers) extinctions of competitor consumers, and these extinctions tend to be evenly distributed in trait space. More specifically, as extinctions occurred this decreased competition on neighbouring consumers, which in turn could outcompete other consumers not directly affected by the invading predator. Such indirect extinctions can be seen by comparing the reference consumer community without (electronic supplementary material, appendix 1, figure S2a) and with (electronic supplementary material, appendix 1, figure S2b) trophic consumers. In electronic supplementary material, appendix 1, figure S2b, competitors have gone extinct (denoted by red X), although they are not directly affected by predation (the consumers most affected by predation are greatly reduced, but not driven extinct, because the predators depend on them). We thus show that classical theory on coexistence and extinction risk associated with trophic interactions [10,11,13] is highly relevant for how we interpret trait distribution patterns in a process inference context. This being said, the variation in our results across parameter space and the discrepancy between MTD- and MNTD-based clustering metrics in parts of parameter space raise several concerns about some of the current inference methods. As an example, although MTD and MNTD are well-known concepts, (e.g. [31,32,34]) and often used for inference, their response to various ecological and stochastic processes (such as randomly distributed extinctions) requires further investigation. Also, defining thresholds that can be used to discriminate between various assembly processes may be difficult or even impossible.

As in any simulation study we make assumptions that may or may not impact our results and conclusions. Most if not all of the assumptions are, however, similar to the assumptions made by current inference techniques (e.g. [2]), making our results (realistic or not) relevant to these techniques. As an example and in addition to our main results, we find that overdispersion of traits calculated from MTD, often associated with competitive exclusion, is only obtained in a relatively small part of parameter space. This may explain dominance of clustering found in empirical data and there may be several reasons for such patterns, ranging from intrinsic properties of the communities to technical issues such as the use and misuse of null models [5]. Furthermore, we gain insights associated with the assumption of a fixed and non-evolving species pool. This issue has been raised several times before but our results, showing a decrease in richness and community clustering for low consumer niche widths (electronic supplementary material, appendix 1, figure S3), point out an issue that to our knowledge has not been raised before. When the niche width of the consumers becomes smaller than the average distance in trait space between island resources, consumers that have trait values that lay in between resources (e.g. light green bird in figure 1b) will have low fitness and may not be able to invade. During such scenarios, resource mismatch rather than habitat filtering, competition or predation excludes species from the island community. We thus identified an additional process that may lead to low levels of community clustering, which is neglected by current inference methods. To avoid such misinterpretation, knowledge about the species pool resource specialization and ‘island’ resource availability and structure should govern species pool construction. Mismatched specialists should not be included in the pool. It may, however, be difficult to identify the correct species pool empirically.

We conduct the analyses on communities at equilibrium, which simplifies our analysis. This is also in concordance with current inference methods that often implicitly assume equilibrium. Such an assumption may of course be violated in natural systems and with this in mind we tried to do our analysis while simulating a never ending succession of invasion events, of both competitive and trophic consumers. A stable community was, however, rarely assembled and instead species composition continued to turnover. This made it difficult to pinpoint the trophic effect on consumer community structure. Such turnover is also likely in nature, so results from inference techniques that compute community clustering on empirical data only provide a snap-shot in time, and the signals found may not be representative for all temporal scales. Furthermore, we make explicit assumptions about the ecological interactions as we assume symmetric niche kernels both for competitive and trophic consumers. This simplifies the fitness analysis but we do not expect other kernels to affect our main conclusions. If anything, much skewed or extremely wide niche kernels of the trophic consumer may possibly facilitate invasions in the extreme parts of the consumer trait space, which may increase competitive consumer clustering. We do however view such a scenario as an unlikely special case and the secondary effect of consumer extinction, which leads to decreased clustering, would still occur.

5. Conclusion

Our findings support Vellend's [1] statement that multiple processes can give rise to similar patterns and that prior information and consideration of a variety of processes may be required to make correct inference about assembly processes from community patterns. In particular, we conclude that trophic effects on community clustering must be considered while interpreting community patterns. We confirm our expectation that invasion of trophic consumers into a competitive community can punctuate the lower level community trait distribution and render decreased clustering. We also found that trophic consumption can induce density-dependent extinctions of competitive consumers that were not directly affected by trophic consumption. These secondary extinctions tended to be evenly distributed and thus also contributed to the decreased community clustering. Our expectation that strong consumption on species associated with extreme ends of the competitive community trait distribution can amplify the habitat filtering effect and thus render increased community clustering was rejected. The main reason for this was the low invasion probability for trophic consumers in the peripheral parts of the consumer trait space. Finally, we found an unexpected source of low clustering as a result of resource mismatch and specialization. The mechanistic link between ecological assembly processes and community patterns presented here can help our endeavour to make correct inference about different assembly processes. However, the complex way in which community structure is affected by different processes, including dependence on clustering metric and parameter values, implies considerable challenges for further investigations of how process inference can be made from trait distributions, and suggests that alternative, perhaps more process oriented inference methods, may be required to correctly interpret observed patterns in nature.

Authors' contributions

M.P. conceived the idea for the study, constructed the model and wrote the code for the simulation software. Both authors contributed to analysis and interpretation of the material and to the writing of the manuscript.

Competing interests

We have no competing interests.

Funding

Financial support for M.P.'s participation in this study was provided by the Swedish Research Council.