Quantification of microcirculatory parameters by joint analysis of flow‐compensated and non‐flow‐compensated intravoxel incoherent motion (IVIM) data

Abstract

The aim of this study was to improve the accuracy and precision of perfusion fraction and blood velocity dispersion estimates in intravoxel incoherent motion (IVIM) imaging, using joint analysis of flow‐compensated and non‐flow‐compensated motion‐encoded MRI data. A double diffusion encoding sequence capable of switching between flow‐compensated and non‐flow‐compensated encoding modes was implemented. In vivo brain data were collected in eight healthy volunteers and processed using the joint analysis. Simulations were used to compare the performance of the proposed analysis method with conventional IVIM analysis. With flow compensation, strong rephasing was observed for the in vivo data, approximately cancelling the IVIM effect. The joint analysis yielded physiologically reasonable perfusion fraction maps. Estimated perfusion fractions were 2.43 ± 0.81% in gray matter, 1.81 ± 0.90% in deep gray matter, and 1.64 ± 0.72% in white matter (mean ± SD, n = 8). Simulations showed improved accuracy and precision when using joint analysis of flow‐compensated and non‐flow‐compensated data, compared with conventional IVIM analysis. Double diffusion encoding with flow compensation was feasible for in vivo imaging of the perfusion fraction in the brain. The strong rephasing implied that blood flowing through the cerebral microvascular system was closer to the ballistic limit than the diffusive limit. © 2016 The Authors NMR in Biomedicine published by John Wiley & Sons Ltd.

Abbreviations used

CBV

cerebral blood volume

CSF

cerebrospinal fluid

DDE

double diffusion encoding

DGM

deep gray matter

FC

flow compensated

GM

gray matter

IVIM

intravoxel incoherent motion

MNI

Montreal Neurological Institute

NC

non‐flow‐compensated

ROI

region of interest

SDE

single diffusion encoding

SNR

signal‐to‐noise ratio

WM

white matter.

Introduction

Non‐invasive motion‐encoded MRI has shown considerable potential for the study of microcirculatory blood flow in tissue 1, 2, 3. The concept of capillary flow imaging was proposed by Nalcioglu et al. 4, and demonstrated in vivo by Ahn et al. using flow‐compensated (FC) and non‐flow‐compensated (NC) motion‐encoded sequences 1. These studies focused on the signal attenuation due to linear blood flow in a randomly ordered capillary system (spatial incoherence), allowing mapping of the relative capillary density 1. Intravoxel incoherent motion (IVIM) is another microcirculatory blood flow imaging method, proposed by Le Bihan et al. 2, 5, which considers the signal attenuation in diffusion experiments caused by pseudo‐random (diffusive) flow of blood through the capillary system (temporal incoherence). The IVIM model allows mapping of the fractional volume of perfused capillaries by modeling the total signal attenuation as the combined effect of diffusion and perfusion 2. As shown by Le Bihan and Turner, the IVIM parameters can be related to traditional perfusion parameters such as cerebral blood flow, cerebral blood volume (CBV) and mean transit time, for a given capillary geometry 6. IVIM thus enables non‐invasive quantification of perfusion‐related parameters, and has recently gained renewed clinical interest, with applications to, for example, liver 7, 8, breast 9, prostate 10, and brain 11. However, conventional IVIM analysis is based on bi‐exponential fitting of diffusion‐weighted data, which suffers from an inordinate sensitivity to noise 12, 13. Although the apparent diffusion coefficient of the flowing blood (referred to as the pseudodiffusion coefficient) is approximately an order of magnitude larger than the regular diffusion coefficient, perfused capillaries contribute to the observable signal by only a small fraction (about 4% in the brain), and the IVIM effect is thus very difficult to detect with a high degree of reliability. Monte Carlo‐based error analysis has shown that a high signal‐to‐noise ratio (SNR) is required for accurate estimation of the perfusion fraction 12, 13, 14. Imaging and processing methods with potential to improve the stability of the IVIM analysis are thus of great importance for the use of IVIM in clinical applications.

It is well known that spatial and temporal flow incoherencies both give rise to signal attenuation (cf. the two models in Reference 2). As suggested by Kennan et al. 15, the attenuation caused by either spatial incoherence (dispersed flow) or temporal incoherence (diffusive flow) can be understood as phenomena occurring in two extreme time scale regimes. The dispersed flow concept assumes that the blood does not change direction during the motion encoding (ballistic limit), and the diffusive flow concept assumes that the blood changes direction several times during the motion encoding (diffusive limit). In the ballistic limit, the attenuated signal can be recovered using FC, allowing for the effects of flow and diffusion to be separated 16. Several studies have demonstrated this rephasing effect by comparing data from FC and NC sequences 1, 16, 17, 18, 19. Most of these studies have relied on the difference or ratio between FC and NC data using a single diffusion encoding strength, while a few recent studies have employed FC and NC with multiple diffusion encoding strengths 18, 19. Since full rephasing of the perfused signal fraction is possible only in the ballistic limit, FC can be used to infer the relevant temporal regime for the blood flow.

To increase the contrast between flowing and non‐flowing spins and thereby improve the stability of IVIM analysis, we here suggest applying a joint analysis of FC and NC data acquired with multiple diffusion encoding strengths. Joint analysis refers to the use of multi‐dimensional data to strengthen the analysis without introducing additional model parameters. We have previously applied the concept of joint analysis to imaging of water exchange through cell membranes 20, 21 and imaging of microscopic diffusion anisotropy 22, 23. In the present study, a global model was used to fit FC and NC data simultaneously, taking advantage of the fact that some fitting parameters are common to the two datasets. An FC and NC single‐refocused double diffusion encoding (DDE) pulse sequence was utilized, where the switching between FC and NC yielded variable flow encoding. To our knowledge, this is the first IVIM study exploiting NC/FC DDE data combined with a velocity dispersion model in the ballistic flow limit. Data were acquired in eight healthy volunteers and analyzed using the proposed method. Using simulated data, our joint analysis was compared with two conventional IVIM analysis methods.

Theory

At the echo time, t _E, the spin‐echo signal S is described by the ensemble average of all signal contributions $⟨e^{-i{\phi }_j\left(t_{\mathit{E}}\right)}⟩$ 24, where φ _j is the phase of contribution j. Using the cumulant expansion in the Gaussian phase approximation 25, the signal can be approximated in terms of the cumulative phase ϕ and the attenuation factor β according to 26

$$S=S_0⟨e^{-i{\phi }_j\left(t_{\mathit{E}}\right)}⟩\hspace{0.17em}\approx \hspace{0.17em}{S}_0{e}^{-i\varphi \left(t_{\mathit{E}}\right)-\beta \left(t_{\mathit{E}}\right)},$$ (1)

where S ₀ is the relaxation‐weighted signal magnitude. The cumulative phase depends on the mean flow velocity of spins, while the attenuation factor depends on velocity fluctuations around the mean velocity. The sensitivity to different aspects of motion can be adjusted by varying the gradient waveform G(t). In the current study, the DDE is implemented as a spin‐echo sequence with bipolar diffusion gradients on both sides of the 180° refocusing pulse. Note that refocusing pulses alter the effective polarity of G(t).

The attenuation factor β is proportional to the diffusion coefficient D according to β(t_E) = bD, where b is the diffusion weighting factor, given by the dephasing factor q(t) according to 25

$$b={\displaystyle {\int }_0^{t_E}q{\left(t\right)}^{2}dt},$$ (2)

where

$$q\left(t\right)=\gamma {\displaystyle {\int }_0^{t}G\left(t^{\prime }\right)d{t}^{\prime }},$$ (3)

and γ is the gyromagnetic ratio.

The cumulative phase φ is proportional to the mean velocity $\overline{\mathit{v}}$ according to

$$\varphi \left(t_{\mathrm{E}}\right)=\alpha \overline{\mathit{v}},$$ (4)

where α is the flow weighting factor, determined by the dephasing factor according to 1

$$\alpha =-{\displaystyle {\int }_0^{t_E}q\left(t\right)dt=\gamma {\displaystyle {\int }_0^{t_{\mathrm{E}}}G\left(t\right)tdt}}.$$ (5)

Equation (5) is valid as long as the spin‐echo condition is fulfilled, i.e., q(t_E) = 0 (zeroth‐order gradient moment nulling). Note that the flow weighting factor is given by the first moment of G(t), and that FC sequences are designed for first‐order gradient moment nulling to eliminate the phase shift due to coherent flow, i.e., α = 0. Figure 1 shows a schematic diagram of the sequence design, indicating how the diffusion and flow weightings depend on the gradient pulses in the NC/FC DDE experiment. The pairs of bipolar gradients are referred to as gradient/encoding blocks 27. For straight flowing spins, the first gradient block gives a phase shift (according to Equation (4)), while the second gradient block nulls this phase shift for the FC acquisition (α = 0), and doubles it for the NC acquisition (Fig. 1).

Figure 1.

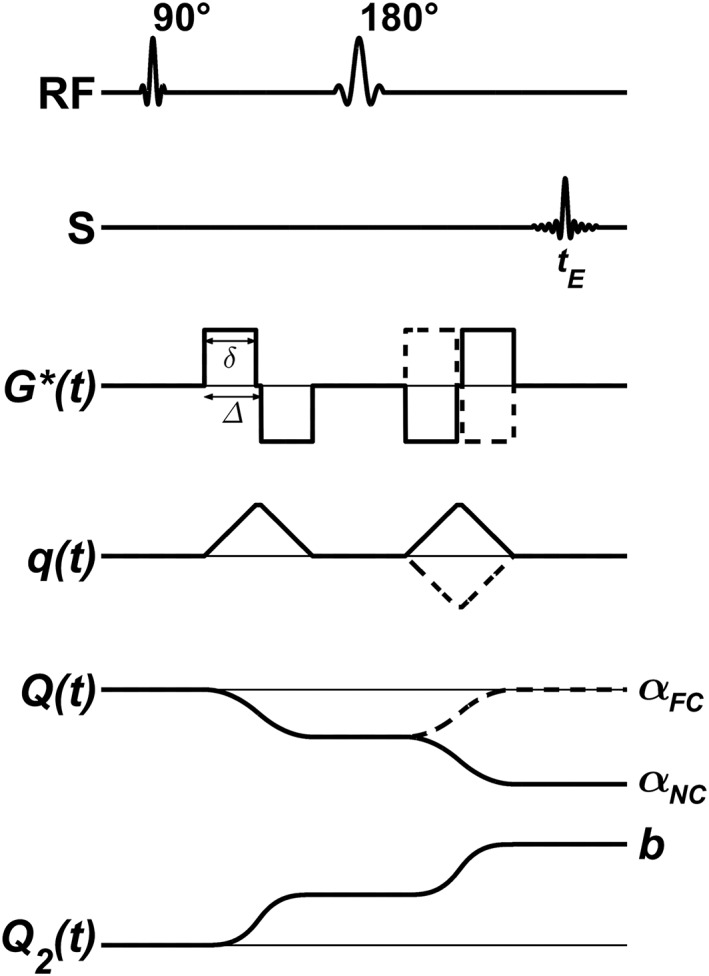
Schematic overview of the NC and FC DDE sequences. RF shows the excitation and refocusing pulses, S displays the acquired spin echo, G^*(t) is the magnetic field gradient waveform of the sequence, q(t) is the dephasing factor (Equation (3)), Q(t) corresponds to the negative integral of q from zero to t, where Q(t_E) = α (Equation (5)), and Q₂(t) is the integral of q ² from zero to t, where Q₂(t_E) = b (Equation (2)). Solid lines correspond to the NC acquisition, and dashed lines to the FC acquisition (i.e., α = 0). Note the resemblance of the FC and NC acquisitions, resulting in identical timings and diffusion weightings b, but different flow weightings α_NC/FC.

We now consider blood flowing through the capillary system as a motion of spins that change velocity (in terms of changing direction) as they pass through curvatures in the microscopic vessels. Depending on the time scale of these velocity fluctuations, two regimes of motion can be identified. If the flow velocity changes several times during the observation time, the phase coherence is lost (regardless of whether the encoding is FC or not), leading to a diffusion‐like signal attenuation 2. This signal attenuation can be characterized by a pseudo‐diffusion coefficient given by D^* = ⟨l⟩⟨v⟩/6, where ⟨v⟩ is the mean flow velocity, and ⟨l⟩ is the characteristic length scale on which flow velocity changes take place 2. This regime corresponds to signal attenuation due to temporal incoherence of flow, and is referred to as the diffusive limit in this work. In IVIM imaging, this limit corresponds to a capillary network model with short capillary segments such that the blood changes direction several times during the observation time. It has been suggested that approximately five changes in direction, or more, are required in order for the diffusive limit to be valid 15.

On the other hand, in this work we assume a capillary network model with straight segments, which are long enough to allow blood to remain within one segment during the observation time 1, 2. Each segment is considered as a separate statistical sub‐ensemble of spins 28, contributing to the total signal according to Equation (1). Non‐uniform velocity profiles within the segments and random orientation of the segments give rise to velocity dispersion. Even though the velocities are constant during the experiment, their phase contributions are incoherent due to the velocity dispersion, resulting in signal attenuation rather than a net phase shift. This regime corresponds to signal attenuation due to spatial incoherence, and is referred to as the ballistic limit in this work. Note that we use the term “velocity dispersion” to describe the effect of a collection of velocity vectors with different amplitudes and directions (i.e. combined effects of blood speeds and segment orientations).

To describe the signal attenuation in the ballistic limit, we consider a collection of sub‐ensembles with different mean velocities ${\bar{v}}_k$ leading to different phase contributions according to $e^{-i{\phi }_k}$, as described by Equations (1), (4). Note that ϕ_j in Equation (1) is the phase of a single contribution within a sub‐ensemble of spins, whereas ϕ_k corresponds to the cumulative phase of signal from the entire sub‐ensemble. Assuming a common diffusion coefficient D, the sum of $e^{-i{\phi }_k}$ over all sub‐ensembles gives the total signal

$$S=e^{-\mathit{bD}}{\displaystyle {\Sigma }_k{S}_k{e}^{-i\alpha {\overline{\mathit{v}}}_k}=S_0{e}^{-\mathit{bD}}{\displaystyle {\int }_{-\infty }^{\infty }P\left(\overline{\mathit{v}}\right)e^{-i\alpha \bar{v}}d\overline{\mathit{v}}}},$$ (6)

where S _k is the relaxation‐weighted signal contribution from sub‐ensemble k, and $P\left(\overline{\mathit{v}}\right)$ is the probability distribution of mean velocities, which can account for different velocity dispersion models. For example, it has been shown that plug flow in randomly oriented segments leads to a sinc‐modulated signal attenuation 1. A plug flow velocity profile is, however, unlikely in vivo, given the non‐uniform blood velocities inside the capillaries and the large number of pseudo‐randomly oriented microvascular networks in every voxel 29. Although it is challenging to establish appropriate velocity dispersion models for capillary blood flow, a large spread in velocities is likely to be present due to the heterogeneity of the microcirculatory system 15. In this work, we assume a distribution of mean velocities, $P\left(\overline{\mathit{v}}\right)$, with variance $⟨{\bar{v}}^2⟩$ and zero mean, yielding

$$S=S_0{e}^{-\mathit{bD}}{e}^{-{\alpha }^2\frac{⟨{\overline{\mathit{v}}}^2⟩}{2}},$$ (7)

where $⟨{\bar{v}}^2⟩$ is the average mean‐squared velocity. We can express the effective diffusion coefficient in terms of the pseudo‐diffusion coefficient D ^* according to

$$D^{*}=D+\frac{{\alpha }^2}{b}{v}_d^2,$$ (8)

where the ratio α²/b depends on the gradient pulse design, and can be maximized for increased sensitivity to flow. Here, v _d is introduced as a measure of velocity dispersion, which scales with velocity depending on the particular dispersion model; e.g., $v_{\mathrm{d}}^2=⟨{\bar{v}}^2⟩/2$ for a Gaussian velocity distribution. Note that, for $P\left(\bar{v}\right)$ with non‐zero odd moments, $\left|\overline{\mathit{v}}\right|,\left|{\overline{\mathit{v}}}^3\right|,\left|{\overline{\mathit{v}}}^5\right|,\dots >0$, Equation (7) would contain a complex phase shift term.

To account for signal contributions from both tissue and blood within a voxel, the signal can be described by

$$S\left(b,\alpha \right)=S_0\left[\left(1-f\right)e^{-b{D}_t}+f{e}^{-b{D}_b}{e}^{-{\alpha }^2{v}_d^2}\right],$$ (9)

where (1 − f) is the intravoxel fraction of diffusing water, D _t is the diffusion coefficient in tissue, f is the intravoxel fraction of flowing water in perfused capillaries (perfusion fraction), D _b is the intrinsic diffusion coefficient of blood and S₀ is the MR signal without diffusion encoding. The FC sequence with α = 0 yields a mono‐exponential signal attenuation if D_t = D_b.

In summary, in the present study, we vary not only the diffusion encoding strength (b value), but also the flow encoding strength (α value). The acquisition of data along an additional dimension makes the separation of different components more stable 30. Hence, assuming ballistic blood flow, joint analysis of two multi‐b data sets with different levels of flow encoding (α > 0 and α = 0) should allow for more robust IVIM parameter estimation.

Methods

Data acquisition

An FC/NC DDE sequence was implemented on a clinical whole‐body MRI scanner. Identical timing parameters were used for the two encoding blocks, and the FC was conveniently activated by reversing the polarity of the second gradient block (see Fig. 1). The sequence was tested on a stationary (zero‐flow) water phantom to confirm equivalency between the FC and NC data

Data from eight healthy volunteers were acquired on a 3 T MRI unit (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany), using the following protocol: EPI readout, GRAPPA =2, BW = 1185 Hz/pixel, T _R = 4000 ms, t _E = 70 ms, 128 × 128matrix, 2 × 2 × 4 mm³ voxel size, 20 slices, six diffusion encoding directions (cube sides), b = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, and 200 s/mm², diffusion gradient separation (within each block) Δ = 7.5 ms, diffusion gradient duration δ = 7.3 ms, total encoding time = 37.7 ms, total scan time = 12 min 32 s. The study was approved by the local ethics committee, and all volunteers gave written informed consent.

Post‐processing

The signal was averaged over the different encoding directions using the geometric mean, which allowed for direct estimation of rotationally invariant mean values of the model parameters 31. The model given by Equation (9) was fitted to the data using nonlinear regression, with S₀, f and v_d as fitting parameters. A fixed value of 1.75 μm²/ms was used for D_b, similarly to Reference 19. The tissue diffusion coefficient D_t was estimated from FC data points with b ≥ 100 s/mm². A regularization term that penalized unreasonable values of v_d was added to the residual sum of squares in the objective function. The regularization term (to be minimized) was based on hyperbolic tangent functions according to λ{1 − 0.5[tanh((v_d − x₁)/s) −  tanh ((v_d − x₂)/s)]}, with parameters empirically set to λ = 0.5, x ₁ = 0.75, x ₂ = 2.75 and s = 0.4 (the latter controlling the smoothness of the regularization function).

The S ₀ map of each subject was normalized to the MNI152 template brain (ICBM, NIH P‐20 project) using SPM12 32. The nonlinear transform was then applied to the other parametric maps, and cerebrospinal fluid (CSF) was masked out in the f and v_d maps using the Montreal Neurological Institute (MNI) tissue probability maps in SPM12. Based on the Neuromorphometrics labels (http://neuromorphometrics.com), gray matter (GM), deep gray matter (DGM), and white matter (WM) regions of interest (ROIs) were created in MNI space, and the parameter estimates were averaged over the subjects and analyzed in these ROIs. In addition, to visualize typical in vivo data and the corresponding model fits, ROIs were drawn directly on an S ₀ image in the native space. Residual bootstrapping 33 was used to estimate confidence intervals for the parameter estimates, based on the mean signal values within the ROI. This ROI analysis was also performed on the phantom data.

Simulations

The performance of the proposed joint analysis of NC and FC data was compared with conventional IVIM analysis in simulations. Note that the simulations assumed ballistic flow and were designed to compare joint analysis with conventional IVIM analysis. They were not designed to compare different flow regimes, i.e. ballistic versus diffusive. Signal data with NC and FC were simulated according to Equation (9) for the same b values and with similar timings as used in the in vivo imaging protocol (Δ = 7.5 ms, δ = 7.5 ms), for different SNR and f values. Other parameters were set to S ₀ = 1, D_t = 0.8 μm²/ms, D_b = 1.75 μm²/ms, and v_d = 1.75 μm/ms, and 10 000 noise realizations were used for each SNR and f value. For conventional IVIM analysis, both bi‐exponential and segmented (asymptotic) 34, 35 fitting were assessed. The segmented fitting was performed in a three‐step approach 35. First, a mono‐exponential signal model was fitted to the data points with b ≥ 100 s/mm², yielding an estimate of D _t and a corresponding intercept $S_0^{*}$. Second, f was estimated from $\left[S\left(0\right)-S_0^{*}\right]/S\left(0\right)$, where S(0) is the measured signal intensity at b = 0. Last, v_d was estimated by fitting the full model (Equation (9)) to all data points, using the estimated D _t and f as fixed parameters and S₀ set to S(0).

The same number of data points was used in all cases, i.e., for bi‐exponential and segmented all 16 NC data points were used, and for the joint analysis 4 FC and 12 NC data points were used. The four FC data points were distributed according to b = 50, 80, 120, and 180 s/mm², and the NC data points were b = 0, 10, 20, 30, 40, 60, 70, 90, 100, 140, 160, and 200 s/mm². No prior estimation of D _t or regularization of v_d was used for the joint or bi‐exponential fitting.

The accuracy and precision of parameter estimates were calculated for the different SNR and f values, using the three analysis approaches. Accuracy was defined as the difference between the parameter estimate and the simulated parameter value (ground truth), averaged over all iterations. Precision was defined as the root‐mean‐square deviation between the parameter estimates and their corresponding means.

Results

Figure 2(a)–(c) shows examples of in vivo data and corresponding model fits in GM, DGM, and WM, respectively. A significant separation of the NC and FC data was observed. With FC, the strong rephasing of the signal resulted in approximately mono‐exponential attenuations for b values up to 200 s/mm². Figure 2(d) presents the corresponding result for the stationary water phantom, where no significant difference between the NC and FC data was observed. Estimated parameter values, including confidence intervals based on residual bootstrapping, are presented in the figure caption. Note that these fits were performed on the mean signal values of the ROIs, as opposed to the ROI analysis on parameter maps reported below.

Figure 2.

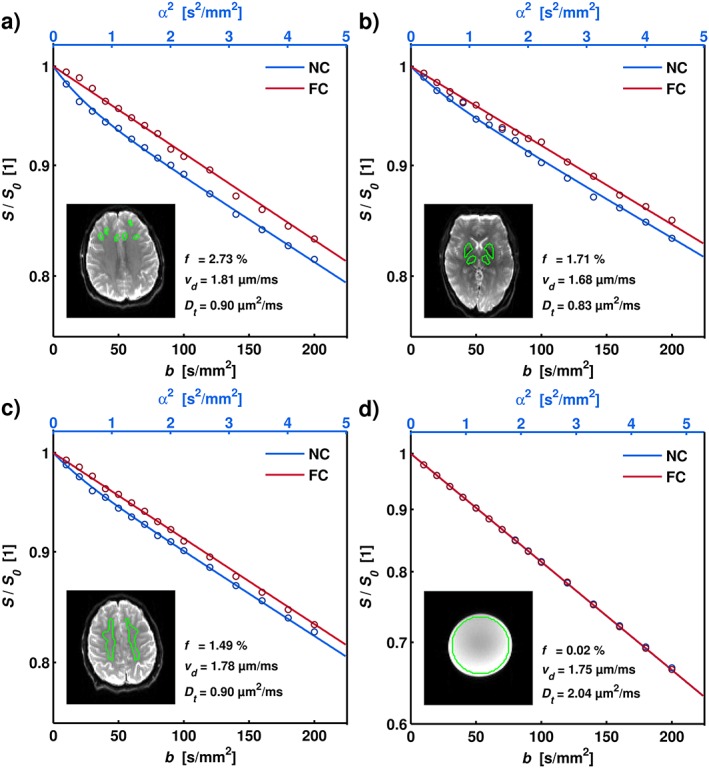
Examples of experimental data and analysis for ROIs corresponding to frontal GM (a), DGM (b), and WM (c), as well as for the stationary water phantom (d). The GM ROIs were drawn to minimize CSF partial volume effects. The insets show the corresponding S₀ images, with the ROIs indicated in green. The graph shows the mean ROI signal (circles) and the corresponding model fit (solid lines) as a function of diffusion and flow weighting. Note the significant rephasing effect in the FC data. The estimated parameters were the following: (a) f = 2.73 [2.33–3.02]%, v_d = 1.81 [1.65–1.94] μm/ms, D _t = 0.90 [0.86–0.98] μm²/ms; (b) f = 1.71 [1.23–2.09]%, v_d = 1.68 [1.61–1.91] μm/ms, D _t = 0.83 [0.75–0.93] μm²/ms; (c) f = 1.49 [1.25–1.69]%, v_d = 1.78 [1.69–1.86] μm/ms, D _t = 0.90 [0.86–0.96] μm²/ms; (d) f = 0.02 [0–0.03]%, v_d = 1.75 [1.73–1.78] μm/ms, D _t = 2.04 [2.02–2.07] μm²/ms. Brackets indicate 95% confidence intervals obtained using residual bootstrapping.

Figure 3 displays the voxel‐by‐voxel analysis, yielding parametric maps of S₀, D _t, v_d, and f. D _t was high in some areas, due to CSF partial volume effects, which also gave rise to artifacts in some f maps (e.g. CSF contamination in lateral ventricles). The map of v_d is fairly isointense, mainly due to the regularization, whereas the map of f shows higher contrast.

Figure 3.

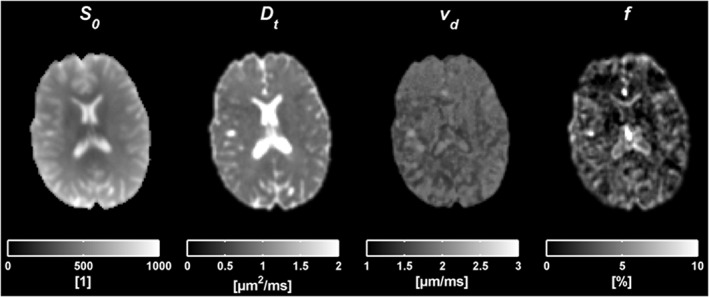
Results from the voxel‐by‐voxel analysis taken from one slice in one subject. The figures from left to right correspond to parametric maps of S₀, D _t, v_d and f.

The average perfusion fraction, velocity dispersion, and diffusion coefficient across all subjects is shown in 15 slices of the MNI space in Figure 4. Figure 5 shows histograms of f, v_d, and D _t values, and a visualization of the corresponding atlas‐based MNI ROIs of GM, DGM, and WM. The perfusion fractions were (mean ± SD over averaged MNI maps) 2.43 ± 0.81%, 1.81 ± 0.90%, and 1.64 ± 0.72% in GM, DGM, and WM, respectively. The corresponding values for v_d were 1.71 ± 0.06 μm/ms, 1.72 ± 0.06 μm/ms, and 1.73 ± 0.04 μm/ms. The v_d values are very homogeneous over the different regions (seen also in Fig. 4), since the subject averaging in combination with the regularization leads to an over‐representation of the mean value of the penalty distribution. For reasons of regularization, we did not attempt to convert the v_d values to average blood velocity. Finally, the D _t values were 1.20 ± 0.22 μm²/ms, 0.96 ± 0.24 μm²/ms, and 0.98 ± 0.13 μm²/ms.

Figure 4.

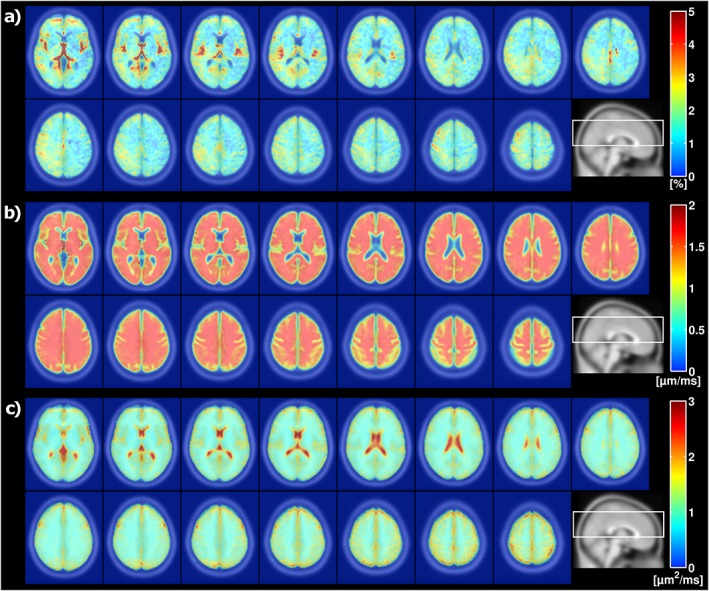
Mean (a) perfusion fraction f, (b) velocity dispersion v_d, and (c) diffusion coefficient D _t, in 15 MNI slices across all eight subjects. CSF is masked out in the f and v_d maps using the MNI tissue probability information in SPM12. The positioning of the slices, indicated on a sagittal image, is shown at the bottom right of the respective sub‐images.

Figure 5.

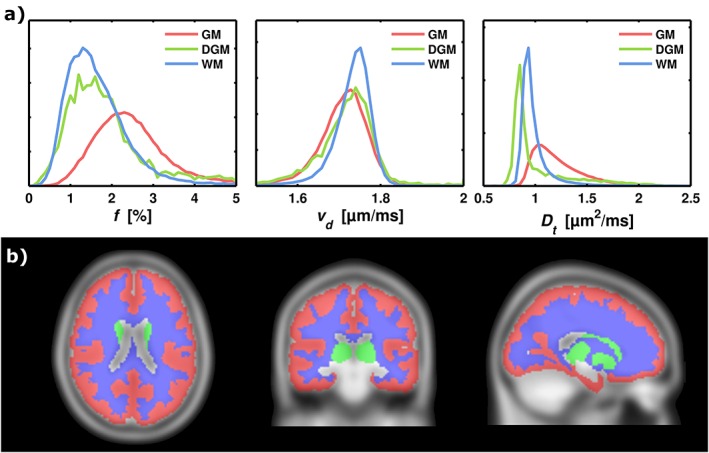
Histogram analysis of the model parameters in the GM, DGM, and WM MNI ROIs. (a) The columns show histograms of f, v_d, and D _t. (b) The MNI template in three projections, with the applied ROIs: GM, DGM, and WM. The color‐encoding corresponds to the histogram curves. The histograms are normalized to unity, so that the y axes correspond to relative frequency.

Figure 6 illustrates the accuracy and precision of f estimates for SNR = 100, as a function of ground‐truth values of f, for the different analysis techniques. The joint analysis showed good performance overall, with superior accuracy and precision for most values of f. The bi‐exponential fitting was clearly inferior to the joint analysis. The segmented fitting showed good performance for low f values, but produced large systematic errors for higher values of f. Figure 7 shows the accuracy and precision of f, v_d, and D _t estimates, as a function of SNR, for a fixed f of 5% (see Simulations sections for the other model parameters). Similarly to Figure 6, the joint analysis showed the best performance overall. The parameter estimates from the joint and bi‐exponential approaches showed a clear convergence towards ideal accuracy and precision, whereas the segmented fitting yielded systematic errors in all model parameters.

Figure 6.

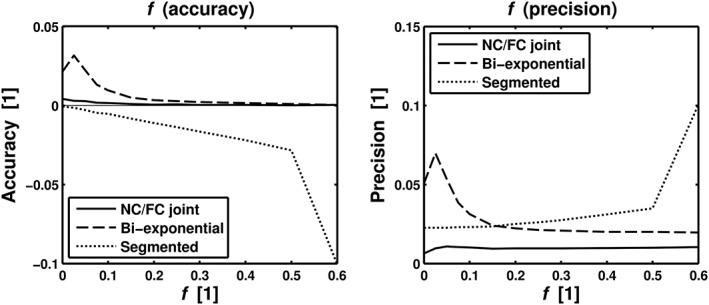
Simulation results for SNR = 100, comparing accuracy and precision of f as a function of f for the joint analysis (“FC/NC joint”) and two different conventional IVIM analysis approaches, i.e. bi‐exponential fit (“Bi‐exponential”) and segmented fit (“Segmented”). The other model parameters were set to v_d = 1.75 μm/ms and D _t = 0.8 μm²/ms in the simulations.

Figure 7.

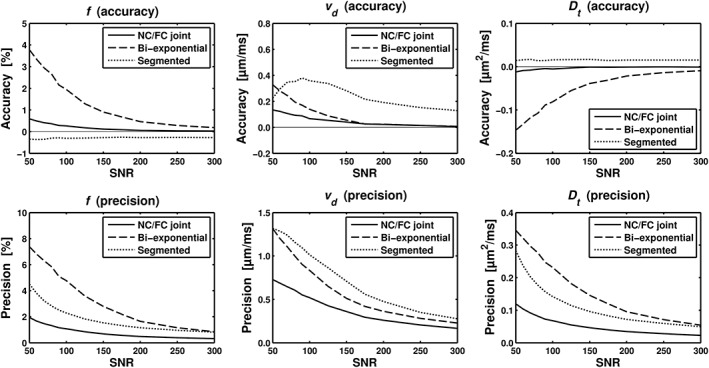
Simulation results comparing accuracy and precision of perfusion parameters estimated with the joint analysis (‘FC/NC joint’) and two different conventional IVIM analysis approaches, i.e., bi‐exponential fit (‘Bi‐exponential’) and segmented fit (‘Segmented’). Graphs show accuracy (top row) and precision (bottom row) for f, v_d and D _t (columns from left to right) as a function of SNR. Simulated parameter values were f = 5%, v_d = 1.75 μm/ms, and D _t = 0.8 μm²/ms.

Discussion

Based on the velocity dispersion model, we suggest a joint analysis of FC and NC motion‐encoded data for improved IVIM analysis. Using an FC/NC sequence, initial tests in eight healthy volunteers showed significant rephasing effects in the FC data. This result is in agreement with previous studies 1, 16, 17, 19 and indicated that the ballistic limit is not an unreasonable assumption for capillary blood flow in the brain. Conversely, the result also suggests that the assumption of the diffusive limit is not valid in the brain under normal experimental conditions. Results of conventional IVIM analysis could thus be prone to misinterpretation due to the dependence of D ^* on protocol parameters (Equation (8)). IVIM imaging is typically performed using single diffusion encoding (SDE) sequences, which enables short encoding times, thereby potentially taking the motion characteristics of the flowing blood even further away from the assumptions of the diffusive limit. Hence, our data suggest that the additional signal attenuation from flowing blood was primarily due to velocity dispersion.

Regularization of the v_d parameter allowed for stable voxel‐by‐voxel analysis in the current approach, yielding perfusion fraction maps of reasonable quality. The regularization was similar to Bayesian model fitting, which has been used previously to improve conventional IVIM analysis 36, 37. Due to the need for regularization, we did not attempt to estimate the average blood velocity in this study. This would otherwise, in principle, have been possible, for example, by assuming a Gaussian velocity distribution so that $v_d^2=⟨{\overline{\mathit{v}}}^2⟩/2$. Voxel‐by‐voxel analysis of brain IVIM is challenging due to the low SNR (low blood volume), and, although the present work suggests promising improvements, more work is needed to make IVIM imaging in the brain more robust 14. The parametric maps of f were found to be sensitive to CSF contamination. This is a common problem in IVIM analysis 38, which also applies to the joint analysis of FC and NC data. Since CSF moves in a pulsatile manner, the FC is expected to affect the CSF signal. Although we tried to avoid CSF contamination by using automatic ROI analysis, some effects are likely to remain in our results, indicated by a higher D _t estimate in the GM compared with the WM. It may be preferable to model the CSF as an additional signal contribution, although it would result in a more complex model. Alternatively, the signal contribution from CSF could be nulled using inversion recovery or T ₂ preparation 38.

The joint analysis yielded plausible perfusion fraction estimates in GM and WM. Although data on brain perfusion fraction are scarce, our values were lower than those reported in previous studies 39, 40. We found that f was highest in GM, whereas DGM showed values in between GM and WM. This result is difficult to assess since there are no comparable reports on regional perfusion fraction in the brain. However, the perfusion fraction is closely linked to CBV 6, and contrast‐agent‐based studies have reported a slightly lower CBV in DGM than in GM, and WM is well known to have lower CBV than GM 41, 42. Still, the perfusion fraction in cortical GM reported here may have been overestimated due to CSF contamination, since the spatial normalization and subject averaging yields an effective smoothing. The diffusion coefficient is known to be fairly homogenous in healthy brain tissue, and is usually reported to be around 0.8 μm²/ms (using b_max= 1000 s/mm²) 43. We found a D _t of around 1 μm²/ms in WM and DGM, and 1.2 μm²/ms in GM. A brain tissue D _t of 1 μm²/ms is reasonable in the low b‐value regime, since these data points are less affected by diffusion kurtosity 44. However, as for the perfusion fraction, cortical D _t values are likely to be overestimated due to CSF partial volume effects. Note that the potential overestimations of the f and D _t in GM values are primarily an effect of the normalization and group averaging, and would therefore be less pronounced in a single‐subject measurement.

Some degree of asymmetry could be identified in the perfusion fraction maps, which could be due to concomitant field effects. Wetscherek et al. used a combination of single refocused SDE (NC) and DDE (FC) sequences with symmetric gradient waveforms 19. Although this effectively compensates for concomitant field effects, it also results in different diffusion experiments with different diffusion times for the NC and FC data, which, in turn, could yield differences in the NC and FC data that are not due to blood flow. To alleviate this, the NC/FC acquisition could be implemented using, for example, a twice‐refocused DDE sequence, with variable polarity of the diffusion encoding blocks. However, this would result in longer encoding times and several unwanted echo pathways that need to be effectively crushed. A few studies have analyzed FC and NC data at multiple b values 17, 18, 19. To the best of our knowledge, only Wetscherek et al. 19 have previously demonstrated FC and NC data at multiple b values in vivo. They used an approach similar to ours, although combing two different types of sequence (SDE and DDE) with unmatched timing parameters. They fitted the acquired signals to simulated phase dispersions, and variation of the encoding time allowed them to analyze motion on different time scales, including the intermediate regime (between the ballistic and diffusive limits). Their findings suggested that blood velocity fluctuations in liver and pancreas were in between the diffusive and ballistic limits. Hence, further work is needed to assess the validity of the ballistic limit in brain tissue, for example, by taking into account possible contributions from blood motion in the intermediate regime.

To compare the reliability of parameter estimates from the proposed joint analysis and the conventional IVIM fitting methods, we performed numerical simulations. The results showed that the joint analysis improved accuracy and precision of estimated perfusion and diffusion parameters across a wide range of SNR levels and values of f. The joint analysis significantly outperformed the conventional approaches particularly for f ≳ 0.1, which suggests that it may be even more suitable in organs with higher blood volumes, such as the liver. In the brain, however, a normal assumption would be that f < 0.1. In this regime, the segmented analysis showed slightly better accuracy in the estimation of f for low perfusion fractions and SNRs, although with a negative bias which increased as a function of f. One obvious advantage of the joint analysis is the robust estimation of D _t from the FC data, which is apparent in the high accuracy of D _t as a function of SNR. We empirically found that a few FC data points (four in the simulations) were enough for a robust joint analysis, which suggests that optimization of the data acquisition protocol may reduce the scan time 45. For example, by acquiring only 4 FC and 12 NC data points, the scan time of our protocol would decrease from approximately 12 to 6 min. The bi‐exponential fitting performed worse than the joint analysis across all performance measures and parameters. This suggests that the application of a joint analysis, i.e. measuring additional information by sampling across both diffusion and flow encoding dimensions, improves the estimation of IVIM parameters.

A limitation of the current work is that we did not use experimental data in the comparison between the proposed joint FC/NC approach and the conventional IVIM approach. Therefore, although the results of the simulations clearly indicated superiority of the joint analysis approach, the robustness of this improvement, as well as its clinical value, needs to be assessed for various in vivo conditions. Furthermore, the specific clinical applications that will benefit most from the acquisition of FC and NC IVIM data are yet to be established. Another limitation is the difficulty in verifying that the signal from flowing blood water is fully rephased in the FC data. Acquisition of FC/NC IVIM data in multiple organs and with variable motion encoding times would help to elucidate for which organs and encoding times the ballistic limit is a valid approximation. Last, we used a generic in vivo acquisition protocol with the same number of FC and NC data points, and with emphasis on low b values. However, IVIM analysis is highly dependent on the exact b‐value distribution 40, and furthermore we empirically found that it could be beneficial to acquire fewer FC than NC data points. Hence, further optimization of our acquisition protocol should allow for an improved distribution of data points and shorter scan times.

The continuation of the present work will include application of the joint analysis to different organs and diseases, further experimental comparisons with conventional IVIM analysis, and improved data acquisition, modeling, and post‐processing.

Conclusions

We analyzed the IVIM effect in NC and FC motion‐encoded brain MRI data. The flow compensation resulted in a strong rephasing effect for the signal contribution from flowing blood, effectively nulling the IVIM effect. This indicates that the ballistic limit is plausible for cerebral blood flow. Conversely, it also suggests that the diffusive limit is inaccurate for IVIM brain imaging. The velocity dispersion model produced reasonable image contrast and numerical values for the perfusion fraction. Simulations showed that the precision and accuracy of microcirculatory parameter estimates were significantly improved when applying the joint analysis. This is of particular importance in systems where the ballistic limit is valid, which was shown to be plausible for the brain. Flow compensation could thus be used in IVIM applications as a way to improve estimation of the perfusion fraction and to probe capillary blood velocity.

Ahlgren, A. , Knutsson, L. , Wirestam, R. , Nilsson, M. , Ståhlberg, F. , Topgaard, D. , and Lasič, S. (2016) Quantification of microcirculatory parameters by joint analysis of flow‐compensated and non‐flow‐compensated intravoxel incoherent motion (IVIM) data. NMR Biomed., 29: 640–649. doi: 10.1002/nbm.3505.