Ion‐driven instabilities in the solar wind: Wind observations of 19 March 2005

Abstract

Intervals of enhanced magnetic fluctuations have been frequently observed in the solar wind. But it remains an open question as to whether these waves are generated at the Sun and then transported outward by the solar wind or generated locally in the interplanetary medium. Magnetic field and plasma measurements from the Wind spacecraft under slow solar wind conditions on 19 March 2005 demonstrate seven events of enhanced magnetic fluctuations at spacecraft‐frame frequencies somewhat above the proton cyclotron frequency and propagation approximately parallel or antiparallel to the background magnetic field B _o. The proton velocity distributions during these events are characterized by two components: a more dense, slower core and a less dense, faster beam. Observed plasma parameters are used in a kinetic linear dispersion equation analysis for electromagnetic fluctuations at k x B _o = 0; for two events the most unstable mode is the Alfvén‐cyclotron instability driven by a proton component temperature anisotropy T_⊥/T_|| > 1 (where the subscripts denote directions relative to B _o), and for three events the most unstable mode is the right‐hand polarized magnetosonic instability driven primarily by ion component relative flows. Thus, both types of ion anisotropies and both types of instabilities are likely to be local sources of these enhanced fluctuation events in the solar wind.

Key Points

• Ion temperature anisotropies and proton beam/core flows are sources of enhanced field observations

• For two events Alfven‐cyclotron modes are most unstable

• For three events magnetosonic modes are most unstable

1. Introduction

The solar wind is a highly ionized, magnetized plasma which flows at supersonic and super‐Alfvénic speeds away from the Sun. In this medium there have been many observations of enhanced magnetic fluctuations at frequencies near the proton cyclotron frequency. There are two hypotheses as to the source of these enhanced fluctuation events [Jian et al., 2014]. One school holds that these large‐amplitude waves are generated close to the Sun and are then transported by the solar wind to observation at planetary distances. The alternative picture is that the expanding solar wind flow leads to nonthermal electron and ion velocity distributions which locally excite short‐wavelength instabilities which are observed near their source. This manuscript uses plasma and magnetic field measurements with kinetic linear dispersion theory to demonstrate that several enhanced magnetic fluctuations events observed by the Wind spacecraft on 19 March 2005 are unstable to one or more kinetic instabilities, thereby providing evidence that these particular events are locally generated.

The hot (tens of eV), tenuous (few particles per cubic centimeter near 1 AU) character of the solar wind implies that it is a collisionless plasma in which a variety of different kinetic instabilities can arise if appropriate sources of free energy are available. Kinetic instabilities are those which are driven by velocity‐space anisotropies and which typically have maximum growth rates arising in the short wavelength regime corresponding to wavelengths the order of or shorter than either the thermal ion gyroradius or the ion inertial length [Gary, 1993].

If a plasma is in equilibrium, the velocity distributions of the constituent species are Maxwellian. All fluctuations in such plasmas either are damped or propagate with no change in amplitude. For frequencies near the proton cyclotron frequency and propagation quasi‐parallel to B _o, the cases of interest here, there are three fundamental normal modes [Gary, 1993, chapter 6]: predominantly electrostatic ion acoustic waves, predominantly electromagnetic Alfvén‐cyclotron waves with left‐hand circular polarization in the limit of k x B _o = 0, and predominantly electromagnetic magnetosonic waves with right‐hand circular polarization at k x B _o = 0. Ion acoustic waves propagate with weak damping only if T_e > > T_p; as this is not a typical condition in the solar wind, we do not consider such modes further. At very long wavelengths and low frequencies Alfvén waves at k x B_o = 0 are nonresonant and essentially undamped. But as the frequencies of such modes approach Ω_p, the proton cyclotron frequency, the waves become dispersive; the resulting Alfvén‐cyclotron fluctuations undergo proton cyclotron damping and propagate with real frequencies only at ω_r < Ω_p. Long‐wavelength magnetosonic fluctuations k x B_o = 0 are also nonresonant and very weakly damped, but because of their right‐hand polarization, they do not suffer proton cyclotron damping and propagate at frequencies through and well above Ω_p where they become strongly dispersive whistler modes.

Although various types of nonthermal ion and electron velocity distributions are observed in the interplanetary medium [Feldman et al., 1973; Marsch, 1991], especially in the fast wind, for purposes of instability analysis nonequilibrium distributions are usually characterized as having temperature anisotropies and/or multiple components with relative flow speeds between component pairs. Here we follow common practice [Feldman et al., 1973; Leubner and Viñas, 1986; Marsch and Livi, 1987; Goldstein et al., 2000; He et al., 2015] and assume that proton velocity distributions can be fit as the sum of two components, a more dense, slower core (denoted by subscript c) and a less dense, faster beam (subscript b). We further assume that both proton components, as well as the electrons (subscript e) and the alpha particles (subscript α), can each be represented as a bi‐Maxwellian distribution with T_⊥ ≠ T_|| (where the subscripts represent directions relative to B _o) and relative flow velocities parallel to B _o. We denote the relative beam/core flow velocity as v _o = v _ob–v _oc where v _oj is the average flow velocity of the jth component in the plasma (center of mass) frame and the relative alpha/core flow velocity as v _oαc  = v _oα–v _oc. We define the ion (electron) inertial length λ_i = c/ω_pi (λ_e = c/ω_pe) where ω _pj is the plasma frequency of the jth species, and the ion (electron) thermal gyroradius ρ_i = v_i/Ω_i (ρ_e = v_e/Ω_e) where v_j is the thermal speed of the jth species, and Ω_j is the cyclotron frequency of the jth species. The jth component parallel plasma beta is defined as β_||j = 8πn_jk_BT_||j/B_o ², and the Alfvén speed is v_A = B_o/(4πn_em_p)^1/2 where n_e = n_p + 2n_α.

Anisotropies in solar wind ion velocity distributions are a rich source of diverse kinetic plasma instabilities. The enhanced fluctuations that arise from such growing modes scatter the nonthermal species, reducing their anisotropies and driving them toward (but not completely to) the Maxwellian distributions of thermal equilibrium [e.g., Gary et al., 1994]. Jian et al. [2009, 2010, 2014] (See also S. A. Boardsen et al., MErcury Surface, Space ENvironment, GEochemistry, and Ranging (MESSENGER) survey of in situ low‐frequency wave storms between 0.3 and 0.7 AU, submitted to Journal of Geophysical Research, 2015) have used high‐resolution magnetometer observations from the STEREO, MESSENGER, and Helios spacecraft to study solar wind events of enhanced magnetic field fluctuations with frequencies near Ω_p at propagation quasi‐parallel to the background magnetic field B _o. By comparing left‐hand versus right‐hand polarizations in the spacecraft frame, they found that the left‐hand waves are generally stronger and appear slightly more often. However, their analyses utilized proton data reduction algorithms which were less general than the beam/core bi‐Maxwellian velocity distributions used in this paper, thereby limiting their ability to compare temperature anisotropy and beam/core distributions as sources of proton‐driven instabilities. Here we follow these earlier papers by identifying events of interest as corresponding to enhanced field fluctuations with frequencies near the proton cyclotron frequency. The new element here is that we correlate these events with particle species observations under the more general and more accurate assumption that the proton distributions can be described as the sum of beam and core components with separate densities, flow speeds, temperatures, and temperature anisotropies. Using this model in kinetic linear dispersion theory, we determine which types of ion‐driven instabilities are the likely sources of these enhanced fluctuation events.

Following the observations of Jian et al. [2009, 2010, 2014], our concerns here are ion‐driven instabilities which propagate at directions quasi‐parallel to B _o. This condition corresponds to three categories of growing modes: Alfvén‐cyclotron instabilities driven by ion component anisotropies such that T_⊥ / T_|| > 1 [Gary et al., 2001], parallel firehose instabilities driven by ion component anisotropies such that T_⊥ / T_|| < 1 [Hellinger et al., 2006], and ion/ion magnetosonic instabilities driven by the relative flow speed of two ion components [Goldstein et al., 2000]. Under the condition k x B _o = 0 Alfvén‐cyclotron waves and instabilities have left‐hand circular polarization, whereas the parallel firehose instability, magnetosonic waves, and magnetosonic proton/proton instabilities all have right‐hand circular polarization in the solar wind frame.

If the proton velocity distribution may be approximated as a single bi‐Maxwellian and heavy ions may be ignored, growth rate predictions of kinetic linear theory of electromagnetic instabilities driven by proton temperature anisotropies may be expressed in terms of two parameters, T_⊥p/T_||p and β_||p. Figure 7.3 of Gary [1993] shows that these two parameters characterize the linear theory thresholds of such instabilities. Gary et al. [1997] used hybrid simulations to show that the Alfvén‐cyclotron instability threshold condition represents an upper bound for T_⊥p/T_||p > 1, and Gary et al. [1998] used the same type of simulations to show that the proton‐parallel firehose instability threshold constitutes an upper bound for the opposite sense of the proton anisotropy. Considering only solar wind conditions in which the proton velocity distribution may be approximated as a single bi‐Maxwellian component, Kasper et al. [2002, 2006], Hellinger et al. [2006], Bale et al. [2009], Maruca et al. [2011, 2012], Osman et al. [2012], and Hellinger and Trávníček [2014] used measurements from the Wind spacecraft to show that instability thresholds in T_⊥p/T_||p versus β_||p parameter space indeed correspond to observed proton anisotropy bounds. However, thresholds of the proton mirror and the oblique proton firehose instabilities, which have wavevectors at substantially oblique angles relative to B _o, provide better constraints to the observations than do the thresholds of the anisotropy‐driven instabilities with maximum growth at parallel propagation.

Furthermore, as discussed above, proton velocity distributions in the relatively fast, relatively collisionless solar wind are usually not well represented as a single bi‐Maxwellian, but rather require at the minimum a two component core/beam description. Linear dispersion theory analyses have demonstrated that a sufficiently large beam/core relative flow speed (typically greater than about 1.5 v_A) can drive both parallel magnetosonic and oblique Alfvén instabilities [Montgomery et al., 1975, 1976; Abraham‐Shrauner et al., 1979; Dum et al., 1980; Marsch and Livi, 1987; Daughton and Gary, 1998; Goldstein et al., 2000]. However, kinetic linear theories of proton beam/core instabilities require at least six independent proton parameters, e.g., the proton core β_||, the proton core relative density n_c/n_e, the dimensionless beam/core relative flow speed v_o/v_A, T_||b/T_||c, and the two proton component temperature anisotropies T_⊥c/T_||c and T_⊥b/T_||b, as well as one or more electron parameters [Daughton and Gary, 1998] and at least four additional parameters characterizing each minor ion species such as the alpha particles. This parametric plethora makes it difficult to present linear theory threshold conditions of beam/core instabilities as two‐dimensional plots, requiring instead a large number of multidimensional figures to clearly expose the plasma physics of these growing modes. Our approach here is to constrain this large parameter space through the use of detailed ion and electron measurements from the plasma instruments on board the Wind spacecraft and to calculate dispersion properties of the enhanced fluctuations for specific conditions observed in the solar wind.

We make two fundamental assumptions. The first is that undetermined processes in the collisionless solar wind (e.g., shocks, diverging flows, and/or large‐scale compressions) act locally to push plasma species velocity distributions away from the Maxwellian condition. The second is that the resulting non‐Maxwellian distributions drive short‐wavelength instabilities which generate enhanced field fluctuations which, in turn, act to stabilize the growing modes by reducing the distribution anisotropies. In this scenario the large‐amplitude wave events we study should correspond to marginally stable or weakly unstable modes. Our conclusion that the plasma observations are indeed subject to modest instability growth implies that these events correspond to local excitation in the solar wind.

2. Magnetic Field and Plasma Observations on 19 March 2005

The Wind spacecraft carries a fast magnetometer [Lepping et al., 1995], a pair of Faraday cup instruments as part of the Solar Wind Experiment (SWE) [Ogilvie et al., 1995] which measures velocity distributions of protons and alpha particles at a 92 s cadence and an electron electrostatic analyzer [Lin et al., 1995] providing a full 3‐D electron velocity distribution at a 97 s cadence. After completing a survey of enhanced magnetic fluctuation events in the observed frequency range 0.01 Hz < f < 5 Hz using 0.092 s magnetic field data, we chose observations of such events in the solar wind on 19 March 2005 to be the subject of a comprehensive study as described below. On this date the Wind spacecraft detected a number of events with wave propagation quasi‐parallel to the background magnetic field. We chose the events on this date because both left‐hand and right‐hand polarized waves in the spacecraft frame are observed within a relatively short time interval, and the individual ion spectra from this period have been examined in detail by the SWE coauthors on this manuscript.

Figure 1 illustrates the dynamic spectrum of the magnetic field data from 19 March 2005. This analysis utilizes a fast Fourier transform based on the Means [1972] quadrature spectrum technique, which is explained in Jian et al. [2010]. As shown in Figure 1, we found seven events of enhanced magnetic fluctuations, with the following common characteristics: (1) the coherence between the two transverse magnetic field components B_y and B_z is enhanced, (2) the transverse power is substantially increased over the background power at earlier and later times, (3) the transverse power is much stronger than the compressional power, (4) the magnetic field fluctuations are nearly circularly polarized as indicated by the high absolute ellipticity, and (5) the propagation direction is within 10° of the background magnetic field direction. Given these seven candidate events, we performed linear dispersion theory analyses for most of these intervals, using the method described below. The events meeting the criteria in Jian et al. [2009] are marked in Figure 2, cyan for left‐hand polarized in the spacecraft frame and yellow for right‐hand polarized in the spacecraft frame. The intervals for the seven events indicated in Figure 1 are as follows: Event #1 (78.380 < DOY < 78.389), Event #2 (78.488 < DOY < 78.494), Event #3 (78.506 < DOY <78.515), Event #4 (78.672 < DOY < 78.685), Event # 5 (78.741 < DOY < 78.748), Event #6 (78.786 < DOY < 78.798), and Event #7 (78.804 < DOY < 78.811).

Figure 1.

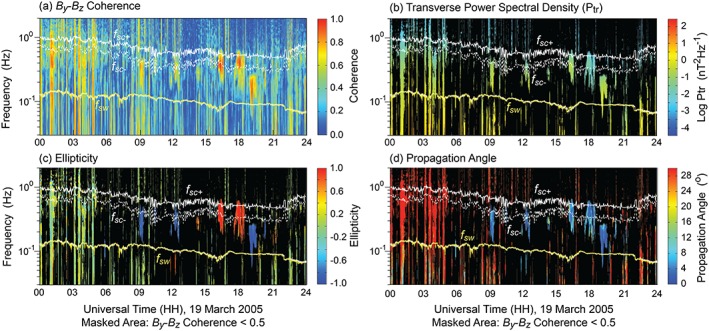
Magnetic field fluctuation measurements from the Wind spacecraft on 19 March 2005. (a) Coherence between the two transverse components, B_y and B_z; (b) transverse power spectral density; (c) the ellipticity in the spacecraft frame where +1 corresponds to right‐hand circular polarization, and −1 corresponds to left‐hand circular polarization; and (d) the propagation angle with respect to B _o. The yellow lines represent the local proton cyclotron frequency. The white solid and dashed lines labeled f_sc+ and f_sc− represent the Doppler‐shifted proton cyclotron frequency if the wave propagates parallel or antiparallel to the solar wind velocity under the assumption that the phase speed of a wave at the proton cyclotron frequency is v _A. The fast Fourier transform is performed for every 2560 points with a shift of 320 points and a bandwidth of 29 points. In Figures 1b through 1d the color black represents parameter values for which the B_y and B_z coherence is less than 0.5.

Figure 2.

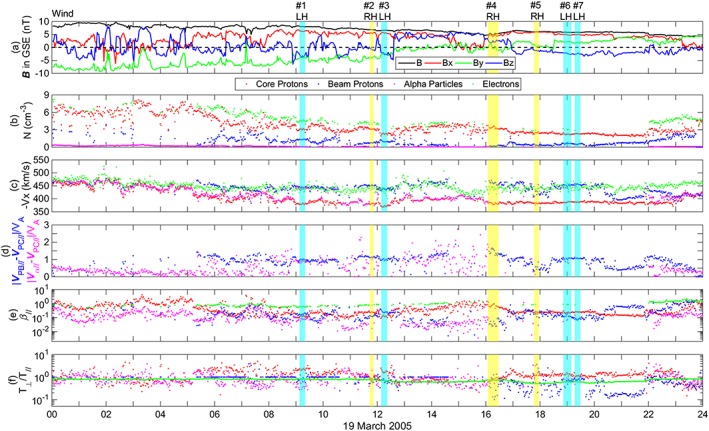
Magnetic field and plasma measurements from the Wind spacecraft as a function of time for 19 March 2005. (a) The magnetic field vector in GSE coordinates, where black represents the field magnitude, and red, green and blue represent B_x, B_y, and B_z, respectively. For the plasma properties shown in the subsequent five panels proton core parameters are indicated by red dots, proton beam parameters as blue dots, alpha particle parameters as magenta dots, and electron parameters as green dots. Here are shown (b) the component number densities, (c) the average velocities in the –x GSE direction, (d) the average flow speed parallel to B _o relative to the core protons and normalized to the Alfvén speed, (e) the component β_||, and (f) the component T_⊥/T_|| values. The seven events corresponding to enhanced proton cyclotron fluctuations discussed in the text are shown as vertical bands with cyan corresponding to left‐hand polarization and yellow representing right‐hand polarization as measured in the spacecraft frame.

For one 92 s measurement cycle of the ions in each event, the proton core, the proton beam, the electrons, and the alpha particles were each fit to bi‐Maxwellian velocity distributions with relative flow velocities parallel to B _o. The proton beam and alpha particle measurements during Event #5 are noisy and poorly defined, so this event is not further considered here. Table 1 presents field and plasma parameters from the other six events analyzed in section 3. Due to weak signal‐to‐noise ratios and/or strongly non‐Maxwellian distributions, the fitting procedures from Events #2 through #7 yield relatively large error bars for many of the alpha parameters. The values of the alpha temperature anisotropies are particularly suspect, so that because of these large uncertainties, we have assumed T_⊥α/T_||α = 1 for Events #2, #3, #4, #6, and #7 in Table 1 and in the linear dispersion theory analyses described in section 3.

Table 1.

Field and Plasma Parameters for Six Enhanced Magnetic Fluctuation Events Observed From Wind Spacecraft on 19 March 2005^a

	Event #1	Event #2	Event #3	Event #4	Event #6	Event #7
Bo (nT)	8.08	6.77	6.64	5.01	5.86	5.85
nc (cm−3)	3.21	3.14	2.45	3.65	2.47	2.29
T||c (eV)	7.015	8.666	7.107	16.17	10.23	9.16
vA/c	2.72 × 10−4	2.47 × 10−4	2.59 × 10−4	1.82 × 10−4	2.39 × 10−4	2.52 × 10−4
β||c	0.139	0.239	0.159	0.947	0.297	0.248
nc/ne	0.687	0.787	0.702	0.910	0.777	0.801
nb/ne	0.274	0.198	0.269	0.060	0.204	0.171
nα/ne	0.019	0.0075	0.014	0.015	0.009	0.014
|vo|/vA	0.964	1.148	1.08	1.649	1.124	1.037
|voαc|/vA	0.929	1.036	0.513	0.669	1.011	1.198
T||b/T||c	2.91	2.139	3.54	0.865	1.506	1.395
T||α/T||c	5.126	3.78	20.21	6.23	3.42	8.85
T||e/T||c	3.06	2.615	4.286	1.375	2.384	2.964
T⊥c/T||c	2.24	1.00	1.448	0.799	0.843	1.00
T⊥b/T||b	0.943	0.587	0.929	1.254	0.773	0.823
T⊥α/T||α	0.609	(1.0)	(1.0)	(1.0)	(1.0)	(1.0)
T⊥e/T||e	0.811	0.753	0.702	0.728	0.602	0.612

^aValues in parenthesis represent the assumption of isotropic alpha particles because of poor fits to the model of flowing bi‐Maxwellian alpha particle velocity distributions.

Figure 2 displays the magnetic field vector in geocentric solar equatorial (GSE) coordinates, the number density, speed in the –X direction (antisunward), the dimensionless beam/core and alpha/core relative flow speeds, β_||j, and temperature anisotropy of core proton (in red), beam proton (in blue), alpha particles (in magenta), and electrons (in green). The relative flow speeds are projected along the magnetic field direction. For all seven events, B_x > 0, implying that this component of the magnetic field points sunward. Also for all seven events v_ocx > 0, v_obx < 0, and v_ox < 0 so that the beam/core relative flow points in the antisunward direction.

Figure 3 illustrates the magnetic fluctuation power spectra for four of these events as labeled. As is typical for solar wind events [Jian et al., 2009, Figure 1b; Jian et al., 2010, Figure 2c; Jian et al., 2014, Figure 7b], the energy density of field fluctuations transverse to B _o is 1 to 2 orders of magnitude greater than that of the compressional fluctuations parallel/antiparallel to the background magnetic field. Polarization analysis shows that the fluctuations of Events #1, #6, and #7 are predominantly left‐hand polarized, whereas Event #4 corresponds primarily to right‐hand polarization fluctuations as measured in the spacecraft frame.

Figure 3.

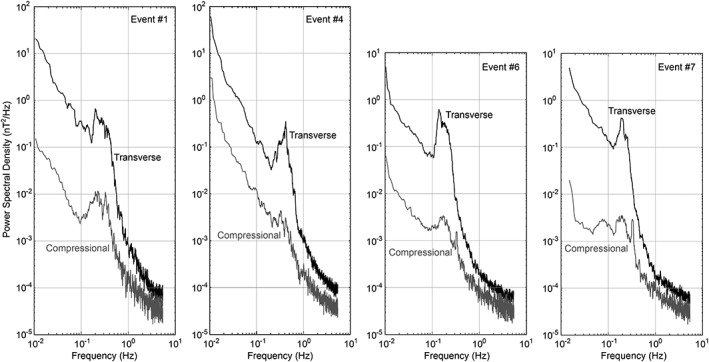
The magnetic fluctuation power spectra during Events #1, #4, #6, and #7 observed from the Wind spacecraft on 19 March 2005.

Figure 4 shows selected ion measurements from the SWE instrument during Event #1. Here θ_Bn indicates the angle between the magnetic field vector and the projection axis on which the distribution was measured (a selection of 5 out of the 40 spin angles that make up the fit). The contour plots show the component fits in the proton core rest frame. The proton beam/core separation is clear here, as is the alpha/core relative flow.

Figure 4.

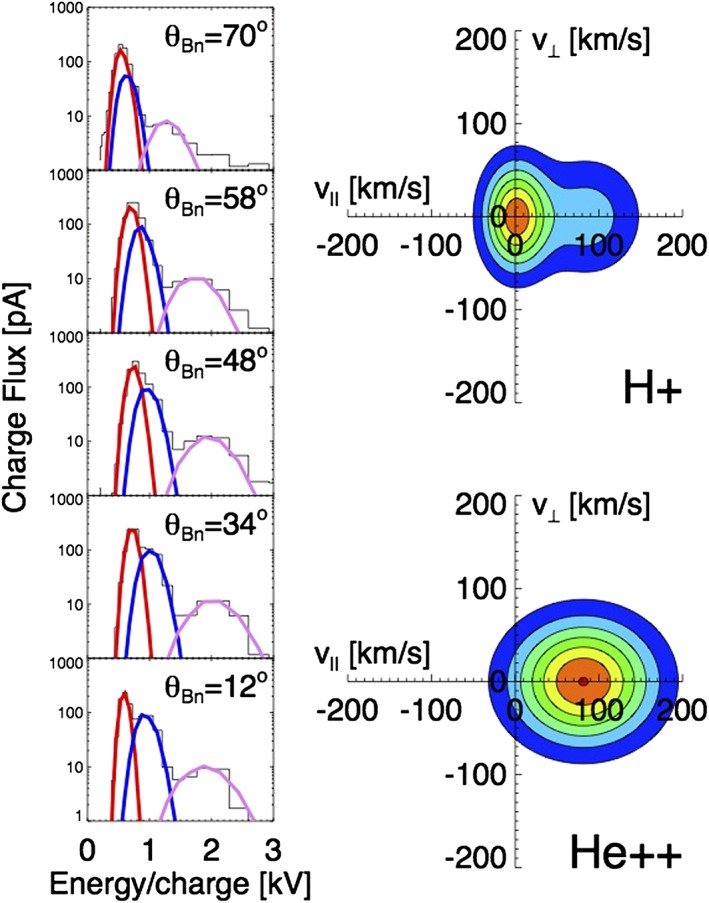
Ion measurements from the Wind spacecraft during Event #1 on 19 March 2005. (first column) The stepwise black lines show the relative flux measurements from the SWE instrument as functions of energy/charge for five different values of θ_Bn, the angle between B _o and the projection axis on which the distribution was measured. The smooth curves display the ion distribution fits for proton core (red), proton beam, (blue), and alpha particle (violet) components. (second column) The proton and alpha particle velocity distributions in v_||‐v_⊥ space as represented by the proton core, proton beam, and alpha particle fits.

3. Kinetic Dispersion Theory Analyses of Six Events on 19 March 2005

This section describes results from kinetic linear dispersion theory of waves and instabilities in collisionless, homogeneous, magnetized plasmas [Gary, 1993], using parameters as measured from Wind during the events of 19 March 2005. Under the assumption that the enhanced fluctuations from each of these events were generated in the local solar wind, we have used magnetic field and plasma measurements as listed in Table 1. Inserting these parameters into the kinetic linear dispersion theory for waves and instabilities at k x B _o = 0, we computed and plotted the dispersion properties, that is, the complex frequency ω = ω_r + iγ as a function of parallel wave number k_||, of the four distinct low‐frequency waves at k x B _o = 0 for each event. All of the linear theory calculations presented here are carried out in the plasma center‐of‐mass frame where B_o > 0 corresponds to the sunward direction.

The parameters for Event #1 given in Table 1 yield Figure 5 which illustrates the dispersion relations (ω_r and γ versus k_||) for each of the modes which propagate near the proton cyclotron frequency. All four modes are essentially undamped in the long‐wavelength limit. The two left‐hand polarized Alfvén‐cyclotron modes are constrained to |ω_r| < Ω_p with one such mode stable and one unstable. If the proton velocity distribution were to consist of a single bi‐Maxwellian component, the sunward and antisunward Alfvén‐cyclotron modes would be unstable with the same growth rates. However, the beam/core character of the observed proton distributions breaks the left‐right symmetry of the system for all the events studied here. In this particular case the positive frequency sunward propagating Alfvén‐cyclotron mode is stable, whereas the negative frequency antisunward propagating Alfvén‐cyclotron mode is moderately unstable (maximum γ/Ω_p ~ 5 × 10⁻³) at k_||c/ω_pp ~ 0.60, where it has a strong proton core cyclotron resonance and is driven by the strong core temperature anisotropy. The two right‐hand polarized magnetosonic modes, in contrast, extend to frequencies well above Ω_p where, in the absence of proton cyclotron resonances, they remain weakly damped and exhibit the beginnings of whistler dispersion.

Figure 5.

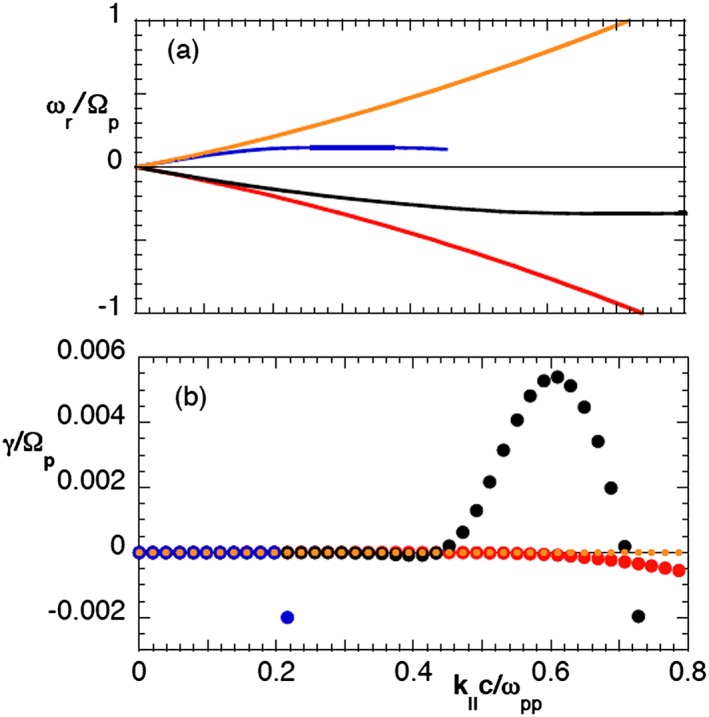
The dispersion properties ((a) real frequencies and (b) damping/growth rates as functions of k_||) of the four low‐frequency electromagnetic normal modes of the plasma computed from the kinetic dispersion equation at k x B _o = 0 for fluctuations in a homogeneous, collisionless plasma. Parameters are those as given in Table 1 for Event #1 on 19 March 2005. Red and orange represent properties of the right‐hand circularly polarized magnetosonic modes, whereas black and blue illustrate dispersion of the left‐hand circularly polarized Alfvén‐cyclotron modes.

The parameters for Event #2 yield Figure 6 which illustrates the dispersion relations for each of the modes that propagate near the proton cyclotron frequency. All four modes are essentially undamped in the long‐wavelength limit. The two left‐hand polarized Alfvén‐cyclotron modes are constrained to |ω_r| < Ω_p and become strongly damped at k_||c/ω_pp > 0.40. The right‐hand polarized magnetosonic modes again extend to higher frequencies with weak damping and whistler dispersion. Here the negative frequency magnetosonic branch is moderately unstable (maximum γ/Ω_p ~ 2 × 10⁻³) at k_||c/ω_pp ~ 0.80 and ω_r/Ω_p ~ 1.0, with a strong proton beam cyclotron resonance and is driven by the super‐Alfvénic beam/core relative flow (This growing mode is also known as the proton/proton right‐hand resonant instability [Gary, 1993, section 8.2]). The negative phase speed again indicates that unstable modes here propagate in the antisunward direction.

Figure 6.

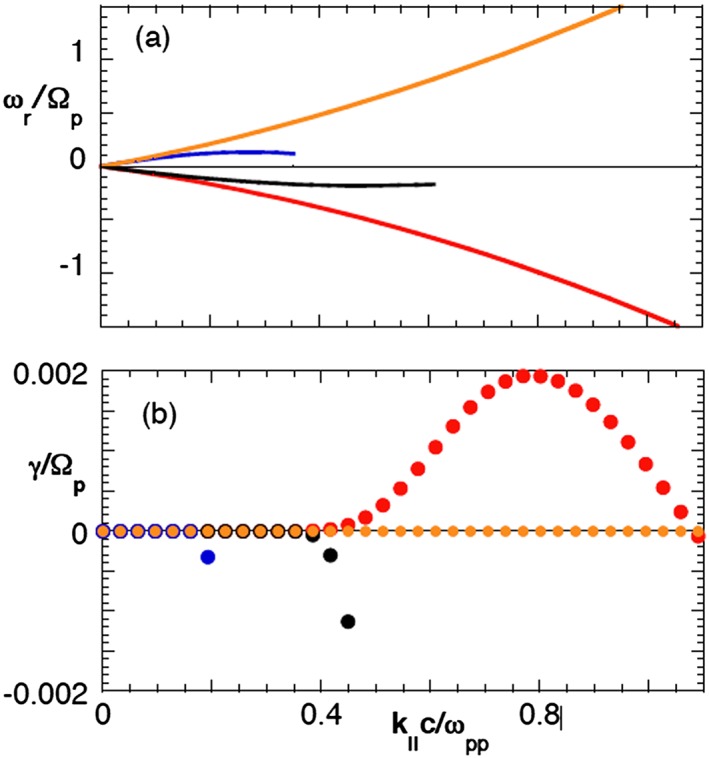
The dispersion properties ((a) real frequencies and (b) damping/growth rates as functions of k_||) of the four low frequency electromagnetic normal modes of the plasma computed from the kinetic dispersion equation at k x B _o = 0 for fluctuations in a homogeneous, collisionless plasma. Parameters are those as given in Table 1 for Event #2 on 19 March 2005. Red and orange represent properties of the right‐hand circularly polarized magnetosonic modes, whereas black and blue illustrate dispersion of the left‐hand circularly polarized Alfvén‐cyclotron modes.

The parameters for Event #3 yield ω_r(k_||) dispersion plots very similar to those for the two preceding events. The Alfvén‐cyclotron modes are stable because of the relatively weak core temperature anisotropy. And beam/core and alpha/core relative flow speeds are not large enough to excite the ion/ion magnetosonic instabilities, so that all four modes are stable for this event and we do not illustrate this case.

The parameters for Event #4 as given in Table 1 yield dispersion plots ω_r(k_||) with two distinct unstable modes as shown in Figure 7. Again, both unstable modes propagate in the antisunward direction. The right‐hand polarized magnetosonic mode is unstable with maximum growth rate γ/Ω_p ~ 7 × 10⁻³ and corresponding wave number k_||c/ω_pp ~ 0.35 and frequency ω_r/Ω_p ~ 0.33, whereas the left‐hand polarized Alfvén‐cyclotron mode is more weakly unstable with maximum growth rate γ/Ω_p ~ 2 × 10⁻⁴ and corresponding wavenumber k_||c/ω_pp ~ 0.24 and frequency ω_r/Ω_p ~ 0.12. It appears that both the beam/core and the alpha/core relative flows contribute to the magnetosonic instability and that the Alfvén‐cyclotron instability is driven primarily by the beam temperature anisotropy. The other two modes are stable, being undamped at long wavelengths and becoming strongly damped at sufficiently large wave numbers.

Figure 7.

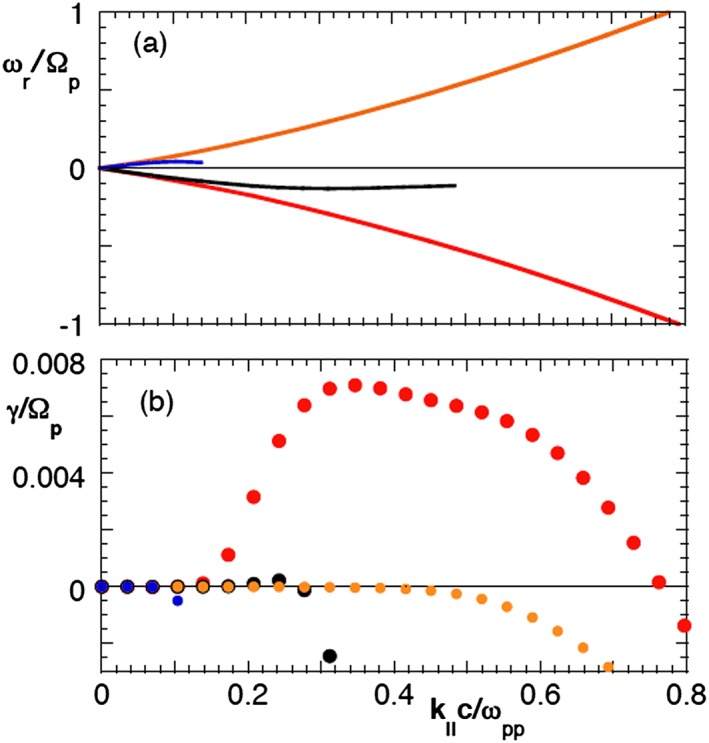
The dispersion properties ((a) real frequencies and (b) damping/growth rates as functions of k_||) of the four low frequency electromagnetic normal modes of the plasma computed from the kinetic dispersion equation at k x B _o = 0 for fluctuations in a homogeneous, collisionless plasma. Parameters are those as given in Table 1 for Event #4 on 19 March 2005. Red and orange represent properties of the right‐hand circularly polarized magnetosonic modes, whereas black and blue illustrate dispersion of the left‐hand circularly polarized Alfvén‐cyclotron modes.

For the parameters of Event #6, the right‐hand polarized magnetosonic mode is again unstable, apparently driven by the beam/core relative flow. Dispersion of both ω_r(k_||) and γ(k_||) is similar to previous cases and is not shown here; the maximum growth rate is very weak with γ/Ω_p < 1 × 10⁻⁴ and corresponds to k_||c/ω_pp ~ 0.63 and ω_r/Ω_p ~ 0.72. Again, the unstable modes propagate in the antisunward direction.

Finally, for the parameters of Event #7, both the Alfvén‐cyclotron and the magnetosonic modes are unstable. Dispersion of both ω_r(k_||) and γ(k_||) is similar to previous cases and is not shown here. The maximum growth rate of the Alfvén‐cyclotron instability is weak with γ/Ω_p ~ 1.3 × 10⁻⁴ and corresponds to k_||c/ω_pp ~ 0.40 and ω_r/Ω_p ~ 0.20, and the magnetosonic mode has very weak growth with γ/Ω_p < 2 × 10⁻⁵ at k_||c/ω_pp ~ 0.25 and ω_r/Ω_p ~ 0.23. Again, both unstable modes propagate antiparallel to B_o, that is, antisunward.

4. Summary and Conclusions

We have used Wind spacecraft magnetic field and plasma observations in the slow solar wind (v_sw ~ 390 km/s) on 19 March 2005 to examine the linear dispersion properties for events of enhanced magnetic fluctuations near the proton cyclotron frequency at propagation parallel/antiparallel to the background magnetic field. We analyze the velocity distributions in terms of two proton components, a more dense, cooler core and a more tenuous, warmer beam with a relative beam/core flow parallel to B _o, and a very tenuous, flowing alpha particle component. We then solve the kinetic linear dispersion equation at k x B_o = 0 and find for two events the most unstable mode is the left‐hand polarized Alfvén‐cyclotron instability driven by a proton component temperature anisotropy T_⊥/T_|| > 1, and for three events the most unstable mode is the right‐hand polarized magnetosonic instability driven primarily by ion component relative flows.

Jian et al. [2014] argued that, for waves propagating parallel to the solar wind flow velocity v _sw, the spacecraft frame polarization should be the same as the polarization in the solar wind frame, whereas for waves at propagation antiparallel to v _sw, the spacecraft frame polarization should be opposite to the intrinsic polarization. The Appendix A of this manuscript provides an alternative derivation of this same result. Our dispersion analysis predicts that, for all five events with unstable modes, the instabilities propagated parallel to the direction of the proton beam, i.e., in the antisunward direction. Thus, as summarized in Table 2, we get agreement between polarizations inferred from observations and polarizations predicted by linear theory for four out of the five events. The single case of disagreement between observations and theory (Event #6) may be due to the fact that in this case theory predicts very weak growth for the right‐hand plasma frame instabilities, so that this disagreement is not as robust as the four cases of agreement.

Table 2.

Polarization Table for the Six Events of 19 March 2005 Analyzed Here^a

	Observed Polarization in Spacecraft Frame	Inferred Polarization in Solar Wind Frame	Theoretical polarization in Solar Wind Frame
Event #1	Left hand	Left hand	Left hand
Event #2	Right hand	Right hand	Right hand
Event #3	Left hand	Left hand	Stable
Event #4	Right hand	Right hand	Right hand
Event #6	Left hand	Left hand	Right hand
Event #7	Left hand	Left hand	Left hand

^aObserved polarizations are as given in Figure 2, inferred polarizations follow from Table A1 assuming antisolar propagation, and theoretical polarizations are obtained from the most unstable modes as predicted by the linear dispersion theory analyses described in section 3.

The observations of enhanced electromagnetic fluctuations near the proton cyclotron frequency in the solar wind have been credited to two distinct sources. The nonlocal hypothesis holds that these waves are generated near the Sun and are then transported by the solar wind flow to observation at planetary distances. An alternate scenario is that the expanding solar wind flow leads to nonthermal particle velocity distributions which excite kinetic instabilities throughout the heliosphere so that the enhanced waves are generated locally, near the source of their observation. Our work demonstrates a clear correlation between such enhanced fluctuations and proton velocity distributions sufficiently anisotropic to locally drive kinetic instabilities. This work does not disprove the nonlocal hypothesis but does demonstrate that local sources of fluctuations should be taken into account in studies of solar wind turbulence and its evolution with distance from the Sun, as suggested by Bale et al. [2009]. Other topics worthy of future study are the sources of the ion anisotropies which drive the kinetic instabilities. What creates the solar wind T_⊥/T_|| > 1 condition which, in turn, drives the Alfvén‐cyclotron instability? What is the source of the beam/core proton distribution [see, for example, Maneva et al., 2013] which, in turn, is the source of the magnetosonic instability?

These results should not be construed as fully representative of enhanced fluctuation activity near the proton cyclotron frequency in the solar wind. As discussed in Jian et al. [2014], such events could also include both intrinsically right‐hand polarized waves driven by the alpha/proton magnetosonic instability [Gomberoff et al., 1996; Gary et al., 2000a, 2000b; Li and Habbal, 2000; Araneda et al., 2002; Lu et al., 2006; Verscharen et al., 2013; Verscharen and Chandran, 2013], and the intrinsically left‐hand polarized waves driven by the T_⊥/T_|| > 1 anisotropy on heavy ion velocity distributions. Understanding which events correspond to which free energies and to which normal modes will require substantial additional studies of proton cyclotron events under a wide variety of solar wind conditions including fast as well as slow wind, both high and low proton β, and a broad range of beam/core relative flow speeds. However, we believe that the present work clearly demonstrates that the sometimes‐invoked assumption that all such events are due to the Alfvén‐cyclotron instability is invalid.

Appendix A.

We begin with the assumption that the ambient magnetic field B _o points toward the Sun in the direction of the x axis in GSE coordinates. In the solar wind frame, a right‐hand circularly polarized (RCP) electromagnetic plane wave propagating parallel to B _o in the x direction has a fluctuating magnetic field of the form:

$$\mathrm{\delta }\mathbf{B}\left(\mathrm{x},\mathrm{t}\right)=\mathrm{A}cos\left(\mathrm{k}\mathrm{x}-\mathrm{\omega }\mathrm{t}\right){\mathbf{ê}}_{\mathbf{y}}–\mathrm{A}sin\left(\mathrm{k}\mathrm{x}-\mathrm{\omega }\mathrm{t}\right){\mathbf{ê}}_{\mathbf{z}}$$ (A1)

where A is the fluctuation amplitude, ω is the frequency, k is the wave number, and ê _j is the unit vector in the jth direction. Here ω is always positive, and k may be either positive or negative; thus, the sign of k indicates the propagation direction of the wave. For a fixed value of x, the vector δB rotates in time about the x axis in the same sense as the gyromotion of an electron, in accord with the plasma physics definition of right‐hand circular polarization. Moreover, it follows from equation (A1) that the sense of rotation of δB is independent of the sign of k or, in other words, the sense of rotation is independent of the direction of propagation of the wave. This means that in the plasma frame the polarization is independent of the sign of the wave number.

To derive the fluctuation polarization in the spacecraft frame, we use the relationship that the spacecraft frame coordinate x′ is related to the plasma frame coordinate x by the Galilean transformation x′ = x–v _sw t, where v _sw > 0 is the radial component of the solar wind velocity. To obtain the fluctuating magnetic field in the spacecraft frame, substitute x = x′ + v _sw t into equation (A1). Then at the origin of the spacecraft frame, x′ = 0, the fluctuation magnetic field is

$$\mathrm{\delta }\mathbf{B}\left(\mathrm{t}\right)=\mathrm{A}cos\left[\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}-\mathrm{\omega }\right)\mathrm{t}\right]{\mathbf{ê}}_{\mathbf{y}}–\mathrm{A}sin\left[\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}-\mathrm{\omega }\right)\mathrm{t}\right]{\mathbf{ê}}_{\mathbf{z}}$$ (A2)

This shows that the wave frequency in the spacecraft frame is the Doppler shifted frequency ω′ = |ω‐kv_sw|. If the phase speed of the wave is much less than the radial solar wind speed, |ω/k| < < v _sw, then equation (A2) is approximately

$$\mathrm{\delta }\mathbf{B}\left(\mathrm{t}\right)\cong \mathrm{A}cos\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}\mathrm{t}\right){\mathbf{ê}}_{\mathbf{y}}–\mathrm{A}sin\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}\mathrm{t}\right){\mathbf{ê}}_{\mathbf{z}}\text{.}$$ (A3)

It follows that the wave polarization in the spacecraft frame is left‐handed (LCP) if k > 0 and right‐handed (RCP) if k < 0. Thus, for waves with phase speeds small compared to v _sw, the polarization in the spacecraft frame depends on the direction of propagation, i.e., the sign of k.

In contrast, if B _o points away from the Sun, that is, in the –x direction, then a wave with right‐circular polarization in the solar wind frame that propagates in the –x direction has a fluctuating magnetic field of the form

$$\mathrm{\delta }\mathbf{B}\left(\mathrm{x},\mathrm{t}\right)=\mathrm{A}cos\left(\mathrm{k}\mathrm{x}-\mathrm{\omega }\mathrm{t}\right){\mathbf{ê}}_{\mathbf{y}}+\mathrm{A}sin\left(\mathrm{k}\mathrm{x}-\mathrm{\omega }\mathrm{t}\right){\mathbf{ê}}_{\mathbf{z}}$$ (A4)

where, as before, ω > 0 and the wave number k may be either positive or negative. Here the fluctuating magnetic field vector rotates about the x axis in the same sense as the gyromotion of an electron, again consistent with the plasma physics definition of right‐hand circular polarization. Then, as above, it follows that the wave magnetic field at the origin of the spacecraft frame is

$$\mathrm{\delta }\mathbf{B}\left(\mathrm{t}\right)\cong \mathrm{A}cos\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}\mathrm{t}\right){\mathbf{ê}}_{\mathbf{y}}+\mathrm{A}sin\left({\mathrm{k}\mathrm{v}}_{\mathrm{s}\mathrm{w}}\mathrm{t}\right){\mathbf{ê}}_{\mathbf{z}}\text{.}$$ (A5)

It follows that the sense of rotation of δB in the spacecraft frame is right‐handed if k > 0, corresponding to an LCP wave and left‐handed if k < 0, corresponding to an RCP wave. In this case, the sense of rotation of the vector δB is the opposite of the sense of polarization.

The above analysis applies to any plane wave that is right‐hand circularly polarized in the plasma frame. The same analysis can be carried out for a wave that is left‐hand circularly polarized in the plasma frame. We leave it to the reader to show that in this case the z components of equations (A1), (A2), (A3), (A4), (A5) all change sign. The results of this Appendix are summarized in Table A1.

Table A1.

Relationships Between Wave Polarizations in the Plasma Frame and in the Spacecraft Frame^a

Direction of B o	Direction of Wave Propagation	Polarization in Plasma Frame	Polarization in Spacecraft Frame
Toward	Toward	RCP	LCP
Toward	Away	RCP	RCP
Away	Toward	RCP	LCP
Away	Away	RCP	RCP
Toward	Toward	LCP	RCP
Toward	Away	LCP	LCP
Away	Toward	LCP	RCP
Away	Away	LCP	LCP

^a“Toward” and “Away” refer to the directions toward the Sun and away from the Sun, respectively. RCP and LCP indicate right‐hand circular polarization and left‐hand circular polarization, respectively. Polarization is defined with respect to rotation with respect to the direction of the ambient magnetic field B _o, that is, in the plasma physics sense.

Gary, S. P. , Jian L. K., Broiles T. W., Stevens M. L., Podesta J. J., and Kasper J. C. (2016), Ion‐driven instabilities in the solar wind: Wind observations of 19 March 2005, J. Geophys. Res. Space Physics, 121, 30–41, doi:10.1002/2015JA021935.