Improved Method to Stratify Elderly Patients With Cancer at Risk for Competing Events

Abstract

Purpose

To compare a novel generalized competing event (GCE) model versus the standard Cox proportional hazards regression model for stratifying elderly patients with cancer who are at risk for competing events.

Methods

We identified 84,319 patients with nonmetastatic prostate, head and neck, and breast cancers from the SEER-Medicare database. Using demographic, tumor, and clinical characteristics, we trained risk scores on the basis of GCE versus Cox models for cancer-specific mortality and all-cause mortality. In test sets, we examined the predictive ability of the risk scores on the different causes of death, including second cancer mortality, noncancer mortality, and cause-specific mortality, using Fine-Gray regression and area under the curve. We compared how well models stratified subpopulations according to the ratio of the cumulative cause-specific hazard for cancer mortality to the cumulative hazard for overall mortality (ω) using the Akaike Information Criterion.

Results

In each sample, increasing GCE risk scores were associated with increased cancer-specific mortality and decreased competing mortality, whereas risk scores from Cox models were associated with both increased cancer-specific mortality and competing mortality. GCE models created greater separation in the area under the curve for cancer-specific mortality versus noncancer mortality (P < .001), indicating better discriminatory ability between these events. Comparing the GCE model to Cox models of cause-specific mortality or all-cause mortality, the respective Akaike Information Criterion scores were superior (lower) in each sample: prostate cancer, 28.6 versus 35.5 versus 39.4; head and neck cancer, 21.1 versus 29.4 versus 40.2; and breast cancer, 24.6 versus 32.3 versus 50.8.

Conclusion

Compared with standard modeling approaches, GCE models improve stratification of elderly patients with cancer according to their risk of dying from cancer relative to overall mortality.

INTRODUCTION

Competing risks settings are those in which an individual may experience multiple different events.¹ Competing events are important to recognize because they complicate the interpretation of effects on primary events of interest.^1-7 With advancing age, the risk of competing mortality for patients increases, and the benefit of intensifying treatment potentially diminishes. Improved methods for stratifying patients according to competing event risk are needed to help individualize treatment.

A common approach to risk stratification is to model variables on a combined end point, such as overall survival or event-free survival, aggregating one or more disease-specific events with death from other causes. This approach is problematic, however, when variables have opposing effects on competing events, because it is not possible to discriminate effects on primary versus competing events when these events are pooled.² As a result, common prognostic models applied do not efficiently distinguish patients at risk for dying of cancer versus noncancer causes, leading to suboptimal risk assessment strategies.

In contrast, competing event models can better discriminate effects of treatments and risk factors on specific events.⁸ We previously developed a generalized competing event (GCE) model that better stratifies patients with endometrial cancer according to risk of death from cancer relative to overall mortality; however, this approach has not been validated in other settings. Therefore, we sought to validate the broader utility of this method by comparing risk scores derived using standard Cox proportional hazards regression models versus the GCE model in three different populations (prostate cancer, head and neck cancer (HNC), and breast cancer), all of which are subject to an appreciable risk of competing cancer and noncancer events.

METHODS

Population and Sampling Methods

This study was institutional review board approved. Using SEER-Medicare database, we identified 51,713 patients with localized prostate cancer diagnosed from 2000 to 2009 and treated with definitive radiotherapy (RT), 9,677 patients with primary nonmetastatic HNC diagnosed from 1996 to 2009 and treated with RT with or without surgery and/or chemotherapy, and 22,929 patients with nonmetastatic primary breast cancer diagnosed from 2004 to 2009 and treated with mastectomy or lumpectomy with or without RT and/or chemotherapy. SEER covers 26% of the US cancer population.⁹ Medicare provides health insurance for 97% of persons age ≥ 65 years. SEER-Medicare links registry data with claims files for beneficiaries enrolled in fee-for-service programs. We excluded patients if their cancer was diagnosed on death certificate or autopsy only or if they had incomplete data or noncontinuous Medicare part A/part B in the year preceding diagnosis. We also excluded 16,546 patients treated with radical prostatectomy because we found too few patients died of cancer (141 deaths, < 1%) to draw definitive conclusions about the impact of GCE models in this population. All patients were age > 66 years.

Main Outcomes

Cancer-specific mortality was defined as death as a result of prostate, HNC, or breast cancer, as appropriate for the context. Competing mortality was defined as either noncancer mortality or second cancer mortality. All-cause mortality was defined as death from any cause. Surviving patients were censored at last follow-up.

Statistical Analysis

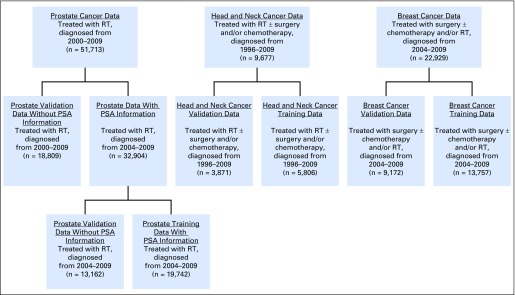
First, we partitioned each sample into training and validation sets (Fig 1), using 60%/40% random samples (without replacement). This was to optimize the tradeoff between robustness of the training sample and number of events in the test sets. Training cohorts were used to build models, whereas validation cohorts were used to compare models. In each training cohort, we used multivariable Cox regression¹⁰ to develop risk scores for all-cause and cause-specific mortality using a standard set of covariates plus additional disease-specific covariates. Risk scores were calculated by taking the inner product of the coefficient vector with the data vector of the patient.^4,8

Fig 1.

Diagram for data abstraction and partitioning into training and validation datasets. PSA, prostate-specific antigen; RT, radiotherapy.

For the GCE models, we performed Fine-Gray regressions¹¹ on both cause-specific and competing mortality as a function of the same covariates, and we computed risk scores in the same fashion, using training cohorts. Second cancer mortality and noncancer mortality events were pooled together as a single competing mortality event in the GCE risk score calculation. Covariates were retained in the final GCE model if they were significant (P < .05) in any individual regression model. We chose this cutoff to guard against overfitting in training samples (note that including fewer covariates reduces variance in the explanatory variables, attenuating the comparisons between GCE and standard models). GCE risk scores were computed by subtracting the competing mortality risk score from the cancer-specific mortality risk score. Note that GCE risk scores can take on any real value, with increasing values corresponding to an increasing ratio of cancer mortality to noncancer mortality risk (Appendix, online only). Despite concerns about the appropriateness of using Cox models for cause-specific mortality,^12,13 we chose this method for comparison because it has been widely applied for this purpose in the oncology literature. Bootstrap resampling with replacement (1,000 iterations) was used to obtain 95% CIs for the coefficients from the GCE model.

Standard covariates included age at diagnosis (continuous), sex, race (black v white/other), marital status (married v unmarried), median household income (lower v higher than mean), stage, grade, and modified Charlson comorbidity index (CCI), calculated using Medicare claims during the year preceding diagnosis.¹⁴ For prostate cancer models, additional covariates included region (West v East v Midwest v South), type of RT (external beam RT only v RT plus brachytherapy v brachytherapy only), and prostate-specific antigen (PSA; continuous). We imputed the mean PSA value where PSA was missing (n = 18,809). Stage was grouped according to American Joint Committee on Cancer staging criteria (3rd and 6th editions), and grade was dichotomized as high (grade 3 and 4) versus intermediate and/or low (grade 1 and 2). For HNC models, additional covariates tested included anatomic subsite and postoperative RT (yes v no). Stage was dichotomized as regional versus localized, and grade was dichotomized as above. Multiple imputation with 20 iterations was performed for missing grade data, given fewer than 20% missing data (n = 1,697). No other variables were imputed. For HNC data, we performed additional analyses controlling for chemotherapy and RT technique (n = 8,920); however, these were not significant in any regression model, and, therefore, were not included in the final GCE model for HNC. For breast cancer models, additional covariates included region (West v East v Midwest v South), teaching hospital (yes v no), tumor size (< 2 cm v ≥ 2 cm to < 5 cm v ≥ 5 cm v size unknown), estrogen receptor and/or progesterone receptor status (positive v negative v unknown), sentinel lymph node biopsy (yes v no), axillary lymph node examination (yes v no), tumor laterality (left v right), surgery (mastectomy v lumpectomy), chemotherapy (yes v no), and RT technique (hypofractionated v conventional). Hypofractionated RT was defined as 13 to 24 daily fractions, and conventional RT was defined as 25 to 36 daily fractions.

Event probabilities were calculated for the whole samples using cumulative incidence functions.^15,16 The predictive ability of the models on the different cause of death incidences was tested in validation cohorts using the area under the curve (AUC) on the basis of receiver operating characteristics curves with competing risks.¹⁷ We also used the Akaike Information Criterion and Bayesian Information Criterion to compare how well the risk scores stratified equally binned subgroups according to the ratio of the cumulative cause-specific hazard for cancer mortality to the cumulative hazard for all-cause mortality (ω). We used the Nelson-Aalen method (ie, negative logarithm of the survival function) to estimate cumulative hazards and plotted ω values for quantiles of the appropriate risk score (Appendix). Last, we performed a second resampling of the training and test sets for all three cohorts, to confirm the robustness of our conclusions. Additional details are provided in the Appendix. All tests were two tailed, and P < .05 indicated statistical significance. Data were extracted using SAS (SAS/STAT User’s Guide, Version 9.3; SAS Institute, Cary, NC) and analyzed in R version 3.2.2 (www.r-project.org). We published an R package called gcerisk to facilitate GCE modeling used in this study.

RESULTS

Cancer Outcomes and Model Comparisons

Sample characteristics are provided in Appendix Tables A1 to A3 (online only). For patients with prostate cancer, the 10-year cumulative incidences of all-cause, cancer-specific, second cancer, and noncancer mortality were 40.2% (95% CI, 39.4% to 41.1%), 4.7% (95% CI, 4.3% to 5.0%), 9.4% (95% CI, 9.0% to 9.9%), and 26.2% (95% CI, 25.4% to 26.9%), respectively. Note that second cancer mortality and noncancer mortality together comprise competing mortality, so the cumulative incidence of competing mortality is the sum of their cumulative incidences (35.6%). Compared with standard models, the effects of stage, grade, and PSA in the GCE model were in the same direction, whereas the effect estimates for age and CCI were generally opposite (Table 1). All-cause mortality was increased for patients in the Midwest and Southern regions, but the effects of region were not significant in the other two models.

Table 1.

Multivariable Regression Analyses for Prostate Cancer

Characteristic	GCE Regression, ω+ Ratio* (95% CI)	PCM Cox Regression, HR (95% CI)	ACM Cox Regression, HR (95% CI)
Age at diagnosis, per year	0.97 (0.94 to 1.00)	1.04 (1.01 to 1.06)	1.06 (1.05 to 1.07)
Married
Yes	1.36 (0.99 to 1.88)	1.10 (0.81 to 1.49)	0.85 (0.77 to 0.93)
Registry region
West	Ref	Ref	Ref
East	0.74 (0.50 to 1.09)	0.79 (0.55 to 1.14)	1.03 (0.92 to 1.16)
Midwest	0.88 (0.57 to 1.36)	1.06 (0.71 to 1.59)	1.17 (1.02 to 1.35)
South	0.77 (0.55 to 1.10)	1.22 (0.88 to 1.70)	1.48 (1.33 to 1.66)
Stage
T1	Ref	Ref	Ref
T2	1.55 (1.16 to 2.07)	1.71 (1.30 to 2.25)	1.16 (1.06 to 1.27)
T3	2.38 (1.16 to 4.87)	2.83 (1.54 to 5.22)	1.39 (1.05 to 1.85)
Grade
Low/intermediate	Ref	Ref	Ref
High	2.92 (2.02 to 4.22)	3.67 (2.57 to 5.23)	1.37 (1.25 to 1.50)
Radiation therapy
EBRT or BT alone	Ref	Ref	Ref
EBRT + BT	1.15 (0.78 to 1.70)	0.97 (0.69 to 1.37)	0.85 (0.74 to 0.97)
CCI
0	Ref	Ref	Ref
1	0.53 (0.37 to 0.76)	0.97 (0.69 to 1.37)	1.64 (1.47 to 1.82)
2	0.69 (0.43 to 1.11)	1.61 (1.03 to 2.53)	2.10 (1.81 to 2.42)
≥ 3	0.35 (0.20 to 0.63)	1.81 (1.02 to 3.19)	3.95 (3.40 to 4.58)
PSA, per unit	1.01 (1.00 to 1.01)	1.01 (1.01 to 1.02)	1.01 (1.00 to 1.01)

Abbreviations: ACM, all-cause mortality; BT, brachytherapy; CCI, Charlson Comorbidity Index; EBRT, external beam radiotherapy; GCE, generalized competing event; HR, hazard ratio; PCM, prostate cancer mortality; PSA, prostate-specific antigen; Ref, reference.

^*Estimate of the ω⁺ ratio for each covariate using the Fine-Gray model for subdistribution hazards. For further explanation of the GCE estimate, see Appendix.

For patients with HNC, the 5-year cumulative incidences of all-cause, cancer-specific, second cancer, and noncancer mortality were 59.3% (95% CI, 58.2% to 60.3%), 24.2% (95% CI, 23.4% to 25.1%), 15.9% (95% CI, 15.1% to 16.7%), and 19.1% (95% CI, 18.3% to 20.0%), respectively. With the GCE model, the effect estimates for stage, anatomic subsite, and postoperative RT were generally comparable to standard models. Compared with standard models, the GCE model gave more weight to female sex, suggesting a potential benefit of treatment intensification for elderly women. The GCE model suggested a null effect of age, and an opposite effect of CCI, in contrast to standard models (Table 2).

Table 2.

Multivariable Regression Analyses for Head and Neck Cancer Training Cohort

Characteristic	GCE Regression, ω+ Ratio* (95% CI)	HNCM Cox Regression, HR (95% CI)	ACM Cox Regression, HR (95%CI)
Age at diagnosis, per year	0.99 (0.98 to 1.00)	1.04 (1.03 to 1.05)	1.05 (1.04 to 1.05)
Sex
Female	1.45 (1.24 to 1.68)	1.14 (1.01 to 1.28)	0.95 (0.88 to 1.02)
Married
Yes	1.03 (0.89 to 1.18)	0.82 (0.73 to 0.91)	0.80 (0.75 to 0.86)
Household income
Higher	1.04 (0.90 to 1.19)	0.91 (0.82 to 1.02)	0.88 (0.83 to 0.95)
Stage
Localized	Ref	Ref	Ref
Regional	1.99 (1.72 to 2.31)	2.49 (2.21 to 2.81)	1.78 (1.67 to 1.91)
Anatomic subsite
Oropharynx	Ref	Ref	Ref
Hypopharynx	1.37 (1.08 to 1.75)	1.64 (1.37 to 1.96)	1.49 (1.32 to 1.67)
Nasopharynx	1.99 (1.28 to 3.10)	1.67 (1.24 to 2.23)	1.24 (1.00 to 1.53)
Oral cavity	1.25 (1.05 to 1.48)	1.76 (1.55 to 2.00)	1.61 (1.49 to 1.75)
CCI
0	Ref	Ref	Ref
1	0.82 (0.70 to 0.96)	1.15 (1.01 to 1.30)	1.32 (1.22 to 1.42)
2	0.76 (0.62 to 0.94)	1.41 (1.20 to 1.66)	1.71 (1.55 to 1.89)
3	0.61 (0.44 to 0.84)	1.51 (1.18 to 1.93)	1.98 (1.72 to 2.28)
≥ 4	0.76 (0.54 to 1.08)	1.97 (1.52 to 2.56)	2.46 (2.10 to 2.88)
Postoperative radiation therapy
Yes	0.67 (0.59 to 0.77)	0.62 (0.55 to 0.69)	0.74 (0.69 to 0.79)

Abbreviations: ACM, all-cause mortality; CCI, Charlson Comorbidity Index; GCE, generalized competing event; HNCM, head and neck cancer mortality; HR, hazard ratio.

^*Estimate of the ω⁺ ratio for each covariate using the Fine-Gray model for subdistribution hazards. For further explanation of the GCE estimate, see Appendix.

For patients with breast cancer, the 5-year cumulative incidences of all-cause, cancer-specific, second cancer, and noncancer mortality were 20.1% (95% CI, 19.5% to 20.8%), 4.8% (95% CI, 4.5% to 5.2%), 3.1% (95% CI, 2.8% to 3.4%), and 12.2% (95% CI, 11.7% to 12.7%), respectively. With the GCE model, effect estimates for stage, grade, tumor size, and nodal examination were comparable to the Cox models in magnitude and direction, in contrast to GCE estimates for age, teaching hospital, and CCI, which were opposite of those from Cox models (Table 3).

Table 3.

Multivariable Regression Analyses for Breast Cancer Training Cohort

Characteristic	GCE Regression, ω+ Ratio* (95% CI)	BCM Cox Regression, HR (95% CI)	ACM Cox Regression, HR (95% CI)
Age at diagnosis, per year	0.94 (0.93 to 0.96)	1.02 (1.01 to 1.04)	1.06 (1.06 to 1.07)
Married
Yes	0.97 (0.77 to 1.23)	0.79 (0.65 to 0.96)	0.81 (0.73 to 0.89)
Teaching hospital
Yes	0.83 (0.67 to 1.02)	1.30 (1.09 to 1.55)	1.46 (1.34 to 1.59)
Registry region
West	Ref	Ref	Ref
Midwest	1.26 (0.92 to 1.72)	1.01 (0.77 to 1.32)	0.87 (0.76 to 1.00)
East	1.10 (0.83 to 1.46)	0.89 (0.70 to 1.13)	0.80 (0.71 to 0.91)
South	1.19 (0.93 to 1.52)	1.35 (1.10 to 1.67)	1.17 (1.05 to 1.30)
Household income
Below mean	Ref	Ref	Ref
Above mean	1.19 (0.97 to 1.46)	1.05 (0.88 to 1.26)	0.93 (0.85 to 1.02)
Stage, ref: localized
Regional	1.82 (1.31 to 2.53)	1.97 (1.55 to 2.52)	1.43 (1.24 to 1.66)
Grade, ref: low/intermediate
High	2.07 (1.64 to 2.62)	1.95 (1.45 to 2.63)	1.20 (1.09 to 1.33)
Tumor size
< 2 cm	Ref	Ref	Ref
≥ 2 to < 5 cm	1.83 (1.46 to 2.30)	2.39 (1.97 to 2.89)	1.50 (1.36 to 1.65)
≥ 5 cm	3.15 (2.06 to 4.80)	4.86 (3.61 to 6.56)	2.45 (2.04 to 2.95)
Unknown size	2.20 (1.16 to 4.17)	1.97 (1.16 to 3.35)	1.10 (0.81 to 1.49)
ER status
Negative	Ref	Ref	Ref
Positive	0.62 (0.45 to 0.86)	0.54 (0.41 to 0.70)	0.71 (0.62 to 0.82)
Unknown	7.19 (2.06 to 25.1)	5.76 (0.23 to 145.4)	0.97 (0.41 to 2.31)
PR status
Negative	Ref	Ref	Ref
Positive	0.77 (0.57 to 1.02)	0.70 (0.54 to 0.89)	0.84 (0.75 to 0.95)
Unknown	0.10 (0.03 to 0.34)	0.10 (0.01 to 2.50)	0.71 (0.30 to 1.66)
Sentinel lymph node biopsy
Yes	0.88 (0.69 to 1.12)	0.74 (0.60 to 0.91)	0.81 (0.73 to 0.90)
Lymph node examination
No	1.33 (1.03 to 1.71)	2.04 (1.66 to 2.50)	1.57 (1.42 to 1.75)
Laterality
Left	1.13 (0.93 to 1.37)	1.15 (0.97 to 1.36)	1.07 (0.98 to 1.16)
CCI
0	Ref	Ref	Ref
1	0.84 (0.66 to 1.05)	1.44 (1.18 to 1.76)	1.59 (1.44 to 1.76)
2	0.51 (0.37 to 0.71)	1.44 (1.08 to 1.91)	2.28 (2.00 to 2.60)
≥ 3	0.39 (0.27 to 0.56)	1.95 (1.45 to 2.63)	3.36 (2.94 to 3.84)
Radiation therapy
Yes	0.97 (0.74 to 1.27)	0.62 (0.49 to 0.79)	0.65 (0.58 to 0.73)
Chemotherapy
Yes	1.01 (0.63 to 1.62)	1.11 (0.77 to 1.60)	1.14 (0.91 to 1.43)

Abbreviations: ACM, all-cause mortality; BCM, breast cancer mortality; CCI, Charlson Comorbidity Index; ER, estrogen receptor; HR, hazard ratio; PR, progesterone receptor.

^*Estimate of the ω⁺ ratio for each covariate using the Fine-Gray model for subdistribution hazards. For further explanation of the GCE estimate, see Appendix.

Predictive Ability of Models on Cause-Specific Events

When Cox models were tested on patients with prostate cancer, increasing risk scores were associated with increased cancer-specific, second cancer, and noncancer mortality (Appendix). In contrast, the GCE risk score was associated with increased cancer-specific mortality (subdistribution hazard ratio [SDHR], 2.12; 95% CI, 1.89 to 2.37; P < .001) and was associated with decreased second cancer mortality (SDHR, 0.88; 95% CI, 0.81 to 0.95; P < .001) and noncancer mortality (SDHR, 0.64; 95% CI, 0.60 to 0.67; P < .001). The GCE model produced a greater difference in AUC for cancer-specific and noncancer mortality (0.64 v 0.42; P < .001) than did the Cox model of all-cause mortality (0.66 v 0.67; P > .05) or cancer-specific mortality (0.72 v 0.59; P < .001). Results did not differ when we tested patients with prostate cancer with or without known PSA information.

When Cox models were tested in patients with HNC, increasing risk scores were associated with increased cancer-specific, second cancer, and noncancer mortality (Appendix). In contrast, the GCE risk score was associated with increased cancer-specific mortality (SDHR, 2.37; 95% CI, 2.09 to 2.70; P < .001) and second cancer mortality (SDHR, 1.44; 95% CI, 1.25 to 1.66; P < .001) but decreased noncancer mortality (SDHR, 0.62; 95% CI, 0.54 to 0.70; P < .001). Again, the GCE model produced a greater difference in AUC for cancer-specific and noncancer mortality (0.66 v 0.55; P < .001) than did the Cox models of all-cause mortality (0.74 v 0.71; P > .05) and cancer-specific mortality (0.75 v 0.68; P < .001). Results were similar when we controlled for treatment or analyzed oropharynx versus nonoropharynx subpopulations separately.

When Cox models were tested in patients with breast cancer, increasing risk scores were associated with increased cancer-specific, second cancer, and noncancer mortality (Appendix). In contrast, the GCE risk score was associated with increased cancer-specific mortality (SDHR, 1.95; 95% CI, 1.71 to 2.23; P < .001) but decreased second cancer mortality (SDHR, 0.76; 95% CI, 0.65 to 0.88; P < .001) and noncancer mortality (SDHR, 0.51; 95% CI, 0.47 to 0.56; P < .001). Again, the GCE model produced a greater difference in AUC for cancer-specific and noncancer mortality (0.64 v 0.36; P < .001) than did the Cox models of all-cause mortality (0.79 v 0.80; P > .05) and cancer-specific mortality (0.82 v 0.73; P < .001).

Predictive Ability of Models on the Relative Hazard for Events of Interest (ω)

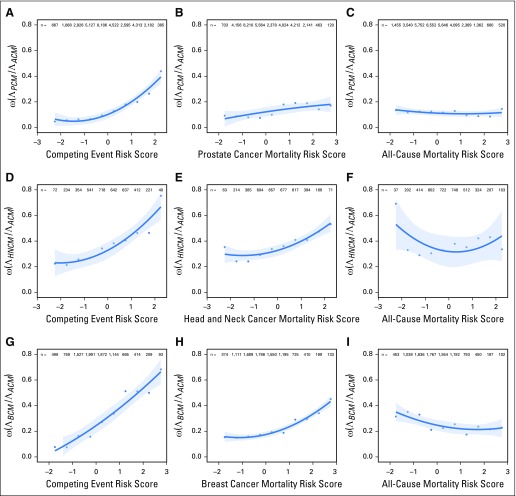
With increasing GCE risk scores, we observed significant increases in the proportion of the hazard for overall mortality attributable to cancer (ω). GCE models better stratified patients according to their risk of dying from cancer relative to other causes. In contrast, risk scores from the Cox models did not optimize the relative event composition (Fig 2). For patients with prostate cancer, the Akaike Information Criterion was superior (lower) for GCE models versus the Cox models of cause-specific and all-cause mortality (25.3 v 31.2 v 35.3). Similar findings were observed for patients with HNC (24.1 v 26.7 v 36.6) and patients with breast cancer (12.7 v 33.2 v 41.6). The Bayesian Information Criterion was also superior for the GCE models in each of the three samples we tested: prostate, 26.2 versus 32.1 versus 36.2; HNC, 25.0 versus 27.6 versus 37.5; and breast, 13.6 versus 34.1 versus 42.5.

Fig 2.

Ratio of the cumulative hazard for cancer mortality to all-cause mortality [ω(Λ_CSM /Λ_ACM)] as a function of the normalized generalized competing event risk score versus normalized cancer mortality risk score versus normalized all-cause mortality risk score for (A-C) prostate cancer, (D-F) head and neck cancer, and (G-I) breast cancer. ω is calculated at 10 years for prostate cancer and 5 years for head and neck and breast cancer.

DISCUSSION

We validated a novel approach to improve prognostication beyond that achievable with traditional methods. Standard approaches to risk stratification typically involve characterizing patient risk of mortality, or event-free survival, and then tailoring treatment according to this risk. This is not a problem when effects of variables on specific events composing the end point are similar. However, this condition often does not hold in oncology, because the causes of cancer recurrence and/or mortality are generally different than for other causes of mortality. Traditional models are constrained, in general, because they assign a mean effect of a variable on both events of interest and competing events. In contrast, the GCE approach, which estimates the effects of a variable on specific events separately before aggregating them in a final model, better stratifies patients according to risk of dying from cancer relative to overall mortality. These findings indicate that measures used to evaluate the net benefit of therapies need not, and perhaps should not, be the same ones used for risk stratification.

The GCE approach can be generalized to other competing risks settings; its potential is therefore broad. In the context of clinical research, better risk stratification will improve the ability to detect treatment benefits within subpopulations, ultimately leading to more powerful and cost-effective clinical trials.^18,19 GCE scores can also be used to better inform patients and physicians about the potential value of intensive treatment, thus leading to more personalized care. In terms of prostate cancer management, controversy still remains regarding when to observe or treat,²⁰ likely because of poorer quality of life associated with local therapies^21,22 and competing mortality risk as a result of comorbidities.²³ Randomized controlled trials have shown that men with prostate cancer will not see the benefits of treatment for at least a decade.²⁴ As a consequence, men with less comorbidity are often not treated for high-risk prostate cancer, whereas younger men with comorbidity are overtreated for low-risk disease.^20,25 In this setting, a widely accepted method to assess prognosis that incorporates patient health status is essential.²⁵

Patients with HNC with comorbidities are also at increased risk of competing mortality,^3,4,6,26,27 making the decision to treat with aggressive therapy difficult. Breast cancer studies have shown that for proper estimation of breast cancer death, risk factors associated with competing mortality should also be considered when evaluating potential treatments.^7,28-30 To this end, numerous prediction models have been used in prostate cancer,³¹ HNC,^26,32 and breast cancer³³ research; however, such models do not directly isolate the effect of the main outcome of interest relative to overall mortality risk. Across oncology, it is imperative to determine how both cancer and noncancer risk factors contribute to risk of cancer death when risks for competing events are present. GCE models have the potential to provide patients with better-informed survivorship information on the basis of their individual health status.

Strengths of our study were the large population-based sample that provided detailed information about demographic and clinical factors and causes of death.³⁴ Although some predictors were not available, such as treatment details, family history, smoking history,³⁵ tissue biomarkers,³⁶ genetic information,^37-39 body mass index, reproductive status, performance status, and pathologic risk factors (eg margin status, extracapsular extension), we were still able to demonstrate better risk stratification and model performance using the GCE approach. Including more variables in the GCE models would likely accentuate the difference between the approaches. Longer follow-up data might improve model parameter selection and estimation by increasing incidences of events. We chose to use Fine-Gray regression models in the construction of GCE risk scores to be consistent with prior studies.⁸ It is also possible to generate GCE scores on the basis of Cox regression,⁸ but often these approaches result in similar estimates¹ and would likely yield similar findings. In theory, the GCE approach will outperform standard methods whenever there is an appreciable incidence of competing events, sufficient variance in the explanatory variables, and low statistical dependence between competing events and events of interest. These conditions appeared to hold in the samples we examined.

In summary, we found that, compared with standard methods, GCE models better stratified patients according to their risk of cancer mortality relative to competing causes of death. Our study directly speaks to the necessity of developing patient-centered risk models,⁴⁰ which use patient-specific characteristics to identify patients likely to benefit from risky or costly therapies.^41,42 Additional studies investigating the value of competing event models are needed, as their use would enhance personalized medical decision making and improve the efficiency of clinical trials.

Appendix

Methods

For each cancer site, we categorized patients on the basis of risk score and calculated the ratio (ω) of the cumulative hazard for cancer-specific mortality (Λ_CSM) to the cumulative hazard for all-cause mortality(Λ_ACM) within strata:

$$\text{ω}=\frac{{\text{Λ}}_{CSM}}{{\text{Λ}}_{CSM}+{\text{Λ}}_{CM}}= \frac{{\text{Λ}}_{CSM}}{{\text{Λ}}_{ACM}} .$$ [1]

ω ranges from zero to one, with lower values of ω indicating that the hazard of cancer-specific mortality is small relative to all-cause mortality. In this situation, intensifying cancer therapy would be expected to have less benefit on overall survival because of the increased risk of mortality from noncancer causes. In contrast, for higher values of ω, the cumulative hazard of cancer-specific mortality dominates, and the potential benefit of intensifying treatment is maximized. Thus, ω may be viewed as a measure of the likelihood to benefit from treatment intensification within a risk group. Its derivation comes from the partitioning of an effect on all-cause mortality (θ) into a weighted average of the cause-specific effects (θ_i; Eq 2), for two events²:

$$\mathrm{\theta }=\frac{{{\displaystyle \sum \mathrm{\theta }}}_i\ast {\Lambda }_i}{{\displaystyle \sum {\Lambda }_i}}= \text{ω }{\mathrm{\theta }}_{CSM}+\left(1-\text{ω}\right){\mathrm{\theta }}_{CM} .$$ [2]

Under this model, we assume proportional hazards for both the composite event and the cause-specific events, that is:

$$\text{λ}\left(t\text{;}x\right){=\text{λ}}_{\text{0}}\left(t\right)\text{exp}\left(\text{β}x\right)$$ [3]

and

$${\text{λ}}_{\text{i}}\left(t\text{;}x\right)={\text{λ}}_{\text{0i}}\left(t\right)\text{exp}\left({\text{β}}_{\text{i}}x\right)$$ [4]

for event time t, data vector x, and a set of K mutually exclusive event types i є {1,…,K}. Because the hazard function can be represented as the sum of the K cause-specific hazard functions, it follows that:

$$\text{λ}\left(t\text{;}x\right)={\displaystyle \sum {\text{λ}}_{\text{0i}}\left(t\right)}\exp \left({\text{β}}_{\text{i}}x\right) .$$ [5]

We define:

$${\text{ω}}_{\text{i}}\left(t\right)={\text{λ}}_{\text{i}}\left(t\right)/\text{λ}\left(t\right) ,$$ [6]

that is, ω_i(t) is the ratio of the cause-specific hazard for event type i to the hazard for all events, hence:

$$\text{λ}\left(t\text{;}x\right)/{\text{λ}}_{\text{0}}\left(t\right)={\displaystyle \sum {\text{ω}}_{\text{0i}}\left(t\right)}\exp \left({\text{β}}_{\text{i}}x\right)$$ [7]

where ω_0i(t) represents the value of ω_i(t) under baseline conditions. We may consider two event types: a (or composite set of) primary event(s) of interest, and a (or composite set of) competing event(s) (eg, cancer mortality and competing mortality). In this case, the proportional hazards assumptions imply that the cause-specific hazards must be proportional to each other, so ω_i(t) is invariant to t. Then Equation 7 reduces to:

$$\text{λ}\left(t\text{;}x\right)/{\text{λ}}_{\text{0}}\left(t\right)={\text{ω}}_{01}\exp \left({\text{β}}_{1}x\right)+\left(1-{\text{ω}}_{01}\right)\exp \left({\text{β}}_{2}x\right) .$$ [8]

If we let ω₀₁ = ω represent the value for cancer-specific mortality, integrating Equation 8 with respect to t gives us Equation 2.

Continuing with the special case of K = 2, we have the following relationship:

$$\begin{array}{l}{\text{ω}}_{\text{i}}\left(x\right)/{\text{ω}}_{\text{0i}}={\text{ω}}_{\text{i}}\left(t\text{;}x\right)/{\text{ω}}_{\text{0i}}\left(t\right)=\left({\text{λ}}_{\text{i}}\left(t;x\right)/\text{λ}\left(t;x\right)\right)/\left({\text{λ}}_{\text{0i}}\left(t\right)/{\text{λ}}_{\text{0}}\left(t\right)\right)\\ =\left({\text{λ}}_{\text{i}}\left(t;x\right)/{\text{λ}}_{\text{0i}}\left(t\right)\right)/\left(\text{λ}\left(t;x\right)/{\text{λ}}_{\text{0}}\left(t\right)\right)=\exp \left({\text{β}}_{\text{i}}x\right)\exp \left(\text{β}x\right)=\exp \left(\left({\text{β}}_{\text{i}}-\text{β}\right)x\right)\end{array} .$$ [9]

Thus, the linear predictor (β_i − β)x quantifies the log(ω_i(x)/ω_0i), or the log of the ω ratio.

Now for the special case K = 2, we define:

$${\text{ω}}^{+}={\text{λ}}_1\left(t\right)/{\text{λ}}_2\left(t\right) .$$ [10]

Then these relationships follow:

$$\text{ω}={\text{ω}}^{+}/\left(1+{\text{ω}}^{+}\right)$$ [11]

and

$${\text{ω}}^{+}=\text{ω}/\left(\text{1}-\text{ω}\right) .$$ [12]

By analogy, exp[(β₁ − β₂)x] quantifies the ω⁺ ratio. Using similar arguments, one can extend this for subdistribution hazard ratios (SDHRs) using estimates from the Fine-Gray model, so the quantity estimated in this experiment can be thought of as the ω⁺ ratio for SDHRs. Appendix Table A1 illustrates the differences in estimates using various generalized competing event models in the head and neck cancer (HNC) training sample.

Results

Sample Characteristics

Most patients with prostate cancer were white, married, from the Western United States, had lower median household income (HHI), Charlson Comorbidity Index (CCI) of zero, T1c stage, mean prostate-specific antigen of 10.3, and lower-grade disease. The majority of patients were treated with radiotherapy (RT) alone (Appendix Table A2). A total of 41,923 patients were alive at last follow-up. Median follow-up times were 57 months for surviving patients and 56 months overall (range, 1 to 131 months). The median times to death from prostate cancer, noncancer causes, and second cancers were 47, 51, and 48 months, respectively. A total of 1,172 patients died of prostate cancer (228 in training cohort, 944 in validation cohort), 6,275 died of noncancer causes (1,304 in training cohort, 4,971 in validation cohort), and 2,343 died of second cancers (522 in training cohort, 1,821 in validation cohort), respectively.

Most patients with HNC were white, male, and married, and had lower HHI, CCI of zero, locoregionally advanced stage, and low- to intermediate-grade disease. Larynx and oral cavity were the most common subsites (Appendix Table A3). A total of 3,355 patients were alive at last follow-up. Median follow-up times were 56 months for surviving patients and 31 months overall (range, 0 to 179 months). The median times to death from HNC, noncancer causes, and second cancers were 13, 22, and 33 months, respectively. A total of 2,378 patients died of HNC (1,429 in training cohort, 949 in validation cohort), 2,274 died of noncancer causes (1,381 in training cohort, 893 in validation cohort), and 1,670 died of second cancers (987 in training cohort, 683 in validation cohort), respectively.

Most patients with breast cancer were white, unmarried, had lower HHI, CCI of zero, localized stage, and low- to intermediate-grade disease, tumor size < 2 cm, estrogen receptor and/or progesterone receptor–positive status, treated with mastectomy and lymph node examination, from the Western United States (Appendix Table A4). A total of 19,237 patients were alive at last follow-up. Median follow-up times were 47 months for surviving patients and 43 months overall (range, 0 to 84 months). The median times to death from breast cancer, noncancer causes, and second cancers were 25, 29, and 30 months, respectively. A total of 905 patients died of breast cancer (568 in training cohort, 337 in validation cohort), 2,220 died of noncancer causes (1,327 in training cohort, 893 in validation cohort), and 567 died of second cancers (333 in training cohort, 234 in validation cohort), respectively.

Predictive Ability of Cox Proportional Hazards Regression Models for Cause-Specific Events

When the Cox model of all-cause mortality was validated on patients with prostate cancer, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 3.00; 95% CI, 2.43 to 3.70; P < .001), second cancer mortality (SDHR, 1.47; 95% CI, 1.25 to 1.74; P < .001), and noncancer mortality (SDHR, 3.07; 95% CI, 2.77 to 3.41; P < .001). With the Cox model of cancer-specific mortality, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 2.62; 95% CI, 2.25 to 3.04; P < .001), second cancer mortality (SDHR, 1.18; 95% CI, 1.06 to 1.31; P < .001), and noncancer mortality (SDHR 1.54; 95% CI, 1.44 to 1.65; P < .001).

When the Cox model of all-cause mortality was validated in patients with HNC, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 2.12; 95% CI, 1.91 to 2.34; P < .001), second cancer mortality (SDHR, 1.38; 95% CI, 1.23 to 1.56; P < .001), and noncancer mortality (SDHR, 1.46; 95% CI, 1.32 to 1.62; P < .001). With the Cox model of cancer-specific mortality, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 2.11; 95% CI, 1.93 to 2.31; P < .001), second cancer mortality (SDHR, 1.37; 95% CI, 1.24 to 1.52; P < .001), and noncancer mortality (SDHR, 1.13; 95% CI, 1.03 to 1.23; P = .19).

When the Cox model of all-cause mortality was validated in patients with breast cancer, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 2.19; 95% CI, 2.00 to 2.40; P < .001), second cancer mortality (SDHR, 1.60; 95% CI, 1.45 to 1.77; P < .001), and noncancer mortality (SDHR, 2.72; 95% CI, 2.55 to 2.89; P < .001). With the Cox model of cancer-specific mortality, an increasing risk score was associated with increased cancer-specific mortality (SDHR, 2.44; 95% CI, 2.24 to 2.65; P < .001), second cancer mortality (SDHR, 1.36; 95% CI, 1.24 to 1.50; P < .001), and noncancer mortality (SDHR, 1.83; 95% CI, 1.74 to 1.92; P < .001).

Table A1.

Alternative Multivariable GCE Regression Results for Head and Neck Cancer Training Cohort

Characteristic	Cause-Specific Hazards (Cox Model), ω Ratio (95% CI)	Cause-Specific Hazards (Cox Model), ω+ Ratio (95% CI)	SDHRs (Fine-Gray Model), ω Ratio (95%CI)
Age at diagnosis, per year	0.99 (0.98 to 1.00)	0.99 (0.98 to 1.00)	0.98 (0.97 to 0.99)
Sex, ref: male
Female	1.20 (1.10 to 1.32)	1.35 (1.17 to 1.57)	1.26 (1.09 to 1.44)
Married, ref: no
Yes	1.02 (0.94 to 1.12)	1.03 (0.90 to 1.19)	1.10 (0.97 to 1.26)
Household income, ref: higher
Lower	0.97 (0.89 to 1.06)	0.96 (0.83 to 1.10)	0.94 (0.82 to 1.07)
Stage, ref: localized
Regional	1.39 (1.27 to 1.55)	1.66 (1.46 to 1.93)	1.21 (1.05 to 1.39)
Anatomic subsite, ref: oropharynx
Hypopharynx	1.10 (0.95 to 1.26)	1.19 (0.92 to 1.52)	1.02 (0.82 to 1.26)
Nasopharynx	1.34 (1.07 to 1.60)	1.77 (1.12 to 2.64)	1.29 (0.87 to 1.90)
Oral cavity	1.09 (0.98 to 1.21)	1.16 (0.97 to 1.38)	0.91 (0.78 to 1.07)
CCI, ref: 0
1	0.87 (0.79 to 0.96)	0.81 (0.69 to 0.94)	0.81 (0.700.94)
2	0.83 (0.73 to 0.94)	0.74 (0.60 to 0.91)	0.68 (0.56 to 0.83)
3	0.76 (0.61 to 0.93)	0.65 (0.47 to 0.89)	0.56 (0.41 to 0.76)
≥ 4	0.80 (0.63 to 0.98)	0.70 (0.49 to 0.98)	0.56 (0.41 to 0.76)
Postoperative RT, ref: no
Yes	0.84 (0.77 to 0.91)	0.76 (0.66 to 0.86)	0.92 (0.81 to 1.05)

NOTE. The data column on the left shows the estimate of the ω ratio for each covariate using the Cox model for cause-specific hazards. The middle data column shows the estimate of the ω⁺ ratio for each covariate using the Cox model for cause-specific hazards. The data column on the right shows the estimate of the ω ratio for each covariate using the Fine-Gray model for subdistribution hazards

Abbreviations: CCI, Charlson comorbidity index; GCE, generalized competing event; ref, reference; RT, radiation therapy; SDHR, subdistribution hazard ratio.

Table A2.

Prostate Cancer Sample Characteristics

Characteristic	With PSA Data	Without PSA Data
No.	32,904	18,809
Age at diagnosis, mean (SD), years	74 (5)	74 (5)
Married, No. (%)	24,379 (74.1)	13,863 (73.7)
Household income*, No. (%)
Higher	13,207 (40.1)	7,481 (39.8)
Lower	19,697 (59.9)	11,328 (60.2)
Race, No. (%)
White	27,159 (82.5)	16,061 (85.4)
Black	3,506 (10.7)	1,807 (9.6)
Other	2,239 (6.8)	941 (5.0)
Registry region, No. (%)
West	12,778 (38.8)	5,928 (31.5)
East	8,112 (24.7)	5,500 (29.2)
Midwest	3,813 (11.6)	2,566 (13.6)
South	8,201 (24.9)	4,815 (25.6)
Stage, No. (%)
T1	19,863 (60.4)	966 (5.1)
T2	12,131 (36.9)	1,024 (5.4)
T3a	299 (0.9)	3 (0)
T3b	264 (0.8)	7 (0)
T3NOS	347 (1.0)	16 (0)
Grade, No. (%)
High	18,071 (54.9)	5,000 (26.6)
Low/intermediate	14,833 (45.1)	13,809 (73.4)
Charlson Comorbidity Index, No. (%)
0	22,005 (66.9)	13,375 (71.1)
1	7,099 (21.6)	3,684 (19.6)
2	2,315 (7.0)	1,151 (6.1)
≥ 3	1,485 (4.5)	599 (3.2)
PSA, mean (SD), ng/mL	10.3 (12.5)	NA
Type of RT, No. (%)
EBRT only	20,427 (62.1)	10,752 (57.2)
Brachytherapy	7,908 (24.0)	4,692 (24.9)
EBRT + brachytherapy	4,569 (13.9)	3,365 (17.9)

Abbreviations: EBRT, external beam radiation therapy; NA, not applicable; NOS, not otherwise specified; PSA, prostate-specific antigen.

^*Lower household income defined as below the mean median household income of $47,290 annual salary.

Table A3.

Head and Neck Cancer Sample Characteristics

Characteristic	Value
No.	9,677
Age at diagnosis, mean (SD), years	75 (6)
Sex, No. (%)
Female	2,808 (29.0)
Race, No. (%)
White	7,973 (82.4)
Black	866 (8.9)
Other	838 (8.7)
Married, No. (%)	5,345 (55.2)
Household income,* No. (%)
Higher	3,738 (38.6)
Lower	5,939 (61.4)
Grade, No. (%)
High	2,458 (25.4)
Low/intermediate	5522 (57.1)
Unknown	1,697 (17.5)
Stage, No. (%)
Localized	4,173 (43.1)
Regional	5,504 (56.9)
Anatomic subsite, No. (%)
Oropharynx	1,087 (11.2)
Larynx	4,199 (43.4)
Hypopharynx	701 (7.2)
Nasopharynx	204 (2.1)
Oral cavity	3,486 (36.0)
Charlson Comorbidity Index, No. (%)
0	5,098 (52.7)
1	2,656 (27.4)
2	1,063 (11.0)
3	475 (4.9)
≥ 4	385 (4.0)
Postoperative RT, No. (%)	3,610 (40.5)
Type of RT, No. (%)
IMRT	2,311 (23.9)
Conventional EBRT	6,609 (68.3)
Unknown	757 (7.8)
Chemotherapy, No. (%)
Yes	2,843 (29.4)
No	6,077 (62.8)
Unknown	757 (7.8)

Abbreviations: EBRT, external beam radiation therapy; IMRT, intensity modulated radiation therapy.

^*Lower household income defined as below the mean median household income of $47,290 annual salary.

Table A4.

Breast Cancer Sample Characteristics

Characteristic	Value
No.	22,929
Age at diagnosis, mean (SD), years	77 (7)
Married, No. (%)	9,622 (42.0)
Household income,* No. (%)
Higher	11,481 (50.1)
Lower	11,448 (49.9)
Race, No. (%)
White	20,291 (88.5)
Black	1,478 (6.4)
Other	1,160 (5.1)
Registry region, No. (%)
West	9,410 (41.0)
East	4,371 (19.1)
Midwest	3,029 (13.2)
South	6,119 (26.7)
Teaching hospital, No. (%)	7,392 (32.2)
Stage, No. (%)
Localized	21,953 (95.7)
Regional	976 (4.3)
Grade, No. (%)
High	5,256 (22.9)
Low/intermediate	17,673 (77.1)
Charlson Comorbidity Index, No. (%)
0	15,594 (68.0)
1	4,776 (20.8)
2	1,483 (6.5)
≥ 3	1,076 (4.7)
Tumor size, No. (%)
< 2 cm	16,756 (73.1)
≥ 2 to < 5cm	5,045 (22.0)
≥ 5 cm	627 (2.7)
Unknown size	501 (2.2)
ER status, No. (%)
Positive	17,990 (78.5)
Negative	3,154 (13.8)
Unknown	1,747 (7.6)
PR status, No. (%)
Positive	15,229 (66.4)
Negative	5,708 (24.9)
Unknown	1,805 (7.8)
Sentinel lymph node biopsy, No. (%)	11,982 (52.2)
Lymph node examination, No. (%)
No	4,702 (20.5)
Yes	18,227 (79.5)
Left sided, No. (%)	11,704 (51.0)
RT, No. (%)
No RT	14,424 (62.9)
Conventional EBRT	7,807 (34.0)
Hypofractionated EBRT	698 (3.0)
Mastectomy ± chemotherapy and/or RT, No. (%)
+ Chemotherapy and RT	171 (0.7)
+ RT only	275 (1.2)
+ Chemotherapy only	19 (0.1)
No chemotherapy or RT	7,248 (31.6)
Lumpectomy ± chemotherapy and/or RT, No. (%)
+ Chemotherapy and RT	1,084 (4.7)
+ RT only	6,975 (30.5)
+ Chemotherapy only	141 (0.6)
No chemotherapy or RT	7,016 (30.6)

Abbreviations: EBRT, external beam radiation therapy; ER/PR, estrogen receptor/progesterone receptor.

^*Lower household income defined as below the mean median household income of $47,290 annual salary.

AUTHOR CONTRIBUTIONS

Conception and design: Ruben Carmona, Kaveh Zakeri, Brent S. Rose, James D. Murphy, Loren K. Mell

Financial support: Loren K. Mell

Administrative support: Loren K. Mell

Provision of study materials or patients: James D. Murphy, Loren K. Mell

Collection and assembly of data: Ruben Carmona, Kaveh Zakeri, Garrett Green, Lindsay Hwang, Sachin Gulaya, Beibei Xu, Rohan Verma, Casey W. Williamson, James D. Murphy, Loren K. Mell

Data analysis and interpretation: Ruben Carmona, Kaveh Zakeri, Garrett Green, Sachin Gulaya, Beibei Xu, Daniel P. Triplett, Brent S. Rose, Hanjie Shen, Florin Vaida, James D. Murphy, Loren K. Mell

Manuscript writing: All authors

Final approval of manuscript: All authors

AUTHORS’ DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

Improved Method to Stratify Elderly Patients With Cancer at Risk for Competing Events

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or jco.ascopubs.org/site/ifc.

Ruben Carmona

No relationship to disclose

Kaveh Zakeri

No relationship to disclose

Garrett Green

No relationship to disclose

Lindsay Hwang

No relationship to disclose

Sachin Gulaya

No relationship to disclose

Beibei Xu

No relationship to disclose

Rohan Verma

No relationship to disclose

Casey W. Williamson

No relationship to disclose

Daniel P. Triplett

No relationship to disclose

Brent S. Rose

No relationship to disclose

Hanjie Shen

No relationship to disclose

Florin Vaida

No relationship to disclose

James D. Murphy

No relationship to disclose

Loren K. Mell

No relationship to disclose