Volumetric CT with sparse detector arrays (and application to Si-strip photon counters)

Abstract

Novel x-ray medical imaging sensors, such as photon counting detectors (PCDs) and large area CCD and CMOS cameras can involve irregular and/or sparse sampling of the detector plane. Application of such detectors to CT involves undersampling that is markedly different from the commonly considered case of sparse angular sampling. This work investigates volumetric sampling in CT systems incorporating sparsely sampled detectors with axial and helical scan orbits and evaluates performance of model-based image reconstruction (MBIR) with spatially varying regularization in mitigating artifacts due to sparse detector sampling.

Volumetric metrics of sampling density and uniformity were introduced. Penalized-likelihood MBIR with a spatially varying penalty that homogenized resolution by accounting for variations in local sampling density (i.e. detector gaps) was evaluated. The proposed methodology was tested in simulations and on an imaging bench based on a Si-strip PCD (total area 5 cm × 25 cm) consisting of an arrangement of line sensors separated by gaps of up to 2.5 mm. The bench was equipped with translation/rotation stages allowing a variety of scanning trajectories, ranging from a simple axial acquisition to helical scans with variable pitch. Statistical (spherical clutter) and anthropomorphic (hand) phantoms were considered. Image quality was compared to that obtained with a conventional uniform penalty in terms of structural similarity index (SSIM), image uniformity, spatial resolution, contrast, and noise.

Scan trajectories with intermediate helical width (~10 mm longitudinal distance per 360° rotation) demonstrated optimal tradeoff between the average sampling density and the homogeneity of sampling throughout the volume. For a scan trajectory with 10.8 mm helical width, the spatially varying penalty resulted in significant visual reduction of sampling artifacts, confirmed by a 10% reduction in minimum SSIM (from 0.88 to 0.8) and a 40% reduction in the dispersion of SSIM in the volume compared to the constant penalty (both penalties applied at optimal regularization strength). Images of the spherical clutter and wrist phantoms confirmed the advantages of the spatially varying penalty, showing a 25% improvement in image uniformity and 1.8 × higher CNR (at matched spatial resolution) compared to the constant penalty.

The studies elucidate the relationship between sampling in the detector plane, acquisition orbit, sampling of the reconstructed volume, and the resulting image quality. They also demonstrate the benefit of spatially varying regularization in MBIR for scenarios with irregular sampling patterns. Such findings are important and integral to the incorporation of a sparsely sampled Si-strip PCD in CT imaging.

1. Introduction

CT techniques involving acquisition of sparsely sampled projection data have been gaining renewed interest, owing largely to the development of novel reconstruction methodologies. Typically, few-view or reduced angular coverage acquisitions are considered, either as a dose reduction technique (Bian et al 2010, Wang et al 2014), or to increase temporal resolution in dynamic (Chen et al 2009a, Tang et al 2010), cardiac (Nielsen et al 2005, Song et al 2007), and respiratory-gated imaging (Abascal et al 2015).

Another form of sparsity arises when the data in each of the projection views are collected with low sampling density, due e.g. to the presence of gaps in the detector matrix. A number of novel detector designs features such gaps, often because of manufacturing constraints that require tiling a number of discrete, individual sensors (each with its own readout electronics) to achieve field of view (FOV) consistent with clinical requirements. For example, CCD and CMOS detectors are being translated from preclinical to clinical cone-beam CT (CBCT) systems, promising faster image acquisition and higher spatial resolution than conventional flat-panel detectors (FPDs) in applications such as breast imaging (Shen et al 2013, Gazi and Boone 2014) or multiresolution imaging (Chen et al 2009b, Jain et al 2015). Manufacturing of large area CCD and CMOS sensors is limited by the size of crystalline Si wafers and thus modular detectors with gaps in the junctions between individual sensors are used (Rong et al 2002, Farrier et al 2009, Konstantinidis et al 2012).

This form of sparsity is not limited to the case of gaps in the detector matrix and could arise in a variety of other scenarios in x-ray imaging such as scatter correction with stationary (Niu and Zhu 2011) or moving blockers (Wang et al 2010) as well as dose reduction techniques that block part of the beam to spare dose to radiation sensitive areas (Cho et al 2012). Furthermore, similar sampling patterns arise in other medical imaging scenarios such as high-resolution PET with gaps between detector elements (De Jong et al 2003), multi-pinhole SPECT imaging (Peterson et al 2009), three-dimensional (3D) photoacoustic imaging with sparse arrays of acoustic detectors (Ephrat et al 2008), diffuse optical tomography (Süzen et al 2010), MRI with sparse k-space sampling (Lustig et al 2007), and even in other imaging applications where sparse or incomplete data are used to estimate complete datasets, as in satellite imaging (Zhang et al 2007) or image in-painting for video applications (Bertalmio et al 2001).

Photon counting detectors (PCDs) are another important example of emerging CT detector technology that may necessitate unconventional sampling patterns in the detector plane. They offer potential benefits in image quality and dose, arising from reduced electronics noise, capability for energy discrimination, and better use of low-energy photons (optimal energy weighting) compared to energy-integrating detectors (Tapiovaara and Wagner 1985, Tanguay et al 2013, Xu et al 2014). A variety of PCD-based x-ray systems have been proposed for applications such as mammography (Thunberg et al 2004, Fredenberg et al 2010a, Cole et al 2012), radiography (Francke et al 2001, Weigel et al 2014), tomography (Maidment et al 2005, Schmitzberger et al 2011, Alivov et al 2014), and energy-resolved imaging (Wang et al 2011, Alessio and MacDonald 2013, Silkwood et al 2013). A comprehensive review of current implementations, potential benefits, and clinical and preclinical applications of PCDs can be found in (Taguchi and Iwanczyk 2013).

Current implementations of PCDs include sensors based on CdTe or CdZnTe crystals (Takahashi and Watanabe 2001, Schlomka et al 2008, Iwanczyk et al 2009), microchannel plates (Shikhaliev et al 2004), Si-strip (Beuville et al 1998, Yoshida and Ohsugi 2005), as well as HgI₂ and GaAs (Schieber et al 2006, d'Aillon et al 2012). Among these technologies, Si-strip detectors offer fast response that accommodates photon fluxes appropriate for x-ray imaging without signal degradation from pileup (Bornefalk and Danielsson 2010). Si-strip PCDs have entered clinical use in scanning-slot mammography (Fredenberg et al 2010b), where an edge-on configuration is used to compensate for the relatively low stopping power of Si at x-ray energies. To accommodate the readout electronics, a sparse arrangement of linear sensors is used, causing gaps in coverage of the detector plane that are significantly larger than those present in tiled CMOS/CCD detectors (Fredenberg et al 2009).

Application of analytical reconstruction methods to sparsely sampled CT data results in noticeable degradation of image quality regardless of the exact form of the sparsity, with streak artifacts in cases of insufficient angular sampling (Crawford and Kak 1979), and ring artifacts in the case of detection gaps (Zbijewski et al 2007). Possible solutions to mitigate the effects of sparse sampling include: (i) estimation of the missing samples (i.e. angular views or detector pixels) using spatial interpolation (Galigekere et al 1999, La Riviere and Pan 1999, Bertram et al 2009, Nelms et al 2009), (ii) Fourier-based data filling methods (Van Velden et al 2008), and (iii) in-painting techniques (Li et al 2012), followed by analytical image reconstruction. The performance of such approaches is dependent on the acquisition trajectory and degrades with increasing sparsity. Application of sinogram consistency conditions was proposed in (Chen and Leng 2005) to estimate missing data for moderate detector gaps (5% to 10% of total detector area). The results showed however residual streak artifacts in the corrected data. Furthermore, the consistency conditions were derived for fan-beam CT and are not directly applicable to cone-beam systems. In some cases, data redundancy weighting schemes such as those used in short-scan conventional CT configurations (Stenner et al 2008, Taguchi and Cammin 2015) could mitigate the effects of gaps in the projection plane, but the applicability of such approaches is likely limited to specific detector sampling patterns and scanning orbits (in particular, to orbits that fulfill data sufficiency conditions regardless of the presence of the gaps, i.e. once the totality of line integrals collected in a scan is considered).

Model-based iterative reconstruction (MBIR) methods have been shown to better handle incomplete data and non-standard geometries than analytical reconstruction and can thus be advantageous in application to sparsely sampled CT acquisitions (Thibault et al 2007, Zbijewski et al 2007, Wang et al 2008). Reconstruction of sparsely sampled CT data benefits in particular from MBIR methods employing the compressed sensing theory, either in the form of constrained minimization of the reconstructed image total variation (TV) (Sidky and Pan 2008, Niu and Zhu 2012) or through edge preserving image roughness penalties based on modifications of the L1 norm of a sparse representation of the image (Jia et al 2011, Wang et al 2014), or of the difference with a high quality, fully sampled prior image (Chen et al 2008, Stayman et al 2013, Dang et al 2014). In a complementary effort to the design of penalty functions appropriate for use with sparsely sampled data, recent work (Cho and Fessler 2015) investigated the effect of spatially varying regularization strength. A previously reported spatially varying penalty design (Fessler and Rogers 1996) was expanded to include voxel under-sampling in CT acquisitions with limited angular span, yielding more homogenous resolution across the volume in penalized weighted least-squares (PWLS) reconstruction.

The performance of MBIR for sparsely distributed projection data depends on the sampling pattern. The impact of the sampling pattern on image quality in constrained TV minimization MBIR was evaluated in (Sidky and Pan 2008, Bian et al 2010, Abbas et al 2013, Jørgensen et al 2013). For the case of angular undersampling, the results point to better image quality for evenly distributed projections compared to clustered projections (which locally reduce to limited angle tomography) with similar sampling density. Furthermore, the general compressed sensing theory (Donoho 2006) indicates that random distribution of projections along the circular orbit is more appropriate for reconstruction with edge-preserving penalties. Recent studies suggest however that this might not be the case for CT acquisitions along circular or helical trajectory (Jørgensen et al 2013, Jørgensen and Sidky 2015), with better image quality achieved using uniform distribution of the angular views than using random sampling.

Compared to the case of angular undersampling, a few studies have explored in detail the effects of sparse sampling in the projection plane (Zbijewski et al 2007, Abbas et al 2013). Results indicate significant degradation of image quality for large gaps at fixed positions in the detector in CT data acquired along a circular orbit even when using MBIR. The effects of penalty design and regularization strength have not yet been fully investigated in the context of sparse sampling in projection plane.

This work investigates the performance of MBIR with edge-preserving penalties and spatially varying regularization for CBCT reconstruction in systems with sparsely sampled detectors. A variety of acquisition trajectories is considered and metrics of volumetric sampling density are proposed to elucidate the relationship between the quality of reconstructed images and local sampling. A benchtop CT implementation based on a mammographic Si-strip PCD was used to test the proposed methodology. As explained above, due to the location of electronics and the edge-on Si-strip configuration, the PCD is an assembly of linear sensors separated by gaps. The pattern of the sensors is designed such that the gaps can be compensated in planar mammography by a linear scanning motion of the source-detector assembly. The extension of this approach to CT is not straightforward, and the benchtop system used here involves very sparse sampling in the projection plane. While silicon has potential advantages over other semiconductors in PCD applications due to its excellent charge transport properties, the mammographic PCD in its current configuration is less optimal for common clinical CT applications owing both to the geometric configuration of the sensors and to the electronics designed for lower energy x-rays. In the context of this work, the PCD-based benchtop setup serves as an illustration of a fairly extreme case of detector undersampling.

Previous work (Zbijewski et al 2013, Sisniega et al 2015) with the same benchtop PCD-based CT system explored the interplay between volumetric sampling and image quality for stacked circular acquisition trajectories and conventional Penalized Likelihood (PL) MBIR with quadratic penalties. In this paper, the analysis is extended to helical acquisition trajectories. MBIR with edge preserving penalties will be evaluated to mitigate artifacts arising from sparse sampling. The benefits of spatially varying penalties in terms of providing homogenous image quality across the densely and poorly sampled regions of the reconstructed volume will be demonstrated.

2. Materials and methods

2.1. PCD imaging bench and experimental setup

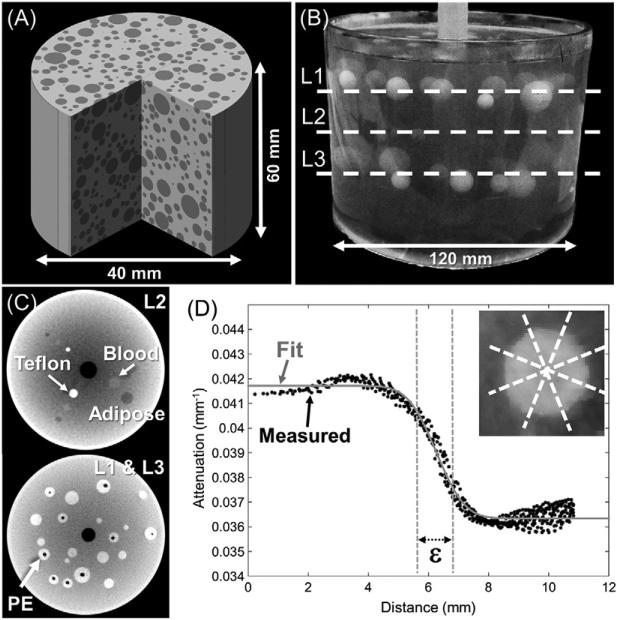
Figure 1(A) shows the imaging bench integrating a Microdose Si-strip PCD (Philips Healthcare, Solna, Sweden). The PCD (figure 1(B)) consists of an array of line sensors with 768 pixels per sensor ‘strip’ and pixels of size 0.05 mm (u direction, axial plane) × 0.5 mm (v direction, slice thickness). The sensors are arranged in edge-on configuration, yielding a 3.6 mm thick Si absorption layer to compensate for the limited stopping power of Si at x-ray energies. The sensors are tilted about the v axis to focus on the x-ray source and about the u axis to avoid filtering of the x-ray beam through the edge of the silicon sensors. The arrangement of tilted strips and the need to accommodate electronics in the edge-on configuration creates large gaps in the detection area up to 2 mm in the horizontal (u) direction and 2.5 mm in the vertical (v) direction (figure 1(C)). The resulting overall fill factor is ~0.25 of the total image size of 25 cm × 5 cm. A pre-patient collimator matched with the sensor positions is integral to the original Microdose system to minimize dose to regions of the object not sampled by the detector. For simplicity in the current experiments, the pre-patient collimator was not used.

Figure 1.

Experimental setup consisting on an imaging bench (A) including a sparse sampling Si-strip photon counting detector (B). (C) shows an illustration of the sampling density of the Si-strip detector (right half) compared to a continuous detector (left half) for a wrist phantom. The sampling pattern of the Si-strip detector presents large gaps in the detector area that would confound conventional acquisition and reconstruction methods.

The PCD was originally developed for scanning multi-slit mammography. In that case, the detector is scanned in the v direction, yielding redundancy in the acquired data that fills detector gaps in the u direction with data from subsequent detector lines. Hence, a continuous two-dimensional (2D) image covering the full FOV without gaps can be acquired.

Each pixel in the detector implements two energy thresholds. Counts below the low threshold are treated as noise and disregarded. The high threshold separates events assigned to low- and high-energy bins to allow dual-energy imaging. The detector also implements coincidence detection by which events triggering two adjacent pixels within a time window of ~20 ns (Xu et al 2014) are treated as a single count and assigned to the high-energy bin of the pixel that received the higher pulse (higher deposited energy). In the current study, the detector was operated in a photon counting mode without energy discrimination. The low threshold was set at ~10 keV to reject electronic noise. The high threshold was set at its maximum value. The high-energy bin stored only the coincidence events, which were disregarded in data processing and image reconstruction.

The bench also included a fixed anode, pulsed x-ray source (XRS-125-7K-P, Source-Ray, Ronkonkoma, NY), and a computer-controlled motion system including a rotation stage (B4872TS, Velmex, Bloomfield, NY) and two linear stages (XSlide and BiSlide, Velmex, Bloomfield, NY) controlled by stepper motor controllers (VXM-3, Velmex, Bloomfield, NY). The x-ray source and PCD were mounted on a rigid arm (identical to that in the Microdose mammography system) to provide proper source-detector alignment and mechanical stability. The source-to-detector distance (SDD) was 65 cm, with source-to-axis distance (SAD) of 50 cm, in a half-fan configuration (figure 1(A)). In addition to rotation, the imaging bench allowed lateral (u) and longitudinal (v) translation of the object, with a maximum stroke of 500 mm and 50.8 mm, respectively. The longitudinal translation and rotation were synchronized during acquisition to perform helical trajectories involving a combination of both movements. Geometric calibration of the CT system as well as dark and flood field calibration were carried out with the method described in (Zbijewski et al 2013).

The motion system allowed three categories of scan orbits: (i) a single circular axial scan, consisting of one 360° rotation with no longitudinal translation; (ii) contiguous axial scans comprising several circular scans separated by a longitudinal shift (of the object); and (iii) helical scan, combining simultaneous rotation and longitudinal translation (of the object). The helical width (HW) for a helical scan was defined as the longitudinal distance (mm) traveled by the sample over one complete rotation (360°), in distinction to the classic definition of pitch in multi-detector CT (equal to helical width normalized by the width of the collimated beam at the axis of rotation). HW was used to avoid any ambiguity that could arise from the fact that the width of the collimated beam does not reflect the actual coverage of the sparsely sampled detector.

The work reported below focused on helical scan orbits, which were found to provide better tradeoff between sampling effects and practical feasibility (namely scan speed) compared to axial scans. Analysis of image quality with stacked axial scans was shown in previous work (Zbijewski et al 2013, Sisniega et al 2015).

All studies were performed using an x-ray source voltage of 40 kV (with 2.0 mm Al inherent filtration), 5 mA tube current, 30 ms pulse duration, and detector readout at 1 frame/s. As reported in Xu et al (2014), such conditions are well below the count rate limit of the PCD (3 × 10⁶ x-rays/pixel/s), well within the linear range of detector response free from pulse pileup effects, and give a zero-frequency detective quantum efficiency (DQE) of ~0.6.

2.2. Experimental studies

2.2.1. Experiment 1: simulation study

The effects of scan orbit and reconstruction parameters on image quality were first evaluated in simulated data using the digital phantom shown in figure 2(A). The phantom consisted of a uniform 40 mm diameter cylinder with attenuation μ_bck = 0.024 mm⁻¹ containing a random arrangement of hypodense spheres (μ_insert = 0.019 mm⁻¹) with radius varying from 1 to 5 mm. The height of the cylinder was 60 mm, slightly larger than the longitudinal FOV of the system. The digital phantom comprised a volume of 800 × 800 × 600 voxels with 0.1 mm × 0.1 mm × 0.1 mm voxel size.

Figure 2.

(A) Digital phantom used in the simulation study. (B) Cylindrical gelatin phantom employed in the experimental benchtop studies. (C) Cone-beam CT images of layers L1, L2, and L3 of spheres in the gelatin phantom. (L1 and L3 had equivalent structure). (D) Spatial resolution was characterized in terms of the ESF width (ε) determined from a fit to oversampled edge profiles of the PE spheres in L1 and L3, obtained from eight 45° conical sections per sphere.

The purpose of the simulation study was to examine the relationship between acquisition orbits, detector sampling, and image quality. Noiseless simulated projection data were thus used to isolate effects associated with sampling from those arising from quantum noise. Line integrals of the digital phantom were computed using an in-house GPU implementation of the separable footprint projector (Long et al 2010, Wu and Fessler 2011). System geometry was set to the nominal configuration of the imaging bench described in section 2.1. The simulated projections included only the active pixels in the sparse Si-strip array of figure 1.

Monochromatic projections were computed as:

$$\breve{y}={\breve{I}}_0\exp (-l),$$ (1)

where Ĭ₀ is the number of photons in the unattenuated monochromatic beam (set to 3000 photons per pixel), and l is the line integral. A monochromatic beam was used in the simulation study to isolate the effects of sampling from artifacts caused by beam hardening. The energy of the beam was 45 keV, approximating the average energy of a 70 kV spectrum (+2 mm Al, +0.2 mm Cu) commonly used in extremities x-ray and CBCT imaging. Note that the experimental study of section 2.1 employed a lower energy beam (40 kV source voltage). While a 70 kV spectrum would be preferable in terms of emulating typical clinical techniques, it was found to result in severe artifacts because the PCD was calibrated for lower energy photons. However, the effects of beam energy and the discrepancy between the simulation and experimental studies are not expected to affect the conclusions of this work, which focuses on projection undersampling and optimization of imaging orbits.

The simulations included helical scans with two rotations (720°) over which 720 projections were acquired. The width of the helix was varied from 0 mm, yielding a pure circular orbit, to 25.2 mm, covering the entire longitudinal extent of the detector in the two rotations. For the circular orbit, only one rotation was performed, since no improvement in sampling is obtained from the second rotation along identical rays.

2.2.2. Experiment 2: benchtop imaging study

The simulation studies of section 2.2.1 identified optimal scan trajectories which were in turn evaluated in physical experiments involving scans acquired using the imaging bench (figure 1(A)). Two physical imaging phantoms were used: a cylindrical phantom with spherical inserts for quantitative evaluation of image quality and an anthropomorphic hand phantom for visual assessment in realistic anatomy.

The first phantom, shown in figure 2(B), consisted of an acrylic cylinder (120 mm diameter, 120 mm height) filled with gelatin. Spherical inserts were arranged in three layers within the cylinder, marked as L1, L2 and L3 in figure 2(B). The top and bottom layers (L1 and L3, figure 2(C)) consisted of polyethylene (PE) spheres with diameters ranging from 2 to 15 mm. Due to the manufacturing process, many of the PE inserts contained air cavities. The central layer (L2, figure 2(C)) presented three linear arrangements containing a high-contrast hyper-dense Teflon sphere, a low-contrast hyper-dense sphere made of simulated blood (QRM, Moehrendorf, Germany), and a low-contrast hypo-dense sphere made of simulated adipose (QRM, Moehrendorf, Germany). The diameter of the inserts in layers L1, L2 and L3 were 4 mm, 6 mm, and 12 mm, respectively.

The second phantom was an anthropomorphic hand / wrist formed from a natural skeleton in soft-tissue equivalent plastic (Rando™, Greenwich, NY). Acquisition trajectories and imaging technique for both phantoms were described in section 2.2.1.

2.3. Image reconstruction

This work used penalized-likelihood (PL) reconstruction to balance data consistency (log-likelihood, L(μ; y)) with a penalty or regularization term R(μ) that determines local image roughness. The reconstructed image is obtained from minimization of the objective function:

$$\widehat{\mu }=\underset{\mu }{\arg \max }L(\mu ;y)-\beta R\left(\mu \right).$$ (2)

The data consistency term was given by the negative log-likelihood:

$$L(\mu ;y)=\sum _i{y}_i\log \left(I_{0i}\exp \left({\left[\mathit{A}\mu \right]}_i\right)\right)-I_{0i}\exp \left({\left[\mathit{A}\mu \right]}_i\right),$$ (3)

assuming a Poisson model for the detected signal:

$$y_i\sim \text{Poisson}\left(I_{0i}\exp (-{\left[\mathit{A}\mu \right]}_i)\right),$$ (4)

where y_i is the signal in the projection data for detector pixel i, I_0i is the number of counts detected in the bare (unattenuated) beam in pixel i, A is the forward projection operator, and μ is a vector of attenuation values in the image volume. In the experimental benchtop study, I_0i was calculated from an average of 50 flood-field frames obtained with the same x-ray technique as in the object scan. Formally, the forward projection operator A includes only contributions to the active pixels (not the gaps). In practical implementation, where A and its adjoint backprojection operator A^T are computed on the fly using ray-tracing or a footprint projector, the gaps are excluded by appropriate masking of the simulated projections. The Poisson statistics of x-ray quanta were assumed to be the major contributor to noise in the projection data, so that the likelihood model in equation (3) was adequate for statistical image reconstruction. Modeling of other sources of non-ideality specific to PCDs (e.g. coincidence or charge sharing (Taguchi et al 2010, Xu et al 2014)) is beyond the scope of this study.

The penalty term in equation (2) is weighted by the scalar parameter β that controls the global tradeoff between the data and regularization. In each experiment, β was varied between 0.01% and 10% of the average detector signal in the acquisition. Consequently, the magnitude of β depended on the object and scan trajectory, but the relative contributions of the data and regularization terms spanned a similar range for all experiments. The lower the value of β, the stronger the relative influence of the data term and weaker the action of the penalty. Note that the numerical values of β used here are low compared to those commonly encountered in other applications of iterative reconstruction in FPD CBCT (Dang et al 2014, Wang et al 2014) due to the different magnitudes of detector signal in PCDs compared to FPDs.

The regularization was designed not only to control the noise in the reconstructions, but also to mitigate image quality degradation due to sparse sampling caused by detector gaps. The roughness penalty in equation (2) had the following general form:

$$R\left(\mu \right)=\sum _j{\kappa }_j^2\sum _{k\in N}\psi ({\mu }_j-{\mu }_k),$$ (5)

where j and k are voxel indices, κ_j is a (voxel-wise) factor that controls local regularization strength, N is the first order neighborhood of voxel j (six nearest neighbors in 3D), and ψ is a potential function.

Specific distributions of κ_j were previously proposed to enforce homogeneity in spatial resolution (or noise) in statistically reconstructed images (Fessler and Rogers 1996). This approach was extended in (Cho and Fessler 2015) to the case of non-uniform sampling due to sparse distribution of projection views and/or short-arc acquisition trajectories. We used a form of κ analogous to that of (Cho and Fessler 2015) to achieve homogenous spatial resolution in the presence of detector gaps (as opposed to gaps in angular coverage due to missing views, for example):

$${\kappa }_j=\sqrt{\frac{{\sum }_{i=1}^{N_d}{a}_{ij}^2{y}_i∕I_{0i}}{{\sum }_{i=1}^{N_g}{g}_{ij}^2}},$$ (6)

where a_ij are the elements of a projection operator A which only contains the N_d sampled (active) projection pixels (excluding the gaps), and g_ij are the elements of an ‘ideal’ hypothetical projection operator G, which represents a continuous sampled detector with no gaps, the same pixel pitch, and the same total area as the real detector (N_g pixels). For a given local neighborhood in the volume, the value of κ_j is lower for voxels which receive less contributions from projection rays due to detector gaps. Consequently, the relative magnitude of the penalty term is reduced for poorly sampled voxels, which prevents over-smoothing and enforces a more homogeneous tradeoff between the data fidelity term and the penalty in equation (2) across the image. Note that for a completely sampled detector G = A and κ reduces to that of (Fessler and Rogers 1996).

This selection of κ assumes relatively smooth variation of the sampling across the volume. However, non-negligible high-frequency structures were observed for some of the scan trajectories considered. The κ maps were therefore smoothed with a 3D Gaussian kernel with 10 voxels FWHM.

The penalty term included an edge-preserving Huber function:

$$\psi \left(x\right)=\{\begin{array}{c}\frac{1}{2\delta }{x}^2,\mid x\mid ⩽\delta \hfill \\ \mid x\mid -\frac{\delta }{2},\mid x\mid >\delta \hfill \end{array}\phantom{\}}.$$ (7)

The value of δ controls the minimum difference in voxel values for which a linear penalty is applied, so that for δ → 0 the regularization approximates total variation (TV), whereas larger values of δ yield a quadratic behavior throughout the volume, with more natural textures but increased blurring. The value of δ was set to 5 × 10⁻⁴ mm⁻¹, approximately an order of magnitude smaller than the typical contrast in the phantoms (e.g. ~6 × 10⁻³ mm⁻¹ for PE and gelatin) and over one order of magnitude smaller than the contrast of the sampling artifacts (e.g. from 5 × 10⁻³ mm⁻¹ to 1 × 10⁻² mm⁻¹ in the simulation study). Such selection of δ relative to image contrast has been shown to yield improved edge preservation compared to a quadratic penalty in earlier studies of intraoperative C-arm CBCT imaging (Wang et al 2014).

The PL objective was iteratively solved using the ordered subsets (OS) separable paraboloidal surrogates (SPS) algorithm (Erdogan and Fessler 1999). 100 iterations of OS-SPS with 50 subsets were used. Forward- and back-projection were carried out using the same separable footprint projector as in the simulation studies of section 2.2.1. The reconstructed volumes were 512 × 512 × 300 voxels with 0.3 mm × 0.3 mm × 0.3 mm voxel size. The constant, shift-invariant penalty with κ = 1 for all voxels was compared to the proposed spatially varying penalty with κ given by equation (6). Calculation of κ involved two squared backprojections—one for the numerator and one for the denominator in equation (6)—both performed with a footprint backprojector and assuming a continuous detector. For the term in the numerator, the gaps were set to zero while the sampled pixels were set to their measured signal (y). For the denominator, all the pixels of the continuous detector were set to one to represent the ideal case of complete sampling.

2.4. Metrics of sampling quality and image reconstruction

The performance of various scan trajectories in the presence of detector gaps was evaluated using quantitative metrics of sampling in the reconstructed volume and by visual assessment of image quality. The effects of image reconstruction algorithm were investigated using the structural similarity index (SSIM) in the simulated data and using quantitative metrics of spatial resolution, uniformity, and contrast-to-noise ratio (CNR) in the real data acquired on the test bench.

2.4.1. Sampling

Sampling in the reconstructed volume was evaluated in terms of sampling density and deviation from uniform sampling. Sampling density for a voxel j was defined as

$${\rho }_{\mathrm{samp}}\left(j\right)=\frac{N_{\mathrm{view}}}{N_{\mathrm{proj}}},$$ (8)

where N_view is the number of projection views contributing to the backprojection into the voxel, N_proj is the total number of projection views in the scan, and j is an index running across voxels.

The value of ρ_samp was computed for the geometry of the imaging bench, as specified in section 2.1, and in a volume of 512 × 512 × 120 voxels with 0.3 mm × 0.3 mm × 0.3 mm voxel size. The longitudinal extent of this test volume was less than the coverage of the detector in a single circular scan, ensuring a fair comparison for all acquisition trajectories independent of their longitudinal range.

The distribution of projection angles (i.e. whether the projection views are uniformly spaced or ‘clustered’) was quantified in terms of the difference from uniform sampling. Considering (i) the angular increment between neighboring projections contributing to a voxel in a given orbit and (ii) the increment that would have been present in a 360° orbit with uniform distribution of projections and the same total number of views, the average absolute difference from uniform sampling is:

$$\delta \Theta \left(j\right)=\frac{1∕N_{\mathrm{view}}{\sum }_{i=1}^{N_{\mathrm{view}}}\mid {\Delta }_i-(360∕N_{\mathrm{view}})\mid }{360∕N_{\mathrm{view}}},$$ (9)

where Δ_i is the angular gap (degrees) between the ith view and the previous view contributing to the signal in the voxel. The angular gap for the first view Δ_Nview) was computed as the difference between the angular position of the last view (i = N_view) and the first view (i = 1) contributing to the voxel. Note that δΘ is normalized to the angular increment in a uniformly sampled scan. Due to large storage requirements for the calculation of δΘ in all voxels of the volume, δΘ was computed for a subset of 10⁶ voxels randomly selected throughout the total volume.

2.4.2. Image similarity

The severity of artifacts in reconstructions of the simulated data was quantified in terms of structural similarity (SSIM) relative to the ‘ground truth’ digital phantom, as defined in (Wang et al 2004). For a small region of interest (ROI) in the volume, the SSIM is:

$$\mathrm{SSIM}=\frac{(2{\stackrel{‒}{\mu }}_{\mathrm{ref}}{\stackrel{‒}{\mu }}_{\mathrm{img}}+c_1)(2{\sigma }_{\mathrm{ref}\text{-}\mathrm{img}}+c_2)}{({\stackrel{‒}{\mu }}_{\mathrm{ref}}^2+{\stackrel{‒}{\mu }}_{\mathrm{img}}^2+c_1)({\sigma }_{\mathrm{ref}}^2+{\sigma }_{\mathrm{img}}^2+c_2)},$$ (10)

where ${\stackrel{‒}{\mu }}_j$ is the mean attenuation value, σ_j is the variance of the attenuation values (both measured in a local ROI) for image j. The index ref denotes the reference digital phantom, img denotes the reconstructed image being evaluated, and σ_ref-img is the covariance between the two images. The scalars c₁ and c₂ guarantee stability when the mean or variance are close to zero (set to c₁ = (0.01 × μ_bck)² and c₂ = (0.03 × μ_bck)², where μ_bck is the background attenuation value in the reference volume (section 2.2.1)). SSIM was computed for spherical ROIs of radius equal to two voxels centered at all non-zero voxels throughout the reference volume.

2.4.3. Image quality: spatial resolution, uniformity, and contrast-to-noise ratio

The effects of penalty design and regularization strength were evaluated in images of the gelatin phantom using the optimal acquisition trajectory identified in the simulation studies. Spatial resolution was measured in terms of the edge spread function (ESF) following the method described in (Wang et al 2014). Separate measurements were obtained for two inserts—one low-contrast hyperdense PE insert in the L1 layer of figure 2(C) and one low-contrast hypodense insert (12 mm diameter adipose) in the L3 layer. This approach recognizes the resolution non-uniformity due to non-uniform sampling and to the dependence on local image contrast associated with MBIR.

Oversampled profiles were obtained for each spherical insert by plotting the voxel values within a 45° cone as a function of their distance to the center of the sphere, as illustrated in figure 2(D). The ESF was obtained by fitting the oversampled edge profiles to an error function (erf):

$$f\left(x\right)=a-\frac{c}{2}\mathrm{erf}\left(\frac{x-r}{\sqrt{2}\epsilon }\right),$$ (11)

where a, c, and r are fitting parameters related to average attenuation, contrast, and edge location, respectively, and ε is the width of the erf function given by:

$$\mathrm{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{\mathrm{e}}^{-t^2}\mathrm{d}t.$$ (12)

The width of the erf function, ε, provided the spatial resolution metric, averaged across 8 conical regions on each sphere. Prior to ESF analysis, air bubbles present in some of the spherical inserts were segmented and filled using a grayscale morphological filling operation.

Image non-uniformity was quantified using a large ROI (~65 cm²) selected in a uniform area of the gelatin background. We used the standard deviation of voxel values in this ROI as a metric of non-uniformity, denoted Δ. Due to the large size of the ROI, the metric Δ captures not only the noise, but also the non-uniformity due to artifacts (as opposed to using a small ROI, where standard deviation typically only captures local noise).

CNR was measured for a low-contrast insert (12 mm diameter adipose) in the central slice (see figure 2(C)). Two 4 mm diameter circular ROIs were used, one at the center of the insert $({\stackrel{‒}{\mu }}_{\text{insert}},{\sigma }_{\text{insert}}^2)$ and one in the background $({\stackrel{‒}{\mu }}_{\mathrm{bck}},{\sigma }_{\mathrm{bkc}}^2)$, 10 mm from the center of the insert.

3. Results

3.1. CT imaging performance with a sparsely sampled detector: simulation study

3.1.1. Impact of scan trajectory on volume sampling

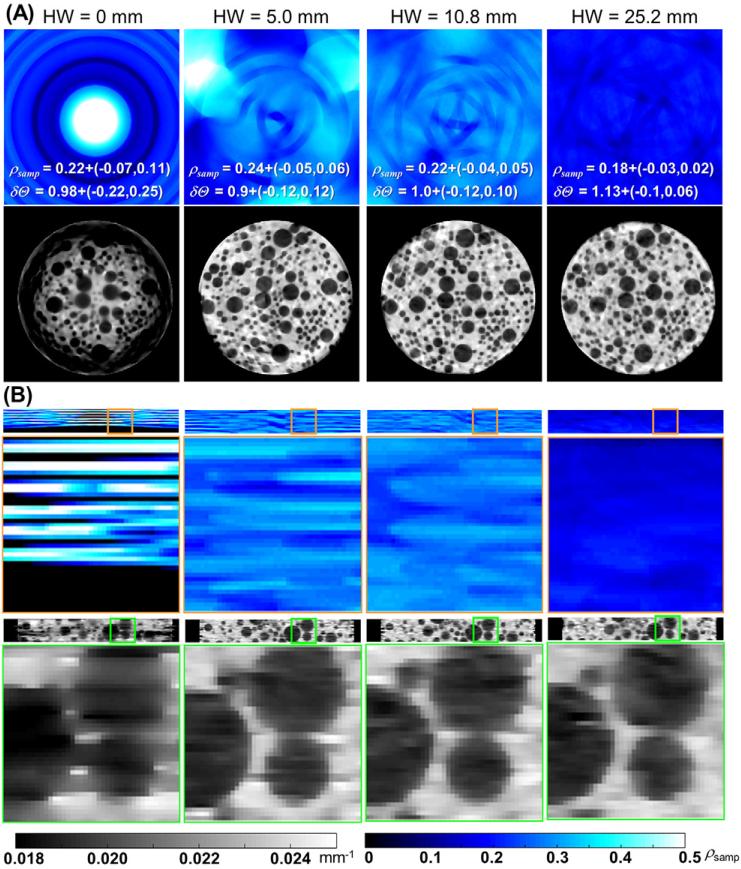
Examination of the line sensor pattern of the Si-strip PCD (figure 1) indicates that in the limiting case of a helical orbit with HW = 0 (equivalent to a single axial scan), the sampling of the volume will consist of disjoint rings of relatively dense sampling, interspersed by regions from which no line integrals are collected due to detector gaps. This is apparent in the axial distributions of the sampling density ρ_samp in figure 3(A) and, even more conspicuously, in the coronal distributions in figure 3(B). The images in figure 3 were obtained with the spatially constant penalty (κ = 1) and low regularization strength (β = 9, equal to 0.01% of the average detector signal) to emphasize the effects of sampling. The areas of low ρ_samp are associated with shading and streak artifacts and reduced spatial resolution due to increased relative contribution of the penalty. By translating the sample along the longitudinal axis in a helical scan, the scan trajectory fills in the gaps using data from line sensors that were initially below the axial plane of interest. For low HW (i.e. a short longitudinal distance covered in one rotation), this yields improved median ρ_samp and reduced variability in ρ_samp throughout the volume, as illustrated by the ρ_samp distributions in figure 3. This results in a marked reduction in the severity and spatial extent of the undersampling artifacts in the reconstructed images. However, because the angular span of the helical scans was held constant at 720°, the increase in HW leads to increased longitudinal travel between consecutive projection views. As a result, although the sampling becomes more homogenous with increasing HW, the angular range of projection views contributing to a voxel decreases above certain HW. In particular, for the voxels at the center of the field of view in figure 3, the axial scan produces higher ρ_samp than any of the helical orbits. This tradeoff between more homogenous sampling and reduced angular separation of views locally contributing to the image results in initial reduction of undersampling artifacts at low HW (up to ~10.8 mm), followed by the increased distortion of the spherical inserts at large HW.

Figure 3.

Axial (A) and coronal (B) planes of sampling density ρ_samp (top row) with increasing helical width HW. The reconstructed images (bottom row) of simulated tomographic data showed direct correspondence between spatial variations in sampling and the presence of artifacts and/or spatially varying image quality. Labels depict median and interquartile range for ρ_samp and δΘ.

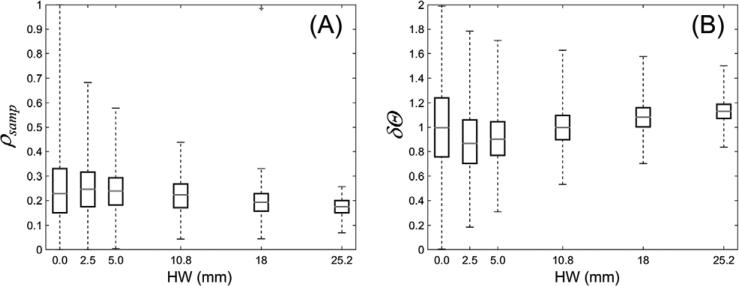
The sampling density ρ_samp measured as a function of HW is shown in figure 4(A). In agreement with the analysis above, the median number of views contributing to a voxel initially increases with increasing HW. This is accompanied by a more uniform distribution of projection angles contributing to a voxel compared to a circular scan, as indicated by the initial decrease in δΘ in figure 4(B) compared to circular scan (HW = 0). Minimum median δΘ was achieved for HW of 2.5 mm, followed by an increase in median δΘ for larger values of HW. For HW above 10.8 mm, the median δΘ exceeded the value for a circular scan due to the larger angular increment between neighboring views, which also results in a decrease in median ρ_samp.

Figure 4.

(A) Sampling density ρ_samp and (B) deviation from uniform sampling δΘ as a function of helical width HW. In the box-and-whisker plots, the gray horizontal bar indicates the median value throughout the volume, the boxes denote the interquartile range, and the whiskers correspond to upper and lower bound throughout the volume.

The interquartile range of ρ_samp and δΘ decreases with increasing HW, indicating a more homogeneous sampling of the volume using helical trajectories. The upper and lower bounds of the whisker plots show the maximum and minimum sampling, with scan trajectories of HW ≥ 10.8 mm achieving minimum ρ_samp larger than 0.05 (i.e. every voxel receives contributions from at least 5% of the projection views in the scan, equal to ~40 views). The increase in minimum ρ_samp for helical widths larger than 10.8 mm is offset by a decrease in median ρ_samp (and eventually is worse than for an axial scan of HW = 0).

Visual evaluation from figure 3 combined with the analysis of trends in ρ_samp and δΘ in figure 4 suggests a value of HW = 10.8 mm as a reasonable choice balancing the average sampling density, angular coverage, and homogeneous sampling properties across the volume. A helical width of 10.8 mm was therefore used in the subsequent experiments reported below.

3.1.2. Effects of spatially varying regularization

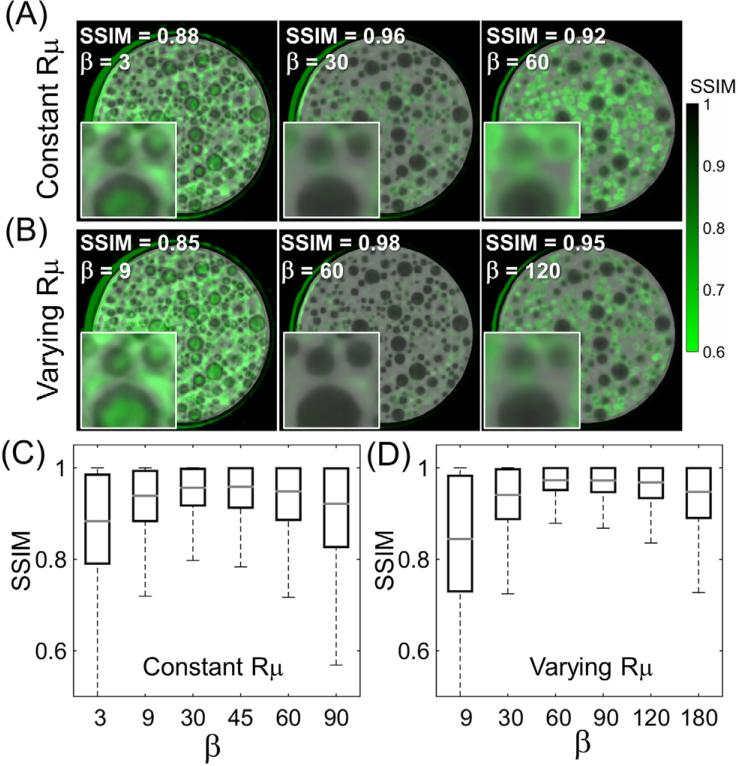
The influence of varying the regularization strength (parameter β in equation (2)) is shown in figure 5(A) for the case of a spatially constant (shift-invariant) penalty. Figure 5(B) shows the effect of the spatially varying penalty (given by equation (6)), using three values of β ranging from light to strong regularization. The local SSIM is overlaid on the reconstructed images (green-scale). Extreme values of β result in poor image similarity. For low β, the action of the penalty is not sufficient to significantly reduce artifacts due to projection gaps and SSIM is degraded primarily in regions corresponding to undersampling artifacts. Excessively high β, on the other hand, introduces over-smoothing, causing reduced SSIM at the edges of the spherical inserts.

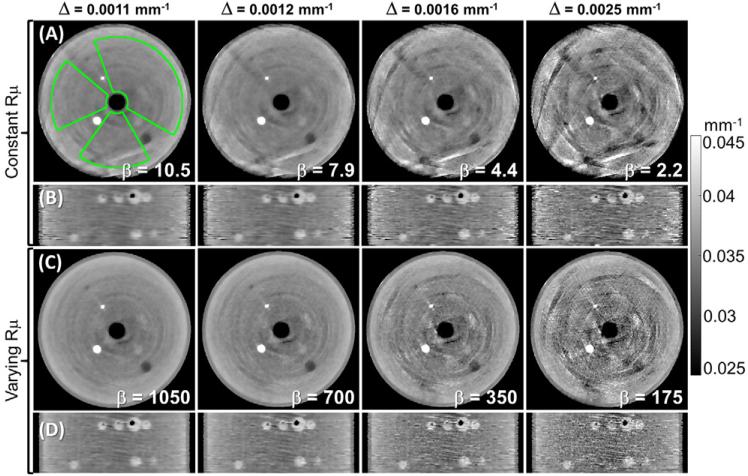
Figure 5.

The effect of (A), (C) constant or (B), (D) spatially varying penalties. In (A) and (B), the SSIM is overlaid in green-scale, and the three columns represent reconstructions at approximately matched median SSIM (shown in the label at the top-left corner of the images). In (C) and (D) the SSIM distributions are quantified as box-and-whisker plots for the spatially constant and spatially varying regularization methods, respectively. Note the larger maximum value of median SSIM and more homogenous distribution in SSIM for the spatially varying penalty.

The SSIM measured as a function of β is shown in figure 5(C) for the spatially constant penalty and in figure 5(D) for the spatially varying penalty. For the spatially constant penalty, a maximum value of median SSIM = 0.96 is achieved at β = 30. For the spatially varying penalty, a maximum median value of SSIM = 0.98 was achieved at β = 60. In both cases, these optimal values of β correspond to the narrowest spread in SSIM throughout the image, with a more homogenous distribution of SSIM observed for the spatially varying penalty than for the constant penalty (minimum SSIM = 0.88 at β = 60 for the spatially varying case compared to 0.80 for the spatially constant penalty at β = 30).

Images for the optimal values of β are shown in the middle columns of figures 5(A) and (B). The spatially varying penalty achieved better fidelity of reconstruction than the spatially constant penalty, yielding a sharper image with reduced artifact. The improved homogeneity of SSIM achieved with the spatially varying penalty is evident across all β values—noting, for example, the prevalence of low SSIM (green spots) at the center of the phantom for the spatially constant penalty. For this cylindrical phantom, the projection values are lowest at the center of the object, and the relative weight between signal and penalty thus favors the effect of the penalty. For the spatially varying penalty, κ is lower for the more strongly attenuated rays at the center, thereby reducing the effect of the penalty in this area and yielding a more uniform SSIM distribution.

Note that the factor κ in equation (6) is bounded between 0 and 1. On average, this results in reduction of the effective regularization strength for the spatially varying penalty, so that the maximum value of median SSIM was achieved for a larger numerical value of β than for the constant penalty. For the sake of fair comparison, the images shown in figure 5 correspond to approximately matched values of SSIM between the two penalty types. Note that since κ is determined by the data term y, the optimal value of β is also object dependent.

3.2. Image quality assessment in real data

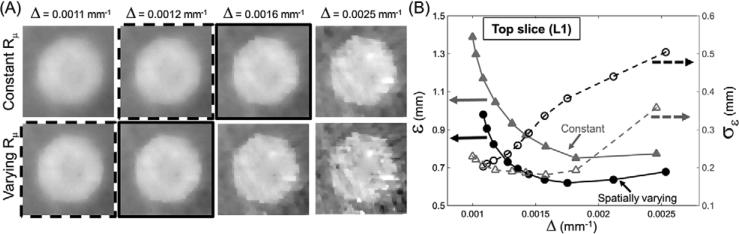
Results from the simulation studies (above) were applied to the acquisition and reconstruction of real data to further characterize the tradeoffs between sampling and noise, including factors that were not included in the simulation study. Reconstructed axial and coronal slices of the gelatin phantom at matched non-uniformity Δ are shown in figure 6, comparing the performance of the spatially constant (figures 6(A) and (B)) and spatially varying (figures 6(C) and (D)) penalties.

Figure 6.

Images of the gelatin phantom reconstructed with various levels of regularization strength. (A), (B) Spatially constant and (C), (D) spatially varying regularization. The non-uniformity Δ was measured in the ROI shown in (A). Columns correspond to images at matched Δ. The spatially varying penalty achieved reduction in artifacts, sharper edges, and superior noise and resolution homogeneity than the spatially constant penalty at matched Δ.

The non-uniformity metric Δ includes the effects of artifacts and quantum noise. Comparable Δ can therefore be obtained for images with a very different tradeoff between noise and artifacts. Figure 6 shows that at equal Δ, the non-uniformity for the spatially constant penalty is dominated by the artifacts, whereas the non-uniformity for the spatially varying penalty is dominated by noise. This indicates that the constant penalty is less effective at reducing the undersampling artifacts and requires stronger regularization to achieve comparable Δ compared to the spatially varying penalty. This stronger regularization results in increased blurring for the spatially constant penalty at matched Δ.

Another effect of the spatially varying regularization is the homogenization of the resolution-noise properties of the image. This can be observed in the coronal views in figure 6, where the constant penalty shows a larger difference between the appearance of the edge of the phantom (sharp and noisy) and of the spheres placed at the center (slightly blurred) compared to the spatially varying penalty.

3.2.1. Spatial resolution

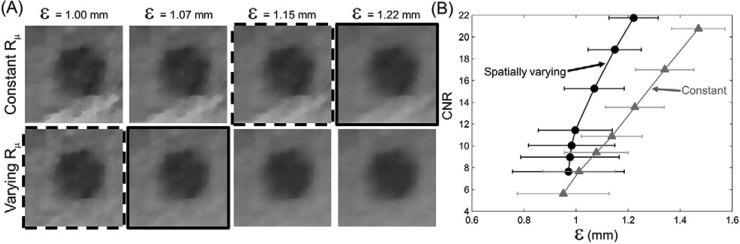
Quantitative evaluation of spatial resolution for the PE insert in the top layer L1 is shown in figure 7. Zoomed images of the insert indicate that the spatially varying penalty exhibits sharper edges at matched non-uniformity Δ than the constant penalty. The spatial resolution is quantified in figure 7(B), where solid lines mark ε and dashed lines mark standard deviation in ε (σ_ε) measured across the eight angular cones on each sphere used for resolution measurement. The spatially varying penalty yielded improved (lower) ε than the spatially constant penalty, corresponding to narrower ESF and better resolution for equal levels of image uniformity.

Figure 7.

Spatial resolution (ε) and image non-uniformity (Δ) for spatially constant and spatially varying penalties. (A) Zoomed images of one of the 8 mm PE inserts in the top layer L1 used for resolution measurement: top row—spatially constant penalty; bottom row—spatially varying penalty. Images in (A) are shown at matched Δ between the two penalty types. (B) Quantitative assessment of spatial resolution. Solid lines denote the width ε of the ESF, and dashed lines denote the standard deviation of ε, σ_ε. The constant penalty is shown in gray, and the spatially varying penalty in black.

For both types of penalty, the spatial resolution was found to exhibit anisotropy that increased with reduced regularization strength, as reflected by increased σ_ε values for higher non-uniformity Δ. Resolution anisotropy σ_ε was higher for the spatially varying penalty, but closer inspection of the σ_ε curves reveals that this occurred at spatial resolutions that were beyond the range achievable by the constant penalty. For cases where ε was matched, the anisotropy was actually comparable between the two types of penalty, indicating that the local action of the penalty is similar for the spatially varying and spatially constant case. This finding is illustrated in the zoomed images framed by solid and dashed lines and representing matched spatial resolution (but different non-uniformity) for the spatially varying and the spatially constant penalties. For the case marked by solid frames, the value of ε is 0.81 mm and σ_ε is 0.18 mm for the spatially constant penalty, compared to 0.82 mm and 0.19 mm for the spatially varying penalty. For the case denoted by dashed frames, σ_ε is also matched at matched spatial resolution, with ε = 0.93 mm and σ_ε = 0.19 mm for the spatially constant penalty, and ε = 0.97 mm and σ_ε = 0.2 mm for the spatially varying penalty. Both cases confirm that for comparable ε, the value of σ_ε is similar for both penalties.

Note that the slightly distorted circular shapes observed in these images are likely due to the penalty function based on voxel differences within a 1-neighborhood (i.e. ignoring diagonal neighbors) as discussed in (Wang et al 2014).

3.2.2. Contrast-to-noise ratio

The measured CNR is plotted as a function of spatial resolution ε for the 12 mm adipose insert in figure 8. The value of ε was measured in the same adipose insert using the method described in section 2.4.3.

Figure 8.

CNR measured as a function of spatial resolution: zoomed images of the 12 mm low-contrast adipose insert are shown in (A) for the constant and spatially varying penalty at matched resolution. CNR curves as a function of resolution (ε) measured in the same insert are presented in (B). The gray curve denotes the spatially constant penalty, the black curve marks the spatially varying penalty. Horizontal error bars represent the standard deviation, σ_ε, of the measured resolution. Zoomed images with solid and dashed frames indicate equal CNR between the spatially constant and spatially varying penalty.

Zoomed images in figure 8(A) indicate improved CNR at matched resolution for the spatially varying penalty. The plot in figure 8(B) confirms this trend, showing moderately improved CNR at matched ε for the spatially varying penalty (black curve) compared to the constant penalty (gray curve). Even after taking into account the dispersion of the resolution measurements (σ_ε) represented by the horizontal error bars, the benefit in CNR is maintained, especially for values of ε larger than ~1.1 mm. The slightly improved CNR performance of the spatially varying penalty at equal resolution, despite the similar local resolution properties observed in section 3.2.1, is associated with the subtle undersampling artifacts that increase standard deviation inside the ROIs used for CNR measurement. The solid and dashed frames in figure 8 indicate two cases with approx. matched CNR (8 and 13–14, respectively). The spatially constant penalty requires additional blurring to reduce the bright sampling artifact located below the insert, so that matched CNR with the image with spatially varying penalty (and less artifact) is achieved at higher ε.

3.3. Imaging performance in anthropomorphic phantom

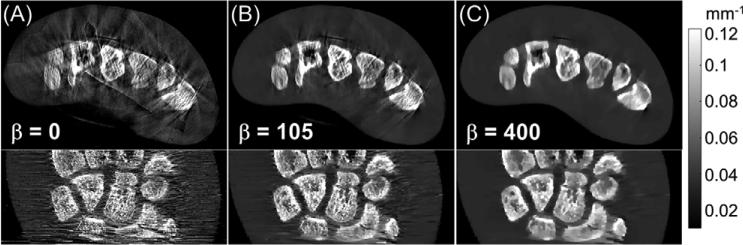
Axial and coronal views of the anthropomorphic hand phantom are shown in figure 9. Data were acquired with HW = 10.8 mm and reconstructed using the spatially varying penalty with three levels of regularization strength. Figure 9(A) shows the case of no regularization (β = 0), included as a baseline for comparison and illustrating the inherent level of artifact and noise in the data. Figure 9(B) illustrates low regularization (β = 105). This relatively low level of regularization provided marked reduction of sampling artifacts, significantly improved homogeneity in soft tissue regions, and improved delineation of fine structures within the bone while preserving spatial resolution. Residual sampling artifacts are still visible, however. As shown in figure 9(C), these artifacts can be further reduced with stronger regularization (β = 400) at the cost of reduced spatial resolution (visible in particular in the inner bone).

Figure 9.

(Top) Axial and (Bottom) coronal reconstructions of an anthropomorphic hand phantom with three levels of regularization: (A) no regularization; (B) low regularization; and (C) strong regularization.

4. Discussion and conclusions

This work investigated the sampling properties of helical trajectories with projection data that are sparsely sampled in the detector plane. The helical acquisition orbit showed significant improvement in image quality compared to an axial circular scan.

Moderate helical widths were found to provide the best tradeoff between maximizing the average sampling density, achieving relatively uniform distribution of projection views, and maintaining homogenous sampling properties throughout the volume. The significance of achieving homogenous sampling has been noted in earlier studies. In (Abbas et al 2013), image quality degradation was found for a sparse detector involving large gaps at fixed positions compared to a detector with comparable average sampling density but a more homogenous distribution of samples achieved through a pattern of more numerous, smaller or moving gaps. Similarly, the observation that trajectories with more uniform distribution of projection views (low δΘ) are preferred over those with more clustered distribution (large δΘ) is in agreement with previous studies (Abbas et al 2013, Jørgensen et al 2013).

A helical width of 10.8 mm was found to yield optimal sampling for the sparse PCD considered in this work. This optimal HW depends however on the particular arrangement of sensors and gaps in the detector. For example, a pattern with a smaller vertical gap between the sensors would likely benefit from shorter HW. While the tradeoffs involved in orbit and regularization design for sparsely sampled detectors are complex, the primary goal of this work was to propose a methodology that is general enough to be applicable to a variety of detector configurations.

In addition to the effects of the acquisition orbits, this work investigated the performance of MBIR in mitigating undersampling artifacts, in particular with respect to the effects of spatially varying penalty (Cho and Fessler 2015). The spatially varying penalty takes into account the variations in sampling density to yield similar relative contributions of the penalty and data throughout the volume. Consequently, over-regularization of poorly sampled sub-volumes and under-regularization of densely sampled sub-volumes are avoided, resulting in more homogenous resolution properties of the reconstruction. This demonstrated improved mitigation of sampling artifacts and thus better resolution and CNR at equal image non-uniformity compared to spatially constant regularization. While the spatially varying penalty considered here presents a straightforward solution to incorporating the sparse sampling pattern in regularization design, future studies could investigate other forms of spatially varying penalty that have recently been proposed, e.g. a penalty designed to homogenize noise (Cho and Fessler 2015), and a penalty that uses an estimate of the local response function (Gang et al 2014) instead of pure sampling considerations.

Furthermore, reconstruction algorithms posed as constrained minimization of the TV of the reconstructed image have been shown to greatly alleviate the effects of undersampling (Sidky and Pan 2008, Niu and Zhu 2012, Rose et al 2015), achieving accurate results when the sampling is complete in the sense of the gradient-magnitude sparsity of the object. In contrast to those TV reconstruction techniques, the MBIR employed here performs unconstrained minimization of an objective function that involves a trade-off between a data fidelity term and an edge-preserving Huber penalty. By setting a sufficiently small value of the parameter δ in the Huber function, a first-order, TV-like penalty is applied across a broad range of image intensities. The effects of varying the value of δ were investigated. Only minor change in the undersampling artifacts was found when δ was decreased by two orders of magnitude from the value used in the experiments described above. This indicates that the Huber penalty employed in this study provides a good approximation of pure TV regularization. Constrained TV reconstruction would likely converge to a somewhat different solution than the reconstructions obtained with TV-like Huber penalty. Nevertheless, the fact that undersampling artifacts were not completely removed with TV-regularized MBIR indicates that complete sampling (in the sense of gradient-magnitude sparsity) was not achieved for the acquisition orbits and phantoms considered in this work. The objective of the study was to identify combinations of acquisition orbits and spatially-varying penalties that mitigate undersampling artifacts for CT systems with sparse detectors, acknowledging that achieving complete sampling in such systems may often be impossible or impractical.

Similarly, the potential of prior image-based regularization (Chen et al 2008, Stayman et al 2013, Dang et al 2014) to mitigate undersampling artifacts is acknowledged. However, the complex optimization that such a penalty would likely require is beyond the scope of this paper, which is concerned with a more general investigation of the fundamental aspects of CT imaging with sparse detectors.

The design of the sampling pattern in the PCD considered here was optimized for planar imaging and not CT and may thus present an extreme case of sparsity. While other detector designs may yield improved image quality, this study demonstrated and quantified the interplay between detector sampling, acquisition trajectory, and image reconstruction algorithm, and it identified a methodology for optimizing CT image quality in the presence of detector gaps. The methods and findings of this study are applicable to other detector sampling patterns and other forms of sparsity and could benefit the development of novel CT systems with non-conventional detector arrays and acquisition trajectories.