Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2015 Dec 2;24(7):1022–1028. doi: 10.1038/ejhg.2015.253

Genome-wide gene–environment interactions on quantitative traits using family data

Colleen M Sitlani 1,*, Josée Dupuis 2, Kenneth M Rice 3, Fangui Sun 2, Achilleas N Pitsillides 2, L Adrienne Cupples 2, Bruce M Psaty 4,5
PMCID: PMC5070904  PMID: 26626313

Abstract

Gene–environment interactions may provide a mechanism for targeting interventions to those individuals who would gain the most benefit from them. Searching for interactions agnostically on a genome-wide scale requires large sample sizes, often achieved through collaboration among multiple studies in a consortium. Family studies can contribute to consortia, but to do so they must account for correlation within families by using specialized analytic methods. In this paper, we investigate the performance of methods that account for within-family correlation, in the context of gene–environment interactions with binary exposures and quantitative outcomes. We simulate both cross-sectional and longitudinal measurements, and analyze the simulated data taking family structure into account, via generalized estimating equations (GEE) and linear mixed-effects models. With sufficient exposure prevalence and correct model specification, all methods perform well. However, when models are misspecified, mixed modeling approaches have seriously inflated type I error rates. GEE methods with robust variance estimates are less sensitive to model misspecification; however, when exposures are infrequent, GEE methods require modifications to preserve type I error rate. We illustrate the practical use of these methods by evaluating gene–drug interactions on fasting glucose levels in data from the Framingham Heart Study, a cohort that includes related individuals.

Introduction

Genome-wide searches for gene–environment interactions represent an agnostic approach for the evaluation of whether genetic markers modify associations between traits and exposures of interest.1 Such interactions could lead to strategies for targeting interventions toward the people who are most likely to benefit from them. For example, many drugs have unintended side effects or variable effectiveness across people. A person's underlying genetics may contribute to whether they experience side effects or respond well to treatment.2, 3 Identifying specific genetic contributions that influence treatment response would permit treatment strategies that minimize side effects or maximize treatment response. Alternatively, variable response to interventions aimed at primary or secondary prevention could also lead to targeted intervention strategies. For example, there is growing evidence that the association between various dietary and behavioral exposures and disease risk may be modified by genetic factors.4, 5 Identifying such interactions could permit personalized strategies for disease prevention. In the case of tailoring drug treatment, interest lies in characterizing gene–environment interactions where the environmental exposure is drug use, whereas in the case of tailoring efforts at prevention, other examples of exposures include pesticide exposure, nutrition, nicotine use, and exercise.

Adequate power for genome-wide investigation of these gene–environment interactions requires large sample sizes,1 which are often obtained by combining information from multiple studies. To properly account for all sources of variability6 and to allow for misspecification of exposure–outcome relationships,7 robust variance estimates are helpful. However, when environmental exposures have low prevalence, common robust methods may not preserve type I error rate at the low significance levels required in genome-wide analyses because of data sparsity.8 The smaller the contributing study, the bigger the problem. Sitlani et al.8 evaluated small-sample modifications in the context of analyses of gene–environment interactions using longitudinal data from samples of unrelated individuals. Comparable methods for genome-wide gene–environment interaction in samples that include related individuals have not yet been evaluated.

In this article, we discuss the available methods for evaluating genome-wide gene–environment interactions in family data, including small-sample modifications to ensure validity when environmental exposures are infrequent. We consider both cross-sectional and longitudinal analyses. We evaluate the type I error rates of these methods via simulations. We then apply the methods to data from the Framingham Heart Study (FHS), evaluating gene–drug interactions on fasting glucose levels, both cross-sectionally and longitudinally. Finally, we discuss the implications of our findings and make practical recommendations for future studies of genome-wide gene–environment interactions that involve family data.

Subjects and methods

Methods

A number of approaches exist for investigating gene–environment interaction on a genome-wide scale.1 In this article, we discuss an agnostic approach that evaluates interaction between single-nucleotide polymorphisms (SNPs) and environmental exposures on quantitative traits. In particular, we are interested in the following statistical model:

graphic file with name ejhg2015253e1.jpg

where i indexes participants, t indexes measurement time, Y is a quantitative outcome of interest, E is an environmental exposure, G is a SNP dosage, and Z is a vector of adjustment variables. There can be multiple measurements over time for each person. SNP dosage, which may be either observed or imputed,9, 10 is modeled additively. This model focuses on associations between SNPs and environmental exposures on the level of the quantitative outcome. Alternatively, with longitudinal data, primary interest could be in associations with the rate of change of the quantitative outcome over time.11 Interactions of G, E, and G × E with time would be required to address questions about associations with rates of change. However, in this article, the coefficient of interest is the interaction coefficient βG:E, and in particular, tests of whether this interaction coefficient is zero.

Several options are available for such tests, using data from related individuals. Typically either linear mixed-effects models (LMMs)12 or generalized estimating equations (GEE methods)13 are used. For LMMs, the correlation among individuals in the same family is accounted for by adding to Equation (1) a random effect with variance–covariance matrix proportional to the relevant kinship matrix. Further, when there are repeated observations within the same individual, a random intercept for each person induces exchangeable patterns of within-person correlation. For GEE methods, a working correlation matrix is specified to account for correlation within families or within individuals. Owing to the constraints of available standard software for fitting GEE models, this working correlation matrix can only explicitly accommodate a single source of clustering; therefore, in the analyses of repeated measures on individuals within families, the working correlation in GEE methods only takes into account within-individual correlation to the extent that it contributes to within-family correlation.

Robustness to model misspecification differs between LMMs and GEE methods, a difference that is reflected in the usual choice of the estimates of the variances of model parameters for each method. Standard use of LMMs assumes correct mean and variance model specification and therefore uses model-based variance estimates.7, 14 Standard implementation of GEE methods, on the other hand, uses semirobust variance estimates that allow for misspecification of the working correlation matrix.15, 16 For canonical link functions, such variance estimates are also robust to misspecification of the mean model.17 In the context of gene–environment interactions, robust variance estimates are often required to properly estimate variability in effect size estimates and to allow for model misspecification.6, 7 Therefore, LMMs are not always appropriate for investigation of gene–environment interactions. GEE methods, using traditional sandwich variance estimates, may be preferable. However, GEE's performance is known to be poor when only a small number of clusters are available.18 In the context of gene–environment interactions, Sitlani et al.8 illustrated that poor performance occurs when small gene–environment strata exist, for example, when binary environmental exposures are infrequent. Use of traditional GEE methods may result in inflated type I error rates.18 Therefore, despite the large sample sizes that are achieved by collaborations within genetic consortia, genome-wide statistical tests of interaction at the individual study level often have inflated type I error rates when traditional sandwich variance estimates are used in the setting of infrequent binary environmental exposures.

Methods exist for improving small-sample properties of robust variance estimates in the context of GEE analysis, but they have not been evaluated in the context of data from related individuals. Specifically, type I error rates can be controlled by modifying the variance estimates and/or the reference distribution used to compute P-values.8, 19

Options for alternate variance estimates include (1) reducing bias in the sandwich variance estimate by incorporating an expression for the leverage of each cluster in estimation of the cluster-specific variance, as proposed by Mancl and DeRouen,20 (2) pooling data across clusters to estimate a common correlation matrix, decreasing the reliance on a single cluster's information in the estimation of the variance, as proposed by Pan,21 and (3) a combination of the previous two methods that further improves small-sample performance, proposed by Wang and Long.19 Pan's method, and thus Wang and Long's (WL's) method, rely more heavily on model assumptions, requiring that the conditional variance of the outcome given covariates be correctly specified and that a common correlation structure exists across all subjects.

Either separately or in combination with alternate variance estimates, control of type I error rate can be improved by changing the reference distribution used to calculate P-values from a normal reference distribution to a t-reference distribution.22, 23 The t-reference distribution requires an estimate of degrees of freedom, which incorporates the variability in the variance estimate, giving a more accurate computation of the P-value. For infrequent binary exposures, a rough approximation to degrees of freedom can be obtained by estimating the size of the smallest gene–environment stratum, which is the SNP-specific number of independent observations with a minor allele and positive exposure status.8 For cross-sectional data, assuming trait correlation of 0.5 between siblings, this approximation would be twice the minor allele frequency (MAF) times the average of the number of exposed participants and the number of sibships with at least one exposed participant, times the imputation quality for imputed SNPs. For longitudinal data, we approximate the degrees of freedom to be twice the MAF times the number of participants exposed at one or more measurement times, times the imputation quality for imputed SNPs. Alternatively, Pan and Wall23 suggested an approximation to degrees of freedom for GEEs that is based on Satterthwaite's approximation.22 Pan and Wall's approximation can be used in the context of alternate standard error (SE) estimates, as discussed by Wang and Long.19

Simulations

We conducted extensive simulation studies to evaluate the relative performance, with respect to type I error rate, of methods for testing gene–environment interactions with family data. Under the null hypothesis of no interaction, uniformity of P-values was assessed visually by plotting the ratio of observed to expected P-values versus expected P-values, with both quantities on a −log10 scale, and inclusion of 95% confidence bands. We evaluated methods across a range of MAF, exposure frequency, family structure, and number of observations per individual.

For each set of simulated data, we included 1000 individuals with exposure status drawn randomly from a binomial distribution, genotype based on random mating and no mutations, and outcomes generated under the null hypothesis of no SNP, exposure, or SNP × exposure effects. We considered two different relationship structures: (1) nuclear families with three offsprings, that is, 200 families each of size five, and (2) three-generational families comprised of first-generation parents with two offspring, those offspring's spouses, and their four children (one from one family and three from the other), as depicted in Supplementary Figure 1,24 that is, 100 families each of size 10. Genotypes were first assigned to founders in the simulated data set based on random generation of each of two alleles from a binomial distribution, and then genotypes were iteratively assigned to individuals in subsequent generations by randomly choosing an allele from each parent's pair. Outcomes were generated from a multivariate normal distribution with mean zero and variance equal to the sum of the heritability times twice the kinship matrix plus one minus the heritability times an identity matrix. Heritability was assumed to be 0.5.

In cross-sectional simulations, we included one observation per person, whereas in longitudinal simulations, we included four observations per person. In the latter scenario, the non-heritable contribution to the variance was split into variability due to a person-specific random intercept and that due to measurement error. Exposure was allowed to change within person, varying randomly across observations. All simulations were conducted in R version 3.0.0,25 and were repeated one million times for each setup, allowing assessment of the P-value behavior to ~1E−5.

Further simulations were carried out to evaluate larger nuclear families, smaller numbers of individuals, exposure clustered within families, exchangeable data generation, a null hypothesis of no SNP × exposure effects in the presence of SNP and exposure main effects, and model misspecification. Specifically, model misspecification was introduced via heterogeneity of outcome variance: variance among exposed individuals was twice as high as variance among unexposed individuals.

LMMs and GEE methods were evaluated. With cross-sectional data, LMMs were fitted using the lmekin function from the kinship package, including a random polygenic effect; with longitudinal data, LMMs were fitted using the pedigreemm function from the pedigreemm package, including both a random polygenic effect and a person-specific normal random effect. With both cross-sectional and longitudinal data, GEE models were fitted using a working independence correlation matrix, clustered on family. In addition to traditional Huber–White (HW) sandwich variance estimates, which were implemented using the boss package, we also computed Mancl and DeRouen's (MD's) alternate estimator and WL's alternate estimator. We do not include Pan's estimator, as it is quite similar to WL's estimator. Because of the additional matrix multiplication and inversion that is necessary for each individual cluster, the MD estimator requires ~15 times more computational time than the HW estimator. Further, we estimated degrees of freedom in two different ways: (1) using Pan and Wall's implementation of Satterthwaite's methods (t), included in the boss package, and (2) using the approximate number of independent observations with a minor allele and positive exposure status (t2). We then calculated alternate P-values using t-reference distributions with these estimates of degrees of freedom in place of the usual normal distribution. R code to compute the alternate variance estimators for GEE methods and the corresponding degrees of freedom for a t-reference distribution can be downloaded from https://goo.gl/F3AMus.

Application description

In the context of the pharmacogenetics working group within the Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE),26 there is strong interest in gene–drug interactions. Several cohorts in the CHARGE consortium, including the FHS,27, 28, 29 have data from multigenerational families. The Original FHS cohort was recruited in 1948 and includes 5209 participants from Framingham, Massachusetts, USA. Original cohort members have attended exams every other year to investigate cardiovascular disease and related risk factors. The Offspring cohort was initiated in 1971 and includes 5124 children of the Original cohort and the children's spouses. Offspring cohort participants have attended exam visits roughly every 4 years. Last, the Third-Generation cohort, recruited in 2002, is comprised of 4095 children of the Offspring cohort and have completed two exams 6 years apart.

To illustrate the methods discussed in this manuscript, we focus on evaluation of drug–gene interactions on fasting glucose levels, and the drug of interest is statins. Statins are well known for their capacity to decrease concentrations of low-density lipoproteins and to reduce the incidence of coronary heart disease,30 but they have also been associated with an increased risk of diabetes. In meta-analyses, patients who use intensive-dose statins have an increased risk of developing diabetes compared with those using moderate-dose statins (odds ratio 1.09).31 The aim of our drug–gene interaction analysis was to identify genetic variants that are associated with interindividual variation in glucose concentration changes in response to statin treatment. Glucose levels serve as a surrogate for diabetes status. If drug-induced changes in glucose levels and diabetes risk have a genetic basis, we may one day be able to assess risk of these side effects before initiating drug use.

Analyses used fasting glucose as the trait of interest, with exposure to statins assessed by medication inventory. Participants were excluded if they were treated with non-statin cholesterol-lowering medications (without concurrent statin use). An additive genetic model, using imputed SNP dosages, was used. Those with diabetes at baseline were excluded. Repeat fasting glucose levels that were obtained while participants were taking anti-diabetic medications were also excluded. Covariates included age, gender, body mass index at baseline, subcohort within FHS, and principal components for ancestry. SNPs with MAF ≤1% were excluded from the analysis. Although the analyses that will contribute to larger CHARGE meta-analyses include longitudinal data from all available visits, we also include baseline cross-sectional analyses in this manuscript to illustrate relative performance of methods.

Results

Simulation results

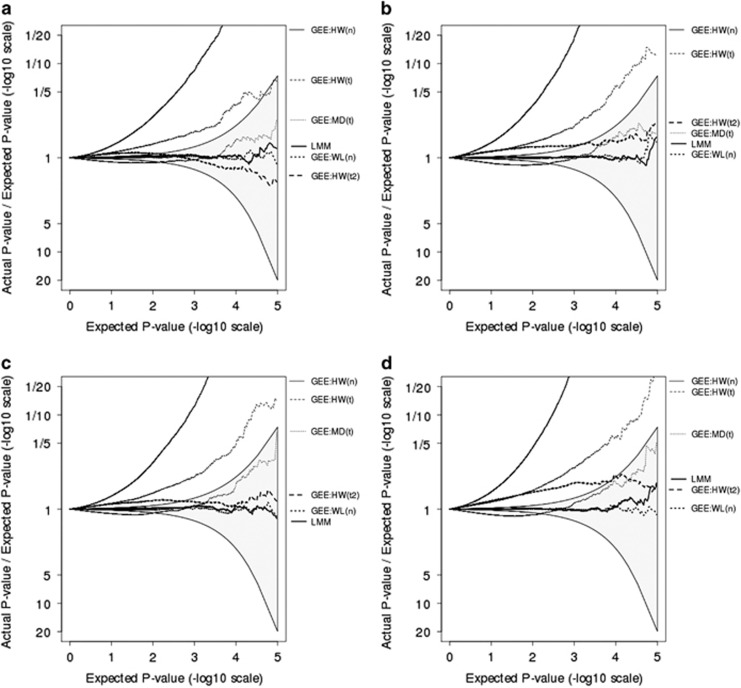
Figure 1 displays results from simulations using data with different family structures and numbers of observations per person. Specifically, the top row (1(a) and 1(b)) uses data from 200 nuclear families, each of size five, whereas the bottom row (1(c) and 1(d)) uses data from 100 three-generational families, each of size 10. The left column (1(a) and 1(c)) uses a single cross-sectional measurement, MAF=0.10 and P(exposure)=10%, whereas the right column (1(b) and 1(d)) uses four longitudinal measurements, MAF=0.05 and P(exposure)=5%. The relative performance of LMMs and GEE methods is consistent across these scenarios. At the low combinations of MAF and exposure frequency that are the focus of our simulations, with a correctly specified model, LMMs perform well, whereas GEE methods with traditional HW variance estimates and a normal reference distribution have inflated type I error rates. The inflation in type I error rate can be attenuated by using methods designed for small numbers of clusters, such as alternate SE estimates and use of a t-reference distribution. Specifically, both the traditional HW variance estimator and the alternate MD variance estimator, both using a t-reference distribution with Satterthwaite estimates of degrees of freedom, decrease type I error rate substantially. The alternate WL estimator, even without a t-reference distribution, decreases type I error rate further, bringing it down to desired levels. The HW estimator with a t-reference distribution using the more approximate degrees of freedom (t2) also decreases type I error rate to desired levels.

Figure 1.

Figure 1

Open in a new tab

Plots showing the ratio, on a −log10 scale, of observed P-values relative to expected P-values. Each plot is derived from one million simulations. Simulated data in the top row are from 200 nuclear families, each of size 5, whereas data in the bottom row are from 100 three-generational families, each of size 10. (a and c) Assumes a single cross-sectional measurement with MAF=0.10 and P(exposure)=10%, whereas (b and d) assumes four longitudinal measurements with MAF=0.05 and P(exposure)=5%. GEE models use either HW, MD, or WL SE estimates, with reference distribution being normal (n), t with Satterthwaite estimates of degrees of freedom (t), or approximate estimates of degrees of freedom (t2).

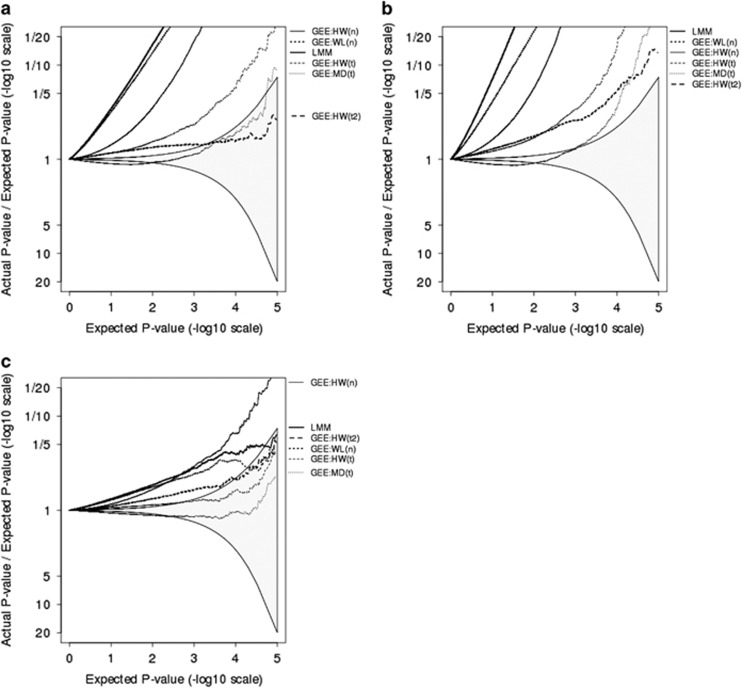
As MAF and exposure prevalence increase, all methods converge to appropriate levels of type I error, with the exception of GEE methods using a normal reference distribution, which would require bigger sample sizes for MAF on the order of 0.10 (Figure 2). At MAF of 0.40 and exposure of 40%, the HW estimator with the t-reference distribution using approximate degrees of freedom (t2) no longer performs much better than the HW estimator with a normal reference distribution, illustrating that this rougher estimate of degrees of freedom has less desirable asymptotic properties than the Satterthwaite estimate of degrees of freedom.

Figure 2.

Figure 2

Open in a new tab

Plots showing the ratio, on a −log10 scale, of observed P-values relative to expected P-values. Each plot is derived from one million simulations. Simulated data are single cross-sectional measurements from 100 three-generational families, each of size 10. (a) Assumes MAF=0.10 and P(exposure)=40%, whereas (b) assumes MAF=0.40 and P(exposure)=40%. GEE models use either HW, MD, or WL SE estimates, with reference distribution being normal (n), t with Satterthwaite estimates of degrees of freedom (t), or approximate estimates of degrees of freedom (t2).

The initial results in Figures 1 and 2 reflect performance of these methods when the model is correctly specified. Both LMM and the WL variance estimator rely, at least in part, on correct model specification. When heteroscedasticity is introduced into simulations, as in Figure 3, both of these methods have inflated type I error rates. Other methods have poorer performance than they did when the model was correctly specified, but their relative performance is unchanged.

Figure 3.

Figure 3

Open in a new tab

Plots showing the ratio, on a −log10 scale, of observed P-values relative to expected P-values. Each plot is derived from one million simulations. Simulated data are from 100 three-generational families, each of size 10. Models are misspecified because outcome variance is twice as high among exposed participants as it is among unexposed participants. (a) Assumes a single cross-sectional measurement with MAF=0.10 and P(exposure)=10% (b) assumes four longitudinal measurements with MAF=0.05 and P(exposure)=5% and (c) assumes a single cross-sectional measurement with MAF=0.10 and P(exposure)=40%. GEE models use either HW, MD, or WL SE estimates, with reference distribution being normal (n), t with Satterthwaite estimates of degrees of freedom (t), or approximate estimates of degrees of freedom (t2).

Quantile–quantile (QQ) plots of −log10 P-values corresponding to Figures 1–3 can be found in Supplementary Figures 2–4.

None of the other sensitivity analyses – allowing exposure to be clustered in families, increasing the size of the nuclear families, generating exchangeable data instead of using a random effect based on kinship, decreasing the total sample size, and simulating under a null hypothesis of no SNP × exposure effects in the presence of SNP and exposure main effects – changed the relative performance of the methods.

Application results

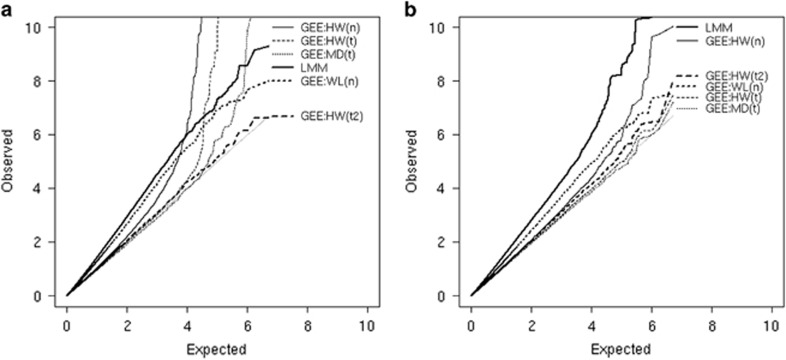
Figure 4 shows results in FHS data from mixed models and the various GEE methods examined in simulations. Based on the anticonservative P-values observed using mixed models and GEE with WL's SE estimates, there is reason for concern about model misspecification, probably due to heterogeneity in outcome variance by drug exposure status. Among the remaining GEE methods, results are consistent with our expectations – there is inflation in QQ plots using HW SE estimates with a normal reference distribution, but this inflation is attenuated with use of a t-reference distribution and/or MD SE estimates. With cross-sectional data, there is not sufficient information to accurately estimate degrees of freedom using Satterthwaite's approximation, so substantial inflation remains unless a more approximate estimate of degrees of freedom is used for the t-distribution. However, with longitudinal data, Sattterthwaite's approximation to degrees of freedom works well.

Figure 4.

Figure 4

Open in a new tab

QQ plots of −log10(P-values) obtained from analysis of SNP–statin interactions on fasting glucose levels in FHS. (a) Uses only data from the first visit for each person, whereas (b) uses data from all visits with available measures of glucose and drug use. GEE models use either HW, MD, or WL SE estimates, with reference distribution being normal (n), t with Satterthwaite estimates of degrees of freedom (t), or approximate estimates of degrees of freedom (t2).

With only data from FHS, in the longitudinal analyses using GEE with modified SE estimates and/or a t-reference distribution, no single SNP has a P-value for interaction that is less than a genome-wide significance level of 5E−8. However, substantial gains in power will be achieved by combining FHS data with data from other studies in the CHARGE consortium; more definitive assessments of SNP–statin interactions on glucose levels will be made in that context.

Discussion

In this article, we have evaluated the performance of methods for genome-wide evaluation of gene–environment interactions in data from related individuals. LMMs perform well in simulations, when model specification is correct. In applications, we will never know for sure that the model is correct, thus we recommend GEE methods that require special handling of small samples, but do not rely on correct model specification. When exposure prevalence and/or MAF is low, standard GEE tests using a normal reference distribution show evidence of inflated type I error rate. This inflation can be attenuated using methods designed for small numbers of clusters, such as more complicated robust SE estimates and/or a t-reference distribution. Alternate SE estimates improve performance, with WL's method performing better than MD's under correct model specification. However, the improvement comes at the cost of computing time for MD's method. Further, WL's estimates rely more heavily on model assumptions, and do not perform well when the model is misspecified; for instance, when there is heterogeneity in outcome variance across exposure groups. Using a t-reference distribution in place of the typical normal reference distribution also improves performance. Using rough estimates of degrees of freedom (t2) can decrease inflation more than using Satterthwaite estimates of degrees of freedom (t); however, when this is true, MD's SE estimate performs better than either modification using typical sandwich SE estimates.

When designing genome-wide analyses of gene–environment interactions in family data, we recommend careful consideration of the potential for model misspecification and of the potential for small-sample problems. Given the importance of allowing for model misspecification when evaluating gene–environment interactions, robust methods are generally recommended; however, in scenarios where model misspecification is unlikely, mixed models using model-based SE estimates could be implemented. When variants with low MAF and/or infrequent exposures are of interest, a modification to standard GEE methods will be useful. If computational burden is a substantial factor, then typical HW SE estimates with a t-reference distribution are recommended; however, in general, MD SE estimates with a t-reference distribution have superior performance.

Our evaluations have focused on the problem of getting type I error correct. However, it is worth considering the relative power of methods with appropriate type I error rates. As might be expected, the methods that exploit modeling assumptions, when these assumptions are valid, have the highest power. For example, when models are correctly specified, LMMs have the highest power and GEE models using WL's method are next best. Both of these methods break down when there is model misspecification, in which case the relative power is not terribly different across the remaining GEE methods. Typical robust variance estimates with a t-reference distribution have slightly higher power than MD's method, but they also break down more easily with small effective sample sizes, making the power gain irrelevant. The bottom line is that there is a tradeoff between robustness to model misspecification and power, with the methods that make stronger assumptions having more power when those assumptions are valid.

The focus in this article has been on analysis of quantitative traits; further research is needed to guide analytic decisions when binary disease traits are of interest. In the cross-sectional case, consideration of two-step, empirical Bayes, and various hybrid approaches32 would be warranted, provided that they could accommodate the correlation within families. Both GEE methods, and LMMs, have standard extensions to binary outcomes using logistic link functions. However, the interpretation of results is complicated by the non-collapsibility of the logistic link function, and non-convergence can be a substantial hurdle in fitting generalized LMMs. Owing to differing interpretations, direct comparisons between GEE methods and LMMs would no longer be justified. However, both the modifications to variance estimates and the small-sample correction that uses a t-reference distribution were derived in the general case that can incorporate the logistic link function, thus the GEE methods discussed here can also be applied to binary disease traits.

Population substructure can lead to spurious findings in genetic analyses. The methods that we discuss in this manuscript use adjustment for principal components to account for genetic substructure. It is known that mixed models provide more robust protection against cryptic relatedness and population structure than GEE models with principal component adjustment.33, 34 Yet in the context of gene–environment interactions, as we have shown, the model-based SEs from mixed models are not always adequate. Given family-based data collection, there are additional alternatives that use the information within families to account for genetic substructure. Moreno-Macias et al.35 discuss relevant methods for exploring gene–environment interactions, both cross-sectionally and longitudinally, by incorporating information from a case-parent design.35 These methods include extensions of the family-based association test and adjusted linear mixed models. Although these within-family methods protect against population substructure, the authors do not compare them to ordinary mixed models that adjust for principal components, which could alleviate some of the bias from using mixed models that do not adjust for principal components. Further, they show substantial loss of power using the within-family methods in scenarios where other methods give unbiased estimates. Therefore, we recommend consideration of within-family methods in family-based studies where population substructure and/or admixture have been shown to be problematic even after adjustment for principal components, with the caveat that the model-based SE estimates may not be adequate. However, for many family-based cohort studies, principal components are adequate to adjust for population substructure,36 thus the increased power gained from using methods that do not make within-family comparisons justifies their use.

In observational cohort studies such as the FHS, confounding by indication and time-dependent confounding (in the longitudinal case) could present additional challenges in the evaluation of gene–environment interactions. Causal methods that incorporate propensity scores or marginal structural models might alleviate these potential biases. However, more work is needed to guide their implementation in the context of GWAS.

In summary, the choice of methods for analyzing gene–environment interactions should take into account multiple factors, including population substructure, model specification, and amount of data that will inform interaction estimates. Particularly when data are sparse, we recommend modified GEE methods that improve small-sample performance and provide robustness to model misspecification.

Acknowledgments

This work was supported by US NIH R01 HL103612, R01 HL105756, R01 DK078616, and U01 DK085526. From the FHS of the National Heart Lung and Blood Institute of the National Institutes of Health and Boston University School of Medicine: This work was supported by the National Heart, Lung, and Blood Institute's FHS (Contract No. N01-HC-25195) and its contract with Affymetrix Inc. for genotyping services (Contract No. N02-HL-6-4278). Analyses reflect intellectual input and resource development from FHS investigators participating in the SNP Health Association Resource (SHARe) project.

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Psaty serves on the Steering Committee for the Yale Open Data Access Project funded by Johnson & Johnson and on the DSMB of a clinical trial of a device funded by the manufacturer (Zoll LifeCor). The other authors have no conflict of interest.

Supplementary Material

Supplementary Information
Click here for additional data file. (260.2KB, pdf)

References

  1. Thomas D: Methods for investigating gene–environment interactions in candidate pathway and genome-wide association studies. Annu Rev Public Health 2010; 31: 21–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Roses A: Pharmacogenetics and the practice of medicine. Nature 2000; 405: 857–865. [DOI] [PubMed] [Google Scholar]
  3. Meyer U: Pharmacogenetics and adverse drug reactions. Lancet 2000; 356: 1667–1671. [DOI] [PubMed] [Google Scholar]
  4. Khoury M, Wagener D: Epidemiological evaluation of the use of genetics to improve the predictive value of disease risk factors. Am J Hum Genet 1995; 56: 835–844. [PMC free article] [PubMed] [Google Scholar]
  5. Song M, Lee KM, Kang D: Breast cancer prevention based on gene–environment interaction. Mol Carcinogen 2011; 50: 280–290. [DOI] [PubMed] [Google Scholar]
  6. Voorman A, Lumley T, McKnight B, Rice K: Behavior of QQ-plots and genomic control in studies of gene–environment interaction. PLoS One 2011; 6: e19416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Tchetgen ET, Kraft P: On the robustness of tests of genetic associations incorporating gene–environment interaction when the environmental exposure is misspecified. Epidemiology 2011; 22: 257–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Sitlani C, Rice K, Lumley T et al: Generalized estimating equations for genome-wide association studies using longitudinal phenotype data. Stat Med 2015; 34: 118–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Burton P, Clayton D, Cardon L et al: Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 2007; 447: 661–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. de Bakker P, Ferreira M, Jia X, Neale B, Raychaudhuri S, Voight B: Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum Mol Genet 2008; 17: R122–R128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gauderman W, Macgregor S, Briollais L et al: Longitudinal data analysis in pedigree studies. Genet Epidemiol 2003; 25: S18–S28. [DOI] [PubMed] [Google Scholar]
  12. Eu-ahsunthornwattana J, Miller E, Fakiola M et al: Comparison of methods to account for relatedness in genome-wide association studies with family-based data. PLoS Genet 2014; 10: e1004445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Suktitipat B, Mathias R, Vaidya D et al: The robustness of generalized estimating equations for association tests in extended family data. Hum Hered 2012; 74: 17–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Laird N, Ware J: Random-effect models for longitudinal data. Biometrics 1982; 38: 963–974. [PubMed] [Google Scholar]
  15. Liang KY, Zeger S: Longitudinal data analysis using generalized linear models. Biometrika 1986; 73: 13–22. [Google Scholar]
  16. Zeger S, Liang KY: Longitudinal data analysis for discrete and continuous outcomes. Biometrics 1986; 42: 121–130. [PubMed] [Google Scholar]
  17. Hardin J, Hilbe J: Generalized Estimating Equations. 2nd edn. CRC Press: Boca Raton, FL USA, 2013. [Google Scholar]
  18. Lipsitz S, Fitzmaurice G, Orav E, Laird N: Performance of generalized estimating equations in practical situations. Biometrics 1994; 50: 270–278. [PubMed] [Google Scholar]
  19. Wang M, Long Q: Modified robust variance estimator for generalized estimating equations with improved small-sample performance. Stat Med 2011; 30: 1278–1291. [DOI] [PubMed] [Google Scholar]
  20. Mancl L, DeRouen T: A covariance estimator for GEE with improved small-sample properties. Biometrics 2001; 57: 126–134. [DOI] [PubMed] [Google Scholar]
  21. Pan W: On the robust variance estimator in generalised estimating equations. Biometrika 2001; 88: 901–906. [Google Scholar]
  22. Satterthwaite F: An approximate distribution of estimates of variance components. Biometrics Bull 1946; 2: 110–114. [PubMed] [Google Scholar]
  23. Pan W, Wall M: Small-sample adjustments in using the sandwich variance estimator in generalized estimating equations. Stat Med 2002; 21: 1429–1441. [DOI] [PubMed] [Google Scholar]
  24. Li B, Chen W, Zhan X et al: A likelihood-based framework for variant calling and de novo mutation detection in families. PLoS Genet 2012; 8: e1002944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. R Core TeamR: A Language and Environment for Statistical Computing. R Core Team: Vienna, Austria, 2014. [Google Scholar]
  26. Psaty B, O'Donnell C, Gudnason V et al: Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) Consortium: design of prospective meta-analyses of genome-wide association studies from five cohorts. Circ Cardiovasc Genet 2009; 2: 73–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dawber T, Meadors G, Moore F Jr: Epidemiological approaches to heart disease: the Framingham Study. Am J Public Health Nations Health 1951; 41: 279–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kannel W, Feinleib M, McNamara P, Garrison R, Castelli W: An investigation of coronary heart disease in families. The Framingham offspring study. Am J Epidemiol 1979; 110: 281–290. [DOI] [PubMed] [Google Scholar]
  29. Splansky G, Corey D, Yang Q et al: The Third Generation Cohort of the National Heart, Lung, and Blood Institute's Framingham Heart Study: design, recruitment, and initial examination. Am J Epidemiol 2007; 165: 1328–1335. [DOI] [PubMed] [Google Scholar]
  30. Baigent C, Blackwell L, Emberson J et al: Efficacy and safety of more intensive lowering of LDL cholesterol: a meta-analysis of data from 170,000 participants in 26 randomised trials. Lancet 2010; 376: 1670–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Preiss D, Seshasai S, Welsh P et al: Risk of incident diabetes with intensive-dose compared with moderate-dose statin therapy: a meta-analysis. JAMA 2011; 305: 2556–2564. [DOI] [PubMed] [Google Scholar]
  32. Mukherjee B, Ahn J, Gruber S, Chatterjee N: Testing gene–environment interaction in large-scale case–control association studies: possible choices and comparisons. Am J Epidemiol 2012; 175: 177–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Astle W, Balding D: Population structure and cryptic relatedness in genetic association studies. Stat Sci 2009; 24: 451–471. [Google Scholar]
  34. Price A, Zaitlen N, Reich D, Patterson N: New approaches to population stratification in genome-wide association studies. Nat Rev Genet 2010; 11: 459–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Moreno-Macias H, Romieu I, London S, Laird N: Gene–environment interaction tests for family studies with quantitative phenotypes: a review and extension to longitudinal measures. Hum Genomics 2010; 4: 302–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhu X, Li S, Cooper R, Elston R: A unified association analysis approach for family and unrelated samples correcting for stratification. Am J Hum Genet 2008; 82: 352–365. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (260.2KB, pdf)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES