Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2016 Oct 18;111(8):1631–1640. doi: 10.1016/j.bpj.2016.08.041

Capturing Invisible Motions in the Transition from Ground to Rare Excited States of T4 Lysozyme L99A

Jamie M Schiffer 1, Victoria A Feher 1,4,∗, Robert D Malmstrom 1,2, Roxana Sida 1,3, Rommie E Amaro 1,2,4,∗∗
PMCID: PMC5071553  PMID: 27760351

Abstract

Proteins commonly sample a number of conformational states to carry out their biological function, often requiring transitions from the ground state to higher-energy states. Characterizing the mechanisms that guide these transitions at the atomic level promises to impact our understanding of functional protein dynamics and energy landscapes. The leucine-99-to-alanine (L99A) mutant of T4 lysozyme is a model system that has an experimentally well characterized excited sparsely populated state as well as a ground state. Despite the exhaustive study of L99A protein dynamics, the conformational changes that permit transitioning to the experimentally detected excited state (∼3%, ΔG ∼2 kcal/mol) remain unclear. Here, we describe the transitions from the ground state to this sparsely populated excited state of L99A as observed through a single molecular dynamics (MD) trajectory on the Anton supercomputer. Aside from detailing the ground-to-excited-state transition, the trajectory samples multiple metastates and an intermediate state en route to the excited state. Dynamic motions between these states enable cavity surface openings large enough to admit benzene on timescales congruent with known rates for benzene binding. Thus, these fluctuations between rare protein states provide an atomic description of the concerted motions that illuminate potential path(s) for ligand binding. These results reveal, to our knowledge, a new level of complexity in the dynamics of buried cavities and their role in creating mobile defects that affect protein dynamics and ligand binding.

Introduction

Proteins function through concerted atomic motions that guide transitions from highly populated ground-state ensembles to higher-energy states (1, 2, 3, 4). Experimentally verified higher-energy states, or “excited states,” typically constitute ∼1% of the protein population, with exchange rates on the microsecond to millisecond timescale. To date, our understanding of these transient protein states has largely been achieved through interpretation of NMR relaxation dispersion spectroscopy (3, 4). Relaxation dispersion measurements provide a high level of detail into the populations, exchange correlation times, and chemical shift differences between two states (3, 4, 5). Until recently, visualizing the specific structural implications of these dispersion measurements has been limited to comparisons with static crystal structures or models, because the slow timescale of these motions was beyond the reach of atomistic molecular simulation (6, 7).

Long-timescale molecular dynamics (MD) simulations now make it possible to witness atomic motions on the nanosecond to microsecond timescale, with a suitable level of agreement with experiment (8, 9, 10, 11). Additionally, with recent advances in specialized computational architectures like Anton, simulation timescales on the order of microseconds to milliseconds in a single trajectory are within reach (7, 12, 13, 14).

Here, we report the transient atomic-level motions that govern the long-timescale dynamics of the L99A mutant of T4 lysozyme. L99A is a model system for studying ligand binding to buried protein cavities and protein excited states, and the conformational changes that govern these phenomena have been enigmatic despite nearly 25 years of experimental study (5, 6, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30). Experimental studies of the L99A mutant of T4 lysozyme have focused on defining the structures of and transition times between the ground state, the excited state, and ligand-bound states. Initial crystal structures of the L99A mutant indicate that the ∼40 Å3 cavity in the C-terminal domain of wild-type protein expands to an ∼150 Å3 cavity (26), a volume capable of accommodating substituted benzenes and noble gases (20, 24, 27, 28, 29, 30). O2 is simulated to bind and escape the buried cavity through openings between the D, E, G, H, and J helices (31), whereas binding of substituted benzenes is accompanied by discrete rearrangements in the F and G helices (30). Substantial rearrangements also occur in these helices in an excited state that comprises ∼3% of the protein ensemble at room temperature (5, 25). NMR relaxation dispersion measurements and chemical-shift-based Rosetta-guided modeling were used previously to design a triple mutant of T4 lysozyme meant to mimic the excited state (5). This chemical-shift-based model places the F114 phenyl group into the center of the buried hydrophobic cavity in the excited state, blocking benzene binding (5). To date, the details of the conformational changes that guide transitions between ground, ligand-accessible, and excited states, at standard temperature and pressure conditions, remain unknown for the L99A mutant.

We performed conventional MD simulations on Anton starting from the ground-state apo crystal structure of L99A with the intention of witnessing the conformational transitions needed for ligand exchange (21). During a 30 μs MD simulation, L99A transitions from the ground state to a rare excited state of L99A. We compare the structures witnessed in the trajectory to chemical shifts and torsion angles determined experimentally. The simulation reveals multiple metastates and a previously unseen intermediate state that exists before the excited state in the trajectory. These transient conformational motions reveal, to our knowledge, a new level of intricacy in the concerted motions of protein interiors and suggest that short-lived metastates in protein ensembles may be critical to dynamic protein function.

Materials and Methods

MD system preparation

We used Schrödinger PrepWizard and MD Desmond setup modules (32) to prepare T4 lysozyme structures for MD simulation. The T4 lysozyme L99A mutant crystal structure (PDB: 1L90) was prepared for the ground-state Anton simulations. The excited-state mimic was prepared using the coordinates from the solution structure of the L99A triple mutant (PDB 2LC9) and Schrödinger’s Maestro (32) to mutate the residues A113 to glycine and P119 to arginine, the residues found in the T4 lysozyme L99A single mutant. We chose to simulate the triple mutant (PDB: 2LC9), ES-3mut, instead of the excited-state model (PDB: 2LCB), ES-Rosetta. However, given the low root mean-square (RMS) differences (∼0.6 Å) between the models, the selection of either would have been appropriate. These systems were protonated at pH 5.5, with the pKa-titratable residues determined using the Maestro integrated PROPKA (33). The pKa of residue E11 is 4.8 for the ground-state crystal structure and >5.5 for the excited-state mimic. For consistency, we deprotonated E11 for both systems. We solvated each system in a TIP3P (32) cubic water box (∼75.7 Å/side), with nine Cl− ions to balance the charge of L99A and 150 mM NaCl. The total numbers of atoms in each system for the L99A crystal structure and each of the nine L99A excited-state mutant (PDB: 2LC9) structures were 43,507, 43,507, 43,540, 43,546, 43,498, 43,483, 43,504, 43,510, 43,504, and 43,525, respectively. Results from the first structure of the ES-3mut (PDB: 2LC9) are shown in the main body of the text, whereas measurements from all other simulations initiated from other 2LC9 structures are shown in Fig. S4 in the Supporting Material.

MD system parameterization

System coordinates from the preparation (above) were converted into an xleap-readable (34) format using in-house Python scripts. Each system was parameterized in xleap using the AMBER99SB (35) force field, and periodic boundary conditions were implemented.

Anton MD simulations

MD simulations on Anton were performed on the same parameterized, minimized, and equilibrated L99A crystal structure system described above. The Anton simulation was run in the NTP ensemble using Anton’s multigrator (34) at 300 K, 1 bar, and with a 2-fs time step, and particle-mesh Ewald (PME) electrostatic approximations.

GPU-enabled MD simulations

Simulations not performed on Anton were performed with NVIDIA GK110 (GeForce GTX Titan, NVIDIA, Santa Clara, CA) graphics processing units (GPUs) using the CUDA version of PMEMD in AMBER12 (35). The L99A crystal structure system (derived from PDB: 1L90) was minimized and equilibrated using the GPU version of AMBER12 (36, 37). We minimized in three stages, including a stage of heating: 1) 40 ps of hydrogen-only minimization with a restraint weight of 20 kcal/mol on the protein and solvent; 2) 4 ps of water minimization with a restraint weight of 20 kcal/mol on the protein and salt atoms; 3) 20 ps of water heating with a restraint weight of 20 kcal/mol on the protein and salt atoms; and 4) 40 ps of full minimization. We equilibrated the system using harmonic equilibration at 300 K over four sequential 500-ps runs, decreasing the restraint potential on the backbone at each step, starting at 4.0 kcal/mol and ending at 1.0 kcal/mol. GPU-enabled AMBER12 production runs were carried out as an NTP ensemble at 300 K and 1 bar with a 2-fs time step and PME (38) electrostatic approximation and nonbonding cutoff of 10.0 Å. MD input files are provided as part of the data-sharing files.

Excited-state mimic MD simulations

The ES-3mut system was also minimized and equilibrated in two stages using the GPU version of AMBER12 (36, 37): 1) 6 ps of hydrogen-only minimization with a restraint weight of 100 kcal/mol were performed, with the 500 steps of steepest-descent algorithm minimization and 2500 steps of conjugate-gradient algorithm minimization; and 2) 12 ps of solvent-only minimization with a restraint weight of 100 kcal/mol, with 500 steps of steepest-descent algorithm minimization and 5500 steps of conjugate-gradient algorithm minimization (39). This protocol was chosen because we did not want to minimize into an arbitrary and nonnative energy minimum. Instead, we performed extensive equilibration so that the remutated L99A protein could more readily search the energetic landscape of L99A. We heated the system to 300 K for 100 ps with a restraint on the protein backbone of 4.0 kcal/mol and equilibrated the system using harmonic equilibration at 300 K over three sequential 100-ps runs, decreasing the restraint potential on the backbone of L99A on each step, starting at 3.0 kcal/mol and ending at 1.0 kcal/mol. GPU-enabled AMBER12 production runs were carried out as an NTP ensemble at 300 K and 1 bar, with Langevin dynamics (40) with a collision frequency of 1.0 ps−1, a pressure relaxation time of 2.0 ps, with SHAKE bond constraints on hydrogen bonds (41), and with a 2-fs time step and PME (38) electrostatic approximation and nonbonding interaction cutoff of 9.0 Å. MD input files are provided as part of the data sharing.

Simulation analysis

MD trajectories were processed using CPPTRAJ (42) and VMD (43). All frames were aligned using the backbone atoms of residues 75–155, which encompasses the C-terminal domain of T4 lysozyme L99A. CPPTRAJ was used to perform dihedral-, distance-, angle-, and hydrogen-bond-based measurements. VMD was used to perform RMS-deviation (RMSD)-based analysis of the F/G helix (residues 108–124), the I helix (residues 135–142), the C/D helix (residues 75–90), and the buried hydrophobic residues (residues 84, 99, 102, 114, 133, 138, and 153).

SHIFTX2 and SHIFTX+ calculations

Two NMR chemical-shift prediction methods were utilized for our studies. SHIFTX+ is an algorithm that takes into account only structural coordinates for chemical-shift prediction. The SHIFTX2 algorithm incorporates a number of sequence-based features from a training set as well as structural coordinates (44). Han et al. (44) report that SHIFTX2 has improved correlation coefficients between observed and predicted backbone chemical shifts compared to the SHIFTX+, so SHIFTX2 was used to predict chemical shifts where direct comparisons were made between MD simulation results and reported experimental values (see Fig. 2). Here, 13Cα chemical shift predictions were calculated for each frame, then averaged over frames 1–12,569, representing the ground state, and frames 112,746–125,691, representing ES-Anton, of the Anton trajectory. A pH of 5.5 was input for the SHIFTX2 algorithm.

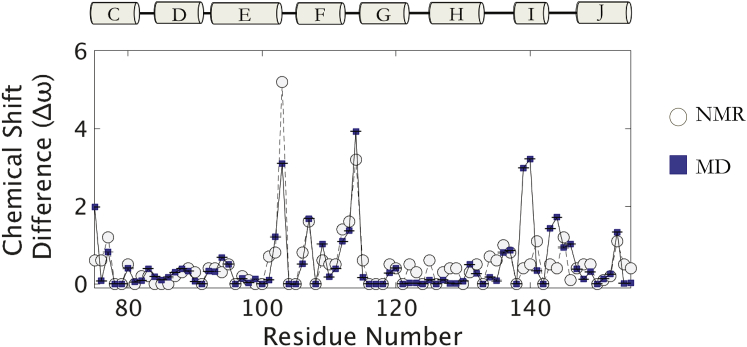
Figure 2.

Figure 2

Open in a new tab

The Anton-simulated excited state agrees with relaxation dispersion data. Absolute values of the 13Cα chemical-shift differences, |Δϖ13Cα|, between the ground and excited states back-calculated with SHIFTX2 from structures from the Anton trajectory (squares) compared to NMR-relaxation-derived |Δϖ13Cα| values (circles) for the C-terminal domain (5). To see this figure in color, go online.

Chemical-shift predictions reported in Fig. 4 d are based on chemical shifts calculated for each frame of the Anton trajectory with the SHIFTX+ algorithm.

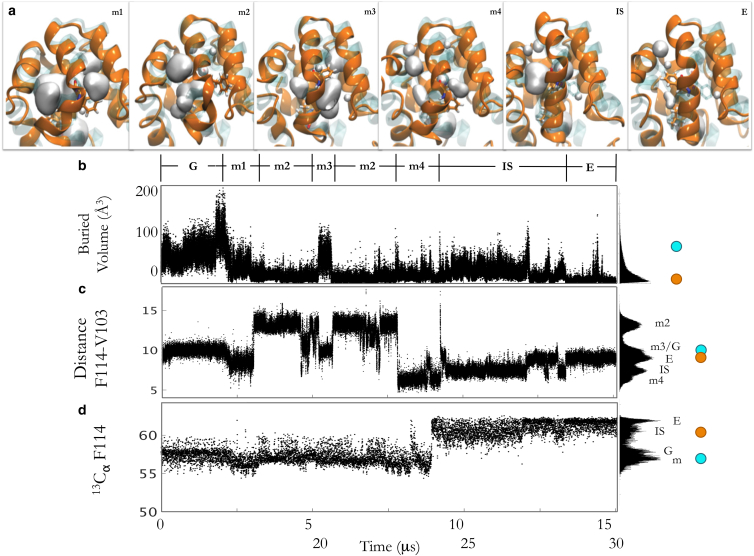
Figure 4.

Figure 4

Open in a new tab

The Anton trajectory samples the transition from ground state to excited state. (a) Representative structures of each of the metastates (m1–m4), the intermediate state (IS), and the excited state (E). The Anton trajectory, the ground state (PDB: 3DMV) as a shadow, and the cavity volumes are depicted. F114 is shown for reference in each representative structure. (b–d) The buried volume, distance between F114 and V103, and back-calculated chemical shifts of the 13Cα for F114 using SHIFTX+ are plotted over time in the Anton trajectory. To the right of each plot is the population histogram for the buried volumes, distances, and back-calculated chemical shifts in the entire trajectory. The circles to the right show the values from the ground state and the excited state from experiment. To see this figure in color, go online.

POVME calculations

A VMD plug-in for POVME 2.0 software (44) was used to calculate pocket volumes and buried surfaces in the L99A C-terminal-domain Anton trajectory. A sphere with 8 Å radius was centered near carbons for residues L84, A99, and M102 (sphere-center coordinates 26.04, 21.48, 25.47). Volume calculations were performed on each cluster centroid, determined by RMSD-based clustering (see below), as well as on every 10th frame of the Anton trajectory. Fig. 4 a depicts cluster centroids from each of the most populated RMSD-based clusters.

RMSD-based clustering

The Anton trajectory structures were clustered using the GROMOS algorithm (45) in GROMACS version 4.5.5 (46) with heavy-atom trace RMSD cutoff of 1.2 Å for T4 lysozyme L99A mutant.

Principal component analysis

The Anton trajectory was stripped of solvent and aligned against the backbone of residues 75–155 in the C-terminal domain. Principal component analysis was performed for all atoms for each frame of the trajectory using CPPTRAJ. Three principal components were specified for calculation.

Results and Discussion

A single Anton trajectory simulates a ground-to-excited-state transition

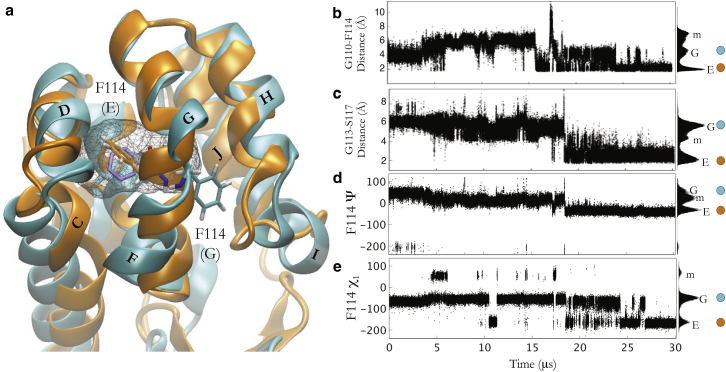
The single Anton trajectory captures a significant conformational change from the ground state to the sparsely populated excited state of the T4 lysozyme L99A mutant. The Anton excited state (ES-Anton) is defined by key structural features that have been experimentally characterized (5, 25). These features are the refolding of the F and G helices into a single helix and changes in the F114 χ1 and ψ torsion angles that position the phenyl ring of F114 into the buried cavity (Figs. 1, S1, and S2). Structural changes from the ground state to the ES-Anton state were followed through hydrogen-bond distances between residues in the F and G helices, changes in dihedral angles of F114 (Fig. 1, b–e), and internal distances between the F114 phenyl group and hydrophobic residues lining the L99A cavity (Fig. 4 c). These internal distances define the same metastates as can be seen with the first principal component of the Anton trajectory (Fig. S6). Folding of the F and G helices into a single helix, as measured by backbone i → i + 4 hydrogen-bond distances (Fig. 1, b and c), starts at 18.6 μs in the Anton trajectory with the G113 to S117 hydrogen-bond formation and completes by 27 μs with the G110-to-F114 hydrogen-bond formation, recapitulating experimental distances (5). Additionally, the F114 ψ and χ1 torsion angles relax to experimentally determined values for the excited state of −60° and −164° at 18.6 μs and 27 μs, respectively (5). These measurements indicate that starting from the ground state, the simulated L99A mutant of T4 lysozyme reaches the sparsely populated excited state within 27 μs of simulation.

Figure 1.

Figure 1

Open in a new tab

The Anton trajectory samples the transition from ground state to excited and cavity-accessible states of T4 lysozyme L99A. (a) Superposition of the C-terminal domain L99A ground-state crystal structure (PDB: 3DMV) and the Anton-simulated average excited-state structure. The gray mesh outlines the buried cavity in the ground state. The positions of F114 in the ground state (G) and the excited state (E) are shown. (b–e) Structural measures for conformational differences over the Anton trajectory. Hydrogen-bond distances between the backbone of helical residues G110 and F114 (b) and G113 and S117 (c) and the F114 ψ (d) and χ1 (e) torsion angle values are shown. The ground (G), meta (m), and excited (E) states are shown in the various populations in the histograms to the right of the plots. The circles indicate the experimentally determined values of the ground and excited states. To see this figure in color, go online.

Verifying the simulated excited state by comparison with experiment

Calculated chemical-shift differences (Δϖ) between the simulated ground-state (1–4 μs) and ES-Anton (27–30 μs) structures agree with experimental Δϖ values measured for the full-length L99A lysozyme protein and for those residues in the F/G helix that have the largest measured Δϖ (Fig. 2).

However, some differences are observed between ES-Anton and what has been previously modeled with the Rosetta mutagenesis approach (5). Specifically, the pitch of the F/G helices and A helix (Fig. S1) and the ϕ, ψ, χ1 torsion angles of residues in the C, D, E, H, I, and J helices (Fig. S3).

For a direct comparison between previous models and our simulated excited state, we performed separate MD simulations initiated on the published excited-state model of L99A, specifically the triple mutant L99A/G113/R119P (PDB: 2LC9) (5), hereafter referred to as ES-3mut.

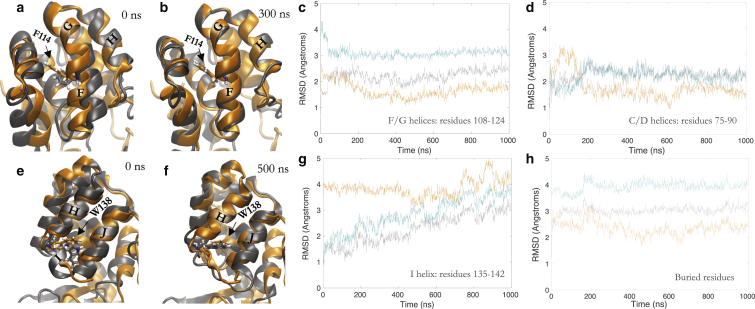
In simulations initiated from ES-3mut, we observe that the majority of the C-terminal domain backbone relaxes to structures more similar to that of ES-Anton than to the starting structure (Figs. 3, a–h, S4, and S5). The pitch of the F/G helices relaxes to the pitch of ES-Anton within a few hundred nanoseconds, as evidenced by backbone RMSD of the F/G helices (Fig. 3, a–c). Additionally, RMSD measurements of residues in the C and D helices (residues 75–90, atoms N, C, Cα, and O) and buried hydrophobic residues (residues 84, 99, 102, 114, 133, 138, and 153, trace atoms) relax to structures more similar to ES-Anton than to ES-3mut (Fig. 3, d and h). Residues in the C, D, F/G, and I helices sample the same ϕ, ψ, χ1 torsion angles as sampled in the ES-Anton model (Figs. 3, S4, and S5), and in one of the triplicate simulations from the ES-3mut model, residues in the I helix also sample ψ torsion angles sampled in the ES-Anton trajectory (Figs. 3, e–g, and S4).

Figure 3.

Figure 3

Open in a new tab

Simulations from a published model of the excited state relax to the excited state simulated with the Anton trajectory. The FG helices (a and b) and the I helix (e and f) of a published excited-state model starting structure (gray; PDB: 2LC9) relax to the excited state from the Anton trajectory (orange) after 300 ns and 500 ns, respectively (b and f, gray). (c, d, g, and h) RMSD time plots of the simulations initiated from coordinates of the excited-state model to the MD Anton excited-state average structure (orange), to the excited-state model starting structure (gray), and to the ground-state crystal structure (teal) are reported as an average over three parallel simulations for the residues of the F/G helices, C/D helices (residues 75–90), I helix (residues 135–142), and buried residues (trace of residues 84, 99, 102, 114, 133, 138, and 153).

Some differences exist in the torsion angles of the residues in the ES-Anton structures and ES-3mut simulations. For example, there are multiple possible explanations for the differences in the ϕ, ψ, χ1 torsion angles of these residues in the ES-Anton model and ES-3mut simulations. The ψ torsion angles sampled in the I helix in both models are outside of the helical regime and occur before the excited-state transition (Fig. S3). It is possible that the structure guidance required in interpretation of relaxation dispersion measurements for the L99A mutant may have confined the conformational ensemble of this excited state. It is also possible that known errors introduced by the force field (47) could have contributed to the local unfolding of the I helix in the ES-Anton and ES-3mut models (5). However, force field bias is also known to increase helical content (48), which could contribute to the increase in timescales we see in the refolding of the F/G helix into a single helix (see below in Discrepancies in Timescales of Excited-State Transitions in Simulation and Experiment). Alternatively, it is also possible that the excited state is composed of multiple states that vary in the conformation of the residues in the C, D, E, H, I, and J helices but are consistent in the position of F114, with a χ1 of ∼160°, and the refolding of the F/G helices into a single helix.

Defining the metastates and intermediate state in the Anton trajectory

To define conformational changes that occur in the Anton trajectory further, we measured the buried pocket volumes (Fig. 4, a and b), the internal distances between the F114 phenyl ring and hydrophobic residues lining the L99A cavity (Fig. 4 c), and back-calculated chemical shifts from every 10th frame of the Anton trajectory using the SHIFTX+ algorithm (Fig. 4 d). Additionally, we performed PCA over the entire Anton trajectory. Taken together, these measurements indicate four metastates and an intermediate state that are sampled in addition to the ground state and the excited state of the L99A mutant of T4 lysozyme (Figs. 1 a and S6; Movie S1. Simulating From the Ground to Excited State of the L99A Cavity Mutant With the Anton Supercomputer, Movie S2. Principal Component 1 of Anton Trajectory, Movie S3. Principal Component 2 of Anton Trajectory, Movie S4. Principal Component 3 of Anton Trajectory). Conformational states defined along both the first and second principal components (PC1/2) align well with the metastates witnessed from the F114-V103 internal distance and buried volume measurements (Fig. S6; Movie S1. Simulating From the Ground to Excited State of the L99A Cavity Mutant With the Anton Supercomputer, Movie S2. Principal Component 1 of Anton Trajectory, Movie S3. Principal Component 2 of Anton Trajectory, Movie S4. Principal Component 3 of Anton Trajectory). The differences between the principal components are motions of the N-terminal domain relative to the C-terminal domain.

As described above for the Anton simulation (Fig. 2), inspection of the back-calculated SHIFTX+ values for F114 13Cα shows that they recapitulate the experimentally derived differences between the ground and excited states over the entire Anton trajectory. Additionally, the back-calculated chemical shifts of the intermediate state and metastates are within error of the chemical shifts for the excited state and ground state, respectively.

The four metastates (m1–m4) witnessed in the single Anton trajectory have chemical shifts similar to those of the ground state, maintain the F helix as a 310 helix separate from the G helix, and position F114 just outside of the buried cavity despite fluctuation in cavity volume and changes in F114-V103 internal distances throughout these metastates (Fig. 1). The internal distance between F114 and V103 was chosen as a metric here because V103 neighbors the buried L99A cavity, and has the largest chemical shift difference (Δϖ) between the ground and the excited state in both 15N and 13Cα spectra. In the following paragraphs, we describe the conformational differences that define each of these states as unique from the ground and excited states and show that these differences are manifested in the back-calculated chemical shifts, calculated using the SHIFTX+ algorithm (49). Interestingly, the back-calculated 13Cα chemical shifts of F114 in these metastates are within error of the back-calculated 13Cα chemical shifts in the ground state despite the wide range of conformations sampled in the four metastates.

The metastates are unique from the ground state, as well as one another, primarily in the angle between the D helix and the G helix, as well as the position of the F114 side chain (Fig. 4). In the m1 state, the angle between the D and G helices is more acute than in the ground state, which manifests in a decreased V103-F114 distances and decreased F114 ψ angle. The m2 state is characterized by an increased distance between F114 and V103, due to D helix cracking that flips the phenyl ring of F114 outside of the cavity between the G and H helices. The m3 state has the F114 χ1 angle similar to that of the excited state, resulting in the phenyl ring of F114 flipped into the buried cavity, but the D and G helices are still two separate helices with a wide angle between the helices. Finally, the m4 state is similar to the m3 state in that F114 is still flipped into the buried cavity, but with a χ1 angle similar to that of the ground state, shortening the distance between F114 and V103.

An intermediate state (IS) (Fig. 4) with distinct conformational features from the excited state (ES-Anton), occurs in the Anton trajectory between 18 and 27 μs. The IS has the same F114 ψ angle as the excited state but differs by the F114 χ1 angle, as it flips between the ground and excited state values (Fig. 1 e). It also contains a larger buried cavity volume (Fig. 4 b). The fluctuation in the F114 χ1 angle was seen in high-temperature simulations of the ES-3mut (15), suggesting that these two states are similar in energy (see Verifying the Simulated Excited State by Comparison with Experiment). Despite the F114 χ1 and cavity-volume differences between the IS and the ES-Anton, the back-calculated chemical shifts from these structures are not distinct and are equal to chemical shifts determined experimentally (Fig. 4 d, orange circle) (5). Thus, the intermediate state, although distinctly observed in the simulation, may represent an equilibration event along the course of the trajectory.

Dynamic fluctuation of the buried cavity of L99A

The C-terminal domain of apo L99A experiences significant core mobility and deformation (Fig. 5; Movie S1). These internal conformational rearrangements result in the overall reduction in the volume of the buried cavity from ∼70 Å3 in the equilibrated ground state to <10 Å3 in the final simulated excited state (Fig. 4 b), as measured with POVME 2.0 (44). These rearrangements are accompanied by mobile defects, or cavity migrations, to other regions of the C-terminal domain. As previously mentioned, the buried cavity in the apo ground-state crystal structure (PDB: 1L90) was initially measured to be ∼150 Å3. However, with the POVME method (44) we used, the volume of the buried cavity in this ground-state crystal structure (PDB: 1L90) was ∼65.5 Å3. We attribute this discrepancy to variability in methods of measuring cavities in proteins (50). The volume reduction seen in the Anton trajectory aligns with the previously described rationale for using high pressure to shift protein conformational equilibria to alternative packing of the hydrophobic core by filling void volumes (51), and has been seen experimentally in L99A for F114 or water filling the void volume (16, 17, 18, 52).

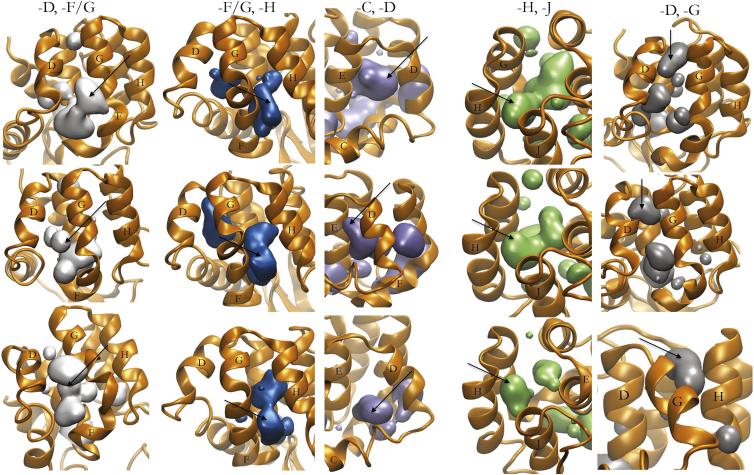
Figure 5.

Figure 5

Open in a new tab

Five mobile defects through the protein surface are seen in the Anton trajectory. Three examples of mobile defects through the protein surface occur between the D and F/G helices (solid surfaces, far left) at 5.38 μs, 6.87 μs, and 8.37 μs (top to bottom), between the F/G and H helices (second from left) at 2.41 μs, 19.22 μs, and 24.21 μs (top to bottom), between the C and D helices (third from left) at 340 ns, 550 ns, and 6.78 μs (top to bottom), between the H and J helices (fourth from left) at 630 ns, 4.95 μs, and 5.14 μs (top to bottom), and between the D and G helices (right) at 7.77 μs, 8.27 μs, 11.66 μs (top to bottom). To see this figure in color, go online.

Occasionally, these internal-cavity deformations reach the protein surface, and over the course of the trajectory, five distinct openings occur from the buried pocket of L99A to solution (Fig. 5). Four of these openings from the buried cavity to solution have been witnessed through enhanced simulation techniques (data not shown). The D/G, D/F/G, and H/J openings (Fig. 5) have also been previously simulated in the egress and ingress of molecular oxygen (31). Although the openings through the D/F/G pocket are larger and able to accommodate benzene, the H/J and D/G pockets form narrower surface openings that cannot, suggesting that different ligands may bind to the buried cavity through different pathways.

The openings of the buried cavity to solvent through the D and F/G helices occur during transitions between the various metastates. Recall that these metastates are defined by the location of the phenyl group of F114 in the buried pocket and the angle between the F and G helices. This suggests that the movement of the F114 side chain and bending of the F and G helices is correlated with the transient sliding of helices that permits the opening of the buried cavity to solution. In other words, transitioning between these metastates may play a role in ligand exchange. Additionally, the D/F/G surface has previously been identified by simulation to both bind benzene and be the opening through which benzene binds to the buried cavity (53, 54).

Discrepancies in timescales of excited-state transitions in simulation and experiment

The opening at the interface of the D and F/G helices, where benzene has been previously simulated to bind and pass through to the buried cavity (54), occurs repeatedly throughout the simulation and on timescales commensurate with experimental rates of benzene binding (μs). Experimentally, the rate of benzene binding is rapid (μs) (27) compared to the transition from the ground state of L99A to the excited state (∼ms) (20). However, in the Anton simulation, we observed the transition to the excited state between 18.6 μs and 27 μs, suggesting a transition timescale two orders of magnitude faster than found in experiment. Although only a single transition in one single long-timescale simulation was observed, and therefore no determination of the timescale for the transition can be made, the order-of-magnitude difference between our observed transition and the experimental rate is consistent with previously reported discrepancies between simulation and experiment for slow ring flips (on the order of microseconds) in proteins (55, 56). The fortuitous observation of this transition is consistent with force-field-induced biases toward greater helical content (48) that could have led to the faster transition timescale, since refolding of the F and G helices into a single helix is a key structural change on the path from the ground state to the excited state of L99A.

Conclusion

Despite the intense study of T4 lysozyme L99A as a model protein system for ligand binding, the Anton supercomputer simulation reported here represents the longest single-trajectory MD simulation for this protein. What emerges are atomistic details for the previously enigmatic conformational changes known to occur for L99A mutant ligand exchange and the ground-to-excited-state transition.

Remarkably, there is a high degree of cavity plasticity, exceeding what might be expected from previous crystallographic studies (18, 19), that involves residues, metastates, and conformations beyond the discrete crystallographic states observed for L99A bound to a congeneric series of benzene-related compounds (24, 30). Further, the number of rotamers observed for buried L99A residues exceeds that seen in the several-hundred-microsecond simulations of other protein cores, such as ubiquitin, RNaseH, and β-lactamase (56). Although dramatic, we find that the torsional, hydrogen-bond, secondary-structure, and back-calculated chemical shifts from the L99A simulation are in agreement with previously measured experimental data. And the extent of the core plasticity is consistent with this protein’s ability to undergo the conformational change that buries the F114 side chain into the engineered C-terminal cavity in the excited state without extensive backbone conformational change.

Our studies demonstrate that the engineered binding pocket of L99A has a much higher degree of plasticity when simulated beyond a few hundred nanoseconds and that the plasticity is not limited to a discrete number of buried side chains. This perhaps presents a challenging dilemma for those utilizing this protein as a model system for free-energy perturbation studies, as a number of different core side-chain rotamers may define the protein ground state and/or ligand-bound states. Furthermore, the residues involved in the plasticity are not limited to a particular region of the binding pocket, but rather are found in all regions surrounding the binding pocket, a fact that is somewhat dissimilar to what is observed for native-protein enzyme pockets where multiple conformations are typically limited to a particular loop or pocket subregion.

Finally, the structural details presented here are consistent with a growing body of data implicating activated volumes and mobile defects of internal cavities in protein conformational change (16, 17, 51). It is possible that mobile defects may not be unique to protein transitions related to excited states, and that fluctuations in small, buried volumes could contribute to conformational change in many protein mechanisms.

Author Contributions

J.M.S. performed simulations and analyses; R.S. performed analyses in Fig. S4 and RMSD calculations; J.M.S. and V.A.F. wrote the article, with significant revisions from R.D.M.; and V.A.F., J.M.S., R.D.M., and R.E.A. planned the study and outlined simulations to perform. R.E.A. was the leading principal investigator, and V.A.F. initiated and directed the study.

Acknowledgments

R.E.A. is a co-founder of Actavalon, Inc., and V.A.F. has financial interest in Actavalon, Inc. Readers are welcome to comment on the online version of this article. Correspondence and requests for materials should be addressed to VAF (vfeher@ucsd.edu) or REA (ramaro@ucsd.edu).

This work was funded in part by the Director’s New Innovator Award Program (NIH DP2 OD007237 to R.E.A.). Funding and support from the National Biomedical Computation Resource (NBCR) was provided through NIH P41 GM103426. J.M.S. was supported by National Institutes of Health Molecular Biophysics Training Grant T32 GM008326. Anton computer time was provided by the Pittsburgh Supercomputing Center (PSC) and the National Center for Multiscale Modeling of Biological Systems (MM Bios) through grant P41GM103712-S1 from the National Institutes of Health. D.E. Shaw Research generously made the Anton machine at PSC available.

Editor: Amedeo Caflisch.

Footnotes

Jamie M. Schiffer and Victoria A. Feher contributed equally to this work.

Six figures and four movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30764-0.

Contributor Information

Victoria A. Feher, Email: vfeher@ucsd.edu.

Rommie E. Amaro, Email: ramaro@ucsd.edu.

Supporting Material

Document S1. Figs. S1–S6
mmc1.pdf (1.4MB, pdf)
Movie S1. Simulating From the Ground to Excited State of the L99A Cavity Mutant With the Anton Supercomputer
mmc2.jpg (841.2KB, jpg)
Movie S2. Principal Component 1 of Anton Trajectory
mmc3.jpg (402.4KB, jpg)
Movie S3. Principal Component 2 of Anton Trajectory
mmc4.jpg (660.9KB, jpg)
Movie S4. Principal Component 3 of Anton Trajectory
mmc5.jpg (366.5KB, jpg)
Document S2. Article plus Supporting Material
mmc6.pdf (4.2MB, pdf)

References

  • 1.Boehr D.D., McElheny D., Wright P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
  • 2.Masterson L.R., Yu T., Veglia G. cAMP-dependent protein kinase A selects the excited state of the membrane substrate phospholamban. J. Mol. Biol. 2011;412:155–164. doi: 10.1016/j.jmb.2011.06.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Baldwin A.J., Kay L.E. NMR spectroscopy brings invisible protein states into focus. Nat. Chem. Biol. 2009;5:808–814. doi: 10.1038/nchembio.238. [DOI] [PubMed] [Google Scholar]
  • 4.Henzler-Wildman K., Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
  • 5.Bouvignies G., Vallurupalli P., Kay L.E. Solution structure of a minor and transiently formed state of a T4 lysozyme mutant. Nature. 2011;477:111–114. doi: 10.1038/nature10349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Xue Y., Ward J.M., Skrynnikov N.R. Microsecond time-scale conformational exchange in proteins: using long molecular dynamics trajectory to simulate NMR relaxation dispersion data. J. Am. Chem. Soc. 2012;134:2555–2562. doi: 10.1021/ja206442c. [DOI] [PubMed] [Google Scholar]
  • 7.Shaw D.E., Dror R.O., Towles B. Millisecond-scale molecular dynamics simulations on Anton. Proc. Conf. High Perform. Comput. Netw. Storage Anal. SC 09. 2009:39. [Google Scholar]
  • 8.Sgourakis N.G., Yan Y., Garcia A.E. The Alzheimer’s peptides Aβ40 and 42 adopt distinct conformations in water: a combined MD/NMR study. J. Mol. Biol. 2007;368:1448–1457. doi: 10.1016/j.jmb.2007.02.093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Sgourakis N.G., Merced-Serrano M., Garcia A.E. Atomic-level characterization of the ensemble of the Aβ(1–42) monomer in water using unbiased molecular dynamics simulations and spectral algorithms. J. Mol. Biol. 2011;405:570–583. doi: 10.1016/j.jmb.2010.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Jensen L.B., Mortensen K., Foged C. Molecular characterization of the interaction between siRNA and PAMAM G7 dendrimers by SAXS, ITC, and molecular dynamics simulations. Biomacromolecules. 2010;11:3571–3577. doi: 10.1021/bm101033g. [DOI] [PubMed] [Google Scholar]
  • 11.Fuglestad B., Gasper P.M., Komives E.A. The dynamic structure of thrombin in solution. Biophys. J. 2012;103:79–88. doi: 10.1016/j.bpj.2012.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Shaw D.E., Maragakis P., Wriggers W. Atomic-level characterization of the structural dynamics of proteins. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
  • 13.Dror R.O., Mildorf T.J., Shaw D.E. SIGNAL TRANSDUCTION. Structural basis for nucleotide exchange in heterotrimeric G proteins. Science. 2015;348:1361–1365. doi: 10.1126/science.aaa5264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Vitalini F., Mey A.S., Keller B.G. Dynamic properties of force fields. J. Chem. Phys. 2015;142:084101. doi: 10.1063/1.4909549. [DOI] [PubMed] [Google Scholar]
  • 15.Vallurupalli P., Chakrabarti N., Kay L. Atomistic picture of conformational exchange in a T4 lysozyme cavity mutant: an experiment-guided molecular dynamics study. Chem. Sci. 2016;7:3602–3613. doi: 10.1039/c5sc03886c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Nucci N.V., Fuglestad B., Wand A.J. Role of cavities and hydration in the pressure unfolding of T4 lysozyme. Proc. Natl. Acad. Sci. USA. 2014;111:13846–13851. doi: 10.1073/pnas.1410655111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Lerch M.T., López C.J., Hubbell W.L. Structure-relaxation mechanism for the response of T4 lysozyme cavity mutants to hydrostatic pressure. Proc. Natl. Acad. Sci. USA. 2015;112:E2437–E2446. doi: 10.1073/pnas.1506505112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Collins M.D., Quillin M.L., Gruner S.M. Structural rigidity of a large cavity-containing protein revealed by high-pressure crystallography. J. Mol. Biol. 2007;367:752–763. doi: 10.1016/j.jmb.2006.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Eriksson A.E., Baase W.A., Matthews B.W. Response of a protein structure to cavity-creating mutations and its relation to the hydrophobic effect. Science. 1992;255:178–183. doi: 10.1126/science.1553543. [DOI] [PubMed] [Google Scholar]
  • 20.Mulder F.A.A., Hon B., Kay L.E. Flexibility and ligand exchange in a buried cavity mutant of T4 lysozyme studied by multinuclear NMR. Biochemistry. 2000;39:12614–12622. doi: 10.1021/bi001351t. [DOI] [PubMed] [Google Scholar]
  • 21.Mulder F.A.A., Hon B., Kay L.E. Slow internal dynamics in proteins: application of NMR relaxation dispersion spectroscopy to methyl groups in a cavity mutant of T4 lysozyme. J. Am. Chem. Soc. 2002;124:1443–1451. doi: 10.1021/ja0119806. [DOI] [PubMed] [Google Scholar]
  • 22.Korzhnev D.M., Orekhov V.Y., Kay L.E. Off-resonance R1ρ relaxation outside of the fast exchange limit: an experimental study of a cavity mutant of T4 lysozyme. J. Biomol. NMR. 2003;26:39–48. doi: 10.1023/a:1023039902737. [DOI] [PubMed] [Google Scholar]
  • 23.Skrynnikov N.R., Dahlquist F.W., Kay L.E. Reconstructing NMR spectra of “invisible” excited protein states using HSQC and HMQC experiments. J. Am. Chem. Soc. 2002;124:12352–12360. doi: 10.1021/ja0207089. [DOI] [PubMed] [Google Scholar]
  • 24.Morton A., Matthews B.W. Specificity of ligand binding in a buried nonpolar cavity of T4 lysozyme: linkage of dynamics and structural plasticity. Biochemistry. 1995;34:8576–8588. doi: 10.1021/bi00027a007. [DOI] [PubMed] [Google Scholar]
  • 25.Mulder F.A.A., Mittermaier A., Kay L.E. Studying excited states of proteins by NMR spectroscopy. Nat. Struct. Biol. 2001;8:932–935. doi: 10.1038/nsb1101-932. [DOI] [PubMed] [Google Scholar]
  • 26.Eriksson A.E., Baase W.A., Matthews B.W. A cavity-containing mutant of T4 lysozyme is stabilized by buried benzene. Nature. 1992;355:371–373. doi: 10.1038/355371a0. [DOI] [PubMed] [Google Scholar]
  • 27.Feher V.A., Baldwin E.P., Dahlquist F.W. Access of ligands to cavities within the core of a protein is rapid. Nat. Struct. Biol. 1996;3:516–521. doi: 10.1038/nsb0696-516. [DOI] [PubMed] [Google Scholar]
  • 28.Morton A., Baase W.A., Matthews B.W. Energetic origins of specificity of ligand binding in an interior nonpolar cavity of T4 lysozyme. Biochem. 1995;34:8564–8575. doi: 10.1021/bi00027a006. [DOI] [PubMed] [Google Scholar]
  • 29.Baldwin E., Baase W.A., Matthews B.W. Generation of ligand binding sites in T4 lysozyme by deficiency-creating substitutions. J. Mol. Biol. 1998;277:467–485. doi: 10.1006/jmbi.1997.1606. [DOI] [PubMed] [Google Scholar]
  • 30.Merski M., Fischer M., Shoichet B.K. Homologous ligands accommodated by discrete conformations of a buried cavity. Proc. Natl. Acad. Sci. USA. 2015;112:5039–5044. doi: 10.1073/pnas.1500806112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Kitahara R., Yoshimura Y., Mulder F.A.A. Detecting O2 binding sites in protein cavities. Sci. Rep. 2016;6:20534. doi: 10.1038/srep20534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
  • 33.Rostkowski M., Olsson M.H.M., Jensen J.H. Graphical analysis of pH-dependent properties of proteins predicted using PROPKA. BMC Struct. Biol. 2011;11:6. doi: 10.1186/1472-6807-11-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Lippert R.A., Predescu C., Shaw D.E. Accurate and efficient integration for molecular dynamics simulations at constant temperature and pressure. J. Chem. Phys. 2013;139:164106. doi: 10.1063/1.4825247. [DOI] [PubMed] [Google Scholar]
  • 35.Hornak V., Abel R., Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Salomon-Ferrer R., Götz A.W., Walker R.C. Routine microsecond molecular dynamics simulations with AMBER. 2. Explicit-solvent particle mesh Ewald. J. Chem. Theory Comput. 2012;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
  • 37.Case D.A., Cheatham T.E., 3rd, Woods R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Darden T., York D., Pedersen L. Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
  • 39.Press W., Flannery B., Teukolsky S., Vetterling W. 3rd ed. Cambridge University Press; Cambridge, United Kingdom: 1986. Numerical Recipes: The Art of Scientific Computing. [Google Scholar]
  • 40.Lamm G., Szabo A. Langevin modes of macromolecules. J. Chem. Phys. 1986;85:7334–7348. [Google Scholar]
  • 41.Ryckaert J.P., Ciccotti G., Berendsen H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
  • 42.Roe D.R., Cheatham T.E., 3rd PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
  • 43.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
  • 44.Durrant J.D., Votapka L., Amaro R.E. POVME 2.0: An enhanced tool for determining pocket shape and volume characteristics. J. Chem. Theory Comput. 2014;10:5047–5056. doi: 10.1021/ct500381c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Baron R., McCammon J.A. Dynamics, hydration, and motional averaging of a loop-gated artificial protein cavity: the W191G mutant of cytochrome c peroxidase in water as revealed by molecular dynamics simulations. Biochemistry. 2007;46:10629–10642. doi: 10.1021/bi700866x. [DOI] [PubMed] [Google Scholar]
  • 46.Hess, B., D. van der Spoel, and E. Lindahl. 2008. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. 4:435–447. [DOI] [PubMed]
  • 47.Thompson E.J., DePaul A.J., Sorin E.J. Evaluating molecular mechanical potentials for helical peptides and proteins. PLoS One. 2010;5:e10056. doi: 10.1371/journal.pone.0010056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Smith M.D., Rao J.S., Cruz L. Force-field induced bias in the structure of Aβ21–30: a comparison of OPLS, AMBER, CHARMM, and GROMOS force fields. J. Chem. Inf. Model. 2015;55:2587–2595. doi: 10.1021/acs.jcim.5b00308. [DOI] [PubMed] [Google Scholar]
  • 49.Han B., Liu Y., Wishart D.S. SHIFTX2: significantly improved protein chemical shift prediction. J. Biomol. NMR. 2011;50:43–57. doi: 10.1007/s10858-011-9478-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Gellatly B.J., Finney J.L. Calculation of protein volumes: an alternative to the Voronoi procedure. J. Mol. Biol. 1982;161:305–322. doi: 10.1016/0022-2836(82)90155-3. [DOI] [PubMed] [Google Scholar]
  • 51.Roche J., Caro J.A., Royer C.A. Cavities determine the pressure unfolding of proteins. Proc. Natl. Acad. Sci. USA. 2012;109:6945–6950. doi: 10.1073/pnas.1200915109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Maeno A., Sindhikara D., Kitahara R. Cavity as a source of conformational fluctuation and high-energy state: high-pressure NMR study of a cavity-enlarged mutant of T4 lysozyme. Biophys. J. 2015;108:133–145. doi: 10.1016/j.bpj.2014.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Wang K., Chodera J.D., Shirts M.R. Identifying ligand binding sites and poses using GPU-accelerated Hamiltonian replica exchange molecular dynamics. J. Comput. Aided Mol. Des. 2013;27:989–1007. doi: 10.1007/s10822-013-9689-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Miao Y., Feher V.A., McCammon J.A. Gaussian accelerated molecular dynamics: unconstrained enhanced sampling and free energy calculation. J. Chem. Theory Comput. 2015;11:3584–3595. doi: 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Weininger U., Modig K., Akke M. Ring flips revisited: 13C relaxation dispersion measurements of aromatic side chain dynamics and activation barriers in basic pancreatic trypsin inhibitor. Biochemistry. 2014;53:4519–4525. doi: 10.1021/bi500462k. [DOI] [PubMed] [Google Scholar]
  • 56.Bowman G.R., Geissler P.L. Extensive conformational heterogeneity within protein cores. J. Phys. Chem. B. 2014;118:6417–6423. doi: 10.1021/jp4105823. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figs. S1–S6
mmc1.pdf (1.4MB, pdf)
Movie S1. Simulating From the Ground to Excited State of the L99A Cavity Mutant With the Anton Supercomputer
mmc2.jpg (841.2KB, jpg)
Movie S2. Principal Component 1 of Anton Trajectory
mmc3.jpg (402.4KB, jpg)
Movie S3. Principal Component 2 of Anton Trajectory
mmc4.jpg (660.9KB, jpg)
Movie S4. Principal Component 3 of Anton Trajectory
mmc5.jpg (366.5KB, jpg)
Document S2. Article plus Supporting Material
mmc6.pdf (4.2MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES