Single-Bond Association Kinetics Determined by Tethered Particle Motion: Concept and Simulations

Abstract

Tethered particle motion (TPM), the motion of a micro- or nanoparticle tethered to a substrate by a macromolecule, is a system that has proven to be extremely useful for its ability to reveal physical features of the tether, because the thermal motion of the bound particle reports sensitively on parameters like the length, the rigidity, or the folding state of its tether. In this article, we survey the applicability of TPM to probe the kinetics of single secondary bonds, bonds that form and break between the tethered particle and a substrate due, for instance, to receptor/ligand pairs on particle and substrate. Much like the tether itself affects the motion pattern, so do the presence and absence of such secondary connections. Keeping the tether properties constant, we demonstrate how raw positional TPM data may be parsed to generate detailed insights into the association and dissociation kinetics of single secondary bonds. We do this using coarse-grained molecular dynamics simulations specifically developed to treat the motion of particles close to interfaces.

Introduction

The precise measurement of the binding and unbinding kinetics of single biomolecular bonds has been an active topic of research in the past two decades (1). A multitude of experimental methods to probe bonds at the single-molecule level are currently available, including AFM (2), optical tweezers (3), magnetic tweezers (4, 5), laminar flow chambers (6), total internal reflection fluorescence microscopy (7, 8), interferometric imaging (9), plasmonic sensing (10), and acoustic force spectroscopy (11). Moreover, the focus on further development of the single-molecule toolbox is projected to intensify in the direct future (12). In this article, we direct our attention to a single-molecule property for which currently few tools are available: the association kinetics of a single pair of noncovalently bonding molecules. A first complicating factor in measuring these properties is the generic difficulty of disentangling extrinsic and intrinsic factors: association is a strongly distance-dependent process that, trivially, may only occur when the two binding partners are within touching proximity. A second complicating factor is that molecular association is a stochastic process, so one needs to be able to gather statistical data of repeated events to be able to extract association parameters with sufficient precision. This requires a stable molecular system and a readout arrangement suited for long observation times.

Here, we propose a method based on tethered particle motion (TPM) to address the above-mentioned problems. The method allows for separation of the encounter and association processes, as well as for repeated probing of the same system and long observation times. The method is based on measuring bond kinetics by tracking the motion of a molecularly tethered particle that can form secondary bonds with a substrate, as sketched in Fig. 1. In its rawest form, the data collected in such an experiment consist of a time series, $\overrightarrow{R}\left(t_i\right)$, of the particle position projected onto the substrate. We will call such a trace a “motion pattern.” The basic idea is straightforward: if a secondary bond is present, the motion pattern of the particle will change, as it is now confined by two, rather than one, bonds to the substrate (13). If no secondary bond is present, the motion pattern is that of a regular noninteracting TPM system. Thus, the motion pattern itself reports on the binding state. There is, however, more information in the time-varying motion pattern: the dynamics of the switching between the different (bound and free) motion patterns reports on the kinetics of the secondary bond.

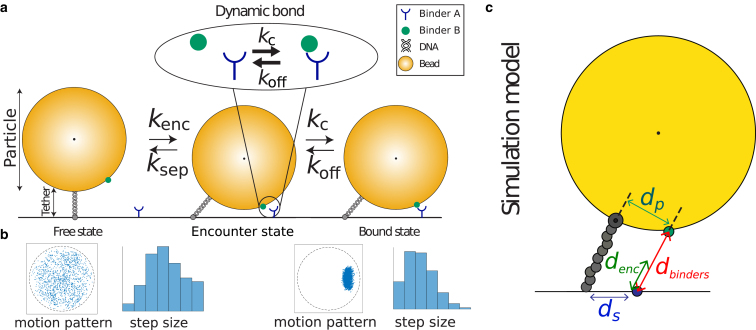
Figure 1.

TPM with a secondary bond. (a) The particle is bound to the substrate by a dsDNA tether. The tether is drawn here as a straight rod, although in reality it is semiflexible. In the simulations, the tether contour length is close to the bending persistence length of dsDNA (∼50 nm). This figure provides an overview of the two-step process, in which the particle reversibly transfers between the free, encounter, and bound states. The first step is governed by the Brownian motion of the particle with encounter rate k_enc and separation rate k_sep. The second step is governed by the binding process between molecules A and B, which are drawn generically in this figure. The molecular complexation and decomplexation rates are k_c and k_off. (b) Motion patterns of the particle in the free state (left) and the bound state (right). A motion pattern is the result of periodically imaging the particle and plotting all observed in-plane particle positions in one figure. The motion pattern of a free particle is fundamentally different from the motion pattern of a bound particle. The step size is the in-plane distance the particle travels between two frames. The step sizes are also affected by the binding process; the average step size is lower in the bound state. (c) Schematic representation of the used simulation model. The tether is modeled as a string of beads. There is a binding patch on the particle at a perpendicular distance, d_p, from the tether point and a binding patch on the substrate at a distance, d_s, from the origin. The encounter distance is denoted by d_enc and the distance between the two binding patches by d_binders. We refer to the encounter state as when $d_{\text{binders}}<d_{\text{enc}}$. To see this figure in color, go online.

In what follows, we present first the basic concepts and definitions required to measure association kinetics by TPM, and then the molecular dynamics (MD) simulations of the process. The insights from these simulations permit us to devise a protocol to extract the association rates from raw experimental data. We provide proof of principle for our method, validating the protocol using simulated raw data.

Motion of tethered particles with secondary bonds

TPM is a proven tool in biophysics. It has been used to determine the transcription of RNA polymerase (14), and after concise validation as a tool to probe tether properties (15), it has been used to determine the persistence length of DNA (16, 17) and the looping kinetics of DNA (18, 19, 20). In all previous TPM-based research, the focus has been on properties and interactions of the tether rather than those of the particle. For the most part, the particle has been a large (and therefore easily visualized) marker for the end of the tether.

There is, however, no reason why one should not assign further functionality to the particle itself. In particular, it will prove useful to consider particles that may form additional bonds with the substrate besides the one effected by the tether. In what follows, we will assume that the double-stranded DNA (dsDNA) tether does not change and will use it solely as a means to keep the functionalized particle close to the substrate and confine its random thermal motion. As explained, there is useful information in both the instantaneous magnitude and the time dependence of the raw signal, $\overrightarrow{R}\left(t_i\right)$. However, although all this information is undoubtedly present, a crucial question is whether $\overrightarrow{R}\left(t_i\right)$ may be dissected to isolate the association rate. We show that this is indeed possible.

A clear advantage of our method is that it is easily parallelized: multiple particles can be tethered to the same substrate, the measurement of their trajectories can be done robustly in wide-field optics, and the change in motion pattern of even a single particle due to binding may constitute a detection and permit the determination of rates, multiple detections obviously improving the accuracy of the method.

Fig. 1 a presents the basic concept of TPM-based single-molecule measurements that we propose. The particle is in one of three states: free, encounter, or bound. The free state is one in which the particle is only bound to the substrate by the tether. The encounter state is a conformation in which the particle and the substrate are close enough for a secondary bond to form, but this bond is not actually connected. The bound state, finally, is where the secondary bond is formed. Four distinct rates characterize the transitions back and forth between the three particle states. By observing the motion pattern we can distinguish only between states where the secondary bond is not present (free or encounter state) and the one where it is (bound state). The entangled, distance-dependent character of this process is obvious: The transition from the free to the bound state is a two-step process that must necessarily pass through the encounter state. An experiment where no changes in binding pattern are observed may either have a complexation rate, k_c, that is low with respect to the reciprocal timescale of the experiment, a dissociation rate, k_off, that is high with respect to the reciprocal time resolution of the experimental detection method, or an encounter rate, k_enc, that is so low that no opportunity for binding occurs on the timescale of the experiment. The first two rates relate to an intrinsic property of the single bond, and the third relates to an extrinsic effect that is dependent on the geometry of the particle-tether construct and its Brownian motion. Clearly, it is important to separate the intrinsic and extrinsic effects. The point of this work is to demonstrate that the contribution of the particle’s Brownian motion to the overall motion can be modeled and understood using MD simulations. Applying this principle allows otherwise inaccessible single-bond properties to be extracted from raw experimental data.

TPM and changing motion patterns

To be able to put real numbers on our axes, and to remain close to experimentally feasible dimensions, we will consider for the most part a 50 nm dsDNA tether that attaches, on each end via single conjugated tags, a 1-μm-diameter particle to a substrate (13). In typical TPM systems, the in-plane motion of this particle is tracked over time, so that a two-dimensional projection, ${\overrightarrow{R}}_{\parallel }\left(t_i\right)$, of the movement of the particles is obtained (20, 21, 22). When such a particle is repeatedly imaged within several consecutive time intervals, Δt = t_{i + 1} − t_i, the combined result is a motion pattern like the one shown in Fig. 1 b. left.

We consider now the case where both the particle and the substrate are coated with complementary binding molecules. This results in the possibility of a tethered particle to form the secondary bond with the substrate. When such a secondary bond is formed, the motion pattern is significantly altered: it is no longer axisymmetric and is much more localized, as shown in Fig. 1 b, right.

The in-plane distance that the particle travels between two frames is indicative of the presence of a secondary bond. We will refer to this traveled distance as the “step size,” defined as $R_{\text{step}}\left(t\right)=\left|{\overrightarrow{R}}_{\parallel }\left(t_{i+1}\right)-{\overrightarrow{R}}_{\parallel }\left(t_i\right)\right|$. Since a secondary bond results in additional confinement of the motion of our tethered particle, the average step size is reduced by secondary bonds. This is graphically represented in the distribution of step sizes in Fig. 1. Moreover, the shape of the motion pattern in the bound state is the result of the specific position of the binding molecules. The typical time between formation and dissociation of these secondary bonds is the kinetic data that we aim to relate to the kinetic binding properties of the individual molecules that form the bond.

A more detailed description on how the step size may be used to distinguish between states can be found in (23). Alternatively, one might consider the Brownian motion amplitude as an indicator of the formation of a secondary bond, as was previously used to study the looping state of DNA (21).

The step size itself is a potential reporter of the presence or absence of a secondary bond. There is, however, additional information in the switches in magnitude of the step size, and this additional information has not been tapped into yet. To extract it, we must understand the temporal behavior of this system. This is why we now turn to MD simulations.

Materials and Methods

Simulation methods

We perform Langevin dynamics simulations using the LAMMPS MD package (24) with one spatially extended spherical particle, the TPM particle, which is connected to a flexible tether represented by a string of N point particles in a bead-spring model. The link between tether and substrate and the link between tether and particle are freely jointed, and the particle is free to rotate with respect to its tether anchoring point. This situation applies when the tether is attached to particle and substrate with single conjugated tags—such conjugations are highly flexible and have rotational freedom. Ours are not the first dynamic simulations of this system: Beausang et al. (25) and later Manghi et al. (26) presented elegant dynamic Monte Carlo (MC) simulations of the TPM process, but these studies focused mostly on its use to assess properties of the tether. The essence of our approach is that we employ coarse-grained (Langevin) MD and include binding between the probe particle and the surface to learn more about the kinetics of the bonds that form between particle and surface.

MD algorithm

In the Langevin dynamics method, each particle is subject to conservative, drag, and random forces, ${\overrightarrow{F}}_{\text{c}}$, ${\overrightarrow{F}}_{\text{d}},$ and ${\overrightarrow{F}}_{\text{r}},$ respectively, and obeys the following translational equation of motion:

$$M\ddot{\overrightarrow{r}}={\overrightarrow{F}}_{\text{c}}+{\overrightarrow{F}}_{\text{d}}+{\overrightarrow{F}}_{\text{r}},$$ (1)

where M is the particle’s mass and $\ddot{\overrightarrow{r}}$ is the particle’s acceleration. Excluded volume, bonding, and angle-bend interactions are explicitly included in ${\overrightarrow{F}}_{\text{c}}$, as described below under Interactions. The drag force is given by ${\overrightarrow{F}}_{\text{d}}=-\gamma \dot{\overrightarrow{r}}$, where γ is the drag coefficient and $\dot{\overrightarrow{r}}$ is the particle’s velocity. The drag coefficient is described in more detail under Drag Coefficients. Both the drag force, ${\overrightarrow{F}}_{\text{d}}$, and the random force, ${\overrightarrow{F}}_{\text{r}}$, are the result of the interaction with the solvent, and by extension, these forces are related. In particular, the fluctuation-dissipation theorem tells us that (27)

$$\langle {\overrightarrow{F}}_{\text{r}}\left(t\right)\cdot {\overrightarrow{F}}_{\text{r}}\left(t^{\prime }\right)\rangle =6k_{\text{B}}T\gamma \delta \left(t-t^{\prime }\right),$$ (2)

with k_B Boltzmann’s constant and T the temperature, noting that in discrete-time MD simulations such as ours, a discrete version of Eq. 2 is implemented (24).

For a spatially extended particle, the rotational motion has to be taken into account as well. This results in the rotational counterpart of Eq. 1:

$$I\ddot{\overrightarrow{\varphi }}={\overrightarrow{\tau }}_{\text{c}}+{\overrightarrow{\tau }}_{\text{d}}+{\overrightarrow{\tau }}_{\text{r}},$$ (3)

where I denotes the moment of inertia, $\ddot{\overrightarrow{\varphi }}$ is the angular acceleration, and the conservative, drag, and random torque are given by ${\overrightarrow{\tau }}_{\text{c}}$, ${\overrightarrow{\tau }}_{\text{d}}$, and ${\overrightarrow{\tau }}_{\text{r}}$, respectively. Similar to the translational force, the translational drag is given by ${\overrightarrow{\tau }}_{\text{d}}=-{\gamma }_{\text{rot}}\dot{\overrightarrow{\varphi }}$, where γ_rot is the rotational drag coefficient and $\dot{\overrightarrow{\varphi }}$ is the angular velocity. Once more, the fluctuation-dissipation theorem provides us with a relation for the effects caused by the solvent, i.e.,

$$\langle {\overrightarrow{\tau }}_{\text{r}}\left(t\right)\cdot {\overrightarrow{\tau }}_{\text{r}}\left(t^{\prime }\right)\rangle =6k_{\text{B}}T{\gamma }_{\text{rot}}\delta \left(t-t^{\prime }\right).$$ (4)

Interactions

There are two main types of interaction included in our simulations, first, interactions that prescribe the behavior of the tether and second, steric exclusion effects.

A bead-spring model is used to represent the tether in the simulations. These beads are held together by a harmonic bond potential given by

$$U_{\text{bond}}=K_{\text{b}}{\left(r-r_0\right)}^2,$$ (5)

with bond coefficient K_b, r₀ the rest distance between two beads, and r the distance between two beads. To ensure that bond lengths are essentially fixed during the simulations, we choose a large value for the strength of the bond potential, $K_{\text{b}}=50k_{\text{B}}T/r_0^2$ (28), where k_BT is the thermal energy.

To include the limited flexibility of a typical dsDNA tether, we include an angle-bending potential,

$$U_{\text{angle}}=K_{\text{a}}{\theta }^2,$$ (6)

where K_a is the angle-bending coefficient and θ is the angle between two adjacent springs. In the limit of $r_0/l_{\text{p}}\to 0$, the angle-bending coefficient can be related to the thermal energy, k_BT, the persistence length, l_p, and the rest distance, r₀, by $K_{\text{a}}=k_{\text{B}}T{l}_{\text{p}}/2r_0$ (29). We construct our model so that $r_0/l_{\text{p}}\ll 1$, which justifies the use of this angle-bend potential.

Moreover, three relevant steric exclusion mechanisms are present in a TPM system: tether-substrate exclusion, particle-substrate exclusion, and tether-particle exclusion. For the tether-substrate exclusion, we use the repulsive part of the Lennard-Jones potential,

$$U_{\text{LJ}}\left(r\right)=4\mathit{ϵ}\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right],r<r_{\text{c}},$$ (7)

where the energy, ϵ, and distance, σ, are the parameters that define the potential and $r_{\text{c}}=2^{1/6}\sigma ,$ so that only the repulsive part is used. r describes the distance beween the interacting elements.

To ensure a steep potential at the edge of the particle, an extra parameter is required. Therefore, for the interactions that involve the particle, we use

$$U_{\text{LJ,exp}}\left(r\right)=4\mathit{ϵ}\left[{\left(\frac{\sigma }{r-\Delta }\right)}^{12}-{\left(\frac{\sigma }{r-\Delta }\right)}^6\right],r<r_{\text{c}}+\Delta ,$$ (8)

as the expanded potential, with extra parameter Δ.

For ϵ, we have used a value of 100 k_BT to ensure repulsion and minimize the overlap of particles. For σ, we have chosen 1 nm, which is small enough to reproduce geometrically sensible results but large enough to create a steepness of the potential that is computationally acceptable. To model a particle with radius 500 nm, we have chosen Δ = 499 nm.

Drag coefficients

Drag on particle. An important feature of a relatively big particle on a small tether is that it is at all times close to the substrate; the distance between the substrate and the edge of the particle is much smaller than the radius of the particle. Hydrodynamic wall effects are therefore important (30, 31), i.e., the drag on a sphere is no longer given by the isotropic Stokes drag, but the drag coefficient is elevated and no longer isotropic.

For a spherical particle with radius R and distance z between the particle center and the substrate, the parallel and perpendicular drag coefficients are given by (32)

$${\gamma }_{\parallel }=\frac{{\gamma }_0}{1-\frac{9}{16}q+\frac{1}{8}{q}^3-\frac{45}{256}{q}^4-\frac{1}{16}{q}^5},$$ (9)

$${\gamma }_{\perp }=\frac{{\gamma }_0}{1-\frac{9}{8}q+\frac{1}{2}{q}^3-\frac{57}{100}{q}^4+\frac{1}{5}{q}^5},$$ (10)

where $q=R/z$, η is the dynamic viscosity of the solvent, and ${\gamma }_0=6\pi \eta R$, the Stokes drag in an unbounded liquid. In Section S1 in the Supporting Material, we discuss in detail how hydrodynamic interactions with the wall are implemented in LAMMPS—this is a feature that will likely have broader applicability in biophysical MD simulations.

Drag on tether. The tether is modeled by a bead-spring system consisting of a number of beads, N_beads, where every bead is subject to a Stokes drag force with drag coefficient

$${\gamma }_{\text{teth}}=6\pi \eta R_{\text{hy}},$$ (11)

where R_hy is the so-called hydrodynamic radius of the beads, an effective parameter that determines the amount of drag on the tether.

In general, a polymer in solution experiences different drag in the direction parallel and perpendicular to its axis. In a TPM experiment, the ends of the tether are attached to the bead and the substrate, so that the tether predominantly moves in the direction perpendicular to its axis. Due to the fact that the drag on the particle, more than the drag on the tether, provides the dominant contribution to the observable timescales in the system, and due to considerations of computational efficiency, we have approximated the drag on the tether by the drag on a cylinder in the perpendicular direction (33), distributed evenly across all beads without preferential direction. This leads to

$${\gamma }_{\text{teth}}=\frac{4\pi \eta l}{N_{\text{beads}}\text{ln}\left(l/b\right)},$$ (12)

where l is the contour length of the tether, b is the width of the cylinder, and for dsDNA, we use b = 2 nm (34). Since the hydrodynamic radius, R_hy, is typically much smaller than the average distance of the beads to the substrate and those beads that are close to the surface move very little, we neglect the hydrodynamic surface effects on the tether and apply a homogeneous Stokes drag to each bead.

Results and Discussion

Validation of the spatial encounter distribution and diffusion kinetics

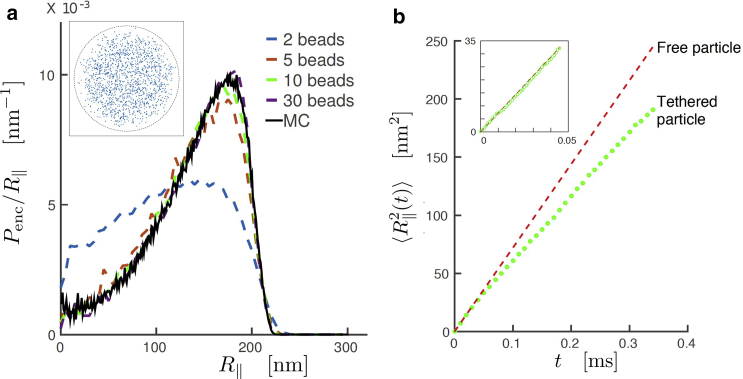
We first compare spatial and kinetic results from our MD simulations to results from reference methods. First, we compare our simulation results to results from previously developed MC simulations, which yield the probability distribution of particle positions in the equilibrium state (13). The spatial encounter distribution describes the probability as a function of the in-plane position that a particle is within the encounter interaction range of the substrate. In Fig. 2 a, the spatial encounter distribution is compared for the MC results and MD results with a varying number of beads that make up the tether while keeping the total tether length constant. We observe that for an increasing number of beads, the two distributions converge. Based on this comparison, we have used a tether consisting of 10 beads in our MD simulations.

Figure 2.

(a) The encounter distribution per in-plane radius, $P_{\text{enc}}/R_{\parallel }$, as a function of the in-plane radius for a particle with diameter of 1 μm and a tether with length 50 nm. The black line represents results obtained by MC simulations with a chain of 50 segments. The dashed lines represent results from MD simulations. The states in which the distance between the edge of the particle and the substrate is <10 nm are defined as encounter states. It can be observed that the MD results converge to the MC results for an increasing number of beads on a string. The inset shows the motion pattern resulting from the MD simulation with 10 beads. The encounter distribution is obtained from these data points in combination with the z-coordinate of the particle. (b) Comparison of the in-plane mean-square displacement of the tethered particle and the mean-square displacement of a free particle starting at the same position. For small times, the mean-square displacement develops equally for a tethered and a free particle, but for larger times, the displacement of the tethered particle is smaller due to its confinement and the fact that it is on average closer to the substrate. Green dots are obtained by averaging over 3000 simulations. To see this figure in color, go online.

Second, we compare results from our MD simulations to the analytical expression for Brownian motion. From conventional Brownian motion theory, it is known that the in-plane mean-square distance traveled by a free diffusing particle is given by

$$\langle R_{\parallel }^2\left(t\right)\rangle =4Dt,$$ (13)

as opposed to the factor of 6 for 3D. Here, D stands for the diffusion coefficient and t for time, and $R_{\parallel }\left(t\right)=\left|{\overrightarrow{R}}_{\parallel }\left(t\right)\right|$.

In the TPM system, the drag on the particle is increased near the surface, as described in above, in Drag Coefficients. This results in a lower effective diffusion coefficient, $D_{\parallel }$. We performed 3000 MD simulations starting out with a TPM system in the upright position and we plot the simulated $\langle R_{\parallel }^2\left(t\right)\rangle$ and the calculated $4D_{\parallel }t$ in one figure. The results are presented in Fig. 2 b.

For small times (see Fig. 2 b, inset) the MD simulation results indeed correspond to the analytical relation for a free particle. For larger times, differences occur, caused both by the confinement of the motion of the particle by the tether and the fact that the particle is, on average, closer to the substrate, resulting in a higher drag and a lower diffusivity.

Determining association kinetics

General algorithm

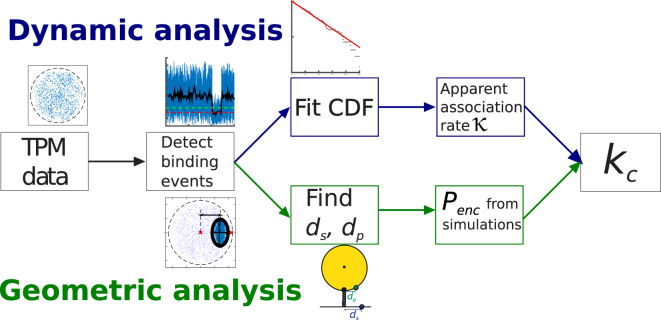
Now that we have introduced the relevant concepts and properties that are involved in the measurement of single-bond kinetics using TPM, we outline an algorithm that allows one to process and interpret measurement data. A schematic outline of the algorithm can be found in Fig. 3. We further expand on both of these steps in this section and clarify how they enable the extraction of single-bond data from a TPM experiment.

Figure 3.

A schematic representation of the data-processing algorithm. The total analysis can be subdivided into dynamic analysis and geometric analysis. The dynamic analysis involves tracking the time between subsequent bonds to end up with an apparent association rate, κ. The geometric analysis involves the characterization of a bound motion pattern, relating this to the most probable values of d_s and d_p and find the corresponding P_enc. The dynamic analysis involves tracking the times of association to find a cumulative distribution function (CDF) and extract an apparent association rate, κ. Finally, both analyses are merged to find our molecular property, the complexation rate, k_c. To see this figure in color, go online.

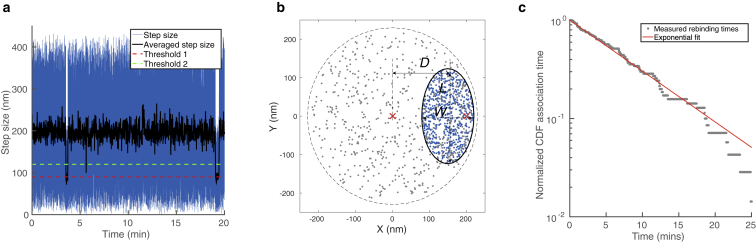
The starting point of our algorithm is the data from a TPM experiment. This is generally the 2D projected position of the particle captured multiple times in a sequence of time intervals. The initial analysis of these data aims to isolate the captured positions that correspond to the particle in the bound state. A means of doing this is by reviewing the step size, that is, the in-plane distance the particle travels between frames. By averaging this over multiple frames and using two separate thresholds, as described in (23), individual binding events can be isolated from the experimental data. An example of this can be found in Fig. 4 a.

Figure 4.

Application of the data-processing algorithm of Fig. 3 to data generated by a mock model. (a) The step sizes obtained from the mock model. Indicated are the step size (blue), the step size averaged over 30 frames (black), threshold 1 (red), and threshold 2 (green). This allows for detection of binding events according to the procedure developed by (23). (b) Motion pattern from the mock model. The blue points are generated in the “bound” state and the gray points belong in the “free” or “encounter” state. Three characteristic geometric parameters may be extracted from the blue points: the length, L, the width, W, and the average distance to the central axis, D. This set of parameters can be linked to the most probable positions of the binders, d_s and d_p. (c) An exponential fit of the cumulative distribution function (CDF) of association times. The vertical axis scales logarithmically. The gray dots represent “measured” rebinding times from our mock model and the red line is an exponential fit of the form $P\left(t\right)=P_0\text{exp}\left(-\kappa t\right)$ with P₀ is 1, which yielded $\kappa =\left(1.7\pm 0.3\right)\times {10}^{-3}$ s^–1 (mean ± SD). To see this figure in color, go online.

Having extracted the frames that correspond to the bound state, these frames are put together to compose the time-independent bound motion pattern. More sophisticated metrics may be employed, but for now we characterize the bound motion pattern using three parameters: its length, L, its width, W, and its average distance to the central axis, D. These parameters are indicated by arrows in Fig. 4 b. Physically, L and W are a measure for the dispersal of the horizontal and vertical components of the position of a bound particle. D is a measure for the average distance from the tether point.

With the bound motion patterns thus characterized, the next step is to determine the location of the binding molecules that is most likely to correspond to that particular binding event. This is where simulation data come in; using the results from simulations with varying binding spots, we can compile the functional relation between binding spot and motion pattern, allowing us to translate the values (L,W,D) into values for d_s and d_p, the distances along substrate and particle where binding most likely occurred. Thus, our simulations permit us to extract new information from experimental data.

Subsequently, simulations are used once more to determine the probability, P_enc, that these two binding spots are within the interaction range. To efficiently do this, we have collected MD data for a large range of combinations of d_s, d_p,and tether length to generate a lookup table which, by straightforward interpolation, yields an accurate estimate for P_enc. We consider here the case where only one molecule is present on the particle and only one on the substrate, but our method is easily extended to include different surface coverages. Whether this is required of course depends on the specific experimental settings, and P_enc should be determined accordingly. Finally, by acquiring the distribution of times between binding events and factoring out P_enc, we can isolate the molecular complexation rate, k_c. If the apparent binding rate is given by κ, then we can find k_c using the relation

$$\kappa =P_{\text{enc}}{k}_{\text{c}}.$$ (14)

In summary, using simulation results, we have created the possibility of extracting otherwise inaccessible single-molecule data from TPM experiments. Clearly, there are design options that could further improve the sensitivity of the method; in Section S2 in the Supporting Material, we assess several optimization strategies.

Example application

As a proof of principle and as a means of demonstrating our algorithm, we have constructed a mock-up model to generate pseudo-TPM data. This model requires three geometric parameters and four rates as input. The geometric parameters L, W, and D describe the shape of the bound motion pattern. It uses preset values for the rates k_enc, k_sep, k_c, and k_off and generates a motion pattern in time as output. The challenge to our analysis protocol is now to back out the value of k_c in the manner described above. The input values are listed in Table 1. We note that our system is in the regime $k_{\text{enc}}\ll k_{\text{sep}}$, so that $P_{\text{enc}}\approx k_{\text{enc}}/k_{\text{sep}}$. The ratio of our input k_enc and k_sep is, by design, such that the resulting P_enc matches with the input L, W, and D.

Table 1.

Input and Reconstructed Values for the Mock Model

Parameter	Input Value	Reconstructed Value	Units
kenc	1.0	–	s−1
ksep	8.3 × 103	–	s−1
kc	1.7 × 101	1.4 × 101	s−1
koff	0.1	–	s−1
L	250	247	nm
W	145	141	nm
D	150	150	nm

The mock model steps through time, and at every time point, the system is in either the “free,” “encounter,” or “bound” state. Every step, the system may change state, and this happens with a probability determined by the relevant transition rates.

In the simulations of the system with a secondary bond, the binding molecule had a fully stretched length of 15 nm. In the simulations without secondary bond, we considered this 15 nm as the encounter range, d_enc.

In the mock model, every time step an x and y coordinate of the particle are generated. When the system is in the “free” state, a random point in a circle with a radius of 220 nm is generated, i.e., within the typical radius of “free” motion patterns in our system. When the system is not in the free state, and is thus in the “encounter” or “bound” state, a random point within a confining ellipse, with a given L, W, and D, is generated. Note that, as one would do with real data, the values of L, W, and D are later established using only the mock data, not the values used to generate it. Clearly, this results in points generated that are, on average, closer to each other in the bound state than in any of the unbound states. This can be seen in Fig. 4 a, where the step size obtained from our mock model is represented. The data points are generated with a frame rate of 30 Hz, so the step size corresponds to the distance traveled in 0.033 s. An averaging window of 30 frames is used, so the black line corresponds to the distance traveled in 1 s.

Using the obtained step size and averaged step size, we now isolate the points of the motion pattern that are classified as belonging to the “bound” state, so that we end up with a motion pattern similar to the pattern in Fig. 4 b. As is indicated, we can extract the L, W, and D from this figure. This leads to a value of L = 247 nm, W = 141 nm, and D = 150 nm, leading to the most probable binding spots d_p = 160 nm and d_s = 200 nm (the resolution of our interpolation table is 20 nm).

Using simulation results of a free tethered particle, we know that the probability of a binder on the substrate and on the particle being within interaction range, d_enc, is $P_{\text{enc}}=1.2\times {10}^{-4}$. This result is obtained by dividing the average number of frames in a simulation in which the two binders are within interaction range by the total number of frames in a simulation. We measure the time it takes for a free particle to become bound throughout the experiment to come up with a cumulative distribution function. This distribution is fit to an exponential function, and the result is represented in Fig. 4 c. From the fit, we obtain the fitting parameter $\kappa =\left(1.7\pm 0.3\right)\times {10}^{-3}$ s⁻¹ (mean ± SD).

Factoring out the encounter probability, P_enc, we end up with a value of $k_{\text{c}}=\left(1.4\pm 0.2\right)\times {10}^1$ s⁻¹, which is to be compared to the input value $k_{\text{c}}=1.7\times {10}^1$ s⁻¹ that was used to generate the data. We hypothesize that the underestimation compared to the actual value may be attributed to a structural issue, also present in experiments, which is that some events are too short lived to be resolved (shorter than one time step), and thus, there is a systematic underestimation of both the bound time and the association rate. An averaging window to detect bonds of 1 s has been used, whereas the typical dissociation time is 10 s ($1/k_{\text{off}}$). Therefore, a detectable difference between the apparent association rate and the actual association rate is expected. In further refinements, this too may be corrected for using the simulations.

Clearly, the sensitivity of the method depends on several other parameters not discussed in this article. Tether length, particle size, and ligand density, too, will affect the determination of the kinetic parameters our method helps determine. In particular, the entire process will slow down considerably as the radius of the probe particle is increased. This effect, first noted in (26) for small particles (20–150 nm radii), is indeed also present in our systems (300–700 nm) (35). These and other dependencies have been assessed in detail in further molecular dynamics simulations. A summary of these findings is found in Section S2 in the Supporting Material and the simulation data themselves are available in (35). The parameters presented in this article are representative of typical experiments.

Conclusions

We have shown that by understanding the contribution of Brownian motion to the overall motion of a tethered particle, a TPM system allows for the probing of single bonds. We have focused on the basic principles of this approach. Several opportunities for future research arise. On the one hand, the understanding of the system and the corresponding simulations could be further developed. On the other hand, experimental validation of this method would be a crucial next cornerstone.

A clear point for improvement is the encounter distance, d_enc, for which we have only a rough approximation at the moment. The next step in developing a TPM-based association measurement would be to increase our understanding of the encounter distance. Two potential experiments come to mind. First, one could investigate the influence of the encounter distance by using linker molecules with different lengths. The length of linker molecules between binder A and the substrate and between binder B and the particle will profoundly influence the encounter distance corresponding to the binder complex. If the apparent association rate, κ, in an experiment with varying linker lengths, ℓ, would display behavior comparable to that of the encounter probability, P_enc, as a function of the encounter distance, d_enc, in the simulations, that would be a strong experimental justification of our approach. Second, by using several different binding molecules, a range of complexation rates, k_c, can be probed. In the upper limit, every encounter will lead to a bond, so for high complexation rates, the apparent association rate should converge to $\kappa =k_{\text{enc}}$.

Concerning experimental conditions and procedures, the proposed method sets requirements on the tethering of the particle, on the number of binders on particle and substrate, and on nonspecific interactions between particle and surface. Measured motion patterns give direct information about the number of tethers between particle and substrate, as we have shown in a recent publication (13). The density of binders on particle and substrate can be controlled by applying suitable dilution steps in the chemical preparation procedures, and observed switching between motion patterns gives information about the occurrence of secondary bonds (13). Nonspecific interactions can be controlled by applying antifouling coatings and by adding blocking agents to the solution. The occurence of nonspecific bonds can be monitored by a statistical analysis of lifetimes (5), which may help to further optimize the conditions and preparation procedures of the experiment

On the simulation side, the next step would be to incorporate the molecular complexation process. The complexation rate, k_c, is the result of distance-dependent physicochemical molecular interactions: charge interactions, van der Waals interactions, steric effects, hydrogen bonds, hydrophobic effects, etc. Simulations with a higher level of detail could provide more insight into the molecular processes involved in TPM experiments.

In summary, what we show here is that the measurement and analysis of surface-binding data in TPM experiments provides a window on single-molecule association dynamics, adding a novel modality to establish these important properties in experiments. Given the measurement concept proposed in this article and the results from the simulations, we believe that the measurement and kinetic analysis of surface-binding data in TPM experiments holds promise to become a new modality for studies on single-molecule association kinetics.

Author Contributions

K.E.M. programmed and performed the simulations. M.W.J.P. conceived the TPM method with the formation of secondary bonds. K.E.M., M.W.J.P., and C.S. developed the computational method, analyzed the data, and together wrote the article.

Editor: Elizabeth Rhoades.