Modeling the Role of Epitope Arrangement on Antibody Binding Stoichiometry in Flaviviruses

Abstract

Cryo-electron-microscopy (cryo-EM) structures of flaviviruses reveal significant variation in epitope occupancy across different monoclonal antibodies that have largely been attributed to epitope-level differences in conformation or accessibility that affect antibody binding. The consequences of these variations for macroscopic properties such as antibody binding and neutralization are the results of the law of mass action—a stochastic process of innumerable binding and unbinding events between antibodies and the multiple binding sites on the flavivirus in equilibrium—that cannot be directly imputed from structure alone. We carried out coarse-grained spatial stochastic binding simulations for nine flavivirus antibodies with epitopes defined by cryo-EM or x-ray crystallography to assess the role of epitope spatial arrangement on antibody-binding stoichiometry, occupancy, and neutralization. In our simulations, all epitopes were equally competent for binding, representing the upper limit of binding stoichiometry that results from epitope spatial arrangement alone. Surprisingly, our simulations closely reproduced the relative occupancy and binding stoichiometry observed in cryo-EM, without having to account for differences in epitope accessibility or conformation, suggesting that epitope spatial arrangement alone may be sufficient to explain differences in binding occupancy and stoichiometry between antibodies. Furthermore, we found that there was significant heterogeneity in binding configurations even at saturating antibody concentrations, and that bivalent antibody binding may be more common than previously thought. Finally, we propose a structure-based explanation for the stoichiometric threshold model of neutralization.

Introduction

Viruses of the Flaviviridae family include dengue (DENV1-4), West Nile (WNV), yellow fever, and tick-borne encephalitis. The flavivirus surface primarily consists of the envelope (E) protein, which is responsible for viral attachment and membrane fusion. X-ray crystallography studies (1) show that the structure of the soluble domain of E-protein consists of three domains (Fig. S1 A in the Supporting Material), domain I (DI), domain II (DII), which contains the fusion loop necessary for membrane fusion, and domain III (DIII), which is responsible for host receptor binding. In the mature dengue virus, 90 E dimers arranged in icosahedral geometry form the outer layer of the virus envelope (Fig. S1 B), and during fusion, the E dimers undergo a dramatic pH-induced conformational change to form a postfusion trimer (2, 3).

During viral infection, the human immune system responds by producing hundreds to thousands of distinct monoclonal antibodies (mAbs) that recognize and bind to the virus and render it noninfectious, thus neutralizing it (see Fig. S1 C). Each mAb has its own variable region (known as a Fab domain) that binds to a distinct region of the virus known as its epitope. Neutralizing Abs that bind to E-proteins is the primary focus of current flavivirus vaccine development efforts such as in WNV or DENV (4, 5). However, studies have shown that not all E-specific Abs contribute equally to neutralization, and that important characteristics of Ab function are related to the particular epitope on E that an Ab binds to. For example, DIII-specific Abs tend to be highly neutralizing (6), whereas Abs directed to the fusion-loop region can be associated with antibody-dependent enhancement of infection (7). Finally, cryo-electron microscopy (cryo-EM) structures show that 180 E-proteins are arranged in an icosahedral “herring bone” geometry on the virus surface, which presents the same epitope in three distinct symmetry environments along the threefold, twofold, and fivefold axes of symmetry (see Fig. S1 B) (8, 9, 10).

The mechanisms that underlie Ab neutralization in flaviviruses are still unclear. Previous studies have identified several steps in the viral infection process that can be disrupted by Ab binding, including receptor binding and attachment, endocytosis, and viral fusion to the host membrane (11, 12, 13). In a landmark study, Pierson et al. (14) advanced the stoichiometric threshold model for antibody neutralization in flaviviruses. Using two independent methods, they showed, for a set of highly neutralizing DIII-specific Abs, that binding of a minimum of ∼30 Abs to the virion was sufficient to neutralize WNV infection, leading to the surprising conclusion that a low binding occupancy of ∼25% was sufficient for neutralization. This stoichiometric threshold of ∼30 Abs corresponds to the coating theory of neutralization (12, 15, 16), which postulates that a threshold density of Abs bound, as a function of virus surface area, is sufficient for neutralization and predicts that flaviviruses, with a surface area of ∼7000 nm², should be neutralized by ∼20–50 Abs. Subsequent experiments have shown that subneutralizing Ab binding stoichiometries facilitate antibody-dependent enhancement of infection (14), underscoring the critical role of antibody binding stoichiometry on flavivirus immunity and pathogenicity.

Recent cryo-EM studies of flaviviruses have provided insight into the structural basis for antibody binding stoichiometry, revealing significant variations in epitope occupancy and binding stoichiometry across different monoclonal Abs. For example, the DENV Ab 1F4 was found to bind exclusively to epitopes along the twofold and fivefold axis of symmetry of the viral envelope, with a total stoichiometry of 120 Abs (17); the DENV Ab 2D22 was found to have a maximum stoichiometry of 180 Abs while binding to epitopes along all three axes of symmetry (18); and the DENV Ab 5J7 was found to have a stoichiometry of 60 Abs, binding to epitopes along only the threefold axis of symmetry (19). Reasons for the observed variations in binding stoichiometry and epitope occupancy are typically attributed to relatively small conformational differences between symmetry-related epitopes that interfere with Ab binding or alter epitope accessibility. Although certainly plausible, such explanations seem at odds with evidence that 1) flaviviruses undergo “breathing” motions that confer considerable conformational heterogeneity (20), and 2) Ab binding can induce significant conformational changes, exposing previously buried epitopes (21). Furthermore, there are technical limits to the use of cryo-EM structures alone in understanding the mechanisms of antibody-based neutralization of flaviviruses. First, these structures are solved under saturating Ab concentrations, whereas neutralization or protection studies are typically carried out at subsaturating concentrations. Second, cryo-EM methods resolve structures with high structural homogeneity and thus may omit heterogeneous binding configurations that nonetheless contribute to neutralization. Third, cryo-EM or x-ray crystallography structures use the Fab, the variable fragment (Fv), or a single-chain variable fragment (scFv) of the full-length mAb and thus cannot directly detect characteristics such as bivalent binding that are unique to the full-length Ab and may play a role in neutralization.

To be clear, cryo-EM and x-ray crystallography structures are essential to our understanding of flaviviruses; without these structures, any subsequent insight into the molecular mechanisms of neutralization would not be possible. However, examination of static structural models alone cannot explain how macroscopic phenomena, such as Ab binding stoichiometry and neutralization activity, arise from the microscopic features of the Ab-flavivirus complex. Such macroscopic characteristics are emergent properties that result from the law of mass action—the Ab and the flavivirus in solution are in a dynamic equilibrium, a stochastic process that results from innumerable binding and unbinding events between free Abs and the multiple binding sites on the flavivirus. The stochastic, heterogeneous nature of this process is even more pronounced at subsaturating Ab concentrations, where there are significant numbers of unbound binding sites. Given that the stoichiometric threshold for neutralization in flavivirus Abs can be achieved at concentrations far below saturation (14, 22), characterizing the ensemble of Ab binding configurations at these concentrations is critical to capturing the microscopic details of neutralization.

Stochastic simulations, which sample the configurational states of a molecular system using a physically realistic potential energy function, can be a useful tool for modeling a system at equilibrium and describing how macroscopic properties of a system emerge from its microscopic characteristics. The sheer size and complexity of a whole virus system typically precludes the use of atomistic-scale simulations, but coarse-grained models that reduce the size of the system while maintaining essential structural features have been used to simulate whole virus systems. Brownian-dynamics-based approaches have been used to simulate virus self-assembly and explore the formation of complex capsid geometries (23, 24). Simplified stochastic models have been used to investigate the membrane fusion in influenza (25, 26, 27, 28). In flavivirus research, Chao et al. (29) recently applied stochastic modeling to validate their experimental work aimed at understanding the mechanism of WNV fusion.

We sought to model the microscopic process of Ab-flavivirus binding by incorporating structural information from x-ray or cryo-EM studies to explore how molecular properties of Ab-flavivirus interactions can influence macroscopic observations such as antibody binding and neutralization. Toward that end, we developed a coarse-grained model of the Ab-flavivirus complex and carried out stochastic simulations using the theory of multiple equilibria in proteins (30) to generate an ensemble of virus-Ab binding configurations at a range of Ab concentrations. We carried out simulations for nine flavivirus monoclonal Abs that have epitopes defined by x-ray crystallography or cryo-EM and investigated the roles of epitope spatial arrangement, steric interactions between antibodies, and bivalent binding in Ab binding stoichiometry, epitope occupancy, and neutralization. In this approach, we assume that all epitopes are equally competent for binding and thus seek to define the upper limit of antibody binding stoichiometry that results purely from the epitope arrangement on the viral surface alone. We used a simplified representation of both the viral envelope and Abs that captures most relevant three-dimensional features of the system. We derived the geometrical parameters of the viral envelope directly from available structural data on Ab-virus complexes obtained through x-ray crystallography and/or cryo-EM studies.

Materials and Methods

We used a structure-based Monte Carlo (MC) approach to simulate Ab binding to the flavivirus whole envelope. In this approach, the virion concentration, [V], is considered infinitely dilute (virion-virion interactions are negligible) and the Ab concentration, [Ab], is much higher than [V]. We assume a Brownian-like process of Ab binding where Abs randomly collide with a virion. We wrote the software program for carrying out the stochastic simulation in FORTRAN and the program, usage instructions, and input files are available upon request.

Coarse-grained structural model of flavivirus-Ab complex

We developed coarse-grained representations of both the Abs and the viral envelope that capture the relevant geometrical features necessary to simulate Ab binding. To that end, we combined homology modeling with existing cryo-EM and x-ray structure data (see Table 1 and Section A in the Supporting Material) to construct all-atom models of the whole virus envelopes in their mature, “smooth” conformation for the four DENV serotypes and for WNV; these constructs were subsequently converted to coarse-grained models.

Table 1.

Flavivirus mAbs in This Study

mAb	Flavivirus	Method	PDB ID(s)	EMDB ID(s)	Epitope	Reference
E16	WNV	x-ray & cryo-EM	1ZTX	EMD-1234; EMD-5115	DIII	(38, 60, 61)
1F4	DENV1	cryo-EM	4C2I	EMD-2442	DI-DII hinge	(17)
14c10	DENV1	cryo-EM	3J05	EMD-5268	DI-DII hinge	(44)
5J7	DENV3	cryo-EM	3J6U; 3J6S; 3J6T	EMD-5935; EMD-5933; EMD-5934	DI-DII hinge + DIIIa	(19)
5H2	DENV4	x-ray	3UAJ; 3UC0		DI	(62)
2D22	DENV2	cryo-EM	4UIF; 5A1Z; 4UIH	EMD-2967; EMD-2996; EMD-2997; EMD-2999; EMD-2968; EMD-2998; EMD-2969	DIII-FLa	(18)
EDE1 C8	DENV2	x-ray	4UTA		DII-DIb	(22, 63)
EDE2 A11	DENV2	x-ray & cryo-EM	4UTB	EMD-2818;	DII-DIb	(22, 63)
D1-E106	DENV1	x-ray	4L5F		DIII	(45, 64)

PDB, Protein Data Bank (http://www.rcsb.org/pdb/home/home.do); EMBD, Electron Microscopy Data Bank (http://www.emdatabank.org/); DI, domain I; DII, domain II; DIII, domain III; FL, fusion loop.

^aQuaternary epitope.

^bDimer interface epitope.

We represented the viral envelope as a tessellated sphere with surface elements of equal size (31). Each surface element represents a pixel on the surface and the total number of pixels defines the resolution of the spherical grid. To compute the radius of such sphere, r_capsid, we used the all-atom homology model of the viral envelope. An epitope, ξ, on the tessellated sphere is represented by a surface patch. To produce this patch, we first selected atoms that constitute the epitope (defined by cryo-EM and x-ray structure data) from the all-atom model. The collection of surface elements on the sphere that are intersected by the radial projections of these epitope atoms constituted the epitope’s simplified representation. The epitope center, q_ξ, was computed using the radial projection onto the sphere of a nonweighted average of the coordinates from atoms belonging to a given epitope.

To simulate Ab binding without explicitly accounting for Ab orientation relative to the virus surface, during binding, we modeled the Ab as a circular “soft disk” that can interact with other Abs through steric interactions. To be considered bound, an Ab landing at a given surface element must occlude an epitope center. It is important to note that Abs can occlude a much larger surface area than their Fabs footprints, because they can bind with the Fab major axis tilted with respect to the virus surface, and because of rotational flexibility of the Fc region (13). As such, the radius of the Ab soft disk, r_Fab, reflects the Ab overall excluded volume, not just its paratope footprint size.

Another important consideration is that all structural data on Ab-virus complexes have been collected from experiments with single Fabs instead of complete Abs. Since we intended to compare our simulation results with such data, we chose a value for r_Fab that reflects the excluded volume of a single Fab. To determine a value of r_Fab, we carried out a set of simulations using the DENV1-1F4 complex. We found that a value of r_Fab = 27.8 Å reproduced the occupancy of ∼120 Fabs determined experimentally for that system (see Section B in the Supporting Material). We found that with two exceptions (2D22 and 5J7), r_Fab=27.8 Å was sufficient to reproduce overall Ab binding stoichiometry for all Abs with available cryo-EM structures. For 2D22 and 5J7, we determined that r_Fab values of 25.0 Å and 32.0 Å, respectively, most closely reproduced the total Ab binding stoichiometry from cryo-EM structures.

Ab-virus interactions

Initially, we focused on monovalent Abs and then expanded our method to accommodate bivalent binding for immunoglobulin G (IgG) Abs. To model Ab binding, we use the theory of multiple equilibria in proteins (30, 32, 33). Under this approach, Abs represent ligands and the virus envelope is the macromolecule whose binding sites correspond to the Ab epitopes. To model the behavior of this system, we adapted the methodology introduced by (34) to study pH titration in proteins.

A binding state of the viral envelope with N sites was described by a vector $\mathit{x}=\left(x_{1,}{x}_2,\mathrm{...},x_{\xi },\mathrm{...},x_N\right)$, where $x_{\xi }$ represents the binding state of the site associated with epitope ξ, and

$$x_{\xi }=\{\begin{array}{l}1\text{if}\text{Ab}\text{is}\text{bound}\text{to}\text{the}\text{site}\hfill \\ 0\text{if}\text{the}\text{epitope}\text{is}\text{free}\hfill \end{array}$$

The free energy, G(x), associated with the x state of the envelope is given by the expression

$$G\left(\mathit{x}\right)=\sum _{\xi =1}^N{x}_{\xi }\left({\epsilon }_{\xi }-{\mu }_{\text{Ab}}\right)+\frac{1}{2}\sum _{\xi =1}^N\sum _{\begin{array}{l}\eta =1\\ \xi \ne \eta \end{array}}^N{W}_{\xi \eta }{x}_{\xi }{x}_{\eta },$$ (1)

where ${\epsilon }_{\xi }$ represents the intrinsic free energy of association of the Ab to site ξ, μ_Ab is the chemical potential of the Ab in solution, W_ξη is the interaction energy between a pair of Abs bound to sites ξ and η, and N represents the total number of epitopes or binding sites in the envelope.

We consider the epitope site ξ as a collection of pixels or subsites. When the center of the Ab coincides with any of these subsites, the Ab is considered bound. The free energy of association of an Ab bound to site ξ is defined by ${\epsilon }_{\xi }={\epsilon }_{\xi }^0+w_{\xi }\left(\Delta r\right)$, where ${\epsilon }_{\xi }^0$ represents the minimum free energy due to the Ab attachment and $w_{\xi }\left(\Delta r\right)$ is the free energy due to formation of H-bonds and other types of favorable interactions. $w_{\xi }\left(\Delta r\right)$ is a function of the distance $\Delta r=\left|q_{\xi }-p\right|$ between the Ab position, p, and the epitope center, $q_{\xi }$ (see Section C in the Supporting Material). Under this assumption, Eq. 1 becomes

$$G\left(\mathit{x}\right)=\sum _{\xi =1}^N{x}_{\xi }\left({\epsilon }_{\xi }^0-{\mu }_{\text{Ab}}\right)+\sum _{\xi =1}^N{x}_{\xi }{w}_{\xi }\left(\Delta r\right)+\frac{1}{2}\sum _{\xi =1}^N\sum _{\begin{array}{l}\eta =1\\ \xi \ne \eta \end{array}}^N{W}_{\xi \eta }{x}_{\xi }{x}_{\eta }.$$ (2)

The term ${\epsilon }_{\xi }^0-{\mu }_{\text{Ab}}$ in Eq. 2 is related to the Ab-epitope intrinsic dissociation constant and the free Ab concentration by the equation

$${\epsilon }_{\xi }^0-{\mu }_{\text{Ab}}=RT\text{ln}10\left(pAb-p{K}_{\text{intr},\xi }\right),$$ (3)

where R is the gas constant; T is the temperature; $pAb=-{\text{log}}_{10}\left[Ab\right]$, where [Ab] is the free Ab concentration; $p{K}_{\text{intr},\xi }=-{\text{log}}_{10}{K}_{\text{intr},\xi }=-{\epsilon }_{\xi }^0/\left(2.303RT\right)$; and $K_{\text{intr},\xi }$ is the intrinsic dissociation constant of Ab to site ξ. All epitopes on the virus envelope are considered equivalent, i.e., $K_{\text{intr},\xi }=K_{\text{intr}}$.

Ab-Ab interactions

We follow the approach introduced by Adamczyk et al. (35, 36) to account for the steric effects between bound Abs and define the Ab-Ab interaction energy term, W_ξη, as

$$W_{\xi \eta }=W_0\frac{2}{2+H_{\xi \eta }}{e}^{-\kappa a{H}_{\xi \eta }},$$ (4)

where $H_{\xi \eta }=r_{\xi \eta }-2r_{\text{Fab}}$ represents the minimum separation between interacting Abs; $r_{\xi \eta }$ is the distance between the centers of a pair of Abs bound at sites ξ and η; W₀ is the interaction energy at zero separation; κa is a parameter that characterizes the “hardness” of the binding Ab; and $\kappa a\to \infty$ corresponds to the limiting hard-sphere behavior, whereas decreasing values are associated with Ab particles that become softer. All simulations in this work were carried out assuming a limiting hard-sphere behavior, with parameters W₀ = 200.0 kcal/mol and κa =100 Å⁻¹.

Monte Carlo-based simulation

To produce a stoichiometric curve for a given Ab-virus complex, we need to determine the average number of bound Abs, $\langle N_{\text{bound}}\rangle ,$ at different concentration values. Toward that end, we used importance sampling using MC methods (34) to simulate the Ab-virus binding process. Briefly, for each simulation run, we specified the concentration of free Abs, [Ab], and initialized the system with an Ab-free viral envelope. During the course of the MC simulation, surface elements are selected randomly, trial moves are carried out where Abs bind to or unbind from that surface element, and then the trial moves are accepted and rejected based on the Metropolis criteria. A flow chart of the algorithm and additional details can be found in Section D in the Supporting Material.

Typically, a run is completed after 10⁹ MC steps; during the run, statistics are collected every 10⁷ steps. To estimate the number of steps between collected samples, we computed a correlation time between approximately independent measurements using the methodology described by Beroza et al. (34). To produce averages for a given concentration, we used all the samples collected from 500 independent runs. All parameters used in the simulation are listed in Section E in the Supporting Material.

Simulating Ab binding and neutralization curves

We generated an Ab-binding curve from the simulation data based on the observed $\langle N_{\text{bound}}\rangle$ from simulated [Ab] conditions ranging from10⁻¹ M to 10⁻¹² M. At each concentration, we carried out 500 binding simulation runs, collecting statistics from 50,000 independent configurations. In addition, we analyzed the simulation trajectories to determine a distribution of states with respect to the number of antibodies bound. We also calculated the binding curve based on an “ideal” noninteracting multisite binding model with N binding sites, the theoretical maximum number of sites for a DENV envelope containing 180 copies of the E-protein, based on the formula (33) given by Eq. 5. This ideal binding curve reflects the binding behavior of Abs to the viral surface if there were no steric effects between Abs, and thus, it is independent of the spatial arrangement of epitopes.

$$\text{Ab}\text{Bound}\left(\left[Ab\right]\right)=\frac{N\times K_{\text{intr}}^{-1}\left[Ab\right]}{1+K_{\text{intr}}^{-1}\left[Ab\right]}$$ (5)

For binding curves, we report the maximum binding stoichiometry as well as the apparent K_d, obtained as the [Ab] value at 50% of maximal Ab occupancy.

Previous studies have suggested that Abs can neutralize flaviviruses at a stoichiometric threshold of ∼30 bound Abs (14). Given a series of M uncorrelated states of the Ab-virus complex, and counting the number of states, k, where $N_{\text{bound}}<30,$ the ratio k/M is a measure of infectivity, whereas (M – k)/M provides a measure of neutralization; these measurements can be used to compute theoretical neutralization or infectivity curves. We define the stoichiometric threshold model of neutralization as the “empirical model.” We also developed “mechanistic models” of neutralization based on definitions of the minimal number of structural elements on the flavivirus envelope necessary for membrane fusion.

Bivalent binding of IgG Abs

We extended our approach to simulate bivalent binding of IgG Abs, which contain two Fab domains capable of binding simultaneously to virus epitopes using the theoretical framework introduced by H.-X. Zhou (37). $K_{\text{Fab}}$ is the binding constant of a single Fab to an epitope, and simultaneous binding of both Fabs of a bivalent Ab leads to enhancement of the binding affinity over that of an individual Fab by a factor $p\left(d_0\right)K_{\text{Fab}},$ i.e., the binding constant, $K_{\text{dAb}}$, of the bivalent Ab becomes

$$K_{\text{dAb}}=p\left(d_0\right)K_{\text{Fab}}\times K_{\text{Fab}},$$ (6)

where p(d₀) is the probability density for the end-to-end vector (r_end-to-end) of the linker to measure d₀, and the linker region joining the Fabs is assumed to be equivalent to a flexible, noninteracting peptide fragment composed of N_AA residues. Zhou found that a good representation of p(d₀), also known as the effective concentration, C_eff, is given by an empirical formula (see Eq. 4 in (37)). For an IgG Ab, we found that the connectivity between the two Fabs is well approximated by a linker of 16–18 residues. The range of p(d₀) associated with the N_AA values used in our application can be found in the Section F in the Supporting Material.

Due to the icosahedral geometry of the flavivirus envelope, the separation and orientation between pairs of epitopes differ depending on the chosen epitope pair. Thus, only a few pairs of epitopes on the viral envelope may be bound bivalently to a single Ab. We used cryo-EM or x-ray structures of the Fabs in complex with the E-protein (see Table 1) superimposed to the whole-envelope model to identify pairs of epitopes compatible with bivalent binding.

Simulating bivalent Ab binding

To account for binding of bivalent Abs, we extended the MC procedure by introducing additional bookkeeping strategies. Fabs bound to the envelope are associated with specific Abs, and an extra set of movements with a different degree of complexity is introduced to account for association/release of the first or second Fab of an Ab.

The binding of the first Fab of an Ab is governed by Eq. 2. The change in binding energy of a bivalent Ab that binds with both Fabs simultaneously to epitopes ξ and τ, at distances Δr₁ and Δr₂, respectively, from the epitope centers is given by

$$\Delta G_{\xi ,\tau }\left(\Delta r_1,\Delta r_2\right)=\Delta x_{\xi }\Delta x_{\tau }\left[RT\text{ln}10\left(pAb-p{K}_{\text{dAb}}\right)+w_{\xi }\left(\Delta r_1\right)+w_{\tau }\left(\Delta r_2\right)+\sum _{\eta =1,\xi \ne \eta }^N{W}_{\xi \eta }{x}_{\eta }+\sum _{\eta =1,\tau \ne \eta }^N{W}_{\tau \eta }{x}_{\eta }\right],$$ (7)

where pAb = −log₁₀[Ab], [Ab] being the free bivalent Ab concentration, and pK_dAb = −log₁₀ K_dAb, K_dAb being the intrinsic association constant of a bivalent Ab, given by Eq. 6. To decide whether the second free Fab of a monovalently bound Ab should bind, we also use the Metropolis criterion. In this case, $\Delta G_{\xi ,\tau }$ is computed as the sum of two energy terms associated with 1) bivalent binding of the Ab, and 2) release of the first bound Fab.

Results and Discussion

We selected nine flavivirus mAbs that have available cryo-EM or x-ray crystal structural information (Table 1). By restricting our analysis to mAbs with high-resolution structure information, we could precisely define the antibody epitopes and parameters for the simulation.

Stochastic model of antibody binding

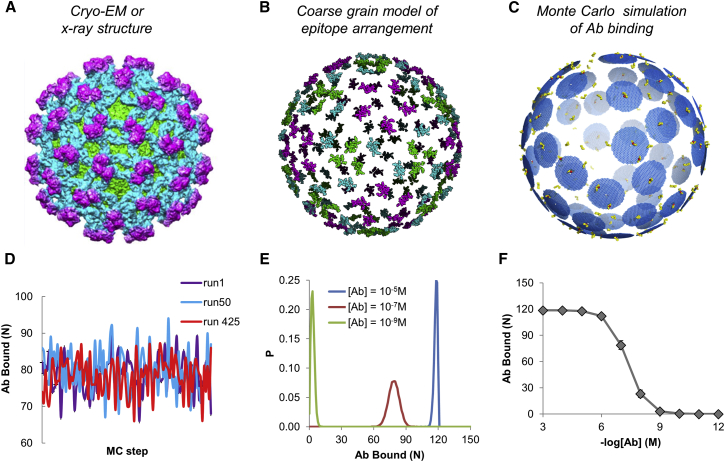
Our approach for carrying out spatial stochastic simulations of Ab binding in flaviviruses is outlined in Fig. 1. We carried out MC-based simulations using coarse-grained representations of virus-Ab complexes. Abs were represented as “soft disks” that sterically interact and interfere with one another as they bind to or unbind from the virus over the course of the simulation (Fig. 1 C). The epitopes on the virus surface are defined using cryo-EM or x-ray crystallography data. All viral epitopes are assumed to be fully accessible for binding to assess the role of epitope spatial arrangement, alone, on Ab binding stoichiometry, epitope occupancy, and neutralization. Besides epitope definitions, the only other aspect of the system that varied between different Abs was r_Fab, the parameter that determines the radius of the soft disk, analogous to a Fab “footprint,” on the virus surface. This footprint reflects the excluded area surrounding a bound Ab in which Ab-Ab steric effects interfere with the binding of a neighboring Ab, and includes other effects, such as the orientation of the Fab on the envelope surface and conformational flexibility and motions of the bound Fab and/or Ab. It is important to note that the excluded area, or footprint, of an Ab is significantly larger than the cross-sectional area of the Fab itself due to excluded volume resulting from the three-dimensional size, orientation, and flexibility of the full-length IgG projected onto the two-dimensional viral surface. We selected a value of r_Fab that most closely reproduced the total binding stoichiometry found in the cryo-EM structure, when available (see Materials and Methods).

Figure 1.

Overview of spatial stochastic model. (A) We use a whole-virus structural model, derived from x-ray or cryo-EM data along with homology modeling. (B) The epitope for a given antibody is mapped to the structure. (C) MC-based spatial stochastic simulations were carried out. (D) Number of Abs bound over the course of three example MC trajectories. (E) Distribution of viral bound states at three Ab concentrations. (F) Ab binding curve derived from MC simulations at a range of Ab concentrations. To see this figure in color, go online.

For each Ab, we carried out 500 independent trajectories per concentration value in the range 10⁻¹ to 10⁻¹² M. Three sample trajectories are displayed in Fig. 1 D, showing how the number of Abs bound $\left(N_{\text{bound}}\right)$ to a single virion varies over the course of the MC trajectory. We used the MC trajectories to calculate a distribution of states with respect to $N_{\text{bound}}$ at each Ab concentration simulated (Fig. 1 E). We used the mean $N_{\text{bound}}$ ($\langle N_{\text{bound}}\rangle$) at each concentration to calculate an Ab binding curve as a function of Ab concentration (Fig. 1 F). For all Abs, we kept several parameters fixed to observe the effect of epitope arrangement alone on the binding stoichiometry and relative occupancy: we set the binding constant $K_{\text{intr}}$ to 10⁻⁶ M, and the Ab radius (r_Fab) was set to 27.8 Å for all but two antibodies (PDB: 2D22 and PDB: 5J7).

Antibody binding stoichiometry and neutralization

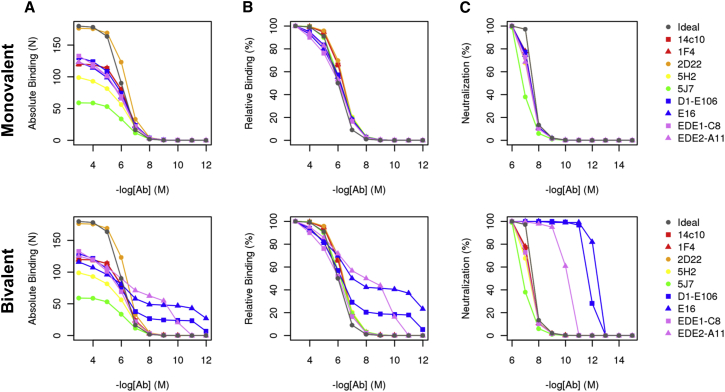
We carried out binding simulations for nine flavivirus Abs at concentrations ranging from 10⁻³ to 10⁻¹² M. The resulting binding curves (Fig. 2 A) reveal significant differences in $\langle N_{\text{bound}}\rangle$ between different flavivirus Abs, especially at higher concentrations. We compared these binding curves to a binding curve based on an “ideal” noninteracting multisite binding model with 180 binding sites (see Materials and Methods). The ideal binding curve showed substantially higher $\langle N_{\text{bound}}\rangle$ values than the stochastic binding simulations for all the Abs except 2D22, demonstrating that most Abs are unable to reach the maximum limit of 180 Abs due to steric interference. On the other hand, the relative binding curves (Fig. 2 B) show that all Abs have results similar to that of the ideal binding curve. These results suggest that Ab steric interactions and epitope arrangement affect the absolute number of Abs bound at a given Ab concentration, but not the overall shape of the binding curve.

Figure 2.

Monovalent and bivalent binding curve and neutralization curves for flavivirus Abs. (A) Absolute binding curve showing the number of Abs bound as a function of Ab concentration for monovalent (top) and bivalent (bottom) binding simulations. (B) Relative binding curve showing the percentage of Abs bound as a function of concentration relative to the maximum number of Abs bound for for monovalent (top) and bivalent (bottom) binding simulations. (C) Neutralization curve, represented by the percentage of the virus population with >30 Abs bound at each concentration for monovalent (top) and bivalent (bottom) binding simulations. To see this figure in color, go online.

We compared $\langle N_{\text{bound}}\rangle$ at saturating conditions in our simulations ([Ab] = 10⁻⁴ M) with the number of Fabs found to be bound in cryo-EM structures (see Table 3). We found that for four of the five cases where cryo-EM information was available, our simulations closely reproduced the cryo-EM binding stoichiometry. For EDE2-A11, our simulation found approximately two-thirds of the total number of antibodies bound. It is important to note that since cryo-EM structures describe the binding stoichiometry at saturating Ab concentration, it is not sensitive to differences in intrinsic K_d values between Abs.

Table 3.

Bivalent Ab Binding

Name	Minimal ${\mathit{r}}_{\text{epi}}\left(\text{Å}\right)$	Minimal $r_{\text{end-to-end}}\left(\mathrm{\AA }\right)$	Total Bound (N)	Peak Bivalently Bound (N)	Kdapp,1 (μM)	Kdapp,2 (nM)	IC50 (nM)	Bivalent IC50 Enhancement
E16	55.5	31.2	120	48	2.2	0.001	0.0004	62,500
D1-E106	51.5	40.2	129	26	1.3	0.002	0.002	12,500
EDE2-A11	52.8	31.4	125	70	12.6	0.3	0.06	42
5H2	54.9	48.1	107	40	0.5	0.02	25	1
2D22	51.9	55.8	176	0	0.5	–	25	1
EDE1-C8	55.0	62.4	141	0	1.3	–	25	1
1F4	47.8	66.6	120	0	0.5	–	25	1
14c10	52.3	82.6	120	0	0.5	–	25	1
5J7	55.0	84.8	59	0	0.6	–	63	1

Previous in vitro studies (14) suggest that a stoichiometric threshold of 25–30 bound antibodies is sufficient for neutralization. To model the implications our simulated binding curves may have for neutralization, we developed a simple empirical model. Using the virus distribution of states at each Ab concentration, we defined neutralization as the percentage of the viral population with $N_{\text{bound}}\ge 30$.We also calculated a simulated IC50 as the Ab concentration that results in 50% neutralization, which is summarized for all Abs in Table 2. We found that despite the differences in the maximum binding stoichiometry of different Abs at saturating concentrations, all Abs that bound had very similar neutralization curves and IC50 values (Fig. 2 C), showing that differences in maximum Ab binding stoichiometry do not play a major role in determining neutralization activity for these highly neutralizing flavivirus Abs.

Table 2.

Maximum Ab Occupancy

Name	${\mathit{r}}_{\text{Fab}}$ (Å)	Cryo-EM				Simulated
		Total	A	B	C	Total	A	B	C	Kdapp (μM)	IC50 (nM)
		(N)				(N)
Ideal	–	–	–	–	–	180	60	60	60	1.0	25
2D22	25.0	180	60	60	60	176	59	59	59	0.4	20
EDE1-C8	27.8	–	–	–	–	141	59	51	31	1.3	25
D1-E106	27.8	–	–	–	–	132	60	60	12	0.4	25
EDE2-A11	27.8	180	60	60	60	131	51	29	51	1.0	25
E16	27.8	120	60	60	0	130	59	59	12	0.8	25
14c10	27.8	120	0	60	60	120	13	47	60	0.5	25
1F4	27.8	120	0	60	60	120	17	43	60	0.5	25
5J7	32.0	60	–	–	60	59	0	13	46	0.7	63
5H2	27.8	–	–	–	–	107	15	43	48	0.5	25

Epitope-level binding preferences

The 180 E-proteins on the flavivirus surface are arranged in an icosahedral geometry in such a manner that there are three distinct symmetrically related environments for a given E-protein epitope. We define epitopes A, B, and C to correspond to epitopes along the threefold, twofold, and fivefold axes of symmetry, respectively. Each of these epitopes is found in a different environment with respect to its spatial relationship to surrounding epitopes, which can affect their binding occupancies. In cases where epitopes involve residues from more than one E-protein, we categorize them according to their proximity to axes of symmetry of the envelope.

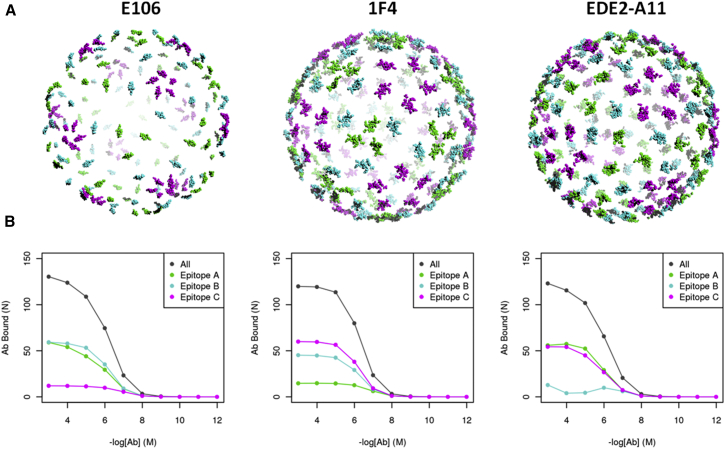
Fig. 3 shows representative examples of epitope binding occupancy for Abs E106 and 1F4. E106, which binds to an epitope on DIII, preferentially binds to A and B epitopes, corresponding to the threefold and twofold axes of symmetry. Steric interactions among Abs lead to a low occupancy of C epitopes, which are in close proximity to one another on the envelope surface, as shown in Fig. 3, top left. By contrast, 1F4, which binds to an epitope on the DI-DII hinge region of E-protein, preferentially binds to B and C epitopes, corresponding to the fivefold and twofold axes of symmetry. As with E106, the close arrangement of A epitopes for 1F4 precludes high-occupancy binding.

Figure 3.

Structure and relative occupancy of symmetry-related epitopes. (A) Whole-virion structure used for binding simulations for flavivirus Abs E106 (left), 1F4 (middle), and EDE2-A1 (right), showing epitopes colored with respect to their symmetry-related epitope environment for the threefold (epitope A, green), twofold (epitope B, cyan), and fivefold (epitope C, magenta) axes of symmetry. (B) Binding curves showing Ab occupancy at epitopes A, B, and C, as well as total Ab occupancy from monovalent binding simulations of the respective Abs. To see this figure in color, go online.

The occupancies at each of the three epitope environments are shown in Fig. S2 A. Overall, Abs, except 5J7, showed at least some binding to all three epitope environments in our simulations. 5J7 binds to an epitope that spans the E-dimer interface and is only coherent in B and C epitopes. Another outlier, 2D22, also binds to an epitope along the E-dimer interface, shows almost total occupancy, with $\langle N_{\text{bound}}\rangle$ of 176, and thus binds equally to all three epitope environments. We also compared the occupancy in each of these three epitope environments through cryo-EM data, when available (Fig. S2 A) and found good agreement of the relative occupancies at epitopes A, B, and C.

We sought to determine whether there were any discernible patterns between the relative occupancies of these epitope regions. A pairwise comparison of the relative occupancies at each epitope type (Fig. S2 B) revealed that occupancy at epitope A was inversely correlated with occupancy at epitope C (R = 0.87) and that occupancy at epitope C was inversely correlated with occupancy at epitope B (R = 0.47). These results suggest that those epitopes associated with high occupancy at the threefold axis of symmetry had correspondingly low occupancy at the fivefold axis, and that epitopes with high occupancy at the fivefold axis of symmetry had relatively lower occupancy at the twofold axis. It is unclear what particular role, if any, E-proteins in the different symmetry environments play in neutralization, beyond the contribution of their epitopes to the overall antibody binding stoichiometry. However, our results show that there is substantial variation in the relative occupancies at these epitopes across flavivirus Abs, and that there is competition between the different epitope regions.

It is important to note that all 180 epitopes were equally competent for binding in our simulation and thus reflect an upper limit of Ab binding stoichiometry that results from epitope spatial arrangement alone. Surprisingly, we found that this upper limit closely reproduced the total binding stoichiometry observed in cryo-EM data and the relative preference of each Ab for epitopes along the threefold, twofold, or fivefold axis (Fig. S2 A). These results suggest that two factors alone, 1) the spatial arrangement of epitopes along the virus envelope and 2) the Fab radius, are sufficient to explain differences in epitope preference between Abs. This represents a plausible alternative explanation for the variation in epitope preferences across flavivirus Abs compared to the traditional explanations that focus on differences in epitope conformation or accessibility. Furthermore, the overall spatial arrangement of epitopes across the viral envelope is robust to relatively large conformational changes in the envelope, explaining how such epitope preferences can persist even in the face of substantial viral conformational heterogeneity or Ab-induced conformational changes.

Partial occupancy and heterogeneity

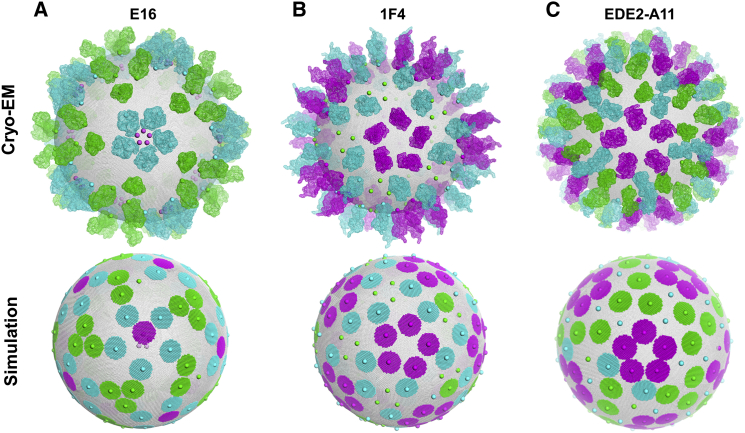
Given that cryo-EM structures are typically determined at saturating Ab concentrations, we compared the binding configurations from simulations at high Ab concentration (10⁻⁴ M) with the electron density maps from the respective cryo-EM structures (Table 1). Fig. 4 A shows a reconstructed cryo-EM model using the electron density map for E16 (38) along with a representative binding configuration from the simulation for E16. In the simulation, E16 shows 100% occupancy at A and B epitopes and 20% occupancy for epitope C, as a result of steric exclusion by neighboring bound Abs. The cryo-EM structure of E16 shows 100% occupancy of epitopes A and B, but shows 0% occupancy for epitope C. In 1F4, we find a similar discrepancy between the cryo-EM structure (17) and the simulation results with respect to binding at epitope A (Fig. 2 B). Our simulations show an ∼20% occupancy at epitope A, whereas the cryo-EM structure shows no Ab bound along that epitope. Other examples of partial occupancy in simulations include Abs D1-E106, 14c10, and 5F7, where we observed occupancies of ≤20% at one of the three epitope environments.

Figure 4.

Comparison of simulated binding configuration with cryo-EM structures. Cryo-EM reconstructions for E16 (A), 1F4 (B), and EDE2-A11 (C) (top) are shown with Fabs colored with respect to binding to epitope A (threefold axis, green), epitope B (twofold axis, cyan), and epitope C (fivefold axis, magenta). Representative binding configurations from simulations run at a saturating Ab concentration (10⁻⁴ M) for E16, 1F4, and EDE2-A11 are shown in the bottom row. Colored circles represent bound Abs, colored with respect to binding to epitopes A, B, and C, as described above. The center of each epitope on the flavivirus envelope surface is shown as a solid sphere, also colored according to epitopes A, B, and C, as described above. Spheres that are covered with a Fab structure (top) or Ab circle (bottom) represent bound epitopes; uncovered spheres represent unbound epitopes. To see this figure in color, go online.

Available cryo-EM structures for all the Abs in the data set show an all-or-nothing pattern of Ab binding—epitopes A, B, and C each show either 100% or 0% occupancy. A complementary example of this pattern can be found in the structure of EDE2-A11 (22) (Fig. 4 C), where the cryo-EM structure shows 100% occupancy at all three epitopes, whereas the simulations of EDE2-A11 show a partial occupancy of 50% at epitope B. In this case, Dejnirattisai et al. (22) noted that there is weaker electron density corresponding to epitope B, supporting the theory that there is partial occupancy at this position. A parsimonious explanation for the discrepancy in occupancy between the simulations and the cryo-EM structures is that a partial occupancy of <20% may be represented by weak or background-level electron density in cryo-EM and thus determined to be unoccupied, whereas a partial occupancy of >80% may be determined to be fully occupied in cryo-EM. In a study of cryo-EM structures of Ab-virus complexes, Thouvenin and Hewat found that the fitting of Ab structures to the cryo-EM density was highly unreliable at partial occupancies of <50% and that the variation in density at regions with full occupancy was ±15% (39), which suggests minimal and maximal limits for detectable partial occupancy of 15% and 85%, respectively. Previous cryo-EM studies of Ab-virus complexes have reported partial occupancies of 40–50% (40, 41), whereas structures with partial occupancy of 20% do not reliably show density in icosahedral averaged structures (42, 43). In the latter cases, low partial occupancy was detected based on the presence of a high-occupancy non-Fab-like overlap density of multiple overlapping low-density Fabs (42) or through the use of asymmetric reconstruction methods (43).

Previous structural studies typically account for the 0% occupancy at certain epitopes (A, B, or C) by suggesting that conformational or environmental differences between those epitopes may be responsible for preventing proper antibody binding. For example, Kaufmann et al. (38) and Fibriansah et al. (17) attribute the lack of binding of E16 to epitope C and of 1F4 to epitope B, respectively, to possible steric hindrance of neighboring E-proteins in those epitopes to Ab binding. Dejnirattisai et al. (22) suggest that differences in epitope presentation between epitope B and epitopes A and C are responsible for the weaker Ab binding to epitope B in EDE2-A11. Most strikingly, Teo et al. explain the fact that 14c10 binds to only B and C epitopes by asserting that its epitope spans across the DII/DIII domain of E in one dimer and the DI domain of E in a neighboring dimer, in such a manner that these two putative epitope regions are only adjacent to each other on the twofold and threefold axes (44). However, a close examination of the structure reveals that 13 of the 16 epitope residues for 14c10 are found on DII/DIII of a single E-protein, and there is little consistency between the DI epitope residues between epitopes along the twofold and threefold axes, calling into question whether those DI residues are critical to binding. In all cases, the apparent lack of Ab binding to epitope A, B, or C, led authors to search for relatively small conformational differences that could be responsible. By contrast, in our simulations, differences in binding preferences and partial occupancy at these epitopes arise purely from the stochastic nature of the binding process and the steric interference from neighboring Abs due to a given epitope arrangement along the flavivirus surface.

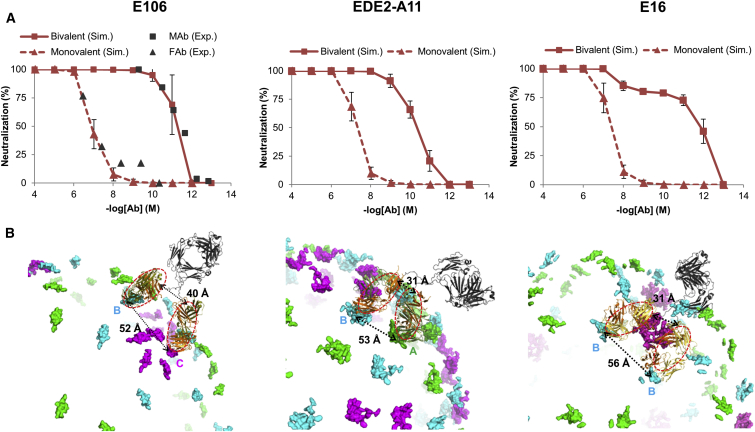
Bivalent antibody binding

Previous structural studies of flavivirus-Ab interactions have been limited to Abs in the form of single Fab, Fv, or scFv fragments bound monovalently to the antigen. However, a full-length IgG mAb contains two identical Fabs that are capable of binding simultaneously, or bivalently, to the same antigen. Previous studies have shown that bivalent binding of Abs can play a major role in viral neutralization (45, 46). We used x-ray and cryo-EM structures to carry out binding simulations explicitly allowing for the formation of bivalent Ab interactions. Using an approach developed by (37), we modeled a full-length mAb as two Fabs connected by a linker, such that the binding of one Fab increased the effective concentration (C_eff) within a given radius around that first bound Fab. C_eff was a function of two parameters, r_end-to-end, which is the distance between the distal ends of a pair of adjacently bound Fabs, and N_AA, the number of amino acids that form the linker between the two Fabs in the IgG. For each Ab in the data set, r_end-to-end was determined from either cryo-EM structures or whole-virus reconstructions modeled using x-ray structures. N_AA was determined from the structure and amino acid sequence of the related IgG2a mAb (47) and was set to 18. Using this model for bivalent antibody binding in our simulations, we sought to assess the role that epitope arrangement along the icosahedral geometry of the envelope plays in mediating bivalent Ab binding interactions in flaviviruses.

Fig. 2, A–C (bottom row) shows binding curves from the simulations that allow for bivalent antibody binding. Overall, we found that three of nine flavivirus Abs—D1-E106 and E16, which have DIII epitopes, and EDE2-A11, which has an epitope along the E-dimer interface—showed substantial bivalent binding. In all three cases, two distinct titration points are apparent in the binding curve, with the second titration point being at a concentration of [Ab] ≪ K_d. Table 3 lists the bivalent binding simulation results for all nine Abs, as well as the r_end-to-end values used for that Ab. We found that only Abs with a minimal interepitope distance of <60 Å, and an r_end-to-end value of <50 Å show bivalent binding. This is a result of the limited ability of the 18-amino-acid linker between the two Fabs to provide an increased C_eff at r_end-to-end > 50 Å.

Our results show that pairwise interepitope distance alone (r_epi) is a poor predictor of whether an Ab would undergo bivalent binding, and that bivalent binding is primarily dependent on the end-to-end distance (r_end-to-end) between the bound pair of Fabs, which is determined by the position and orientation of the bound Fab on the virus surface. For example, EDE2-A11 and EDE1-C8 have similar epitopes with nearly identical interepitope distances of 53 Å and 55 Å, respectively. However, EDE2-A11 displays modest bivalent binding, whereas EDE1-C8 displays none, because EDE2-A11 and EDE1-C8 Fabs engage their epitopes at very different orientations, resulting in drastically different Ab end-to-end distances (31 Å and 62 Å, respectively).

For Abs E16, E106, and EDE2-A11, we found that bivalent binding leads to increased binding to the virus compared to the monovalent simulations at concentrations of [Ab] < K_intr. We note that the bivalent binding curve can be represented as the sum of two monovalent binding curves, each with their own maximum occupancy and K_d (referred to as K_d1 and K_d2 for monovalent and bivalent curves, respectively) (Fig. S3). As in the monovalent simulations, in the bivalent simulations, K_d1 is similar across all three Abs, ranging from 1.3 to 12.6 μM. However, K_d2 varied over a greater range, from 0.001 nM to 0.3 nM for E16 and EDE2-A11, respectively. Furthermore, the peak number of sites that was engaged by bivalent Abs varied as well, from 26 for D1-E106 to 70 for EDE2-A11. These results show that 1) some flavivirus Abs are capable of bivalent binding given the constraints imposed by the icosahedral viral geometry; 2) enhancement of neutralization due to bivalent binding (relative to monovalent binding) is primarily seen at concentrations of [Ab] < K_d; and 3) the degree of neutralization enhancement due to bivalent binding is highly sensitive to both the arrangement of epitopes and the orientation of the bound Fab on the viral surface.

A closer look at bivalent binding in E106, E16, and EDE2-A11

To our knowledge, only a single study (Edeling et al. (45)) has examined the possibility of bivalent Ab binding in flaviviruses. In that study, Ab E106 was found to have significant bivalent binding, and as such, we compared monovalent and bivalent binding simulations of Ab E106 with experimental data from Edeling et al. (45) to determine whether our simulation could model the enhancement of neutralization between the full-length mAb and the Fab observed in that study. We set the intrinsic K_d in the simulations to the experimentally observed K_d value of 4.8 μM (45), and then carried out the bivalent simulation of E106 using the same parameters. Fig. 5 A shows that the neutralization curves of E106 in the monovalent and bivalent simulations closely matched the experimentally derived neutralization curves for the Fab and the mAb, demonstrating that the monovalent simulation quantitatively reproduces the neutralization curve from the experimental data, and that the bivalent simulation successfully captures the neutralization enhancement of bivalent binding. Furthermore, our model provides some structural insights into E106 interactions. Edeling et al. (45) used molecular modeling to predict that bivalent binding for E106 happened across pairs of epitopes along the twofold (B-B pairs) and two- and fivefold axes (B-C pairs), leading to up to 48 sites being paired in bivalent engagement. Our simulations reveal that bivalent binding between B and C epitopes alone (26 binding sites) is sufficient to reproduce the neutralization enhancement seen experimentally, and that binding between B epitopes is unlikely due to a large end-to-end distance (∼49 Å) between a pair of Fabs bound along a B-B epitope pair.

Figure 5.

Modeling bivalent binding of IgG antibodies to flavivirus. (A) Neutralization curves from monovalent and bivalent binding simulations for Abs E106, EDE2-A11, and E16. Experimental data for Fab and MAb neutralization for E106 was derived from (45). (B) Molecular models of bivalent binding for IgG Abs E106, EDE2-A11, and E16. Epitopes A (threefold axis), B (twofold axis), and C (fivefold axis) on the flavivirus envelope are colored green, cyan, and magenta, respectively. Fabs are noted with a red dotted circle. To see this figure in color, go online.

We used molecular modeling to reconstruct the structures of the full-length IgG Ab bound to the flavivirus surface for the three bivalent-binding Abs E16, E106, and EDE2-A1. For each Ab, we used superposition of x-ray structures of the Fab-E-protein complex with cryo-EM structures of the whole flavivirus envelope to define the Fab positions of the bound full-length mAb. We used loop modeling and a representative Fc region structure (PDB: 1IGT) to reconstruct the entire full-length IgG. For each Ab that showed bivalent binding in simulation, we were able to generate plausible molecular models that satisfied the steric and geometric constraints imposed on the flavivirus envelope structure for bivalent binding (Fig. 5 B).

A structure-based explanation for the stoichiometric threshold of neutralization

Using two independent approaches, Pierson et al. (14) found that ∼30 Abs bound, achieved by a relatively low occupancy of 25% of binding sites occupied, was sufficient to neutralize WNV using a set of DIII-specific Abs. This threshold of $N_{\text{bound}}$ = 30 formed the basis of our empirical model of neutralization. Although this range of values is in line with what is expected based on the “coating” theory of antibody neutralization (12, 15, 16), as yet, there is no structural explanation as to the mechanism that underlies this threshold. Current theories of flavivirus infection suggest that the formation of at least two or more fusogenic E-protein trimers, formed from prefusion E-protein dimers, is necessary to initiate membrane fusion (48). The fact that the number of Abs sufficient for neutralization (N = 30) is lower than the number of potential trimers that can form from dimers on the viral envelope (N = 60), suggests that higher-order arrangements of trimers are necessary for fusion. We hypothesized that Abs that inhibit infection at the postattachment stage disrupt the formation of these fusogenic trimers, and that the number of Abs needed to neutralize the virus is related to the number and spatial arrangement of these fusogenic trimers necessary for fusion. In other words, flaviviruses require a minimal number and/or arrangement of fusogenic trimers for fusion, which we term a “minimal fusogenic element,” and the stoichiometric threshold of 30 Abs corresponds to the average minimal number of bound Abs needed to disrupt all possible fusogenic elements on the viral surface.

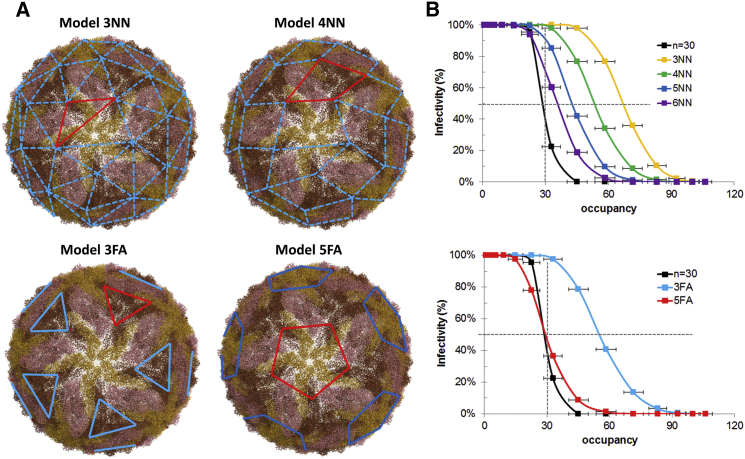
We developed a structure-based model for neutralization to explore the link between the binding configurations generated in our simulations with the neutralization stoichiometry determined experimentally. First, we randomly assigned each E-protein monomer on the virus surface to belong to one of 60 possible E-protein trimers. Then, we defined minimal fusogenic elements as a combination or arrangement of N putative trimers. Finally, we defined a fusogenic element as “obstructed” if an Ab was bound to at least one of its component E-protein monomers, and we defined a particular virus-Ab binding configuration as neutralized if all possible fusogenic elements on that virus were obstructed. We used the binding configurations from simulation to calculate the percentage of bound states that had at least one unobstructed fusogenic element, and was thus infectious, for each simulated Ab concentration.

We defined two types of minimal-fusogenic-element models, a nearest-neighbor (NN) model, which postulates that some number of adjacent fusogenic trimers is necessary for membrane fusion, and a fold-axis (FA) model, which postulates that fusogenic trimers along one of the icosahedral axes of symmetry is necessary for fusion. We tested four NN models assuming coordination among a progressively larger number of fusogenic trimers, from three to six (3NN to 6NN models, respectively) and two FA models that assume coordination among fusogenic trimers along the threefold and fivefold axes (3FA and 5FA models, respectively). Fig. 6 A illustrates putative trimer positions for fusogenic elements for each model. We defined the percent infectivity of a viral population as the percentage of that population that has at least one fusogenic element free from Ab binding. Using binding configurations generated at the range of Ab concentrations for each Ab in the data set, we calculate the percentage (%) of infectivity as a function of Ab concentration using each of the NN and FA models for Ab E16, which was one of the Abs used by Pierson et al. (14) to determine the stoichiometric threshold of ∼30 Abs.

Figure 6.

Minimal fusogenic element model of flavivirus neutralization. (A) Representative fusogenic elements are shown as a red line for nearest-neighbor models 3NN and 4NN and symmetry-axis models 3FA and 5FA. Dotted lines represent degenerate fusogenic element definitions; straight lines indicate a single defined fusogenic element. (B) Percentage of infectivity, measured as the percentage of the viral population with at least one unbound fusogenic element according to the NN models (top) or FA models (bottom), are plotted against occupancy, the number of antibodies bound, for Ab E16. The infectivity and occupancy for the empirical neutralization model (n = 30) is also shown. The data points were collected from binding simulations at Ab concentrations ranging from 10⁻⁶ to 10⁻¹² M. Dotted lines show 50% infectivity at an occupancy of 30 Ab, determined experimentally for E16 (14). To see this figure in color, go online.

We compared the infectivity-versus-occupancy curves for each of the neutralization models with the empirical neutralization model used earlier in this study (Fig. 6 B). For the NN model, our results show that even at unexpectedly high numbers of coordinating trimers, such as six trimers, there is at least one minimal fusogenic element that is free of Ab binding at an occupancy of $\langle N_{\text{bound}}\rangle$ = 30. This is because the fusogenic elements in NN models have a high degree of degeneracy, and a large number of Abs must be bound to block all possible fusogenic elements. By contrast, in FA models, we find that the 5FA model, which postulates that trimer formation along the fivefold axis is necessary for fusion, closely reproduces the empirical model and shows ∼50% neutralization at $\langle N_{\text{bound}}\rangle$ = 30. Based on our results, the observation that a relatively low occupancy of 30 Abs is sufficient for neutralization suggests that a higher-order assembly is required for fusion that either contains a very large number of trimers (more than six) or is restricted to a particular spatial arrangement, such as trimers along the fivefold axis of symmetry.

Although no one, to our knowledge, has previously proposed the importance of conformational changes along the fivefold axis of symmetry as being important for fusion in flaviviruses, such a finding is not without precedent. Sanchez-San Martin et al. reported that the E1 envelope from Semliki Forest virus, was found to associate with membranes in an in vitro assay in its truncated (soluble) form by forming clusters of five and six trimers (49). Of more importance, using a combination of x-ray crystallography and cryo-EM, Gibbons et al. found that the same E1 protein in Semliki Forest virus forms a ring of five trimers along the fivefold axis in an early step of membrane fusion, before the formation of a fusion pore or channel (48). Both the E-protein of flaviviruses and the E1-protein of alphaviruses are classified as class II fusion proteins and share similar domain architecture, and thus, they may have similar mechanisms of fusion.

Conclusions

Recent cryo-EM studies of flaviviruses reveal significant variations in epitope occupancy and binding stoichiometry across different mAbs. Reasons for these variations are typically attributed to relatively small conformational differences between symmetry-related epitopes that interfere with Ab binding or alter epitope accessibility. Although certainly plausible, such explanations seem at odds with evidence that 1) flaviviruses undergo considerable conformational fluctuations in solution, and 2) Ab binding can induce significant conformational changes. Using stochastic binding simulation based on cryo-EM structures, we found that epitope arrangement and antibody steric interactions alone were sufficient to explain differences in Ab binding preferences, suggesting that minor differences in epitope accessibility do not play a significant role in determining relative epitope occupancies in these highly neutralizing flavivirus Abs. Our results also showed that there was considerable heterogeneity in Ab binding configurations, even at saturating concentrations, that bivalent Ab binding was possible within the structural constraints imposed by the icosahedral geometry of the flavivirus envelope, and that the relatively low stoichiometric threshold of neutralization in flaviviruses may be a result of a fusion mechanism that involves the coordination of higher-order arrangements of E-protein trimers.

Author Contributions

D.R. and I.K. developed the stochastic model for antibody binding. D.R. carried out the simulations and the data analysis. D.R., A.W., and S.C. prepared the manuscript.

Editor: Tamar Schlick.

Supporting Citations

References (50, 51, 52, 53, 54, 55, 56, 57, 58, 59) appear in the Supporting Material.