Charge Distribution Fine-Tunes the Translocation of α-Helical Amphipathic Peptides across Membranes

Abstract

Hundreds of cationic antimicrobial and cell-penetrating peptides (CPPs) form amphipathic α-helices when bound to lipid membranes. Here, we test two hypotheses for the differences in the ability of these peptides to translocate across membranes. The first, which we now call the hydrophobicity hypothesis, is that peptide translocation is determined by the Gibbs energy of insertion into the bilayer from the membrane interface. The second, which we call the charge-distribution hypothesis, is that translocation is determined by whether the distribution of cationic residues in the peptide can transiently stabilize a high-energy inserted intermediate by forming salt bridges to the phosphates of lipid headgroups. To test these hypotheses, we measured translocation of two series of peptide variants. The first series was based on TP10W, a peptide derived from the amphipathic CPP transportan 10; the second was based on DL1a, a synthetic peptide derived from staphylococcal δ-lysin. The peptides in those two series had small sequence changes relative to TP10W and DL1a: either single-residue substitutions or two-residue switches, which were designed to increase or decrease translocation differently according to the two hypotheses. We found that with regard to the changes introduced in the sequences, five out of six peptide variants translocated in agreement with the charge-distribution hypothesis, whereas none showed agreement with the hydrophobicity hypothesis. We conclude that large effects on translocation are probably determined by hydrophobicity, but the fine tuning appears to arise from the distribution of cationic residues along the peptide sequence.

Introduction

The discovery of cell-penetrating peptides (CPPs) was an exciting event for two reasons (1, 2, 3, 4). From a biological point of view, CPPs could be carriers of cargo into cells, with a vast field of potential applications, especially in human health (5). From a physical chemistry point of view, they present an intriguing problem: How can these peptides, the majority of which bear large positive net charges, cross the nonpolar interior of a lipid bilayer? The energy required to place a charge in a membrane was estimated to be ∼40 kcal/mol (6). Even forming an ion pair would not make matters much more favorable, as long as the interaction is electrostatic (noncovalent). The establishment of a salt bridge—a hydrogen bond between an anion and a cation—between the side chains of aspartate or glutamate and arginine or lysine has been estimated to lower the Gibbs energy of those groups by 4 kcal/mol in octanol (7). Octanol was used as a mimic of the lipid-bilayer interior (8, 9). Slightly less unfavorable Gibbs energies may thus be obtained for the movement of charged peptides across a membrane. These values, however, are still much too large for direct movement through the membrane to appear to be a realistic mechanism for CPP translocation. Yet these peptides cross membranes, and some even cross pure lipid bilayers.

Various mechanisms have been proposed for the translocation of CPPs across membranes and their entry into cells (10). Initially, some peptides, such as the HIV tat peptide and penetratin, were thought to cross cell plasma membranes passively. In lipid vesicles containing negatively charged phospholipids, polylysine appears to translocate by first associating with the membrane surface and then forming various types of invaginations that culminate in their release in the vesicle lumen (11). CPPs have also been shown to move through nonpolar solvents if coupled with phosphates or other anionic counterions (12, 13, 14). Most of these CPPs are highly cationic, often with a high density of arginine residues, including peptides such as nonarginine (15, 16). However, studies in lipid vesicles have cast much doubt on the ability of some of these CPPs (penetratin, tat, or polyarginine) to cross bilayers (17, 18). In cells, the mechanism probably involves endocytosis (5).

Other CPPs also contain a large fraction of hydrophobic residues in addition to many cationic residues. In some cases, this combination results in the formation of an amphipathic structure on the membrane, as, for example, in transportan 10 (TP10) (19, 20, 21). There is now strong evidence that peptides with large fractions of cationic and hydrophobic residues are indeed able to translocate passively across the bilayers of simple lipid vesicles (22, 23, 24, 25, 26).

We have concentrated our investigations on these peptides, which are positively charged but also amphipathic, and which form an α-helix when bound to the membrane surface (27, 28, 29). We have examined the interactions of a large number of such peptides with lipid vesicles composed exclusively of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC). These lipids are zwitterionic, and therefore, the membrane has no net charge. In particular, we have measured peptide binding to vesicles, peptide-induced flux into or out of lipid vesicles, and, more recently, peptide translocation (26). We observed that peptides for which the Gibbs energy of insertion $\left(\Delta G_{\text{ins}}^{\text{o}}\right)$ was <$\sim 20$ kcal/mol caused graded flux of dye (carboxyfluorescein (CF)) from large unilamellar vesicles (LUVs; diameter, $\sim 0.1$ μm) prepared by extrusion, whereas peptides with $\Delta G_{\text{ins}}^{\text{o}}\gg 20$ kcal/mol caused all-or-none flux (27). We hypothesized that those peptides with $\Delta G_{\text{ins}}^{\text{o}}<20$ kcal/mol translocated across the bilayer, whereas those with $\Delta G_{\text{ins}}^{\text{o}}\gg 20$ kcal/mol did not. We call this the hydrophobicity hypothesis (Fig. 1 A). The rationale is that a smaller Gibbs energy of insertion allows the peptides to move through the bilayer nonpolar interior to dissipate their mass imbalance across the membrane. On the other hand, above that energetic threshold, insertion would be too costly; thus, the peptides accumulate on the membrane surface until the mass imbalance across the membrane is too high to accommodate, resulting in a more drastic membrane disrupture, perhaps by forming a large pore (27). We further conjectured that graded dye flux occurred as peptides translocated, whereas all-or-none flux was a consequence of large pores formed in membranes by peptides that were not able to translocate. We later examined dye flux into giant unilamellar vesicles (GUVs; diameter, $\sim 0.1$–100 μm) caused by the same peptides and realized that there is no general relation between flux type (graded or all-or-none) and $\Delta G_{\text{ins}}^{\text{o}}$ (30).

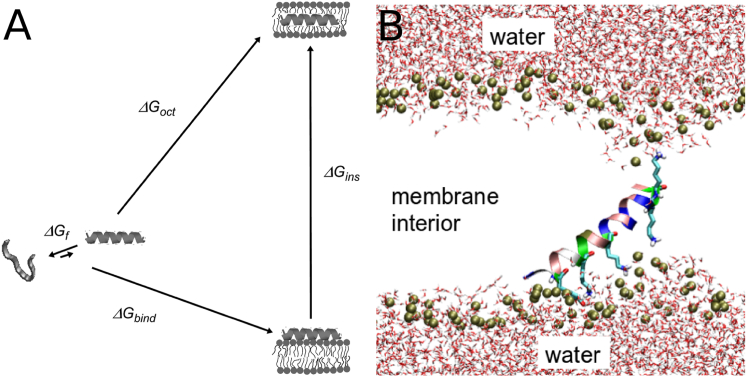
Figure 1.

(A) The hydrophobicity hypothesis. Shown is the thermodynamic cycle for the interactions of a membrane-active peptide with a membrane. The peptide is shown in water (left) and on the membrane interface (bottom right) or inserted into the bilayer (top right)—no orientation is implied. The Gibbs energies in each step are $\Delta G_{\text{bind}}$, binding to the bilayer interface; $\Delta G_{\text{oct}}$, insertion into the bilayer core, approximated by transfer to octanol; $\Delta G_{\text{ins}}=\Delta G_{\text{oct}}-\Delta G_{\text{bind}}$, insertion into the bilayer interior; and $\Delta G_{\text{f}}$, folding in water. (B) The charge-distribution hypothesis. Shown is the final state of an MD simulation of TP10W placed in a lipid bilayer. The salt bridges between the lysine residues of the peptide and the phosphate headgroups of the lipids stabilize the high-energy inserted intermediate. The scheme in (A) was reprinted with permission from Yandek et al. (21). The image in (B) was reprinted with permission from Dunkin et al. (31). To see this figure in color, go online.

However, independent of graded or all-or-none flux, the question remains whether there is a relation between $\Delta G_{\text{ins}}^{\text{o}}$ and peptide translocation consistent with the hydrophobicity hypothesis (27). To assess its plausibility, we examined the translocation of some of those peptides in GUVs using a new method (26). The results essentially supported the conjecture that the lower the Gibbs energy of peptide insertion, the more likely is translocation. We examined translocation of three peptides with very different sizes: TP10W (AGWLLGKINLKALAALAKKIL-amide), which is derived from TP10 (19–21), DL1a (MAQKIISTIGKLVKWIIKTVNKFTKK-amide), derived from δ-lysin (both labeled with rhodamine (Rh) through a linker on their N-terminal amino groups: Lissamine rhodamine B-NH-(CH₂)₅-CO-peptide (Rh-peptide)), and CE-2 (KWKLLKKLEKAGAALREGLLKAGPALALLGAAAALAK-amide), derived from cecropin A. These three peptides are positively charged at pH 7: Rh-TP10W has a charge of +4 and Rh-DL1a has a charge of +7; neither contains acidic residues. CE-2 has a net charge of +7. We found that Rh-TP10W, Rh-DL1a, and CE2 translocate with very different probabilities, which are inversely correlated with their Gibbs energy of insertion calculated according to the hydrophobicity hypothesis. $\Delta G_{\text{ins}}^{\text{o}}\approx 17$ kcal/mol for Rh-TP10W, ∼24 kcal/mol for Rh-DL1a, and ∼35 kcal/mol for CE2. The fraction of GUV inner vesicles that showed influx, used as a measure of translocation, was 53% for Rh-TP10W, 25% for Rh-DL1a, and 2% for CE2. These results are consistent with the hydrophobicity hypothesis.

An alternative hypothesis emerged from observations in molecular dynamics (MD) simulations (Fig. 1 B). An inserted peptide can be stabilized by salt bridges between basic residues (Arg and Lys) on the peptide and phosphate headgroups of the lipids (31, 32, 33, 34, 35, 36). We thus arrive at the charge-distribution hypothesis. The idea is that for cationic peptides to translocate across the membrane, the high-energy intermediate state must be stabilized by salt bridges between peptide basic residues and lipid phosphate groups. If this intermediate can be stabilized, the peptide has an equal chance of crossing the membrane or returning to the original side. To achieve this stabilization, the distribution of basic residues must be such that they interact with the headgroups of both monolayers of the bilayer. Namely, basic residues must be placed both at the N- and C-terminal stretches of the sequence.

A few studies have addressed the interplay of charge and hydrophobicity on the interactions of antimicrobial peptides with membranes, but the role of charge distribution along the peptide sequence remains very poorly understood (37, 38, 39). Here, we are concerned with fine-tuning the membrane translocation of peptides that already translocate. The two hypotheses formulated about the importance of charge distribution and hydrophobicity in membrane-active peptides can be tested experimentally. This test is now reported using peptide variants of TP10W and DL1a. These petpides were not chosen because of function (neither is natural), but because we have sufficient knowledge about them to make reasonable predictions regarding the properties we wanted to test. Among all the peptides we have studied, DL1a and TP10W are some of the best behaved in the experiments we proposed to perform. For example, they do not aggregate, they bind well to POPC membranes, and they cause flux across the membrane in a practically useful time.

Materials and Methods

Chemicals

N-terminal modified peptides acetyl (Ac)-TP10W and Ac-DL1a and their variants, as well as lissamine rhodamine B (Rh)-TP10W and Rh-DL1a (purity $>95$ %) were purchased from American Peptide Company (Sunnyvale, CA). The peptide identity was ascertained by mass spectrometry, and the purity was determined by high-performance liquid chromatography provided by the manufacturer. Peptide stock solutions were prepared in water/ethyl alcohol 1:1 (v/v) (AAPER Alcohol and Chemical, Shelbyville, KY), stored at $-{80}^o$ C, and kept on ice during experiments. Peptide concentrations were determined by tryptophan (Trp) absorbance at 280 nm ($\mathit{ϵ}=5.6\times {10}^3$ × M^–1 cm^–1) or Rh absorbance at 559 nm ($\mathit{ϵ}=8.8\times {10}^4$ M^–1 cm^–1). POPC and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-lissamine rhodamine B (Rh-DOPE) in chloroform solution were purchased from Avanti Polar Lipids (Alabaster, AL). CF and 7-methoxycoumarin-3-carboxylic acid (7MC) succinimidyl ester were purchased from Molecular Probes/Invitrogen (Carlsbad, CA). 7MC-POPE was synthesized as previously described in detail (40, 41, 42, 43). Fatty-acid-free bovine serum albumin (BSA) was purchased from ICN (Aurora, OH). Organic solvents (high-performance liquid chromatography/American Chemical Society grade) were purchased from Burdick & Jackson (Muskegon, MI).

Confocal fluorescence microscopy of GUVs

GUVs were prepared from POPC by electroformation (44, 45), as previously described (26, 30). The samples for microscopy were prepared by adding 10 μL of GUV suspension in 0.1 M sucrose to $\sim 240$ μL of 0.75 μM peptide, 50 μM CF, and 0.1 M glucose in a culture dish coated with BSA (26, 30). Fluorescence microscopy was performed with an Olympus (Center Valley, PA) Fluoview FV1000 scanning confocal microscope. Quantification of CF fluorescence emission from each vesicle was performed with ImageJ (30, 46). The degree of filling of each vesicle was calculated from the ratio of the CF fluorescence intensity inside the GUV to that outside (30).

Kinetics of peptide binding to LUVs

LUVs were prepared by extrusion through polycarbonate filters of 0.1 μm pore size (Nuclepore, Whatman, Florham, NJ) in buffer containing 20 mM MOPS (pH 7.5), 0.1 mM EGTA, 0.02% NaN₃, and 100 mM KCl, as previously described (43, 47, 48). Lipid concentrations were determined by a modified Bartlett phosphate assay (49, 50). The kinetics of peptide binding to LUVs were measured by stopped-flow fluorescence (using the SX.18MV instrument from Applied Photophysics (Leatherhead, United Kingdom)), as previously described (42, 43, 47, 51). The signal monitored was the change in fluorescence emission intensity of rhodamine covalently attached to the peptides upon binding to the membrane, or the emission of 7MC-POPE incorporated into the bilayer (at 2 mol %) upon Förster resonance energy transfer (FRET) from the intrinsic Trp residue on the peptide. Trp was excited at 280 nm, and the emission of 7MC (${\lambda }_{\text{max}}=396$ nm) was measured with a cut-off filter (GG-385, Edmund Industrial Optics, Barrington, NJ). Rhodamine was excited at 550 nm and emission was recorded through a long-pass filter (OG 590, Edmund Industrial Optics). After mixing, the concentration of peptide was 1 μM. The binding kinetics were analyzed as previously described (42, 43).

Kinetics of peptide-induced CF efflux in LUVs

LUVs containing 50 mM CF in 20 mM MOPS buffer (pH 7.5), 0.1 mM EGTA, and 0.02% NaN₃ were prepared. Efflux kinetics were measured by the relief of self-quenching of CF fluorescence inside the vesicles by stopped-flow fluorescence, as previously described (21, 42, 43, 47, 48, 51). The dye-efflux kinetics were characterized by the average time constant of CF efflux, ${\tau }_{\text{cf}}=\int tf\left(t\right)dt/\int f\left(t\right)dt$, obtained by numerical integration, where $f\left(t\right)$ is the experimentally measured time derivative of the fraction, $F\left(t\right)$, of CF released, as previously described in detail (47, 51, 52, 53).

Circular dichroism

Peptide secondary structure was determined by circular dichroism (CD) on a Chirascan CD spectrometer (Applied Photophysics), as previously described (47). CD spectra of the peptide were obtained in aqueous 10 mM phosphate buffer (pH 7.5), using $\sim 10$ μM peptide in the absence of lipid and $\sim 20$ μM peptide in the presence of 5 mM POPC LUVs (peptide/lipid $<$ 1:200) (54). The fractional helical content on the membrane $\left(f_{\text{H}}\right)$ was calculated from the average of three independent samples using the the CD signal at 222 nm (55).

Results

Dye flux and peptide translocation across GUV membranes

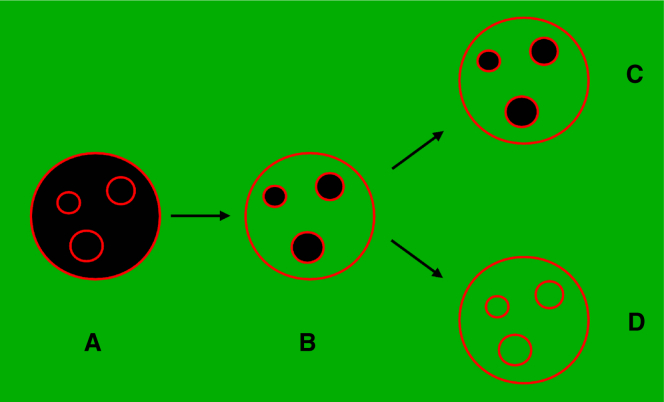
GUV samples prepared by electroformation include a small number of large GUVs that contain (smaller) inner vesicles (26). Peptide translocation was assessed by determining the flux of an external, aqueous fluorescent dye (CF) into the inner vesicles of those large GUVs. The idea is illustrated in Fig. 2. To cause flux of an external dye into the inner vesicles of a GUV, a peptide must cross the membrane of the outer GUV and reach the membranes of the inner vesicles (26). Initially, the interior of the vesicles has no fluorescence (Fig. 2 A, black vesicles). Over time, the peptide induces dye flux into the outer vesicle (Fig. 2 B). If the peptide does not translocate across the outer membrane, the inner vesicles remain dark (Fig. 2 C). However, if fluorescence appears inside the inner vesicles (Fig. 2 D), the peptide must have translocated across the membrane of the outer GUV.

Figure 2.

Concept of the experiment. GUVs prepared with inner vesicles are added to a solution containing peptide and a water-soluble fluorophore (green). The membrane of the vesicles is shown in red. Initially (A), the interior of the vesicles has no fluorescence (black circles). (B) The peptide induces flux into the outer vesicle. If the peptide does not translocate across the outer membrane, the inner vesicles remain dark (C). The appearance of fluorescence inside inner vesicles indicates that the peptide did translocate across the membrane of the outer vesicle (D). The scheme here was reprinted with permission from Wheaten et al. (26). To see this figure in color, go online.

We used this method to examine a series of variants of the two parent peptides Ac-TP10W and Ac-DL1a (Fig. 3). All peptides are acetylated on the N-terminus and amidated on the C-terminus to restrict possible salt-bridge formation to the side chains of basic residues. Two types of mutations were incorporated into the peptide variants: switches of the positions of two residues and mutations of one residue to another. Switches of pairs of residues are denoted by their positions in the mutated peptides. For example, Ac-DL1a-G4-K10 contains Gly at position 4 and Lys at position 10 (whereas the original Ac-DL1a contains Lys at position 4 and Gly at position 10). Single-residue mutations are indicated by the identity of the original residue, its position, and the identity of the new residue. For example, in Ac-DL1a-K26L, Lys26 was replaced by Leu.

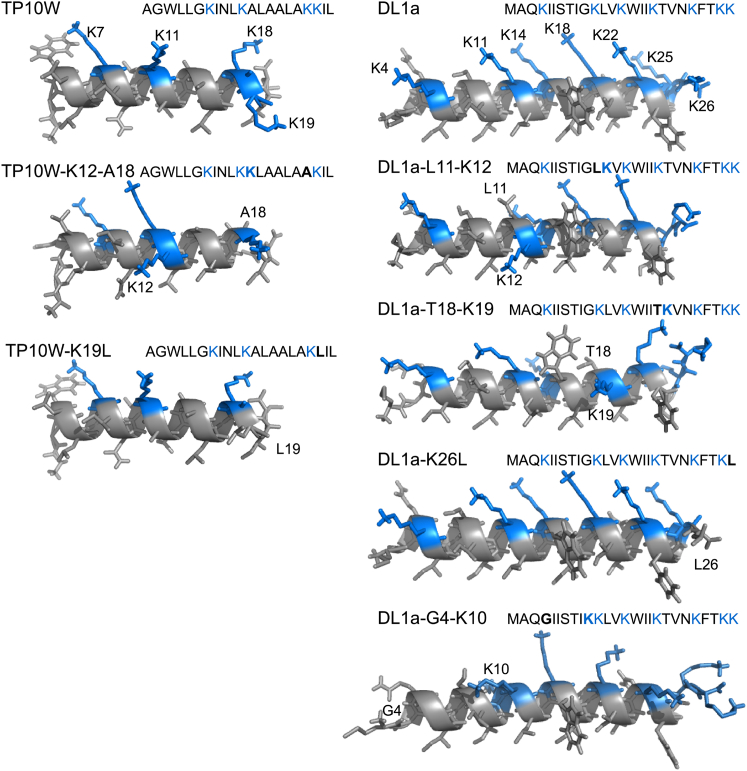
Figure 3.

Location of mutations in TP10W (left) and DL1a (right) variants. The structures were generated with the program PEPFOLD (63, 64, 65) and rendered with open-source PyMol. They do not represent the structures of the peptides on the membrane, which are mostly, but not fully, helical. To see this figure in color, go online.

Fig. 3, left, shows models of Ac-TP10W and its variants K12-A18 and K19L. In Ac-TP10W-K12-A18, Lys-18 was moved to the middle of the sequence. According to the hydrophobicity hypothesis, the mutation was expected to have little effect, but according to the charge-distribution hypothesis, it was expected to reduce translocation. In Ac-TP10W-K19L, the last Lys residue was replaced by Leu. This mutation was predicted to increase peptide translocation according to the hydrophobicity hypothesis, but to reduce it according to the charge-distribution hypothesis. Fig. 3, right, shows models of Ac-DL1a and its variants L11-K12, T18-K19, G4-K10, and K26L. According to the hydrophobicity hypothesis, the first three mutations were not expected to significantly alter translocation, but the mutation K26L was expected to enhance it. According to the charge-distribution hypothesis, the mutations L11-K12 and T18-K19 were expected to marginally enhance and reduce translocation, respectively, compared to Ac-DL1a; the mutations G4-K10 and K26L were both expected to reduce translocation.

Fig. 4 shows examples of GUVs with inner vesicles in the presence of Ac-DL1a (Fig. 4 A), Ac-DL1a-K26L (Fig. 4 B), and Ac-DL1a-G4-K10 (Fig. 4 C). In these experiments, the GUV suspension (in 0.1 M sucrose) was added to a 0.1 M glucose solution containing the peptide (0.5–0.75 μM) and CF (50 μM). Based on the number of vesicles in the field of view, we estimate the lipid concentration to be $\sim 30$–100 μM, which yields a peptide/lipid ratio of $\sim 1:100$ in the preparation. The higher density of the sucrose solution makes the GUVs sink to the bottom of the microscope slide, where they are observed by fluorescence confocal microscopy.

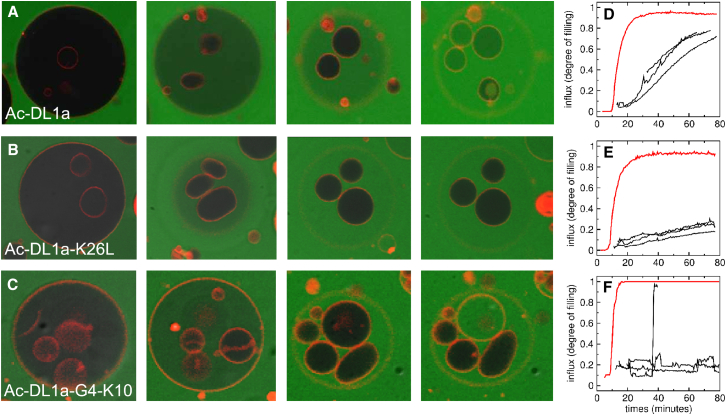
Figure 4.

Examples of dye flux into POPC GUVs containing inner vesicles. (A–C) Time series showing influx into GUVs added to a solution containing CF and a peptide. The pictures were taken at different times after addition of the GUVs to the peptide solution. (A) Ac-DL1a at 4.5, 13.5, 17.5, and 64.5 min. (B) Ac-DL1a-K26L at 2.5, 12.5, 40, and 77.5 min. (C) Ac-DL1a-G4-K10 at 5, 10.5, 33.5, and 39 min. The outer GUVs (leftmost images) have diameters of $\sim 50$–100 μm. The inner vesicles (rightmost images) have diameters of $\sim 10$–20 μm. (D–F) Plots show the dye flux into GUVs as a function of time for the same peptides in each series: (D) Ac-DL1a, (E) Ac-DL1a-K26L, and (F) Ac-DL1a-G4-K10. The red lines indicate flux into the outer GUV, and the black lines indicate flux into inner vesicles. To see this figure in color, go online.

In the initial pictures of each time series (Fig. 4, left), the outer GUVs are dark, because no dye influx has yet occurred. As influx occurs, the lumen of the outer GUVs becomes progressively greener, and the inner vesicles become visible. The inner GUVs then sink to the bottom of the outer GUV, because the density in their lumens is still high (sucrose), whereas the density of the solution in the outer GUV decreases as it is replaced by the external glucose solution. We then focus the microscope on the bottom of the large GUV, which is why its diameter appears smaller. (Some inner vesicles are out of the focal plane in the second images, and therefore not visible). In the third and fourth images of each set, we can observe that the dye entered some of the inner GUVs. At the end of this experiment (last image), in Fig. 4 A (Ac-DL1a), all inner vesicles show complete dye influx; in Fig. 4 B (K26L), none of the inner vesicles shows significant influx; and in Fig. 4 C, the larger of the inner GUVs shows complete influx, but none of the smaller ones does. The plots at the right (Fig. 4, D–F) show the time courses of dye flux into the GUVs of the corresponding time series (Fig. 4, A–C, respectively). The red line shows dye flux into the outer GUV and the black lines show flux into the inner vesicles. We define the characteristic times of influx as the midpoints of these influx curves for the outer GUV $\left({\tau }_{\text{o}}\right)$ and for the inner vesicles $\left({\tau }_{\text{i}}\right)$.

The results of these experiments are summarized in Table 1. Translocation efficiency is assessed by the number of inner vesicles that undergo dye influx. All variants translocated less than did the parent peptides. Also indicated in the table are the mean influx times for the outer GUV $\left({\tau }_{\text{o}}\right)$ and the inner GUVs $\left({\tau }_{\text{i}}\right)$. Finally, for comparison, we also list the mean times $\left({\tau }_{\text{cf}}\right)$ for CF efflux from LUVs, as determined by stopped-flow fluorescence, upon addition of 0.5 μM peptide to 50 mM POPC LUVs. Our previous data on Rh-TP10W and Rh-DL1a (26) are included for comparison. To our surprise, we found no correlation between dye flux in GUVs and LUVs. Even in GUVs alone, there is only a weak correlation between the percent of inner vesicles exhibiting dye influx and the time, ${\tau }_{\text{o}}$, of flux into the outer GUV (Table 1).

Table 1.

Flux of CF into GUVs and out of LUVs of POPC Caused by Ac-DL1a and Ac-TP10W Variants

Peptide	GUVs					LUVs
	No. Outer GUVs	No. Inner GUVs	% Inner GUV with Influx	Parent GUV
				${\tau }_{\text{o}}$ (min)	${\tau }_{\text{i}}/{\tau }_{\text{o}}$	${\tau }_{\text{cf}}$ (s)
Rh-TP10W	13	53	53%	$21\pm 17$	2.4	8.0
Ac-TP10W	15	29	83%	$21\pm 14$	2.6	6.3
Ac-TP10W-K12-A18	30	45	47%	$28\pm 26$	2.4	5.6
Ac-TP10W-K19L	25	57	58%	$21\pm 11$	3.4	2.2
Rh-DL1a	14	85	25%	$34\pm 23$	2.7	1.7
Ac-DL1a	10	38	84%	$10\pm 5$	4.2	8.7
Ac-DL1a-L11-K12	8	33	18%	$11\pm 4$	2.6	64
Ac-DL1a-T18-K19	20	52	50%	$16\pm 15$	4.3	5.5
Ac-DL1a-K26L	12	44	5%	$28\pm 15$	3.8	4.9
Ac-DL1a-G4-K10	17	27	48%	$21\pm 6$	2.3	ND

The data for Rh-TP10W and Rh-DL1a are from Wheaten et al. (26).

Kinetics and thermodynamics of peptide binding to membranes

To fully test the predictions of the hydrophobicity hypothesis, it is necessary to determine the Gibbs energy of binding to the membrane $\left(\Delta G_{\text{bind}}\right)$. The Gibbs energy of insertion is estimated through $\Delta G_{\text{ins}}=\Delta G_{\text{oct}}-\Delta G_{\text{bind}}$, where $\Delta G_{\text{oct}}$ is the Gibbs energy of transfer from water to octanol in the Wimley-White octanol scale (8, 56). We determined $\Delta G_{\text{bind}}$ by measuring the kinetics of peptide binding to the membrane by stopped-flow fluorescence. Binding was measured by the increase in FRET from a Trp residue in the peptide to a lipid fluorophore incorporated in the membrane (7MC-POPE) as a function of time. The experiments yield the on- and off-rate constants ($k_{\text{on}}$ and $k_{\text{off}}$), from which the equilibrium dissociation constant is obtained as $K_{\text{D}}=k_{\text{off}}/k_{\text{on}}$. The Gibbs energy of binding is calculated from $\Delta G_{\text{bind}}^{\text{o}}=RT\text{ln}{K}_{\text{D}}-2.4$ kcal/mol, where the last term is included to convert the results from a molar to a mole fraction concentration scale, to use the same units as the Wimley-White hydrophobicity scales.

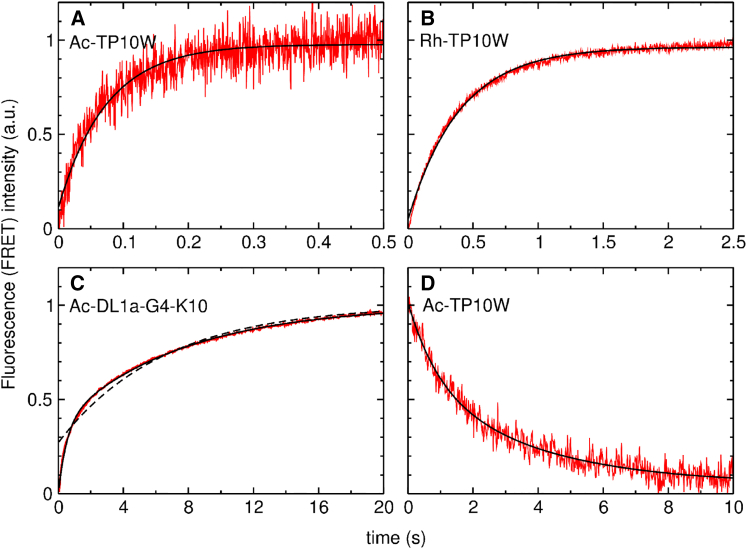
Fig. 5 shows examples of the kinetics of peptide binding to POPC LUVs. The experimental data are shown in red. The curves for Ac-TP10W and Ac-DL1a-G4-K10 (Fig. 5, A and C) were measured by FRET from the intrinsic Trp to 7MC-POPE. A curve for Rh-TP10W (26), measured through the change in the Rh fluorescence upon binding, is shown for comparison in Fig. 5 B. In most cases, the time-dependent fluorescence curves were reasonably well described by a single exponential function of the form $f\left(t\right)=1-e^{-k_{\text{app}}t}$, where $k_{\text{app}}$ is the apparent rate constant, which is the reciprocal of the relaxation time, τ. Single-exponential fits to the experimental data are shown in Fig. 5, A and B (black lines). Sometimes a small deviation from single-exponential behavior is observed, which is especially noticeable in the very beginning of the curves. This fast component may correspond to an initial interaction of the peptide with the membrane, in a state that precedes stable binding. We used single-exponential fits in all cases for which the approximation was acceptable. However, in the Ac-DL1a variants T18-K19 and G4-K10, the deviation from single-exponential behavior is significant. The dashed line in Fig. 5 C is a fit to a single exponential, which is very poor. In those cases, a double-exponential fit was used, shown by the solid black line in Fig. 5 C. The interpretation of the double-exponential fit is not straightforward, but we have refrained from a more complicated analysis. Instead, we calculated an apparent relaxation time, ${\tau }_{\text{app}}$, that characterizes the kinetics as a weighted average of the time constants for the two exponentials (${\tau }_{\text{app}}={\alpha }_1{\tau }_1+{\alpha }_2{\tau }_2$, where the α values are the amplitudes obtained from the fit). The apparent rate constant was then obtained from $k_{\text{app}}=1/{\tau }_{\text{app}}$.

Figure 5.

(A–C) Binding kinetics for (A) Ac-TP10W, (B) Rh-TP10W, and (C) Ac-DL1a-G4-K10. In (A) and (C), FRET from Trp in the peptide to a lipid fluorophore (2 mol % 7MC-POPE) in POPC vesicles (1 μM peptide and 100 μM POPC LUVs). (B) Fluorescence intensity of the Rh-labeled peptide (26). (D) Dissociation kinetics of Ac-TP10W from POPC LUVs. The figure shows the decay in FRET from the Trp residue in the peptide to a lipid fluorophore present in the (donor) vesicles (0.5 μM peptide prebound to donor vesicles containing 2 mol % 7MC-POPE, mixed with 150 μM POPC LUVs containing no fluorophore). The data are shown in red. The black lines in (A), (B), and (D) are fits to single-exponential functions. In (C), the solid black line is a fit to a double exponential and the dashed line is a fit to a single exponential. To see this figure in color, go online.

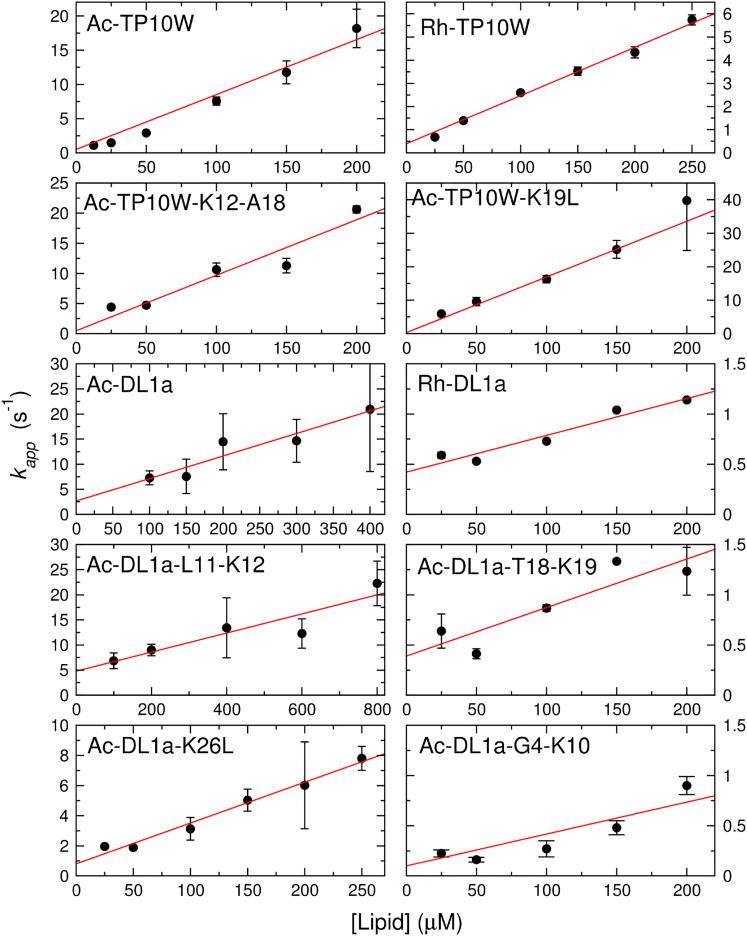
Fig. 6 shows plots of the apparent rate constant $\left(k_{\text{app}}\right)$ as a function of lipid concentration for all TP10W and DL1a variants. In a single-exponential process, the apparent rate constant is given exactly by $k_{\text{app}}=k_{\text{on}}\left[\text{Lipid}\right]+k_{\text{off}}$. Thus, these plots yield $k_{\text{on}}$ from the slope and $k_{\text{off}}$ from the y-intercept of the line. This equation is only an approximation in the case of double-exponential fits.

Figure 6.

Kinetics of peptide binding to lipid vesicles (POPC LUVs). The apparent rate constant, $k_{\text{app}}$, for the kinetic binding experiments is plotted as a function of lipid concentration to extract the on- and off-rate constants ($k_{\text{on}}$ and $k_{\text{off}}$) from the slope and the y-intercept of the line, respectively. The binding kinetics were measured using the change in FRET signal from an intrinsic Trp in the peptide to a lipid fluorophore (7MC-POPE) incorporated in the membrane. The data for the Rh-peptides are from (26). An experiment on one vesicle preparation is shown for each peptide, except in the case of Ac-DL1a-G4-K10, where the data from three independent experiments were combined. The error bars are standard deviations of $\sim 5$ curves for each data point (when not visible, they are contained inside the points). To see this figure in color, go online.

In the Ac-TP10W variants, the y-intercept occurred very close to the origin, and obtaining $k_{\text{off}}$ from these linear regressions would carry a large error. Therefore, in these cases, $k_{\text{off}}$ was obtained through a dissociation kinetics experiment (42, 43, 47). The peptide was first bound to donor vesicles that included 2 mol % 7MC-POPE, which were then mixed, in the stopped-flow fluorometer, with a large excess of acceptor vesicles of POPC only using a 1:10 syringe volume ratio. As the peptide dissociates from the donor vesicles and binds to the acceptors, the FRET signal decreases, yielding kinetics that are now determined mainly by $k_{\text{off}}$ (43). An example is shown in Fig. 5 D for Ac-TP10W. The kinetics in this experiment often contain a long-time tail, but $k_{\text{off}}$ is reasonably well approximated by the largest rate constant, which is obtained by a single-exponential fit to the initial part of the curve (43, 47). Table 2 summarizes the results obtained for $k_{\text{on}}$, $k_{\text{off}}$, and $K_{\text{D}}=k_{\text{off}}/k_{\text{on}}$.

Table 2.

Rate Constants and Equilibrium Constant for Peptide Binding to POPC LUVs

Peptide	kona (M–1 s–1)	$k_{\text{off}}$ (s–1)	$K_{\text{D}}$ (μM)
TP10Wb	$\left(9.4\pm 0.7\right)\times {10}^4$	$13\pm 1.6$	$140\pm 20$
Rh-TP10Wb	$\left(2.3\pm 0.6\right)\times {10}^4$	$0.4\pm 0.2$	$16\pm 4$
Ac-TP10W	$\left(8.3\pm 2.3\right)\times {10}^4$	$0.5\pm 0.1$	$6\pm 2$
Ac-TP10W-K12/A18	$\left(1.3\pm 0.3\right)\times {10}^5$	$0.5\pm 0.1$	$3.6\pm 1.3$
Ac-TP10W-K19L	$\left(1.6\pm 0.3\right)\times {10}^5$	$0.32\pm 0.02$	$2.0\pm 0.5$
Formyl-DL1b	$2.5\times {10}^4$	10	400
Rh-DL1ab	$\left(3.8\pm 0.2\right)\times {10}^3$	$0.37\pm 0.07$	96
Ac-DL1a	$\left(3.1\pm 1.7\right)\times {10}^4$	$1.4\pm 1.1$	$40\pm 20$
Ac-DL1a-L11-K12	$\left(2.0\pm 0.1\right)\times {10}^4$	$3.9\pm 1.3$	$200\pm 80$
Ac-DL1a-T18-K19	$\left(4.4\pm 0.6\right)\times {10}^3$	$0.29\pm 0.14$	$65\pm 23$
Ac-DL1a-K26L	$\left(3.7\pm 1.0\right)\times {10}^4$	$0.58\pm 0.37$	$17\pm 13$
Ac-DL1a-G4-K10	$\left(3.2\pm 1.0\right)\times {10}^3$	$\sim 0.1\pm 0.1$	$30\pm 30$

^aThe data for all constants are represented as the mean ± SD from two to four independent samples (except in the case of Ac-DL1a-G4-K10, where they are the result of linear regression of all data combined).

^bThe data for TP10W (47), Rh-labeled peptides (26), and formyl-DL1 (51) are included for comparison.

Secondary structures and Wimley-White interfacial binding

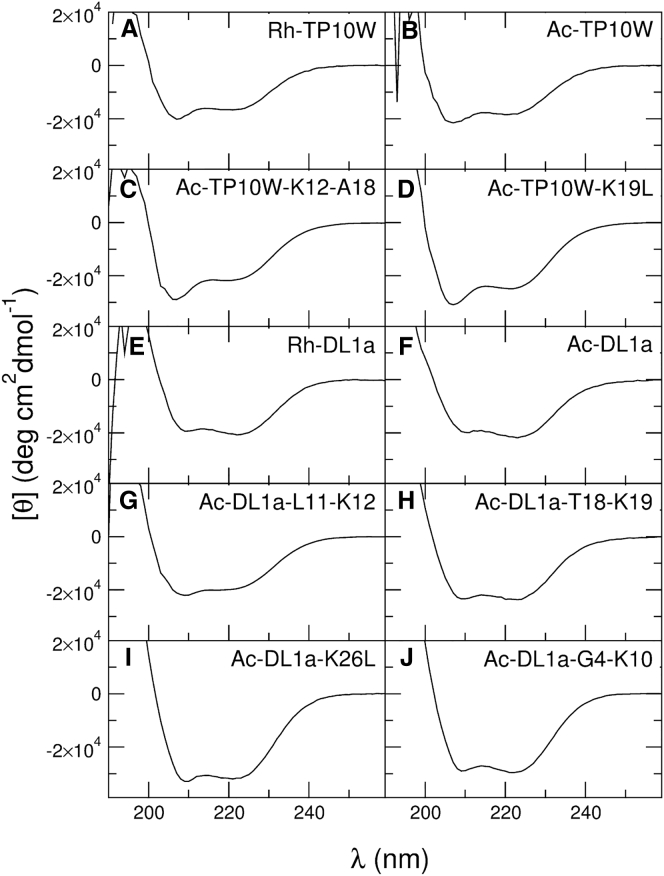
To ensure that the mutations introduced did not produce major changes in peptide structure, we measured the CD spectra of all peptide variants in lipid membranes ($\sim 20$ μM peptide in 5 mM POPC LUVs). The results, shown in Fig. 7, indicate that all peptides are helical on the membrane. We also recorded the CD spectra in solution (not shown) for the sake of completeness, although the results were not used in the analysis. The helical contents of the peptides, on the membrane and in solution, are listed in Table 3.

Figure 7.

(A–J) CD spectra of the peptides (20 μM) bound to POPC vesicles (5 mM POPC LUVs). The spectra shown are averages of three independent experiments. Rh-TP10W and Rh-DL1a are included for comparison (26).

Table 3.

Translocation of DL1a and TP10W Variants

Peptide	$\Delta G_{\text{bind}}^{\text{o}}$a	$\Delta G_{\text{if}}^{\text{o}}$	$\Delta G_{\text{ins}}^{\text{o}}$b	% α-helix		% inner GUVs
	(kcal/mol)			Membc	Waterd	with influx
TP10We	$-7.7$	$-7.3$	17	57f	28	–
Rh-TP10We	$-8.9$	–	$\sim$ 17	50	54	53%
Ac-TP10W	$-9.5$	$-8.1$	17	61	21	83%
Ac-TP10W-K12-A18	$-9.8$	$-9.0$	17	71	22	47%
Ac-TP10W-K19L	$-10.1$	$-10.7$	13	74	31	58%
Formyl-DL1e	$-7.0$	$-1.3$	26	52	20	–
Rh-DL1ae	$-7.9$	–	$\sim$ 24	61	49	25%
Ac-DL1a	$-8.3$	$-5.2$	22	63	51	84%
Ac-DL1a-L11-K12	$-7.4$	$-4.9$	21	58	29	18%
Ac-DL1a-T18-K19	$-8.1$	$-6.2$	22	69	13	50%
Ac-DL1a-K26L	$-9.0$	$-9.7$	19	91	49	5%
Ac-DL1a-G4-K10	$-8.5$	$-7.5$	22	86	58	48%

^a$\Delta G_{\text{bind}}^{\text{o}}=RT\text{ln}{K}_{\text{D}}-2.4$ kcal/mol.

^b$\Delta G_{\text{ins}}=\Delta G_{\text{oct}}-\Delta G_{\text{bind}}$.

^cThe values for membrane helical content are averages of three independent experiments with 20 μM peptide in 5 mM POPC LUV suspensions in phosphate buffer (pH 7.4).

^dThe solution contained 10 μM peptide in aqueous phosphate buffer (pH 7.4).

^eThe data for TP10W (47), Rh-labeled peptides (26), and formyl-DL1 (51) are included for comparison.

^fThe error in fractional helicity in these measurements is ∼10% (relative error).

We determined the Gibbs energy of binding to the membrane $\left(\Delta G_{\text{bind}}^{\text{o}}\right)$ from $K_{\text{D}}$ after converting it to a mole fraction partition coefficient. $\Delta G_{\text{bind}}^{\text{o}}$ is the experimental equivalent of the Gibbs energy of binding to the interface $\left(\Delta G_{\text{if}}^{\text{o}}\right)$ calculated with the Wimley-White interfacial hydrophobicity scale (56, 57). The calculation can be done using the MPEx software (58). Because each hydrogen bond established by the backbone peptide groups in the helix contributes about $-0.4$ kcal/mol to the Gibbs energy of binding (59), $\Delta G_{\text{if}}^{\text{o}}$ becomes more negative as the peptide helical content on the membrane increases. The importance of helical structure and the roles of hydrophobicity and amphiphilicity in peptide binding and folding on the membrane interface were subject to a systematic investigation (60). However, when the calculation of the Gibbs energy of peptide folding in the membrane interface is correctly performed (61), it is clear that the peptide amphipathicity (hydrophobic moment) itself has little or no effect on peptide partitioning to the membrane interface other than through an increase in helix propensity already evident in water. What leads to improved folding and binding are the more favorable internal hydrogen bonds established by the peptide backbone when located in the membrane interface. In the TP10W variants, using the helicity values from Table 3, the calculated $\Delta G_{\text{if}}^{\text{o}}$ values are in good agreement with experimental values. This is not true for the DL1a variants, however, as we previously observed (29, 47, 51). The values of $\Delta G_{\text{bind}}^{\text{o}}$ and $\Delta G_{\text{if}}^{\text{o}}$ are summarized in Table 3.

Discussion

We now confront the two hypotheses proposed with the translocation results obtained in GUVs. We take the fraction of inner vesicles that showed dye influx as a measure of peptide translocation across the membrane of the outer GUV that contains those inner vesicles. Table 3 summarizes this information. The table also lists the values of the Gibbs energy changes of binding and insertion necessary for the interpretation of the results. To recapitulate, the hydrophobicity hypothesis states that the probability of peptide translocation is determined by the Gibbs energy of insertion, $\Delta G_{\text{ins}}^{\text{o}}$, from the membrane interface-bound state into the bilayer interior, operationally measured by $\Delta G_{\text{oct}}^{\text{o}}-G_{\text{bind}}^{\text{o}}$. (Note that it is the value of the Gibbs energy of binding to the membrane interface determined experimentally $\left(\Delta G_{\text{bind}}^{\text{o}}\right)$, not the value calculated from the Wimley-White interfacial scale $\left(\Delta G_{\text{if}}^{\text{o}}\right)$, that is used to calculate $\Delta G_{\text{ins}}^{\text{o}}$). Thus defined, $\Delta G_{\text{ins}}^{\text{o}}$ is simply a measure of the peptide hydrophobicity difference between the membrane interior and the interface. The smaller the value of $\Delta G_{\text{ins}}^{\text{o}},$ the greater is the likelihood of translocation. The charge-distribution hypothesis states that the probability of translocation is determined by the ability of the distribution of positive charges in the peptide to transiently stabilize the inserted intermediate state. The idea is that translocation occurs if the high-energy intermediate can be stabilized by salt bridges to the phosphate of the lipid headgroups. Fig. 3 shows models of the peptide variants examined in a helical conformation. (These structures show the positions of the residues discussed but do not represent the actual peptide structures on membranes. As shown in Table 3, these peptides are mainly helical on the membrane, but not fully helical).

We begin with the TP10W variants (Fig. 3, left column). The parent peptide is Ac-TP10W, for which the inner vesicle flux (translocation index) was 83%. The variants examined were K12-A18 and K19L. According to the hydrophobicity hypothesis, Ac-TP10W-K12-A18 was expected to show translocation similar to that observed for Ac-TP10W, because this mutation is a simple switch of two residues and $\Delta G_{\text{ins}}^{\text{o}}$ is identical to that of Ac-TP10W (17 kcal/mol). According to the charge-distribution hypothesis, however, we predicted less translocation, because one of the terminal lysine residues (K18) was moved to the middle (K12), where it is less likely to interact with the lipid headgroups in the inserted intermediate state. The experiment showed a decrease of percent flux from 83% to 47%, consistent with the charge-distribution hypothesis. The second variant was Ac-TP10W-K19L, where the C-terminal lysine residue was replaced by leucine. According to the hydrophobicity hypothesis, this peptide was expected to show significantly better translocation, because $\Delta G_{\text{ins}}^{\text{o}}$ decreased from 17 kcal/mol for Ac-TP10W to 13 kcal/mol, which is a reflection of the much higher hydrophobicity of Leu compared to Lys. According to the charge-distribution hypothesis, Ac-TP10W-K19L was expected to show lower levels of translocation because the terminal lysine, which is believed to participate in salt bridges with the lipid phosphate headgroups in the inserted intermediate, was replaced by a leucine. The results showed a reduction of percent flux from 83% to 58%, consistent with the charge-distribution hypothesis but not with the hydrophobicity hypothesis.

Consider now the DL1a variants (Fig. 3, right column). The parent peptide for this series is Ac-DL1a, for which the inner vesicle flux (translocation index) was 84%. $\Delta G_{\text{ins}}^{\text{o}}$ for Ac-DL1a is 22 kcal/mol, which is about the threshold value that we proposed for translocation. Clearly, translocation occurs efficiently. Four variants of Ac-DL1a were examined: L11-K12, T18-K19, K26L, and G4-K10. The values of $\Delta G_{\text{ins}}^{\text{o}}$ for L11-K12, T18-K19, and G4-K10 are within 1 kcal/mol of that of Ac-DL1a. Thus, the prediction from the hydrophobicity hypothesis is that these three peptides should translocate as efficiently as Ac-DL1a. In Ac-DL1a-K26L, the replacement of a lysine by a leucine renders the peptide more hydrophobic. According to the hydrophobicity hypothesis, $\Delta G_{\text{ins}}^{\text{o}}=19$ kcal/mol for this variant, which is 3 kcal/mol smaller than for Ac-DL1a; consequently, translocation should increase. The predictions of the charge-distribution hypothesis are very different. The switch of the position of lysine with the preceding residue in the variant L11-K12 moves the lysine away from the the N-terminus, toward the center of the peptide, which should make translocation slightly worse compared with translocation for Ac-DL1a. In T18-K19, the lysine moves toward the C-terminus, away from the center of the peptide, which should make translocation slightly better compared to that for Ac-DL1a. In Ac-DL1a-K26L, the C-terminal lysine is removed, which should be detrimental to translocation because it removes a potential salt-bridge partner for the phosphate headgroups in the inserted intermediate state. And in Ac-DL1a-G4-K10, the first lysine is significantly moved away from the N-terminus, toward the center of the peptide; thus, a decrease in translocation is expected according to the charge-distribution hypothesis. We found that the translocation index decreased for all peptide variants compared with Ac-DL1a. In none of the cases was the prediction by the hydrophobicity hypothesis correct. The outcome agrees with the charge-distribution hypothesis in L11-K12, K26L, and G4-K10. The prediction failed only in the case of T18-K19, in which the inner vesicle flux decreased to 50% (compared to 84% in Ac-DL1a) rather than increasing slightly. However, the most striking case is that of Ac-DL1a-K26L, in which a dramatic decrease of inner vesicle flux occurred (5%), as predicted by the charge-distribution hypothesis and completely opposite the prediction by the hydrophobicity hypothesis.

Before closing, we need to recognize that there are two weaknesses in this study. The first is that the parent peptides of both series, Ac-TP10W and Ac-DL1a, already have a high translocation efficiency ($\sim 80$% inner vesicle flux), so it is difficult to produce improvements by mutations. Thus, most peptide variants will necessarily translocate less. We had assumed that the replacement of the N-terminal modifier from rhodamine to acetyl would have a negligible effect on translocation, because its effect is minimal on $\Delta G_{\text{bind}}^{\text{o}}$ measured experimentally (Table 3). That assumption, however, turned out to be wrong. Second, the mutations initially designed were too conservative. This was done by design, because we did not want to cause major changes in the peptide structure or in its membrane binding affinity (62). Later, bolder changes were made, as seen in the variants Ac-TP10W-K19L, Ac-DL1a-K26L, and Ac-DL1a-G4-K10. We think that these three peptides provide the most stringent tests of the two hypotheses. Their translocation results argue against the hydrophobicity hypothesis and are consistent with the charge-distribution hypothesis.

In summary, the charge-distribution hypothesis predicted the correct translocation outcome in five of the six peptide variants examined. The hydrophobicity hypothesis was wrong in all six cases. However, when we previously compared translocation of three peptides with very different $\Delta G_{\text{ins}}^{\text{o}}$ values, we found good agreement with the hydrophobicity hypothesis (26). Specifically, we examined Rh-TP10W ($\Delta G_{\text{ins}}^{\text{o}}\approx 17$ kcal/mol), Rh-DL1a ($\Delta G_{\text{ins}}^{\text{o}}\approx 24$ kcal/mol), and CE2 ($\Delta G_{\text{ins}}^{\text{o}}\approx 35$ kcal/mol) and found fractions of inner vesicle influx of 53% for Rh-TP10W, 25% for Rh-DL1a, and 2% for CE2. It thus appears that if the differences in peptide insertion propensity are large, the hydrophobicity hypothesis successfully predicts the relative translocation efficiency, but for fine differences, it fails. We now posit that the coarse translocation propensity is determined by hydrophobicity, corresponding to differences of $\sim 10$ kcal/mol in $\Delta G_{\text{ins}}^{\text{o}}$. However, fine-tuning depends on the charge distribution. These results suggest a possible path to design a translocating peptide de novo. We can envision that the hydrophobicity hypothesis would be used to design or select peptides that translocate, and the charge-distribution hypothesis would be used to fine-tune the behavior of those peptides.

Author Contributions

F.D.O.A. performed the confocal fluorescence microscopy experiments on GUVs and the binding and efflux kinetics on LUVs, analyzed the corresponding data, and interpreted results; B.L.S. performed and analyzed binding and efflux kinetics on LUVs; K.I.A. performed and analyzed the CD experiments; and P.F.A. designed the work, analyzed data, interpreted results, and wrote the manuscript.

Editor: Kalina Hristova.