The reaction of methyl peroxy and hydroxyl radicals as a major source of atmospheric methanol

Abstract

Methyl peroxy, a key radical in tropospheric chemistry, was recently shown to react with the hydroxyl radical at an unexpectedly high rate. Here, the molecular reaction mechanisms are elucidated using high-level quantum chemical methodologies and statistical rate theory. Formation of activated methylhydrotrioxide, followed by dissociation into methoxy and hydroperoxy radicals, is found to be the main reaction pathway, whereas methylhydrotrioxide stabilization and methanol formation (from activated and stabilized methylhydrotrioxide) are viable minor channels. Criegee intermediate formation is found to be negligible. Given the theoretical uncertainties, useful constraints on the yields are provided by atmospheric methanol measurements. Using a global chemistry-transport model, we show that the only explanation for the high observed methanol abundances over remote oceans is the title reaction with an overall methanol yield of ∼30%, consistent with the theoretical estimates given their uncertainties. This makes the title reaction a major methanol source (115 Tg per year), comparable to global terrestrial emissions.

The high observed abundance of atmospheric methanol over remote oceans is still not well-explained. Here the authors use quantum calculations and atmospheric modelling to show the reaction of methyl peroxy and hydroxyl radicals is a major methanol source (115 Tg/yr), comparable to global terrestrial emissions.

Methyl peroxy radical (CH₃O₂) is the most important organic peroxy radical in the atmosphere, with a global production (∼50 Tmoles or 2,500 Tg per year) primarily due to the oxidation of ubiquitous methane by hydroxyl (OH) radicals¹. Its reaction with nitric oxide (NO) accounts for ∼25% of the global production of tropospheric ozone²,³, second in importance only to HO₂+NO. Under pristine conditions, CH₃O₂ reacts chiefly with hydroperoxy radicals HO₂ to form methyl hydroperoxide CH₃OOH, depleting odd hydrogen radicals (HOx≡OH+HO₂) directly and through the further reaction of CH₃OOH with OH. The reaction of CH₃O₂ with organic peroxy radicals (RO₂) is only a minor sink⁴, but it is also the only well-documented photochemical source of atmospheric methanol, amounting to 18–38 Tg per year globally according to model estimates⁵. Note that a much larger total photochemical source (50–100 Tg per year) was invoked by Jacob et al.⁴ to rationalize serious model underestimations of methanol observations during an aircraft campaign over the Pacific⁶.

Although the possibility of a reaction of CH₃O₂ with OH was previously considered⁷,⁸, it is only recently that a direct, absolute determination of its rate has been reported. Coupling Laser Induced Fluorescence and cw-Cavity Ring-Down Spectroscopy to laser photolysis, Bossolasco et al.⁹ measured a rate of (2.8±1.4) × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹. This unexpectedly high value makes this reaction a major sink of CH₃O₂ in pristine conditions. Using campaign data in Cape Verde, Fittschen et al.¹⁰ estimated that it accounts for ∼25% of the overall CH₃O₂ sink at that remote site, rivalling the reaction with HO₂. Its impact on atmospheric chemistry is however critically dependent on the nature and yields of the products. Three exothermic overall reaction channels were envisaged⁸:

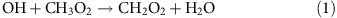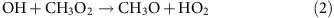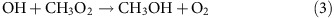with CH₂O₂ the singlet Criegee intermediate, H₂C=O⁽⁺⁾−O⁽⁻⁾. The Criegee channel (1) has been invoked as the possible source of a missing oxidant of SO₂ inferred from observations at a coastal site¹¹. A large Criegee yield would also lead to a very large source of formic acid through reaction of stabilized CH₂O₂ with water¹². The reaction was therefore speculated⁸,¹³ to explain part of the missing source of HCOOH required to sustain the high HCOOH levels observed in the atmosphere¹⁴,¹⁵, although it was found to degrade model/data correlation for measurement campaigns over the U.S.¹³ The methoxy channel (2) leads ultimately to two HO₂ radicals and formaldehyde, which is the end product of both CH₃O₂+NO and (through CH₃OOH) CH₃O₂+HO₂. The methanol channel (2) was noted to be a potentially very significant source of methanol⁸,¹³, but no quantitative assessment has been made to this date.

A recent quantum chemical study of CH₃O₂+OH by Bian et al.¹⁶ could identify only one thermally accessible pathway commensurate with the high measured rate constant: combination of the reactants into an activated methylhydrotrioxide CH₃OOOH (TRIOX), followed by direct dissociation into CH₃O and HO₂, which are about 4 kcal mol⁻¹ more stable than the reactant radicals. Another recent theoretical study by Nguyen et al.¹⁷ briefly addressed the reaction, concluding that the dominant pathway in atmospheric conditions is collisional stabilization of CH₃OOOH, whereas production of Criegee is negligible.

In view of the likely major importance of the title reaction for key oxygenated organic compounds and its potentially large impact on HOx radicals in the remote troposphere, this work proposes to: (i) elucidate the molecular mechanisms of the reaction by constructing detailed potential energy surfaces, using suitable high-level density functional theory (DFT) and ab initio methodologies for the singlet and triplet (biradical) intermediates; (ii) identify the kinetically viable reaction channels and distinguish between the major and minor product routes using appropriate statistical rate theories; (iii) use a global chemistry-transport model, the Intermediate Model for the Annual and Global Evolution of Species (IMAGES, see the ‘Methods section'), to assess the impact of the reaction and constrain the yields through comparisons with atmospheric measurements. For those readers most interested in the implications for atmospheric chemistry, the results relating to goals (i) and (ii) are succinctly summed up before the section on atmospheric modelling, and we invite such readers to move directly to this summary.

Results

Potential energy surface and reaction kinetics

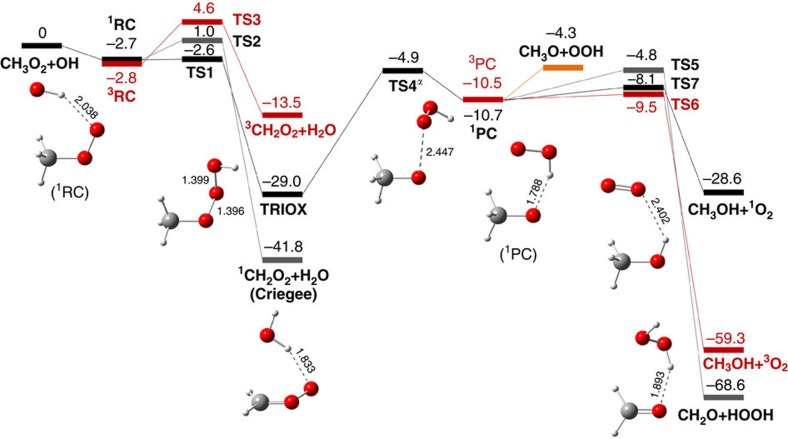
We characterized all three exothermic overall reaction channels (reactions (1), (2), (3)) and all other relevant pathways of the title reaction using quantum chemical methods. Structures and vibrational frequencies were computed with DFT, at the M06-2X-D3/6-311++G(3df,3pd) level of theory (Supplementary Fig. 1, Supplementary Fig. 2, and Supplementary Table 1). More accurate energies were computed using coupled-cluster theory, with explicit (‘F12') treatment of electron–electron distances, as shown in Fig. 1. The DFT and coupled-cluster calculated properties of various complexes and transition states are summarized in Table 1.

Figure 1. Potential energy surface for CH₃OO+OH biradical reactions.

Coupled-cluster energies (kcal mol⁻¹) relative to separated reactants CH₃O₂ and OH, based on DFT geometries (CCSD(T)-F12/cc-pVTZ-F12//M06-2X-D3/6-311++G(3df,3pd) level of theory). TS, transition state; RC, reactant complex; PC, product complex. The singlet reaction pathways are depicted in black and grey, while the triplet reaction pathways are depicted in red for clarity. ^aTS4 was optimized at M06-D3/6-311++G(3df,3pd) level of theory, see text (each structure with formula or acronym is depicted separately in Supplementary Fig. 2).

Table 1. Relative energies with inclusion of ZPVE for all structures involved in the title reaction.

Complexes	ΔE*	ΔE†	T1 diag.‡
CH3O2+OH	0	0	–
1RC	−4.4	−2.7	0.025
3RC	−4.5	−2.8	0.024
TRIOX	−29.9	−29.0	0.015
1PC	−12.3	−10.7	0.028
3PC	−12.1	−10.5	0.025
TS1	−4.3	−2.6	0.026
TS2	−0.1	1.0	0.035
TS3	3.0	4.6	0.028
TS4	−7.1	−4.9	0.027
TS5	−6.3	−4.8	0.038
TS6	−12.0	−9.5	0.044
TS7	−10.9	−8.1	0.081
CH3O+HO2	−4.8	−4.3	–
CH3OH+3O2	−60.1	−59.3	–
CH2O+H2O2	−67.4	−68.6	–

^*Computed at M06-2X-D3/6-311++G(3df, 3pd) level of theory.

^†Computed at CCSD(T)-F12/cc-pVTZ-F12//M06-2X-D3/6-311++G(3df, 3pd) level of theory.

^‡T1 diagnostic for CCSD(T)-F12 calculations.

The reaction of CH₃OO with OH starts by the barrier-less formation of singlet reactant complex ¹RC and triplet reactant complex ³RC, in which OH donates a hydrogen bond to CH₃OO, and in which the singlet and triplet states are near degenerate. Hydrogen abstraction starting from ¹RC and ³RC to form the Criegee intermediate ¹CH₂OO and the triplet biradical ³CH₂OO via TS2 and TS3, respectively, involve significant barriers. In absence of intersystem crossing (ISC) ³RC→¹RC, the reaction CH₃O₂+OH ↔ ³RC will be quasi-equilibrated such that the bimolecular rate constant for the overall triplet channel CH₃O₂+OH→³CH₂O₂+H₂O can be found from transition state theory (TST)¹⁸,¹⁹,²⁰, yielding ³k_bi,3(298 K)=2.6 × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹. This channel is therefore entirely negligible, as are the other triplet entrance routes described by Bian et al.¹⁶, all proceeding through transition states that lie even much higher. Instead, rapid ISC of ³RC to the nearly-degenerate ¹RC could channel much of the triplet entrance flux also towards the singlet surface and hence to TRIOX (see below), rationalizing the high measured overall rate constant⁹ of 2.8 × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹.

The favoured reaction channel of the chemically activated ¹RC is the formation of the stable methylhydrotrioxide TRIOX over the very low-energy TS1. Direct dissociation of TRIOX into CH₃O and HO₂ is not a minimum energy pathway; instead, the energetically favoured decomposition route passes through the singlet product complex ¹PC over TS4, which involves concerted CH₃O–OOH bond-breaking and formation of a CH₃O–HOO hydrogen bond. The relative energy and vibrational properties of saddle-point TS4 play an important role in determining selectivity, but this point is also very difficult to characterize accurately. As explained below, the best results are obtained by using a structure optimized with the M06-D3 DFT method, rather than M06-2X-D3 as used for the other stationary points. Like the reactant complex, the hydrogen-bonded PC has near-degenerate singlet and triplet states. From ¹PC, CH₂O+HOOH can be formed through TS5, or CH₃OH+¹O₂ can be obtained through TS7. Equally, ¹PC can convert to triplet product complex ³PC, and ³PC can form CH₃OH+³O₂ through the very low TS6.

Transition states TS2, TS3, TS5, TS6 and TS7 corresponding to the abstraction or transfer of a hydrogen atom are straightforward and their identity has been carefully confirmed using intrinsic reaction coordinate (IRC) calculations. The coupled-cluster relative energies agree well with those from DFT, supporting the use of the M06-2X-D3 functional for geometry optimization. However, TS1 and TS4 are more problematic and need further discussion, in particular as these crucial transition states (TSs) largely determine the dominant reactant pathways. Both TSs can be considered to correspond to breaking of one of the O–O bonds in TRIOX. However, this step does not proceed with monotonously increasing energy towards the fragments, due to the existence of the hydrogen-bonded RC and PC. As the relative orientation of the fragments in the complexes differs from that in TRIOX, the TSs have combined O–O bond breaking and fragment reorientation character. Also, TRIOX has a closed-shell singlet electronic structure, with the transition to the open-shell radical pair nature of PC or RC occurring in the region near the TSs. For open-shell singlets with completely uncoupled electrons, singlet and triplet states are near-degenerate (as in RC and PC). Unrestricted DFT calculations and coupled-cluster calculations based on unrestricted Hartree-Fock reference wavefunctions are reasonably accurate in this case. However, for partially uncoupled electrons, the triplet is significantly higher in energy, and unrestricted approaches are less accurate, introducing artefacts in the shape of the energy curve. For TS1, we are able to locate two saddle points, TS1 and TS1′, with the M06-2X-D3 functional. The first one corresponds mostly to reorientation of the OH fragment, while TS1′ has essentially only O–O bond stretching character. Large-active-space CASSCF (complete active space self-consistent field) and CASPT2 (complete active space perturbation theory 2) calculations (Supplementary Fig. 3 and Supplementary Note 1), which can treat systems with partially uncoupled electrons in a balanced way, strongly suggest TS1′ to be purely an artefact based on inaccurate description of the developing low-spin open-shell electronic structure, whereas the TS1 is more reliable.

For TS4, only one TS structure, TS4′, is obtained with M06-2X-D3, but CASSCF and CASPT2 calculations show it is an artefact, similar to TS1′. In contrast, the M06-D3 functional yields a TS structure, denoted TS4, which is closer to the correct TS according to CASSCF and CASPT2. The difference in structure is quite large: the M06-2X-D3 TS4′ structure is very ‘early' (O–O distance of 1.967 Å) whereas the M06-D3 TS4 has an O–O distance of 2.447 Å. Accordingly, we have used the TS4 structure in this study. For the other stationary points, the CCSD(T)-F12 (coupled cluster—single, double and triple excitation theory) total energies at the M06-D3 and M06-2X-D3 structures differ by <0.2 kcal mol⁻¹, and the vibrational frequencies are very similar also.

The chemically activated singlet reactant complex ¹RC, with average vibrational energy <E_v>=4.8 kcal mol⁻¹, including an average 2.1 kcal mol⁻¹ thermal energy at 298 K inherited from the reactants (see the ‘Methods section'), reacts nearly barrier-free (TS1) to form the closed-shell CH₃OOOH molecule, TRIOX, much faster than forming Criegee ¹CH₂O₂ and H₂O over a barrier of 3.7 kcal mol⁻¹ (TS2). The RRKM-based (Rice, Ramsperger, Kassel, Marcus)²¹,²² unimolecular rate coefficients averaged over the (narrow) distribution function of formation F(E_th,v) (see the ‘Methods section') are <k₁>=1.8 × 10¹³ s⁻¹ and <k₂>=3.4 × 10¹⁰ s⁻¹, respectively. The k-subscripts refer to the TS numbering in Fig. 1. All F(E_th,v)-averaged rate coefficients of the activated reaction steps given in this subsection are for 298 K and 1,013 hPa (air). They are listed also in Table 2, together with the values for 285 K and 750 hPa, as well as these for 256 K and 400 hPa (see next subsection). Since the other pathways to ¹CH₂O₂+H₂O theoretically characterized by Bian et al.¹⁶ and Nguyen et al.¹⁷ contribute even less as they involve TSs lying ≥7 kcal mol⁻¹ above the initial reactants, it is clear that Criegee formation contributes not more than ∼1% overall.

Table 2. RRKM-calculated rate coefficients <k(E _v)> averaged over the thermal energy distribution of formation F(E _th,v)^* for the various chemically activated reactions.

Reaction step	Notation	k(s−1) (298 K) (1,013 hPa)	k(s−1) (285 K) (750 hPa)	k(s−1) (256 K) (400 hPa)
1RC→TRIOX	<k1>	1.82 × 1013	1.81 × 1013	1.76 × 1013
1RC→1CH2O2+H2O	<k2>	3.36 × 1010	2.56 × 1010	1.20 × 1010
TRIOX→1PC	<k4>	2.38 × 1010	2.25 × 1010	1.90 × 1010
1PC→TRIOX	<k-4>	1.29 × 1011	1.29 × 1011	1.23 × 1011
1PC→CH3O+HO2	<kdiss>†	2.43 × 1012	2.41 × 1012	2.32 × 1012
1PC→3PC	<kisc>	3.50 × 1012	3.50 × 1012	3.44 × 1012
3PC→1PC	<3k-isc>‡	1.87 × 1012	1.87 × 1012	1.84 × 1012
1PC→CH2O+H2O2	<k5>	9.67 × 109	9.67 × 109	9.29 × 109
3PC→CH3O+HO2	<3kdiss>†,‡	3.37 × 1012	3.36 × 1012	3.23 × 1012
3PC→CH3OH+3O2	<3k6>‡	4.14 × 1011	4.14 × 1011	4.14 × 1011
1PC→CH3OH+1O2	<k7>	1.20 × 1011	1.20 × 1011	1.20 × 1011

^*For formation of ¹RC and TRIOX, F(E_th,v) is the initial thermal distribution; for ¹PC and ³PC, F(E_th,v) is shifted down by collisions, by 0.45, 0.35 and 0.25 kcal mol⁻¹ at 298, 285 and 256 K, respectively (see text).

^†k-value obtained using variational RRKM.

^‡Rate coefficient of triplet ³PC reaction preceded by superscript 3 for clarity.

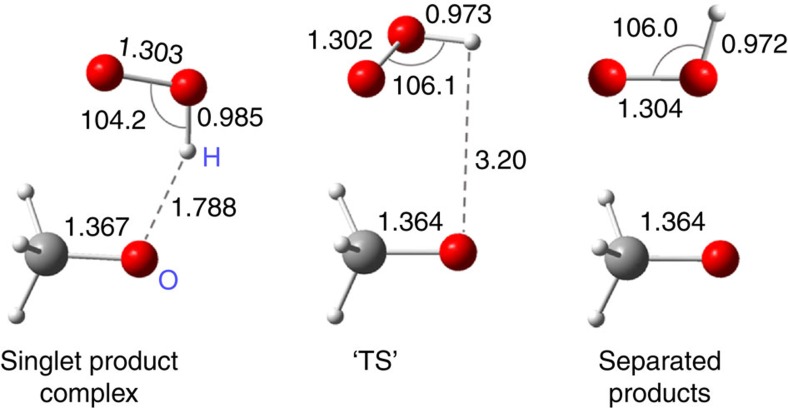
TRIOX, with average chemical activation energy <E_v> of 31.1 kcal mol⁻¹ (at 298 K) converts rapidly to the product complex ¹PC over the low-lying and very loose TS4, characterized above, far outrunning the other isomerization/decomposition reactions through high-lying transition states¹⁶. The rate coefficient integrated over the formation distribution function F(E_th,v) is evaluated at <k₄>=2.4 × 10¹⁰ s⁻¹, implying a TRIOX lifetime of ∼40 ps during which it should lose ∼0.45 kcal mol⁻¹ by collisions at 298 K and 1,013 hPa (see below), shifting down also the energy distribution F(E_th,v) for ¹PC. The CH₃O·HO₂ complex ¹PC has a decisive role in our system; the ∼7 kcal mol⁻¹ strong CH₃O–HOO hydrogen bond explains why the minimum energy pathway of CH₃OOOH to CH₃O+HO₂ passes through it. The fastest reaction of ¹PC, with <E_v>(¹PC)≈12.4 kcal mol⁻¹, is dissociation into these radicals by breaking the H-bond without exit barrier. The F(E_th,v)- averaged <k_diss> was estimated by variational RRKM²¹,²². The energy, zero-point vibrational energy (ZPVE) and integrated density of states G^var(E_v—E^var) were computed for a series of structures with increasing H-bond length, using the unprojected vibrational frequencies, as listed in Supplementary Table 2; the use of projected frequencies²³,²⁴,²⁵ for the sum of states would have resulted in ∼12% higher <k_diss> and <³k_diss>, with a minor effect on the overall product yields (see Supplementary Note 3). The variational bottleneck that minimizes G^var(E_v—E^var), shown in Fig. 2, was found for an H-bond length of 3.2 Å, and relative energy 1.7 kcal mol⁻¹ below the separated CH₃O+HO₂, giving <k_diss>≈2.4 × 10¹² s⁻¹.

Figure 2. Dissociation of product complex and the variational transition state.

Bond lengths are in angstrom. Angles are in degrees.

The decomposition of ¹PC into CH₂O+H₂O₂ over the fairly high TS5, with RRKM-calculated rate of only <k₅>=9.7 × 10⁹ s⁻¹ is negligibly slow, whereas decomposition into CH₃OH+O₂(¹Δ) over TS7, at averaged rate <k₇>=1.2 × 10¹¹ s⁻¹, is a channel of atmospheric relevance. Importantly, conversion of the initially formed ¹PC to ³PC will affect the relative yields of the different products. Spin–orbit coupling between the lowest singlet and triplet states in PC is very small, but the spin–orbit coupling between the lowest singlet state and the second-lowest triplet state (or between the second-lowest singlet and the lowest triplet) is much larger, as there is now an orbital angular momentum difference, and we calculate a root-mean-square coupling matrix element of 58 cm⁻¹ in both cases. Simply assuming Rabi cycling between the two states, a ‘rate constant' for singlet-triplet conversion of 1.7 × 10¹² s⁻¹ is estimated. Using a more rigorous statistical rate theory for reactions with spin-state change²⁶,²⁷ (see Supplementary Note 2), we obtain a remarkably similar estimate of <k_ISC>=3.5 × 10¹² s⁻¹, while the reverse <k_−ISC>=1.9 × 10¹² s⁻¹. The reverse reaction ¹PC→TRIOX occurs with an average rate <k₋₄> of 1.3 × 10¹¹ s⁻¹, which is ∼3% of the total ¹PC removal rate, such that the net TRIOX→¹PC conversion rate k₄ⁿ(E_v)=0.97 × k₄(E_v).

³PC decomposes into CH₃OH and ground state ³O₂ over a very low barrier (TS6), with RRKM-calculated average <³k₆> of 4.1 × 10¹¹ s⁻¹, faster than the singlet ¹PC reaction to CH₃OH, above. It must compete with the reverse ISC, above and also with the fast dissociation of ³PC into CH₃O+HO₂ at variational-RRKM rate <³k_diss>≈3.4 × 10¹² s⁻¹ (see data in Supplementary Table 3), but still results in twice more CH₃OH+³O₂ production than the CH₃OH+¹O₂ afforded by ¹PC, above. Accounting for the rates of all reactions of ¹PC and ³PC, the two latter routes together are found to result in a CH₃OH yield through activated TRIOX of 7.8% at 298 K and 1,013 hPa. Given the possible error of ∼1.5 kcal mol⁻¹ on the energies of the transition states to CH₃OH relative to the (variational) transition states of the PC dissociations, and taking into account also a likely error of a factor of ∼2 on the ratio of k_ISC/k_diss, we estimate an uncertainty margin on the CH₃OH yield of a factor of ∼3.5. Note that about 45% of the products of activated TRIOX arise via ISC of ¹PC to ³PC. Of major importance is that TRIOX does not decompose directly but via the complex ¹PC, which enables production of CH₃OH, while direct methanol formation from CH₃OOOH would face a quasi-unsurmountable barrier¹⁶.

A (minor) fraction of the activated TRIOX will suffer energy loss by successive collisions with air molecules to yield thermalized CH₃OOOH, of which the subsequent fates are discussed in Supplementary Note 4. Using the bi-exponential energy transfer model of Troe²⁸ with an assumed average energy transferred per collision <ΔE>_all of −0.9 kcal mol⁻¹—fairly high because TRIOX has several low-frequency vibration modes—and taking into account the distribution function F(E_th,v) of the activated TRIOX, the fraction of stabilization at a collision frequency of 1.2 × 10¹⁰ s⁻¹ at 298 K and 1,013 hPa was evaluated (see the ‘Methods section') to be f_stab≈10.7%. However, this result is quite uncertain, first of all because it is very sensitive to the assumed value of <ΔE>_all: doubling it increases f_stab nearly threefold while halving it reduces f_stab to <2%. Moreover, the calculated f_stab depends also strongly on k₄(E_v), which itself bears a possible error of a factor ∼1.5–2. We therefore estimate a stabilized CH₃OOOH yield at 298 K and 1 atm in the range 0–35%. The much higher f_stab of ∼90% predicted by Nguyen et al.¹⁷ can be ascribed to their TS for TRIOX→¹PC conversion being our artefactual TS4′, which on account of its far higher rigidity than TS4 leads to a much lower calculated rate of TRIOX→¹PC and hence much more TRIOX stabilization.

Reaction products and estimated yields in the troposphere

The theoretical investigation above predicts that the dominant product route of the title reaction is channel (2) yielding the radicals CH₃O+HO₂, whereas the suggested channel (1)⁸,⁹ producing the Criegee Intermediate CH₂O₂ is found to be entirely negligible. On the other hand, we find that the title reaction yields a sizable fraction of collisionally thermalized (but chemically labile) CH₃OOOH, of order of 10% at 1 atm and 298 K, while we also uncovered two parallel pathways leading directly to CH₃OH+O₂ with overall yield around 7% in the same conditions. No evidence could be found for any other significant product routes. It must be stressed that the yield estimates of CH₃OOOH and CH₃OH given above and listed in Table 3 are subject to large uncertainty factors of ∼3.5 for each, as detailed in the previous subsection.

Table 3. Predicted products of the CH₃O₂+OH reaction and best-estimate yields at various pressures and corresponding average temperatures in the troposphere above the tropics.

Reaction products	Reaction channel	1,013 hPa, 298 K	750 hPa, 285 K	400 hPa, 256 K
CH3O+HO2	(2)	0.82	0.85	0.88
CH3OOOH*	(4)*	0.107	0.074	0.035
CH3OH+O2†	(3)	0.069	0.072	0.078

^*Channel 4: CH₃O₂+OH→thermalized CH₃OOOH.

^†Overall yield of CH₃OH formed through activated CH₃OOOH^†.

As detailed in the next subsection, the title reaction is most important above the tropical oceans, where NO levels are low but OH concentrations moderate to high. The rate of the reaction as a function of decreasing pressure (or of increasing altitude) and as a function of latitude is depicted in Supplementary Fig. 4. Near the Equator, accounting for the temperature profile, ∼50% of the reaction occurs below 750 hPa (altitude ∼2.4 km) where the average temperature is 285 K, and nearly ∼95% below 400 hPa (altitude ∼7.5 km) where temperature is 256 K. Given that the CH₃OOOH stabilization fraction should show a considerable pressure and temperature dependence, and a minor temperature dependence is also expected for other pathways (see the ‘Methods section') we have evaluated the CH₃OOOH and CH₃OH yields also for the ‘median' conditions 750 hPa and 285 K, and for the ‘limit' conditions 400 hPa and 256 K, above. The results, together with those for 1,013 hPa and 298 K, are listed in Table 3. The pronounced pressure- and temperature dependences of the CH₃OOOH stabilization fraction can be expressed within a few per cent by the power function f_stab(P,T)=0.107 × (P/1,013 hPa)^2.0 × (298 K/T)^5.0.

Modelled global impact

Adopting the measured rate⁹ of CH₃O₂+OH, the reaction accounts for 20% of the global CH₃O₂ sink according to IMAGES simulations. The global flux through that reaction is considerable: ∼11 Tmoles per year, comparable to, for example, the global source of isoprene²⁹. Although it is only a minor sink (∼10%) of CH₃O₂ at high latitudes and over polluted continental regions (Fig. 3) where the reaction with NO is by far the largest sink (Supplementary Fig. 5), the reaction with OH represents 20–30% of the sink over tropical oceans and deserts, where CH₃O₂+HO₂ is however still dominant (30–50% of total sink).

Figure 3. Contribution of CH₃O₂+OH to the sink of CH₃O_2.

Modelled yearly averaged contribution (%) of the reaction to the vertically integrated sink of CH₃O₂. Map created using IDL version 8.2.3.

Table 4 summarizes the model simulations. The best theoretical estimates are used in run B, while runs C and D adopt yields approaching respectively the high end and low end of the estimated uncertainty range of both the direct CH₃OH yield and the TRIOX stabilization fraction. Relative to a simulation neglecting the title reaction, the HO₂ radical abundances are increased by 10–20% over tropical oceans (Supplementary Fig. 6). Unsurprisingly, the impact is highest when the HO₂ yield is highest (run D). The changes are negligible or even negative in high-NOx areas.

Table 4. Overview of model simulations with assumed product yields.

Run	CH3O2+OH	CH3O	TRIOX	CH3OH	CH2OO
A	Ignored	–	–	–	–
B	Best estimate	0.86	0.07	0.07	0
C	High methanol case*	0.61	0.21	0.18	0
D	Low methanol case*	0.975	0	0.025	0
E	High Criegee case†	0.6	0	0	0.4
A_NO	As A, no ocean source‡	–	–	–	–
C_NO	As C, no ocean source‡	0.61	0.21	0.18	0
C_VR	As C, low k(CH3OOH+OH)§	0.61	0.21	0.18	0

^*Methanol yield from activated trioxide multiplied (divided) by 3 in run C (D) relative to best estimate. Stabilisation fraction multiplied by 3 in run C, taken equal to zero in run D.

^†Not a theoretical prediction.

^‡Oceanic methanol emission omitted.

^§Use lower rate for reaction CH₃OOH+OH, within recommended uncertainty range.

Globally averaged molar yields of CH₃O, stabilized trioxide, CH₃OH and CH₂OO adopted in model runs. The yields are pressure- and temperature-dependent (see text).

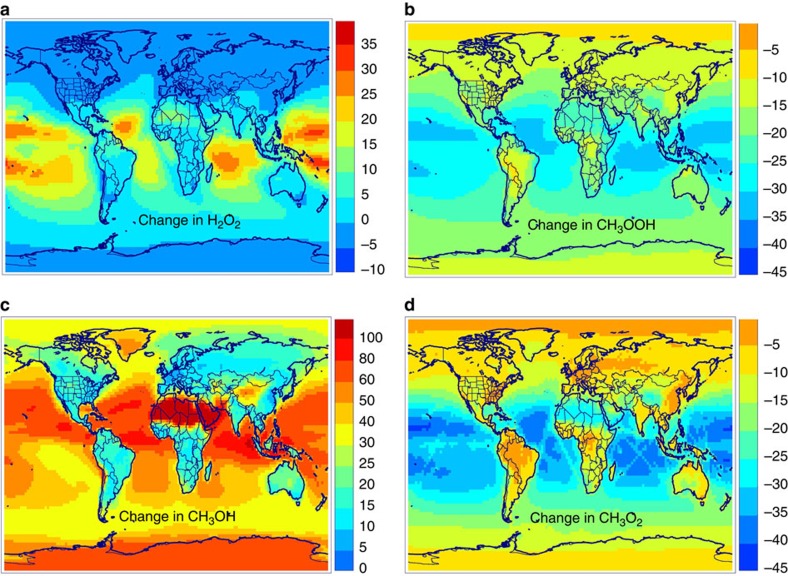
The changes in OH are of opposite sign to those of HO₂, reaching up to −7% over remote oceans. Loss of OH due to reaction with CH₃O₂ and the products CH₃OOH and CH₃OH is partially offset by OH recycled from enhanced HO₂. The globally averaged OH concentration decreases by 1.5–3.2% depending on the simulation, increasing the methane lifetime by up to 0.3 years in run C. The largest OH changes are calculated in run C, due to its lower HO₂ yield and higher OH loss through reaction with CH₃OOOH and CH₃OH. Surface ozone is decreased due to the CH₃O₂+OH reaction, by up to 6% over remote oceans, and by 1–2% (<1 ppbv) over Europe, North America and East Asia in July (Supplementary Fig. 7). Hydrogen peroxide (H₂O₂) is strongly impacted, owing to the quadratic dependence of its production on HO₂ levels. Its concentrations increase by up to 30% in run C (Fig. 4) and ∼50% in runs B and D.

Figure 4. Impact of CH₃O₂+OH on key compounds abundances.

Annually averaged modelled changes (in %) in near-surface concentrations of (a) H₂O₂, (b) CH₃OOH, (c) CH₃OH and (d) CH₃O₂ in the high methanol simulation (run C). Maps created using IDL version 8.2.3.

Methyl peroxy radical abundances are reduced by up to 40% over tropical oceans (Fig. 4), irrespective of the yield assumption. This strong drop in concentration reflects increased loss through reaction with OH and HO₂, and slightly decreased production from CH₄+OH. The decreases in CH₃OOH are also substantial (up to −30%). Formaldehyde is almost unaffected, being an end product to all CH₃O₂ sink pathways. Methanol, however, shows drastic differences among the simulations: whereas its concentrations increase or decrease by ∼20% at most in runs B and D, the global methanol burden is increased by 60% in run C, with concentration increases reaching 30–100% over remote oceans (Fig. 4). Even over continents, methanol increases by 10–20% over most areas and by 80–200% over desert regions with very low methanol emissions. Methanol formation from CH₃O₂+OH is largely due to the direct pathway to CH₃OH+O₂ (56%), but indirect formation through stabilized TRIOX is significant (44%). Reaction on aerosols is calculated to be the largest TRIOX sink globally, followed by reaction with OH and reaction with (H₂O)₂ (Supplementary Fig. 8, Supplementary Note 4). The calculated average yield of methanol from stabilized TRIOX is 65%.

Model evaluation for peroxides and formaldehyde

We limit our evaluation to stable compounds over oceans, where strongest impacts are expected. Both the modelled vertical profile and latitudinal profile of H₂O₂ agree generally fairly well with the observations from aircraft and ship campaigns (Supplementary Fig. 9, Supplementary Fig. 10, and Supplementary Fig. 11), indicating that its sources and sinks are reasonably well described by the model. As seen in Supplementary Table 4, the average model bias across all campaigns is improved when including the title reaction, from −14% in run A to +3 and −2% in runs B and C, respectively. Although this improvement could be fortuitous, given the known uncertainties in HO_x modelling³⁰, the title reaction clearly does not lead to noticeable inconsistencies with the data. As expected, the reaction has negligible impact on modelled CH₂O (Supplementary Fig. 12) which agrees very well with aircraft data over oceans.

For CH₃OOH, the title reaction leads to model underestimations (>∼25%) of airborne measurements, but it improves significantly the model agreement with ship measurements (Supplementary Fig. 11, Supplementary Fig. 13, and Supplementary Table 5). The contradiction between the conclusions from either ship or aircraft data is difficult to explain given the wide geographical area covered by both platforms. As in a previous modelling study¹³, the largest biases are found for INTEX-B (ref. ³¹). Since even the run ignoring the title reaction largely underestimates the observations in several campaigns, measurement issues and/or model uncertainties likely cause the discrepancies. For example, the estimated uncertainty in the rate constant of the CH₃OOH+OH reaction is a factor of 1.4 (ref. ³²). Adopting a rate constant measurement³³ about 25% lower than the current Jet Propulsion Laboratory recommendation³² used in the model increases the CH₃OOH concentrations by 15–20% and goes already a long way to compensating the deterioration of model performance against aircraft campaigns (Supplementary Fig. 13 and Supplementary Table 5). Other relevant processes might be also uncertain. More work is needed to address those issues.

A large source of methanol

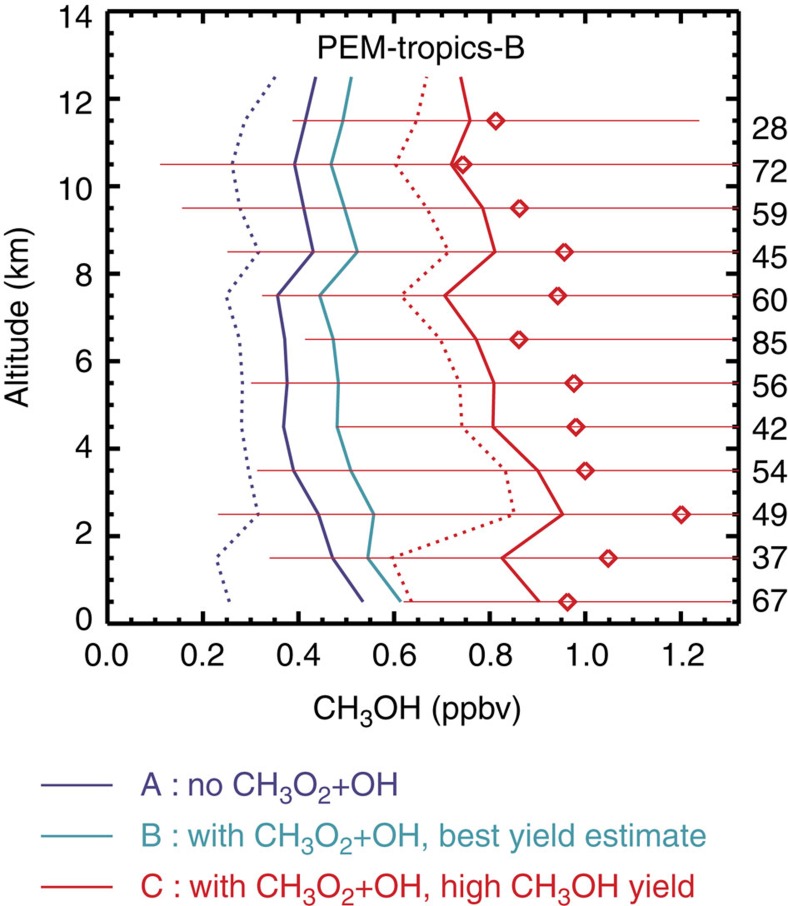
In agreement with previous studies⁴,⁵,³⁴,³⁵, our simulation omitting CH₃O₂+OH underestimates CH₃OH observations by a factor of ∼2 over the remote Pacific (Fig. 5). When including the reaction, methanol production from CH₃O₂+RO₂ is halved, from 33 to 15 Tg per year (Supplementary Table 6) due to its near-quadratic dependence on CH₃O₂ levels. The CH₃O₂+OH reaction would therefore worsen the model underestimations unless methanol is produced by the reaction with a sufficient yield. The model/data mismatch is barely reduced in run B, with its low overall methanol yield (∼12%), while it nearly vanishes in run C, with an overall yield of 32%. Both the average concentration and vertical profile shape are greatly improved in this case.

Figure 5. Measured and modelled methanol over the remote Tropical Pacific.

Measurements from the Pacific Exploratory Mission in the tropical Pacific (PEM-Tropics-B)⁶. Solid (dotted) lines denote simulations including (excluding) the oceanic source of methanol. The number of measurements per altitude bin is indicated on the right. The error bars represent the s.d.'s of the measurements. The nominal precision of the measurements was 25% (ref. ⁶⁵).

Similar conclusions hold for comparisons at the most remote sites Mauna Loa and Cape Verde, which was shown to be under mostly maritime and Saharan influences³⁶ (Table 5, Supplementary Fig. 15). The other campaigns listed in Table 5 were probably more impacted by continental emissions, which are likely overestimated in the model since they were derived by inverse modelling³⁴ while neglecting the contribution of CH₃O₂+OH. Nevertheless, including the reaction improves the model performance against airborne measurement at mid-latitudes (Supplementary Fig. 16). An overestimation of oceanic emissions likely contributes also to the strong model overestimation for the Atlantic Meridional Transect cruise AMT-22 (Supplementary Fig. 17), since flux measurements by eddy covariance during that campaign³⁷ indicated no emission, only deposition with an average dry deposition velocity (0.68 cm s⁻¹) close to the corresponding model value (0.63 cm s⁻¹). Suppressing oceanic emissions in the model (run C_NO) leads to a much closer agreement with the latitudinal profile of AMT-22 data. That this setting leads however to large underestimations at other sites (Table 5) suggests that ocean/atmosphere exchanges are more variable than currently assumed.

Table 5. Measured CH₃OH over oceans and model biases.

Campaign	Area	Obs.	A	A_NO	B	C	C_NO
PEM-Tropics-B	Pacific	934	0.44	0.30	0.54	0.87	0.74
PEM-West-B	N.-W. Pacific	702	0.83	0.71	0.99	1.35	1.26
INTEX-A	N. Atlantic	1,689	0.76	0.73	0.83	0.97	0.93
ITCT	N. Atlantic	991	0.98	0.95	0.96	1.15	1.12
INTEX-B	Pacific	1,012	0.60	0.53	0.67	0.80	0.73
Mauna Loa	N. Pacific	900	0.50	0.23	0.63	0.89	0.64
Cape Verde	N. Atlantic	768	0.38	0.18	0.73	1.06	0.68
AMT-22	Atlantic	420	1.12	0.52	1.33	1.96	1.35
INDOEX-1999	S. Indian	708	0.79	0.43	0.94	1.56	1.19
Mean model bias factor*			0.73	0.45	0.82	1.12	0.92
Mean discrepancy factor†			1.47	2.25	1.31	1.26	1.31

^*Defined as 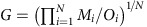, with M_i/O_i the ratio of the averaged modelled values to the averaged observed values for campaign i.

^†Defined as 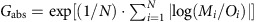,that is, it is the geometrically averaged ratio of the higher to the lower among the model and observed averages.

Averaged observed mixing ratios (pptv) and ratios of averaged modelled to averaged observed values for model runs defined in Table 4. See Supplementary Fig. 14 for more information on the measurements.

Discussion

The theoretical results presented above leave little doubt that the Criegee pathway (1) is negligible in atmospheric conditions, that is, CH₂O₂ is not formed in any significant amount from CH₃O₂+OH which therefore cannot be an important source of formic acid. Actually, any sizable contribution of the reaction to HCOOH formation would lead to huge overestimations of its modelled concentrations over the Southern Pacific (Supplementary Fig. 18) where median concentrations of only 19 pptv were measured in the boundary layer during spring³⁸, almost an order of magnitude below modelled values assuming a 40% stabilized CH₂O₂ yield.

The theoretical calculations further inform us that the methoxy pathway (2) is expected to dominate, whereas both methanol formation (3) and stabilization of the trioxide are viable, but likely minor. Of fundamental interest is that significant direct methanol production can occur only because the activated CH₃OOOH intermediate decomposes indirectly through the CH₃O·HO₂ complex. The share of each of the two minor channels likely does not exceed ∼20% of the total reaction rate. Theory alone cannot provide precise yield estimates, due to uncertainties in key parameters, that is, precise barrier heights, average energy losses per collision, and the singlet ↔ triplet ISC rate that impacts methanol production.

Fortunately, atmospheric measurements provide valuable constraints. The persistent model underestimation of CH₃OH measurements over the remote Pacific⁴,⁵,³⁴,³⁵ cannot be explained by ocean/atmosphere exchanges, since higher emissions would cause strong decreasing vertical gradients not seen in campaign data; on the contrary, eddy covariance measurements³⁷ indicate that oceanic emissions might be very low. Another remote source of methanol, the photochemical production due to CH₃O₂+RO₂ reactions, could be underestimated. But since it is largely dominated by the CH₃O₂ self-reaction of which the methanol yield (∼0.63) cannot be much underestimated, and since CH₃O₂ production from CH₄+OH is also well constrained, only a large production of organic peroxy radicals from non-methane organic precursors could boost this source of methanol. High observed acetaldehyde over oceans⁶,³⁶,³⁹ suggested indeed the existence of unknown sources of CH₃CHO or of its precursors. However, besides the noted inconsistency³⁹ of those observations with measured PAN:NOx ratios, the good agreement of modelled CH₂O with observations over oceans (Supplementary Fig. 12) shows that those potential sources cannot weigh heavily on CH₂O and CH₃O₂ production.

The only viable candidate for the missing remote source of methanol is therefore CH₃O₂+OH, with an overall methanol yield crudely estimated to be ∼30%, consistent with theoretical estimates given their uncertainties. Given the experimental uncertainty (50%) in the total rate constant of the reaction⁹, this inferred overall yield could be even higher, or possibly lower. The total photochemical source of methanol in run C (130 Tg per year) slightly exceeds the range (50–100 Tg per year) estimated by Jacob et al.⁴, because of a higher net ocean sink and lower continental emissions in our simulations. The contribution of CH₃O₂+OH (115 Tg per year globally) is comparable in magnitude to the total terrestrial emission source. Further work will be needed to evaluate how this source will impact our understanding of the methanol budget. Clearly, a better understanding of ocean-atmosphere exchanges is required to refine the top–down yield estimation presented above. It is not currently possible to determine which of the direct methanol formation channel or indirect pathway through the stabilised TRIOX is dominant. A more direct experimental determination is obviously needed. Hopefully TRIOX can be measured, although loss to walls might prove challenging, and atmospheric concentrations should be very low, a few pptv at most.

Reaction with OH might be also significant for other peroxy radicals, such as those formed from biogenic terpenoids. We expect that for the much larger activated ROOOH^†, conversion to a complex RO—HO₂ and eventual dissociation to RO+HO₂ will be substantially slower than for CH₃OOOH^†, such that collisional stabilisation of ROOOH^† should be a major if not dominant product route. However, the global relevance for large peroxys formed from biogenic terpenoids is expected to be lower compared with CH₃O₂+OH, because OH levels are generally lower in the boundary layer over forests than in the oceanic lower troposphere, and because the reaction of HO₂ with large peroxys is considerably faster than the reaction of CH₃O₂ with HO₂ (ref. ⁴⁰). Assuming a rate constant similar to that of CH₃O₂+OH, the reaction of large biogenic peroxy radicals with OH is estimated here to account for ∼3% of their total sink over remote forests.

Methods

Quantum chemistry

All the structures presented on the potential energy surface were fully optimized with DFT using the M06-2X-D3/6-311++G(3df,3pd) level of theory in Gaussian 09 version D.01 (ref. ⁴¹; see Supplementary Table 7), except where explicitly stated otherwise. The M06-2X-D3 method was benchmarked and recommended for the general main group elements including the evaluation of thermochemistry, kinetics and noncovalent interactions⁴². For the geometry optimization and the corresponding frequency calculations, a tight convergence criterion and a superfine integration grid (150,974) were adopted. Wherever appropriate, an unrestricted ansatz was used, and careful checks were made to ensure that low-spin open-shell solutions were found to the Kohn–Sham equations. The calculated vibrational frequencies have been used for evaluation of zero-point energies and RRKM rate calculations. All the transition states for the reactions involving the abstraction or transfer of a hydrogen atom were confirmed by IRC calculations, while for the reactions from the reactant complex ¹RC via TRIOX to the product complex ¹PC, attempts to generate IRC curves failed due to the low curvature of the potential energy surface, so instead, various scans were used to explore the behaviour of those two loose TSs (Supplementary Fig. 3 and Supplementary Note 1).

Various single-point calculations were carried out using CASSCF, CASPT2 and CCSD(T)-F12. The CASSCF and CASPT2 calculations were performed with Molpro 2012.1 (refs ^{43, 44}) with an active space of 18 electrons in 13 active orbitals (which corresponds to a full-valence active space, but omitting the O–H and C–H bonding orbitals and the C–H anti-bonding orbitals), with the cc-pVTZ basis set⁴⁵. We also calculated the spin–orbit coupling constant with Molpro at CASSCF(18,13)/cc-pVTZ level of theory.

Explicitly correlated CCSD(T)-F12 energies were obtained with the ORCA 3.03 package⁴⁶, using an unrestricted HF-reference wavefunction for reactant and product radicals and the open-shell singlet intermediates, and a restricted reference otherwise. The cc-pVTZ-F12 basis set⁴⁷ and appropriate auxiliary basis sets were used. Unless mentioned otherwise, all reported energies derive from CCSD(T)-F12/cc-pVTZ-F12 calculations with ZPVE corrections from M06-2X-D3/6-311++G(3df,3pd).

Theoretical reaction kinetics

The statistical-kinetics rates for thermal as well as chemically activated reactions were estimated using the energies obtained at our highest level and including the ZPVE (scaled by a factor 0.97 (ref. ⁴⁸)) as stated above, while partition functions or integrated sums of vibration states and vibration state densities were based on the M06-2X-D3 harmonic vibration frequencies (scaled by a factor 0.983 (ref. ⁴⁸)) and rigid-rotor rotation constants. For all structures and transition states involved we adopted the harmonic oscillator approximation, commensurate with our aim of identifying the relevant reaction pathways and distinguishing between major and minor routes based on an approximate, semi-quantitative assessment of end-product yields.

As detailed in the Results section, the only thermal bimolecular reaction that needs to be considered was found to be unimportant if not negligible. Its thermal rate coefficient at 298 K was computed using conventional transition state theory²², with tunnelling factor estimated assuming an asymmetric Eckart potential⁴⁹,⁵⁰.

The majority of the relevant reaction steps are chemically activated unimolecular reactions of (i) the initial singlet reactant complex ¹RC, (ii) the closed-shell singlet intermediate TRIOX and (iii) the resulting product complexes ¹PC and ³PC. We employed RRKM theory²¹,²² to estimate the micro-canonical rate coefficients for each of the steps:

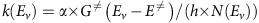in which α is the reaction path degeneracy, h Planck's constant, E^≠ the TS energy, E_v the vibration energy of the reacting activated intermediate, N(E_v) its density of vibration states and G^≠(E_v−E^≠) the sum of accessible vibration states of the TS; both the latter were evaluated by exact count²². The conservation of angular momentum was accounted for in reasonable approximation by correcting the potential energies (inclusive ZPVE) of the activated reactants and transition structures by their average rotation energy relative to that of the reactant complex ¹RC, adopting the quasi-diatom approximation (see Supplementary Note 5). The changes in effective potential energy²¹,²² are at most ±0.3 kcal mol⁻¹ and the rotational effects on the chemically activated rate coefficients remain minor for all reactions (1–20%). Tunnelling corrections for all relevant activated reactions were found negligible because of the relatively high excess vibration energies (E_v–E^≠) and low imaginary frequencies (see Supplementary Table 1). The rate constants for the dissociation of the singlet and triplet product complexes ¹PC and ³PC were calculated using variational RRKM²¹,²² by locating the structure ‘var' that minimizes G^var(E_v−E^var). The rate constant for ISC of ¹PC to ³PC was calculated based on locating the minimum energy crossing point using the code developed by Harvey and Aschi⁵¹,⁵². (see Supplementary Note 2)

In the total distributable energy E_v, we duly include the thermal vibration energy E_th,v that the intermediates inherit from the thermal reactants CH₃O₂+OH, and for each step the rates k(E_v) were averaged over the thermal distribution function F(E_th,v) of formation. As the lifetime of the initial complex ¹RC is <1 ps, the original thermal distribution F(E_th,v) remains conserved up to the TRIOX intermediate, but it shifts down for ¹PC and ³PC by ∼0.45 kcal mol⁻¹ at 298 K/1,013 hPa, ∼0.35 kcal mol⁻¹ at 285 K/750 hPa and ∼0.25 kcal mol⁻¹ at 256 K/400 hPa, respectively, due to the average of ∼0.5, 0.4 and 0.3 collisions, respectively, that TRIOX suffers in the atmosphere during its lifetime (see <k₄> rate values in Table 2). The lifetime of <0.3 ps of ¹PC and ³PC is too short for further collisional losses. The width of F(E_th,v), of ∼2 kcal mol⁻¹, is much less than the average excess energy (E_v−E^≠) for most reaction steps, and the k(E_v) are generally not far from their high-energy asymptotes, such that the F(E_th,v)-averaged <k(E_v)> differ only 1–20% from k(<E_v>). The only exception is the ¹PC reaction through TS2, which anyway is negligibly slow compared with the competing reaction through TS1. As a result, the precise shape of F(E_th,v) is of little importance for the overall kinetics of the chemically activated unimolecular reactions of our system, though the average value of the thermal <E_th,v> is of some significance. As there is no entrance barrier and the entrance transition state TS_in is variational (see Fig. 1), the formation distribution function F(E_th,v) cannot be evaluated in the usual way²¹. However, the average initial <E_th,v>, of ∼2.1, 2.0 and 1.75 kcal mol⁻¹ at 298, 285 and 256 K, respectively, could be estimated with sufficient accuracy for our purpose and a reasonable F(E_th,v) could be derived accordingly as detailed in Supplementary Note 6.

Different from the effective rates of the unimolecular reactions, the (minor) fraction f_stab of the activated TRIOX that becomes collisionally stabilized depends markedly on the vibration energy of the activated TRIOX and is therefore quite sensitive to F(E_th,v). The stabilization competes with the much faster rearrangement TRIOX→¹PC through TS4 at net rate kⁿ₄(E_v) (≈0.97 × k₄(E_v) due to the reverse reaction). The Lennard-Jones collision frequency of CH₃OOOH with air molecules, k_coll=Z_LJ[M], is estimated⁵³ to be about 1.2, 0.92 and 0.55 × 10¹⁰ s⁻¹ at 298 K/1,013 hPa, 285 K/750 hPa and 256 K/400 hPa, respectively. The bi-exponential energy transfer model of Troe²⁸ was used and implemented in a quasi-stochastic approach; the average energy transferred per collision, a critical quantity for the overall f_stab but highly uncertain, was assumed to be <ΔE>_all=−0.9 kcal mol⁻¹, amounting at 298 K to an average energy lost per down-collision α≈1.34 kcal mol⁻¹ and average energy gained per up-collision β≈0.44 . For a given initial energy E_v,in of TRIOX, the stabilization fraction was found as the repetitive product of the successive, increasing probabilities of a (new) jth collision at constant rate k_coll in competition with TRIOX→¹PC rearrangement at net rate kⁿ₄(E_j−1) that decreases on average after each collision:

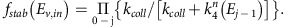Given the initial excess energy of TS4 of ∼7 kcal mol⁻¹, this product converges rapidly after some 8–10 collisions for the adopted <ΔE>_all. The overall f_stab was finally found by integrating over the distribution function F(E_th,v). As the net TRIOX conversion rate kⁿ₄(E_v) at the initial energies is relatively high, f_stab is small and depends strongly on <ΔE>_all but also markedly on kⁿ₄(E_v) itself. Obviously, at higher altitudes in the troposphere, f_stab decreases with decreasing pressures, but this is partially offset by the pronounced, multiple effect of the simultaneous temperature decrease: through the lower kⁿ₄(E_v), the lower average E_th,v to be lost for stabilization, the effect on the number density of N₂/O₂ and the higher Ω^2,2 collision integral. Thus, the combined effects of the decreasing pressure P and temperature T in the troposphere above tropical oceans result in a dependence f_stab∼P² × T⁻⁵.

Overall and net reaction rates and end-product yields were obtained in a straightforward way by duly considering the fractional contribution of each competing reaction for each intermediate in the complete scheme.

Global modelling

IMAGES⁵⁴,⁵⁵ calculates the distribution of 172 compounds at 2° × 2.5° resolution, using meteorological fields from ERA-Interim analyses of the European Centre of Medium-Range Weather Forecasts (ECMWF). Simulations were made for the year 2010 with a spin-up time of 6 months starting in July 2009. Anthropogenic emissions are obtained from a global inventory (edgar.jrc.ec.europa.eu/overview.php?v=42) overwritten by regional inventories over Europe, Asia and the U.S. Biomass burning emissions are provided by the Global Fire Emissions Database GFEDv4s (www.globalfiredata.org). Isoprene fluxes are based on the Model of Emissions of Gases and Aerosols from Nature (MEGAN)⁵⁵. Biogenic methanol emissions (100 Tg per year globally) are obtained from an inverse modelling study³⁴ using IMAGES and methanol total columns from Infrared Atmospheric Sounding Interferometer. Parameterization of ocean-atmosphere methanol exchanges follows a two-layer model resulting in an oceanic source of 39 Tg (in 2010) and an oceanic uptake represented as dry deposition (between 46 and 66 Tg per year depending on the model simulation). The isoprene degradation mechanism has been updated to account for the revised peroxy radical kinetics of the Leuven Isoprene Mechanism LIM1 (ref. ⁵⁶) as well as for the chemistry of isoprene epoxides⁵⁷. Wet scavenging is parameterized based on ECMWF cloud and precipitation fields⁵⁸. Dry deposition follows Wesely's resistance-in-series scheme⁵⁹, with aerodynamic resistances based on Monin-Obukhov similarity theory (ECMWF, IFS Documentation—Cy40r1, Operational implementation 22 November 2013, Part IV: Physical processes, European Centre for Medium-Range Weather Forecasts, Shinfield Park, Reading, England, 2014.) using sensible heat fluxes and friction velocities from ECMWF operational analyses and quasi-laminar layer resistances dependent on gas-phase diffusivity⁶⁰. Surface resistances are calculated depending on mesophyll, cuticular, ground and in-canopy aerodynamic resistances⁵⁹,⁶¹,⁶². The surface resistances are adjusted to provide a better match of modelled dry deposition velocities with eddy-covariance estimates over a forest by Nguyen et al.⁶³; in particular, the H₂O₂ surface resistance becomes negligible after this adjustment.

As detailed in Supplementary Note 4, the reactions of the stabilized trioxide include the thermal conversion to the product complex ¹PC; reaction with OH; reaction with the water dimer; and reactive uptake on aqueous aerosols. Aerosol uptake is calculated⁵⁴ based on sulfate/ammonium/nitrate and carbonaceous aerosols calculated by IMAGES, and sea salt aerosols obtained from the MACC (Monitoring Atmospheric Composition & Climate) Reanalysis (apps.ecmwf.int/datasets/data/macc-reanalysis/levtype=sfc/). The water dimer concentrations are calculated using an equilibrium constant expression⁶⁴ validated with available experimental data.

Data availability

The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information file. Any further relevant code and data used in the paper are available from the authors upon request.

Additional information

How to cite this article: Müller, J.-F. et al. The reaction of methyl peroxy and hydroxyl radicals as a major source of atmospheric methanol. Nat. Commun. 7, 13213 doi: 10.1038/ncomms13213 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-18, Supplementary Tables 1-7, Supplementary Notes 1-6 and Supplementary References