A multiple imputation approach to the analysis of clustered interval-censored failure time data with the additive hazards model

Abstract

Clustered interval-censored failure time data can occur when the failure time of interest is collected from several clusters and known only within certain time intervals. Regression analysis of clustered interval-censored failure time data is discussed assuming that the data arise from the semiparametric additive hazards model. A multiple imputation approach is proposed for inference. A major advantage of the approach is its simplicity because it avoids estimating the correlation within clusters by implementing a resampling-based method. The presented approach can be easily implemented by using the existing software packages for right-censored failure time data. Extensive simulation studies are conducted, indicating that the proposed imputation approach performs well for practical situations. The proposed approach also performs well compared to the existing methods and can be more conveniently applied to various types of data representation. The proposed methodology is further demonstrated by applying it to a lymphatic filariasis study.

1. Introduction

Correlated or clustered failure time data occur in many areas such as medical studies (Cai and Prentice, 1997). In many situations, the exact time of failure cannot be observed but is known to fall between two observation times. Such data are usually referred to as interval-censored failure time data. Clustered interval-censored failure time data may naturally arise in periodic follow-up studies where each study subject is repeatedly measured at discrete time points and some subjects come from the same cluster or group such as sibling, family and community. In this case, the interval-censored observations from the same cluster share certain unknown characteristics and are correlated as a result.

Several methods have been proposed for regression analysis of clustered interval-censored failure time data. These include parametric approaches (Bellamy et al., 2004; Zhang and Sun, 2010; Lam et al., 2010) and semiparametric approaches (Xiang et al., 2011; Zhang and Sun, 2013; Li et al., 2014). For most of the existing semiparametric methods, it is assumed that the failure time of interest follows the proportional hazards model (Pan, 2000). It is known that the proportional hazards model may not fit failure time data well sometimes and in this case, one of the alternatives is the additive hazards model. The additive hazards model describes a different aspect of the relationship between survival time and covariates and could be more plausible than the proportional hazards model in many situations (Lin and Ying, 1994). For example, in public health studies, people may be more interested in the risk difference described by the additive hazards model than the risk ratio described by the proportional hazards model (Breslow and Day, 1987). Li et al. (2012) investigated regression analysis of clustered interval-censored failure time data. However, they considered only the simple situation where each subject is observed only twice, or the failure time is left-, interval-, or right-censored. In the following, we will discuss general clustered interval-censored failure time data.

We develop a multiple imputation approach to analyze clustered interval-censored failure time data. Our method reduces the analysis of clustered interval-censored data to that of right-censored failure time data. The algorithm is implemented in two steps. First, we apply a within-cluster resampling (WCR) procedure (Hoffman et al., 2001) to sample a single subject from each cluster and obtain independent interval-censored failure time data. In other words, one observation is randomly sampled with replacement from each of the N clusters and an independent interval-censored dataset of size N is formed. Then a multiple imputation procedure is applied to convert the interval-censored dataset to right-censored failure time data. Inference is made based on the right-censored failure time data taking advantage of an existing estimation procedure developed by Lin and Ying (1994). If the resampling process is repeated a large number of times, say Q, where each of the Q analyses provides a consistent estimator of parameter of interest, one can obtain the WCR estimate by taking the average of the Q resampling-based estimates.

The multiple imputation approach has been used in many fields. In particular, Lam et al. (2010) developed such a procedure for the same type of the data considered here but under a parametric gamma frailty model. In addition, their method requires some strong assumptions on the distribution of the unobserved frailty and the use of the EM algorithm for the implementation. In contrast, the presented procedure has the advantage of simplicity because it can be easily implemented by using a standard software for the additive hazards model. Another advantage of the proposed approach is the use of a semiparametric additive hazards model, which provides more flexibility in describing the relationship between the failure time and covariates than a fully parametric model. In addition, the procedure given below does not need the estimation of the unobserved frailty.

In the following, before presenting the multiple imputation approach, we will first briefly introduce in Section 2 the additive hazards model and the inference procedure proposed by Lin and Ying (1994) for independent right-censored failure time data. The proposed estimation procedure is then presented in Section 3 and as mentioned above, it makes use of the method given in Lin and Ying (1994). Results from an extensive simulation study are reported in Section 4 for assessing the performance of our proposed approach and comparing to the existing method. Section 5 applies the proposed method to a set of well-known clustered interval-censored failure time data arising from a lymphatic filariasis study. Section 6 contains some concluding remarks.

2. The additive hazards model and right-censored failure time data with independent samples

Consider a survival study and let T denote the failure time of interest and Z a vector of covariates that may depend on time t. We assume that given Z, the hazard function of T has the form

$$\lambda (t;Z)={\lambda }_0\left(t\right)+{\beta }^{\prime }Z\left(t\right),$$ (1)

where λ₀(t) denotes the unknown baseline function and β is the vector of unknown regression coefficients. That is, T follows the additive hazards model (Cox and Oakes, 1984). In the following, as most authors, it will be assumed that the covariate Z(t) is known or can be observed at any time.

In this section, we will assume that instead of clustered data, one observes right-censored failure time data given by {X_i, δ_i, Z_i, i = 1, … , n} from n independent subjects. Here X_i denotes the observed failure time defined as the minimum of the true failure time T_i and the censoring time for subject i and δ_i = 1 if the true failure time is observed and 0 otherwise. Also it will be assumed that the failure time and the censoring time are independent given covariates. Define Y_i(t) = I(X_i ≥ t), the risk indicator process, and N_i(t) = I(X_i ≤ t, δ_i = 1), a counting process, i = 1, … , n.

To estimate β in model (1), Lin and Ying (1994) proposed to use the following estimating equation

$$U\left(\beta \right)=\sum _{i=1}^n{\int }_0^{\infty }\left\{Z_i\right(t)-\stackrel{‒}{Z}(t\left)\right\}\left\{{\mathit{dN}}_i\right(t)-Y_i(t\left){\beta }^{\prime }{Z}_i\right(t\left)\mathit{dt}\right\}=0,$$

where

$$\stackrel{‒}{Z}\left(t\right)=\frac{\sum _{i=1}^n{Y}_i\left(t\right)Z_i\left(t\right)}{\sum _{i=1}^n{Y}_i\left(t\right)}.$$

It can be easily shown that the solution to the equation above has the explicit form

$$\widehat{\beta }={\left[\sum _{i=1}^n{\int }_0^{\infty }{Y}_i\left(t\right){\left\{Z_i\right(t)-\stackrel{‒}{Z}(t\left)\right\}}^{\otimes 2}\mathit{dt}\right]}^{-1}\left[\sum _{i=1}^n{\int }_0^{\infty }\left\{Z_i\right(t)-\stackrel{‒}{Z}(t\left)\right\}{\mathit{dN}}_i\left(t\right)\right],$$ (2)

where $a^{\otimes 2}=a{a}^{\prime }$ for a vector a. Furthermore, Lin and Ying (1994) showed that $n^{1∕2}(\widehat{\beta }-{\beta }_0)$ converges weakly to a normal vector with mean zero and a covariance matrix that can be consistently estimated by Σ = A⁻¹ B A⁻¹, where β₀ denotes the true value of β,

$$A=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\infty }{Y}_i\left(t\right){\left\{Z_i\right(t)-\stackrel{‒}{Z}(t\left)\right\}}^{\otimes 2}\mathit{dt},$$

and

$$B=\frac{1}{n}\sum _{i=1}^n{\int }_0^{\infty }{\left\{Z_i\right(t)-\stackrel{‒}{Z}(t\left)\right\}}^{\otimes 2}{\mathit{dN}}_i\left(t\right).$$

Given $\widehat{\beta }$, a natural estimate of the baseline cumulative hazard function ${\Lambda }_0\left(t\right)={\int }_0^t{\lambda }_0\left(s\right)\mathit{ds}$ is given by

$${\widehat{\Lambda }}_0(t;\widehat{\beta })={\int }_0^t\frac{\sum _{i=1}^n\left\{{\mathit{dN}}_i\right(s)-Y_i(s\left){\widehat{\beta }}^{\prime }{Z}_i\right(s\left)\mathit{ds}\right\}}{\sum _{i=1}^n{Y}_i\left(s\right)}.$$ (3)

Note that the estimator (3) may not always be monotone in t. For this, Lin and Ying (1994) suggested using ${\widehat{\Lambda }}_0^{\ast }(t;\widehat{\beta })={\max }_{s\le t}{\widehat{\Lambda }}_0(s;\widehat{\beta })$. In the next section, we will discuss the use of the estimators (2) and (3) in estimation of β when one observes clustered interval-censored failure time data.

3. A multiple imputation approach for estimation of β with clustered interval-censored failure time data

Now we consider a survival study that includes n independent clusters with n_i denoting the size of the ith cluster, where i = 1, … , n. Let T_ij denote the failure time of interest for subject j in cluster i, j = 1, … , n_i. Suppose that one observes clustered interval-censored failure time data on the T_ij’s denoted by {(L_ij, R_ij], Z_ij(t), i = 1, … , n; j = 1, … , n_i}, where L_ij ≤ R_ij. Here L_ij = 0 represents a left-censored observation, R_ij = ∞ corresponds to a right-censored one, and Z_ij(t) is a possibly time-dependent covariate vector associated with subject j in cluster i. Note that for interval-censored data, all available information about T_ij is the interval (L_ij, R_ij] with T_ij ∈ (L_ij, R_ij]. We assume that L_ij and R_ij are independent of T_ij given the covariates Z_ij(t). Throughout this paper the T_ij′s are considered to be independent for subjects in different clusters but could be dependent for subjects within the same cluster.

To describe the association within each cluster, we will assume that there exists a cluster-specific latent variable b_i with mean zero and unknown variance. Furthermore suppose that given covariates and b_i, the failure times within each cluster are independent and T_ij follows the additive hazards model

$${\lambda }_{\mathit{ij}}(t\mid Z_{\mathit{ij}},b_i)={\lambda }_0\left(t\right)+{\beta }^{\prime }{Z}_{\mathit{ij}}\left(t\right)+b_i.$$ (4)

Here λ₀(t) and β are defined as in model (1). To make inference about β, we propose to randomly sample with replacement one interval-censored observation from each cluster using the WCR approach (Hoffman et al., 2001) and construct a new independent sample of interval-censored observations. The left-censored and interval-censored observations in this resampled interval-censored data will be imputed to generate a right-censored failure time data. Then the problem is reduced to analyzing the imputed (right-censored) data, which can be handled with the inference procedure discussed in Section 2.

More specifically, we randomly select one data point {(L_i, R_i], Z_i(t) with replacement from each cluster and generate a set of interval-censored failure time data. Let Q be a positive integer denoting the number of resamples. We repeat the resampling process Q times and generate Q sets of independent samples of interval-censored failure time data. For each set of the interval-censored failure time data, we propose the following estimation procedure to estimate β. Let K be a prespecified integer representing number of imputations.

Step 1. Choose initial estimates ${\widehat{\beta }}^{\left(0\right)}$ and ${\widehat{S}}_0^{\left(0\right)}$ of β and the baseline survival function S₀(t) = exp{−Λ₀(t)}, respectively.

Step 2. At the lth iteration, let ${\widehat{\beta }}^{(l-1)}$ and ${\widehat{S}}_0^{(l-1)}$ denote the estimates of β and S₀(t) obtained at the (l − 1)th iteration and generate K sets of right-censored data {X_ik, δ_ik, Z_ik, i = 1, … , n; k = 1, … , K} as follows. If R_i = ∞ (right-censored), define X_ik = L_i and δ_ik = 0; if R_i < ∞, define δ_ik = 1 and X_ik to be a random number drawn from the survival function

$${\widehat{S}}_0^{(l-1)}(t;{\widehat{\beta }}^{(l-1)})\exp \{-{\widehat{\beta }}^{(l-1)\prime }{Z}_i^{\ast }(t\left)\right\}$$ (*)

given L_i ≤ X_ik < R_i, where $Z_i^{\ast }\left(t\right)={\int }_0^t$ Z_i(s) ds. The imputed value was drawn this way: suppose that, in interval (L_i, R_i], the survival function (*) has probability mass {p₁, … , p_Si} at time points {t₁, … , t_Si}, then X_ik was randomly drawn from {t₁, … , t_Si} with probability proportional to {p₁, … , p_Si}. Also for all i and k, define Z_ik = Z_i.

Step 3. First define the estimate ${\widehat{\beta }}_k^{\left(l\right)}$ as $\widehat{\beta }$ given in (2) with {X_i, δ_i, Z_i, i = 1, … , n} replaced by {X_ik, δ_ik, Z_ik, i = 1, … , n}. Then determine the estimate ${\widehat{S}}_{0k}^{\left(l\right)}(t;{\widehat{\beta }}_k^{\left(l\right)})=\exp \{-{\widehat{\Lambda }}_{0k}^{\left(l\right)}(t;{\widehat{\beta }}_k^{\left(l\right)}\left)\right\}$, where ${\widehat{\Lambda }}_{0k}^{\left(l\right)}(t;{\widehat{\beta }}_k^{\left(l\right)})$ is given by (3) with {X_i, δ_i, Z_i, i = 1, … , n} replaced by {X_ik, δ_ik, Z_ik, i = 1, … , n}. Also calculate the covariance matrix ${\Sigma }_k^{\left(l\right)}$ as Σ given in the previous section based on {X_ik, δ_ik, Z_ik, i = 1, … , n}.

Step 4. Define the updated regression estimate ${\widehat{\beta }}^{\left(l\right)}$ and the estimate of baseline survival ${\widehat{S}}_0^{\left(l\right)}$ as

$${\widehat{\beta }}^{\left(l\right)}=\frac{1}{K}\sum _{k=1}^K{\widehat{\beta }}_k^{\left(l\right)},{\widehat{S}}_0^{\left(l\right)}(t;{\widehat{\beta }}^{\left(l\right)})=\frac{1}{K}\sum _{k=1}^K{\widehat{S}}_{0k}^{\left(l\right)}(t;{\widehat{\beta }}_k^{\left(l\right)}),$$

and the covariance matrix can be estimated by

$${\widehat{\Sigma }}^{\left(l\right)}=\frac{1}{K}\sum _{k=1}^K{\widehat{\Sigma }}_k^{\left(l\right)}+\left(1+\frac{1}{K}\right)\sum _{k=1}^K\frac{({\widehat{\beta }}_k^{\left(l\right)}-{\widehat{\beta }}^{\left(l\right)}){({\widehat{\beta }}_k^{\left(l\right)}-{\widehat{\beta }}^{\left(l\right)})}^{\prime }}{K-1}.$$

Step 5. Return to step 2 until the convergence is achieved.

To implement the procedure above, one needs to choose the initial estimates of β and S₀. For β, a simple choice is to let ${\widehat{\beta }}^{\left(0\right)}=0$ or use the estimate (2) based on the right-censored data {X_i, δ_i, Z_i, i = 1, … , n}. To generate the X_i’s, one can simply impute X_i = (L_i +R_i)/2 for the left- and interval-censored observations. Another alternative is to generate a uniform random variable from the interval (L_i, R_i]. For ${\widehat{S}}_0^{\left(0\right)}$, as with the second approach for β, one could apply the estimate (3) based on the same set of right-censored data and the relationship S₀(t) = exp{−Λ₀(t). For the convergence of the procedure, since the main purpose is to estimate β, one can apply the criterion

$$\mid \frac{{\widehat{\beta }}^{\left(l\right)}-{\widehat{\beta }}^{(l-1)}}{{\widehat{\beta }}^{(l-1)}}\mid \le ϵ\text{or}\mid {\widehat{\beta }}^{\left(l\right)}-{\widehat{\beta }}^{(l-1)}\mid \le ϵ$$

for a given positive constant ϵ.

Note that as the estimator (3), the estimator ${\widehat{S}}_0^{\left(l\right)}(t;{\widehat{\beta }}^{\left(l\right)})$ may not be monotone. In this case, we replace it by min_s≤t ${\widehat{S}}_0^{\left(l\right)}(s;{\widehat{\beta }}^{\left(l\right)})$ in Step 4. Let $\widehat{\beta }={\widehat{\beta }}^{\left(L\right)}$ denote the estimate of β at convergence with the multiple imputation procedure above for a resampled interval-censored data. When n is large, the distribution of $\widehat{\beta }$ can be approximated by the normal distribution (Rubin, 1987) with mean β₀ and the covariance matrix that can be estimated by

$${\widehat{\Sigma }}^{\left(L\right)}=\frac{1}{K}\sum _{k=1}^K{\widehat{\Sigma }}_k^{\left(L\right)}+\left(1+\frac{1}{K}\right)\sum _{k=1}^K\frac{({\widehat{\beta }}_k^{\left(L\right)}-{\widehat{\beta }}^{\left(L\right)}){({\widehat{\beta }}_k^{\left(L\right)}-{\widehat{\beta }}^{\left(L\right)})}^{\prime }}{K-1}.$$

Let ${\widehat{\beta }}_q^{\left(L\right)}$ and ${\widehat{\Sigma }}_q^{\left(L\right)}$ denote the final estimate of β and Σ, respectively, for the qth resampled interval-censored failure time data with q = 1, … , Q. Following Hoffman et al. (2001), we estimate β by

$$\widehat{\beta }=\frac{1}{Q}\sum _{q=1}^Q{\widehat{\beta }}_q^{\left(L\right)}$$

and Σ by

$$\widehat{\Sigma }=\frac{1}{Q}\sum _{q=1}^Q{\widehat{\Sigma }}_q^{\left(L\right)}-\frac{1}{Q}\sum _{q=1}^Q({\widehat{\beta }}_q^{\left(L\right)}-\widehat{\beta }){({\widehat{\beta }}_q^{\left(L\right)}-\widehat{\beta })}^{\prime }.$$

In the numerical studies reported below, we used Fortran 77 for the implementation of the computational algorithm above on Redhat (2.6.9–34.EL), and the computational cost seems to be affordable for moderate sample sizes. For example, with a dataset of 100 clusters with the cluster size being between 2 and 5, it took about 50 s of CPU time on average on Dell Desktop (OPTIPLEX 7010 of 10 GB RAM, 1 TB hard disk) to achieve convergence with 10 imputations and 1000 resamplings.

4. A simulation study

An extensive simulation study is conducted to assess the performance of the multiple imputation approach presented in the previous sections. In the study, we investigated the performance of the imputation method with clustered interval-censored observations represented in (L_ij, R_ij], i = 1, … , n, j = 1, … , n_i. For comparison, we also studied the estimating equation-based procedure proposed by Li et al. (2012) under the same additive hazards model. For the generation of the censoring intervals, we considered both the situation where they are independent of covariates and the situation where they may be covariate-dependent.

To generate the failure time of interest, we took λ₀(t) = 2 in model (4) and generated the Z_ij’s from the Bernoulli distribution with success probability p = 0.5. The latent variable b_i was assumed to follow a normal distribution with mean zero and variance $\frac{1}{4}$. For the generation of covariate-independent censoring intervals, we first generated multiple examination times for each subject to mimic many medical follow-up studies. For example, this would be the case if each subject is repeatedly monitored at discrete time points and some subjects are siblings or from the same family. More specifically, it was supposed that there were potentially eight examination times for each subject and the length or period between two consecutive examination times, denoted as len, was assumed to be a uniform random variable over (0, 0.2). Denote τ₀ = 0 and τ₉ = +∞ for each subject, and suppose that τ_1ij is the first random examination time generated from the uniform distribution U(0, 0.2). Then the following seven examination times were calculated as τ_kij = τ_1ij + (k − 1) × len, k = 2, 3, … , 8. It was assumed that a subject may miss the scheduled examination times with probability 0.1 for the first four and 0.2 for the latter four. Then the observed interval (L_ij, R_ij] was defined with L_ij = τ_sij and R_ij = τ_qij, where τ_sij and τ_qij with 0 ≤ s < q ≤ 9 are the two real adjacent observation times such that (τ_sij, τ_qij) contains the true failure time T_ij.

For the generation of covariate-dependent censoring intervals, we used the same procedure as above except that the eight examination times τ_k, k = 1, … , 8 were assumed to follow the Cox models

$${\lambda }_{\mathit{ij}}^k(t\mid Z_{\mathit{ij}}(s),s\le t)={\lambda }_k\left(t\right)\exp \left\{{\gamma }^{\prime }{Z}_{\mathit{ij}}\right(t\left)\right\}$$

with λ_k(t) = 9 − k and under the restricted order τ_1ij < τ_2ij < τ_3ij < τ_4ij < τ_5ij < τ_6ij < τ_7ij < τ_8ij. Here as before, we also assume τ_0ij = 0 and τ_9ij = +∞. For all situations, the cluster size n_i was assumed to follow a uniform distribution U{2, 3, 4, 5}.

In the simulation study, for comparison, we also considered the estimating equation-based procedure given by Li et al. (2012), which assumed that each subject is observed twice at U_ij and V_ij with U_ij ≤ V_ij and T_ij is known only T_ij ≤ U_ij, U_ij < T_ij ≤ V_ij or T_ij > V_ij. That is, the observation on T_ij is left-, interval- or right-censored. It is apparent that such data cannot give exact or right-censored data as the type of interval-censored considered here. To transform the observations with format (L_ij, R_ij] to that with (U_ij, V_ij), we set U_ij = R_ij and let V_ij to be the largest observation times in the study if L_ij 0. In the case of 0 < L_ij < R_ij < +∞, we set U_ij = R_ij and let V_ij to be the largest observation times in the study if L_ij = 0. In the case of 0 < L_ij < R_ij < +∞, we set U_ij = L_ij and V_ij = R_ij and if R_ij = +∞, we took V_ij = L_ij and U_ij to be the smallest observation time in the study. The results given below are based on 1000 replications with K = 10 and Q = 1000 for the multiple imputation approach.

Table 1 presents the simulation results for estimation of β with the true value, denoted by β0, of β taken to be −0.25, 0 and 0.25 with covariate-independent censoring intervals. The results with covariate-dependent censoring intervals are given in Tables 2 and 3 with the true value γ₀ = −0.25 and 0.25, respectively. In both cases, we considered n = 100 and 200, and the results include the bias of β (BIAS), the means of the estimated standard deviations (ESD), the sample standard errors of the estimated β (SSE), and the 95% empirical converge probabilities (CP). It can be seen from the three tables that the imputation approach performs well as the estimator has negligible bias and the estimated standard deviation is close to the empirical standard error with proper coverage probability. But the estimates given in Li et al. (2012) seem to be biased and the biases appear to be more severe with covariate-dependent censoring intervals. A possible reason for this is that the data structure may not satisfy the requirement needed in Li et al. (2012). One can also see from the tables that as expected, both bias and variance decrease when the number of cluster increases.

Table 1.

Estimation of β with γ₀ = 0 and covariate-independent censoring intervals.

β 0	n	The proposed estimator				Li–Wang–Sun’s estimator
		BIAS	ESD	SSE	CP	BIAS	ESD	SSE	CP
−0.25	100	−0.0134	0.2445	0.2516	0.936	0.0832	0.1779	0.2049	0.894
0	100	−0.0091	0.2585	0.2599	0.942	−0.0008	0.1846	0.2199	0.907
0.25	100	−0.0139	0.2708	0.2911	0.941	−0.1053	0.1916	0.2325	0.860
−0.25	200	−0.0037	0.1744	0.1792	0.943	0.0885	0.1238	0.1422	0.855
0	200	−0.0059	0.1839	0.1773	0.954	0.0053	0.1290	0.1480	0.912
0.25	200	0.0031	0.1932	0.2029	0.943	0.1433	0.1339	0.1564	0.840

Table 2.

Estimation of β with γ₀ = −0.25 and covariate-dependent censoring intervals.

β 0	n	The proposed estimator				Li–Wang–Sun’s estimator
		BIAS	ESD	SSE	CP	BIAS	ESD	SSE	CP
−0.25	100	0.0056	0.2472	0.2521	0.952	0.0967	0.1958	0.2270	0.725
0	100	−0.0011	0.2578	0.2572	0.958	0.1830	0.2077	0.2289	0.835
0.25	100	0.0005	0.2720	0.2755	0.941	0.0964	0.2189	0.2441	0.903
−0.25	200	0.0044	0.1746	0.1715	0.952	0.2886	0.1376	0.1551	0.534
0	200	−0.0002	0.1828	0.1819	0.954	0.1733	0.1461	0.1655	0.766
0.25	200	0.0000	0.1928	0.1979	0.941	0.0947	0.1526	0.1793	0.849

Table 3.

Estimation of β with γ₀ = 0.25 and covariate-dependent censoring intervals.

β 0	n	The proposed estimator				Li–Wang–Sun’s estimator
		BIAS	ESD	SSE	CP	BIAS	ESD	SSE	CP
−0.25	100	−0.0039	0.2565	0.2584	0.945	−0.0968	0.2191	0.2448	0.901
0	100	−0.0135	0.2702	0.2871	0.936	−0.1745	0.2274	0.2579	0.870
0.25	100	−0.0126	0.2859	0.2946	0.939	−0.2820	0.2357	0.2626	0.768
−0.25	200	−0.0016	0.1810	0.1755	0.942	−0.0852	0.1536	0.1642	0.893
0	200	−0.0005	0.1900	0.1883	0.961	−0.1635	0.1592	0.1759	0.815
0.25	200	0.0020	0.2025	0.2081	0.949	−0.2636	0.1655	0.1909	0.641

Note that in the above, we only considered the situation with one covariate. As suggested by a reviewer, we also performed some simulations with two covariates and Table 4 presents some results on estimation of two regression parameters β₁ and β₂ with Z₁ and Z₂ generated from the Bernoulli distribution with success probability p = 0.5 and the uniform distribution U(0, 5), respectively. Here the censoring intervals were assumed to be covariate-independent and all other set-ups were the same as with Table 1. The results again indicate that the presented approach seems to work well for the situations considered. We also investigated other set-ups and obtained similar results. Also suggested by a reviewer, we also investigated some different ways for generating covariate-dependent censoring intervals. In the results given in Table 5, for example, the observation times and censored intervals were generated as in Table 1, but with the length len following the uniform distribution U(0, 0.2) if Z ≤ 0.5 and the uniform distribution U(0.2, 0.8) if Z > 0.5. Note that here the covariate Z was assumed to follow the uniform distribution U(0, 1). One can see that the results are similar to those given in Tables 2 and 3.

Table 4.

Estimation of β with two covariates and covariate-independent censoring intervals.

β 0	n	BIAS	ESD	SSE	CP
β10 = 0	100	−0.0115	0.1971	0.2023	0.942
β20 = 0	100	−0.0062	0.0703	0.0754	0.947
β10 = 0.5	100	0.0093	0.2103	0.2091	0.937
β20 = −0.25	100	0.0039	0.0767	0.0725	0.945
β10 = −0.25	100	−0.0156	0.3142	0.3210	0.941
β20 = 0.5	100	0.0197	0.1406	0.1338	0.930
β10 = 0	200	−0.0066	0.1429	0.1521	0.947
β20 = 0	200	0.0010	0.0675	0.0698	0.951
β10 = 0.5	200	−0.0067	0.1479	0.1470	0.943
β20 = −0.25	200	−0.0013	0.0519	0.0496	0.950
β10 = −0.25	200	−0.0078	0.2393	0.2381	0.946
β20 = 0.5	200	0.0083	0.0941	0.0956	0.938

Table 5.

Estimation of β with covariate-dependent censoring intervals.

β 0	n	BIAS	ESD	SSE	CP
−0.25	100	−0.0215	0.3974	0.4202	0.930
0	100	−0.0051	0.4267	0.4724	0.914
0.25	100	0.0067	0.4466	0.4770	0.922
−0.25	200	−0.0106	0.2835	0.2918	0.946
0	200	−0.0021	0.2998	0.3171	0.940
0.25	200	−0.0041	0.3192	0.3272	0.945

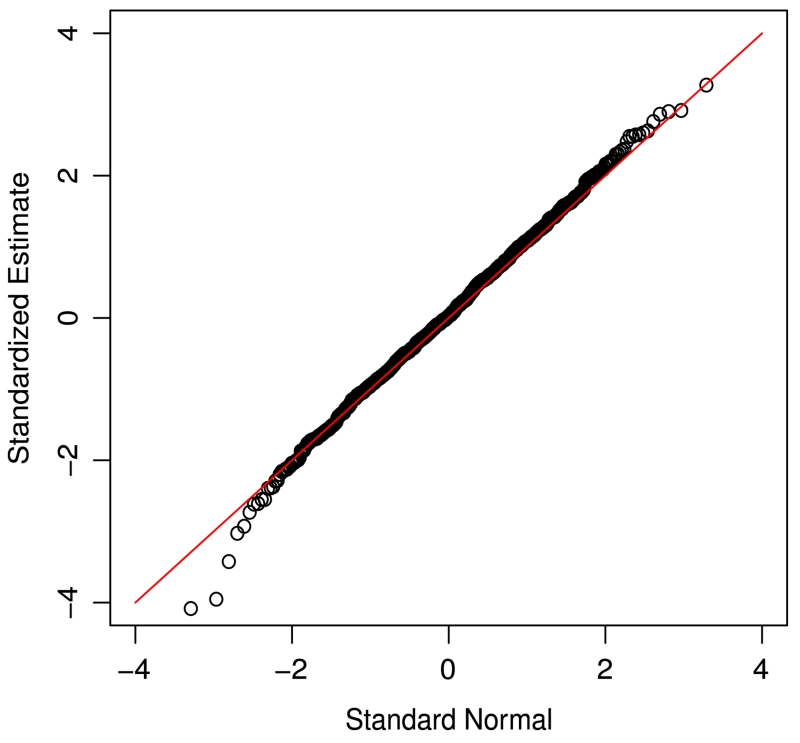
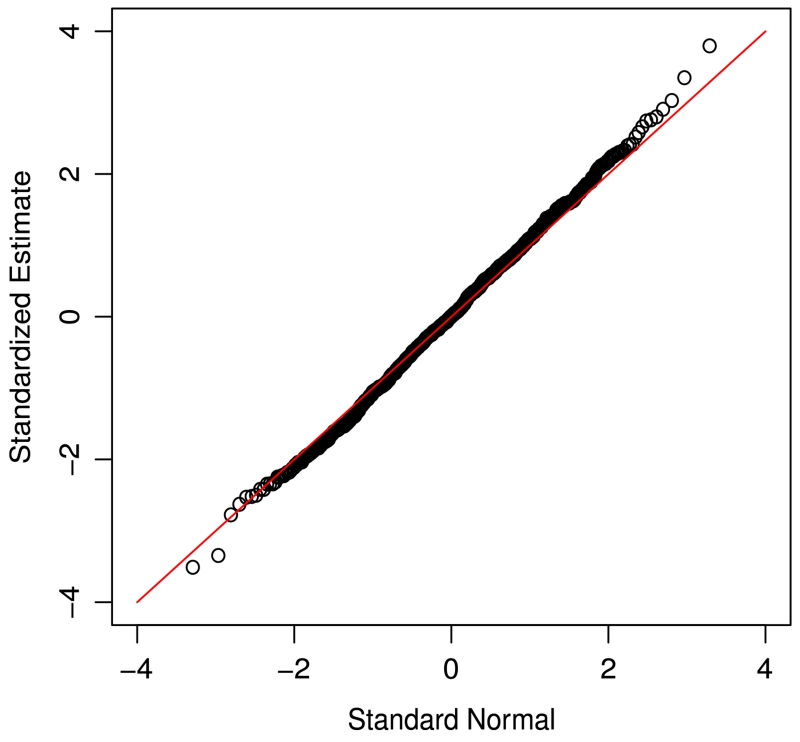
For the simulation results given above, we used Q = 1000 for resampling. To investigate the effect of Q on the performance of the procedure, we used Q = 2000 and obtained similar results. As mentioned above, in practice, one can approximate the distribution of the proposed estimator $\widehat{\beta }$ by the normal distribution. To see this, based on the simulated data generated above, we obtained and evaluated the quantile plots of the standardized $\widehat{\beta }$ against the standard normal variable. Figs. 1 and 2 present two such plots from the set-ups in Tables 1 and 3, respectively. Both plots suggest that the normal approximation seems to be reasonable and the plots for other set-ups were similar.

Fig. 1.

Quantile plot of the estimates with covariate-independent censoring intervals (γ₀ = 0, β₀ = −0.25, n = 200).

Fig. 2.

Quantile plot of the estimates with covariate-dependent censoring intervals (γ₀ = 0.25, β₀ = 0.25, n = 200).

5. An application

In this section, we apply the presented estimation procedure to a set of clustered interval-censored failure time data arising from a lymphatic filariasis (LF) study (Dreyer et al., 2006). It followed 47 men with LF, a debilitating parasitic disease that worms live in nests in human body. Among them, 22 received the co-administration of diethylcarbamazine (DEC) and albendazole (ALB) (new treatment), and the others were given DEC alone (standard treatment). ALB is an anti-parasitic drug, which is commonly used to treat interstim worm infections. When co-administered with DEC, it helps break the cycle of LF transmission between mosquitoes and humans. Using ultrasound a doctor can detect the movement of the living adult worms. One main goal of the study was to compare the effect of the co-administration of DEC and ALB versus DEC alone for the treatment of LF. The variable of interest is the time to clearance of worms in each nest. The patients in the study were followed for one year since their treatment and periodically examined by ultrasound to see if the worms were still alive. Therefore only interval-censored data were observed with each patient as a cluster with n = 47 and the cluster size is number of nests of adult filial worms in each patient. In total, 78 adult worm nests were detected by ultrasound and the cluster size, n_i, ranged from 1 to 5. Two covariates were of particular interest to the investigators. One is the treatment indicator, and the other is age of the patient in years at baseline. In the analysis, we define X_1i to be 0 if the patient i was given the co-administration of DEC and ALB and 1 otherwise and let X_2i be age of the patient at baseline, i = 1, … , 47. Note that here we only have cluster-specific covariates. The data are given in the formulation T_ij ∈ (L_ij, R_ij].

To analyze the data, we applied the multiple imputation procedure with Q = 1000 to the observation of the time to clearance of worms in a nest. We also investigated the effect of the number of imputations K on the performance of the procedure with K = 5, 10 and 500 and obtained similar results. The procedure yielded ${\widehat{\beta }}_1$ = 0.0025 with the estimated standard error of 0.0015 for treatment effect (p-value = 0.0895 for testing of treatment effect) and ${\widehat{\beta }}_2$ = −2.2611 × 10⁻⁵ with the estimated standard error of 5.8895 × 10⁻⁵ for age effect (p-value = 0.7011 for testing of age effect). These results suggest that there seems to be no difference in cleaning the worms between the two treatments and the clearance of the worms is not significantly related to the age of the patients at baseline. These results are similar to those given in Li et al. (2012) under the same additive hazards model. However, one must be careful about interpreting the results due to the small number of patients.

6. Discussion and concluding remarks

This paper discussed regression analysis of interval-censored failure time data under the additive hazards model and for the analysis, a multiple imputation approach was presented and investigated. Compared to the existing methods for the problem, a major advantage of the imputation approach is its simplicity. It avoids estimating the correlation of interval-censored observations within the same cluster by using a resampling-based method. The imputation approach converts the regression problem of interval-censored failure time data to that of right-censored failure time data which can be easily implemented by using existing software packages. The numerical studies showed that the imputation approach presented here is efficient and performs well for practical situations.

Compared to the regression approach proposed by Li et al. (2012), the imputation approach is less biased and provides much better coverage probabilities for all the situations considered. The approach by Li et al. (2012) only applies to clustered interval-censored failure time data given in (U_ij, V_ij) where U and V are two monitoring times assumed to follow a Cox model. However, in real situations, the failure time may only be known to lie within a time interval in the form of (L_ij, R_ij] with L ≤ R and both L and R belonging to (0, +∞). In this paper, we considered general clustered interval-censored failure time data given by (L_ij, R_ij] which arise naturally from longitudinal studies with periodic follow-up. The proposed approach can also be conveniently implemented with clustered interval-censored failure time data given by (U_ij, V_ij). It should be noted that the proposed approach does require estimation of the cumulative baseline hazard function.

There exist several directions for future research. One is that although the simulation suggests that the normal approximation seems reasonable to the distribution of $\widehat{\beta }$ and $\widehat{\beta }$ is efficient, it would be helpful to provide rigorous justification to it. By looking at the lymphatic filariasis study, one may be also interested in developing a procedure to measure the strength of correlation among subjects within the same cluster and incorporate the correlation in the imputation model. In this paper, we have focused on the situation where covariates are time-independent and subject-specific and it is easy to see that sometimes we may face time-dependent and/or cluster-specific covariates. Although the proposed approach cannot be directly applied to this latter situation, it can be easily generalized to the situation. Note that the simulation studies have shown that the proposed method works well on the scenarios with moderate to larger number of clusters and small cluster size. Suggested by a reviewer, we also investigated the performance of the method for the scenarios with small number of clusters but large cluster size that may occur in practice, and the results indicate that one needs to be careful for the application of the method to the latter situations and may need to develop a more proper approach. Our simulation results suggest that one needs 50 or more clusters for the presented approach to perform properly.

Another possible direction is that sometimes one may face situations with an informative cluster size in the sense that cluster size is related to the failure time (Williamson et al., 2008). It is apparent that it would be useful to generalize the proposed estimation procedure to the case of clustered interval-censored failure time data with informative cluster sizes under a semiparametric failure time model. In addition, one can see that the additive hazards model (4) assumes a normal distribution for the latent variable b_i and one may want to consider the situation where the covariates may affect the latent variable.