Abstract
PURPOSE
The high-dimensional propensity score algorithm attempts to improve control of confounding in typical treatment effect studies in pharmacoepidemiology and is increasingly being used for the analysis of large administrative databases. Within this multi-step variable selection algorithm, the marginal prevalence of non-zero covariate values is considered to be an indicator for a count variable's potential confounding impact. We investigate the role of the marginal prevalence of confounder variables on potentially caused bias magnitudes when estimating risk ratios in point exposure studies with binary outcomes.
METHODS
We apply the law of total probability in conjunction with an established bias formula to derive and illustrate relative bias boundaries with respect to marginal confounder prevalence.
RESULTS
We show that maximum possible bias magnitudes can occur at any marginal prevalence level of a binary confounder variable. In particular, we demonstrate that, in case of rare or very common exposures, low and high prevalent confounder variables can still have large confounding impact on estimated risk ratios.
CONCLUSIONS
Covariate pre-selection by prevalence may lead to sub-optimal confounder sampling within the high-dimensional propensity score algorithm. While we believe that the high-dimensional propensity score has important benefits in large-scale pharmacoepidemiologic studies, we recommend omitting the prevalence-based empirical identification of candidate covariates.
1. INTRODUCTION
The high-dimensional propensity score (hd-PS) algorithm introduced and established by Schneeweiss and colleagues1–6 attempts to reduce residual confounding in typical treatment effect studies in pharmacoepidemiology and is increasingly being used by large, collaborative drug safety networks such as the U.S. Mini-Sentinel7 and the Canadian Network for Observational Drug Effect Studies8.
It is assumed that adjustment for large numbers of covariates, as commonly available in administrative databases, may serve as sufficient proxy for unobserved confounders which, if not considered, would yield biased estimates of treatment effects. In general an ideal hd-PS algorithm will either select all relevant confounders in a given data set or, due to the latent correlation structure of all potential confounder variables, will select enough confounder-associated variables so that unobserved or non-selected confounders are sufficiently mirrored in the final propensity score model. In order to achieve confounder-adjusted treatment or exposure effect estimates, the fitted propensity score usually serves as a balancing score in a multivariable outcome model, as matching criterion or is used to define inverse probability weights for the estimation of marginal treatment or exposure effects.
The hd-PS variable selection algorithm considers the marginal prevalence of non-zero values of a covariate (either binary or count variable) as an indicator for its potential confounding magnitude. Accordingly, candidate covariates to be included in the final propensity score model are empirically identified. The idea of assessing the potential confounding impact of extraneous variables is not entirely new and has received broad attention in the epidemiological literature9–14. However, so far, the proposed formulas and illustrations focus mainly on the conditional prevalence of confounder variables, i.e. dissimilarities in confounder prevalence between the exposure groups. In this article we investigate the theoretical justification for assessing potential bias impact based on the marginal prevalence of confounder variables as implied by the hd-PS algorithm.
The article is structured as follows: Section 2 provides a brief review of the high-dimensional propensity score covariate selection procedure. Section 3 gives formal insights in confounding mechanisms and the role of marginal confounder prevalence. Section 4 provides a comprehensible data example and illustrates the formally determined boundaries for bias magnitudes in dependency on marginal confounder prevalence and confounder-outcome association. Section 5 closes with discussion and conclusion.
2. THE HD-PS COVARIATE SELECTION PROCEDURE
The hd-PS confounder selection algorithm is essentially comprised of three steps: First, among all count variables (codes from the claims database), candidate empirical covariates are selected according to their marginal prevalence (proportion of subjects with a count value of at least one). Here, variables with marginal prevalence values closer to 0.5 is given higher priority. Second, the selected count variables are recoded into three binary variables indicating i) if a subject has at least one count, ii) if a subject has a count value greater or equal to the median of all non-zero counts in this variable and iii) if a subject has a count value greater or equal to the 75th percentile of all non-zero counts. Third, after dichotomization, ranking and selection of potential confounder variables according to a multiplicative bias term which reflects the relative magnitude of bias potentially caused by each of the created dummy variables. This calculation is performed using a formula based on an earlier work of Bross9:
| (1) |
Here, ARRED refers to the apparent (unconditional) relative risk on a binary outcome variable D associated with a binary point-exposure or treatment E. The relative risk between exposed and unexposed individuals conditional on the binary confounding variable C is given by RRED. Furthermore, RRCD depicts the relative risk between subjects with and without the confounder attribute and PC1 = P(C = 1|E = 1) and PC 0 = P(C = 1|E = 0) the prevalence of the confounder in exposed and unexposed individuals respectively.
3. CONFOUNDING AND THE ROLE OF MARGINAL CONFOUNDER PREVALENCE
The maximum possible magnitude of the multiplicative bias term of a confounder variable is a clearly defined function of P(C), P(E), and RRCD. According to the law of total probability, the marginal prevalence of C is given by the weighted sum of the respective conditional prevalences:
| (2) |
As indicated by equation (1), and as universally known as the key point in confounding mechanism, the magnitude of confounder-induced bias is strictly increasing with increased imbalance of the confounder distribution in the exposure groups. Accordingly, at fixed values of P(E) and RRCD, the highest magnitude of bias potentially caused by a confounder variable appears in the most extreme cases of pure imbalance either if P(C = 1|E = 1) = 1 and P(C = 1|E = 0) = 0 or if P(C = 1|E = 1) = 0 and P(C = 1|E = 0) = 1. In these cases the effect of the confounder variable cannot be differentiated from the effect of the exposure so that RRCD immediately bonds with RRED and the apparent relative risk becomes simply the product of these two effect measures. Therefore, the maximum reachable magnitude of the multiplicative bias term corresponds to the value of RRCD or 1/RRCD in the worst two possible confounder distribution scenarios among the exposure groups. Equation 2 illustrates the crucial implications P(C) = P(E) or P(C) = 1 − P(E) induced by such extreme confounding situations. However, since neither P(C) nor P(E) are restricted to a value of 0.5 and the bias magnitude is a monotone decreasing function with increasing confounder balance among the exposure groups, the rationale to pre-select potential confounders according to marginal prevalence values close to 0.5 may lead to an inappropriate choice of propensity score variables.
4. EXAMPLE DATA AND ILLUSTRATION
The following example provides a simple hypothetical data scenario in which the marginal prevalence of a confounder variable is low but the magnitude of bias caused is still substantial.
Panel A of Table 1 displays the unconditional exposure-outcome association indicating an about 1.5 fold higher risk for exposed individuals. Exposure (E) is high prevalent (96%) in the study population. Panel B shows for the same study sample the distribution of a low prevalent (3%) binary confounding variable (C). A strong imbalance of the confounder between the exposure groups is present, as P(C = 1|E = 1) = 0.02 and P(C = 1|E = 0) = 0.41. Panels C and D indicate, in contrast to Panel A, no exposure-outcome association conditional on the confounder variable. Thus, despite the given low marginal confounder prevalence, the confounder-associated multiplicative bias still yields a magnitude of 1.5 in this example scenario. This is because the confounder distribution is strongly imbalanced between the exposure groups, a fact which cannot be deduced from the marginal confounder prevalence.
Table 1.
Hypothetical data example demonstrating relevant confounding magnitude in estimating an exposure-outcome association in presence of a low prevalent binary confounder.
| A | B | C | D | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| total sample | total sample | confounder = 'no' | confounder = 'yes' | ||||||||||||
| exposure | exposure | exposure | exposure | ||||||||||||
| no | yes | no | yes | no | yes | no | yes | ||||||||
|
|
|
|
|
||||||||||||
| outcome | no | 25 | 488 | confounder | no | 22 | 948 | outcome | no | 11 | 474 | outcome | no | 14 | 14 |
| yes | 12 | 475 | yes | 15 | 15 | yes | 11 | 474 | yes | 1 | 1 | ||||
|
|
|
|
|
||||||||||||
| 37 | 963 | 37 | 963 | 22 | 948 | 15 | 15 | ||||||||
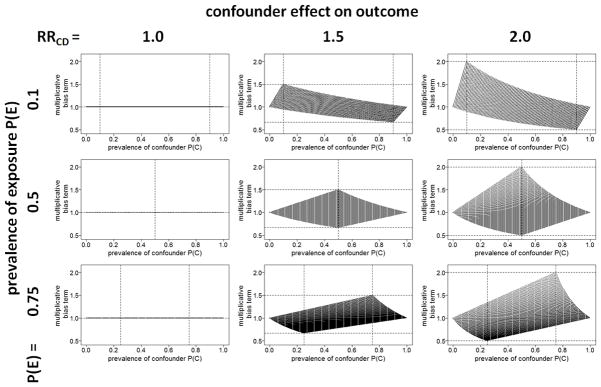
Figure 1 provides a comprehensive illustration of the described multivariable impact of P(C), P(E), and RRCD on the confounding magnitude potentially caused by C. We simply plotted the multiplicative bias term from equation 1 for all possible values resulting from a grid { PC 0, PC 1} ∈ {(0, 0.1,.., 0.9, 1)×(0, 0.1,..,0.9, 1)} conditional on the respective marginal confounder prevalence P(C). We considered nine exemplary configurations by setting RRCD={1, 1.5, 2} and P(E) ={0.1, 0.5, 0.75}. In the resulting graphs we added horizontal dashed lines on angle of the respective value of RRCD and 1/RRCD as well as vertical dashed lines for values of P(C) and 1 − P(C). As can be seen from the figure, the maximum multiplicative bias magnitude for a given scenario corresponds to the value of RRCD (or 1/RRCD) and is achieved at the respective value of P(C) = P(E) (or 1− P(E)). Therefore, only in case of P(E) =0.5 a pre-selection of confounders according to their marginal prevalence value would be appropriate. However, since the multiplicative bias term already reflects the impact of the marginal prevalence on the confounding magnitude, such pre-selection would be superfluous.
Figure 1.
Multiplicative bias term depending on P(C), RRCD and P(E).
The R code15 to reproduce Figure 1 is provided as supplementary material.
5. DISCUSSION AND CONCLUSION
We formally explained and illustrated the definite role of the marginal prevalence of an uncontrolled binary variable on its confounding impact when estimating risk ratios in point-exposure studies with a binary outcome. We showed that low prevalent confounder variables can become highly influential in scenarios where the prevalence of at least one exposure category is low.
Propensity score methods such as the hd-PS are commonly not used in situations where the exposure prevalence is low. However, in the analysis of large pharmacoepidemiological data sets, low relative frequencies of exposed individuals often translate to sufficient absolute numbers that allow for reliable effect estimation using propensity score methods.
In light of the presented results, while we believe that the high-dimensional propensity score has important benefits in large-scale pharmacoepidemiologic studies in administrative data, we recommend the deletion of the prevalence-targeted pre-selection step within the hd-PS confounder selection procedure.
Supplementary Material
Acknowledgments
FUNDING: This project was supported by the Canadian Network for Observational Drug Effect Studies (CNODES). CNODES, a collaborating centre of the Drug Safety and Effectiveness Network (DSEN), is funded by the Canadian Institutes of Health Research (CIHR).
Dr. Schuster is supported by a CNODES post-doctoral award. Miss Pang is also supported by CNODES funding. Dr. Platt is supported in part by a National Scholar (Chercheur-national) of the Fonds de Récherche du Québec-Santé (FQR-S) and is a member of the Research Institute of the McGill University Health Centre, which is supported by core funds from FQR-S.
Footnotes
CONFLICT OF INTERESTS
The authors declare that there is no conflict of interest in the context of the submitted work.
References
- 1.Schneeweiss S, Rassen JA, Glynn RJ, et al. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology. 2009;20(4):512–522. doi: 10.1097/EDE.0b013e3181a663cc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rassen JA, Avorn J, Schneeweiss S. Multivariate-adjusted pharmacoepidemiologic analyses of confidential information pooled from multiple health care utilization databases. Pharmacoepidemiol Drug Saf. 2010;19(8):848–57. doi: 10.1002/pds.1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Toh S, García Rodríguez LA, Hernán MA. Confounding adjustment via a semi-automated high-dimensional propensity score algorithm: an application to electronic medical records. Pharmacoepidemiol Drug Saf. 2011;20(8):849–57. doi: 10.1002/pds.2152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Polinski JM, Schneeweiss S, Glynn RJ, et al. Confronting "confounding by health system use" in Medicare Part D: comparative effectiveness of propensity score approaches to confounding adjustment. Pharmacoepidemiol Drug Saf. 2012;21(Suppl 2):90–8. doi: 10.1002/pds.3250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Garbe E, Kloss S, Suling M, et al. High-dimensional versus conventional propensity scores in a comparative effectiveness study of coxibs and reduced upper gastrointestinal complications. Eur J Clin Pharmacol. 2013;69(3):549–57. doi: 10.1007/s00228-012-1334-2. [DOI] [PubMed] [Google Scholar]
- 6.Neugebauer R, Schmittdiel JA, Zhu Z, Rassen JA, Seeger JD, Schneeweiss S. High-dimensional propensity score algorithm in comparative effectiveness research with time-varying interventions. Statistics in Medicine. 2014 doi: 10.1002/sim.6377. [DOI] [PubMed] [Google Scholar]
- 7.Mini-Sentinel Coordinating Center. [Accessed January 19, 2015]; ( http://www.mini-sentinel.org)
- 8.Suissa S, Henry D, Caetano P, et al. CNODES: the Canadian Network for Observational Drug Effect Studies. Open Medicine. 2012;6(4):134–140. [PMC free article] [PubMed] [Google Scholar]
- 9.Bross IDJ. Spurious effects from an extraneous variable. J Chronic Dis. 1966;19:637–647. doi: 10.1016/0021-9681(66)90062-2. [DOI] [PubMed] [Google Scholar]
- 10.Schlesselman JJ. Assessing effects of confounding variables. American Journal of Epidemiology. 1978;108(1):3–8. [PubMed] [Google Scholar]
- 11.Flanders WD, Khoury MJ. Indirect assessment of confounding: graphic description and limits on effect of adjusting for covariates. Epidemiology. 1990;1(3):239–246. doi: 10.1097/00001648-199005000-00010. [DOI] [PubMed] [Google Scholar]
- 12.Arah OA, Chiba Y, Greenland S. Bias formulas for external adjustment and sensitivity analysis of unmeasured confounders. Annals of Epidemiology. 2008;18(8):637–646. doi: 10.1016/j.annepidem.2008.04.003. [DOI] [PubMed] [Google Scholar]
- 13.Chiba Y. Simple Formulae for Evaluating the Potential Impact of Confounding Bias. Communications in Statistics-Theory and Methods. 2011;40(23):4278–4288. doi: 10.1080/03610926.2010.508864. [DOI] [Google Scholar]
- 14.VanderWeele TJ, Arah OA. Unmeasured Confounding for General Outcomes, Treatments, and Confounders: Bias Formulas for Sensitivity Analysis. Epidemiology (Cambridge Mass) 2011;22(1):42–52. doi: 10.1097/EDE.0b013e3181f74493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.R Core Team. R Foundation for Statistical Computing. Vienna, Austria: 2014. R: A language and environment for statistical computing. http://www.R-project.org/ [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.