Extracellular Linkers Completely Transplant the Voltage Dependence from Kv1.2 Ion Channels to Kv2.1

Abstract

The transmembrane voltage needed to open different voltage-gated K (Kv) channels differs by up to 50 mV from each other. In this study we test the hypothesis that the channels’ voltage dependences to a large extent are set by charged amino-acid residues of the extracellular linkers of the Kv channels, which electrostatically affect the charged amino-acid residues of the voltage sensor S4. Extracellular cations shift the conductance-versus-voltage curve, G(V), by interfering with these extracellular charges. We have explored these issues by analyzing the effects of the divalent strontium ion (Sr²⁺) on the voltage dependence of the G(V) curves of wild-type and chimeric Kv channels expressed in Xenopus oocytes, using the voltage-clamp technique. Out of seven Kv channels, Kv1.2 was found to be most sensitive to Sr²⁺ (50 mM shifted G(V) by +21.7 mV), and Kv2.1 to be the least sensitive (+7.8 mV). Experiments on 25 chimeras, constructed from Kv1.2 and Kv2.1, showed that the large Sr²⁺-induced G(V) shift of Kv1.2 can be transferred to Kv2.1 by exchanging the extracellular linker between S3 and S4 (L3/4) in combination with either the extracellular linker between S5 and the pore (L5/P) or that between the pore and S6 (LP/6). The effects of the linker substitutions were nonadditive, suggesting specific structural interactions. The free energy of these interactions was ∼20 kJ/mol, suggesting involvement of hydrophobic interactions and/or hydrogen bonds. Using principles from double-layer theory we derived an approximate linear equation (relating the voltage shifts to altered ionic strength), which proved to well match experimental data, suggesting that Sr²⁺ acts on these channels mainly by screening surface charges. Taken together, these results highlight the extracellular surface potential at the voltage sensor as an important determinant of the channels’ voltage dependence, making the extracellular linkers essential targets for evolutionary selection.

Introduction

Given the diversity of voltage-gated ion channels (143 channel genes in the human genome (1)), it is of general interest to consider what constitutes the variability and what functional role it plays in forming and regulating neuronal firing patterns (2, 3, 4, 5, 6, 7, 8, 9, 10). The basic functional channel parameters are ion selectivity and gating, the latter characterized by opening/closing kinetics and the voltage dependence of the channel’s open probability. In this study we focus on the role of the channel’s voltage dependence (measured as the steady-state conductance versus voltage, G(V), in characterizing voltage-gated potassium (Kv) channels and consequently its role in the evolution of these channels.

In theory, the G(V) curve depends on the outer (ψ_out) and the inner (ψ_in) (surface) potentials at the voltage sensor, and on a component independent of electrostatic forces (ΔG₀ / F), where ΔG₀ is the difference in Gibbs energy between the closed and open states at zero electric field. In the following, (ΔG₀ / F) + (ψ_in) will be referred to as the residual field potential. At the midpoint voltage (V_1/2) of the G(V) curve these entities are encapsulated by the following formula:

$$V_{1/2}={\psi }_{out}-\left(\frac{\mathit{\Delta }{G}_0}{F}+{\psi }_{in}\right).$$ (1)

We want to explore these parameters for different Kv channel types to obtain information about the principles that regulate the evolution of these channels. V_1/2 has been shown to depend on the existence of certain charged residues on the external surface of the channel protein (11, 12, 13), suggesting these charges contribute to an electric potential at the external surface (14, 15, 16).

Metal ions were early recognized to alter the excitability of neurons by shifting the G(V) curve of ion channels along the voltage axis (17, 18, 19, 20). For certain metal ions most of this effect is likely to be caused by screening (i.e., damping the electric field by mobile charges rather than by bound charges) of the critical negative charges at the external surface of the channel protein, modifying φ_out at the voltage sensor (14, 15, 20). Thus, such metal ions can be used as probes to explore the external surface potential. For other metal ions, also binding to the voltage sensor (21, 22, 23) and binding to the pore (24, 25) have been suggested to contribute.

Assuming that the metal-ion induced shift of the G(V) curve, ΔV_Me, depends exclusively on a screening effect (and not by binding, henceforth called the screening hypothesis), we can derive the relation between ΔV_Me and ψ_out from simple principles of the double-layer theory. Based on the model of Gouy and Chapman (26, 27), the Grahame equation (28) describes the relation between surface charge and surface potential in terms of the ionic composition of the solution. Even though this equation is based on the simplistic assumption of smeared surface charges it has been shown that it rather well describes the surface potential of a plane with moderately spread out point charges (29) and thus that of most ion channels (15). Approximating the Grahame equation, as shown in the Appendix, we obtain the following:

$${\psi }_{out}={\left(\sqrt{\frac{I_0}{I_1}}-1\right)}^{-1}\times \mathit{\Delta }{\mathit{V}}_{Me},$$ (2)

where I₀ and I₁ are the ionic strengths of the control and test solutions, respectively. This approximation is fairly accurate when compared with the exact solution of the Grahame equation (for a solution containing monovalent ions and one divalent cation, the Grahame equation can be solved analytically, see Appendix).

Interestingly, Eq. 2 is closely related to the surface-potential equation derived by Helmholtz (30) to describe his “double layer model,” assuming that the fixed surface charges are counteracted by a fixed layer of ions with opposite charge. Assuming the distance between the layers is proportional to the inverse square root of the ionic strength (cf. the Debye length (31)), Eq. 2 follows directly from the Helmholtz model. The Helmholtz model is also the high concentration limit of the more sophisticated Stern model (32), which is why our approximation is “exact” for higher concentrations.

From Eqs. 1 and 2 we obtain the following:

$$V_{1/2}={\left(\sqrt{\frac{I_0}{I_1}}-1\right)}^{-1}\times \mathit{\Delta }{\mathit{V}}_{Me}-\left(\frac{\mathit{\Delta }{G}_0}{F}+{\psi }_{in}\right).$$ (3)

Thus, assuming exclusive screening of the outer surface charges and a membrane/internal potential component that is independent of φ_out, then the relation between V_1/2 and ΔV_Me should be described by Eq. 3. This fact provides us with a tool to test the validity of the screening hypothesis. In our study we used the strontium ion (Sr²⁺) as probe, because it seems to act exclusively via a screening mechanism; together with the magnesium ion (Mg²⁺), it shifts the G(V) curve less than other tested metal ions, and activation time courses, deactivation time courses, gating currents, and G(V) curves are equally affected, as if these metal ions only alter the membrane voltage (11, 15, 21, 22, 33, 34, 35, 36).

In previous studies of effects of Sr²⁺ and Mg²⁺ on Kv channels (of Kv1, Kv2, and Kv3 type), we have shown that critical surface charges are located in the extracellular linker connecting S5 and the pore (P) loop (L5/P). It was found that it was enough to swap two amino acids of the L5/P linker of the Kv1-type Shaker channel to emulate the Kv2.1 behavior with reference to Mg²⁺ sensitivity, but it was also clear that the effects were dependent on the molecular background (13). However, we also found that the charged amino acids in that linker did not generally act independently of each other in impacting the voltage sensor; assuming independent effects (37) we could only partially predict the point mutation results (38). This is most likely because of altered locations of the linker’s charged residues, caused by electrostatic interactions (exemplified by the electrostatic domino effect in the Kv2.1 channel between 425K and 427K in the turret, and 419K at the top of S5, close to S4; residue numbering from the Shaker K channel (13)).

In this study we aimed to quantitatively analyze the structural determinants of the voltage sensitivity of Kv channels to clarify which components determine their function and thus their evolution. We have estimated and analyzed G(V) curves and surface potentials with reference to effects of Sr²⁺ in 25 chimeras constructed from the most Sr²⁺ sensitive Kv channel (Kv1.2) and the least sensitive (Kv2.1). The results are discussed with respect to the atomic structure of a Kv channel (39), as well as to their role as targets for evolutionary selection.

Materials and Methods

Ethical approval

The local ethical committee of Münster University approved this project.

In vitro mutagenesis and RNA synthesis

The cDNA for the chimeras between rat Kv1.2 (Acc. No. X16003) and human Kv2.1 (Acc. No. X68302) were obtained using an overlap polymerase chain reaction (40) and were cloned into the pGEM vector (41). For the different chimeras, fragments containing the nucleotides given in Table 1 were fused together. The numbers refer to the open reading frame of the respective channel. DNA sequences amplified by the polymerase chain reaction were verified by sequencing using the BigDye terminator cycle sequencing kit (Perkin-Elmer, Waltham, MA). The sequence reactions were analyzed on an ABI 377 or Prism 310 automated sequencer (Perkin-Elmer). The cDNAs encoding for the rat Kv channel subunits Kv1.1, Kv1.2, Kv1.3, Kv1.6, Kv3.1, and Kv3.2 and for the human subunit Kv2.1 were either cloned into the pAKS2, pNKS2 (42), or pGEM vector. For cRNA synthesis, the corresponding plasmid DNAs were linearized. The transcription reactions were performed using a commercial kit (mMessage mMachine; Ambion, Austin, TX) and T7 RNA polymerase. Denaturating agarose gel electrophoresis was used to check the quality of cRNA product of each reaction and to quantify the yield.

Table 1.

Nucleotide Compositions of Chimeras between Kv1.2 and Kv2.1

	Kv2.1	Kv1.2	Kv2.1	Kv1.2	Kv2.1	Kv1.2	Kv2.1
Transmembrane and intracellular parts
N-term		1-492	571-stop
S1−S3	1-555	478-843	862-stop
S1−S4	1-555	478-936	946-stop
S3 + L3/4	1-774	754-879	889-stop
L3/4 + S4	1-840	820-936	946-stop
S4−S6	1-882	874-1230	1240-stop
L4/5	1-954	946-996	1006-stop
S5	1-1005	997-1035	1042-stop
S5 + L5/6	1-1005	997-1164	1171-stop
P1	1-1113	1105-1113	1123-stop
P2	1-1146	1138-1143	1153-stop
P3	1-1095	1087-1092	1102-stop
S6 + C-term	1-1182	1174-stop
C-term	1-1239	1231-stop
Extracellular linkers
L1/2	1-624	547-663	685-stop
L3/4	1-840	820-879	889-stop
L5/6	1-1059	1051-1164	1171-stop
L5/P	1-1059	1051-1077	1087-stop
LP/6	1-1155	1147-1164	1174-stop
L3/4 + L5/6	1-828	808-879	889-1059	1051-1158	1168-stop
L3/4 + L5/P	1-840	820-879	889-1059	1051-1077	1087-stop
L3/4 + LP/6	1-840	820-879	889-1155	1147-1164	1174-stop
L5/P + LP/6	1-1059	1051-1077	1087-1155	1147-1164	1174-stop
L3/4 + L5/P + LP/6	1-840	820-879	889-1059	1051-1077	1087-1155	1147-1164	1174-stop
L1/2 + L3/4 + L5/6	1-624	547-663	685-828	808-879	889-1059	1051-1158	1168-stop

The cDNA for the chimeras was constructed from rat potassium channel Kv1.2 (Acc. No. X16003) and human potassium channel Kv2.1 (Acc. No. X68302). The numbers refer to the open reading frame of the respective channel. The denomination of the chimera refers to the exchanged linker (L1/2 to L5/6), transmembraneous segment (S1 to S6), pore loop (P), amino terminus (N-term), and carboxy terminus (C-term).

Preparation and injection of oocytes

South African clawed frogs (Xenopus laevis) were anesthetized in ethyl m-aminobenzoate (Sandoz, Basel, Switzerland) and small sections of the ovary were removed surgically. Oocytes (stage V or VI (43)) were injected with 0.1 or 1.0 ng of cRNA in 50 nl distilled water and were maintained under tissue culture conditions at 20°C until used for experiments. The tissue culture solution was a modified Barth medium (in mM): NaCl 88, KCl 1, CaCl₂ 1.5, NaHCO₃ 2.4, MgSO₄ 0.8, HEPES 5 (pH 7.4), which was supplemented with penicillin (100 IU/ml) and streptomycin (100 μg/ml).

Electrophysiological techniques

The investigations were performed with the two-electrode voltage-clamp technique. Microelectrodes were made from borosilicate glass and had resistances of 0.5–1 MΩ for the current electrode and 1–2 MΩ for the voltage electrode when filled with 3 M KCl. The holding voltage was −80 mV and command voltages were applied up to a voltage of +100 mV. The control bath fluid was a Ringer solution (in mM): NaCl 115, KCl 2, CaCl₂ 1.8, HEPES 10 (pH 7.2), yielding the solution an ionic strength of ∼145 mM. Strontium in the form of chloride (SrCl₂, 50 mM; Aldrich, Deisenhofen, Germany), nitrate (Sr(NO₃)_2, 50 mM, Sigma-Aldrich, Steinheim, Germany) or gluconate (Sr(C₆H₁₁O₇)₂; 50 mM; Sigma-Aldrich, Steinheim, Germany), and/or urea (120 mM, Sigma-Aldrich) were added to the bath solution and applied at least 30 s before eliciting currents. The resulting ionic strength of the strontium chloride solution was ∼445 mM, which gives the proportionality factor ${\left(\sqrt{I_0/I_1}-1\right)}^{-1}$ in Eq. 3 a value of −2.33. The osmolarity of solutions was measured with a cryoscopic osmometer (Gonotec, Berlin, Germany). Solutions were applied with a concentration-clamp technique (44) allowing an exchange of more than 90% of the extracellular solution within less than 10 ms. All experiments were performed at days 3 and 4 after injection of cRNA and were carried out at room temperature (22 ± 1°C).

Data acquisition, analysis, and statistics

The potassium currents (I_K) obtained in two-electrode recordings were low-pass filtered at 1 kHz and transferred to a computer system (pClamp program, Axon instruments, Foster City, CA). Leakage currents and capacitive transients were subtracted online using a p/−4 pulse protocol. I_K was measured at the peak of current obtained during the voltage step (V). The conductance was calculated as follows:

$$G\left(V\right)=\frac{I_K}{V+80\text{mV}}.$$ (4)

The conductance normalized to the maximal conductance under control conditions (G_maxCTRL) were fitted to the following Boltzmann equation:

$$\frac{G\left(V\right)}{G_{\max CTRL}}=\frac{A}{1+\text{exp}\left(\left(V_{1/2}-V\right)/s\right)},$$ (5)

where A is the relative (to control) maximal conductance, V_1/2 is the voltage of half-maximal G(V), i.e., midpoint voltage, and s is the slope.

To calculate φ_out, we used Eq. 2. The residual field potential, ((ΔG₀ / F) + ψ_in) was obtained from Eq. 1. To test the suggested relations of Eq. 1 we used Deming regression (45). This method assumes that the ratio (δ) between variances of both y and x axis data are known. Let the measured values (y_i,x_i) be related to the true values $\left({\hat{y}}_i,{\hat{x}}_i\right)$ by the following:

$$y_i={\hat{y}}_i+{\epsilon }_i,$$ (6)

$$x_i={\hat{x}}_i+{\eta }_i.$$ (7)

Under our model (Eq. 1) we obtain the following:

$${\hat{y}}_i={\hat{x}}_i+{\hat{z}}_i,$$ (8)

where ${\hat{x}}_i$ and ${\hat{z}}_i$ are the two components of the field. Since we had multiple measures of x_i and y_i, the variability (including measurement errors) could be estimated. For the regression line of the relation between the outer field component and the midpoint, we obtain the following:

$${\delta }_{xy}=\frac{{\sigma }_y^2}{{\sigma }_x^2}=\frac{{\sigma }_y}{{\sigma }_x}.$$ (9)

For the relation between the residual field component z (obtained from Eq. 1) and the midpoint, we obtain the following:

$${\delta }_{xz}=\frac{{\sigma }_y^2}{{\sigma }_y^2+{\sigma }_x^2}.$$ (10)

The measured values are given as mean or mean ± SE. Statistical significance was tested using a t-test or a Mann-Whitney rank sum test. Values of p < 0.05 were taken as statistically significant.

Sequence similarity estimations

The similarity between the amino acid sequences of the studied channels were analyzed using the Smith-Waterman algorithm (46). Chosen segments were pairwise aligned and the fraction of identical amino acids was taken as a measure of similarity. The significance of the similarity was assessed by bootstrapping, i.e., by randomly sampling from the sequences and thereby constructing an empirical distribution. Then, the statistics were assessed by comparing the true belongings (e.g., to the transmembranal segments) with the obtained distribution.

Results

Strontium effects on seven wild-type Kv channels

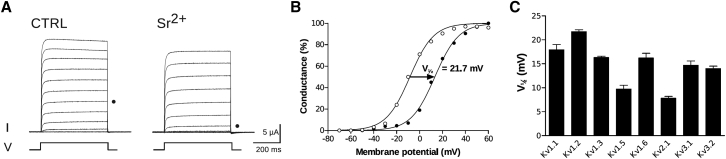
The range of V_1/2 for seven studied noninactivating wild-type Kv channels covers 41 mV, from −21 to +20 mV (Table 2), reflecting the functional variability of the channels; varying V_1/2 may alter neuronal excitability. The working hypothesis of this investigation is that ψ_out at the voltage sensor is an important regulator of V_1/2 and consequently the function of the channel. Assuming an exclusive screening effect (thus no binding), ψ_out is possible to estimate from Eq. 2, using a suitable metal ion. Of reasons given above, Sr²⁺ was chosen as probe metal ion. Application of 50 mM SrCl₂ shifted the G(V) for Kv1.2 by +21.7 ± 0.4 mV by altering V_1/2 from –8.0 ± 1.1 mV to +13.7 ± 1.0 mV (n = 16, Fig. 1, A and B; Table 2). The slope of the G(V) was not affected while the maximal conductance was slightly decreased (by 13 ± 2%) (Table 2). Of all studied Kv channels, Kv1.2 showed the largest shift (+21.7 mV) and Kv2.1 the smallest (+7.8 mV) (Fig. 1 C; Table 2).

Table 2.

Effects of 50 mM SrCl₂ on Conductance Parameters of Cloned wt Kv Channels

Channel	Control		Sr		Differences
	V1/2 (mV)	s (mV)	V1/2 (mV)	s (mV)	ΔV1/2 (mV)	Δs (mV)	ΔGmax (%)	n
Kv1.1	−20.7 ± 1.5	12.2 ± 0.7	+0.2 ± 1.6	11.0 ± 0.5	+20.8 ± 0.7	−1.2 ± 0.3	−8 ± 6	6
Kv1.2	−8.0 ± 1.1	10.4 ± 0.7	+13.7 ± 1.0	10.7 ± 0.5	+21.7 ± 0.4	0.3 ± 0.2	−13 ± 2	16
Kv1.3	−20.0 ± 0.8	6.3 ± 0.2	−3.4 ± 1.0	8.9 ± 0.5	+16.3 ± 0.3	2.6 ± 0.5	−19 ± 2	5
Kv1.6	−4.7 ± 1.6	9.5 ± 0.4	+12.8 ± 1.9	11.3 ± 0.8	+17.5 ± 1.2	1.8 ± 1.0	−12 ± 6	3
Kv2.1	+8.3 ± 0.5	13.3 ± 0.3	+16.1 ± 0.3	12.9 ± 0.2	+7.8 ± 0.4	−0.4 ± 0.4	+13 ± 1	13
Kv3.1	+19.9 ± 1.6	11.1 ± 0.5	+34.6 ± 1.1	11.0 ± 0.4	+14.7 ± 0.9	−0.1 ± 0.5	+2 ± 2	5
Kv3.2	+7.5 ± 2.2	9.3 ± 1.0	+21.5 ± 2.7	11.0 ± 1.3	+14.0 ± 0.5	1.7 ± 0.4	−1 ± 3	5

V_1/2 and s are the midpoint voltage and slope, respectively, for the G(V) curve calculated from Eq. 2. ΔV_1/2 is the difference between V_1/2 in control and Sr²⁺ conditions. Δs is the difference between s in control and Sr²⁺ conditions. ΔG_max is quotient of G_max in control and Sr²⁺ conditions minus 1. n is the number of experiments. All data given as mean ± SE.

Figure 1.

Effect of Sr²⁺ on steady-state conductance of wild-type Kv channels. (A) K currents through Kv1.2 channels are elicited from a holding voltage of –80 mV by voltage steps of 500 ms duration up to +60 mV in steps of 10 mV under control conditions and with 50 mM SrCl₂ added to the control solution. The dots mark the currents at 0 mV. One voltage pulse is illustrated below the current traces. (B) G(V) curves in control (open symbols) and 50 mM SrCl₂ (solid symbols) (n = 16) are shown. The conductance values were normalized to their respective maximal value. The error bars represent mean ± SE. (C) Summary of Sr²⁺-induced shifts of midpoint values (ΔV_1/2) of the G(V) curves from seven wild-type channels are shown.

Evidence that the strontium effect on Kv channels is caused by screening

Analyzing the relevance of ψ_out for V_1/2 using Eq. 1 requires, as mentioned, that the effect of Sr²⁺ is due to screening (and no binding of the ions). Beside the arguments for Sr²⁺ being a pure screener, stated in the Introduction, we here add some further arguments. Screening (of negative surface charges) implicates 1) that the induced shifts should be relatively unaffected by the negatively charged Cl⁻ ion, 2) that the induced shifts should be unaffected by the increased osmolarity of the test solution (50 mM SrCl₂ added to control solution), and 3) that the G(V) shifts should be paralleled by equivalent effects on ion channel kinetics. We tested all these predictions using Kv1.2, being the most Sr²⁺-sensitive channel and therefore providing the best experimental resolution.

• 1)To test the lack of influence of Cl⁻ on the G(V) shifts, we compared the effects of SrCl₂ with that of other Sr²⁺ salts. If Cl⁻ binds to the channel it will mask the Sr²⁺ effect. If so, other Sr²⁺ salts may exist, where the anion binds less and where the salt shifts more than SrCl₂. We found, however, that among the tested Sr²⁺ salts (Table 3), SrCl² was the most potent, suggesting that Cl⁻ is relatively inert, with no or low binding to the channel. These results are in line with previous reports, where the relative anion effects follow the lyotropic series (47).
• 2)To investigate possible effects of osmolarity on the Sr²⁺-induced shifts, we added equimolar concentrations of the uncharged compound urea to the control solution and measured the effect on G(V). Application of 50 mM SrCl₂ increased the osmolarity from 240 mosmol/l to 364 mosmol/l (measured values). We therefore applied 120 mM urea to the control solution to obtain an osmolarity of 360 mosmol/l of the test solution. The mean shift was –1.4 mV (Table 3), suggesting negligible effects of the osmolarity increase when applying 50 mM SrCl₂.
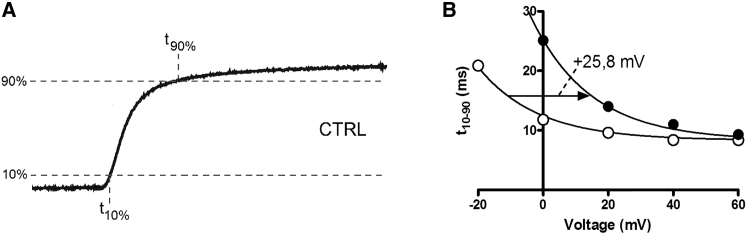
• 3)To compare the shift of the G(V) curve with effects on kinetics, we measured the rise time from 10% to 90% of maximum current (t_10-90) (Fig. 2 A) and plotted it versus voltage (Fig. 2 B). Application of 50 mM SrCl₂ shifted the curve by +19.1 ± 0.7 mV, thus close to that for G(V) (21.7 mV; Table 3). Thus, for the Kv1.2 channel the Sr²⁺-induced shift of t_10-90(V) follows that of the G(V) shifts.

Table 3.

Shifts of Conductance and Rise-Time Curves for Kv1.2 with Different Sr²⁺ Salts and Urea

Substance	c (mM)	ΔV1/2 (mV)	ΔVt10-90 (mV)	ΔGmax (%)	Δs (mV)	n
SrCl2	50	21.7 ± 0.4	19.1 ± 0.7	−13 ± 2	+0.6 ± 0.4	16
Sr(NO3)2	50	18.2 ± 0.2	16.9 ± 1.1	−7 ± 2	−0.6 ± 0.2	5
Sr(C6H11O7)2	50	12.1 ± 0.6	12.5 ± 1.6	−8 ± 2	−0.5 ± 0.0	5
Urea	120	−1.4 ± 0.4	−3.8 ± 2.4	−1 ± 1	+0.1 ± 0.1	5

The applied substances were strontium chloride (SrCl₂), strontium nitrate (Sr(NO₃)₂), strontium gluconate (Sr(C₆H₁₁O₇)₂), and urea. c is concentration. ΔV_1/2 is difference between V_1/2 in control and test conditions (with the applied substance; shift of G(V)). ΔV_t10-90 is the shift of t_10-90(V), where t_10-90 is the rising time from 10% to 90% of maximum current in control and test conditions. n is the number of experiments. Data is given as mean ± SE.

Figure 2.

Sr²⁺ effects on Kv1.2 channel opening kinetics. (A) Currents at a step from −80 mV to 0 mV in control solution are shown. Rise time measured as difference between times at 10% and 90% of steady-state value (t₁₀₋₉₀ = t_90% − t_10%). (B) Plots of t₁₀₋₉₀ versus voltage are shown. Additional 50 mM SrCl₂ (solid symbols) to the control solution (open symbols) shifts the curve along the voltage axis. The continuous lines are fitted exponential curves where the exponent and the plateau are constrained to be equal.

In summary, these results strengthen the hypothesis that Sr²⁺ acts on the studied channels mainly by screening surface charges.

ψ_out is a major determinant of V_1/2 of the wild-type channels

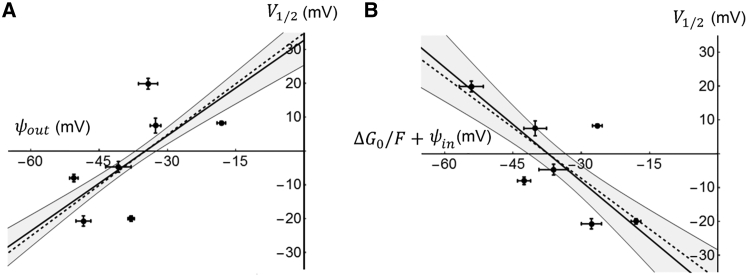
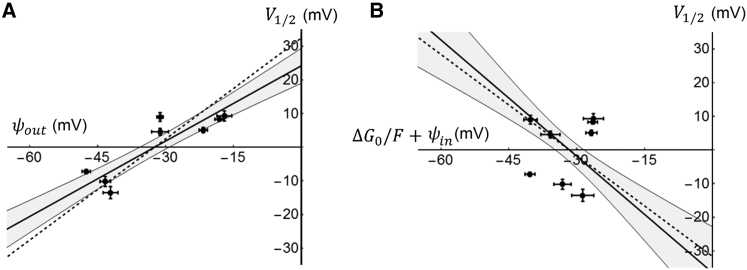
Given that the Sr²⁺ effects allows us to calculate ψ_out from Eq. 2, we are able to plot V_1/2 against ψ_out for the seven studied wild-type channels (Fig. 3 A). If ψ_out and the residual field potential (i.e., (ΔG₀ / F) + ψ_in) are independent of each other, we expect the curve of V_1/2 versus ψ_out to be linear and have a slope of 1 (see Eq. 1). The reason for this is that even though the residual field potential affects V_1/2, the effect is not correlated to ψ_out and therefore random with respect to ψ_out. Thus we expect a 1:1 relation between ψ_out and V_1/2. The regression line, constructed by using Deming distances (45), had a slope of 0.94 and the corresponding correlation coefficient (r) was 0.62 (Fig. 3 A). The found slope value, close to 1, is predicted by Eq. 1 and strengthens the view that the effect of Sr²⁺ ions is caused by screening. A similar analysis for the residual field potential was consistent with these findings. Since the residual field potential is obtained from Eq. 1 and assumed to be independent of ψ_out, the slope of the potential relation of the V_1/2 versus residual field is predicted to be −1 at large numbers of data points. Of the same reason the correlation coefficient is predicted to be $\sqrt{1-r^2}$, where r is the correlation coefficient for the relation of the V_1/2 versus ψ_out relation. The analysis of the experimental data yielded a slope of −1.12 and a correlation coefficient of 0.70, reasonably close to the predicted values −1 and 0.78, respectively (Fig. 3 B), strengthening Eq. 1 and the reasoning above. Altogether, the data in Fig. 3 supports the view that Eq. 1 is valid, that the shifts are caused by screening of fixed surface charges, and that the electrostatic effects caused by the small extracellular loops plays about equally large roles as the rest of the channel proteins to regulate the midpoint of the G(V) curves.

Figure 3.

Midpoint voltage (V_1/2) among wild-type Kv channels as a function of the electric field components. (A) The influence of ψ_out on V_1/2 of seven Kv channels is shown. Thick continuous line is the estimated regression line (V_1/2 = 0.94 × φ_out + 32.7), surrounded by a shaded area representing a 95% confidence interval. The line was obtained by Deming regression (n = 53, r = 0.62). The dashed line represents a linear function with a slope of +1. (B) The influence of the residual field potential (ΔG₀ / F + ψ_in) on V_1/2 is shown. Thick continuous line is the estimated regression line (V_1/2 = −1.12 × (ΔG₀ / F + ψ_in) − 41.9), surrounded by a shaded area representing a 95% confidence interval. The line was obtained by Deming regression (n = 53, r = 0.70). The dashed line represents a linear function with a slope of −1.

Combinations of extracellular linkers transfer ψ_out of Kv1.2 to Kv1.2

We have previously identified charged residues that contribute to ψ_out and to V_1/2 (13, 15, 48). However, we have not been able to completely transfer the effective surface charges from a metal-ion sensitive channel to a relatively metal ion-insensitive channel. In an attempt to do this, we analyzed the Sr²⁺ effect on 25 chimeric constructs by introducing segments from Kv1.2 (most sensitive to Sr²⁺) into Kv2.1 (least sensitive) (Table 4; Fig. 4).

Table 4.

Parameters of Kv1.2, Kv2.1 and Chimera Currents and Effects of 50 mM SrCl₂

	Control		Strontium
	V1/2 (mV)	s (mV)	ΔV1/2 (mV)	Δs (mV)	ΔGmax (%)	n
Wt channels
Kv1.2	−8.0 ± 1.1	10.4 ± 0.7	21.7 ± 0.4	0.3 ± 0.2	−13 ± 2	16
Kv2.1	8.3 ± 0.5	13.3 ± 0.3	7.8 ± 0.4	−0.4 ± 0.4	13 ± 1	13
Extracellular linkers
L1/2	−0.6 ± 1.6	27.1 ± 0.3	ND	ND	ND	9
L3/4	9.3 ± 1.5	20.8 ± 0.5	7.3 ± 0.7	−2.7 ± 0.2	30 ± 3	16
L5/P	9.0 ± 1.3	15.9 ± 0.3	13.4 ± 0.3	0.8 ± 0.3	3 ± 2	6
LP/6	5.1 ± 0.8	14.7 ± 0.3	9.3 ± 0.4	−0.3 ± 0.1	14 ± 2	6
L5/6	16.9 ± 0.3	13.7 ± 0.2	13.9 ± 0.6	0.5 ± 0.6	−7 ± 2	6
L3/4 + L5/P	−7.2 ± 0.6	20.0 ± 0.3	20.4 ± 0.4	−1.8 ± 0.2	−1 ± 2	9
L3/4 + LP/6	−13.5 ± 1.8	20.6 ± 0.4	18.1 ± 0.7	−1.6 ± 0.2	14 ± 1	6
L3/4 + L5/6	−10.2 ± 1.2	17.3 ± 0.2	23.9 ± 0.7	−1.6 ± 0.2	−4 ± 2	16
L5/P + LP/6	4.6 ± 1.0	13.8 ± 0.5	13.4 ± 0.8	2.9 ± 1.2	11 ± 6	9
L3/4 + L5/P + LP/6	−10.2 ± 1.5	19.0 ± 0.6	18.6 ± 0.5	−1.7 ± 0.4	12 ± 1	16
L1/2 + L3/4 + L5/6	−29.9 ± 1.7	19.5 ± 0.6	27.3 ± 2.4	0.2 ± 1.4	4 ± 7	6
Transmembrane and intracellular parts
N-term	9.5 ± 0.9	9.0 ± 0.6	7.5 ± 0.3	−0.1 ± 0.1	0 ± 1	6
S1−S3	19.0 ± 2.2	18.9 ± 0.7	14.0 ± 0.7	−0.8 ± 0.2	2 ± 3	6
S1−S4	−3.2 ± 1.9	17.1 ± 0.1	16.8 ± 1.1	−1.4 ± 0.3	2 ± 2	6
S3 + L3/4	25.7 ± 1.1	15.5 ± 0.8	10.2 ± 0.6	0.6 ± 0.6	30 ± 7	6
L3/4 + S4	2.5 ± 1.5	14.2 ± 0.6	8.1 ± 1.0	−1.4 ± 0.6	10 ± 2	6
S4−S6	26.7 ± 0.6	11.9 ± 0.1	ND	ND	ND	6
L4/5	21.0 ± 2.1	12.5 ± 0.4	5.7 ± 0.3	1.4 ± 0.5	24 ± 2	5
S5	8.8 ± 1.5	13.7 ± 0.3	9.0 ± 0.7	−0.5 ± 0.3	7 ± 1	5
S5 + L5/6	17.6 ± 0.4	14.4 ± 0.2	ND	ND	ND	6
P1	16.1 ± 1.2	15.0 ± 0.2	7.5 ± 0.4	−0.3 ± 0.2	10 ± 2	6
P2	0.7 ± 1.0	12.0 ± 0.6	8.8 ± 0.4	1.8 ± 0.7	20 ± 5	6
P3	7.4 ± 0.5	14.0 ± 0.1	8.3 ± 0.4	−0.6 ± 0.3	4 ± 1	6
S6 + C-term	12.1 ± 0.5	13.0 ± 0.2	8.7 ± 0.2	−1.0 ± 0.1	1 ± 2	6
C-term	3.7 ± 0.7	10.2 ± 0.3	11.8 ± 0.5	1.6 ± 0.4	23 ± 5	6

V_1/2 is midpoint voltage of G(V) from Eq. 2, s is slope of G(V) from Eq. 2, ΔV_1/2 is Sr²⁺-induced shift of G(V) at 1/2 of G_max, Δs is the difference between s in control and Sr²⁺ conditions, ΔG_max is quotient of G_max in control and Sr²⁺ conditions minus 1, and n is the number of experiments. ND, not determinable. Data is given as mean ± SE.

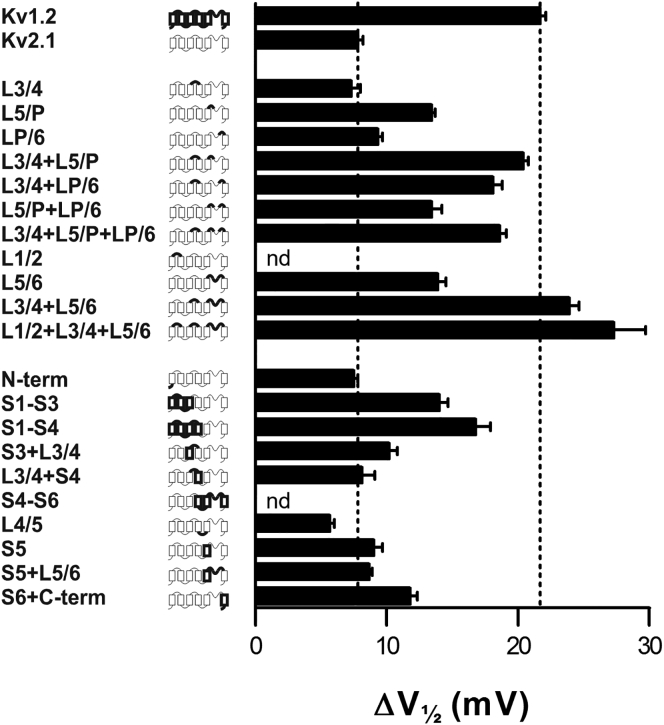
Figure 4.

Effect of Sr²⁺ on G(V) curves for chimeras measured as midpoint shifts. Data taken from Table 4. The hatched vertical lines indicate the mean shift value of the Kv1.2 and Kv2.1 channels, respectively.

For 5 of the 25 chimeras the Sr²⁺-induced G(V) shift was successfully transferred from Kv1.2 to Kv2.1 (G(V) shift >18 mV). These five chimeras comprised L3/4 in different combinations with L5/P and LP/6. It has been suggested that the pore region in itself is responsible for the G(V) shifts caused by Ca²⁺ on Na channels (25). Data from our investigation do not support this view for Sr²⁺ on K channels. For instance, none of the chimeras containing parts of the channel forming the proper pore (S5 up to S6 + C-Term) yielded shifts comparable with that of the Kv1.2 channel (Table 4). In contrast, it is possible to transfer the Sr²⁺-sensitivity without moving the pore loop (e.g., transferring L3/4 + L5/P from Kv1.2 to Kv2.1), and despite using very high concentrations of SrCl₂, only small block effects were seen (Table 4). Thus, the extracellular linkers L3/4, L5/P, and LP/6, are important determinants of ψ_out at the voltage sensor. As we show below, these extracellular linkers are also important determinants of the activation midpoint voltage V_1/2.

Eq. 1 implies that the correlation between ψ_out and V_1/2 depends on the variability of ψ_in + G₀/F. This component, the residual field potential, has been shown to influence V_1/2 in various channels: for instance, electroneutral mutations at the interior of the Shaker Kv channel (not expected to affect ψ_out) have considerable effects on V_1/2 (49, 50, 51, 52). Because the extracellular linkers L3/4, L5/P, and LP/6 were sufficient to transfer the alteration in ψ_out we analyzed the contribution of the different components in more detail, assuming that the unchanged parts would remain relatively constant (Fig. 5 A). As predicted, the slope of the regression line for V_1/2(ψ_out) (calculated from Deming distances) is close to 1 (0.75), suggesting that Eqs. 1 and 2 and our reasoning are valid. The correlation coefficient is high, 0.87. The corresponding plot for the residual field potentials, V_1/2(ΔG₀/F + ψ_in), is logically dependent on the data in Fig. 5 A and shows a much lower correlation coefficient, 0.16 (Fig. 5 B).

Figure 5.

Midpoint voltage (V_1/2) among mutant Kv channels as a function of electric field components. (A) Dependence on ψ_out when external linkers are mutated (n = 81 distributed among seven mutation sites, r = 0.87). Deming regression line shown by the thick continuous line. Slope is 0.75 and intercept is 24.2 mV. The dashed line shows a slope of +1. A 95% confidence band is represented by shaded gray areas. (B) Dependence on the residual field potential (ΔG₀ / F + ψ_in) is shown for the same channels as in (A). Slope and intercept of the Deming regression line are −1.15 and −36.4 mV, respectively (r = 0.16). The dashed line shows a slope of −1. A 95% confidence band is represented by shaded gray areas.

The substitution experiments suggest interaction between the linkers

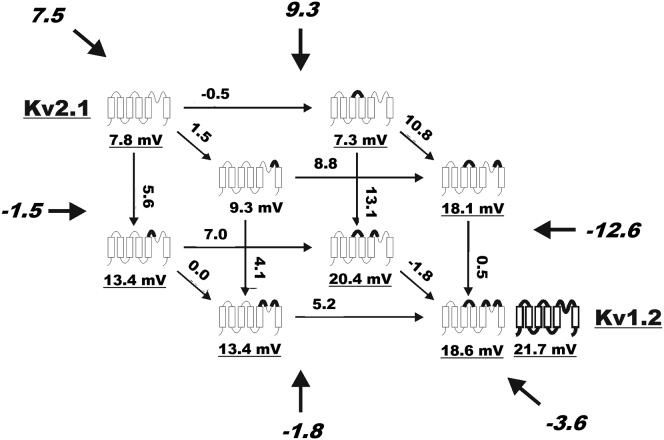
The interactions between L3/4, L5/P, and LP/6 were analyzed in more detail by a substitution-cycle analysis. Fig. 6 shows how the Sr²⁺-induced shifts are altered when the channel is transformed, in three subsequent steps, from Kv2.1 to L3/4 + L5/P + LP/6, which is close to Kv1.2 with respect to Sr²⁺’s G(V)-shifting properties. Each face in the cubic scheme represents a substitution cycle, with the Sr²⁺-induced shifts (ΔV_Sr, underlined numbers below each channel cartoon) and differences between the shifts (Δ²V_Sr, numbers above the arrows) given in the cube. Assuming that the effect of the substitutions in a cycle is independent of each other and that the total effect is additive, the difference between the shift differences (Δ³V_Sr, numbers in italics) in that cycle should be zero. It is clear that this is not the case and the effects are clearly nonadditive in at least three of the cycles of the L3/4-L5/P-LP/6 substitution scheme ((|Δ³V_Sr| > 7 mV). Thus, the substituted linkers interact with each other, most likely by moving charged residues relative to the voltage sensor.

Figure 6.

Mutant cycles cube of Sr²⁺-induced (50 mM) shifts. Data taken from Table 4.

Transplanting L3/4 and LP/6 separately from Kv1.2 to Kv2.1 causes almost no effects on the Sr²⁺-induced shifts, but transplanting them together makes this chimera almost as sensitive as Kv1.2 (Fig. 6). In contrast, transplanting L5/P from Kv1.2 to 2.1 has a relatively large effect alone. In addition, this effect is clearly increased in the presence of L3/4 from Kv1.2. However, the largest interaction occurs between L5/P and LP/6, both from Kv1.2, in the presence of L3/4 from Kv1.2; Δ³V_Sr is considerably higher in combination with L3/4 from Kv1.2 (–12.6 mV) than in the cycle of the Kv2.1 background (−1.5 mV), suggesting a higher energy coupling between the linkers L5/P and LP/6 when in the L3/4 background. Similar analyses of the other substitution cycles yield absolute Δ³V_Sr values between 1.5 and 12.6 mV (italicized numbers outside the cube in Fig. 6). In summary, three chimeras have high sensitivity to Sr²⁺ (ΔV_Sr = 18.1–20.4 mV) and five have relatively low sensitivity (ΔV_Sr = 7.3–13.4 mV). The three high-sensitivity chimeras contain L3/4 transferred from Kv1.2 in combination with L5/P from Kv1.2 or with LP/6 from Kv1.2 or with both together.

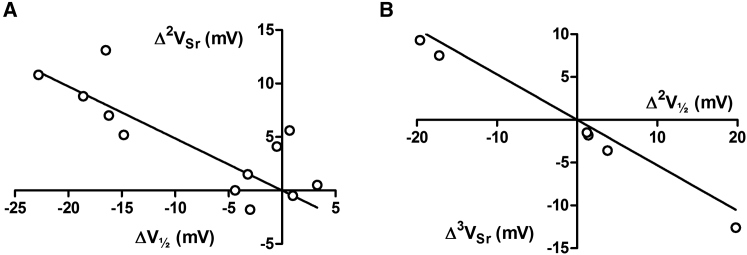
The interactions between the linkers with respect to the Sr²⁺-induced shifts should also be paralleled by equal interactions with respect to V_1/2 in the absence of Sr²⁺ if ψ_out is a strong determinant of V_1/2. This is in fact the case; alterations in V_1/2 (i.e., ΔV_1/2) is strongly correlated with Δ²V_Sr (Fig. 7 A, slope = −0.49 close to the predicted −0.43 (i.e., 1/2.33, from Materials and Methods); p < 0.0001). There is a clear clustering of data in two distinct groups, suggesting that either the linkers interact or they do not. However, our data does not rule out that point mutations can cause intermediate variants. In addition, the higher-order values Δ²V_1/2 and Δ³V_Sr are also strongly correlated (Fig. 7 B, slope = −0.53 close to the predicted −0.43; p = 0.0001). Taken together, these data show an exceedingly strong connection between (alterations in) the voltage dependence (i.e., midpoint of the G(V) curve) of the ion channel, and (alterations in) the Sr²⁺-induced G(V) shift.

Figure 7.

Correlations in higher-order effects. (A) Alterations in Sr²⁺-induced G(V) shifts plotted versus alterations in V_1/2 caused by transplantation of extracellular linkers from Kv1.2 to Kv2.1. Based on data taken from Table 4 (slope = −0.49, p < 0.0001). (B) Alterations in alterations of Sr²⁺-induced G(V) shifts plotted versus alterations in alterations of V_1/2 caused by transplantation of extracellular linkers from Kv1.2 to Kv2.1. Based on data from Fig. 6 (slope = −0.53, p = 0.0001).

Discussion

In this study we have quantitatively evaluated the structural determinants of Kv channel activation, looking for possible principles explaining their evolution. Analyzing Sr²⁺ effects on G(V) curves of 7 wild-type Kv channels and 25 chimeric constructs between Kv1.2 and Kv2.1, we conclude that 1) Sr²⁺ acts on these channels mainly by screening surface charges (the strong screening hypothesis); 2) the surface potential at the voltage sensor is a major determinant of V_1/2; 3) the three interacting extracellular linkers L3/4, L5/P, and LP/6 are the main contributors to the external surface potential at the voltage sensor of Kv1.2; and 4) these critical linkers interact nonadditively to influence the voltage-sensing mechanism.

This means that in addition to linker L5/P (11, 13, 37), the linker L3/4 also plays an important role for the Sr²⁺ sensitivity. It also means that the pore segment does not seem to be involved in mediating the shift effect for Sr²⁺ acting on the Kv channel as has been suggested for Ca²⁺ acting on Na channels (25).

No indication of direct strontium effects on the gating machinery

Despite the fact that no observation in our study falsified the strong screening hypothesis, we nevertheless explored other mechanisms that could explain the experimental results. The strong screening hypothesis assumes that Sr²⁺ indirectly affects the gating machinery via screening the extracellular surface charges, thereby making ψ_out more positive. We therefore looked for hypotheses that directly affected the gating machinery. Especially we looked for mechanisms that showed the observed coupling between the Sr²⁺-induced shift of the G(V) curve and the V_1/2 value, i.e., a mechanism that limits the Sr²⁺-induced shift at higher V_1/2 values.

One such mechanism is based on the assumption that the construction of the chimera and Sr²⁺ selectively affect different steps along the activation path. Kv channels are known to first undergo a series of relatively voltage sensitive steps and then a less voltage sensitive opening step when activated. Using a quantitative model of a Shaker Kv channel (53) we can show that if the construction of a chimera is assumed to selectively affect a transition step (by shifting the midpoint of the transition voltage function along the voltage axis), and that Sr²⁺ is assumed to selectively affect another transition step (by shifting the midpoint), the Sr²⁺-induced shift of the G(V) curve decreases with increasing V_1/2 in accordance with the experimental results. However, the G(V) curve is also systematically steeper at higher V_1/2. As pointed out above, the experimental results listed in Table 4 show that there is no correlation between the Sr²⁺-induced slope change and the G(V) shift, thus making the hypothesis of selective effects less likely as explanation of the results.

Although we have shown above that the assumption of specific effects of Sr²⁺ and the chimerization on specific steps in the activation path does not explain the experimental results, it is too simplistic to assume that the effects on the steps are equal. Inherent in the strong screening hypothesis is the assumption that Sr²⁺ has less effect on the channel during the final step than during the early steps. It has been shown for Shaker channels that ψ_out close to S4 changes by +35 mV when the channel changes from a closed state with fully retracted gating charges to an open state with the gating charges exposed on the extracellular surface (54). Thus, ψ_out as determined from Eq. 2 is not likely to correspond to ψ_out in a specific state, but rather to an average ψ_out, which also determines the midpoint of the G(V) curve. However, this does not change the overall conclusions.

The linkers are the most diverse part of the channel protein

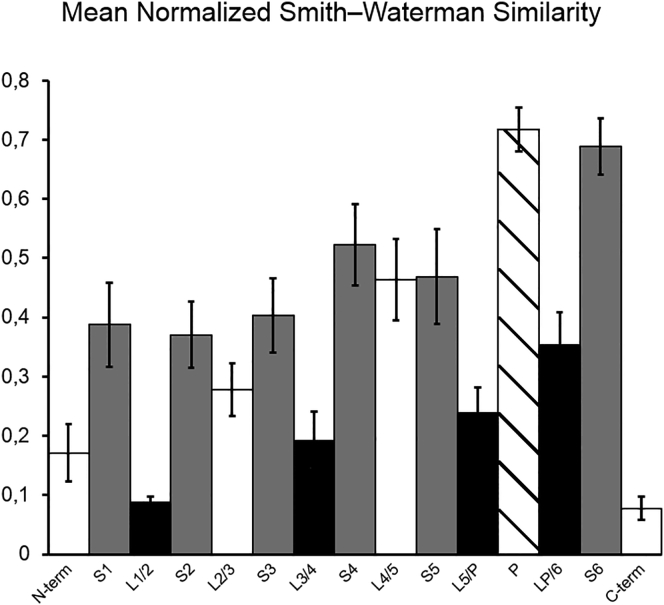
The K channels are the most abundant of the channels in the human channelome, forming a plethora of types varying in kinetics and distribution (14). We have shown here that the extracellular linkers L3/4, L5/P, and LP/6 are the main determinants of V_1/2 and thus of the location of the G(V) curve on the voltage axis. Since this curve is a key factor in the differential functioning of Kv channels, this suggests that the sequences forming these segments should be more diverse than those of other segments of the channel proteins when comparing wild-type channels. We analyzed this issue by comparing the similarity of extracellular, intracellular, and intramembranous segments of the investigated wild-type channels (Fig. 8), using the normalized Smith-Waterman similarities as measures (46). As can be clearly inferred the linkers (black bars are the extracellular and white are the intracellular) are most variable, suggesting that these segments may play a crucial role in the function and evolution of Kv channels.

Figure 8.

Similarity in the amino acid sequence of the studied Kv channels. Using the Smith-Waterman algorithm (46), the segments were pairwise locally aligned and the fraction of identical amino acids was taken as a measure of similarity (see Materials and Methods for details). The bars show the mean similarity between the seven Kv channels studied (21 pairwise comparisons). The white bars represent intracellular segments, the gray bars represent the transmembrane segments, the black bars represent the extracellular segments, and the striped bar represents the pore. The pore is the most conserved part, whereas the extra- and intracellular linkers are the least-conserved parts of the protein (p < 0.05). Significance assessed by bootstrapping. Error bars represent mean ± SE.

Molecular interpretation of linker substitutions

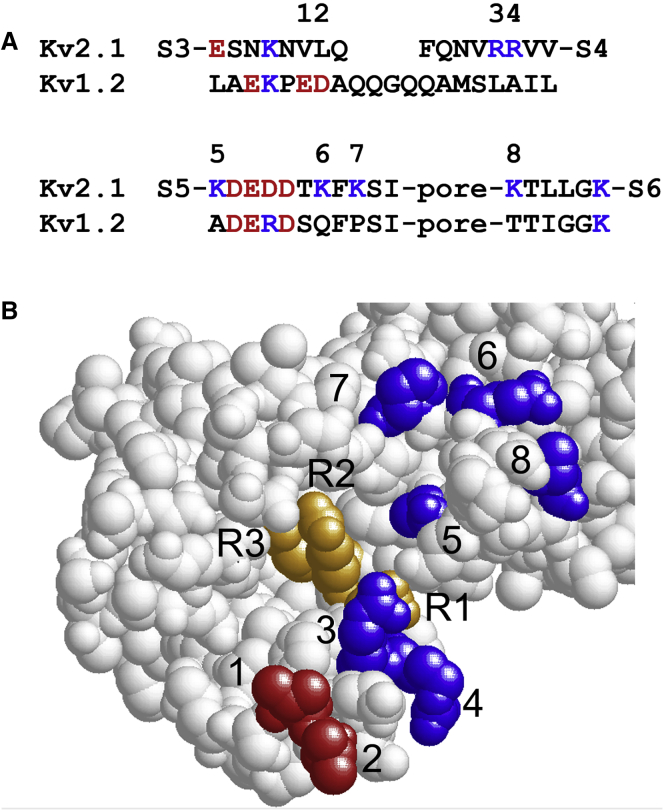
In structural terms, our data suggest that charged residues in L3/4, L5/P, or LP/6 are close to the most extracellular positive charges of S4, and that L3/4, L5/P, or LP/6 are sufficiently close to each other to interact positionally. How do these predictions and the quantitative results from the substitution experiments summarized in Fig. 4 fit structural data? For such a comparison we here use the results from a high-resolution structure of a Kv1.2/2.1 chimera, crystallized in the presence of phospholipids (39). This chimera is essentially a Kv1.2 channel with the extracellular end of S3, the L3/4 linker, and the extracellular end of S4 from Kv2.1, and this structure most likely captures the detailed structural features of a native Kv channel (16, 49, 55). Kv2.1 and Kv1.2 differs in a few positions in the extracellular linkers L3/4, L5/P, and LP/6 with respect to charged amino acid residues (Fig. 9 A). Eight residues on the surface of the channel protein are more positively charged in Kv2.1 than in Kv1.2 (labeled 1 to 8 in Fig. 9, A and B), making them possible candidates as functional surface charges in explaining the difference between Kv1.2 and Kv2.1. Residues 1 and 2 are negatively charged in Kv1.2 (red) and residues 3–8 are positively charged in Kv2.1 (blue). The three top charges of S4 (R1 to R3) are shown in orange.

Figure 9.

Sequences and structure of the extracellular linkers of a Kv1.2/2.1 channel. (A) Sequences of the extracellular linkers of Kv1.2 and Kv2.1 are presented. Negatively charged residues are red and positively charged residues are blue. The numbers 1–8 above the sequences denote the residues where the Kv2.1 channel is more positively charged than Kv1.2. (B) Extracellular view of the Kv1.2/2.1 chimera (39) is shown. The numbered residues in (A) are colored and numbered in the molecular structure. The three top gating charges in S4 (R1–R3) are colored in gold. To see this figure in color, go online.

Charges 1 and 2 are too distant from S4 to electrostatically affect S4 more than marginally (55, 56), whereas residues close to residues 3 and 4 affect the voltage sensitivity in HCN channels (57, 58), and in the Shaker K channel residue 4 has a large effect on the position of G(V) along the voltage axis depending on the valence of the residue, +30 mV for a positively charged arginine compared with a negatively charged glutamate (59). Shortening of L3/4 shifts the G(V) in positive direction along the voltage axis (60). Whether or not this affects the effect of Sr²⁺ has not been investigated, but for reasons given above, it is not likely that the shortening per se, limiting the S4 movement, will affect the Sr²⁺ effect if not charged amino acid residues are moved closer or more distant to S4. Charges 5–7 electrostatically affect S4, most prominently the residue closest to S4 (position 419 in Shaker) (13, 38). Charge 8 has only small effects on S4 (13, 38). How do alterations of the charge patterns shown in Fig. 8 match the results of the linker substitutions? Introducing single linkers L3/4, L5/P, or LP/6 from Kv1.2 to Kv2.1 only have modest effects, whereas combinations of L3/4 and L5/P or LP/6 lead to considerably large effects. The details of the mechanism are not clear. The most surprising effect is that of the L3/4 → L3/4 + LP/6 transition, in which removing one positive charge in LP/6 (residue 8 in Fig. 9) increases the shift value by 10.8 mV and shift G(V) by −22.8 mV. A reasonable explanation is that the transition leads to a new position of L5/P, where the positive charges are moved away from S4 and the negative charges moved closer to S4.

Bond formation between the extracellular loops

Which physical mechanisms mediate the structural interaction between the linkers, causing the resulting chimeras to behave nonadditively with respect to Sr²⁺ sensitivity? The substitutions of the extracellular loops involve relatively high energies. For instance, introducing LP/6 in the Kv2.1 background shifts G(V) by –3 mV while introducing the same linker in the L3/4 background shifts G(V) by −23 mV, a 20 mV difference. Similar differences are found for other combinations of the extracellular linkers. This difference could be due to bond formation between certain extracellular loops, forcing the surface charges in suitable positions in relation to the voltage sensor. This would mean an energy difference of the following:

$$\mathit{\Delta }W=\mathit{\Delta }V{Q}_g=\mathit{\Delta }VFz=20\text{mV}\times \mathrm{96,480}\text{C}/\text{mol}\times 12\approx 24\text{kJ}/\text{mol},$$ (11)

where z is the number of charges that have to move to open the gate (52). This energy amount is sufficient to break or form a hydrogen bond (10–30 kJ/mol), a couple of dipole-dipole interactions (10–15 kJ/mol), several van der Waals (1–10 kJ/mol), or multiple hydrophobic interactions (<1 kJ/mol (61)). We suggest that such bond modifications alter the L3/4, L5/P, and LP/6 configurations and thus the effective surface-charge density around the voltage sensor and the consequent channel sensitivity to Sr²⁺.

Conclusions

In summary, we have shown that the charged residues close to S4 in the extracellular linker L3/4 (residues 3 and 4 in Fig. 9) and in the turret loop S5/P (residues 5–7 in Fig. 9) determine the activation curve of Kv channels. In addition, charged residues in the linker LP/6 (residue 8 in Fig. 9) affect the position of residues in L5/P via the domino network of L5/P previously described (13). The linkers interact by forming bonds, most likely hydrogen bonds, affecting the distance between charged residues and S4. This implies that many residues, not only the charged ones, are important in shaping the surface-charge geometry.

Author Contributions

F.E., M.M., and P.Å. designed research; M.M. performed research; F.E., M.M., H.Z., and P.Å. analyzed data; and F.E., M.M., H.Z., and P.Å. wrote the manuscript.

Editor: Henry Colecraft

Appendix A: Approximate and Analytical Solution of the Grahame Equation

Approximative solution

Consider the Grahame equation:

$${\sigma }^2=2{\epsilon }_r{\epsilon }_0\sum _i{c}_i\left(e^{-z_i\psi F/RT}-1\right),$$

which can be represented by the following Maclaurin series:

$${\sigma }^2=2{\epsilon }_r{\epsilon }_0\sum _{n=2}^{\infty }\sum _i\frac{c_i}{n!}{\left(-\frac{z_i\psi F}{RT}\right)}^n.$$

The power series starts at n = 2, since the two first terms vanish (trivially for n = 0, for n = 1 by the general electroneutrality relationship ${\sum }_i{z}_i{c}_i=0$). Let c_i,0 and ψ₀ be the initial concentration and surface potential, and c_i,1 and ψ₁ be the altered concentration and potential. Given that the surface charge σ is preserved, the following equation is obtained:

$$\sum _{n=2}^{\infty }\sum _i\frac{c_{i,0}{\psi }_0^n-c_{i,1}{\psi }_1^n}{n!}{\left(-\frac{z_{i}F}{RT}\right)}^n=0.$$

Taking the first term of the power series (n = 2) yields the following approximation:

$${\psi }_0^2\frac{1}{2}\sum _i{c}_{i,0}{z}_i^2\approx {\psi }_1^2\frac{1}{2}\sum _i{c}_{i,1}{z}_i^2,$$

which contains expression for the ionic strength and can be written as follows:

$${\psi }_0^2{I}_0\approx {\psi }_1^2{I}_1.$$

Let ψ₁ = ψ₀ + h and express ψ₀ as a function of the ionic strengths and h

$${\psi }_0\approx {\left(\sqrt{\frac{I_0}{I_1}}-1\right)}^{-1}\times h.$$

Note that in this article the notation ΔV_me is used (to indicate the specific shift induced by Sr²⁺) and not h.

Analytical solution

In a solution with monovalent ions and divalent cations, express σ² using the variable substitution t = e^{ψF / RT}:

$${\sigma }^2=2{\epsilon }_r{\epsilon }_0\left(c_1{t}^{-1}+c_2{t}^{-2}+c_{3}t\right).$$

The Grahame equation must give the same charge after addition of SrCl₂. This condition is equivalent to the following third-order equation:

$$a{t}^3+b{t}^2+ct+d=0,$$

which in turn can be transformed to a depressed cubic t³ + pt + q = 0 (the coefficients are given below). Analyzing the discriminant of this equation reveals that there are always three real roots and by Descartes rule of sign, one root is always negative and the other two positive. The negative root corresponds to a complex potential and the smallest positive root to a negative σ and the largest positive root to a positive σ. Thus, after substituting back, the geometrical solution (by the French 16th-century mathematician François Viète) to the intermediate potential is the following:

$$\psi =\frac{RT}{F}\text{ln}\left(2\sqrt{-p}\text{cos}\left(\frac{\theta }{3}+\frac{2\pi }{3}\right)-\frac{b}{3a}\right),$$

where $\text{cos}\left(\theta \right)=q/\sqrt{-p^3}$ (where p = 3ac + b³ / 3a² and q = 2b³ − 9abc + 27a²d / 27a³) and the coefficients are given by $a={\left[C{l}^{-}\right]}_0-{\left[C{l}^{-}\right]}_1{e}^{hF/RT}$, $b=\left[S{r}^{2+}\right]+\left({\left[C{l}^{-}\right]}_1-{\left[C{l}^{-}\right]}_0\right)$, $c=\left[N{a}^{+}\right]\left(1-e^{-\left(hF/RT\right)}\right)$ and $d=\left[C{a}^{2+}\right]-\left(\left[C{a}^{2+}\right]+\left[S{r}^{2+}\right]\right)e^{-2\left(hF/RT\right)}])$.