Use and Interpretation of Propensity Scores in Aging Research: A Guide for Clinical Researchers

Abstract

Observational studies are an important source of evidence to evaluate treatment benefits and harms in older adults, but lack of comparability in the outcome risk factors between the treatment groups leads to confounding. Propensity score (PS) analysis is widely used in aging research to reduce confounding. Understanding the assumptions and pitfalls of common PS analysis methods is fundamental to apply and interpret PS analysis. This review was developed based on a symposium of the American Geriatrics Society Annual Meeting on the use and interpretation of PS analysis in May 2014. PS analysis involves 2 steps: estimation of PS and estimation of the treatment effect using PS. Typically estimated from a logistic model, PS reflects the probability of receiving a treatment given observed characteristics possessed by an individual. PS can be viewed as a summary score that contains information on multiple confounders, and this score is used in matching, weighting, or stratification to achieve confounder balance between the treatment groups to estimate the treatment effect. Among these methods, matching and weighting generally reduce confounding more effectively than stratification. Although PS is often included as a covariate in the outcome regression model, this is no longer a best practice due to its sensitivity to modeling assumption. None of these methods reduce confounding by unmeasured variables. In this review, we explain the rationale, best practices, and caveats in conducting PS analysis using a case study that examined the effectiveness of angiotensin-converting enzyme inhibitors on mortality and hospitalization in older adults with heart failure.

1. Introduction to Propensity Score Analysis

Observational studies are an important source of evidence to evaluate treatment effects in a more generalizable, routine practice population that includes a large number of older adults who are underrepresented in randomized controlled trials (RCTs). Unlike RCTs in which risk factors between the treatment groups are likely to be balanced by randomization, treatments in observational studies are chosen based on several factors, such as disease status, severity, or prognosis. As a result, the difference in the outcome between the treatment groups may not reflect true treatment effect but the difference in risk factors that pre-existed treatment.

Case study. In a retrospective study, Mujib et al. examined the benefit of angiotensin-converting enzyme inhibitors (ACEIs) in older adults with heart failure with preserved ejection fraction (see the summary in Table 1).¹ Patients who were prescribed an ACEI had 16% lower mortality or heart failure hospitalizations than untreated patients. Since ACEIs were more likely to be given to lower-risk patients, this 16% reduction cannot be interpreted as the true effect of ACEIs.

Table 1. Summary of a Case Study of Propensity Score Analysis (Am J Med 2013; 126: 401-410)¹.

Components	Summary
Research question	Does ACEI prevent all-cause mortality or heart failure hospitalizations in older adults with HFpEF?
Study design	Retrospective cohort study in a national registry (2003-2004) linked to Medicare (through 2008)
Study population	4189 older patients with HFpEF who were not taking ACEIs prior to admission and eligible for ACEIs
Treatment exposure	Treatment group: 1706 patients who were newly treated with ACEIs on discharge Comparison group: 2483 patients who did not receive ACEIs on discharge
Primary outcome	A composite endpoint of all-cause mortality or heart failure hospitalizations
Median follow-up	2.4 years
Potential confounders	114 patient-level and hospital-level characteristics
PS analysis	PS model: logistic model for initiation of ACEI as a function of 114 patient-level and hospital-level characteristics PS matching: 1:1 nearest neighbor matching without caliper resulted in 1337 pairs of treated and untreated patients. Evaluation of PS model: SMD of selected characteristics (treated vs. untreated groups) before and after matching ○ Before matching: COPD, −0.11 (27% vs. 32%); CKD, −0.14 (58% vs. 65%); diuretics, −0.26 (49% vs. 62%) ○ After matching: COPD, 0.00 (28% vs. 28%); CKD, 0.00 (60% vs. 60%); diuretics, −0.02 (54% vs. 55%)
Results	Risk of primary outcome in treated vs. untreated groups: 79% vs. 84% Unadjusted: HR 0.84 (95% CI: 0.78-0.90) PS matching (main analysis): HR 0.91 (95% CI: 0.84-0.99) PS covariate adjustment: HR 0.94 (95% CI: 0.87-1.01) PS weighting or PS stratification was not performed. Multivariable regression model: HR 0.93 (95% CI: 0.86-1.00)
Sensitivity analysis	The observed HR 0.91 could be explained by an unmeasured strong risk factor that would increase the odds of receiving ACEI by 1%.

Abbreviations: ACEI, angiotensin-converting enzyme inhibitors; CI, confidence interval; CKD, chronic kidney disease; HFpEF, heart failure with preserved ejection fraction; HR, hazard ratio; PS, propensity score; SMD, standardized mean difference.

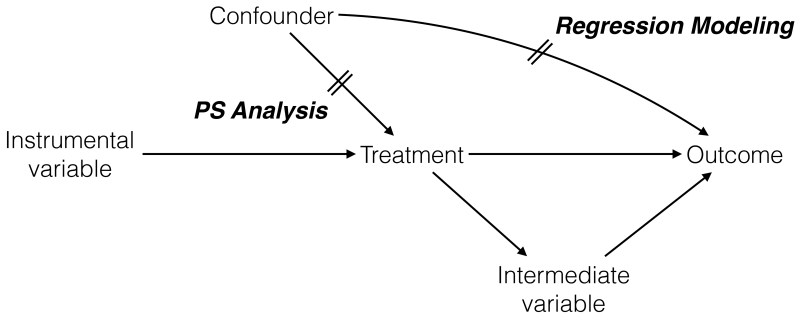
The discrepancy between the estimated and true treatment effects is called bias; a particular bias caused by lack of comparability in the outcome risk factors between the treatment groups is confounding. A confounder refers to a variable that satisfies the following 3 conditions: 1) it is associated with the treatment (i.e., unbalanced between the treatment groups); 2) it is associated with the outcome in the absence of treatment (i.e., a risk factor of the outcome); and 3) it is not affected by the treatment (Figure 1).²

Figure 1. Causal Diagram Representing Confounder, Instrumental Variable, and Intermediate Variable.

In this causal diagram, a variable is called a confounder if 1) it is associated with the treatment (confounder → treatment); 2) it is associated with the outcome, independently of the treatment (confounder → outcome without its effect through treatment); and 3) it is not affected by the treatment (not treatment→confounder). A variable is called an instrumental variable if it is only associated with the treatment (instrumental variable → treatment) and not with confounder or outcome. A variable that mediates the effect of the treatment on the outcome (treatment → intermediate variable → outcome) is called an intermediate variable. To reduce confounding, propensity score analysis focuses on the confounder-treatment relationship, while regression modeling focuses on the confounder-outcome relationship.

Case study. Certain comorbidities (e.g., chronic obstructive pulmonary disease and chronic kidney disease) and diuretic use were less prevalent in the treated patients, and they are known risk factors of the outcome in the absence of ACEI treatment (Table 1).¹ Since they were present before ACEI initiation, they could not be affected by the treatment. Therefore, these variables are confounders.

Estimating treatment effects in observational studies requires careful adjustment for confounding. Investigators should think about all potential confounders and measure them accurately; any measurement error or lack of measurement on confounders can lead to residual or unmeasured confounding. Once it is assumed that all confounders are accurately measured (i.e., no measurement error and no unmeasured confounding), statistical techniques can be employed to reduce confounding. A popular technique is regression modeling in which investigators specify a mathematical relationship of how the treatment and confounders relate to the outcome. If this relationship is correctly specified, the model can estimate the unbiased treatment effect.

Case study. The investigators identified 114 patient-level and hospital-level characteristics as potential confounders.¹ To reduce confounding using regression modeling, the investigators would have to specify how each of the 114 covariates is related to the outcome, which could lead to model misspecification and overfitting. Furthermore, the treatment effect estimate can change depending on how covariates are modeled; one may explore multiple models to obtain more satisfactory results.

Propensity score (PS) analysis is another useful technique for confounding adjustment. It involves 2 steps: estimation of PS and estimation of treatment effects using PS. Typically estimated from a regression model that relates confounders to the treatment, PS reflects the probability of receiving a treatment given the observed characteristics (confounders) possessed by an individual. PS can be viewed as a “confounder summary score” that contains information on multiple confounders.^3-5 In theory, if no unmeasured confounders exist and treated and untreated patients have similar PS, all confounders included in the PS model will be balanced within this sample and the unbiased treatment effect can be estimated. In contrast to regression modeling that handles individual confounders, PS analysis uses this single score in design (matching) or analysis (weighting or stratification) to reduce confounding.

Case study. Instead of modeling the relationship between the 114 covariates and the outcome in a regression model, the investigators first modeled how the 114 covariates are related to the treatment to estimate a PS. The estimated PS from this model was then used to estimate the treatment effect. This 2-step process generally offers several advantages to regression modeling, including robustness to model misspecification, handling a large number of confounders, and transparent analysis by limiting data exploration.

There have been several tutorials on PS analysis,^6,7 but less emphasis has been placed on explaining the assumptions and pitfalls of common PS analysis methods for clinical researchers. In particular, while PS analysis assumes no unmeasured confounding, it is not often discussed what can be done to minimize unmeasured confounding and to explore the influence of such confounding on study results. This review is developed based on a research method symposium of the American Geriatrics Society Annual Meeting on the use and interpretation of PS analysis that took place in Orlando, Florida, on May 15, 2014. It is intended to guide clinical researchers who want to apply PS analysis as well as clinician readers who want to critically appraise research papers that employed PS analysis. In the sections that follow, we 1) outline the steps to estimate PS; 2) explain PS analysis methods (matching, weighting, stratification, and covariate adjustment) to estimate the treatment effect; 3) review advantages of PS analysis to regression modeling; 4) list strategies to address unmeasured confounding; and 5) conclude with best practices of PS analysis. We explain the rationale, best practices, and caveats, using a case study (Table 1).¹ Although PS analysis can be applied to any exposure with ≥2 groups,⁸ we only consider a binary treatment in this review.

2. Estimation of PS

PS is estimated most commonly using logistic regression, although semi-parametric models (e.g., generalized method of moments) and data mining techniques can be used.^9,10 A logistic regression model can be developed using the treatment indicator as dependent variable, and baseline covariates and their interaction terms as independent variables (see Appendix for equation).⁷ Since patients with the same characteristics at different time periods may not have the same chance of receiving a treatment, it is important to consider the impact of time and the possible interaction between time and baseline covariates.

2.1. What variables should be included in the PS model?

PS models should include confounders. Some variables may only be associated with the treatment, not with the outcome or confounders (Figure 1); these variables are called instrumental variables (IVs). Including IVs may help predicting the treatment, but it decreases the precision of treatment effect estimates (i.e., a wider 95% confidence interval [CI])¹¹ or may increase bias when unmeasured confounders are present.^12,13 Variables that mediate the effect of the treatment in the causal pathway are called intermediate variables (Figure 1). Including such variables will bias the results by obscuring a part of treatment effect mediated by intermediate variables.

Best practices and caveats

The distinction among confounders, IVs, and intermediate variables is important in variable selection for PS models. Subject-matter knowledge should be the basis of evaluating whether or not a variable is a confounder; it cannot be determined based on statistical criteria alone (e.g., p-value or 10% change in coefficient).¹⁴ This principle applies to any observational study, regardless of the use of PS analysis. Perfect predictors of the treatment should not be included in PS models. To avoid adjusting for IVs, one should only include the outcome risk factors, regardless of their association with the treatment.^12,15 Even if risk factors may not be associated with the treatment, including them in a PS model can improve the precision of treatment effect estimates.¹¹ To prevent including intermediate variables, one can compare patients who are newly prescribed treatments (i.e., incident users) rather than those who are already receiving treatments (i.e., prevalent users), and measure confounders before treatment initiation. This is called “new-user design”.¹⁶

Case study. Based on clinical knowledge, the authors identified 114 patient-level and hospital-level characteristics as potential confounders.¹ From a logistic model that included 114 variables, the PS (i.e., probability of receiving an ACEI) was estimated for all individuals in the dataset. Because the included variables were risk factors of mortality and heart failure hospitalizations and measured before treatment initiation, IVs and intermediate variables were unlikely to be included in the PS model.

2.2. How can we evaluate the PS model?

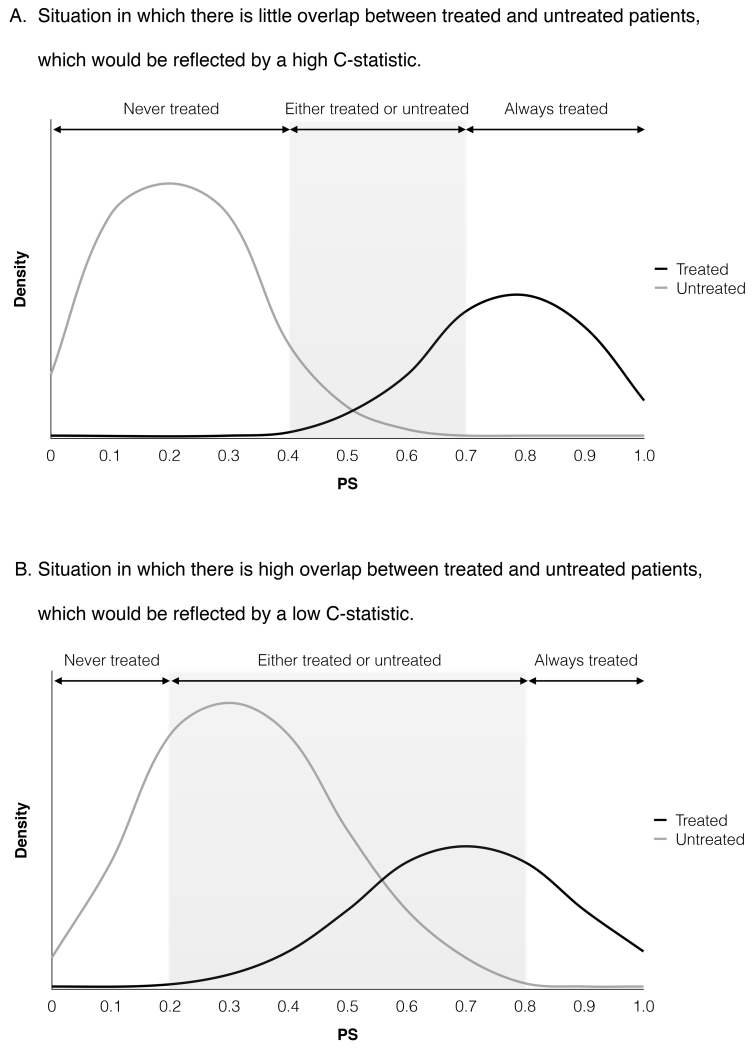
PS models should be evaluated based on the balance in potential confounders between treated and untreated groups with similar PS levels. If imbalance persists, PS model may be misspecified; one can include additional variables, interaction terms, and non-linear terms of continuous variables. This process is repeated until an acceptable level of balance (see below) is achieved. In addition, a graphical presentation of PS distribution has important implications in interpreting the results of PS analysis (Figure 2). The treatment effect can be reliably estimated for treated and untreated patients in the overlapping range of PS (“common support”), because confounders are balanced within the sample of similar PS. Little overlap in the PS distribution indicates that the difference between the treatment groups cannot be reduced, and the estimated treatment effect may remain confounded.¹⁷ More details on assessment of PS models are available elsewhere.¹⁸

Figure 2. Hypothetical Distribution of Propensity Scores Between Treated and Untreated Patients.

Abbreviation: PS, propensity score.

Figure 2A depicts a situation with high C statistic, in which the propensity score clearly distinguishes treated patients from untreated patients and there is a small overlap in propensity score. This may reflect a consistent clinical practice regarding treatment use or inclusion of strong predictors of the treatment, such as instrumental variables. Figure 2B depicts a situation with low C statistic, in which the propensity score modestly distinguishes treated patients from untreated patients and there is a large overlap in propensity score. This may indicate that a majority of patients have a chance of being treated or untreated, or that important confounders may have been omitted.

Best practices and caveats

In assessing balance, one should use a metric that is specific to the sample and not affected by sample size, such as standardized difference (<0.1 is considered acceptable).^19,20 Significance testing (e.g., p-value) that is influenced by sample size should be avoided.²¹ Because the main purpose of PS analysis is not the best prediction of treatment status, metrics to evaluate prediction models (e.g., goodness-of-fit statistic and C statistic) do not inform whether PS models are correctly specified or include important confounders.²² High C statistics indicate a wide separation of PS distribution between the treatment groups (Figure 2A), which may result from consistent clinical practice or inclusion of IVs. In contrast, low C statistics (Figure 2B) may reflect a situation in which clinical uncertainty exists or omission of important confounders. Thus, C statistics cannot be relied upon to evaluate PS models.

Case study. The authors used standardized differences to assess balance in potential confounders before and after PS matching. After PS matching, standardized differences for all covariates were <0.1, suggesting adequate balance (Table 1).¹

3. Use of PS to Estimate Treatment Effects

Having developed a PS, there are 4 methods that are commonly employed to estimate the treatment effect: matching, weighting, stratification, and covariate adjustment. Depending on the method used, the treatment effect can be estimated for all treated and untreated patients (average treatment effect [ATE]) or for treated patients (average treatment effect for the treated [ATT]). These quantities may not be the same when treatment effects vary within study population. This section describes all 4 methods and their advantages and disadvantages (Table 2). Refer to tutorial papers for implementation of these methods.^6,7

Table 2. Comparison of Commonly Used Propensity Score Analysis Methods.

PS Method	Advantages	Disadvantages
Matching	Allows intuitive analysis and transparent presentation of covariate balance Removes covariate imbalance more effectively (less bias) than other stratification or covariate adjustment Does not require specification of the PS-outcome association	Limits generalizability and reduces power by excluding unmatched patients Subject to residual and unmeasured confounding
Weighting	Can be extended to account for time-dependent confounding and censoring Removes covariate imbalance more effectively (less bias) than other stratification or covariate adjustment Does not require specification of the PS-outcome association Analyzes study population within range of common support	May be subject to the influence of few patients with extreme weights PS model misspecification can result in extreme weights. Subject to residual and unmeasured confounding
Stratification	Allows relatively straightforward analysis and transparent presentation of covariate balance for each stratum Does not require specification of the PS-outcome association Analyzes study population within range of common support	In the presence of non-uniform treatment effects across strata, a single summary estimate is not meaningful. Subject to residual and unmeasured confounding
Covariate Adjustment	Analyzes the entire study population	Requires specification of the PS-outcome association; if misspecified, the estimated effect can be biased. Does not allow transparent assessment of covariate balance Subject to residual and unmeasured confounding Due to these limitations, this method is no longer considered a best practice.

Abbreviation: PS, propensity score.

3.1. Matching

For each treated patient, ≥1 untreated patients with similar PS can be selected to form a PS-matched cohort. Typically, there are more untreated patients than treated patients; the matched cohort resembles the treated patients in the original population. Thus, the treatment effect estimated from the matched cohort represents ATT. In the matched cohort, treated and untreated patients have similar distribution of variables included in the PS model; treatment effects can be estimated by directly comparing the outcome risks in the PS-matched cohort. A major advantage of matching is that it removes covariate imbalance more effectively than PS stratification or covariate adjustment^23,24 and offers transparency by giving an intuitive look similar to that of a RCT. Typically, in the PS-matched cohort, the nature of baseline covariates relating to the outcome need not be specified in the outcome model. However, it has been shown that specifying the covariate-outcome relationship in the outcome regression model after PS matching can generate results less prone to model misspecification.²⁵ Because matching excludes patients in the tails of PS distribution and untreated patients who do not have a match (depending on the size of untreated group and matching algorithm), the treatment effect is estimated only for patients who are in the common support range of PS distribution (shaded area in Figure 2). If matching is overdone beyond the point of approximating a RCT, it can paradoxically exacerbate covariate imbalance and confounding.²⁶ Other disadvantages include limited generalizability and decreased statistical power due to exclusion of patients. However, this loss of power is counterbalanced by increased precision of comparing the matched pair of treated and untreated patients.

Best practices and caveats

The choice of matching algorithm (optimal or greedy), use of caliper (maximum difference in PS allowed within a matched pair), matching ratio of treated-to-untreated patients, and matching with or without replacement can affect matching samples and treatment effect estimates.^27,28 Refer to a review paper for further explanation of matching analysis.²⁹ The emphasis is placed on finding the approach that achieves the best covariate balance. Using a smaller caliper achieves better covariate balance and less bias, but it reduces the number of matched pairs. Statistical methods appropriate for matched data may be used (e.g., paired t-test, McNemar test, or regression adjustment for the matching variable).^30,31 However, when one is interested in estimating the treatment effect at the population level instead of individual matched-pair level, simply analyzing data without consideration of matching process is also acceptable.²⁹ Standard bootstrap-based standard errors of treatment effect may not provide valid inference in the matched sample.³²

Case study. Of the 1706 treated and 2483 untreated patients, 1337 untreated patients were matched to the treated patients using a 1:1 nearest neighbor matching without caliper (Table 1).¹ Note the matched cohort had characteristics (e.g., chronic obstructive pulmonary disease, 28%) that were more comparable to those of treated patients (27%) than untreated patients (32%). After PS matching, ACEI use was associated with a modest reduction of the composite endpoint (hazard ratio [HR]: 0.91; 95% CI: 0.84-0.99), as opposed to the larger unadjusted HR 0.84 (95% CI: 0.78-0.90). This estimated HR in the PS-matched sample reflects ATT.

3.2. Weighting

PS weighting adjusts for confounding by weighting treated and untreated patients using PS-based weights to make the treatment groups similar, rather than creating individual matches as in PS matching. This procedure is analogous to a survey sampling in which each participant is given a specific weight to represent the population from which the participant was sampled. Treatment effects are estimated using a weighted regression. A commonly used weight is the inverse of the probability of receiving the treatment that they actually received: this probability equals PS for treated patients, whereas it equals 1-PS for untreated patients. Thus, the weight (w) to estimate ATE is $w=\frac{1}{\mathit{PS}}$ for treated patients and $w=\frac{1}{1-\mathit{PS}}$ for untreated patients. Alternatively, the weight to estimate ATT is w = 1 for treated patients and $w=\frac{\mathit{PS}}{1-\mathit{PS}}$ for untreated patients; this kind of weighting is also sometimes called weighting by the odds or standardized mortality/morbidity ratio weighting. Advantages of PS weighting are that more patients are analyzed (as opposed to matching that excludes unmatched patients) and the method can be extended to account for censoring and time-dependent confounding.^33,34 A disadvantage is that the results can be sensitive to the influence of extreme weights.

Best practice and caveats

A small number of patients who had very low probability of receiving the treatment they actually received (i.e., treated patients with very low PS and untreated patients with very high PS) may dominate the weighted analysis and result in biased or imprecise estimates of treatment effect. Because extreme weights may result from PS model misspecification, one should attempt to improve the PS model by including interaction or non-linear terms³⁵ or using machine learning methods.^10,36 Weights that are above or below certain thresholds are often replaced with the threshold values (“weight trimming or truncation”),³⁷ but such practice is no longer considered a best practice.³⁵ Stabilized weights have been proposed to improve precision of treatment effect estimates.³³

3.3. Stratification

Patients are ranked based on their PS and stratified into mutually exclusive, equal-size subsets. Within each stratum, treated and untreated patients have similar PS and, therefore, the distribution of confounders is likely to be similar. Assuming that treatment effects remain constant across strata, stratum-specific treatment effects can be pooled into a weighted average.⁴ When strata are weighted based on the number of patients in each stratum, ATE is estimated; when strata are weighted based on the number of treated patients in each stratum, ATT is estimated. Advantages include transparency in presentation (i.e., confounder balance can be explicitly shown for each stratum) and straightforward analysis. A disadvantage is that stratification may not be as effective in achieving covariate balance as matching or weighting.²⁴ If stratum-specific treatment effects are not constant, they cannot be pooled. Furthermore, it is not possible to determine whether stratum-specific treatment effects reflect true variation or different amount of residual confounding due to imbalance in covariates within strata.^22,38

Best practices and caveats

An increased number of strata (e.g., 5-10 strata) generally result in better covariate balance within strata and larger bias reduction. If imbalance persists for some covariates within each stratum, those variables can be included in the regression model to estimate stratum-specific treatment effects. Before pooling stratum-specific effects, one should examine whether the treatment effect across PS strata remains constant.

3.4. Covariate adjustment in regression models

PS or its function (e.g., splines) can be included in the outcome regression model as a covariate; this method estimates ATE. The risk of this approach is that misspecification of the PS-outcome association in the regression model can lead to biased results. It is difficult to predict this association from prior knowledge, as the PS contains information from multiple confounders. Compared with other PS methods, this method does not allow evaluation of confounder balance and often includes individuals outside the range of PS overlap in whom treatment effect cannot be estimated. Due to these limitations, covariate adjustment is not considered a best practice.

4. PS Analysis vs. Regression Modeling for Confounding Adjustment

PS analysis and regression modeling generally give comparable results,^39-41 but PS analysis offers advantages in certain situations.^17,41,42 First, it is often easier to specify how confounders are related to the treatment (PS analysis) than how confounders are related to the outcome (regression modeling). Misspecified PS model tends to cause less bias than misspecified outcome model.⁴³ Second, PS analysis seems to perform better than regression modeling when the number of confounders is large relative to the number of outcome events.^44,45 Third, the examination of PS distribution between the treatment groups allows one to explicitly identify the population in whom treatment effect is estimated. In regression modeling that does not allow such examination, the results may be based on extrapolation beyond what data can support.²⁹ Finally, PS matching and weighting separates the “design” (i.e., creating a balanced cohort) from the “analysis” (i.e., estimating the treatment effect), which allows more transparent analysis and limits data exploration.^46,47

5. Strategies to Address Unmeasured Confounding

Because PS analysis can only adjust for measured confounders, it is critical to discuss the likely direction and magnitude of unmeasured confounders in interpreting the results from PS analysis. An overview of strategies to address unmeasured confounding is available elsewhere.^48,49 This section introduces 2 methods that are easy to implement in conjunction with PS analysis: active comparator design and sensitivity analysis for unmeasured confounding.

5.1. Active comparator design

Patients who initiate and adhere to a treatment may have different health-seeking behaviors from those who are untreated.⁵⁰ Therefore, a non-randomized comparison of treated vs. untreated patients is likely to be confounded by such characteristics that are not readily measured. Instead of untreated patients, the use of patients who receive an alternative active treatment as a comparison group can effectively minimize the difference in such characteristics. Ideally, the comparison treatment should have similar indications to the treatment of interest (e.g., typical vs. atypical antipsychotics).⁵¹ Active comparator design is a form of restriction that is generally more effective in minimizing confounding than statistical adjustment.⁵² Limitations include decreased sample size, limited generalizability, and difficulty in finding an appropriate comparison treatment.

5.2. Sensitivity analysis for unmeasured confounding

The impact of a binary confounder depends on its prevalence in the treated group and untreated group and the confounder-outcome association. One can estimate what the true treatment effect would be by assigning the prevalence of an unmeasured binary confounder and its association with the outcome in a mathematical equation.⁴⁸ One can also show how much confounding can fully explain the observed treatment effect, and discuss how likely such an unmeasured confounder exists. If there is another dataset that contains data on the treatment and unmeasured confounders in the main dataset, the prevalence of unmeasured confounder in the treated and untreated groups can be directly estimated from this dataset (see published examples^53-56). A similar approach can be applied to continuous confounders.⁵⁷ However, these methods do not account for joint distribution among measured and unmeasured confounders.⁴⁸ Alternatively, one can estimate the effect of treatment on an outcome that is known to be unaffected by the treatment: if the estimated effect is null, unmeasured confounding is unlikely.

Case study. The investigators showed that the observed HR could be explained by an unmeasured strong risk factor that would increase the odds of receiving ACEI by 1%. It suggests that the results are somewhat sensitive to unmeasured confounding.¹

6. Conclusions

PS analysis is a useful technique to reduce confounding in observational studies and offers several advantages over regression modeling in certain situations. Although confounding is a major threat to validity of observational studies, minimizing other types of bias, such as measurement error and selection bias, is also important. In this paper, we explained the concepts, assumptions, pitfalls, and current best practices in PS analysis (Table 3). Since PS analysis methods are evolving, best practices may change in the future. Nonetheless, the concepts discussed in this review can help clinical researchers broaden their understanding about PS analysis.

Table 3. Considerations and Recommendations for Propensity Score Analysis.

Item	Steps	Considerations and Recommendations
1	Estimation of PS
1.1	Identify potential confounders	Use subject-matter knowledge; do not rely on statistical criteria alone (e.g., p-value). Instrumental variables and intermediate variables should not be included in the PS model.
1.2	Estimate PS	Logistic model is typically used; other machine learning techniques can be used alternatively. Model continuous variables in more flexible terms (e.g., multiple categories or splines). Consider clinically plausible interactions (e.g., interaction between confounders and time period). Avoid modeling strategies to build a best prediction model for treatment status; the main purpose of PS is to balance potential confounders between treated and untreated patients.
1.3	Evaluate PS model	Use standardized difference, not significance testing (e.g., p-value), to assess balance in potential confounders between treated and untreated groups with similar PS values. Examine the distribution of PS between treated and untreated groups to assess the extent of overlap. C statistics do not inform whether PS models are correctly specified or include all confounders.
2	Estimation of treatment effect *
2.1	PS matching
2.1.1	Match untreated patient to treated patient based on PS	Matching algorithm: nearest neighbor matching vs. optimal matching, 1:k (k≥1) matching ratio, caliper (maximum difference in PS allowed within a matched pair), and matching with or without replacement. Choose the matching algorithm that results in the best covariate balance between the treatment groups.
2.1.2	Evaluate balance in potential confounders	Use standardized difference, not significance testing (e.g. p-value), to assess covariate balance in the PS-matched sample.
2.1.3	Estimate treatment effect	Consider using appropriate statistical methods for matched data (e.g., paired t-test and McNemar test). When one is interested in estimating the treatment effect at the population level instead of individual matched-pair level, simply analyzing data ignoring matching process is acceptable.
2.2	PS weighting
2.2.1	Estimate PS-based weights	Present the distribution of weights; pay attention to extreme weights. If extreme weights are present, check misspecification of PS logistic model; consider alternative methods for weight estimation or trimming to minimize the influence of extreme weights. Consider stabilized weight to improve precision of treatment effect estimate.
2.2.2	Estimate treatment effect	Use a weighted regression to estimate the treatment effect.
2.3	PS stratification
2.3.1	Create PS strata	Typically, 5 strata are used; increased number of PS strata leads to larger bias reduction.
2.3.2	Evaluate balance in potential confounders	Use standardized difference, not significance testing (e.g. p-value), to assess confounder balance within each PS stratum.
2.3.3	Estimate treatment effect	Estimate the stratum-specific treatment effect. Lack of constant treatment effect across strata indicates true treatment effect variation by PS or residual confounding within the stratum. Calculate a weighted average of stratum-specific treatment effects if there is constant treatment effect across strata.

Abbreviations: ATE, average treatment effect; ATT, average treatment effect in the treated; PS, propensity score.

^*Covariate adjustment is omitted because it is no longer considered a best practice.

APPENDIX. An Example of Propensity Score Model

A logistic model can be developed using the treatment indicator as outcome and baseline covariates and their interaction terms as predictors (see the equation below).⁷

$$\ln \frac{\mathrm{Pr}(A=1)}{1-\mathrm{Pr}(A=1)}={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_k{X}_k+\cdots +{\beta }_{k+l}{X}_m{X}_n$$

where A = treatment (1: yes, 0: no); X₀ to X_k = k covariates at baseline; X_mX_n = interaction terms between X_m (1 ≤ m ≤ k) and X_n(1 ≤ n ≤ k); and β₁ to β_{k + l} = coefficients for k main-effect terms and l interaction terms estimated from the dataset.