A Quantitative Model for cAMP Binding to the Binding Domain of MloK1

Abstract

Ligand-protein binding processes are essential in biological systems. A well-studied system is the binding of cyclic adenosine monophosphate to the cyclic nucleotide binding domain of the bacterial potassium channel MloK1. Strikingly, the measured on-rate for cyclic adenosine monophosphate binding is two orders of magnitude slower than a simple Smoluchowski diffusion model would suggest. To resolve this discrepancy and to characterize the ligand-binding path in structural and energetic terms, we calculated 1100 ligand-binding molecular dynamics trajectories and tested two scenarios: In the first scenario, the ligand transiently binds to the protein surface and then diffuses along the surface into the binding site. In the second scenario, only ligands that reach the protein surface in the vicinity of the binding site proceed into the binding site. Here, a binding funnel, which increasingly confines the translational as well as the rotational degrees of freedom, determines the binding pathways and limits the on-rate. From the simulations, we identified five surface binding states and calculated the rates between these surface binding states, the binding site, and the bulk. We find that the transient binding of the ligands to the surface binding states does not affect the on-rate, such that this effect alone cannot explain the observed low on-rate. Rather, by quantifying the translational and rotational degrees of freedom and by calculating the binding committor, our simulations confirmed the existence of a binding funnel as the main bottleneck. Direct binding via the binding funnel dominates the binding kinetics, and only ∼10% of all ligands proceed via the surface into the binding site. The simulations further predict an on-rate between 15 and $40\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$, which agrees with the measured on-rate.

Introduction

Ligand-protein binding is essential for many biological systems, e.g., immune response (1, 2), enzymatic activity, or signaling (3, 4). An important class of ligands involved in many signaling pathways are cyclic nucleotides, such as cyclic adenosine monophosphate (cAMP) (4, 5, 6, 7), which bind to a cyclic-nucleotide-binding domain (CNBD) and regulate cyclic-nucleotide-gated (CNG) channels (4, 8).

An experimentally well characterized system is the potassium channel MloK1 and its CNBD of the bacterium Mesorhizobium loti (9, 10, 11, 12, 13). X-ray (14) and NMR (15, 16) structures revealed two different conformations for the cAMP-bound and cAMP-free CNBDs. This conformational change controls ion conductivity, which has been shown to be higher in the ligand-bound conformation (14). The complete binding process thus involves the ligand-protein encounter, including the ligand’s path into the binding site, and a conformational change of the protein. Here, we focus on the ligand-protein encounter and, in particular, the kinetics of this process.

The on-rate of the ligand-binding process has been measured by Peuker et al. (17) via stopped-flow experiments using the CNBD of MloK1 and a dye-labeled analog of cAMP, 8-NBD-cAMP. The fluorescence of 8-NBD-cAMP is low in aqueous solvents and high in the hydrophobic environment of a binding pocket. The increase of fluorescence after rapid mixing yielded an on-rate coefficient of $k_{\text{on}}=26\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$ (17). This on-rate is strikingly slow. In fact, a simple radial diffusion model (18) would predict an on-rate that is faster by more than two orders of magnitude. Vice versa, for a diffusion model to agree with the observed on-rate, an unrealistically small radius of the binding site of ∼10 pm would be required.

To resolve this striking discrepancy, and to develop a theoretical model of the binding process, we considered two possible scenarios. First, the ligand may initially bind to the protein surface (or at least certain parts thereof) and subsequently, in a second step, diffuse along the surface toward and into the binding site. In this scenario, the low on-rate would be caused by transient and unproductive ligand trapping at the surface and governed by the rates for surface diffusion and surface detachment. In the second scenario, only ligands that reach the protein surface in the vicinity of the binding site proceed into the binding site. We assume here that a binding funnel, which increasingly confines the translational and rotational degrees of freedom of the ligand, determines the binding pathways and the on-rate. Such binding funnels have been discussed and observed previously (19, 20), as have various models of ligand binding within the scope of enzyme reaction kinetics (21, 22, 23). However, no quantitative theory that connects simulation, experiment, and structure has so far been achieved.

To differentiate between these two possibilities, we carried out 1100 spontaneous ligand-binding molecular dynamics (MD) simulations (20, 24, 25, 26, 27) to the ligand-free CNBD, each starting from unbound solvated cAMP. From these simulations, we estimated rates for transitions between the bulk phase, surface states, and the binding site. Taken together, this set of rates establishes that transient surface binding and diffusion does not markedly slow down binding kinetics. Rather, transitions from the bulk directly into the binding site via a narrow funnel constitute the dominant binding pathway. We characterized this pathway by translational and rotational ligand confinement as well as by the committor function for ligand binding. This model predicts a ligand-binding on-rate, which agrees with the measured rate. Thus, a quantitative microscopic picture of cAMP binding to the CNBD of MloK1 is obtained that explains the measured on-rate and resolves the above discrepancy.

Materials and Methods

MD simulations

Simulation parameters

All simulations were carried out using the Gromacs 4.6 simulation package (28, 29, 30). In all simulations, the Amber99sb (31) force field was used together with the TIP3P water model (32). Electrostatic interactions were calculated using particle-mesh Ewald (33) with a real-space cut-off distance of 1.2 nm, a grid spacing of 0.145 nm, and cubic interpolation. van der Waals interactions were cut off at 1.2 nm. Nonbonded interactions were calculated using Verlet neighbor lists (34). The Verlet buffer was chosen such that the maximal error for pair interactions was <$0.005\text{kJ}{\text{mol}}^{-1}{\text{ps}}^{-1}$. All simulations were performed in the constant temperature, pressure, and particle-number ensemble using the velocity-rescaling method (35) for temperature coupling with a heat-bath temperature of 300 K and a coupling time constant of 0.1 ps, and Berendsen pressure coupling (36) with a reference pressure of 1000 hPa and a respective time constant of 1 ps. Cubic simulation boxes and periodic boundary conditions were used for all simulations. All atom bonds were constrained using the LINCS algorithm (37). Additionally, fast fluctuations of angles defined by at least one hydrogen atom were removed by changing the respective hydrogen atoms into virtual sites and fixing the angle (38). The equations of motion were integrated using the Verlet algorithm (34) with a 4 fs time step. In all simulations, sodium chloride ions were added at a concentration of 113 mM.

Ligand parametrization

Force-field parameters for unprotonated cAMP were calculated using the general Amber force field (39) and the antechamber toolkit (40). Atomic point charges were obtained in a restrained fitting procedure such that the resulting electrostatic potential fits best to the electrostatic potential generated by the electronic wave function (restrained-electrostatic-potential charges) (41). The wave function was calculated with Gaussian03 software (42) at a Hartree-Fock level using the 6-31G^∗ basis set. A convergence criterion of ${10}^{-8}$ was applied for the self-consistent field calculations; six points per unit area were calculated in the electrostatic potential fit. Before the calculation of the electronic wave function, a geometry optimization of the molecule was performed.

Modeling of the protein structure

All simulations of ligand binding to the CNBD were based on the R384A mutant (PDB: 1U12) (14) of the CNBD. The mutation was reverted by replacing residue Ala384 with Arg384 and the missing atoms were added using the Modeler 9v10 software (43).

Simulation setup

A total of 900 “high-ligand-concentration” simulations, each 200 ns long, of solvated cAMP and CNBD were carried out using a cubic simulation box with a box length of 7 nm. In each of the simulations, a single cAMP molecule was placed in random orientation at a random position, avoiding overlap with the protein. In addition, 99 simulations, each 300 ns long, and 99 simulations, each 200 ns long, were carried out using a cubic simulation box with a box length of 14 nm. In the latter two sets of simulations (“low-ligand-concentration simulations”), ligand molecules were placed in random orientation on random points on a sphere at a distance of 6.5 nm around the center of the protein.

Data analysis

Surface-flow model

Markov state model. The stationary probability distribution of the positions of the ligand centers of mass (COMs) was determined from a Markov state model (44, 45). To build this model, the set of high-ligand-concentration simulations was used. To that aim, all ligand trajectories were translated and rotated such that the position and orientation of the CNBD was fixed. Subsequently, the ligand’s COM position space was discretized, using ${30}^3=\mathrm{27,000}$ bins, each with a volume of $V={\left(0.4\text{nm}\right)}^3$.

The count matrix was calculated using a lag time of 60 ns as an empirical trade-off between statistical convergence and small memory effects. After converting this count matrix into a transition matrix, the first left eigenvector, representing the stationary probability distribution, was calculated. Neighboring bins in which the COM position probability was >1.1% were identified as surface binding states. This cutoff was chosen as a trade-off between separability of the states and high population coverage. The cutoff distance, $d_{\text{surface}/\text{bulk}}$, which separates surface states from bulk states, was considered as a free parameter, and therefore, all rates were calculated for several values of this parameter.

Determination of rates and rate coefficients. From the set of high-ligand-concentration simulations, rates were calculated for transition between the surface states (including the binding site) via the rest of the protein surface (i.e., without intermediate unbinding or transitions through other surface states) as well as for unbinding into the bulk. All rates were determined from the average waiting time of the respective transition. The rate coefficients, $\left\{k_i\right\}$, for transitions from the bulk into the surface states, $\left\{i\right\}$, including the binding site, were estimated from the product of the surface-attachment rate coefficient,

$$k_{\text{bulk}\to \text{surface}}=4\pi N_{\text{A}}Dr,$$ (1)

and the probabilities, $p_i$, of entering state i. Here, $D=0.44\times {10}^{-9}{\text{m}}^2{\text{s}}^{-1}$ is the diffusion coefficient of cAMP (46), $r=2.2\text{nm}$ is the protein radius, estimated from the structure, and $N_{\text{A}}$ is the Avogadro constant.

We estimated the uncertainty of the protein radius as ${\sigma }_r=0.3\text{nm}$ and that of the diffusion coefficient as ${\sigma }_{\text{D}}=0.03\times {10}^{-9}{\text{m}}^2{\text{s}}^{-1}$. The latter uncertainty was derived from the difference between the measured and geometrically expected diffusion coefficients (46). The resulting error range of $k_{\text{bulk}\to \text{surface}}$ is thus

$${\sigma }_{k_{\text{bulk}\to \text{surface}}}=4\pi N_{\text{A}}\sqrt{D^2{\sigma }_r^2+r^2{\sigma }_{\text{D}}^2}.$$ (2)

All transition probabilities, $p_i$, were determined from the frequencies of transitions, as observed in the trajectories, from the bulk ($p_{\text{bulk}\to {\text{state}}_i}$, $p_{\text{bulk}\to \text{surface rest}}$) and from the remaining surface ($p_{\text{surface rest}\to {\text{state}}_i}$, $p_{\text{surface rest}\to \text{bulk}})$. Using these counts,

$$k_i=k_{\text{bulk}\to \text{surface}}\times \underset{p_i}{\underbrace{\left(p_{\text{bulk}\to {\text{state}}_i}+p_{\text{bulk}\to \text{surface rest}}\times p_{\text{surface rest}\to {\text{surface state}}_i}\right)}}.$$ (3)

Comparison of surface binding and diffusion. To test whether transitions of the ligand from the bulk phase to the protein surface are controlled by diffusion, we determined for all low-concentration MD simulations the time of the first ligand-protein contact. To this aim, the simulation time-dependent fraction, ${\tilde{p}}_{\text{nonbinding}}\left(t\right)$, of no-surface-contact occurrence was determined. The probability predicted by a Smoluchowski model (18) was calculated via

$$p_{\text{nonbinding}}\left(t\right)=\text{exp}\left[-\frac{4\pi Dr}{V}\times t\left(1+\frac{2r}{\sqrt{\pi Dt}}\right)\right].$$ (4)

Here, $D=1.42\times {10}^{-9}{\text{m}}^2{\text{s}}^{-1}$ is the diffusion coefficient of cAMP in TIP3P water observed in the MD simulations, $r=2.2\text{nm}$ is the approximate protein radius, and $V=2744{\text{nm}}^3$ is the simulation box volume. D was determined independently using the average squared COM displacement in bulk water over time during the simulations.

Determination of the effective on-rate coefficient. The mean first-passage time for transitions from the bulk phase to the binding site was calculated using the group general inverse (47) for different ligand concentrations. This calculation was carried out 1) for the full set of rates, 2) for an alternative scenario in which the rate for direct transitions from the bulk to the binding site is zero (meaning binding is limited to the surface diffusion pathway), and 3) for an alternative scenario in which the rate for direct transitions from the bulk to the binding site equals the Smoluchowski rate. The effective rates $k_{\text{on}}$ and $k_{\text{surface diffusion}}$ were calculated as the inverse of the mean first-passage time.

Binding-funnel parameters

To describe how the ligand proceeds toward the binding site, the ligand root mean-square deviation (RMSD) to the bound-state configuration (which we refer to as the “binding-site RMSD”) was chosen as a reaction coordinate, subsequently denoted by x. The bound-state configuration was extracted from the x-ray structure of the cAMP-bound CNBD (PDB: 1VP6) (14).

Translational confinement. To estimate the radius of the effective target sphere, we identified those configurations for which similar configurations were sampled in all other trajectories for which successful ligand binding occurred. To that end, first a pairwise ligand RMSD matrix was calculated for all pairs of trajectories for which ligand binding occurred. These matrices were then used to identify, for every ligand-configuration snapshot and for every ligand-binding trajectory, a “neighborhood cloud.” The latter thus consists of the set of ligand configurations—one for each binding trajectory—that has the smallest RMSD from the reference configuration. The spatial extension of each neighborhood cloud was defined as the maximal pairwise distance between the COMs of two neighborhood-cloud members. Finally, all ligand configurations were binned according to their RMSD from the binding site. For each bin, a “target sphere radius”, $r\left(x\right)$, was determined from the smallest neighborhood-cloud radius.

Rotational confinement. The rotational confinement was estimated from the scatter of the major orientation axis of the ligand: For every binding site, the RMSD value of the corresponding structure ensemble was determined from the ligand-binding trajectories, as well as the solid angle covered by these configurations.

To that end, all structures with a particular reaction coordinate x were extracted from the ligand-binding trajectories, and the vector defined by the phosphor atom and the nitrogen atom closest to the amino group was taken to represent the major axis of the molecule. Of the resulting ensemble of vectors, the central vector, as well as the angular deviation, ${\alpha }_i\left(x\right)$, from the central vector, were determined as a function of the reaction coordinate. The solid angle, $\text{Ω}\left(x\right)$, of the cone was then estimated from the mean of this angle distribution, plus one standard deviation of the angle distribution,

$$\text{Ω}\left(x\right)={\text{sin}}^2\frac{\text{E}\left(\left\{{\alpha }_i\right\}\left(x\right)\right)+\sqrt{\text{Var}\left(\left\{{\alpha }_i\right\}\left(x\right)\right)}}{2}.$$ (5)

Note that for an isotropic and uniform angle distribution, $\text{Ω}=0.9$. The same procedure was applied to the whole set of trajectories, irrespective of whether binding actually occurred. Also note that since the target sphere is located on the protein surface, it is only accessible from half of all possible access directions. This confinement, which corresponds to a rotational confinement of the protein, is taken into account by introducing a factor of 0.5 into the rotational confinement.

Binding committor. Binding committors $p\left(\text{bind}|x\right)$ along the reaction coordinate x, i.e., the probability that binding occurs before unbinding from the funnel, were calculated from the whole set of binding trajectories. Here, binding and unbinding were defined by crossing a lower threshold, $x_{\text{bound}}$, and an upper threshold, $x_{\text{unbound}}=1.0\text{nm}$, respectively. For $x_{\text{bound}}$, several values between 0.1 nm and 0.6 nm were considered. Binding and, similarly, unbinding committors were calculated for several values of the reaction coordinate x between $x_{\text{bound}}$ and $x_{\text{unbound}}$, as well as for all trajectories, by monitoring whether the system subsequently first crossed the threshold $x_{\text{bound}}$ or $x_{\text{unbound}}$.

Brownian dynamics in a one-dimensional model landscape

The committor functions determined from our MD simulations were compared with committor functions obtained from Brownian dynamics (BD) simulations in an inverted harmonic potential, $U=-(\alpha /2){\left(x-x_{\text{barrier}}\right)}^2$. All BD trajectories were generated by integrating the overdamped stochastic dynamics equation of motion using the Euler-Maruyama method. The BD simulations were aborted whenever $x\left(t\right)$ exceeded $x_{\text{unbound}}=1\text{nm}$ or dropped below $x_{\text{bound}}$. Starting positions, $x_0$, were varied between $x_{\text{bound}}$ and $x_{\text{unbound}}$, and 5000 simulations were carried out for each starting position. This procedure was repeated for 11 different values for $x_{\text{bound}}$ between 0.1 nm and 0.6 nm.

Counts of how often $x_{\text{bound}}$ and $x_{\text{unbound}}$ were crossed ($n_{\text{bind}}$ and $n_{\text{unbind}}$, respectively) yielded committors in a similar way as done in the analysis of the MD simulations. To quantify the similarity between MD and BD committors, a measure

$$\epsilon \left(\alpha ,x_{\text{barrier}}\right)=\sum _{\text{lower}\text{cut}-\text{off}}\sum _{\left\{x_i\right\}}\left[\text{log}\left(\frac{n_{\text{unbind}}\left(x_i;\alpha ,x_{\text{barrier}}\right)}{n_{\text{bind}}\left(x_i;\alpha ,x_{\text{barrier}}\right)}\right)-\text{log}\left(\frac{p_{\text{unbind}}\left(x_i\right)}{p_{\text{bind}}\left(x_i\right)}\right)\right]$$ (6)

was calculated for force constants α ranging from $5\text{kJ}{\text{mol}}^{-1}{\text{nm}}^{-2}$ to $30\text{kJ}{\text{mol}}^{-1}{\text{nm}}^{-2}$, as well as for “transition state” maxima, $x_{\text{barrier}}$, between 0.2 nm and 0.8 nm. Finally, the pair α and $x_{\text{barrier}}$ yielding the best agreement with the acMD committors (smallest ε) was determined.

Results and Discussion

Binding in a Smoluchowski model

A first analytical estimate for the on-rate of ligand binding is given by the Smoluchowski model (18). This model assumes only radial diffusion toward an absorbing spherical surface and yields an on-rate coefficient of $k_{\text{on}}=4\pi N_{\text{A}}Dr$. Here, D is the diffusion coefficient of the ligand, r is the protein radius, and $N_{\text{A}}$ is the Avogadro constant.

One critical assumption in this model is that all ligands that reach the protein surface rapidly enter the binding site, i.e., the entire protein surface represents the absorbing sphere. With a protein radius of $r=\left(2.2\pm 0.3\right)\text{nm}$ and a cAMP diffusion coefficient of $D=\left(0.44\pm 0.03\right)\times {10}^{-9}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ (46), the on-rate would be $k_{\text{on}}=\left(7300\pm 1100\right)\mu {\text{s}}^{-1}{\left(\text{mol}/\text{l}\right)}^{-1}$, by far exceeding the experimentally obtained value of $26\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$. Vice versa, for the Smoluchowski model to yield the measured on-rate, one would have to assume an absorbing surface, representing the binding site, with a radius of 10 pm, which also seems unrealistic.

Mesoscopic binding model

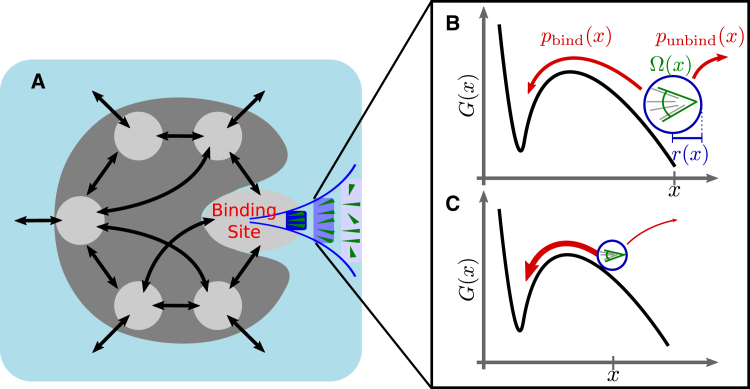
To resolve this discrepancy, we developed a more detailed, Markov-type model of the binding process, depicted schematically in Fig. 1. Such a model should also enable us to estimate the relative contributions of surface-diffusion pathways versus direct binding to the total on-rate coefficient. As indicated in Fig. 1 A, the model involves several substates and transitions (arrows) between these substates. As relevant substates, we considered a) ligand in bulk (light blue), b) ligand bound to one of several regions of the protein surface (dark gray), and c) ligand in the binding site. The model also includes a “funnel” toward the binding site (Fig. 1, B and C), which will be explained below. By design, the model describes the two above scenarios as limiting cases: in the surface-diffusion model, where the ligand binds to surface regions and then diffuses along the surface into the binding site, the flux through the funnel should be small with respect to the flux through the surface states; vice versa, in the funnel model, the flux via the direct binding funnel should dominate. Comparison of these two fluxes, therefore, should allow discriminating between these two models. Comparison of a Smoluchowski model including surface trapping and diffusion with the simple Smoluchowski model should, further, identify the main cause of the observed drastically reduced binding rate.

Figure 1.

(A) Mesoscopic binding model (schematic) consisting of the bulk (light blue), the binding site, and multiple surface (light gray) substates, as well as transitions between them (black arrows). Ligands bind either via the surface states or directly to the binding site. For the latter option, a binding funnel (blue sketch) is proposed. (B and C) In the funnel model, the on-rate is given by diffusion toward a translationally (blue) and rotationally (green) confined target volume (blue circle) near the binding site, combined with the probability, $p_{\text{bind}}\left(x\right)$, of crossing the remaining free-energy barrier (red arrow). The rate is independent of the position, x, of the target volume (blue circle) if the lower rate to reach a smaller target volume (C, blue circle) is compensated by a higher probability of overcoming the remaining barrier (C, thick red arrow). To see this figure in color, go online.

To calculate the required states and rates, 1100 binding simulations from random starting positions in the bulk were carried out as described in Materials and Methods. In these simulations, many direct ligand-binding events, as well as events of binding via the protein surface, were both observed, indicating that our general model is indeed adequate.

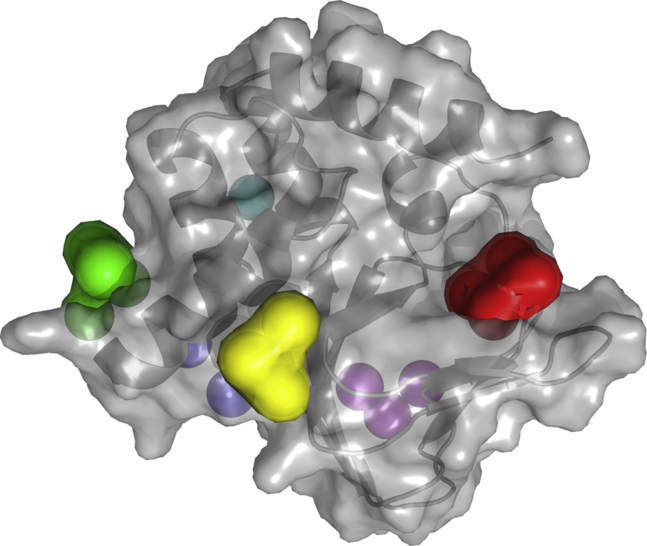
To identify suitable surface states, we built a Markov model (44, 45) by binning the ligand’s COM position into a grid of 30 $\times$ 30 $\times$ 30 cubes of 0.4 nm size and by counting transition frequencies between pairs of these “microstates” as described in Materials and Methods. The first eigenvector of the resulting transition matrix was used to estimate the stationary probability distribution. Closer analysis of this surface distribution revealed five major well-separated maxima, which we considered as relevant surface states, in addition to the binding site (Fig. 2).

Figure 2.

Locations of the binding site (red) and surface-binding states. The stationary probability distribution of the ligand position revealed six distinct maxima. These maxima were identified as the binding site (red) and surface-binding states (yellow, green, blue, cyan, and magenta). To see this figure in color, go online.

Next, we calculated from the set of MD trajectories all rates and rate coefficients between bulk phase, the five surface states, and the binding site, from the respective average waiting times (see Materials and Methods). Note that the exact definition of a surface-bound state is somewhat arbitrary, and the calculated rates will vary depending on the particular choice of the cutoff value, $d_{\text{surface}/\text{bulk}}$. To capture to what extent this ambiguity affects the obtained rates, we treated this surface-bulk cutoff as a free parameter and determined all rates for various values in the range 0.7–1.35 nm, centered around the approximate size of the ligand.

As described in Materials and Methods, each of these rate coefficients, $k_i$, was calculated as the product of the surface attachment rate coefficient, $k_{\text{bulk}\to \text{surface}}$, and the transition probability, $p_i$, to the respective state i. The former, $k_{\text{bulk}\to \text{surface}}=\left(7300\pm 1100\right)\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$, was calculated from the Smoluchowski model (compare Eqs. 1 and 2) assuming a protein radius of $2.2\pm 0.3\text{nm}$, which was estimated from the structure. To test whether the (long-time) behavior is actually described by a single rate coefficient, we first tested whether the binding from the bulk to the entire surface is determined by diffusion only, in which case the Smoluchowski model should provide an accurate description.

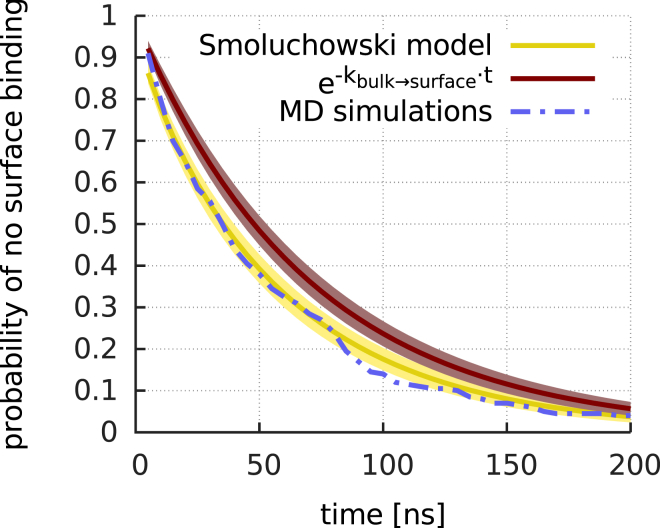
To that end, Fig. 3 compares the (time-dependent) fraction, ${\tilde{p}}_{\text{nonbinding}}\left(t\right)$, of molecules that have not yet bound to the protein surface at time t, determined from all binding trajectories of the low-concentration simulations, with the probability, $p_{\text{nonbinding}}\left(t\right)$, expected from Eq. 4. Given that no fit parameters were used (the diffusion coefficient, D, was determined from independent simulations), the agreement is remarkable and justifies the use of the Smoluchowski model for calculating $k_{\text{bulk}\to \text{surface}}$.

Figure 3.

Surface binding is dominated by diffusion. Shown are the fraction of trajectories where, until the specified time, no surface contact occurred, ${\tilde{p}}_{\text{nonbinding}}\left(t\right)$ (blue dashed line); the expected fraction from the full Smoluchowski model, $p_{\text{nonbinding}}\left(t\right)$ (yellow; cf. Eq. 4); and the fraction predicted by the long-time approximation of the Smoluchowski model, $\text{exp}\left(-k_{\text{bulk}\to \text{surface}}\times t\right)$ (brown). The depicted error ranges indicate the statistical uncertainty due to the finite number of MD trajectories. To see this figure in color, go online.

Notably, because our simulations capture the binding statistics only on relatively short timescales, inclusion of the initial influx term in Eq. 4 beyond the long-time limit, $k_{\text{bulk}\to \text{surface}}\approx 4\pi N_{\text{A}}Dr$ (Fig. 3, brown line), is essential. Combined with transition frequencies, $p_i$, which were also calculated from the binding trajectories, the effective rate coefficients, $k_i$, were estimated.

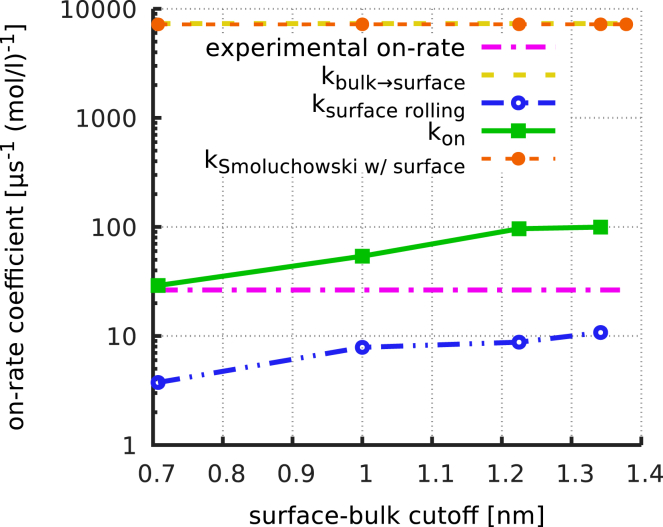
With these rates and their dependence on $d_{\text{surface}/\text{bulk}}$ at hand, we can now compare the contributions of surface diffusion and direct binding to the total on-rate coefficient. To that end, all rates and rate coefficients were combined into an effective on-rate coefficient, $k_{\text{on}}\left(d_{\text{surface}/\text{bulk}}\right)$ (more precisely, a reciprocal mean binding time, as described in Materials and Methods), from the bulk into the binding site (Fig. 4, green line). To quantify the contributions of surface diffusion to $k_{\text{on}}$, the figure also shows the effective on-rate coefficient excluding the rate coefficient for direct bulk-to-binding-site transitions, $k_{\text{surface}\text{diffusion}}$ (Fig. 4, dashed blue line). Finally, to estimate the effect of only the surface-bound states on the binding rate, we have calculated from the Markov-type model by how much the Smoluchowski rate is affected by the presence of the surface-bound states (Fig. 4, dashed orange line)

Figure 4.

Surface diffusion versus direct binding. Shown are binding rates $k_{\text{on}}$ (green line) and $k_{\text{surface}\text{diffusion}}$ (blue dash-dotted line) as a function of the surface-state cut-off, $d_{\text{surface}/\text{bulk}}$. For comparison, $k_{\text{bulk}\to \text{surface}}$ from the simple Smoluchowski model (yellow dashed line) and a Smoluchowski model including transient surface-binding states (orange dashed line), as well as the measured on-rate coefficient (magenta dash-dotted line), are also shown. To see this figure in color, go online.

As expected, both $k_{\text{on}}$ and $k_{\text{surface}\text{diffusion}}$ vary within a factor of 3 for the different values of $d_{\text{surface}/\text{bulk}}$. Notably, the best agreement with the measured on-rate coefficient (Fig. 4, magenta line) is seen for the most restrictive definition of the surface state. Importantly, and independent of the particular choice of the surface-state definition, $k_{\text{surface}\text{diffusion}}$ is consistently almost 10 times smaller than $k_{\text{on}}$. Apparently, the contribution of surface diffusion to the overall on-rate is small, such that the dominant process is direct binding via the funnel. Further, because the binding rate of the Smoluchowski model is essentially unchanged by inclusion of the surface binding states and surface diffusion (Fig. 4, orange line), we conclude that the funnel is the main cause for the slow measured on-rate.

Binding-funnel model

This finding suggests that the observed slow binding should be accounted for by an appropriate funnel model. We will therefore derive such a funnel model from our MD simulations and test whether it correctly predicts the measured on-rate.

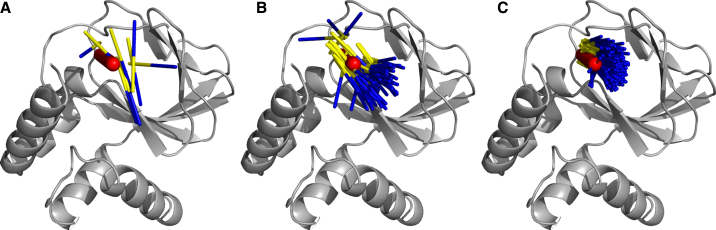
Visual inspection of ligand ensembles at three different binding reaction coordinates x (defined by RMSD to the bound configuration; see Fig. 5) readily reveals that during binding, the configurations of the ensembles become increasingly restricted and oriented. Apparently, binding occurs via gradual translational and rotational confinement, motivating the funnel model.

Figure 5.

Ligand ensembles for three different distances to the binding site, measured by their binding-site RMSD values of 0.8 nm (A), 0.6 nm (B),and 0.3 nm (C). The ligand configurations are drawn as colored sticks, showing their main orientation. The bound ligand configuration is shown in red. With decreasing RMSD, increasing translational and rotational confinement was observed, as described by the funnel model. To see this figure in color, go online.

This translational and rotational confinement implies an entropic cost. Combined with the enthalpic contribution from interactions with the binding site, this entropic cost leads to a free-energy barrier that may explain the experimental slow on-rate. To calculate the on-rate coefficient, $k_{\text{on},\text{funnel}}$, via the funnel from our simulations, we expressed the on-rate as a product of two factors, 1) the (diffusive) rate to reach a translationally and rotationally confined volume (Fig. 1, B and C, blue and green sketches), and 2) the probability, $p\left(\text{bind}\right)$, of overcoming the remaining free-energy barrier toward the binding site (Fig. 1 B, red arrows).

A study by Šolc and Stockmayer (48) showed that the rate coefficient to reach such a translationally and rotationally confined volume adopts the same form as that of the simple Smoluchowski model, albeit with an additional factor, $\text{Ω}\left(x\right)<1$, which describes the effect of the rotational confinement,

$$k_{\text{on},\text{funnel}}=4\pi N_{\text{A}}Dr\left(x\right)\times \text{Ω}\left(x\right)\times p\left(\text{bind}|x\right).$$ (7)

Here, the translational confinement within the binding funnel is described by a Smoluchowski term, $4\pi N_{\text{A}}Dr\left(x\right)$, where $r\left(x\right)$ (Fig. 1 B, blue circle radius) is the effective radius of the target volume at a given reaction coordinate x, here defined as the above RMSD of the ligand from its bound conformation.

Šolc and Stockmayer (49) also showed that rotational confinement of fast rotational degrees of freedom does not affect the on-rate. Because cAMP is roughly six times more extended along its main axis, we assume that rotation around the main ligand axis is fast with respect to the mean first-passage time from the target volume to the free-energy barrier and can thus be neglected. Hence, in Eq. 7, only the confinement of the orientation of the main axis (Fig. 1 B, green) is considered, approximated by the solid angle, $\text{Ω}\left(x\right)$, sampled by the ligand axis at a given reaction coordinate x within the binding funnel.

So far, no specific choice of x has been made. Indeed, we will assume that the on-rate given by Eq. 7 is independent of x for values of x outside the maximum of the binding free energy. Comparing Fig. 1, B and C, this assumption is plausible as long as, within this uphill part, there are no other contributions to the free-energy barrier. In this case, the slower rate to the more confined volume shown in Fig. 1 C is compensated by the increased probability of crossing the barrier.

To test whether the rate estimate (Eq. 7) is indeed independent of x, we quantified the confinement by determining $r\left(x\right)$, $\text{Ω}\left(x\right)$, and $p\left(\text{bind}|x\right)$ from our simulation data as functions of x; subsequently, we will calculate $k_{\text{on},\text{funnel}}$ via Eq. 7. Further, it will be tested whether a one-dimensional coordinate suffices to describe the binding kinetics.

Translational and rotational confinement

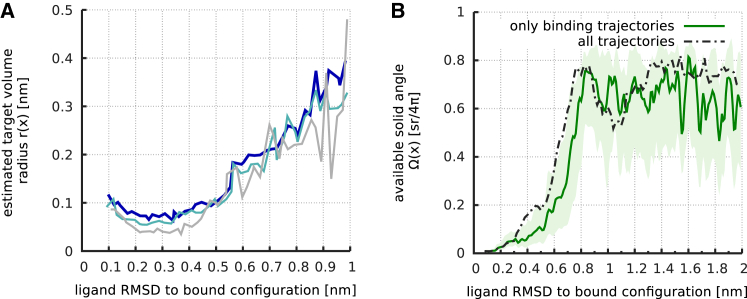
To quantify the translational confinement, we determined for every ligand configuration the most similar configuration, in terms of RMSD, among the other binding trajectories. The radius of the ensemble of COMs of these ligand configurations (see Materials and Methods), subesequently referred to as the “neighborhood-cloud” radius, serves as an estimate for $r\left(x\right)$ (Fig. 6 A, blue line). As can be seen, $r\left(x\right)$ decreases monotonously with decreasing binding-site RMSD x, which is consistent with the picture of a binding funnel.

Figure 6.

Translational (A) and rotational (B) confinement of the ligand during binding. (A) The blue line indicates the target radii, $r\left(x\right)$ (compare Fig. 1B, blue circle), during binding, estimated from the binding trajectories, as described in the text. The turquoise and gray lines show the same estimate using only 50% and 20%, respectively, of the binding trajectories as data. (B) Available rotational space, measured by the estimated solid angle, $\text{Ω}\left(x\right)$, formed by the major axes of an ensemble of ligand configurations. The accessible solid angle is shown for the subset of trajectories for which ligand binding occurs (green), as well as for the full set of trajectories (black dashed line). Due to the construction, a value of $\text{Ω}=0.9$ corresponds to no rotational confinement. For a reaction coordinate value of x < [0.8] nm, a rapidly increasing rotational confinement was observed. To see this figure in color, go online.

To test whether the estimate of the target radius is subject to potentially insufficient sampling, we performed the same analysis using only every second and every fifth binding trajectory (Fig. 6, turquoise and gray lines). Apparently, the estimated target radius depends only weakly on sample size and thus can be considered sufficiently converged.

To quantify the rotational confinement, Fig. 6 B (solid line) shows the solid angle, $\text{Ω}\left(x\right)$, covered by an ensemble of ligand configurations from those trajectories for which successful binding occurred as a function of their reaction coordinate x (see Materials and Methods). As can be seen, the ligand is free to assume almost any orientation for $x>0.8\text{nm}$, whereas for smaller RMSD values, the available rotational space abruptly narrows down within a relatively short reaction coordinate interval. Interestingly, when also including in the analysis those trajectories that do not proceed toward binding (Fig. 6 B, dashed line), a weaker rotational confinement is seen, which commences at smaller x. Apparently, correct ligand orientation increases the probability for subsequent binding.

Barrier-crossing probability

Next, we determined the binding committor, $p\left(\text{bind}|x\right)$ (Fig. 1 B, red arrow). Here, successful binding was defined as reaching a lower threshold, $x_{\text{bind}}$ (resembling the point at which the ligand becomes fluorescent in the experiments), before reaching a larger threshold, $x_{\text{unbound}}$.

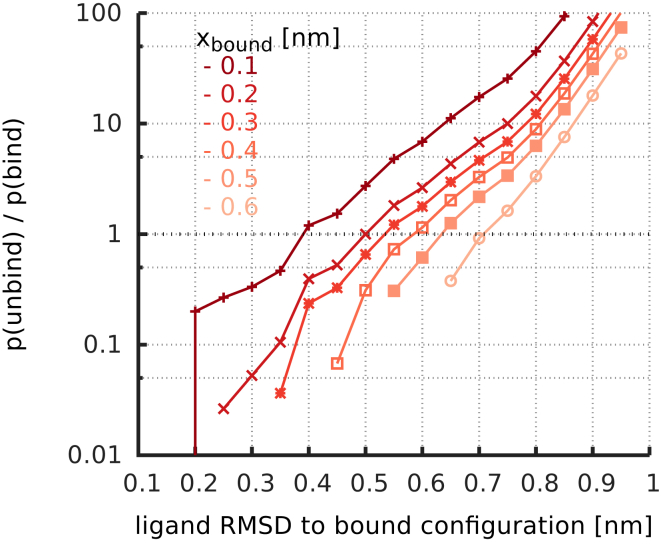
Fig. 7 shows ratios of the unbinding committor and the binding committor as a function of x. Because the experimental value of $x_{\text{bound}}$ is not known, the ratios are shown for six different values of $x_{\text{bound}}$ chosen from a large range. As expected, the ratio increases monotonously with increasing x. A similar log-linear dependency is seen for all choices of $x_{\text{bound}}$, albeit with a horizontal displacement. Such displacement may be due to recrossing events, which are more likely for smaller $x_{\text{bound}}$, or, alternatively, to the fact that a single one-dimensional time-independent free-energy barrier does not describe the binding kinetics properly.

Figure 7.

Ratio of unbinding and binding committor functions, $p\left(\text{unbind}|x\right)/p\left(\text{bind}|x\right)$. Different color intensities represent different values of the lower threshold, $x_{\text{bound}}$. To see this figure in color, go online.

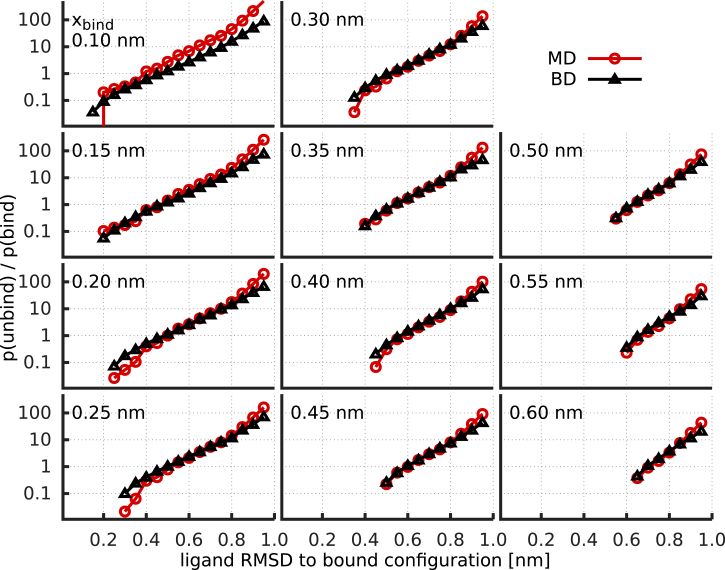
To distinguish between these two cases and to test whether a funnel model with a one-dimensional reaction coordinate is indeed an accurate description of the binding observed in the atomistic simulations, we compared the above binding committors with binding committors from BD simulations in a one-dimensional diffusion model. To that end, we generated BD trajectories in an inverse harmonic potential, $U\left(x\right)=-\left(\alpha /2\right){\left(x-x_{\text{barrier}}\right)}^2$, with two free parameters, α and $x_{\text{barrier}}$, representing the position and curvature of the barrier, respectively. From these trajectories, committor curves were calculated similarly to those in the MD simulations, i.e., by counting how often identical lower and upper thresholds were crossed (Fig. 8). Best agreement between all MD and BD committor ratios simultaneously was obtained for $\alpha =18\text{kJ}{\text{mol}}^{-1}{\text{nm}}^{-2}$ and $x_{\text{barrier}}=0.45\text{nm}$.

Figure 8.

Comparison of $p\left(\text{unbind}|x\right)/p\left(\text{bind}|x\right)$ ratios derived from MD simulations (red) with those obtained for a simple inverted harmonic potential BD model (black). With only two fitting parameters (barrier top position, $x_{\text{barrier}}$, and curvature, α), simultaneous agreement for all reaction coordinate values, x, and binding thresholds, $x_{\text{bound}}$, is achieved. To see this figure in color, go online.

As can be seen, all committor functions of the one-dimensional diffusion model and the MD simulations agree remarkably well, despite the choice of the simplest possible potential function. This result shows that the observed binding kinetics can indeed be described well by a one-dimensional binding-funnel model with a harmonic shaped free-energy barrier. Already, at the barrier top ($x=0.45\text{nm}$), considerable orientational restriction of the ligand ensemble is observed (Fig. 9), underscoring the relevance of orientational restriction for the free-energy barrier and, hence, the binding kinetics.

Figure 9.

Barrier top ensemble with a binding-site RMSD of $x=0.45\text{nm}$. The protein (cyan) is shown as an average structure. To see this figure in color, go online.

Determination of on-rate estimate

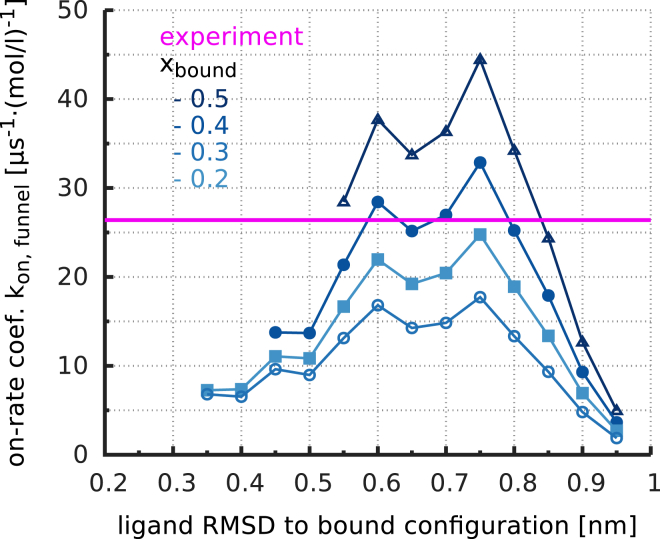
With $r\left(x\right)$, $\text{Ω}\left(x\right)$, and $p\left(\text{bind}|x\right)$ at hand, Eq. 7 can be used to calculate the binding on-rate coefficient, $k_{\text{on},\text{funnel}}$. Prerequisite for the description of the binding kinetics with a single rate coefficient is that the rate is independent—at least over a certain range—of the particular choice of x. To test whether this is actually the case, Fig. 10 shows $k_{\text{on},\text{funnel}}$ as a function of x for different bound-state threshold values, $x_{\text{bound}}$.

Figure 10.

Comparison of the estimated on-rate coefficient, $k_{\text{on},\text{funnel}}$ (blue lines), with the measured one (magenta) as a function of the target volume position, x, for multiple lower thresholds, $x_{\text{bound}}$. For $0.6\text{nm}<x<0.8\text{nm}$, the estimated on-rate coefficient is almost independent of x, justifying the assumption of the funnel model. Within the range of considered values of $x_{\text{bound}}$, the on-rate estimate varies only by a factor of 3. To see this figure in color, go online.

As can be seen, the on-rate estimate is indeed essentially independent of x between 0.6 nm and 0.8 nm, supporting the notion of a single rate. For positions $x<0.55\text{nm}$ of the target volume close to the barrier top, the rate coefficient deviates from this constant value. Reconsidering the assumptions of our model, we speculate that enthalpic interactions between the ligand and the protein become relevant in this region, such that the free-diffusion (Smoluchowski) estimate for the bulk-to-target-volume kinetics is no longer valid. Vice versa, this result shows that before crossing the barrier top, the free-energy landscape for ligand binding is dominated by entropy, i.e., translational and orientational restriction of the ligand. The decrease of $k_{\text{on},\text{funnel}}$ for $x>0.8\text{nm}$ to zero results from our choice of the unbinding threshold value, $x_{\text{unbound}}=1\text{nm}$ and is irrelevant in this context.

Depending on the particular choice of $x_{\text{bound}}$, the estimated on-rate between 15 and $40\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$ varies by less than a factor of 3, reflecting the fact that, in the experiment, the bound state is defined by the complex photophysics of the dye and, in the absence of a more accurate quantum-mechanical treatment, is not precisely defined. We should also note that the bound state considered here and probed by the dye label differs from the NMR bound structure (15, 16) in that the latter is characterized by a subsequent closure of the binding site, which markedly enhances the affinity and slows down the ligand dissociation rate, but does not severely affect the on-rate. Given this experimental uncertainty, comparison with the experimentally determined on-rate of $26\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$ (17) (Fig. 10, magenta line) shows that our model predicts the binding kinetics quite accurately. Such quantitative agreement is remarkable and underscores the accuracy of the MD binding simulations as well as that of the funnel model.

Conclusions

Motivated by the striking discrepancy between the slow measured on-rate and an estimate from a simple Smoluchowski model, we have quantified the kinetics of cAMP binding to the binding site of the CNBD of MloK1. Using over 900 MD simulations of spontaneous ligand binding, two possible models for the binding pathway were considered.

According to the first model, the dominant process is transient and unspecific ligand binding to the protein surface, with subsequent diffusion along the surface to the binding site via several intermediate surface binding states. In this scenario, the surface diffusion rates and the surface detachment rates would determine the on-rate. According to the second model, the ligand approaches the binding site directly via a binding funnel which constrains the translational and rotational degrees of freedom. Here, these constraints would imply an entropic barrier, which in turn would determine the on-rate.

Multiple binding events were observed in the simulations, including both transient binding to five main surface binding sites with subsequent diffusion and direct binding to the ligand-binding site. From this trajectory set, all associated surface diffusion, detachment, and binding rates were determined, thus providing a quantitative mesoscopic description of the unexpectedly complex ligand-binding process. According to this model, the surface diffusion pathways—taken together—contribute only ∼10% to the total binding rate, and most ligands bind directly to the binding site. Further, the presence of the surface binding “traps” alone leaves the Smoluchowski binding rate essentially unchanged and therefore is not the main cause for the drastically reduced binding rate.

We therefore asked if the above discrepancy can be explained in terms of an appropriate funnel model, the key determinants of which are a gradual confinement of the ligand motion and an associated free-energy barrier. Quantifying translational and rotational confinement and the binding committor from the MD trajectories, we estimated the on-rate coefficient to be between 15 and $40\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$. This on-rate coefficient agrees well with the experimentally determined value (17) of $k_{\text{on}}=26\mu {\mathrm{s}}^{-1}{\left(\mathrm{mol}/\mathrm{l}\right)}^{-1}$.

The exclusion of the surface diffusion model and the agreement of the prediction from the funnel model with the measured on-rate strongly supports the binding funnel model. Further, the uphill part of its free-energy barrier seems to be mainly entropic and caused by translational and rotational confinement of the ligand.

Although only cAMP binding to the CNBD of MloK1 was studied here, we consider it likely that similar binding models can properly describe the binding of other secondary messengers such as cyclic guanosine monophosphate, as well as many other ligand/receptor systems.

In the binding funnel model presented here, the on-rate is mainly limited by the spatial and rotational confinement, i.e., by entropic effects. Our funnel model therefore predicts that the on-rate should only depend weakly on temperature, and should mainly correlate with the temperature dependency of the diffusion coefficient of the respective ligand. This prediction suggests an experimental test for the proposed funnel model.

Author Contributions

B.V. designed research, performed research, analyzed data, and wrote the article. H.G. designed research and wrote the article. U.B.K. discussed and designed research and wrote the article. R.S. discussed and designed research.

Editor: Michael Feig.