The control of the discrimination between dNTP and rNTP in DNA and RNA polymerase

Abstract

Understanding the origin of discrimination between rNTP and dNTP by DNA/RNA polymerases is important both for gaining fundamental knowledge on the corresponding systems and for advancing the design of specific drugs. This work explores the nature of this discrimination by systematic calculations of the transition state (TS) binding energy in RB69 DNA polymerase (gp43) and T7 RNA polymerase. The calculations reproduced the observed trend, in particular when they included the water contribution obtained by the water flooding approach. Our detailed study confirms the idea that the discrimination is due to the steric interaction between the 2′OH and Tyr416 in DNA polymerase, while the electrostatic interaction is the source of the discrimination in RNA polymerase.

I. Introduction

Gene replication and transcription play a key role in the development of biological systems. These processes are catalyzed by DNA/RNA polymerases with high fidelity that maintains very low error rates. Such high fidelity is essential for the stability of reproduction and cellular activity but the occasional errors are also important source of evolution. The mechanism that DNA polymerases adopt to selectively choose the right Watson-Crick base pair between the template strand and the incoming nucleotide substrate has received a great attention in many studies. [1–15] Another important selective behavior of DNA and RNA polymerases is the discrimination against rNTP and dNTP, respectively. It is believed that DNA was evolved from RNA to stabilize earlier genetic system by giving a specific role to DNA as an information carrier in cells [16, 17]. One of the evidence that supports the RNA-to-DNA transition hypothesis is the analogous active site that uses two divalent ions mechanism, as well as the finding that rNTP is reduced to dNTP by reductases. [18, 19]

Understanding the rNTP and dNTP discrimination should help in advancing the fundamental description of replication processes and can also provide a powerful way for developing selective drugs that act against viruses and cancers. [20, 21]

In trying to understand the above selectivity, it is useful to consider a highly conserved tyrosine (e.g. Y416 and Y639 in RB69 DNA polymerase and T7 RNA polymerase, respectively). This residue is thought to be the key residue that contributes to the sugar selectivity, since it is the only residue near the 2′ position of the ribose sugar (see Figure 1) and [10, 22, 23]). Yang et al. [24] has shown that the mutant, Y416A, of RB69 DNA polymerase incorporates rNTP much more efficiently than its wild type. (Table 1) Similarly, but in an opposite way, Sousa et al. [25] mutated the corresponding tyrosine residue of T7 RNA polymerase, Y639, to phenylalanine (since in RNA polymerase, the extra 2′OH is probably preferred by its hydrogen bonds with the hydroxyl in Y639, and the mutant behaved as a DNA polymerase). (Table 4) These experiments were aimed at exploring the assumption [26, 27] that the tyrosine in DNA polymerase acts as a steric gate to the ribose of the incoming rNTP, while the corresponding tyrosine residue in RNA polymerase stabilizes the incoming rNTP by making a hydrogen bond with the hydroxyl group of the ribose.

Figure 1.

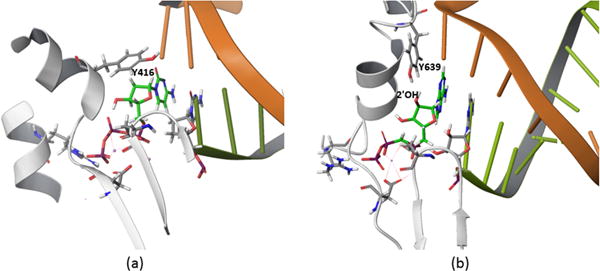
Analogous active sites of DNA polymerase (a) and RNA polymerase (b). These two polymerase catalyze the same reaction with the same key groups; two aspartate acids and magnesium ions. Furthermore, both have a tyrosine right above the 2′ of the ribose sugar.

Table 1.

Experimental data set from Yang et al. [24] and the catalytic effect of changing from deoxyribose to ribose sugar in RB69 DNA polymerase

	WT				Y416A				Y416F
	Kd	kpol	kpol/Kd	log Ω	Kd	kpol	kpol/Kd	log Ω	Kd	kpol	kpol/Kd	log Ω
dCTP	69	2.0×102	2.9	−4.8	70	22	0.31	−1.3	2.1×102	3.6×10	0.17	−4.2
rCTP	1.6×104	0.74	4.6×10−5		5.2×102	8.6	1.7×10−2		1.8×104	0.2	1.1×10−5

Table 4.

Experimental data set from [25] and the catalytic effect of changing from deoxyribose to ribose sugar in T7 RNA polymerase

	WT				Y639F
	KD	kpol	kpol/KD	log Ω	KD	kpol	kpol/KD	log Ω
rATP	0.1	205.0	4100.0	−3.3	0.1	180.0	1914.9	−0.9
dATP	3.5	7.5	2.1		0.3	60.0	222.2

The above hypothesis cannot be established uniquely by experimental studies, since it is hard to distinguish experimentally between electrostatic and steric contributions. Fortunately, computational approaches can help to determine what are the actual energy contributions that lead to the selectivity. Our previous studies have successfully elucidated sources of the high replication fidelity and the catalytic mechanism of DNA polymerase β [4–6, 13] Thus we apply in this paper the same approach to explore the origin of the sugar selectivity by RB69 DNA polymerase, using our empirical valence bond/free energy perturbation (EVB/FEP) calculations [28–31] and pKa calculations by the semi macroscopic version of the protein dipoles Langavin dipoles (LDLD/S-LRA) approach. [32–34]

II. Methods

Our task is to evaluate the barriers that correspond to k_pol and/or the TS binding energies, which are related to k_pol/K_D through (See [35])

$${\mathrm{\Delta }\mathrm{G}}_{\mathit{bind}}^{TS}={\mathrm{\Delta }\mathrm{g}}_{\mathit{protein}}^{‡}-{\mathrm{\Delta }\mathrm{g}}_{\mathit{water}}^{‡}=-\text{RT}\ln \frac{k_{\mathit{pol}}}{K_D}+\text{RT}\ln k_{\mathit{wat}}$$ (1)

The evaluation of this relationship should be done with a sufficiently reliable strategy and the approaches used towards this aim are mentioned below.

II.1 EVB/FEP calculations

To date, arguably the most effective way of evaluating activation free energies of enzymatic reactions is the empirical valence-bond (EVB) method described elsewhere. [28–31] Our previous studies with the EVB have successfully revealed the important factors for the high replication fidelity of DNA pol beta. [4–6, 13] Here, we applied the same method for exploring the selectivity of RB69 DNA polymerase with the following three different substrates ; the natural substrate (PDB: 4FK0) and the mismatched Watson-Crick base pair substrate (PDB: 4FK4), which are reported in Ref. [36]. We also explored the incorrect sugar with the 2′OH, which was obtained by substituting the 2′H by a hydroxyl group for the incorrect sugar structure and relaxing the structure by the same procedure used for the wild type. The stepwise associative mechanism was considered, as it was found out in our previous studies [37–40] that it gives similar trend to that obtained by the concerted mechanism, but it makes it simpler to explore the TS energy (by evaluating the energy of the pentacovalent intermediate that is being formed between the nucleophilic attack and the bond breaking steps).

The starting structures were immersed in a 18 Å sphere of water molecules subject to the surface-constraint all-atom solvent (SCAAS) type boundary conditions [33]. Long range effects were treated by the local reaction field (LRF) method (which is equivalent to having no cut-off for the electrostatic interactions) [33]. The center of the simulations sphere was defined by the geometric center of the EVB reacting atoms (defined in figure S1). The parameters used in the EVB calculations are described in section SI.

The positions of all atoms beyond 18 Å from this center were fixed at their crystallographic positions and their nonbonded interactions with the atoms within the simulation sphere were turned off. Note that the SCAAS allows one to obtain reliable results using smaller explicit systems than those used by most other methods. The protonation states were determined by calculating the pK_a s with our coarse grained (CG) model[41] and then keeping the ionizable residues within 12 Å from the simulation center in their ionization states. The effect of the more distanced ionizable residues was determined macroscopically while using a large charge–charge dielectric [42]. The immersed structures were equilibrated by increasing the temperature from 10 K to 300 K during 200 ps run, while imposing on the protein atoms 100 kcal/mol Ų harmonic constraint. The temperature was decreased back to 10K over another 200 ps with the same harmonic constraint and the constraint was then released over 100 ps. The systems were reheated to 310 K over 200 ps with fully released constraint followed by 800 ps relaxation. A further relaxation was done for another200 ps to generate 5 different starting configurations for the EVB and FEP calculations by picking a structure at each 40ps. The resulting structures were used in starting the free energy calculations, and the corresponding final results were taken as the average of the 5 runs.

The EVB simulation used 51 frames with each 10 ps for moving the potential from the reactant to the product potential at 300 K with a time step of 1 fs. 10 kcal/mol Ų harmonic constraint was applied to two magnesium ions for both simulations in protein and reference system (water) which otherwise do not keep their positions close to the reactive site in the water simulation, which are used for the calibration. We note here that the effect of the Mg ions has been explored in many of our studies (e.g. [43, 44]) that include examination of the predictively of the binding of the second metal ions and the late binding of the second ion. More recent studies (e.g.[45, 46] also addressed related questions. However, when the Mg is treated classically without our six dummy atom model it is justified to use harmonic constraint for fixing the mg ions near their observed position.

The FEP simulation of the alchemical transformation used the intermediate state (see below) structures from the EVB simulations. The alchemical simulations were run with the same number of frames and time step as the EVB simulations. As stated above the FEP and EVB calculations were obtained by averaging over the 5 different starting configurations.

We note here that choosing the intermediate state as the model for the TS exploits above mention the fact that the TS for concerted path has similar energetics as the intermediate state (IS), but it provides more stable results for the binding energy calculations. We are well aware of different studies of the TS structure (e.g. [47, 48]) but we believe that our QM/MM analysis [49] is quiet reliable and clearly sufficient for exploring the selectivity towards the hydroxyl of the ribose group which is mainly influenced from the environment of this group. At any rate, in this work we refer to the IS as the TS because of the above considerations.

Our analysis of the reaction mechanism indicated that it is most likely to involve proton transfer (PT) to the bulk and that the PT reaction is not likely to be the rate [50], and thus it is sufficient to calculate ∆G_PT instead of ∆g^‡_PT. This is equivalent to calculating the pK_a shift of the proton donor (the 3′OH group). The calculations of the pKa shift were done by PDLD/S-LRA in the MOLARIS package. [33] The PDLD/S-LRA method is a semimacroscopic method that take the Protein Dipole Langevin Dipoles (PDLD) method and scale it with a physically based dielectric constants. This method evaluates the charging energies with MD relaxation runs for the charged and uncharged stated in the framework of the LRA formulation. The details of this method as been described extensively and can be found for example in ref. [51]

II.2 The Water Flooding approach

The evaluation of binding free energies should involve the use of correct configuration of the water molecules in the active site, in both the bound and unbound states. However, obtaining the corresponding configurations can be very challenging, since overcoming the barriers for water penetration may require very long simulation times. In principle, one may try to randomly insert water molecules and find by Monte Carlo (MC) approach the configuration with the lowest free energy. However, such an approach can take enormous time since most insertion attempt will not be accepted. Our strategy for resolving this challenging problem is the “water flooding “ approach[52], where we first insert clusters of water molecules into the active site, relax and optimize the energy of the selected internal water molecules and use the very efficient LRA approach to estimate the energy of each of the internal water molecule in the given cluster. Next we take the energy of the internal water and evaluate the probability that a water molecule will be inside the protein by running a postprocessing MC simulation with an external program that simply iterate on the energy obtained from the LRA run relative to the energy of water in solution. In this work, we applied the water flooding approach in the TS configuration, and evaluated the TS binding energy in the presence of the most probable water cluster. In the actual simulations we started with standard calculations of the TS in the presence of the original water molecules (obtained by our standard procedure of using an initial grid), but then we removed the water molecules within a radius of 8 Å from the center of our system and reevaluates the population of the internal water by the water flooding approach. In other word, after using MD LRA calculations to estimate the free energy of each water molecule in a relaxed configuration, we then ranked the different configurations by an external MC treatment that obtains the lowest free energy configurations. Next, these processed structures were used in the specific calculation.

In the generation of the relaxed water clusters we solvated the protein with excess water molecules with a minimum distance (r_cut) of 1.8Å between the protein atoms and the oxygen of the water molecules (note that the water molecules that are found to be unstable after the LRA relaxation will not be accepted by the MC procedure). Water molecules that are out of the 8 Å radius are inserted normally with r_cut = 2.8Å. MD was performed for 100 ps with 0.3 kcal/mol constraints on water. Finally, the solvated structures obtained by the water flooding and the external MC calculation were treated as standard starting structure files and the same protocol and length of the equilibration and relaxation were performed as the simulations without the water flooding.

III. Result

III.1. Analyzing of the selectivity of DNA polymerase

EVB calculations

In first step of our analysis we performed EVB/FEP calculations of the reaction profiles of the different systems. The results of the calculations are given in Fig. 2 As found in our previous studies [4–6, 13], the difference in the activation barrier between the correct and incorrect Watson-Crick base pair substrates was reproduced in this case as well. However, the calculations did not reproduce a significant difference between the calculated barrier of the deoxyribose and ribose sugars systems. Apparently, it is challenging to capture throughout the entire reaction pathway the effect of the small differences in the partial charges of the 2′OH between rNTP and dNTP, because most of the contributions are obtained from the highly charged triphosphate and the base. In fact, Figure 2 shows slightly unfavorable barrier due to the extra hydroxyl group of the ribose sugar. The difficulties of obtaining converging results that reproduce the observed trend reflects in part the fact that the contribution to selectivity from k_pol is significantly smaller than that from k_pol/K_D. Thus we should try to use the thermodynamic cycle needed to the evaluation of k_pol/K_D. With this on mind we considered the cycle in Fig. 3 (see below)

Figure 2.

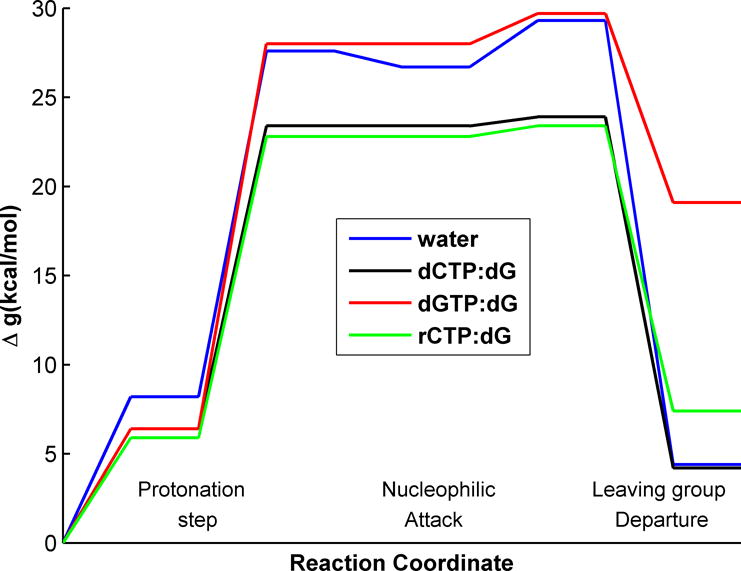
The EVB free energy profiles for the catalytic reaction with different substrates.

Figure 3.

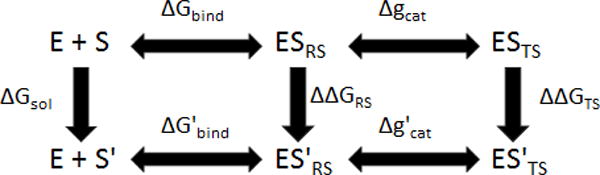
The thermodynamic cycle for the alchemical transformation of the ribose sugar in NTP. E, S, and S′ represent enzyme, cognate substrate, and non-cognate substrate, respectively. The energetics of the states involved is described schematically in Fig. 4

FEP calculation of alchemistic transformations

In view of the discussion above we turn to the use of alchemical transformations in evaluating the energies of the cycle of Fig 3. That is, we evaluated the catalytic efficiency (k_pol/K_m), for the wt and the Y416 mutants, by FEP simulations of the relevant alchemical transformations based on the thermodynamic cycles of Fig. 3 (where the energetics of the relevant states is described in Fig.4). We note here that this type of alchemical cycle was used in previous related works ([53, 54]). Finally, it also useful to point out that our alchemical study served also a useful purpose in allowing us to explore the performance of our water flooding approach in an attempt to improve the agreement between the calculated and observed free energies.

Figure 4.

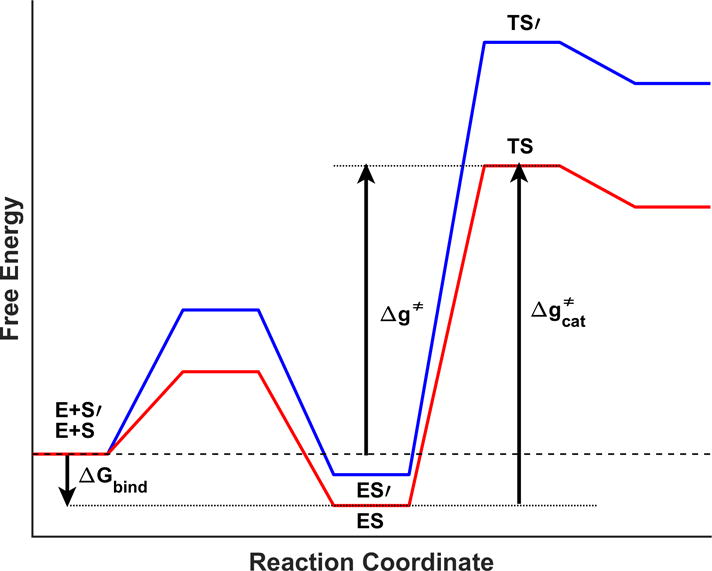
Schematic description of the energetics of the states considered in the thermodynamic cycle of Fig.3

Our study explored the effect of mutating the deoxy-ribose sugar of dCTP to the ribose sugar of rCTP using the alchemical pathway, trying to obtain the contribution from the hydroxyl group while leaving other parts of substrate unchanged. More specifically, the relative catalytic efficiency,

$$\mathrm{\Omega }={\left({\mathrm{k}}_{\mathrm{pol}}/{\mathrm{K}}_{\mathrm{D}}\right)}^{[\mathrm{OH}]}/{\left({\mathrm{k}}_{\mathrm{pol}}/{\mathrm{K}}_{\mathrm{D}}\right)}^{[\mathrm{H}]}$$ (2)

can be expressed in terms of the corresponding free energies using the thermodynamic cycle of Fig. 3 as

$$\log \mathrm{\Omega }=-\mathrm{\beta }(\mathrm{\Delta \Delta }{{\mathrm{G}}_{\mathrm{TS}}}^{[\mathrm{H}]->[\text{OH}]}-\mathrm{\Delta }{{\mathrm{G}}_{\mathrm{sol}}}^{[\mathrm{H}]->[\text{OH}]})/2.303$$ (3)

where ΔΔG_TS^[H] −^>[OH] and ΔG_sol^[H] −^>[OH] are the free energies of substituting the 2′H of the dNTP to an hydroxyl group in the TS of the reaction in the protein and in solution, respectively. The actual simulations were done in the opposite direction, mutating rCTP to dCTP, since it is more practical to mutate the hydroxyl group to a hydrogen atom and a dummy atom than to perform the opposite transformation. It is known that free energy calculations associated with mutations to dummy atoms frequently experience an extremely large vdW energy explosion, when the mapping parameter, λ, approaches the limit when we the run on the state were the forces are given almost entirely from the potential with the dummy atom (in this case we can obtain enormous artificial free energy contributions from the van der Waals (vdW) energy of the state with the real atom). This situation is known as “vdW catastrophe” [55]. To avoid this problem, we used a modified vdW function whose exponential repulsion part is linear below a cutoff set at 1.8 Å for the hydrogen and 3.0 Å for the oxygen.

The results of our calculations of the relative catalytic efficiency (log Ω) are given in Table 2 and the energy contributions from the FEP procedure are listed in Table 3 and Table S2. We also depict in Figure 5 the relative catalytic efficiency.

Table 2.

The relative catalytic efficiency (log Ω) calculated for DNA polymerase with and without the water flooding postprocessing and 4.0 kcal/mol Ų hydrogen bond constraint between the backbone nitrogen of the Y416 and 3OH′ in the substrate.

		Without H bond const		With H bond const
	exp	Original	Water Flooding	Original	Water Flooding
WT	−4.80	−7.29	−5.78	−8.48	−7.03
Y416A	−1.28	−1.78	−2.00	−1.24	−1.52
Y416F	−4.19	−6.25	−4.57	−9.32	−6.37

^aThe calculations are based on the alchemical thermodynamic cycle described in Figure 4. The last column includes the effect of using our water flooding approach.

Table 3.

Breakdown of the calculated free energy contributions to the TS binding in RB69 DNA polymerase^a

	Electrostatic	VDW
solvent	9.08	−3.05
WT	4.43	−5.76
Y416A	5.58	−2.40
Y416F	7.29	−6.83

^aEnergies in kcal/mol. The calculations involve the water flooding approach and no H bond constraint.

Figure 5.

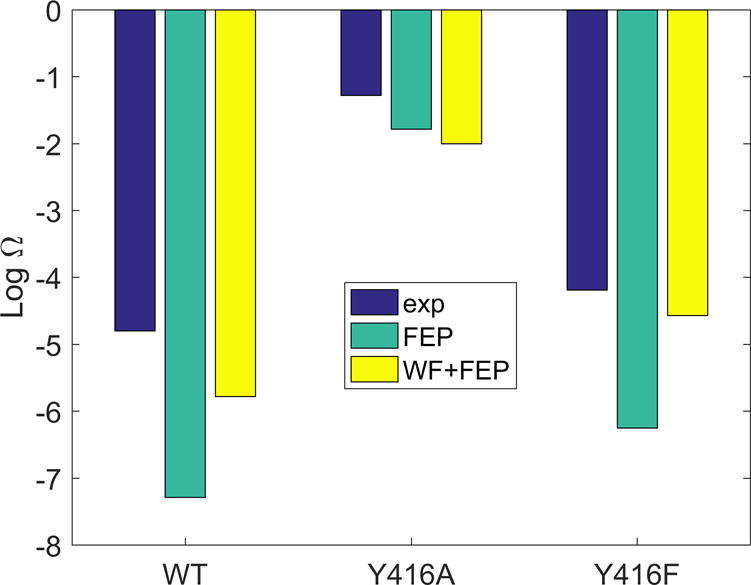
The relative catalytic efficiency (log Ω) calculated for DNA polymerase

In the first set of calculations we obtained overestimates for both the wild type and Y416F, while the results for Y416A agreed with the experimental trend. It is hard to tell whether such overestimates reflect the electrostatics or vdW contributions, since both terms showed about 5 kcal/mol differences compared to the calculations in solution.

Next, we used our water flooding approach, and the corresponding results (Table 3 and Table S2) did improve the agreement with the observed values for the wild type and Y416F (the result for Y416A was slightly worse, but the difference is not significant to be meaningful). The detail comparison between the electrostatic and vdW contributions in Table 3 shows that the improvement comes mostly from the increase in the vdW contributions.

As seen from Figure 6, it is hard to see a clear differences between structures generated by the water flooding approach and the structures obtained by the regular protein solvation procedure. However, there are always extra water molecule besides the tyrosine. Thus, it seems that the water flooding treatment has improved the results by better relaxation rather than by direct interactions between the substrate and the optimally selected water molecules.

Figure 6.

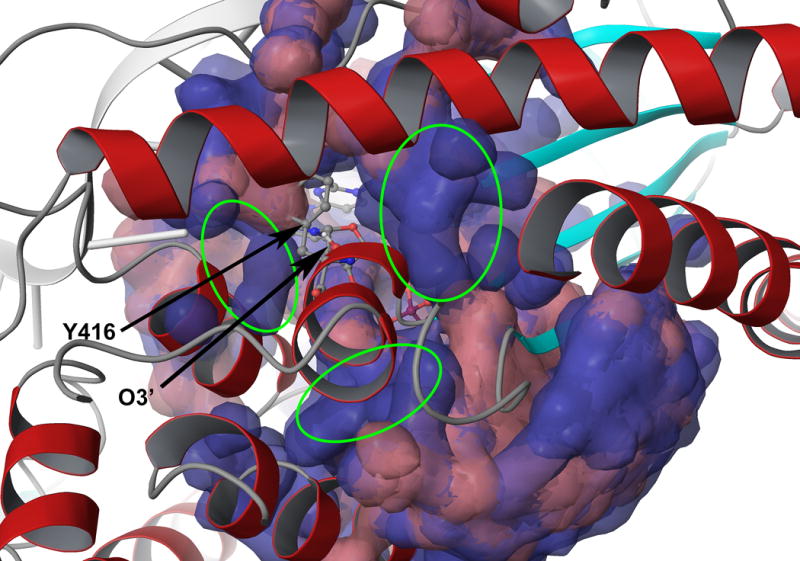
A comparison between normally solvated structures (red) and structures processed by the water flooding approach (blue). All initial trajectories used were superimposed and the water molecules are presented as molecular surface with transparency. The extra water molecules found around the Y416 after the water flooding are highlighted with circles.

To further inspect the source of improvements we calculated the distances between the sugar and the tyrosine (Figure 7). The original structural study [36] has suggested that the 3′OH makes an hydrogen bond with the backbone nitrogen of Y416, and thus increase the binding energy of the incoming nucleotide. Indeed, the hydrogen bond during the calculation with the original structure (without the water flooding) was observed for most of times (Figure 7-a). Interestingly, however, after the structure was processed by the water flooding approach and then simulated by the FEP approach, it almost always showed a longer H-bonds distance. Note that all results reported in this paper are averaged over 5~10 different initial trajectories. Some trajectories did not even make a hydrogen bonds and still reproduced the observed energetics better than without the water flooding. To see this effect more clearly, we also performed FEP mutation, subjecting the hydrogen bond length to a constraint with an equilibrium length of 2 Å and a force constant of 4.0 kcal/mol Ų. As shown in Table 3, regardless of the use of the water flooding approach, the results were worse with the hydrogen bond constraint except for the alanine mutant. As a consequence of this ‘loosen’ hydrogen bond in the structures generated by the water flooding approach, the distance between the 2′OH and the Cγ of Y416 was also slightly further as well. This explains the alleviated vdW contributions in the wild type and the Y416F calculations.

Figure 7.

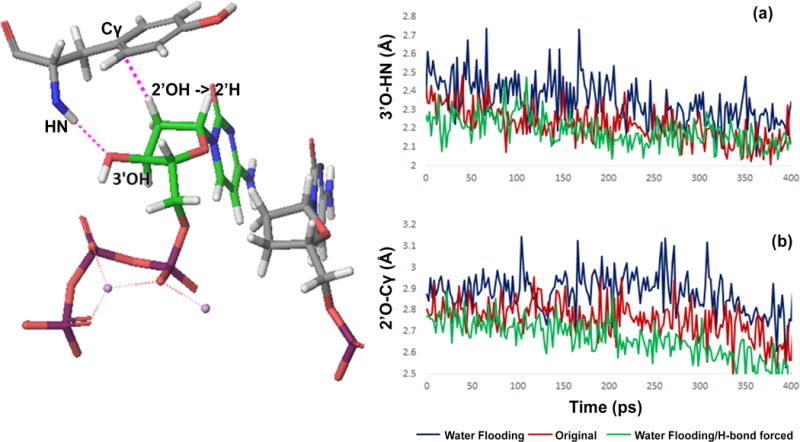
(a) Hydrogen bond distances between 3′OH and the Y416 backbone during the FEP calculation for structures. (b) The distance between 2′O and Cγ of the side chain of Y416 during the FEP calculation. Three cases were tested with the original structure (red), with the structure processed by water flooding (blue), and the same structure by water flooding but the hydrogen bond 3′O and HN is forced by a 4.0 kcal/mol Ų harmonic constraint at 2 Å (green).

III.2 Analyzing the selectivity of RNA polymerase

Building on the success in the evaluation the selectivity in DNA polymerase we used the same alchemical procedure for T7 RNA polymerase. In this case we used the α β methylene ATP elongation complex structure (PDB:1S76 [56]), where we modified the substrate to ATP and mutated Y416 to a phenylalanine, in order to simulate the corresponding mutant. The results are summarized in Tables 5 and 6. Apparently, when we just ran the simulations with our ENZYMIX force field, the proposed ([13, 15]) hydrogen bond between the O2′ and the hydroxyl group of Y416 was not obtained and the observed effect of the mutation was not reproduced. Thus, we imposed a 15 kcal/mol Ų distance constraint with a 1.9 Å equilibrium value, to force the hydrogen bond in the wild type. To position the mutated phenylalanine in a similar position to that of the tyrosine in the constrained wild type system, a similar distance constraint of 15 kcal/mol Ų and equilibrium distance of 2.8 Å were imposed on the distance between O2′ and the substituted hydrogen of the side chain of the phenylalanine. With these modifications, we could reproduce the experimental data (a reasonable trend was also obtained when the force constant was reduced to 6 kcal/mol Ų). As seen from Table 6 the sugar discrimination in T7 RNA polymerase is most probably due to electrostatic effects since the only difference between the wild type and the mutant is obtained from the electrostatic contribution. One may assume that imposing constraint on the H bond leads to our conclusions. However, it is quite likely that the hydrogen bond classical function should be refined by comparing to ab initio calculations and also should be represented by an EVB hydrogen bond potential. Exploring this issue is left for future studies.

Table 5.

The relative catalytic efficiency (log Ω) for T7 RNA polymerase structures with and without the constrained hydrogen bond^a.

	exp	normal	H bond forced
Wild Type	−3.3	1.1	−3.2
Y639F	−0.9	−2.3	−1.4

^awith 15kcal/mol hydrogen bond constraint between O2′ and the hydroxyl group in Y416 at 1.9 Å was imposed in the wild type while a corresponding distance constraint at 2.8 Å between O2′ and Hζ in F416 was imposed in the mutant

Table 6.

Free energy contributions of the alchemical mutation in T7 RNA polymerase^a

	WT/H-bond	Y639F with const	Solution
Electrostatic	10.1	6.8	9.1
VDW	0.3	0.5	−3.0

^aEnergies in kcal/mol. The results were obtained with a hydrogen bond constraint between O2′ and the hydroxyl group. In Y639F, a corresponding constraint was imposed to position the mutated phenylalanine at the constrained wild type.

III. Concluding remarks

This work explored the origin of discrimination between rNTP and to dNTP by DNA/RNA polymerases, using systematic calculations of the change in the transition state (TS) binding free energy in RB69 DNA polymerase and T7 RNA polymerase. The calculations reproduced the observed trend and supported the idea that the discrimination is due to the steric interaction between of the 2′OH and Tyr416 in DNA polymerase, while the electrostatics is the source of the discrimination in RNA polymerase.

The calculations demonstrate the importance of the water contribution by the improvement of the results by using the water flooding approach, and indicate that the determination of the correct water configuration can be crucial for reliable binding calculations.

Overall, we believe that the elucidation of the source of the discrimination can help significantly in developing selective drugs that act against viruses and cancers.