Abstract
Purpose
Develop a minimal mechanistic model based on in vitro–in vivo extrapolation (IVIVE) principles to predict extent of passive tubular reabsorption. Assess the ability of the model developed to predict extent of passive tubular reabsorption (Freab) and renal excretion clearance (CLR) from in vitro permeability data and tubular physiological parameters.
Methods
Model system parameters were informed by physiological data collated following extensive literature analysis. A database of clinical CLR was collated for 157 drugs. A subset of 45 drugs was selected for model validation; for those, Caco-2 permeability (Papp) data were measured under pH 6.5–7.4 gradient conditions and used to predict Freab and subsequently CLR. An empirical calibration approach was proposed to account for the effect of inter-assay/laboratory variation in Papp on the IVIVE of Freab.
Results
The 5-compartmental model accounted for regional differences in tubular surface area and flow rates and successfully predicted the extent of tubular reabsorption of 45 drugs for which filtration and reabsorption were contributing to renal excretion. Subsequently, predicted CLR was within 3-fold of the observed values for 87% of drugs in this dataset, with an overall gmfe of 1.96. Consideration of the empirical calibration method improved overall prediction of CLR (gmfe = 1.73 for 34 drugs in the internal validation dataset), in particular for basic drugs and drugs with low extent of tubular reabsorption.
Conclusions
The novel 5-compartment model represents an important addition to the IVIVE toolbox for physiologically-based prediction of renal tubular reabsorption and CLR. Physiological basis of the model proposed allows its application in future mechanistic kidney models in preclinical species and human.
Abbreviations: AUC, area under the plasma concentration-time profile; BCRP, breast cancer resistance protein; CD, collecting duct; Cp, plasma concentration; CLR, renal excretion clearance; CLR, filt, renal filtration clearance; CLR, int,reab, intrinsic permeability clearance in renal tubule; CLR,sec, renal secretion clearance; DT, distal tubule; fu,p, fraction of drug unbound in plasma; Freab, fraction of the drug reabsorbed in the renal tubule; Freab’, intermediate model parameter, representing the fraction of the equilibrium reached between unbound drug concentration in the plasma and urine; GFR, glomerular filtration rate; gmfe, geometric mean fold error; IVIVE, in vitro–in vivo extrapolation; LogD, octanol-buffer distribution coefficient; LoH, loop of Henle; MATE, multidrug and toxin extrusion protein; MRP, multidrug resistance protein; OAT, organic anion transporter; OCT, organic cation transporter; OATP, organic anion-transporting peptides; OCTN, organic cation/l-carnitine transporter; Papp, apparent permeability; PBPK, physiologically-based pharmacokinetic; P-gp, P-glycoprotein; PT, proximal tubule; RMSE, root mean squared error; TFR, tubular flow rate; TSA, tubular surface area
Keywords: In vitro–in vivo extrapolation, Tubular reabsorption, Renal excretion clearance
Graphical abstract
1. Introduction
Renal excretion is considered a major route of elimination for many drugs (e.g., metformin, acyclovir and digoxin) (Morrissey et al., 2013, Tucker, 1981, Varma et al., 2009). Prediction of human renal excretion clearance (CLR) prior to commencing first-in-man clinical studies currently relies on in silico methods based on physico-chemical properties (Dave and Morris, 2015a, Ito et al., 2013, Paine et al., 2010, Varma et al., 2009) and/or allometric scaling (Huh et al., 2011, Paine et al., 2011). Despite wide use of these methods, they do not provide mechanistic insight into the underlying processes contributing to renal excretion and have limited ability to account for any changes in the renal physiology. Mechanistic understanding of various pharmacokinetic (PK) processes has become a necessary part of model-informed decision making for special populations (e.g., obese or patients with renal impairment), as well as devising dosage regimens for use in such populations (Jadhav et al., 2015). The mechanistic approach becomes even more important when certain sub-groups (‘complex’ patients) exhibit various co-morbidities which make clinical studies very difficult, if not impossible (Rostami-Hodjegan, 2015). Thus, understanding various elements of renal excretion may offer advantages through prediction of potential differences in various patients under the framework of physiologically-based pharmacokinetic (PBPK) modelling (Zhao et al., 2011). In addition, many currently developed drugs undergo extensive active tubular secretion (Morrissey et al., 2013) for which prediction of CLR by mechanistic PBPK models (Felmlee et al., 2013, Neuhoff et al., 2013, Posada et al., 2015) is considered more promising in comparison with in silico and allometric scaling.
While efforts have been made at predicting renal metabolic clearance from in vitro data (Gill et al., 2012, Gill et al., 2013), successful prediction of CLR using in vitro–in vivo extrapolation (IVIVE) remains a challenge. In order to quantitatively and mechanistically predict CLR using IVIVE, each of the contributing processes (glomerular filtration, active secretion and tubular reabsorption, Eq. (1)) must be considered independently.
| (1) |
Filtration clearance (CLR,filt) is readily predicted from glomerular filtration rate (GFR) and fraction unbound in plasma (fu,p). In cases where both secretion and reabsorption contribute to elimination, confidence in prediction of the fraction reabsorbed (Freab) is equally important as the accurate prediction of renal secretion clearance (CLR,sec). Whereas reabsorption is predominantly a passive process, secretion is actively mediated by a range of drug transporters expressed in the kidney such as OAT1, OAT3, OCT2 and MATE2-K (Morrissey et al., 2013).
A number of mathematical models concerning physiological functions of the kidney (e.g., urine concentrating mechanism, solute transport regulation) exist (Layton, 2011, Weinstein, 2015), but may not be readily adaptable for use in renal PBPK models. Further, these models were developed based on physiological and experimental data in rat kidney (e.g., from micropuncture studies) for which analogous data in human are lacking. Recently, a static model for the prediction of CLR using in vitro permeability data from LLC-PK1 cell monolayers was proposed and its performance was assessed against a relatively small and restricted dataset (Kunze et al., 2014). The model considered both active secretion and tubular reabsorption, and used the proximal tubule surface area as the IVIVE scaling factor for the apparent permeability (Papp) data. However, the remaining tubular regions (e.g., collecting duct), which may contribute to passive tubular reabsorption, were not considered (Kunze et al., 2014).
A dynamic kidney model that facilitates IVIVE of renal transporter kinetics and passive permeability has recently been reported (Neuhoff et al., 2013). Although very promising, paucity of data on relevant physiological scaling factors and some of the system data (e.g., transporter abundance) limit model application and validation. In addition, adequate consideration of the heterogeneity of the renal tubule, important for prediction of passive permeability clearance in each tubular segment, is lacking. Current reports on the use of physiologically-based kidney models for ‘bottom-up’ prediction of renal drug disposition often rely on clinical plasma and/or urine drug concentration data for derivation/optimisation of transporter kinetic parameters and their scaling factors (Dave and Morris, 2015b, Felmlee et al., 2013, Hsu et al., 2014, Watanabe et al., 2011), analogous to the trends seen with prediction of hepatic clearance (Galetin, 2014, Zamek-Gliszczynski et al., 2013). For example, IVIVE of human CLR,sec from in vitro uptake data obtained in precision cut kidney slices required an empirical scaling factor of 10 in order to obtain agreement between predicted and observed values (Watanabe et al., 2011). In an analogous manner OAT3 maximal uptake rate (Vmax) was optimised using plasma concentration–time profiles to refine prediction of pemetrexed CLR using a PBPK kidney model, and account for differences in transporter expression and activity between the in vitro transfected cell system and in vivo (Posada et al., 2015).
The aim of this study was to develop a mechanistic model to predict extent of passive tubular reabsorption from in vitro permeability data and tubular physiological parameters. The second aim was to assess the ability of the model developed to predict CLR for a range of drugs for which filtration or reabsorption appeared to be the dominant mechanisms contributing to CLR. The physiological aspects of the model were informed from the data collated following an extensive literature analysis. A database of in vivo CLR and corresponding Freab was collated for 157 drugs. For a subset of 45 selected drugs, in vitro permeability data were generated in Caco-2 cell monolayer under pH 6.5–7.4 gradient conditions. Subsequently, the tubular reabsorption model developed was applied to predict regional and overall passive tubular reabsorption for the selected drug subset (n = 45). An empirical calibration approach was proposed to account for the effect of inter-assay/laboratory variation in Papp on the IVIVE of Freab using a set of reference drugs as calibrators (n = 11). The novel mechanistic 5-compartment model developed enables prediction of the contribution of passive tubular reabsorption to CLR in a physiologically-based manner and is seen as an integral part of complex kidney models.
2. Materials and methods
2.1. Clinical data collation
CLR data were collated from literature sources and, wherever possible, data were acquired from primary studies. Further data were gathered from review papers where sufficient details on the trial design had been reported. In addition, data from unpublished clinical studies available at https://www.clinicaltrials.gov were also included in the analysis. Where CLR values were not reported in the study, Eqs. (2), (3) were used to calculate CLR from published urinary excretion and plasma concentration data. Reports of a drug not being detected unchanged in urine, or having “negligible” CLR, were not considered for collation. Data available in graphical format were digitised using GetData Graph Digitizer v2.25 (http://getdata-graph-digitizer.com/).
| (2) |
| (3) |
where AUC0-t represents the area under the plasma concentration–time profile, and Cp,midpoint represents the plasma concentration at the midpoint of the urinary collection interval from which the urinary excretion rate was measured.
Only CLR data acquired following administration of a drug to healthy adult subjects were included in the database. Data from diseased, obese, elderly or alcoholic subjects were excluded, but exclusion criteria based on sex or ethnicity were not applied. Data acquired after co-administration of multiple drugs (e.g., from drug–drug interaction studies) were generally excluded. An exception was made for trimethoprim and sulfamethoxazole because these drugs are generally co-administered and there is a paucity of data following single drug administration. These studies were considered acceptable as there have been no reports in the literature of interactions at the level of renal excretion between sulfamethoxazole–trimethoprim. Aminoglycosides (amikacin, gentamicin, isepamicin, netilmicin, sisomicin and tobramycin) were excluded. These drugs are reported to accumulate in proximal tubule cells, possibly due to endocytotic luminal uptake mediated by the megalin receptor, causing nephrotoxicity (Moestrup et al., 1995, Nagai and Takano, 2004, Schmitz et al., 2002). Drugs with enantiomer specific renal excretion were excluded, an example being cetirizine (Strolin et al., 2008).
In contrast to previous databases (Varma et al., 2009), CLR data in this database are reported as absolute values, i.e. without normalisation for body weight or body surface area. Normalisation was not considered as the majority of literature studies (> 75%) reported absolute CLR values and substantial portion of studies did not report either body weight or body surface area of subjects. In addition, recent publications favour the use of absolute values of markers like GFR and creatinine clearance for the drug dosing recommendation, in contrast to body surface area normalised values (Chew-Harris et al., 2015, Dooley and Poole, 2000, Jones, 2011, Pai, 2010). In cases where CLR data were reported following normalisation to body weight (e.g., mL/min/kg or mL/min/70 kg), CLR data were corrected according to the mean weight or midpoint of the range reported in the study. The CLR data were corrected using an assumed body weight of 70 kg for those studies in which body weights had not been reported, which could have introduced some bias. An analogous approach was applied for CLR data reported following normalisation to body surface area, using a standard value of 1.73 m2 for studies where subject body surface area data was not reported.
When clearance values for the same drug were available from multiple sources, anomalies in studies/trials reported for individual drugs were initially identified using the I2 statistic for data heterogeneity (Eqs. (4), (5)) (Higgins and Thompson, 2002, Higgins et al., 2003). High heterogeneity was observed for 20 drugs (I2 greater than 0.5), of which 8 had very high heterogeneity (I2 greater than 0.75). The presence and subsequent exclusion of anomalous studies/trials was identified for drugs with I2 greater than 0.5 through visual analyses of study/trial mean and standard deviation data.
| (4) |
where Q is Cochran's heterogeneity statistic, and df is the degrees of freedom
| (5) |
where yi is the mean CLR reported by study i, and σ2i is the variance in CLR reported by study i.
In addition to CLR, any measured or estimated creatinine clearances and GFR that had been reported in the same clinical studies were collated where available. These data were corrected for any normalisations that had been applied, as performed for CLR. Data reported on fu,p were also collated from the same study. Further fu,p data were obtained using other literature sources. Where nonlinear plasma protein binding was reported for a drug, the fu,p at concentrations consistent with plasma concentrations reported for CLR clinical studies were used for the analysis.
The fu,p data were collated from a variety of in vivo and in vitro sources using a number of different experimental techniques (ultrafiltration or membrane dialysis). Therefore, the average fu,p value for each drug was obtained without applying a weighting, whilst ensuring good agreement was achieved between the data used to obtain the average.
Overall weighted mean CLR and standard deviation were calculated using Eqs. (6), (7), respectively.
| (6) |
where is the weighted mean, nj is the number of subjects in the jth study, and is the mean of the jth study. Here a “study” is defined as the data associated with a group of subjects being administered a specific dose regime, on a particular occasion, with “n” number of subjects.
| (7) |
where σ is the overall weighted standard deviation and σj is the standard deviation of the jth study.
2.2. Calculation of observed clearance ratio and Freab
The clearance ratio was calculated from clinical data using Eqs. (8), (9), in agreement with reported studies (Giacomini et al., 2010, Ito et al., 2013). Drugs with a clearance ratio greater than 1.5 were considered to undergo net secretion, and were therefore excluded from subsequent analyses and assessment of the model developed for prediction of tubular reabsorption. For the remaining drugs the fraction reabsorbed (Freab) was calculated using Eq. (10).
| (8) |
| (9) |
| (10) |
N.B. In certain instances, calculated Freab was negative based on Eq. (10). For these drugs (6/45 drugs), data in figures were presented as Freab = 0 (actual negative values were used for numerical analyses). The most extreme example was atenolol, with the observed weighted overall CLR of 145 ± 48 mL/min (fu,p of 0.97) which exceeded GFR assumed in the current study.
GFR values for healthy subjects may vary as a result of biological as well as inter-individual variation and also the method of measurement. As the more robust methods for measuring GFR, such as inulin or iohexol renal clearance, are impractical and time consuming (Sterner et al., 2008), GFR measurements during clinical studies are typically based on the renal clearance of endogenous creatinine. This method is associated with a degree of inaccuracy, due to the proposed contribution of active secretion by the OCT2, MATE1 and MATE2-K transporters to creatinine clearance (Soveri et al., 2014, Tanihara et al., 2007, Urakami et al., 2004). More frequently GFR is not measured but estimated using creatinine plasma concentrations using either the ‘Cockcroft–Gault’ or ‘Modification of Diet in Renal Disease’ equations (Nyman et al., 2011). Individual GFR values for subjects in clinical trials databases were generally not available. Therefore, for the purposes of this study, a GFR value of 120 mL/min was assumed for all drugs, consistent with precedent set in the literature and value used in the recently developed physiologically-based kidney model (Delanaye et al., 2012, Neuhoff et al., 2013).
2.3. In vitro permeability data, physico-chemical properties and drug affinity for renal transporter proteins
In the absence of a robust and validated in vitro model for assessing passive permeability in the renal nephron tubule, it was hypothesised that permeability data obtained in Caco-2 cell monolayers may offer a potential substitute. Apparent permeability (Papp) of drugs was measured in the apical to basolateral direction in Caco-2 cell monolayers using an AstraZeneca in-house assay (Hilgendorf, C. and Fredlund, L., Intrinsic permeability in-vitro — a transporter independent measure of Caco-2 permeability in drug design and development; poster presented at World Conference on Drug Absorption, Transport and Delivery (WCDATD): responding to challenging situations; Uppsala, Sweden June 24–26, 2013). The assay was performed using the apical to basolateral pH gradient format of pH 6.5 to pH 7.4. Permeability assays were performed in the presence of an efflux transporter inhibitor cocktail (50 μM quinidine, 20 μM sulfasalazine, 100 μM benzbromarone) over a 2 h incubation period. The pH gradient was applied in order to mimic typical conditions observed in the renal tubule, where the urine pH can vary between 4.5 and 8, but is typically more acidic relative to plasma (pH 5.5–6.5) (Simerville et al., 2005). The efflux transporter inhibitor cocktail was used to minimise the effect of efflux transporters expressed in Caco-2 cells (e.g. P-glycoprotein, BCRP and MRP2) on the estimate of apical to basolateral Papp of substrates for such transporters. Papp data were obtained for a subset of drugs that exhibited a variety of physico-chemical properties, range of CLR, Freab and expected Papp values (based on historical AstraZeneca in-house data and literature analysis of permeability data generated under isotonic pH 7.4 conditions).
The octanol-buffer (pH 7.4) distribution coefficient (LogD7.4) and pKa data were generated using slight modification of the shake-flask (Wenlock et al., 2011) and potentiometric AstraZeneca in-house assays respectively. Where measured LogD7.4 or pKa data could not be obtained, values reported in the BioByte Masterfile database (BioByte Corporation, Claremont, CA, USA, http://www.biobyte.com/index.html) or calculated using ACD/LogD program v.14.02 (Advanced Chemistry Development, Inc., Toronto, On, Canada, www.acdlabs.com, 2014) were used. The pKa values associated with ionisable centres identified within a given drug were used to calculate the fraction of drug ionised at pH 6.5. Drugs were then classified into groups as follows: drugs with > 50% unionised at pH 6.5 were classified as “Neutral”; drugs with > 50% ionised as mono −/di −/tri-protic acids or bases were classified as “Acid” or “Base”, respectively; “Zwitterions” were classified as drugs with > 50% ionised, with the major ionised species having no net charge; all other drugs were classified as amphoteric. The LogD6.5 of acids and bases were estimated from LogD7.4 and pKa data assuming that only the neutral species partitions into the octanol phase (Kah and Brown, 2008). LogD6.5 for neutral, amphoteric and zwitterion drugs were assumed to be equal to LogD7.4. Although melagatran, oxytetracycline and tetracycline have an isoelectric point > 7.4 or < 6.5, the difference between LogD7.4and LogD6.5 predicted by ACD was less than 0.5, confirming the validity of the assumption above.
The potential impact of renal transporter mediated secretion of drugs on the assessment of the prediction of CLR using the minimal model of reabsorption was investigated. A thorough literature search was performed in PubMed (http://www.ncbi.nlm.nih.gov/pubmed) to identify drugs reported to be substrates of OAT1, OAT3, OAT4, OATP4C1, OCT2, OCTN1, OCTN2, MATE1, MATE2K, P-gp, MRP2, MRP4 or BCRP (Morrissey et al., 2013). To expand this dataset, the UCSF-FDA Transportal and TP-search databases were also searched (Morrissey et al., 2012, Ozawa et al., 2004). Only reports of drugs interacting as substrates of human drug transporters were included. In addition, clinical data indicating occurrence of renal transporter mediated drug–drug interactions (i.e., decrease in CLR following co-administration of another drug) were used as indirect evidence of drugs being substrates of renal drug transporters.
2.4. Overall structure of the minimal model of tubular reabsorption
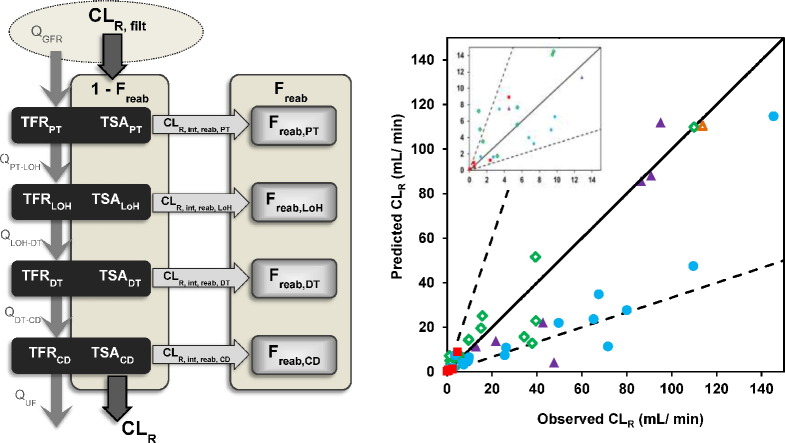
In the proposed model, the nephron is represented as five compartments, namely the glomerulus and four tubular regions, as depicted in Fig. 1. The tubular compartments in the model, listed in anatomical order starting from the glomerulus are: the proximal tubule (PT), the loop of Henle (LoH), the distal tubule (DT) and the collecting duct (CD). In the absence of active processes, tubular reabsorption proceeds until the urinary concentration is in equilibrium with the unbound drug plasma concentration. Thus a Freab value of 1, and CLR of 0, is not strictly possible in this case. The minimal model of reabsorption was developed by introducing an intermediary parameter, Freab′, the value of which could range from 0 to 1, representing the fraction of the equilibrium reached between urine and plasma. The relationship between Freab′ and Freab is shown in Eq. (11). The predicted overall Freab′ was calculated from the predicted Freab′ in each (i) tubular region (Freab,i′), as shown in Eq. (12). Regional Freab,i′ (Eq. (13)) were predicted from the intrinsic permeability clearance of the drug of interest for each tubule region (CLR,int,reab,i) and the tubular flow rate (TFR) of the filtrate/urine in the corresponding region (TFRi), approach adapted from previous studies (Kunze et al., 2014).
| (11) |
where UF is the urine flow, which was assumed to be 1 mL/min
| (12) |
| (13) |
Fig. 1.
Schematic diagram of the minimal physiologically-based model for tubular reabsorption of drugs in the kidney. The nephron is represented by a glomerulus compartment in addition to four compartments representing different regions of the nephron tubule (proximal tubule (PT), loop of Henle (LoH), distal tubule (DT) and collecting duct (CD) in descending anatomical order). Physiological parameters, tubular flow rate (TFRi) and tubular surface area (TSAi), for each individual tubular region are indicated. Tubular filtrate flow (Q) is represented by grey arrows connecting tubular compartments and used to calculate TFRi (average midpoint flow rates). The intrinsic reabsorption clearance of each individual region (CLR,int,reab,i) is calculated using the corresponding TSAi. Total renal excretion clearance (CLR) is obtained from the filtration clearance (CLR,filt) and the overall fraction reabsorbed (Freab), by rearrangement of Eq. (9).
CLR,int,reab,i for each drug and tubular region combination was calculated using an IVIVE approach, as per Eq. (14) (Kunze et al., 2014).
| (14) |
where TSAi is the tubule surface area for each individual tubular region.
Based on the scope of the model, renal drug metabolism was not considered. In addition, there was no evidence of renal metabolism for the majority of drugs used to assess the predictive performance of the model of reabsorption.
2.5. Minimal model of tubular reabsorption: Physiological system parameters
Final values of physiological input parameters for the four tubular compartments are shown in Table 1, with the full detail on the individual parameters (e.g., tubular region diameters and length) presented in the Supplementary Methods. In general, TFRi values were the midpoint flow rates for each tubular compartment (Table S1.1 and S1.2). TSAi values were initially calculated following the assumption of the surface area of a cylinder, using length and diameter of tubular region (Tables S1.3 and S1.4), and the number of nephrons of 900,000 nephrons/kidney. Special consideration was made for the CD compartment, due to the merging of nephrons to form the cortical CD, and merging of CDs in the inner medulla. To account for this, the number of nephrons was reduced to 90,000 nephrons/kidney for the cortical and outer medulla CD, with surface area calculated following assumption of a cylinder. The surface area of the inner medulla CD was calculated using an exponential function shown in Eq. (15) (details provided in Supplementary Methods, Section 2 and Fig. S1.1) which accounts for the concomitant decrease in number and increase in diameter of CD, as they traverse towards the renal pelvis.
| (15) |
where d0 and dn are the diameter of inner medulla collecting ducts at the papilla apex and at the outer medulla-inner medulla boundary, NCD0 is the number of inner medulla CD at the papilla apex, and F is the number of fusion events. Cx represents the total circumference of inner medulla CD throughout this region at ‘x’ mm from the papilla apex. The inner medulla CD surface area is the area under the curve of this function between 0 and n, where n is the length of the IMCD (length = inner medulla width = 11 mm).
Table 1.
Physiological parameter values used for tubular compartments in the minimal physiologically-based reabsorption model.
| TSAi (m2) | TFRi (mL/min)a | |
|---|---|---|
| PT | 6.1 | 81.6 (120–43.2) |
| LoH | 0.16b | 33.6 (43.2–24.0) |
| DT | 0.21b | 17.8 (24.0–11.6) |
| CD | 0.045b, c | 6.3 (11.6–1.0) |
Values represent midpoint flow rates, ranges in parentheses represent flows at beginning and end of tubule regions.
TSALoH, TSADT and TSACD calculated accounting for microvilli.
TSACD includes an exponential function for calculating surface area of inner medulla CD. Details are listed in the Supplementary Methods.
Microvilli are present extensively in epithelial cells of the proximal tubule where they form a brush border; in contrast, microvilli are sparse in tubular cells of other regions (Welling et al., 1981, Welling and Welling, 1988). Additionally, there is evidence of the expression of microvilli in the Caco-2 cells. Therefore, a microvilli correction factor was applied to TSAi values in the DT, LoH and CD compartments to account for the differential presence of microvilli along the renal tubule relative to the PT region and Caco-2 cells. This approach resulted in a 7.5-fold decrease in the estimated surface area compared to that calculated using the assumption of open cylinder for the LoH, DT and CD compartments. The method used here is analogous to a recently published approach to estimate specific regional effective permeability for intestinal PBPK models used to predict drug absorption (Olivares-Morales et al., 2015).
2.6. Empirical relationship between Papp and observed Freab′
The empirical relationship between Papp and Freab′ was best described by the Hill model (Eq. (16)), consistent with the relationship already defined between Papp across Caco-2 cell monolayers and fraction absorbed following oral administration (Artursson et al., 2001).
| (16) |
where a represents the slope factor and b is the value of Papp at which Freab′ equals 0.5. The Hill model was fitted to the data using nonlinear regression to estimate best-fit values and 95% confidence interval (CI) of parameters.
2.7. Calibration of Caco-2 permeability data
Permeability data from Caco-2 cell monolayer assays generally show inter-laboratory variation (Artursson et al., 2001). To account for this and to allow the Caco-2 data in the present study to be transferable to other assay formats/laboratories, a Papp–Freab′ calibration method was explored by splitting the available Papp and Freab′ data into ‘reference’ and internal ‘validation’ subsets. It is important to clarify that this calibration is not intended to predict Freab′ using a data driven empirical model, as done in quantitative structure–pharmacokinetic relationship models, which require formal internal and external validation (Dave and Morris, 2015a). The calibration approach is proposed as a pragmatic method to account for inter-assay/inter-laboratory differences; herein it is applied to the current dataset only, and not external data as intended for future studies.
The reference drugs (n = 11) were selected to cover a range of Papp and Freab′ values and were representative of the overall relationship between Papp and Freab′. The relationship between Papp and the predicted Freab′ based on the minimal reabsorption model was best described by the Hill model, analogous to the relationship between Papp and observed Freab′ discussed above. Empirical calibration was performed using the reference dataset of 11 drugs to account for any discrepancy between predicted and observed Freab′. This approach allowed subsequent calculation of calibrated Papp values for the drugs in the internal validation dataset (n = 34), using Eq. (17) (see Supplementary Methods for derivation).
| (17) |
where a1 and b1 are the slope factor and Papp value at which Freab′ is equal to 0.5 for the Papp vs Freab′ Hill equation fitted against data predicted by the minimal model for the reference dataset; a2 and b2 are the Hill equation parameters obtained from fitting Papp values for the reference drugs (Papp,ref) and corresponding observed Freab′.
2.8. Data analysis
Nonlinear regression was carried out using MATLAB R2012a (The MathWorks Inc., Natick, MA, USA, www.mathworks.com). All other data analyses were performed using MS Excel. The model performance was assessed based on the R2 of the predicted vs. observed linear regression, and by considering the number and percent of drugs predicted within 3-fold of the observed CLR. The performance of models with different physiological complexity was assessed for drugs with low (Freab < 0.25), medium (Freab = 0.25–0.75) and high passive tubular reabsorption (Freab > 0.75). These cut-off values were arbitrarily selected to assess potential differences in trends between these groups of drugs.
Bias and precision in predicting CLR and Freab were calculated as geometric fold error (gmfe) in Eq. (18) and root mean squared error (rmse) in Eq. (19) (Gertz et al., 2010). The gmfe indicates an absolute deviation from the observed data, as this metric does not allow over- and under-predictions to cancel each other out.
| (18) |
| (19) |
3. Results
3.1. Collation of a comprehensive renal clearance database
CLR, fu,p and transporter interaction data were collated for 157 drugs; details are listed in Supplementary Material, Tables S2.1 and S3.1. On average 4–5 clinical studies and 40 CLR measurements were obtained per individual drug, although this varied depending on availability of data. No attempt was made to separate intra- and inter-subject variability. Following analysis using the I2 statistic, three studies/trials were classified as anomalous results and excluded; details are presented in the Supplementary Results, Table S4.1. Overall weighted mean CLR ranged from 0.022 (isoxicam) to 526 mL/min (metformin), while fu,p ranged from 0.01 (olmesartan) to 1 (metformin). Measurements and estimates of GFR (n = 1686) were reported from 200 clinical studies (28% of studies collated). Only two of the studies collated used inulin to measure GFR; the remainder used either creatinine clearance, estimated GFR from plasma creatinine concentrations, or did not specify the method. Overall weighted mean GFR was 112.9 ± 25.2 mL/min, with study mean values ranging from 69.2 to 168.0 mL/min.
Of the 157 drugs, 72 were classified as net secreted (clearance ratio > 1.5). As such, they were regarded unsuitable for assessing a model of tubular reabsorption and therefore excluded from further analysis. Glomerular filtration or reabsorption was the dominant mechanism for the remaining 85 drugs (clearance ratio < 1.5). Of these, a representative subset of 45 drugs was selected for the assessment of the predictive performance of the mechanistic tubular reabsorption model. These drugs covered a range of CLR values, from 0.02 (isoxicam) to 145 mL/min (atenolol); the extent of tubular reabsorption ranged from none (six drugs including atenolol and verapamil) to reaching complete equilibrium (Freab′ = 1, isoxicam). Drugs were also selected to ensure a range of physico-chemical properties were represented, although neutral and basic drugs represented the majority, with 15 and 16 drugs, out of the set of 45, falling into these categories, respectively (Table 2). Approximately one third of the drugs have been reported to be substrates of human drug transporters known to be expressed in the kidney. Corresponding Papp values obtained in the Caco-2 cells under the 6.5–7.4 pH gradient conditions covered approximately 3 orders of magnitude, as shown in Table 2.
Table 2.
In vivo, physico-chemical properties and in vitro data for 45 drugs used to assess the minimal model of tubular reabsorption.
References for CLR and indications of transporter affinity are provided in Supplementary Results Tables S2.1 and S3.1.
| Drug | CLR (mL/min) | Freaba | Papp (× 10− 6 cm/s) | fu,p | pKa (acid) | pKa (base) | Ionisation at pH 6.5b | LogD7.4 | LogD6.5c | Indication of transporter affinity |
|---|---|---|---|---|---|---|---|---|---|---|
| Antipyrine | 1.22 | 0.99 | 125 | 0.89 | – | – | Neutral | 0.11 | 0.11 | N/A |
| Aprindine | 1.28 | 0.78 | 31.8 | 0.05 | – | 9.95, 5.85d | Base | 2.50 | 1.53 | N/A |
| Atenolol | 145 | − 0.25 | 0.256 | 0.97 | – | 9.39 | Base | − 2.65 c | − 3.55 | OCT2 |
| Betamethasone | 9.50 | 0.78 | 26.5 | 0.36 | – | – | Neutral | 1.99 | 1.99 | P-gp |
| Betaxolol | 49.6 | 0.08 | 20.0 | 0.45 | – | 9.53 | Base | 0.63 | − 0.27 | N/A |
| Caffeine | 1.06 | 0.99 | 81.1 | 0.67 | – | – | Neutral | 0.11 c | 0.11 | N/A |
| Chlorpheniramine | 26.2 | 0.26 | 28.5 | 0.30 | – | 9.35, 5.15 | Base | 1.22 | 0.31 | N/A |
| Chlorpropamide | 0.56 | 0.91 | 88.1 | 0.05 | 4.69 | – | Acid | − 0.33 | 0.56 | N/A |
| Citalopram | 65.2 | − 0.09 | 20.9 | 0.50 | – | 9.57d | Base | 1.55 | 0.65 | N/A |
| Dapsone | 5.50 | 0.83 | 49.7 | 0.27 | – | – | Neutral | 0.85 | 0.85 | N/A |
| Difloxacin | 4.54 | 0.94 | 74.6 | 0.62 | 5.81 | 7.39 | Zwitterion | 0.70 | 0.70 | N/A |
| Doxepin | 9.75 | 0.64 | 36.5 | 0.22 | – | 8.00d | Base | 2.23 | 1.41 | N/A |
| Fluconazole | 15.7 | 0.85 | 36.3 | 0.86 | – | – | Neutral | 0.46 | 0.46 | P-gp |
| Gabapentin | 95.1 | 0.18 | 0.67 | 0.97 | 4.72d | 10.27d | Zwitterion | − 1.10 | − 1.79 | OCTN1 |
| Grepafloxacin | 47.6 | 0.35 | 110 | 0.61 | 6.44d | 8.74d | Zwitterion | 0.50 | 0.50 | P-gp |
| Imipramine | 6.80 | 0.55 | 33.4 | 0.13 | – | 9.17 | Base | 2.49 | 1.60 | N/A |
| Irbesartan | 2.37 | 0.62 | 44.0 | 0.05 | 3.91 | – | Acid | 1.29 | 2.19 | N/A |
| Isoxicam | 0.02 | 1.00 | 142 | 0.04 | 3.84 | – | Acid | − 0.20 | 0.70 | N/A |
| Levetiracetam | 39.4 | 0.64 | 15.7 | 0.90 | – | – | Neutral | − 0.63 c | − 0.63 | N/A |
| Linezolid | 39.5 | 0.58 | 36.1 | 0.78 | – | – | Neutral | 0.67 | 0.67 | N/A |
| Melagatran | 114 | − 0.02 | 0.145 | 0.93 | 2.12 | 11.62, 8.16d | Amphoteric | − 1.42 | − 1.42 | P-gp |
| Metoprolol | 110 | − 0.05 | 17.0 | 0.87 | – | 9.40 | Base | − 0.29 | − 1.19 | OCT2 |
| Metronidazole | 9.64 | 0.92 | 64.7 | 0.98 | – | – | Neutral | − 0.11 | − 0.11 | N/A |
| Mexiletine | 71.6 | − 0.25 | 43.8 | 0.48 | – | 9.13 | Base | 0.62 | − 0.27 | N/A |
| Moclobemide | 3.42 | 0.94 | 64.4 | 0.50 | – | 6.53d | Base | 1.60 | 1.34 | N/A |
| Moxifloxacin | 42.7 | 0.37 | 26.7 | 0.57 | 6.31 | 9.51 | Zwitterion | − 0.24 | − 0.24 | P-gp, MRP2 |
| Oxprenolol | 9.35 | 0.44 | 30.0 | 0.14 | – | 9.60 | Base | 0.23 | − 0.67 | N/A |
| Oxytetracycline | 90.8 | 0.02 | 0.850 | 0.77 | 3.27, 7.32, 9.11d | 10.80d | Zwitterion | − 4.7c | − 4.70 | P-gp |
| Pefloxacin | 12.9 | 0.86 | 63.7 | 0.75 | 6.28 | 7.55 | Zwitterion | 0.30 | 0.35 | P-gp |
| Prednisolone | 34.3 | 0.10 | 19.7 | 0.32 | – | – | Neutral | 1.62c | 1.62 | P-gp |
| Prednisone | 37.9 | 0.30 | 37.3 | 0.45 | – | – | Neutral | 1.25 | 1.25 | Weak P-gp interaction |
| Probenecid | 0.50 | 0.96 | 84.5 | 0.09 | 3.36 | – | Acid | − 0.14 | 0.76 | N/A |
| Propafenone | 7.37 | 0.26 | 26.4 | 0.08 | – | 9.62d | Base | 1.72 | 0.82 | N/A |
| Propylthiouracil | 3.20 | 0.83 | 80.8 | 0.16 | 8.01 | – | Neutral | 0.70 | 0.78 | N/A |
| Ribavirin | 109.9 | 0.08 | 1.55 | 1.00 | – | – | Neutral | − 2.14c | − 2.14 | N/A |
| Ropivacaine | 2.73 | 0.55 | 32.3 | 0.05 | – | 8.10 | Base | 2.10 | 1.27 | N/A |
| Sparfloxacin | 21.7 | 0.73 | 49.8 | 0.67 | 6.31 | 8.94 | Zwitterion | − 0.15 | − 0.91 | P-gp |
| Sulfamethoxazole | 4.52 | 0.89 | 41.7 | 0.35 | 5.81 | – | Acid | − 0.63 | 0.20 | N/A |
| Tetracycline | 86.4 | 0.05 | 1.10 | 0.76 | 5.06, 7.63, 8.77d | 10.52d | Zwitterion | − 0.90 | − 0.90 | Weak OAT3 interaction |
| Theophylline | 5.50 | 0.91 | 65.1 | 0.52 | 8.51 | – | Neutral | − 0.09 | − 0.06 | N/A |
| Tocainide | 67.5 | 0.18 | 19.0 | 0.69 | – | 7.75d | Base | 0.03 | − 0.73 | N/A |
| Topiramate | 15.1 | 0.86 | 46.2 | 0.87 | 9.22d | – | Neutral | 0.60 | 0.61 | MATE2K |
| Venlafaxine | 80.0 | 0.09 | 27.6 | 0.73 | – | 9.64 | Base | 0.95 | 0.05 | N/A |
| Verapamil | 25.6 | − 0.35 | 20.9 | 0.16 | – | 8.74 | Base | 2.61 | 1.73 | P-gp, OCTN1, OCTN2 |
| Voriconazole | 1.57 | 0.97 | 96.5 | 0.42 | – | – | Neutral | 1.70 | 1.70 | N/A |
N/A No information available whether a drug was a substrate for renal drug transporters.
Apparent negative Freab are result of inclusion criteria (CR < 1.5) and were changed to 0 for graphical presentation.
Drugs were classified using the predominant species (> 50%) at pH 6.5, using either measured or calculated pKa data.
LogD6.5 calculated from pKa and LogD7.4, as described in the methods.
LogD7.4 and pKa values predicted using ACD (v.14.02) or obtained from BioBytes Masterfile (otherwise measured experimentally as described in the methods).
Lipophilic drugs, and those unionised at physiological pH, were associated with low CLR, (Supplementary Results, Figs. S4.1 and S4.2), in agreement with previous studies (Paine et al., 2010, Varma et al., 2009). No clear trends could be established between LogD7.4 or LogD6.5 and observed Freab of 45 drugs investigated (data not shown). High LogD7.4 did not appear to be predictive of high tubular reabsorption (Freab > 0.75), as a wide range of LogD7.4 values were associated with drugs in moderate to low Freab category (Supplementary Results Fig. S4.1). The majority of neutral drugs (62%) had high tubular reabsorption (Freab > 0.75), whereas the majority of ionised drugs had low Freab (< 0.25). The percent of acidic, basic, zwitterion and amphoteric drugs with Freab < 0.25 was 43%, 56%, 61% and 100%, respectively (data presented in detail in the Supplementary Results, Fig. S4.2).
3.2. Prediction of CLR from glomerular filtration only
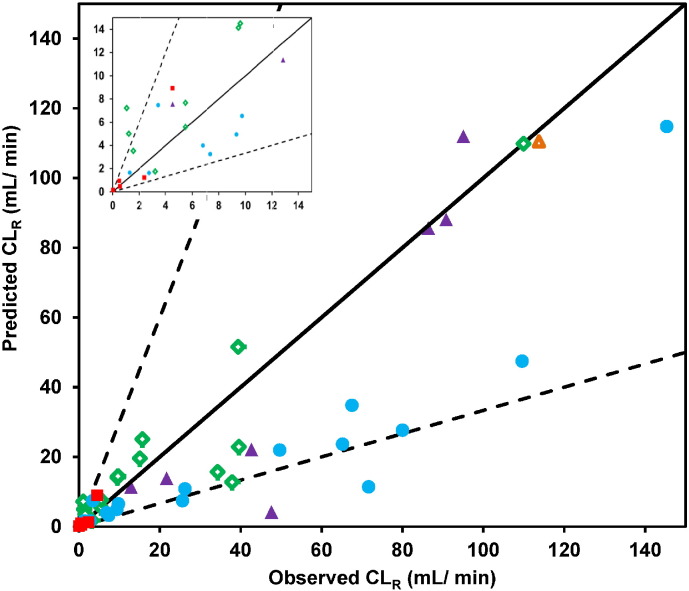
Predictive performance of the tubular reabsorption model was assessed using a subset of 45 drugs. Initial analysis was performed by assessing CLR prediction assuming that the glomerular filtration was the only contributing mechanism (Eq. (8)). This approach resulted in general over-prediction of CLR, as shown in Fig. 2 and Table 3; the predicted CLR for each individual drug are listed in the Supplementary Results, Table S4.2. The extent of over-prediction (> 3-fold) was particularly apparent for neutral (10 out of 15 drugs) and acidic drugs (4 out of 5 drugs). Antipyrine (neutral), caffeine (neutral), and isoxicam (acid) were the most pronounced outliers with the extent of over-prediction of CLR ranging from 75- to 202-fold for these drugs. Conversely, the majority of basic drugs were predicted well, especially betaxolol, citalopram, metoprolol and venlafaxine. For these four basic drugs, the assumption of glomerular filtration in isolation resulted in predicted CLR within 10% of the observed values.
Fig. 2.
Comparison of predicted and observed CLR using CLR,filt alone to predict CLR. Neutral ( ), basic (
), basic ( ), acidic (
), acidic ( ), zwitterion (
), zwitterion ( ) and amphoteric (
) and amphoteric ( ) drugs are indicated. Solid and dashed lines represent line of unity and 3-fold error, respectively.
) drugs are indicated. Solid and dashed lines represent line of unity and 3-fold error, respectively.
Table 3.
Assessment of the physiologically-based tubular reabsorption model for prediction of CLR. Performance of the mechanistic model was assessed initially for all drugs with a measured Caco-2 Papp value with the exception of those that showed evidence of net secretion (clearance ratio > 1.5). Subsequently, the tubular reabsorption model was reassessed after excluding drugs currently identified as substrates for drug transporters expressed within kidney.
| R2 | # (%) of drugs within 3-fold of observed CLR | gmfe | RMSE | |
|---|---|---|---|---|
| CLR,filt only | ||||
| All drugs (45) | 0.38 | 26 (58%) | 3.73 | 43.0 |
| Neutral (15) | 0.15 | 5 (33%) | 6.69 | 63.4 |
| Acid (5) | 0.75 | 1 (20%) | 16.45 | 18.0 |
| Basic (16) | 0.84 | 14 (88%) | 1.80 | 18.0 |
| Zwitterion (8) | 0.41 | 5 (63%) | 2.47 | 44.9 |
| Amphoteric (1) | N/A | 1 (100%) | 1.02 | 2.3 |
| Minimal model | ||||
| All drugs (45) | 0.76 | 39 (87%) | 1.96 | 20.9 |
| Neutral (15) | 0.86 | 13 (87%) | 1.86 | 10.4 |
| Acid (5) | 0.84 | 4 (80%) | 2.29 | 2.1 |
| Basic (16) | 0.79 | 14 (88%) | 2.18 | 31.0 |
| Zwitterion (8) | 0.84 | 7 (88%) | 1.73 | 18.3 |
| Amphoteric (1) | N/A | 1 (100%) | 1.03 | 3.3 |
| Non-substrates of renal transporters (29) | 0.65 | 25 (86%) | 2.07 | 19.3 |
| Neutral (10) | 0.95 | 8 (80%) | 1.88 | 7.2 |
| Acid (5) | 0.84 | 4 (80%) | 2.29 | 2.1 |
| Basic (13) | 0.76 | 12 (92%) | 2.19 | 28.0 |
| Zwitterion (1) | N/A | 1 (100%) | 1.66 | 3.0 |
| Amphoteric (0) | N/A | N/A | N/A | N/A |
3.3. Prediction of Freab using the minimal physiologically-based tubular reabsorption model
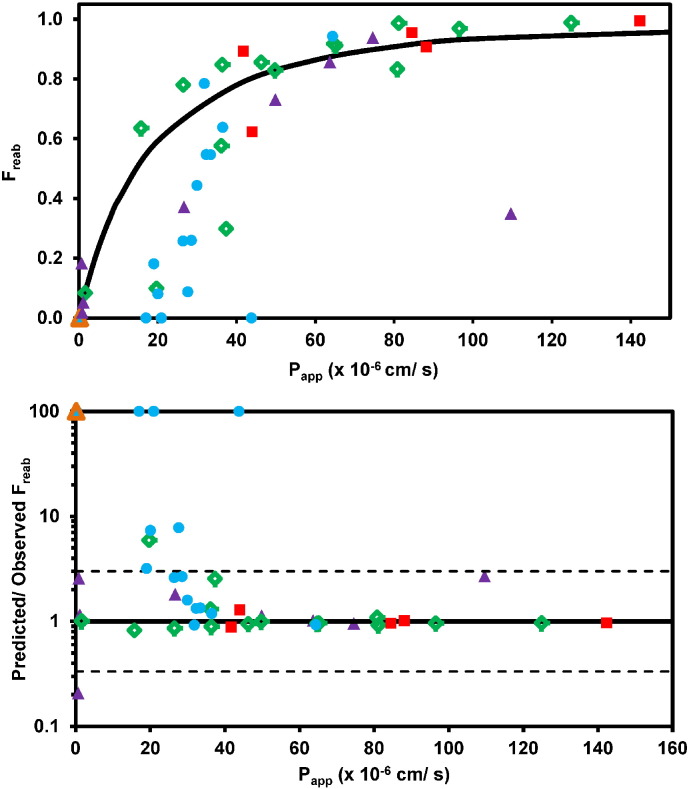
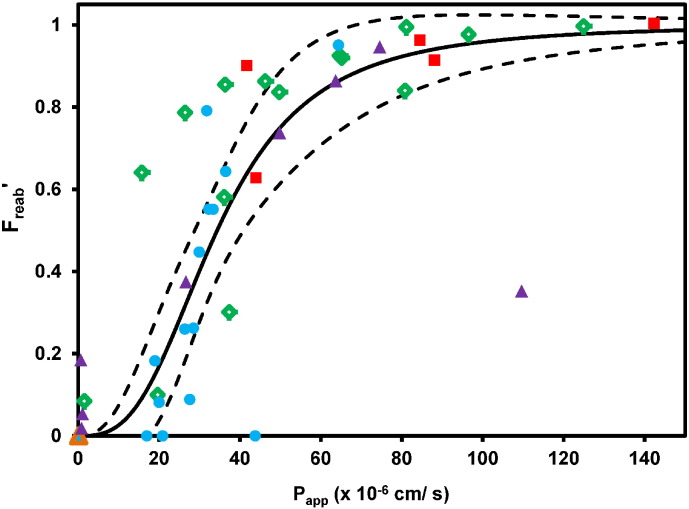
The IVIVE approach was used to predict the Freab and CLR from Caco-2 Papp data using the minimal mechanistic tubular reabsorption model, as outlined in the Materials and methods (Eqs. (11), (14)). The observed Freab was calculated from reported CLR and fu,p data, assuming the GFR value of 120 mL/min (Fig. 3). In some instances, apparently negative Freab and Freab′ values were obtained (e.g., atenolol and verapamil); this is an artefact of the inclusion criteria applied, given that the renal clearance ratio was used as cut off for net secretion (> 1.5). Overall there was a good agreement between predicted and observed Freab, albeit with over-prediction of Freab for some drugs with moderate Papp values (~ 20–40 × 10− 6 cm/s).
Fig. 3.
Comparison of observed and predicted Freab using the mechanistic tubular reabsorption model and Papp data obtained in Caco-2 cells. Panel A: Predicted relationship between Freab and Papp is shown by the solid black line, whereas observed data are shown by symbols; Panel B: Predicted/observed Freab are plotted as symbols, whereas solid and dashed black lines indicate Predicted/observed = 1 and 3-fold error, respectively. Symbols indicate neutral ( ), basic (
), basic ( ), acidic (
), acidic ( ), zwitterion (
), zwitterion ( ) and amphoteric (
) and amphoteric ( ) drugs. Drugs with negative values for observed Freab are plotted as Freab = 0 in Panel A, or predicted/observed Freab = 100 in Panel B, as described in the Materials and methods.
) drugs. Drugs with negative values for observed Freab are plotted as Freab = 0 in Panel A, or predicted/observed Freab = 100 in Panel B, as described in the Materials and methods.
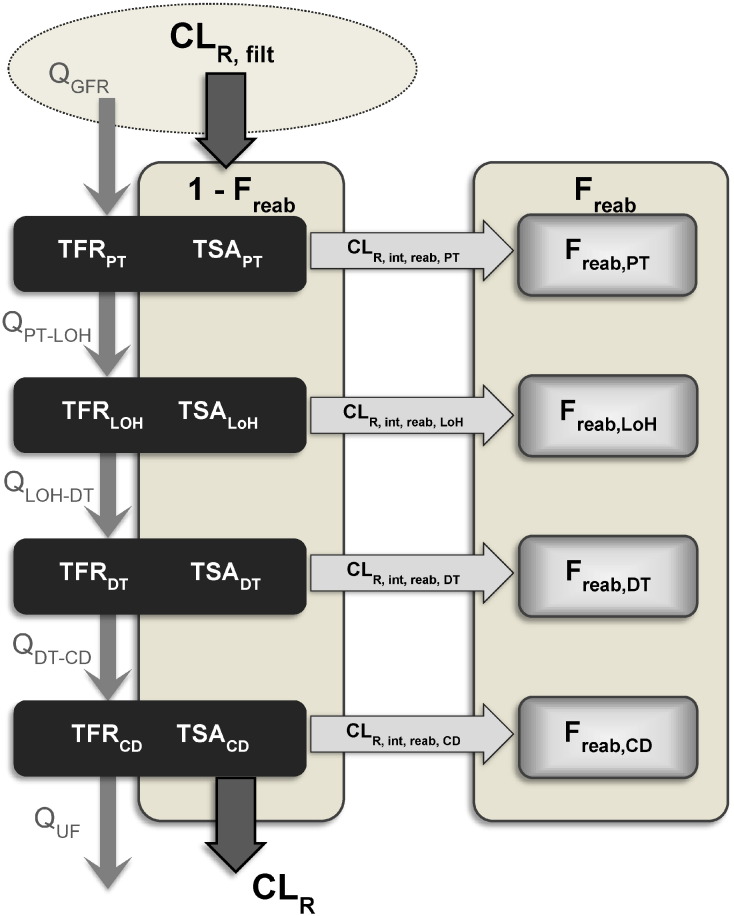
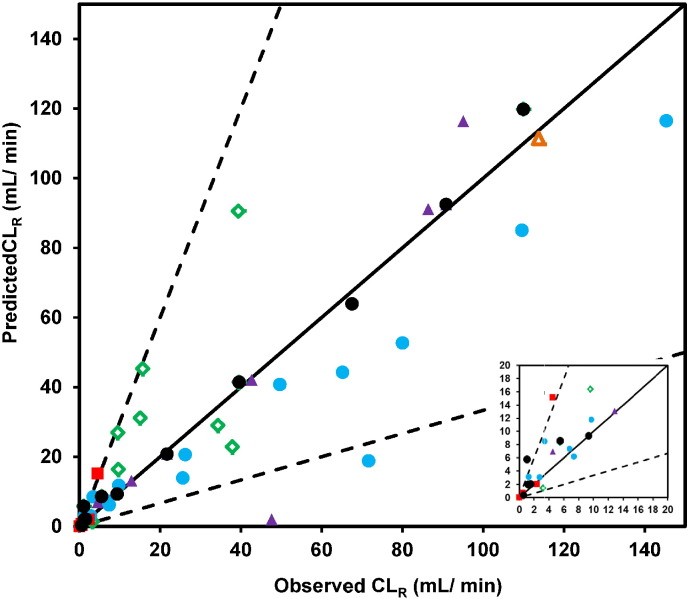
The predicted CLR were calculated for 45 drugs using the predicted Freab, together with GFR and urine flow (full results listed in Supplementary Results, Table S4.2). There was a good agreement between predicted and observed CLR data with < 2-fold bias for the whole dataset (Fig. 4 and Table 3). In particular, this trend was evident for neutral drugs (gmfe = 1.86), where 87% of CLR were predicted within 3-fold error of the observed value with antipyrine and caffeine being the only exceptions (over-prediction of 4.1 and 6.8-fold, respectively). In the case of basic drugs, a general CLR under-prediction trend was noted, as well as poor precision (RMSE = 31.0), in agreement with the over-prediction of Freab seen for this class of drugs (Fig. 3). Consideration of both glomerular filtration and reabsorption reduced the prediction accuracy in the case of betaxolol, citalopram, metoprolol and venlafaxine. However, the predicted CLR was still within 50–65% of the observed data. Despite this overall CLR under-prediction trend, it is important to note that the values for the majority of basic drugs (14/16) were predicted within 3-fold of the observed. Mexiletine and verapamil were the most pronounced outliers as the predicted CLR represented only 16 and 29% of the observed value, respectively. Consideration of pH gradient and ionisation was of particular relevance for this class of drugs, as the use of Papp data obtained under isotonic pH 7.4 conditions resulted in pronounced under-prediction of CLR for half of basic drugs in the dataset, with predicted CLR < 35% of the observed value (Supplementary Results Fig. S4.3).
Fig. 4.
Comparison between observed and predicted CLR by the mechanistic tubular reabsorption model. Symbols indicate neutral ( ), basic (
), basic ( ), acidic (
), acidic ( ), zwitterion (
), zwitterion ( ) and amphoteric (
) and amphoteric ( ) drugs respectively. Solid and dashed lines represent line of unity and 3-fold error, respectively. The inset shows the data for lower CLR values for clarity.
) drugs respectively. Solid and dashed lines represent line of unity and 3-fold error, respectively. The inset shows the data for lower CLR values for clarity.
Excluding drugs which were known/reported substrates of human kidney transporters had negligible impact on the success of CLR prediction (Table 3). In contrast, failing to account for the presence/absence of microvilli expressed by Caco-2 cell monolayers and nephron tubular cells resulted in reduced prediction success with only 27% of drugs predicted within 3-fold of the observed CLR. Comparison of predictive performances of different models stratified according to low, medium and highly reabsorption drug status is shown in Table 4.
Table 4.
Assessment of the predictive performance of various CLR prediction methods using gmfe and % predicted within 3-fold of observed CLR.
| gmfe (% predicted within 3-fold of observed) |
|||||
|---|---|---|---|---|---|
| Filtration onlya | No correction for microvillib | Proximal tubule onlyc | Reabsorption modeld | Papp–Freab′ calibratione | |
| All drugs (n = 45) | 3.73 (58%) | 5.35 (27%) | 2.17 (76%) | 1.96 (87%) | 1.65 (91%) |
| Low Freab (n = 17) | 1.17 (100%) | 5.02 (35%) | 1.59 (94%) | 1.97 (88%) | 1.34 (94%) |
| Medium Freab (n = 12) | 2.56 (75%) | 8.52 (17%) | 1.44 (92%) | 1.90 (92%) | 1.73 (92%) |
| High Freab (n = 16) | 16.86 (0%) | 4.03 (25%) | 4.11 (44%) | 2.01 (81%) | 1.98 (88%) |
CLR,filt calculated using Eq. (7) in main text.
No correction was made for surface area attributable to the presence/absence of microvilli when calculating CLR,int,reab,i.
CLR predicted using a model with only one tubular compartment representing proximal tubule (main contributor to reabsorption predicted by the model).
CLR predicted using the tubular reabsorption model after calibration of Papp data using Eq. (14), data are for all drugs including reference subset.
3.4. Empirical relationship between Freab′ and Papp and calibration approach
The Hill model was fitted to the observed Freab′ and Papp data for the 45 drugs selected (Fig. 5). The best-fit value and 95% confidence interval for Caco-2 Papp corresponding to Freab′ = 0.5 was estimated to be 34.4 (28.9–39.9) × 10− 6 cm/s. In addition, the Hill model was fitted to the Papp values and Freab′ predicted by the mechanistic tubular reabsorption model for 45 drugs. The resultant estimate of Papp corresponding to Freab′ = 0.5 was 14.8 (14.3–15.2) × 10− 6 cm/s.
Fig. 5.
Best-fit curve and 90% confidence interval of the Hill equation to the Papp and Freab′ data for 45 drugs (solid and dashed lines respectively). Symbols indicate neutral ( ), basic (
), basic ( ), acidic (
), acidic ( ), zwitterion (
), zwitterion ( ) and amphoteric (
) and amphoteric ( ) drugs. Drugs with negative values for observed Freab′ are plotted as Freab′ = 0, as described in the text.
) drugs. Drugs with negative values for observed Freab′ are plotted as Freab′ = 0, as described in the text.
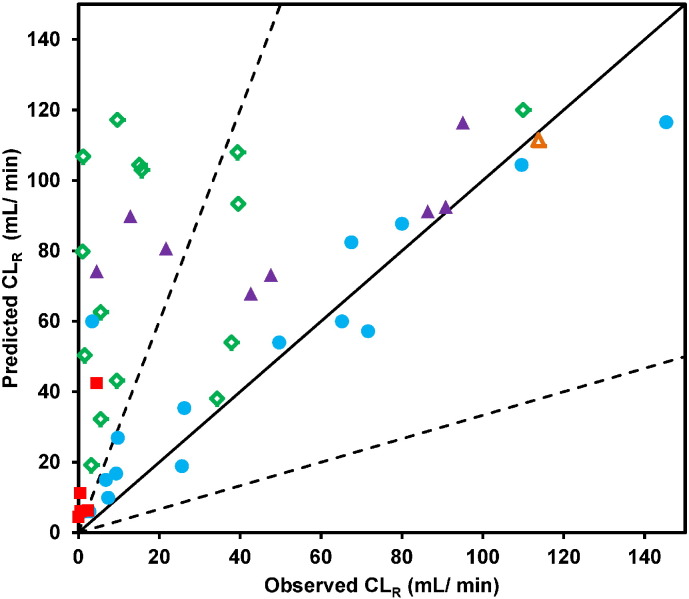
In order to evaluate the application of Papp–Freab′ calibration (Eq. (17)), 11 drugs were selected as reference ‘calibrator’ drugs (Papp,ref) covering a representative range of Freab′ and Papp values (Table 5). The remaining 34 drugs were treated as an internal ‘validation’ set. Following the fitting of the Hill equation to observed Freab′ and Papp,ref data for these 11 reference drugs, the best-fit estimates for a2 and b2 were 2.74 and 33.1 × 10− 6 cm/s. These were used to calculate values of Papp,calibrated for the validation dataset, and were subsequently applied for prediction of Freab′, Freab and CLR using the minimal physiologically-based reabsorption model, as done initially. Use of this calibrated approach led to considerable improvement in the predictive performance with 31/34 drugs in the internal validation set predicted within 3-fold of the observed CLR (gmfe = 1.73, Fig. 6). Comparable success was seen for the full dataset, with 41/45 drugs predicted within 3-fold of the observed CLR, and reduced bias (gmfe = 1.65) compared to the model before applying the Papp calibration. Particular improvement in the prediction of CLR following the Papp–Freab′ calibration was apparent for basic drugs, as 15/16 drugs were successfully predicted. An increase in prediction accuracy was also observed for neutral drugs (e.g., prednisone) and zwitterions (e.g., moxifloxacin) with moderate Papp values (20–40 × 10− 6 cm/s). The calibration approach resulted in marginal overall improvement in the prediction of CLR for drugs with Freab > 0.75. However, substantial improvement was noted for 9/11 highly reabsorbed drugs (Freab > 0.9), including isoxicam, probenecid, caffeine and antipyrine.
Table 5.
Reference drugs used for calibration of Caco-2 Papp data.
| Drug | CLR (mL/min) | Freab | Papp,ref (× 10− 6 cm/s) | Papp,ref,calibrateda (× 10− 6 cm/s) | Ionisation at pH 6.5 |
|---|---|---|---|---|---|
| Antipyrine | 1.22 | 0.99 | 124.9 | 229.49 | Neutral |
| Caffeine | 1.06 | 0.99 | 81.12 | 94.06 | Neutral |
| Chlorpropamide | 0.56 | 0.91 | 88.12 | 111.60 | Acid |
| Linezolid | 39.5 | 0.58 | 36.1 | 17.65 | Neutral |
| Oxprenolol | 9.35 | 0.44 | 29.95 | 12.00 | Base |
| Oxytetracycline | 90.8 | 0.02 | 0.85 | 0.01 | Zwitterion |
| Ribavirin | 110 | 0.08 | 1.55 | 0.03 | Neutral |
| Sparfloxacin | 21.7 | 0.73 | 49.83 | 34.35 | Zwitterion |
| Theophylline | 5.50 | 0.91 | 65.13 | 59.75 | Neutral |
| Tocainide | 67.5 | 0.18 | 19 | 4.68 | Base |
| Voriconazole | 1.57 | 0.97 | 96.51 | 134.68 | Neutral |
Papp,ref,calibrated calculated using Eq. (15) after fitting of the Hill equation to the Caco-2 Papp data and either observed or predicted (using minimal model of reabsorption) Freab.
Fig. 6.
Prediction of CLR using the minimal model following calibration of Papp data using reference drugs (n = 45 drugs). Symbols indicate neutral ( ), basic (
), basic ( ), acidic (
), acidic ( ), zwitterion (
), zwitterion ( ) and amphoteric (
) and amphoteric ( ) drugs in the internal ‘validation’ dataset and drugs in the reference dataset (●; n = 11). Solid and dashed lines represent line of unity and 3-fold error, respectively. The inset shows the data for lower CLR values for clarity.
) drugs in the internal ‘validation’ dataset and drugs in the reference dataset (●; n = 11). Solid and dashed lines represent line of unity and 3-fold error, respectively. The inset shows the data for lower CLR values for clarity.
4. Discussion
4.1. Physiological considerations for predicting tubular reabsorption
The 5-compartment minimal physiologically-based model was developed for the prediction of tubular reabsorption. Although static, the model accounted for physiological differences between regions of the nephron and captured complex underlying physiology of the kidney in a mechanistic manner. In addition to the model development, a comprehensive database of physiological parameters with relevance to pharmacokinetics of drugs in human kidney was collated. Quantitative human physiological data were sparse in general and available from a few primary research articles, but were supported by data in preclinical species where possible (see Supplementary Methods, Tables S1.1–4). For some physiological parameters, such as glomerular filtration rate, considerable inter-individual variability, as well as bias in some of the commonly used methods has been reported (Delanaye et al., 2012, Soveri et al., 2014, Sterner et al., 2008). The lack of data and information on variability in reported values for physiological parameters will inevitably result in a level of uncertainty associated with the relevant input model parameters. For example, calculation of apparent Freab was dependent on the value of GFR; the sensitivity of Freab to changes in GFR was evident for drugs exhibiting low tubular reabsorption (Freab < 0.25). However, as the reported data on the inter-individual variability in GFR were limited in the clinical studies in the database, its potential impact on the estimation of apparent Freab was not considered in the current analysis.
Predictive performance of the mechanistic tubular reabsorption model was assessed against a representative set of 45 drugs, focusing in particular on the impact of the tubular surface area in the model development (Table 1, Table 4). The mechanistic tubular reabsorption model was applied to predict both regional and overall Freab′ for the selected dataset. The analysis has shown that reabsorption in the proximal tubule compartment was the major contributor to the overall predicted Freab for most of the drugs. Consideration of tubular reabsorption solely in this region within the model had marginal impact on the prediction of CLR for drugs with low Freab (e.g., atenolol and melagatran). In contrast, this approach resulted in reduced CLR prediction accuracy compared with the ultimate 5-compartment model for extensively reabsorbed drugs such as antipyrine and isoxicam (Table 4). The reabsorption in other tubular regions was not considered in the previously reported static model (Kunze et al., 2014). However, it is important to note that in the study by Kunze et al. only one drug in the dataset exhibited notable net reabsorption (desipramine, apparent Freab of 0.31) and drugs showing extensive reabsorption (Freab′ ~ 1, CLR approaching 1–2 mL/min, (Tucker, 1981)) were not included in the analysis.
The 5-compartment tubular reabsorption model was also able to account for regional differences in the expression of microvilli and subsequent effect on the surface area to be used for scaling of permeability data. A pronounced under-prediction of CLR was observed for most of the drugs in the dataset if differences in microvilli related surface area between Caco-2 monolayers and the loop of Henle, distal tubule and collecting duct regions were ignored (Supplementary Results Fig. S.4.4); the exceptions were drugs with low Papp (e.g., melagatran). All of the above emphasises the necessity for appropriate interpretation and implementation of complex physiological features of human kidney in the model to allow mechanistic prediction of CLR.
4.2. Validity of Caco-2 cell monolayers as in vitro model for renal tubular reabsorption
The ability to cross biological membranes is an important determinant of rate of absorption and rate and route of elimination (Smith et al., 2014, Varma et al., 2015). Existing in vitro proximal tubule models express a range of functional drug transporters, confounding measurement of passive permeability in the nephron (Brown et al., 2008, Fouda et al., 1990, Kunze et al., 2014). Although primary cultured collecting duct cells can be used for this purpose, these methods require a consistent supply of high quality kidney tissue (Trifillis and Kahng, 1990). Caco-2 cell monolayer assay performed in the presence of a transporter inhibitor cocktail is widely used to measure passive permeability and was therefore considered in the current work. Alternatively, permeability data obtained in MDCK cells (Avdeef and Tam, 2010, Irvine et al., 1999) can be considered for prediction of Freab. The application of the MDCK data in this model would require adequate implementation of the microvilli/surface area considerations highlighted, together with the use of transporter inhibitor cocktail in the in vitro assay to minimise the impact of differences in endogenous transporter expression on Papp data.
Beyond inter-system differences in permeability (e.g. Caco-2 vs. MDCK vs. nephron tubule cells), inter-laboratory variability has been widely reported for experimental data generated in either Caco-2 or MDCK cells (Artursson et al., 2001, Bentz et al., 2013). Reference compounds are often used to standardise in vitro assay data and minimise the impact of this variability on the subsequent IVIVE (Artursson et al., 2001, Hasegawa et al., 2003, Sohlenius-Sternbeck et al., 2012). The Papp–Freab′ calibration approach proposed here can be used in that context. While this method resulted in the improved prediction of CLR (Fig. 6 and Table 4), the choice of drugs used as reference dataset was fundamental. As such, the Papp–Freab′ calibration proposed here should be applied with caution; further work is needed to refine and validate this approach using an external dataset of Caco-2 (or MDCK) Papp data.
The Caco-2 permeability data were measured under a pH-gradient in order to mimic the slightly acidic nature of urine typically found in vivo. The pH consideration was particularly important for basic drugs because the use of permeability data under iso-pH conditions resulted in systematic under-prediction of CLR for this class (Supplementary Results, Fig. S4.3). However, despite the use of the pH-gradient, an apparent over-prediction of Freab was still evident for some basic drugs, mostly those with moderate Papp (approx. 20–40 × 10− 6 cm/s). Two pH-related mechanisms could potentially contribute to this under-prediction. Firstly, a reduced fraction of unionised drug in acidic conditions may affect the permeation rate of the total (ionised and unionised) drug. Secondly, the concentration gradient of the unionised basic drug in vivo could be reduced in acidic conditions (due to water reabsorption), or in extreme cases reversed which would not be represented by the typical in vitro permeability assay. Additionally, it is important to consider that if left uncontrolled, urine pH can vary substantially in clinical studies (Özdemir et al., 2004), which can confound subsequent pharmacokinetic analyses and estimation of CLR and Freab used for model validation. Finally, potential contribution of tubular reabsorption via active transport in vivo via as yet unknown transporter-substrate interactions should not be disregarded.
4.3. Application of the mechanistic tubular reabsorption model and existing gaps
Use of the mechanistic tubular reabsorption model in conjunction with in vitro permeability data in a pure ‘bottom-up’ manner resulted in CLR prediction accuracy comparable with quantitative structure-pharmacokinetic relationships and allometric approaches. In contrast to other methods, the added advantage of this IVIVE approach is the mechanistic insight into renal drug elimination because of the physiological nature of the model. This model provides solid foundation to inform future PBPK efforts towards understanding mechanisms behind changes in CLR following pathophysiological changes in kidney, by accounting for the effects of factors such as age and renal impairment on the values of physiological parameters. For example, the lengths of each region of the tubule used in the model are representative of values reported for the healthy adult population (see Table S1.4 in the supplementary methods). Proximal tubule length has been reported to change with age (Darmady et al., 1973, Fetterman et al., 1965). Accounting for this, as well as any changes in other physiological parameters, could be used to investigate potential differences in tubular reabsorption in paediatric and geriatric populations.
Accuracy of CLR prediction using the tubular reabsorption model was consistent across all ionisation groups, with a slightly higher bias seen for acidic drugs (Table 3). CLR was over-predicted by more than 4-fold for three drugs (antipyrine, caffeine and isoxicam), which all had apparent Freab values ≥ 0.99. For these drugs, predicted CLR were very sensitive to even minor relative changes in Freab. However, the differences between predicted and observed CLR for drugs with very high Freab represented ≤ 15% of the plasma clearance of these drugs in healthy subjects, as they are also extensively metabolised by the liver (Huffman et al., 1974, Shaw et al., 1985, Tang-Liu et al., 1982). Therefore, potential errors in prediction of CLR for extensively reabsorbed drugs were less likely to have a substantial impact on the prediction of the overall in vivo clearance for such drugs.
The dataset used for model assessment here included several drugs (e.g., caffeine, antipyrine) which are extensively reabsorbed and are known to exhibit urine flow and pH dependent CLR (Birkett and Miners, 1991, Mawer and Lee, 1968, Taylor and Blaschke, 1984). It is beyond capability (and purpose) of the model to describe/predict urine flow dependent CLR quantitatively, as reported by some of the previous modelling efforts (Hall and Rowland, 1984, Neuhoff et al., 2013, Tang-Liu et al., 1983). However, modulation of the TFRCD and urine flow rate parameters in the model can be used to indicate whether a drug is expected to exhibit urine flow dependent CLR, as shown by the sensitivity analysis presented in Supplementary Results, Fig. S4.5. It is anticipated that incorporation of the mechanistic prediction of tubular reabsorption into existing PBPK kidney models, e.g., (Neuhoff et al., 2013), will allow for more accurate predictions of changes in tubular reabsorption and CLR due to changes in urine flow rates.
IVIVE of renal metabolic clearance has been investigated in several studies (Gill et al., 2012, Gill et al., 2013, Knights et al., 2016). In contrast, prediction of CLR,sec using ‘bottom-up’ approach is currently challenging due to lack of a ‘gold standard’ in vitro system and physiologically relevant scaling factors (Felmlee et al., 2013, Hsu et al., 2014, Kunze et al., 2014, Posada et al., 2015, Watanabe et al., 2011). Static models of CLR,sec (Watanabe et al., 2011) could be used alongside the current reabsorption model for prediction of CLR; however, such an approach is unlikely to be adequate when metabolism is simultaneously involved. Consideration of metabolism and secretion was outside of the scope of the current model, but these elements could potentially be incorporated by expansion of the current model. While such expansion would not be beneficial for the majority of drugs investigated in the current study, it might be of interest for probenecid which has high apparent Freab (0.955) and may undergo renal glucuronidation (Vree et al., 1993). Dynamic models, such as PBPK kidney models, which feature reabsorption, secretion and metabolism processes can be adapted/refined to incorporate mechanistic description of tubular reabsorption using the principles of the current model. Although some PBPK kidney models allow for metabolism-transport interplay to be investigated (Neuhoff et al., 2013), obtaining suitable clinical data to validate such models remains challenging (Tucker, 1981). Finally, considering a conservation of the tissue level organisation between mammalian species (e.g., regional differentiation of nephron), the mechanistic tubular reabsorption model could be adapted for prediction of Freab and CLR in preclinical species, by accounting for specific differences in surface area and flow rate parameters.
4.4. Conclusion
A novel 5-compartment mechanistic tubular reabsorption model was developed for prediction of Freab and CLR from Caco-2 Papp data. A database of clinical CLR values for 157 drugs was collated, as well as a comprehensive database of physiological parameters with relevance to IVIVE of renal excretion clearance. The mechanistic model successfully predicted CLR for 45 chemically diverse drugs for which filtration or reabsorption appeared to be the dominant mechanism. In addition, empirical Papp–Freab′ calibration method was proposed to account for inter-assay variability in permeability data. The physiological assumptions of the model represent an excellent basis for future studies, e.g., simultaneous consideration of secretion and reabsorption for mechanistic predictions of CLR and prediction of Freab in different pathophysiological conditions (e.g., renal impairment). Overall, the mechanistic model represents an important addition to the currently existing IVIVE toolbox, and a step towards enabling physiologically-based predictions of renal tubular reabsorption, and its contribution to CLR.
Conflict of interest
The authors have no conflict of interest to declare.
Acknowledgements
D.S. was supported by a PhD studentship from the Biotechnology and Biological Sciences Research Council UK (BB/J500379/1) and AstraZeneca, Cambridge, UK. The authors would like to acknowledge Mark Wenlock and Neil Shearer for assistance with generating pKa data, and members of the Centre for Applied Pharmacokinetic Research of The University of Manchester, in particular Andres Olivares-Morales, Drs Hitesh Mistry and Frauke Assmus for valuable discussions and comments.
Footnotes
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.ejps.2016.03.018.
Appendix A. Supplementary data
Supplementary Methods
Supplementary Results (Table S2.1)
Supplementary Results (Table S3.1)
Supplementary Results
References
- Artursson P., Palm K., Luthman K. Caco-2 monolayers in experimental and theoretical predictions of drug transport. Adv. Drug Deliv. Rev. 2001;46:27. doi: 10.1016/s0169-409x(00)00128-9. [DOI] [PubMed] [Google Scholar]
- Avdeef A., Tam K.Y. How well can the Caco-2/Madin–Darby canine kidney models predict effective human jejunal permeability? J. Med. Chem. 2010;53(9):3566. doi: 10.1021/jm901846t. [DOI] [PubMed] [Google Scholar]
- Bentz J., O'Connor M.P., Bednarczyk D., Coleman J., Lee C., Palm J., Pak Y.A., Perloff E.S., Reyner E., Balimane P. Variability in P-glycoprotein inhibitory potency (IC50) using various in vitro experimental systems: implications for universal digoxin drug–drug interaction risk assessment decision criteria. Drug Metab. Dispos. 2013;41(7):1347. doi: 10.1124/dmd.112.050500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birkett D., Miners J. Caffeine renal clearance and urine caffeine concentrations during steady state dosing. Implications for monitoring caffeine intake during sports events. Br. J. Clin. Pharmacol. 1991;31(4):405. doi: 10.1111/j.1365-2125.1991.tb05553.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown C., Sayer R., Windass A., Haslam I., De Broe M., D'Haese P., Verhulst A. Characterisation of human tubular cell monolayers as a model of proximal tubular xenobiotic handling. Toxicol. Appl. Pharmacol. 2008;233(3):428. doi: 10.1016/j.taap.2008.09.018. [DOI] [PubMed] [Google Scholar]
- Chew-Harris J.S., Chin P.K., Florkowski C.M., George P., Endre Z. Removal of body surface area normalisation improves raw-measured GFR estimation by the CKD-EPI equation and drug dosing in the obese. Intern. Med. J. 2015;45(7):466. doi: 10.1111/imj.12791. [DOI] [PubMed] [Google Scholar]
- Darmady E., Offer J., Woodhouse M. The parameters of the ageing kidney. J. Pathol. 1973;109(3):195. doi: 10.1002/path.1711090304. [DOI] [PubMed] [Google Scholar]
- Dave R., Morris M. Quantitative structure–pharmacokinetic relationships for the prediction of renal clearance in humans. Drug Metab. Dispos. 2015;43(1):73. doi: 10.1124/dmd.114.059857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dave R.A., Morris M.E. Semi-mechanistic kidney model incorporating physiologically-relevant fluid reabsorption and transporter-mediated renal reabsorption: pharmacokinetics of γ-hydroxybutyric acid and l-lactate in rats. J. Pharmacokinet. Pharmacodyn. 2015;42(5):497. doi: 10.1007/s10928-015-9441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delanaye P., Schaeffner E., Ebert N., Cavalier E., Mariat C., Krzesinski J., Moranne O. Normal reference values for glomerular filtration rate: what do we really know? Nephrol. Dial. Transplant. 2012;27(7):2664. doi: 10.1093/ndt/gfs265. [DOI] [PubMed] [Google Scholar]
- Dooley M.J., Poole S.G. Poor correlation between body surface area and glomerular filtration rate. Cancer Chemother. Pharmacol. 2000;46(6):523. doi: 10.1007/PL00006751. [DOI] [PubMed] [Google Scholar]
- Felmlee M.A., Dave R.A., Morris M.E. Mechanistic models describing active renal reabsorption and secretion: a simulation-based study. AAPS J. 2013;15(1):278. doi: 10.1208/s12248-012-9437-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetterman G., Shuplock N., Philipp F., Gregg H. The growth and maturation of human glomeruli and proximal convolutions from term to adulthood: studies by microdissection. Pediatrics. 1965;35:601. [PubMed] [Google Scholar]
- Fouda A., Fauth C., Roch-Ramel F. Transport of organic cations by kidney epithelial cell line LLC-PK1. J. Pharmacol. Exp. Ther. 1990;252(1):286. [PubMed] [Google Scholar]
- Galetin A. Rationalizing underprediction of drug clearance from enzyme and transporter kinetic data: from in vitro tools to mechanistic modeling. In: Nagar S., Argikar A.U., Tweedie J.D., editors. Enzyme Kinetics in Drug Metabolism: Fundamentals and Applications. Humana Press; Totowa, NJ: 2014. p. 255. [DOI] [PubMed] [Google Scholar]
- Gertz M., Harrison A., Houston J.B., Galetin A. Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab. Dispos. 2010;38(7):1147. doi: 10.1124/dmd.110.032649. [DOI] [PubMed] [Google Scholar]
- Giacomini K.M., Huang S.-M., Tweedie D.J., Benet L.Z., Brouwer K.L., Chu X., Dahlin A., Evers R., Fischer V., Hillgren K.M. Membrane transporters in drug development. Nat. Rev. Drug Discov. 2010;9(3):215. doi: 10.1038/nrd3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill K.L., Houston J.B., Galetin A. Characterization of in vitro glucuronidation clearance of a range of drugs in human kidney microsomes: comparison with liver and intestinal glucuronidation and impact of albumin. Drug Metab. Dispos. 2012;40(4):825. doi: 10.1124/dmd.111.043984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill K.L., Gertz M., Houston J.B., Galetin A. Application of a physiologically based pharmacokinetic model to assess propofol hepatic and renal glucuronidation in isolation: utility of in vitro and in vivo data. Drug Metab. Dispos. 2013;41(4):744. doi: 10.1124/dmd.112.050294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall S., Rowland M. Relationship between renal clearance, protein binding and urine flow for digitoxin, a compound of low clearance in the isolated perfused rat kidney. J. Pharmacol. Exp. Ther. 1984;228(1):174. [PubMed] [Google Scholar]
- Hasegawa M., Kusuhara H., Endou H., Sugiyama Y. Contribution of organic anion transporters to the renal uptake of anionic compounds and nucleoside derivatives in rat. J. Pharmacol. Exp. Ther. 2003;305(3):1087. [Google Scholar]
- Higgins J., Thompson S.G. Quantifying heterogeneity in a meta-analysis. Stat. Med. 2002;21(11):1539. doi: 10.1002/sim.1186. [DOI] [PubMed] [Google Scholar]
- Higgins J.P., Thompson S.G., Deeks J.J., Altman D.G. Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu V., de LT Vieira M., Zhao P., Zhang L., Zheng J.H., Nordmark A., Berglund E.G., Giacomini K.M., Huang S.-M. Towards quantitation of the effects of renal impairment and probenecid Inhibition on kidney uptake and efflux transporters, using physiologically based pharmacokinetic modelling and simulations. Clin. Pharmacokinet. 2014;53(3):283. doi: 10.1007/s40262-013-0117-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huffman D., Shoeman D., Azarnoff D. Correlation of the plasma elimination of antipyrine and the appearance of 4-hydroxy antipyrine in the urine of man. Biochem. Pharmacol. 1974;23(2):197. doi: 10.1016/0006-2952(74)90410-9. [DOI] [PubMed] [Google Scholar]
- Huh Y., Smith D.E., Rose Feng M. Interspecies scaling and prediction of human clearance: comparison of small-and macro-molecule drugs. Xenobiotica. 2011;41(11):972. doi: 10.3109/00498254.2011.598582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irvine J.D., Takahashi L., Lockhart K., Cheong J., Tolan J.W., Selick H., Grove J.R. MDCK (Madin–Darby canine kidney) cells: a tool for membrane permeability screening. J. Pharm. Sci. 1999;88(1):28. doi: 10.1021/js9803205. [DOI] [PubMed] [Google Scholar]
- Ito S., Ando H., Ose A., Kitamura Y., Ando T., Kusuhara H., Sugiyama Y. Relationship between the urinary excretion mechanisms of drugs and their physicochemical properties. J. Pharm. Sci. 2013;102(9):3294. doi: 10.1002/jps.23599. [DOI] [PubMed] [Google Scholar]
- Jadhav P.R., Cook J., Sinha V., Zhao P., Rostami-Hodjegan A., Sahasrabudhe V., Stockbridge N., Powell J.R. A proposal for scientific framework enabling specific population drug dosing recommendations. J. Clin. Pharmacol. 2015;55(10):1073. doi: 10.1002/jcph.579. [DOI] [PubMed] [Google Scholar]
- Jones G.R. Estimating renal function for drug dosing decisions. Clin. Biochem. Rev. 2011;32(2):81. [PMC free article] [PubMed] [Google Scholar]
- Kah M., Brown C.D. LogD: lipophilicity for ionisable compounds. Chemosphere. 2008;72(10):1401. doi: 10.1016/j.chemosphere.2008.04.074. [DOI] [PubMed] [Google Scholar]
- Knights K.M., Spencer S.M., Fallon J.K., Chau N., Smith P.C., Miners J.O. Scaling factors for the in vitro-in vivo extrapolation (IV-IVE) of renal drug and xenobiotic glucuronidation clearance. Br. J. Clin. Pharmacol. 2016 doi: 10.1111/bcp.12889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunze A., Huwyler J., Poller B., Gutmann H., Camenisch G. In vitro-in vivo extrapolation method to predict human renal clearance of drugs. J. Pharm. Sci. 2014;103(3):994. doi: 10.1002/jps.23851. [DOI] [PubMed] [Google Scholar]
- Layton A.T. A mathematical model of the urine concentrating mechanism in the rat renal medulla. I. Formulation and base-case results. Am. J. Physiol. Ren. Physiol. 2011;300(2):F356. doi: 10.1152/ajprenal.00203.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mawer G., Lee H. Value of forced diuresis in acute barbiturate poisoning. BMJ. 1968;2(5608):790. doi: 10.1136/bmj.2.5608.790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moestrup S.K., Cui S., Vorum H., Bregengård C., Bjørn S., Norris K., Gliemann J., Christensen E.I. Evidence that epithelial glycoprotein 330/megalin mediates uptake of polybasic drugs. J. Clin. Invest. 1995;96(3):1404. doi: 10.1172/JCI118176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrissey K., Wen C., Johns S., Zhang L., Huang S., Giacomini K. The UCSF-FDA TransPortal: a public drug transporter database. Clin. Pharmacol. Ther. 2012;92(5):545. doi: 10.1038/clpt.2012.44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrissey K., Stocker S., Wittwer M., Xu L., Giacomini K. Renal transporters in drug development. Annu. Rev. Pharmacol. Toxicol. 2013;53:503. doi: 10.1146/annurev-pharmtox-011112-140317. [DOI] [PubMed] [Google Scholar]
- Nagai J., Takano M. Molecular aspects of renal handling of aminoglycosides and strategies for preventing the nephrotoxicity. Drug Metab. Pharmacokinet. 2004;19(3):159. doi: 10.2133/dmpk.19.159. [DOI] [PubMed] [Google Scholar]
- Neuhoff S., Gaohua L., Burt H., Jamei M., Li L., Tucker G.T., Rostami-Hodjegan A. Accounting for transporters in renal clearance: towards a mechanistic kidney model (Mech KiM) In: Sugiyama Y., Steffansen B., editors. Transporters in Drug Development. Springer; 2013. p. 155. [Google Scholar]
- Nyman H., Dowling T., Hudson J., Peter W., Joy M., Nolin T. Comparative evaluation of the Cockcroft–Gault equation and the Modification of Diet in Renal Disease (MDRD) study equation for drug dosing: an opinion of the Nephrology Practice and Research Network of the American College of Clinical Pharmacy. Pharmacotherapy. 2011;31(11):1130. doi: 10.1592/phco.31.11.1130. [DOI] [PubMed] [Google Scholar]
- Olivares-Morales A., Lennernäs H., Aarons L., Rostami-Hodjegan A. Translating human effective jejunal intestinal permeability to surface-dependent intrinsic permeability: a pragmatic method for a more mechanistic prediction of regional oral drug absorption. AAPS J. 2015;17(5):1177. doi: 10.1208/s12248-015-9758-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozawa N., Shimizu T., Morita R., Yokono Y., Ochiai T., Munesada K., Ohashi A., Aida Y., Hama Y., Taki K. Transporter database, TP-search: a web-accessible comprehensive database for research in pharmacokinetics of drugs. Pharm. Res. 2004;21(11):2133. doi: 10.1023/b:pham.0000048207.11160.d0. [DOI] [PubMed] [Google Scholar]
- Özdemir M., Crewe K.H., Tucker G.T., Rostami-Hodjegan A. Assessment of in vivo CYP2D6 activity: differential sensitivity of commonly used probes to urine pH. J. Clin. Pharmacol. 2004;44(12):1398. doi: 10.1177/0091270004269582. [DOI] [PubMed] [Google Scholar]
- Pai M.P. Estimating the glomerular filtration rate in obese adult patients for drug dosing. Adv. Chronic Kidney Dis. 2010;17(5) doi: 10.1053/j.ackd.2010.05.010. [DOI] [PubMed] [Google Scholar]
- Paine S., Barton P., Bird J., Denton R., Menochet K., Smith A., Tomkinson N., Chohan K. A rapid computational filter for predicting the rate of human renal clearance. J. Mol. Graphics Modell. 2010;29(4):529. doi: 10.1016/j.jmgm.2010.10.003. [DOI] [PubMed] [Google Scholar]
- Paine S., Ménochet K., Denton R., McGinnity D., Riley R. Prediction of human renal clearance from preclinical species for a diverse set of drugs that exhibit both active secretion and net reabsorption. Drug Metab. Dispos. 2011;39(6):1008. doi: 10.1124/dmd.110.037267. [DOI] [PubMed] [Google Scholar]
- Posada M., Bacon J., Schneck K., Tirona R., Kim R., Higgins J., Pak Y., Hall S., Hillgren K. Prediction of renal transporter mediated drug–drug interactions for pemetrexed using physiologically based pharmacokinetic modeling. Drug Metab. Dispos. 2015;43(3):325. doi: 10.1124/dmd.114.059618. [DOI] [PubMed] [Google Scholar]
- Rostami-Hodjegan A. Complex patients-complex DDI: is there a straight way forward? Biopharm. Drug Dispos. 2015;36(2):69. doi: 10.1002/bdd.1939. [DOI] [PubMed] [Google Scholar]
- Schmitz C., Hilpert J., Jacobsen C., Boensch C., Christensen E., Luft F., Willnow T. Megalin deficiency offers protection from renal aminoglycoside accumulation. J. Biol. Chem. 2002;277(1):618. doi: 10.1074/jbc.M109959200. [DOI] [PubMed] [Google Scholar]
- Shaw P., Houston J., Rowland M., Hopkins K., Thiercelin J., Morselli P. Antipyrine metabolite kinetics in healthy human volunteers during multiple dosing of phenytoin and carbamazepine. Br. J. Clin. Pharmacol. 1985;20(6):611. doi: 10.1111/j.1365-2125.1985.tb05119.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simerville J., Maxted W., Pahira J. Urinalysis: a comprehensive review. Am. Fam. Physician. 2005;71(6):1153. [PubMed] [Google Scholar]
- Smith D., Artursson P., Avdeef A., Di L., Ecker G.F., Faller B., Houston J.B., Kansy M., Kerns E.H., Krämer S.D. Passive lipoidal diffusion and carrier-mediated cell uptake are both important mechanisms of membrane permeation in drug disposition. Mol. Pharm. 2014;11(6):1727. doi: 10.1021/mp400713v. [DOI] [PubMed] [Google Scholar]
- Sohlenius-Sternbeck A.-K., Jones C., Ferguson D., Middleton B.J., Projean D., Floby E., Bylund J., Afzelius L. Practical use of the regression offset approach for the prediction of in vivo intrinsic clearance from hepatocytes. Xenobiotica. 2012;42(9):841. doi: 10.3109/00498254.2012.669080. [DOI] [PubMed] [Google Scholar]
- Soveri I., Berg U., Björk J., Elinder C., Grubb A., Mejare I., Sterner G., Bäck S., SBU G. Measuring GFR: a systematic review. Am. J. Kidney Dis. 2014;64(3):411. doi: 10.1053/j.ajkd.2014.04.010. [DOI] [PubMed] [Google Scholar]
- Sterner G., Frennby B., Mansson S., Nyman U., Van Westen D., Almén T. Determining ‘true’ glomerular filtration rate in healthy adults using infusion of inulin and comparing it with values obtained using other clearance techniques or prediction equations. Scand. J. Urol. Nephrol. 2008;42(3):278. doi: 10.1080/00365590701701806. [DOI] [PubMed] [Google Scholar]
- Strolin B.M., Whomsley R., Mathy F., Jacques P., Espie P., Canning M. Stereoselective renal tubular secretion of levocetirizine and dextrocetirizine, the two enantiomers of the H1-antihistamine cetirizine. Fundam. Clin. Pharmacol. 2008;22(1):19. doi: 10.1111/j.1472-8206.2007.00543.x. [DOI] [PubMed] [Google Scholar]
- Tang-Liu D., Williams R., Riegelman S. Nonlinear theophylline elimination. Clin. Pharmacol. Ther. 1982;31(3):358. doi: 10.1038/clpt.1982.46. [DOI] [PubMed] [Google Scholar]
- Tang-Liu D., Tozer T., Riegelman S. Dependence of renal clearance on urine flow: a mathematical model and its application. J. Pharm. Sci. 1983;72(2):154. doi: 10.1002/jps.2600720215. [DOI] [PubMed] [Google Scholar]
- Tanihara Y., Masuda S., Sato T., Katsura T., Ogawa O., Inui K. Substrate specificity of MATE1 and MATE2-K, human multidrug and toxin extrusions/H (+)-organic cation antiporters. Biochem. Pharmacol. 2007;74(2):359. doi: 10.1016/j.bcp.2007.04.010. [DOI] [PubMed] [Google Scholar]
- Taylor G., Blaschke T. Measurement of antipyrine half-life from urinary drug concentrations [letter] Br. J. Clin. Pharmacol. 1984;18(4):650. doi: 10.1111/j.1365-2125.1984.tb02524.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trifillis A., Kahng M. Characterization of an in vitro system of human renal papillary collecting duct cells. In Vitro Cell. Dev. Biol. 1990;26(5):441. doi: 10.1007/BF02624085. [DOI] [PubMed] [Google Scholar]
- Tucker G. Measurement of the renal clearance of drugs. Br. J. Clin. Pharmacol. 1981;12(6):761. doi: 10.1111/j.1365-2125.1981.tb01304.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urakami Y., Kimura N., Okuda M., Inui K. Creatinine transport by basolateral organic cation transporter hOCT2 in the human kidney. Pharm. Res. 2004;21(6):976. doi: 10.1023/b:pham.0000029286.45788.ad. [DOI] [PubMed] [Google Scholar]
- Varma M., Feng B., Obach R., Troutman M., Chupka J., Miller H., El-Kattan A. Physicochemical determinants of human renal clearance. J. Med. Chem. 2009;52(15):4844. doi: 10.1021/jm900403j. [DOI] [PubMed] [Google Scholar]
- Varma M.V., Steyn S.J., Allerton C., El-Kattan A.F. Predicting clearance mechanism in drug discovery: Extended Clearance Classification System (ECCS) Pharm. Res. 2015;32(12):3785. doi: 10.1007/s11095-015-1749-4. [DOI] [PubMed] [Google Scholar]
- Vree T.B., van Ewijk-Beneken Kolmer E.W.J., Wuis E.W., Hekster Y.A., Broekman M.M.M. Interindividual variation in the capacity-limited renal glucuronidation of probenecid by humans. Pharm. World Sci. 1993;15(5):197. doi: 10.1007/BF01880626. [DOI] [PubMed] [Google Scholar]
- Watanabe T., Kusuhara H., Watanabe T., Debori Y., Maeda K., Kondo T., Nakayama H., Horita S., Ogilvie B., Parkinson A. Prediction of the overall renal tubular secretion and hepatic clearance of anionic drugs and a renal drug–drug interaction involving organic anion transporter 3 in humans by in vitro uptake experiments. Drug Metab. Dispos. 2011;39(6):1031. doi: 10.1124/dmd.110.036129. [DOI] [PubMed] [Google Scholar]
- Weinstein A.M. A mathematical model of rat proximal tubule and loop of Henle. Am. J. Physiol. Ren. Physiol. 2015;308(10):F1076. doi: 10.1152/ajprenal.00504.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welling L., Welling D. Relationship between structure and function in renal proximal tubule. J. Electron Microsc. Tech. 1988;9(2):171. doi: 10.1002/jemt.1060090205. [DOI] [PubMed] [Google Scholar]
- Welling L., Evan A., Welling D. Shape of cells and extracellular channels in rabbit cortical collecting ducts. Kidney Int. 1981;20(2):211. doi: 10.1038/ki.1981.123. [DOI] [PubMed] [Google Scholar]
- Wenlock M.C., Potter T., Barton P., Austin R.P. A method for measuring the lipophilicity of compounds in mixtures of 10. J. Biomol. Screen. 2011;16(3):348. doi: 10.1177/1087057110396372. [DOI] [PubMed] [Google Scholar]
- Zamek-Gliszczynski M.J., Lee C.A., Poirier A., Bentz J., Chu X., Ellens H., Ishikawa T., Jamei M., Kalvass J.C., Nagar S. ITC recommendations for transporter kinetic parameter estimation and translational modeling of transport-mediated PK and DDIs in humans. Clin. Pharmacol. Ther. 2013;94(1):64. doi: 10.1038/clpt.2013.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao P., Zhang L., Grillo J., Liu Q., Bullock J., Moon Y., Song P., Brar S., Madabushi R., Wu T. Applications of physiologically based pharmacokinetic (PBPK) modeling and simulation during regulatory review. Clin. Pharmacol. Ther. 2011;89(2):259. doi: 10.1038/clpt.2010.298. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Methods
Supplementary Results (Table S2.1)
Supplementary Results (Table S3.1)
Supplementary Results