Contributions of organic and inorganic matter to sediment volume and accretion in tidal wetlands at steady state

Abstract

A mixing model derived from first principles describes the bulk density (BD) of intertidal wetland sediments as a function of loss on ignition (LOI). The model assumes that the bulk volume of sediment equates to the sum of self‐packing volumes of organic and mineral components or BD = 1/[LOI/k₁ + (1‐LOI)/k₂], where k₁ and k₂ are the self‐packing densities of the pure organic and inorganic components, respectively. The model explained 78% of the variability in total BD when fitted to 5075 measurements drawn from 33 wetlands distributed around the conterminous United States. The values of k₁ and k₂ were estimated to be 0.085 ± 0.0007 g cm⁻³ and 1.99 ± 0.028 g cm⁻³, respectively. Based on the fitted organic density (k₁) and constrained by primary production, the model suggests that the maximum steady state accretion arising from the sequestration of refractory organic matter is ≤ 0.3 cm yr⁻¹. Thus, tidal peatlands are unlikely to indefinitely survive a higher rate of sea‐level rise in the absence of a significant source of mineral sediment. Application of k₂ to a mineral sediment load typical of East and eastern Gulf Coast estuaries gives a vertical accretion rate from inorganic sediment of 0.2 cm yr⁻¹. Total steady state accretion is the sum of the parts and therefore should not be greater than 0.5 cm yr⁻¹ under the assumptions of the model. Accretion rates could deviate from this value depending on variation in plant productivity, root:shoot ratio, suspended sediment concentration, sediment‐capture efficiency, and episodic events.

Key Points

• Sediment bulk density can be largely explained by its organic matter concentration

• Bulk volume approximates the summed volumes of the mineral and organic fractions

• Upper bound of steady‐state accretion defines sustainability of coastal marshes under SLR

1. Introduction

Tidal wetlands have survived in place within the intertidal zone for millennia of rising sea level through biophysical processes that lead to the accumulation of mineral and organic matter, thereby increasing soil volume and surface elevation. Long‐term wetland stability requires that the soil surface elevation must increase at a rate similar to the local rate of relative sea‐level rise (SLR), i.e., they must be in equilibrium with the sea level. Many contemporary tidal wetlands formed during the late Holocene and accumulated up to several meters of deposits at a time when rates of SLR were relatively slow [Redfield and Rubin, 1962; Kelley et al., 1988; Engelhart and Horton, 2012; Engelhart et al., 2015]. With accelerating rates of relative SLR [Vermeer and Rahmstorf, 2009; Horton et al., 2014] and many examples of tidal wetlands converting to open water [Craft et al., 2009], there is an increasing need to understand the limits of the biophysical processes that expand soil volume and elevation.

Wetland elevation and its rate of change represent a balance between local rates of accretion and erosion as these factors ultimately determine the net change in sediment volume per unit area. Sediment volume decreases as a consequence of organic matter decomposition, compaction, and erosion. Sediment volume increases with additions of refractory root and rhizome tissue and deposition onto the sediment surface of mineral and refractory organic particles, which in turn is influenced by aboveground plant biomass. Empirical studies [e.g., Nyman et al., 1993; Turner et al., 2000; Neubauer, 2008] and simulation models [e.g., Kirwan et al., 2010] have illustrated the interactive roles of organic matter and mineral inputs on wetland accretion rates.

The annual surface deposition of mineral and organic material creates a lamination that can be conceptualized as a sediment cohort [Morris and Bowden, 1986], the volume of which will change over time as a consequence of compaction and the subsequent ingrowth and turnover of roots and rhizomes. The final volume of a cohort is achieved when its organic matter content has stabilized, a process that occurs over many years of burial by generations of younger cohorts until the cohort has reached a depth below the root zone [Morris and Bowden, 1986; Davis et al., 2015]. When the wetland is in equilibrium with a constant rate of SLR (i.e., the system is in steady state), the final mass of a cohort and its bulk density will determine the rate of vertical accretion. Many studies have described a variety of transient perturbations—including nutrient pollution, changing atmospheric chemistry, abrupt sea‐level change, and watershed development—that can alter or disrupt steady‐state accretion processes of tidal wetlands [Langley et al., 2009; Kirwan et al., 2011; Deegan et al., 2012; Kirwan and Megonigal, 2013; Mariotti and Fagherazzi, 2013; Weston, 2014; Ratliff et al., 2015]. Nevertheless, in light of the persistence of marsh habitat over centuries of rising sea level [Kemp et al., 2011, 2013], wetland survival must be viewed in the context of the steady state. Transient perturbations return to equilibrium with mean sea level, or they lead to wetland loss and a state change.

A central requirement in many empirical and mechanistic studies of wetland accretion is the need to convert mineral and organic mass to a volume (and therefore thickness) of sediment. The analysis presented here was motivated by the simple objective of describing the physical relationship between sediment dry bulk density (BD) and organic matter concentration expressed as loss on ignition (LOI) in coastal wetlands. A number of publications have explored this relationship for upland or wetland soils, using either empirical models or first principles [Jeffrey, 1970; Stewart et al., 1970; Adams, 1973; Harrison and Bocock, 1981; Gosselink et al., 1984; Grigal et al., 1989; Honeysett and Ratkowsky, 1989; Manrique and Jones, 1991; Federer et al., 1993; Turner et al., 2000; Neubauer, 2008; Périé and Ouime, 2008]. Common limitations of this previous work include datasets that are limited geographically, by a narrow range of possible soil conditions, and by sample size. Herein, we extend these previous analyses to a wide sample of herbaceous and forested tidal wetland ecosystems (>5000 samples across 33 riverine and estuarine systems) from the coastal region of the conterminous United States. The present study tests a quantitative mixing model wherein the proportions and compositions of the two end‐member components, organic and inorganic material, govern the density and volume of tidal wetland sediments and therefore influence steady‐state rates of vertical accretion in tidal wetlands. The results suggest a simple and robust rule for setting upper limits on steady‐state vertical accretion rates in coastal wetlands, a rule that is defensible from first principles.

2. Data and Methods

2.1. Sampling Protocol

We compiled a database of 5075 samples of sediment BD and LOI from 33 wetland sites in estuaries in Maine, Massachusetts, New York, Rhode Island, Delaware, Maryland, Virginia, North and South Carolina, Florida, Alabama, Mississippi, Louisiana, and California. The data were either unpublished and provided by the authors or published and publically available.

The methods for estimating bulk density and LOI in sediment vary in details, such as the operation, type, and dimension of the coring device, the volume of samples analyzed, etc. Despite this variation, they all share a common protocol of drying samples of known wet volume, weighing the dried samples, combusting the samples in a furnace, and reweighing to obtain the weight loss on ignition (LOI) [e.g., Dean, 1974; Percival and Lindsay, 1997]. There are numerous opportunities for error, including compression of the sediment when taking the core and/or when extracting the core from the core tube, imprecise sectioning of the core into known volumes, variation in drying temperature, furnace temperature, and presence of salts that precipitate when the pore water is evaporated from the sample [Heiri et al., 2001]. We think that compression during the coring operation is the most significant source of error, but to our knowledge, the relative sizes of these errors have not been evaluated.

2.2. Statistics

The Marquardt‐Levenberg method [Levenberg, 1944] of the SAS 9.4 PROC MODEL was used to estimate the unknown parameters in several alternative nonlinear models describing the relationship between sediment BD and LOI. PROC MODEL is an iterative procedure that finds the combination of parameters that minimizes the sum of squares of residuals. The procedure reports an adjusted R² value for the model being fitted and significance tests with associated probabilities that the parameters differ significantly from zero. Nonlinear regression analysis has an advantage over linear regression, which requires that nonlinear data must first be linearized. Linear transformation introduces a bias by changing the relative weights of individual observations. Additional tests were performed (PROC REG, PROC GLM) with log‐transformed data to test for differences across sites, including homogeneity of slopes and LOI‐by‐site interactions. A massive dataset (N > 6000) from the Louisiana Coastwide Reference Monitoring System (CRMS) was randomly subsampled using PROC SURVEYSELECT to bring it in line with the number of samples from other sites and to prevent a deltaic bias.

3. Results

3.1. Site Characteristics

The 33 sites analyzed (Table 1) represented varied climatic conditions, tidal amplitudes, soil compositions, and species. Most samples are from the near surface (50 cm), except for cores from Sand Hill, NC that were nearly 3 m in length and cores from Maine, Patuxent River, MD, and Otter Point, MD, where 1–2 m of sediment was sampled. Sediments were predominately siliciclastic, with varying amounts of organic matter, but also included calcareous sediments from the coastal Everglades (FCE). The sites spanned 14 degrees of latitude. Across sites, mean sediment LOI ranged from 0.12 g g⁻¹ at Grand Bay, MS; China Camp, CA; and Otter Creek, MD to 0.79 g g⁻¹ at GCREW near Edgewater, MD. Mean dry bulk density ranged from 0.12 g cm⁻³ at GCREW to 0.78 g cm⁻³ at North Inlet, SC.

Table 1.

Sites Included in the Analysis, Their Geographical and Physical Characteristics, Mean (±SD) Loss on Ignition (LOI) and Bulk Density (BD), Sample Size (N), and Data Sources

Site	Community Type	Latitude (oN)	Tidal Amp (cm)	Loss on Ignition  (g g−1)	Bulk Density (g cm−3)	N
Apcola, FLa	Tidal brackish marsh	29.8	25	0.43 ± 0.12	0.14 ± 0.07	297
FCEman, FLb	Everglades brackish mangrove	25.2	10	0.26 ± 0.14	0.37 ± 0.14	72
FCEmmm, FLb	Everglades mixed mangrove‐marsh	25.2	5	0.17 ± 0.15	0.35 ± 0.13	41
FCEbtf, FLb	Everglades brackish tidal forested	25.4	20	0.81 ± 0.13	0.14 ± 0.03	39
FCEbtma, FLb	Everglades brackish tidal mangrove	25.4	30	0.37 ± 0.18	.032 ± 0.14	80
CRMS, LAh	Tidal salt to tidal fresh marsh	29		0.38 ± 0.24	0.28 ± 0.22	500
GrandB, MSa	S. alterniflora/Juncus tidal marsh	30	22	0.12 ± 0.04	0.39 ± 0.15	59
WeeksB, ALa	Tidal brackish marsh	30.4	20	0.17 ± 0.04	0.35 ± 0.08	60
NorthI, SCa	Tidal salt marsh, S. alterniflora	33.3	70	0.13 ± 0.08	0.78 ± 0.34	278
Waccam, SCa	Tidal fresh marsh	33.5	60	0.55 ± 0.16	0.13 ± 0.09	337
Smyrna, NCa	Tidal brackish marsh Juncus roemerianus	34.8	19	0.27 ± 0.15	0.43 ± 0.37	416
SandH, NCa	Tidal brackish marsh Juncus roemerianus	35	5	0.56 ± 0.20	0.23 ± 0.26	145
James, VAa	Tidal fresh marsh, Polygonum, Peltandra, Zizania, others, & forest	37.3	40	0.21 ± 0.06	0.44 ± 0.13	25
Pamunk, VAa,e	Tidal fresh marsh	37.6	44	0.21 ± 0.08	0.35 ± 0.15	401
Browns Isl, CAl	Tidal brackish marsh, Schoenoplectus spp.	38.0	46	0.35 ± 0.17	0.29 ± 0.15	113
ChinaCp, CAl	Tidal salt marsh, Spartina foliosa, Sarcocornia pacifica.	38.0	66	0.12 ± 0.04	0.50 ± 0.10	134
CoonIs, CAl	Tidal salt marsh, S. foliosa, S. pacifica	38.2	72	0.16 ± 0.09	0.44 ± 0.22	172
MonieBay, MDc,d	Tidal brackish marsh, S. alterniflora	38.2	15	0.27 ± 0.18	0.49 ± 0.49	189
PetalumaR, CAl	Tidal salt marsh, S. foliosa, S. pacificia	38.2	75	0.18 ± 0.08	0.4 ± 0.21	111
RushRa, CAl	Tidal brackish marsh, Schoenoplectus spp.	38.2	86	0.27 ± 0.15	0.38 ± 0.19	138
Choptk, MDc	Tidal fresh marsh	38.7	16	0.27 ± 0.05	0.30 ± 0.07	45
PatuxR, MDc,g	Tidal fresh marsh, mixed	38.7	28	0.34 ± 0.17	0.29 ± 0.14	230
GCREW, MDa	Brackish tidal marsh, Schoenoplectus americanus, Spartina patens	38.9	14	0.79 ± 0.05	0.12 ± 0.02	117
OttCr, MDc	Tidal fresh marsh	39.4	19	0.12 ± 0.02	0.68 ± 0.19	45
DelRiv, DEf	Tidal fresh marsh	39.8	91	0.14 ± 0.04	0.27 ± 0.17	11
JamBay, NYj,k	S. alterniflora salt marsh	40.6	80	0.41 ± 0.18	0.31 ± 0.32	133
NarrBay, RIa,i	Tidal salt marsh, S. patens, D. spicata, S. alterniflora	41.6	65	0.28 ± 0.19	0.41 ± 0.31	127
Hudson, NYc	Tidal fresh marsh	42	61	0.16 ± 0.1	0.58 ± 0.21	103
PlumIs, MAa	S. patens, S. alterniflora salt marsh	43	150	0.29 ± 0.14	0.26 ± 0.12	320
Moody, MEa	Tidal salt marsh, S. patens, D. spicata, S. alterniflora	43.2	134	0.31 ± 0.14	0.34 ± 0.22	52
Webhannet, MEa	Tidal salt marsh, S. patens, D. spicata, S. alterniflora	43.3	134	0.25 ± 0.13	0.44 ± 0.20	36
Morse, MEa	Tidal salt marsh, S. patens, D. spicata, S. alterniflora	43.7	139	0.22 ± 0.12	0.42 ± 0.21	37
Sprague, MEa	Tidal salt marsh, S. patens, D. spicata, S. alterniflora	43.7	139	0.20 ± 0.12	0.43 ± 0.24	212
Grand Means				0.30 ± 0.17	0.36 ± 0.14	5075

^aoriginal data; ^b Chambers and Pederson, 2006 and http://fcelter.fiu.edu/data/; ^c Merrill, 1999; ^d Ward et al., 1988; ^e Neubauer, 2000; ^f Church et al., 2006; Orson et al., 1992; ^g Khan and Brush, 1994; ^h http://cims.coastal.la.gov/monitoring‐data/; ⁱ Wigand et al., 2003; ^j Wigand et al., 2014; ^k Swanson and Wilson, 2008; ^l Callaway et al., 2012

The dominant species vary among sites, with Spartina patens and Spartina alterniflora most common in northeastern and southeastern estuaries, respectively; Spartina foliosa and Schoenoplectus in the San Francisco estuary; a mix of Spartina species and brackish species (S. cynosuroides and/or Juncus roemerianus) in the Gulf Coast and North Carolina estuaries; and the red mangrove Rhizophora mangle in several Everglades sites. The tidal freshwater wetlands typically contained a diverse mixture of herbaceous species, including Peltandra virginica, Pontederia cordata, Zizania aquatica, and Zizaniopsis miliacea, with some locations also containing trees (e.g., Nyssa aquatica, Taxodium distichum). There was a weak, but insignificant (p = 0.25) decline of mean LOI by site with increasing latitude (−0.01 per degree) and a weak decline in LOI with tidal amplitude (−0.002 per cm, R ² = 0.27, p = 0.05).

Tests of homogeneity of slopes of log‐normalized data were significant (p < 0.0001). Likewise, an analysis of covariance established that LOI varies among sites: the independent variables site, ln(LOI), and the ln(LOI) x site interaction term were all significant (p < 0.0001) for type I and type III errors, meaning that there is no reasonable chance that these samples behave in the same way with respect to the dependence of log‐transformed BD on log‐transformed LOI.

3.2. Model 1 Power Function

The first model tested (Figure 1) is one that is commonly used to estimate bulk density (BD) from LOI measurements. It is an empirical power function of the form

$$\mathrm{B}\mathrm{D}=a{\mathrm{L}\mathrm{O}\mathrm{I}}^b$$ (1)

where a and b are empirical constants. The equation was fitted with an R ² of 0.73. Parameter a = 0.141 ± 0.002 (p < 0.0001) and b = −0.59 ± 0.004 (p < 0.0001).

Figure 1.

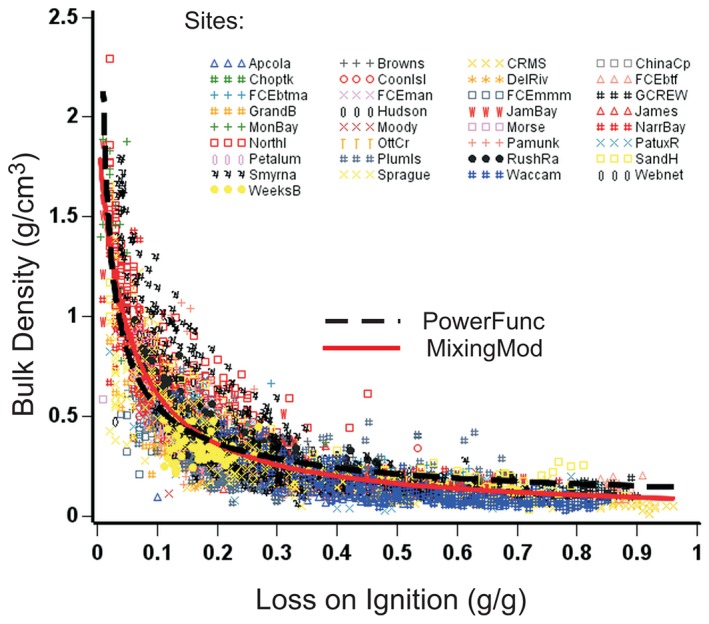
Best fits of the power function () BD = a LOI^b and ideal mixing model () BD = 1/[LOI/k₁ + (1 − LOI)/k₂)] to the complete collection of 5075 sediment samples from 33 tidal marshes and mangroves distributed around the United States. The data in Figure 1 are available in Appendix S1, Supporting Information

3.3. Model 2 Power Function With Intercept

This model differs from the first only in having a nonzero intercept c. It is an empirical power function of the form

$$\mathrm{B}\mathrm{D}=a{\mathrm{L}\mathrm{O}\mathrm{I}}^b+c$$ (2)

where a, b, and c are empirical constants. The equation was fitted with an R ² of 0.77. Parameter a = 0.569 ± 0.03 (p < 0.0001), b = −0.31 ± 0.01 (p < 0.0001), and c = −0.55 ± 0.04 (p < 0.0001).

3.4. Model 3 Ideal Mixing Model

Stewart et al. [1970] suggested that in natural soils containing organic matter, there is a relationship between soil apparent density and organic matter content, namely that the bulk volume of a soil approximates to the summed self‐packing volumes of the organic and mineral components. In other words, it is assumed that the bulk densities of pure organic matter and pure mineral matter are assumed constants, and in a mixture, the volumes occupied by the organic and mineral components are additive [Federer et al., 1993]. For example, starting with dry weights W_o and W_i of organic and inorganic matter having bulk densities of k₁ and k₂, and volumes V_o = W_o/k₁ and V_i = W_i/k₂, when the two are mixed, the resulting bulk density BD = (W _o + W_i)/(W _o/k₁ + W_i/k₂). The mixture will have a loss on ignition LOI = W_o/(W _o + W _i). Rearranging W _o + W _i = W _o/LOI and substituting gives BD = (W _o/LOI)/(W _o/k₁ + W_i/k₂). Substituting for W_i gives BD = (W _o/LOI)/[W _o/k₁ + (W _o/LOI − W _o)/k₂] , which reduces to

$$\mathrm{B}\mathrm{D}=1/\left[\mathrm{L}\mathrm{O}\mathrm{I}/k_1+\left(1-\mathrm{L}\mathrm{O}\mathrm{I}\right)/k_2)\right]$$ (3)

This is known as the ideal mixing model [Adams, 1973]. Coefficients k₁ and k₂ are the bulk, self‐packing densities of pure organic and mineral matter, respectively.

The best fit over all sites (R ² = 0.78) gave k₁ and k₂ coefficients of 0.085 ± 0.0007 g cm⁻³ (p < 0.0001) and 1.99 ± 0.028 g cm⁻³ (p < 0.0001), respectively (Figure 1). Note that when LOI = 0, Eq. 3 reduces to BD = k₂, and Eq. 3 reduces to BD = k₁ when LOI = 1. When fitted specifically to each site, the resulting k₁ values varied from 0.05 to 0.168 g cm⁻³ and k₂ from 0.59 to 2.87 g cm⁻³. Parameter estimates made from site‐specific data were unreliable because few sites possessed the full spectrum of BD and LOI values needed for a good fit.

3.5. Vertical Accretion

There have been several analyses of the relative contribution of organic and inorganic accretion to vertical accretion using a top–down approach [Nyman et al., 1993, 2006; Turner et al., 2000; Neubauer, 2008]. Starting with known accretion rates and composition, Turner et al. [2000] and Neubauer [2008] calculated the densities of organic and mineral matter that best fit the total accretion rates by linear regression. From their published inventories of mineral and organic matter above the 1963 ¹³⁷Cs maxima, we calculated vertical accretion by dividing the mass accretion rates (g cm⁻² yr⁻¹) by the k₁ and k₂ densities, 0.085 and 1.99 g cm⁻³, respectively, from the present study. Our calculated vertical accretion rates and their measured rates (Figure 2) were highly correlated (r ² = 0.6, p < 0.0001).

Figure 2.

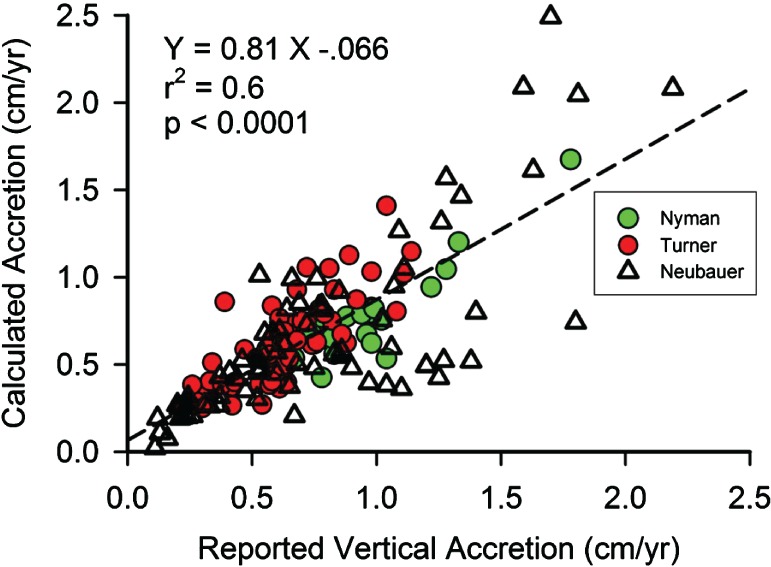
Mixing model‐calculated accretion rates and reported ¹³⁷Cs‐based vertical accretion rates. Calculations used published mass accretion rates (g m⁻² yr⁻¹) of inorganic and organic matter as reported in Nyman et al. [1993, 2006], Turner et al. [2000], and Neubauer [2008].

With estimates of k₁ and k₂, using a bottom–up approach, it is possible to parse vertical accretion between its organic and mineral fractions and to reasonably estimate rates of vertical accretion across a range of suspended sediment concentrations and LOI (Figure 3). We used suspended sediment (TSS) concentrations ranging from 10 to 200 mg L⁻¹ and assumed depths of high water over the marsh surface of 1, 5, and 20 cm—flood depths representative of high, mid, and low marsh. Following the logic of Krone [1987], the depth of high water determines the volume of water over the marsh surface and, together with the tide range, approximately defines the hydroperiod or duration of flooding, but as we are assuming a 100% capture efficiency, the explicit calculation of the hydroperiod is avoided. A marsh surface that captures all of the suspended sediment when flooded semi‐diurnally (704 floods per year) by 20 cm of water at high tide would receive an annual deposit of 0.42 g cm⁻² yr⁻¹ (=3 × 10⁻⁵ g cm⁻³ × 20 cm × 704 yr⁻¹), using a flow‐weighted, average suspended sediment concentration of 30 mg/liter for East and eastern Gulf Coast estuaries [Weston, 2014]. Dividing by k₂ (1.99 g cm⁻³) gives 0.2 cm/yr.

Figure 3.

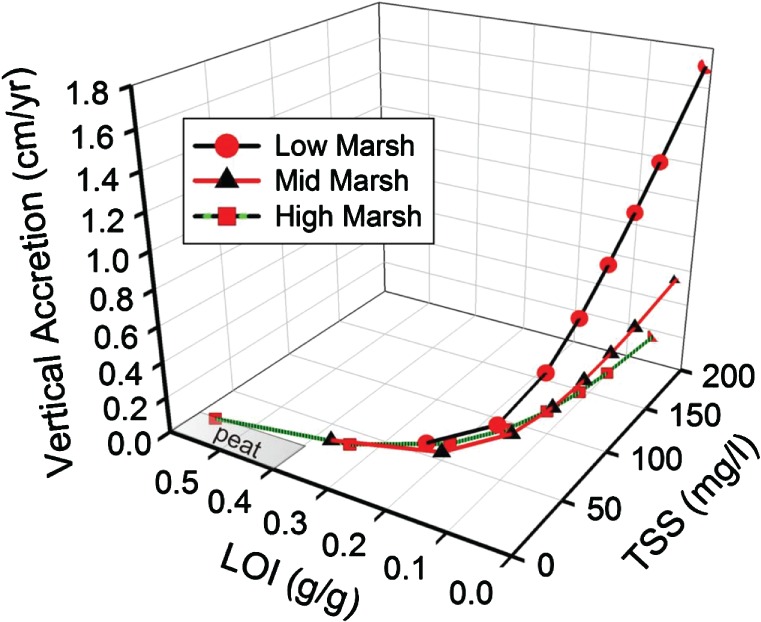
A curve family describing relationships among vertical accretion, soil organic content (LOI), and total suspended inorganic sediment (TSS) in hypothetical high‐, mid‐, and low‐marsh habitats. Calculations of vertical accretion due to organic production and mineral sedimentation are based on the pure packing densities k₁ and k₂ (see text) derived from a fit of the mixing model to the entire dataset. High, mid, and low marshes were defined as having high tides that flood the surface semi‐diurnally, with average water depths of 1, 5, and 20 cm, and with belowground refractory organic matter inputs of 80, 160, and 250 dry g m⁻² yr⁻¹, respectively. The grey area is the domain of peat formation, truncated at LOI = 0.6.

As the production of the vegetation is also sensitive to flood depth [Morris et al., 2002, 2013], we assumed belowground productivities of 800, 1600, and 2500 g dry weight m⁻² yr⁻¹ in high, mid, and low marsh, respectively, with 10% preservation. The organic contribution to vertical accretion is determined by the input of the refractory organic production, which should be nearly equal to the production of lignin. Using a lignin concentration of 10% [Hodson et al., 1984; Wilson et al., 1986; Buth and Voesenek, 1987], the vertical accretion due to a theoretical maximum belowground dry weight production of 2500 g m⁻² yr⁻¹ for Spartina alterniflora [Morris et al., 1984] should be about 0.3 cm yr⁻¹ ≈ (0.25 g cm⁻² yr⁻¹ × 0.1 g lignin/g dry weight)/ 0.085 g cm⁻³. Shown here (Figure 3) are the vertical accretion rate and LOI resulting from various combinations of inputs. The results show that the highest vertical accretion rates are possible only at the highest TSS concentrations, that is, the highest inputs of mineral matter (Figure 3). However, for conditions typical of East Coast estuaries (high production, low TSS), organic matter probably contributes about 3/5 or 60% to vertical accretion, which is in line with Neubauer's [2008] estimate of 62%.

4. Discussion

The variability in BD not explained by the mixing model can be due to sampling and analytical errors, as discussed earlier, and to violations of the model assumptions, namely that k₁ and k₂ are constant and their volumes additive. Additivity is not strictly true because organic molecules encapsulated within the lattices of clay minerals or sorbed to the surfaces of clay minerals [Mortland, 1970; van Veen and Kuikman, 1990; Mayer, 1994; Hedges and Keil, 1995; Bergamaschi et al., 1997; Mayer et al., 2004] may raise the LOI without adding to the total volume. Furthermore, a portion of the variability also could be due to compaction or differences in sediment grain size. The mass per unit volume of the solid inorganic component, that is, excluding voids and water, is commonly taken to be 2.65 g cm⁻³ [Skopp, 2000; Blanco‐Canqui et al., 2004]. The difference between the solid inorganic density and k₂ equates to an average porosity of 25%, but porosity and bulk density are functions of grain size [Manrique and Jones, 1991; Jackson et al., 2014], which is variable. However, the fidelity of the mixing model (Figure 1) suggests that these deviations from the model assumptions are minor, at least within the universe of data analyzed here.

There was a weak, but insignificant (p = 0.25) decline of mean LOI by site with increasing latitude (−0.01 per degree). If the concentration of organic matter in sediment was reduced by rising temperature, perhaps due to an increase in decay rate [Kirschbaum, 1995], then we would have expected an increase in LOI with latitude. Alternatively, a decline with latitude would be consistent with a trend of decreasing aboveground productivity in salt marshes with increasing latitude [Kirwan et al., 2009]. This decline with latitude is also consistent with the interpretation of Philben et al. [2014, 2015] who found that peat formed at more southerly latitudes and, during the Holocene Climatic Optimum, did not appear to be any more decomposed than peat formed in cooler latitudes or during subsequent cooler periods in younger sections of the cores. They suggested that decomposition in peatlands was regulated primarily by oxygen‐exposure time, not by temperature.

We found a weakly negative (−0.002 cm⁻¹) but significant (p = 0.05) effect of tidal amplitude on LOI. Tidal amplitude could affect LOI in a number of ways, for example, by affecting dewatering and oxygen exposure, hydroperiod, and/or the effect of tidal energy on mineral sediment transport. For a fixed input of organic matter, the resulting LOI will be determined by the input of mineral matter. The latter would be controlled by the concentration of suspended sediment as well as the hydroperiod or settling time for suspended sediment.

Mixing model parameters k₁ and k₂ were used to parse total vertical accretion into its organic and mineral fractions and to place upper limits on vertical accretion. With respect to the contributions from organic production, it can be assumed that only belowground biomass contributes to soil organic matter in tidal salt marshes because we do not observe the accumulation of a litter layer on the marsh surface. Furthermore, excluding sites of marsh restoration or newly emerging marshes where the live biomass may build over a period of years, the input of labile organic matter does not add new volume because its production and decay rate are in equilibrium, that is, the volume of living and labile organic matter exists in steady state. The refractory fraction of belowground production, however, does contribute to the change in soil volume, and we can equate this to the production of lignin, which is considered to be the most refractory part of plant tissue and is a significant component of soil organic matter in anaerobic environments such as peatlands [Morita, 1962]. Its decomposition depends primarily on the supply of oxygen [Andriesse, 1988; Williams and Yavitt, 2003]. An upper limit for belowground dry weight production of 2500 g m⁻² yr⁻¹ containing 10% lignin gives a theoretical steady‐state vertical accretion of about 0.3 cm yr⁻¹ (3 mm yr⁻¹). Thus, peat marshes are not likely to indefinitely survive an accelerating SLR without a source of mineral sediment.

Empirical measures of belowground production sometimes exceed the generalized estimate above 2500 g m⁻² yr⁻¹, for example, 3500 g m⁻² yr⁻¹ in Great Sippewissett marsh [Valiela et al., 1976], 6500 g m⁻² yr⁻¹ in Delaware Bay [Roman and Daiber, 1984], and 7900 g m⁻² yr⁻¹ in Narragansett Bay [Wigand, 2008]. Measurements of belowground production are subject to significant sampling error [Singh et al., 1984], but theoretical estimates associated with model assumptions also have uncertainty. Moreover, maximum productivity varies greatly among plant communities and species. The productivity of tidal freshwater marshes, for example, exceeds that of salt marshes [Odum, 1988]. Primary production can also vary strongly with factors such as interannual variation in sea level [Morris et al., 2002], nitrogen loading, and atmospheric CO₂ concentration [Langley et al., 2009]. Therefore, belowground production might provide greater accretion than the 0.3 cm yr⁻¹ estimated here and also potentially greater rates of carbon sequestration.

The relative importance of inorganic and organic contributions to vertical accretion is dynamic over long timescales [Kearney et al., 1994; Drexler, 2011] and can vary spatially in contemporary settings [Craft et al., 1993]. Vertical accretion is ultimately limited by the mass inputs of mineral and refractory organic material, constrained by their bulk densities. Mass accretion rates of mineral and organic matter in tidal freshwater and salt water wetlands and ¹³⁷Cs‐based vertical accretion have been reported by Nyman et al. [1993, 2006], Turner et al. [2000], and Neubauer [2008] among others, and these authors have advanced the argument that organic matter accretion is the principal means by which marshes accrete vertically. Our analysis supports this view, considering the low TSS concentrations typical of many estuaries, but we would argue that vertical accretion is limited by low availability of mineral sediment. Using a top–down approach, Turner et al. [2000] regressed the vertical accretion rate against organic matter accumulation and found a slope of 11 cm³ g⁻¹. Its reciprocal is k₁ and, ignoring a regression intercept, is equivalent to 0.09 g cm⁻³. His regression of vertical accretion rate against inorganic accumulation rate gave a slope of 1.36 cm³ g⁻¹ or 0.73 g cm⁻³, which is significantly less than k₂ derived in our study. Using multiple linear regression of vertical accretion rate against organic plus mineral accumulation, Neubauer [2008] derived densities equivalent to 0.182 g cm⁻³ and 0.847 g cm⁻³ for the organic and mineral fractions, respectively. The differences between coefficients derived by Turner et al. [2000] and Neubauer [2008] and our calculated values of k₁ and k₂ reflect the limited range of soil properties in those other studies, notably a near absence of high LOI samples.

Several generalities emerge from our bottom–up calculations of vertical accretion (Figure 3). Firstly, the theoretical maximum vertical accretion rate at steady state for a typical marsh on the East Coast and eastern Gulf is probably not greater than 0.5 cm yr⁻¹. This is the expected vertical accretion from the combined inputs of organics and inorganics at the highest loading rates, that is, complete capture of 30 mg L⁻¹ suspended sediment under 20 cm of water flooding the surface semi‐diurnally and with the addition of 250 g dry weight m⁻² yr⁻¹ of refractory organic matter. However, a significantly higher sediment load, like that available in a deltaic environment, for example, 200 mg L⁻¹, could support a vertical accretion rate of 1.7 cm yr⁻¹ (Figure 3). Secondly, the lowest concentration of sediment organic matter or LOI occurs at the highest vertical accretion rates for a marsh at steady‐state equilibrium with sea level, reflecting low marsh conditions with high mineral inputs. Conversely, the highest LOI occurs at the lowest accretion rates and in high marsh habitat with little flooding (Figure 3). High marsh habitat has the lowest opportunity for mineral loading from tidal flooding and, thus, little supplement to organic accretion by inorganic material.

Our analysis addresses marshes operating in steady state with typical rates of plant production and sediment availability. However, marshes often accrete sediment at different rates (Figure 2) because they are not always constrained by the limits we have assumed on mineral and organic matter accretion. Locally, there may be erosion of marsh edge and redeposition onto the remaining marsh platform [Wilson et al., 2014] or episodes of rapid sedimentation following hurricanes [Cahoon et al., 1995; Turner et al., 2006; McKee and Cherry, 2009; Baustian and Mendelssohn, 2015]. However, storm impacts also can be negative [Chabreck and Palmisano, 1973; Cahoon, 2006; Howes et al., 2010; Morton and Barras, 2011; Leonardi et al., 2016], and it seems unlikely that storms could contribute globally to a positive, steady‐state accretion or that they could accommodate an acceleration in sea‐level rise. There are also situations when a system may be far removed from the local equilibrium state. What follows is a rapid recovery and accretion toward the equilibrium [French and Burningham, 2003]. This could happen following a wetland restoration, an emergence of a bar at the mouth of a delta, or a sudden loss in relative elevation due to storm‐induced erosion or to mechanical means. These are transient conditions that could affect short‐term accretion rates but that should not affect the steady‐state accretion rate. Also possible are changes in state following a change in nutrient loading, which could affect organic matter production and preservation or a change in sediment loading. These could increase or decrease the steady‐state accretion rate, therefore affecting the ability of tidal wetlands to maintain elevation relative to a rising sea level.

A tidal wetland with a high LOI and low accretion rate is not necessarily at its maximum rate of vertical accretion because the mineral loading rate and primary productivity will depend on its relative elevation, depth of flooding, and suspended sediment concentration. With an accelerated rate of SLR, the relative, equilibrium marsh elevation will fall, and the vertical accretion rate will rise [Morris et al., 2002]. It is only when the equilibrium elevation falls below the optimum for primary production that the marsh will fail to keep up with the acceleration in SLR. Our analysis, which assumes only chronic inputs, suggests that this will most likely occur when the local rate of SLR (including subsidence) exceeds about 0.5 cm yr⁻¹ in most East Coast estuaries or 1.7 cm yr⁻¹ in a sediment‐rich estuary. Thus, even current rates of SLR along the East Coast (mean = 0.34 cm yr⁻¹, range = 0.18–0.60 cm yr⁻¹) (http://tidesandcurrents.noaa.gov/sltrends/sltrends.html) are near the point that will lead to long‐term elevation loss and eventual drowning of coastal wetlands.

Supporting information

Supporting Information S1