Ultrafast Excited State Relaxation of a Metalloporphyrin Revealed by Femtosecond X-ray Absorption Spectroscopy

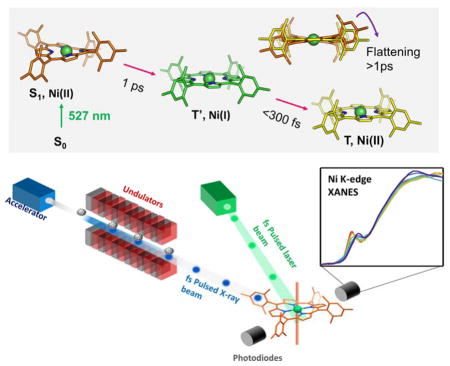
Abstract

Photoexcited Nickel(II) tetramesitylporphyrin (NiTMP), like many open-shell metalloporphyrins, relaxes rapidly through multiple electronic states following an initial porphyrin-based excitation, some involving metal centered electronic configuration changes that could be harnessed catalytically before excited state relaxation. While a NiTMP excited state present at 100 ps was previously identified by X-ray transient absorption (XTA) spectroscopy at a synchrotron source as a relaxed (d,d) state, the lowest energy excited state,^1,2 structural dynamics before thermalization were not resolved due to the ~100 ps duration of the available X-ray probe pulse. Using the femtosecond (fs) X-ray pulses of the Linac Coherent Light Source (LCLS), the Ni center electronic configuration from the initial excited state to the relaxed (d,d) state has been obtained via ultrafast Ni K-edge XANES (X-ray Absorption Near Edge Structure) on a time scale from hundreds of femtoseconds to 100 ps. This enabled the identification of a short-lived Ni(I) species aided by time-dependent density functional theory (TDDFT) methods. Computed electronic and nuclear structure for critical excited electronic states in the relaxation pathway characterize the dependence of the complex’s geometry on the electron occupation of the 3d orbitals. Calculated XANES transitions for these excited states assign a short-lived transient signal to the spectroscopic signature of the Ni(I) species, resulting from intramolecular charge transfer on a timescale that has eluded previous synchrotron studies. These combined results enable us to examine the excited state structural dynamics of NiTMP prior to thermal relaxation and to capture intermediates of potential photocatalytic significance.

Graphical abstract

INTRODUCTION

Molecular photoexcitation generates high-energy transient species capable of driving subsequent chemical reactions. The challenge for energy conversion from light entails directing these transient species to minimize unwanted processes, such as heat generation and geminate charge recombination. Transition metal complexes (TMCs) have previously been selected for photochemical applications primarily based on the condition of possessing nanosecond or longer triplet excited state lifetimes (and large redox potentials).^3–5 While such selection criteria are sufficient to ensure that a reactive species will persist, recent studies have shown that some excited TMCs can initiate photochemical processes on the picosecond or sub-picosecond timescales via singlet excited states, timescales that are competitive with vibrational relaxation, and faster than intersystem-crossing to a triplet excited state. ^1,7–12 Such short-lived excited states are less susceptible to energy dissipation processes that would reduce the potential driving force of a reaction. However, experimentally characterizing the TMC electronic and nuclear configurations of excited states on these timescales is challenging, making rational control difficult. Recent ultrafast optical spectroscopic measurements have provided substantial information on the reaction dynamics of TMCs,^13–21 but optical signatures of metal-centered electronic transitions for these critical TMC intermediates are frequently nonexistent or obscured by π → π* optical signatures localized on aromatic ligands. A greater understanding of the electronic and nuclear structural response to excitation on fs to ps timescales is needed to utilize these potentially catalytic intermediates and could be pivotal to identifying a new regime of efficient metal based photocatalysts, light sensitizers, and electron donor/acceptors that might otherwise be neglected on the basis of selection criteria focused on triplet state lifetimes.

Pump-probe X-ray spectroscopies are element specific, and can selectively probe both the dynamic electronic structure of a TMC’s metal center and its local nuclear dynamics following photoexcitation without interference from ligand-localized transitions.^22–30 Recently, X-ray free electron laser (XFEL) sources capable of producing femtosecond X-ray pulses^31,32 have become available for these studies.²² We show here that combining an ultrafast X-ray source with an ultrafast optical laser pulse capable of triggering photochemical processes, allows quantitative analysis of the evolution of the electronic and nuclear dynamics of TMCs. By implementing this experimental approach along with accurate theoretical modeling, rational control over transient, catalytically-active TMC species becomes a possibility.

Metalloporphyrins possess versatile functionality as light harvesting/electron transfer cofactors, both in biological processes (natural photosynthesis,^33,34 physiological oxygen transport,³⁵ and small molecule sensing) and photocatalytic processes where they act as redox centers,^36–38 and sensitizers in molecular devices.³⁹ Such functional versatility is enabled by a high degree of chemical tunability in both the choice of metal center and the ligated macrocycle. Changes in macrocycle functionalization can dramatically impact metalloporphyrin ring conformation and rigidity, leading to varied redox and ligand binding properties, as well as the ability to impact relaxation dynamics by altering the energetic ordering of excited states. Open-shell transition metal porphyrins have not historically been seen as candidates for solar energy conversion due to their relatively fast excited state deactivation through d-orbital vacancies. While originally thought to be a disadvantage when judged with the triplet lifetime criteria, the ability to rationally control this ultrafast deactivation mechanism presents an exciting possibility for funneling the photon energy absorbed via porphyrin-based π → π* transitions to redox equivalents at the metal centers via intramolecular charge transfer.

Nickel porphyrins and phthalocyanines have been of particular interest as model complexes to provide guidance for targeted molecular design in part due to their conformational flexibility brought on by the small Ni core size and the ease with which certain ring conformers can be stabilized to tune relaxation kinetics. Nickel (II) tetramesitylporphyrin (NiTMP), which exists in the ground state as an ensemble of ring conformers, and its analogs, have complicated photochemical dynamics and have been extensively studied by optical absorption^6,40 and Raman spectroscopy.^41–46 These studies, combined with quantum-mechanical calculations, proposed a plausible pathway for the photoexcitation. Within 20 ps of the photoexcitation that initiates the S₀ → S₁ transition, a porphyrin macrocycle based π → π* transition, the electron promoted to the π* orbital moves to an empty 3d_x2-y2 orbital, the highest energy ligand field state for a square-planar complex, and an electron from an originally filled 3d_z2 orbital moves to fill the hole in the π orbital of the macrocycle left by the initial photoexcitation, resulting ultimately in the lowest-lying triplet state, (3d_z2, 3d_x2-y2). This state has a 3d electronic configuration of (3d_x2-y2)¹(3d_z2)¹ and is here denoted T(d,d) (Figure 1).^41,47 A pump-pump-probe transient absorption measurement of Ni(II) porphyrin excited state dynamics suggested that a transient Ni(I) charge transfer state may exist with a lifetime of a few picoseconds, ⁴⁰ but previously such a reaction pathway could not be substantiated by monitoring the temporal evolution of the nickel electronic configuration. In comparison to these previous optical and vibrational spectroscopic studies, X-ray transient absorption (XTA) spectroscopy,^22,23 which combines a laser excitation and conventional X-ray absorption spectroscopy,⁴⁸ can directly probe the metal center electronic structure and local geometry rather than relying on the indirect deduction of excited state dynamics from relatively broad transient optical spectral features.

Figure 1.

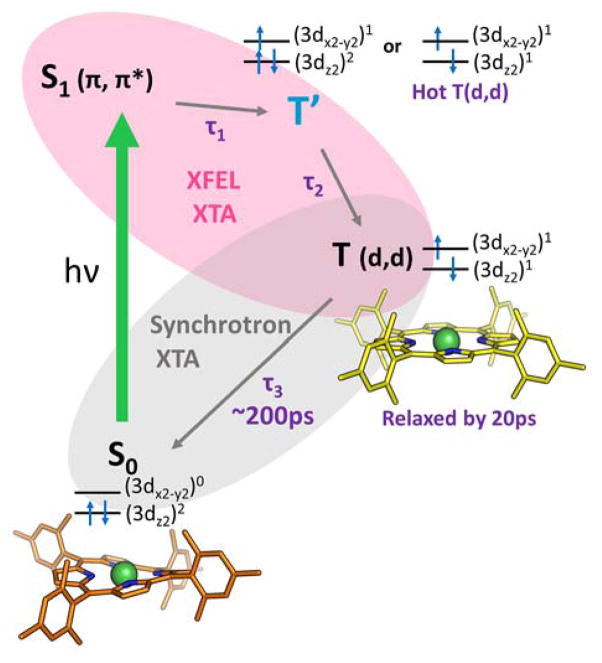
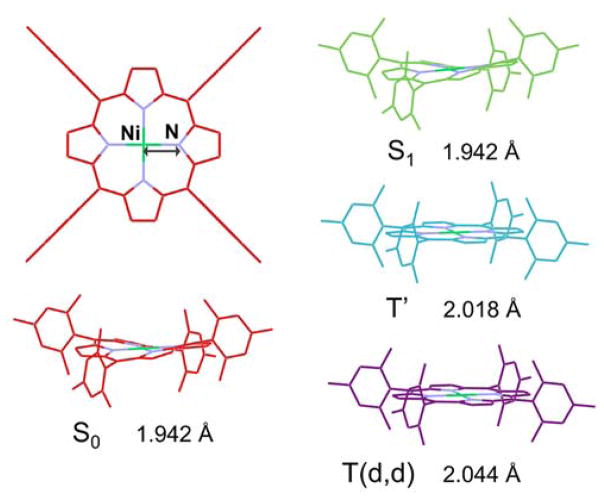
The relaxation pathway of NiTMP following Q-band excitation (e.g. at 527 nm). Structures for states characterized by XTA are shown. Within a few ps the porphyrin macrocycle S₁(π, π*) population has dissipated by transfer of the excitation to the metal center. The resulting state (T′) is therefore either a hot (3d_z2, 3d_x2-y2) state which decays to the relaxed (3d_z2, 3d_x2-y2) state T(d,d) via vibrational relaxation or a (π, 3d_x2-y2) state with Ni(I) character that transfers an electron back to the ligand. By 20 ps the T(d,d) state is fully populated and vibrationally relaxed, and has adopted a flattened structure with elongated Ni-N bonds.² This T(d,d) state decays back to the ground state with a 200 ps lifetime.⁶

Previous XTA studies at a synchrotron source (the Advanced Photon Source, Argonne National Laboratory) with ~100 ps time resolution^1,2 have conclusively verified that the thermalized excited T(d,d) state has an (3d_x2-y2)¹(3d_z2)¹ electronic configuration, and have captured this state’s elongated Ni-N bond length and flattened macrocycle conformation through analysis of the Extended X-ray Absorption Fine Structure (EXAFS), which arises from scattering processes with atoms neighboring the absorbing Ni.^1,2,49 However, the time resolution of the synchrotron X-ray pulses was insufficient to detect detailed excited state structural dynamics before the development of the relaxed T(d,d) state. In this study, this missing time window in the evolution of excited Ni(II)TMP is obtained by collection of XTA spectra near the nickel K-edge (8333 eV) with the sub-picosecond time resolution provided by the Linac Coherent Light Source (LCLS), an X-ray free electron capable of delivering femtosecond X-ray pulses of incredible intensity.^28,50 This study has in fact disclosed a transient charge transfer state, denoted T′ for consistency with previous work,⁵¹ that occurs prior to the appearance of T(d,d) (Figure 1) and, importantly, the X-ray absorption near edge spectra (XANES) of electronic states and geometries in the proposed photochemical trajectory were calculated and the effects of different orbital occupancies, Ni-N bond lengths, and the magnitude of repulsive potential acting on the Ni 1s electrons were correlated with trends in the experimental spectra.

METHODS

1. Ultrafast XANES spectroscopy

Ultrafast XANES spectra were collected for an 8 mM solution of NiTMP in toluene at the X-ray Pump-Probe (XPP) instrument of the LCLS⁵² using a similar experimental configuration as previous XANES measurements at XPP.²⁸ The sample solution was delivered to the point of spatial X-ray/laser overlap within a nitrogen filled chamber as a flat 100 μm liquid jet angled at 45° with respect to the incoming beam, where a pulsed laser beam nearly collinear with the incoming X-ray beam intersect. Each laser pulse generates an excited population probed by an X-ray pulse at a specified delay time with a “pump-probe” cycle of 120 Hz. A 527 nm excitation pulse from the output of an optical parametric amplifier (OPA) pumped by a Ti:Sapphire laser with a pulse duration of 50 fs (FWHM) was used to excite NiTMP through the porphyrin macrocycle centered S₀ → S₁ (π → π*) transition. The laser pulse energy at the sample was between 15 and 18 μJ with a spot size of ~0.3 mm diameter. At this pulse energy, simultaneous two-photon absorption (TPA) is not expected to contribute meaningfully to the excited XAS signal due to the low TPA cross section noted for symmetrically substituted porphyrins at this energy (~10 GM). Under these excitation conditions, the TPA excitation rate is less than 1% of the linear absorption transition rate (See Supporting Information 2 for a more detailed discussion). The absorption of the S1 state at the Q-band is very weak for similar porphyrins and sequential two photon absorption is similarly discounted.

Ni K-edge (8.333 keV) XANES spectra were collected at specific pump-probe time delays by scanning a Si(111) double crystal X-ray monochromator, which at this energy has a resolution of 1.2 eV, across the XFEL spontaneously amplified stimulated emission (SASE) bandwidth. The ~50 fs pulse duration X-ray probe pulses have significant bunch-to-bunch spectral and temporal fluctuations due to the variation in electron bunch characteristics, resulting in a time-integrated energy bandwidth of ~50 eV at the Ni K-edge. The peak intensity position of this distribution was tuned to the X-ray photon energy at the center of the Ni K-edge to optimize X-ray flux in the energy region of interest. The monochromatic X-ray beam was focused to a ~0.1 mm diameter spot at the sample with a series of Beryllium lenses. To obtain the kinetics at a specific energy, scans of the pump-probe delay were performed at fixed photon energies. For both scan types, the XANES signal for each individual X-ray pulse was collected at the 120 Hz repetition rate of the X-ray pulse and integrated for two seconds for a total of 240 single pulses per point.

XANES spectra were collected via Ni K_α X-ray fluorescence using two solid state passivated implanted planar silicon (PIPS) point detectors (Canberra, Inc.) at 90° with respect to the incoming X-ray beam. To minimize the contribution of background counts for each fluorescence detector, the majority of the elastic scattering photons were blocked by a cobalt oxide filter mounted on a Soller slit designed for a fixed distance between the detector and the sample liquid jet (6 mm) and placed in front of each detector diode. The incoming monochromatic X-ray pulse intensity was monitored for later pulse-by-pulse signal normalization by another PIPS detector located upstream of the sample chamber. XANES spectra were obtained for pump-probe delay times from −5 ps (where the X-ray pulse precedes the laser pulse) to 100 ps to obtain spectra for both a fully ground state population and for a comparable T(d,d)-ground state population mixture measured in previous experiments limited temporally by the 100 ps pulse of APS.^1,2 XANES scans were smoothed with the locally weighted regression method using the number of local data points about each energy equal to 5% of the total number of points to fit the regression. Due to variation of energy step size through the scan, the energy window used in smoothing is therefore 0.6 eV, 1.8 eV, and 6.6 eV respectively for the pre edge, 4p_z, and white line regions of the scan, comparable or less than the 1.2 eV energy resolution of the Si(111) monochromater where sharp features are interpreted.

UV-Vis absorption spectra of the sample taken before and after the XTA experiment were identical, verifying the integrity of the sample throughout data collection and discounting any contribution of irreversible damaging processes (e.g. interactions with solvated electrons, demetalation of the porphyrin, etc.) to the transient signal.

2. Characterization of XFEL pulses and the XAS signal

The stochastic nature of the XFEL pulse energy distribution and temporal jitter require additional characterization of both the incoming X-ray pulse and the X-ray fluorescence signal at the sample. For each scan step, 240 individual shots were collected and characterized according to initial intensity (I₀) and fluorescence detector response (D₁ and D₂). The XAS signal amplitude at each energy step was determined from the average of normalized shots after rejection of selected individual shots when the normalized XAS signal deviated significantly from the median XAS value as described in the Supporting Information. To account for timing jitter in the X-ray pulses, individual shots were re-binned in time for time delay scans according to up-stream diagnostic RF cavities (“phase cavities”) that record the average electron bunch arrival time (see Supporting Information 1 for details). Importantly, this serves to account for the long-term drift in the average pulse arrival time relative to the laser delay and replaces and reduces the contribution of the timing jitter to the overall time resolution with the uncertainty in the phase cavity response. After phase cavity rebinning, the time resolution of the experiment was reduced from an estimated 400 fs to 300 fs based on the FWHM of the Gaussian instrument response function obtained as a fitted variable in the fits of the time delay scans (see Methods 3 and Supporting Information 3).

3. Global analysis of excited state kinetics

To obtain kinetics for the NiTMP XANES evolution, pump-probe delay scans at selected characteristic X-ray photon energies were performed, primarily at those energies showing the largest signal amplitudes in the difference XANES spectra (Figure 2C). These kinetic traces were fit globally to simulated traces assuming a sequential kinetic scheme to describe the excited state decay, S₁ → T′ → T → S₀. Based on this scheme, the relative populations of each species as a function of the delay time were simulated by numerical integration of a system of differential equations. These are the differential rate expressions for each species included in the kinetic scheme. τ₁, τ_2, and τ₃ are assigned to the first second and third steps in the sequential scheme, respectively (see Supporting Information 3). These components were weighted by their relative absorption at each energy and the total simulated kinetic traces were fit to the experimental traces using a nonlinear least squares method to obtain time constants for each step. The total absorption signals are expressed as functions of the X-ray photon energy E and the pump-probe delay time t,

Figure 2.

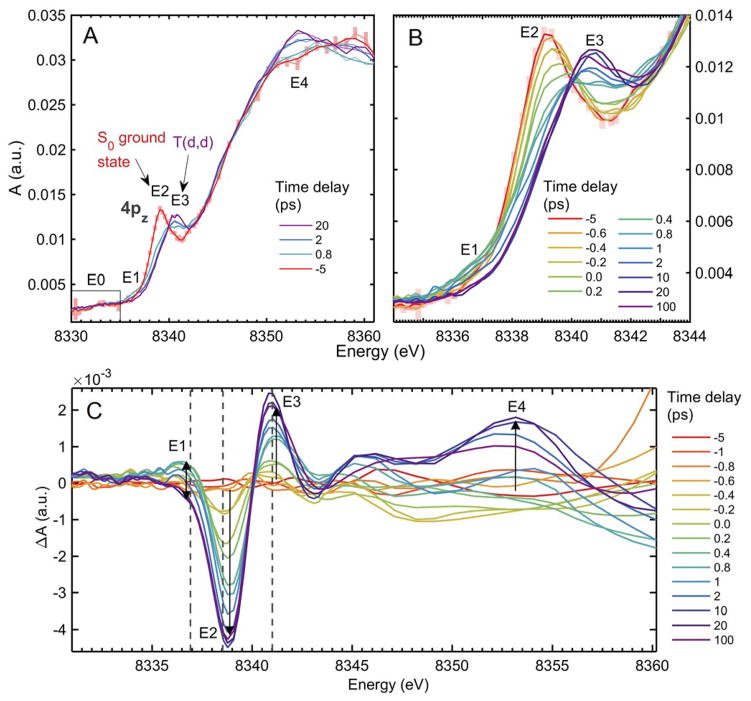
Smoothed Ni K-edge XANES spectra of NiTMP between −5 and 100 ps following 527 nm excitation. Numbered energies correspond to: E0. The 1s → 3d transition (“pre edge”) region E1. a transient at the low-energy end of the 1s → 4p_z region, E2. the S₀ 1s → 4p_z transition, E3. the T(d,d) 1s → 4p_z transition, and E4. the white-line feature associated with shortened Ni-N bonds in the T(d,d) state. (A) Time delays characteristic of (−5 ps) S_0, plotted with 95% confidence intervals to show the level of the error throughout the data set, (0.4 ps) the peak of the transient signal at 8337 eV, (2 ps) the partial disappearance of the transient at 8337 eV, the appearance of the T(d,d) 1s → 4p_z peak at E2., and the shift of the primary white line feature to E4., and (20 ps) T(d,d). (B) The evolution of the XANES from −5 ps to 100 ps within the 1s → 4p_z region. (C) Difference spectra relative to S₀ spectrum for delays between −5 and 100 ps, showing the dynamics of the S₀ bleach (E1), the rise of the T(d,d) 1s → 4p_z peak (E2), the rise and fall of the transient at 8337 eV within 2 ps (E3) and the rise of the white line feature (E4). Dotted lines correspond to energies at which delay scans were taken (Figure 3A).

$$A_{\mathit{total}}(E,t)=\sum _{i=0}^3{A}_i(E)P_i(t)$$ (1)

Where i is the index of the states, i = 0 – 3, corresponding to S_0, S₁(π, π*), T′, and T(d,d) states, A_i(E) is the relative absorption of the i-th state at E, and P_i(t) is the population of i-th state at t. The relative absorption of the ground state S₀, A₀(E) and that of the T(d,d) state, A₃(E) were respectively obtained from XANES spectra before the laser pump pulse and at 20 ps time delay where a mixture of only the T(d,d) and S₀ states are present. The relative absorption of the S₁(π, π*) state A₁(E) is assumed to be identical to A₀(E) because the (π, π*) excitation is confined on the macrocycle porphine and has little impact on the nickel center. The relative absorption of the T′ state A₂(E) was treated as a variable during the fits. The calculated A_total was then convoluted with a Gaussian instrument response function (IRF), the width of which is also treated as a variable.

4. XANES scans in the 1s → 3d transition pre-edge region

In order to capture excitation induced changes in the Ni 3d-orbital occupation, the time evolution of the 1s → 3d quadrupole-allowed transition features was also investigated by tuning the center of the SASE spectral bandwidth to this pre-edge region (8349 eV) and collecting energy scans. Due to relatively low signal intensities of the pre-edge features, a modified scheme to compute the XTA signal at each energy step was implemented using the slope of a linear fit of D₁ or D₂ vs I₀ rather than the average of the normalized signal for all individual shots. (see Supporting Information 1). Monochromator scans were taken only at selected time delays of −5 ps, 1 ps, 10 ps and 50 ps. Because XAS signals in the pre-edge region contain a significant background contribution from the rising edge that varies with the time delay as the nearby 1s → 4p_z transition peak shifts in energy, a second order polynomial was used to fit the background contribution of the averaged scans for each time delay. This contribution was removed to extract the individual peaks.

5. Electronic structure calculations

To understand the overall electronic and structural evolution of the NiTMP excited states and to ascertain how changes in the electronic and nuclear structure as the molecule relaxes are reflected in the experimentally observed XTA signals, each electronic state in the proposed mechanism (Figure 1) was modeled separately. Initial DFT and TDDFT calculations using the BP86 functional were employed to probe the basic orbital structure of NiTMP and its excited states using the ADF package (ADF2013.01^53,54). A double-ζ polarized (DZP) basis set was used for the description of C, N, and H atoms, and a triple-ζ polarized (TZP) basis set was used to describe the atomic orbitals of Ni. This combination of functional and basis set has previously described the orbital structure of a related Ni compound with high accuracy.⁵⁵ Subsequently, the geometries of the ground and each intermediate excited state were optimized with the BP86 functional^56–58 and the 6-31G(d) basis set^59,60 using a development version of the Gaussian software package.⁵⁸ The X-ray absorption was calculated with energy-specific TDDFT (ES-TDDFT)^61,62 using the PBE1PBE and Ahlrichs’ def2-TZVP basis set⁶³ with diffuse functions on the nickel atom.^64–66 For all calculations of X-ray absorption spectra, the mesityl groups on the porphyrin have been replaced with methyl groups to reduce computational cost.

RESULTS

1. Experimental results

1.1 Ni K-edge XANES describes excited state electronic and structural dynamics

In the Ni K-edge XANES spectra shown in Figure 2, the spectrum at a −5 ps pump-probe time delay (before the laser arrives) is identical to the previously obtained spectrum for the ground state S₀,^1,67 while the spectra at the 20 ps time delay and longer resemble the spectrum identified by the same study as the T(d,d) state.^1,2

Comparing the spectra at 100 ps delay with the T(d,d) spectrum and considering the 200 ps T(d,d) state decay time constant obtained previously, we estimate the initial excited state fraction to be ~60% (see Supporting Information 2). XANES features for the S₀ and T(d,d) states have been assigned and share attributes characteristic of a square planar Ni(II) coordination geometry. A distinct peak at 8339 eV in the S₀ state spectrum and at 8341 eV in the T(d,d) state spectrum (Figure 2A, labeled E2 and E3), respectively, are assigned to the strong dipole-allowed 1s → 4p_z transition.⁶⁸ Features near the “white line” absorption peak at 8351 eV are ascribed to contributions from multiple scattering resonances and transitions from Ni 1s to σ* antibonding molecular orbitals resulting from the hybridization of Ni 4p_x and 4p_y orbitals with porphyrin N 2s orbitals. Below the rising edge in the pre-edge region from 8330 to 8336 eV are weak quadrupole-allowed 1s → vacant 3d transitions, which directly probe the 3d orbital energies and electronic occupation,⁶⁹ determined by the coordination geometry and electronic state of the Ni center. The 4p orbitals are vacant for Ni complexes, so changes in transition energies to these orbitals, as well as to all high energy bound states, are determined by perturbations to the 4p energies and changes in the energy of the core orbitals due to structural or oxidation state changes.

The progression of the electronic state population S₀ → S₁ →T(d,d) is captured by XANES spectra taken as a function of the pump-probe delay time. The peak position of the 1s → 4p_z transition for the S₀ state at 8339 eV (Figure 2A, label E2) clearly shifts to 8341 eV, the energy for the same transition in the T(d,d) state. Meanwhile in the less well-resolved white line region, the prominent peak feature shifts from 8359 eV to 8353 eV.

While the σ*_x,y orbitals should shift to lower energy in the excited state as the Ni-N distances expand and the hybridization between the Ni 4p_x,y and Ni 2s orbitals is weakened,⁷⁰ the 4p_z transition blue shift has not yet been well explained due to the fact that coupling between the Ni 4p_z orbital and porphyrin π-orbitals is minimal.

At a glance, the spectra at time delays of −5 ps to 20 ps seem to resemble mixtures of the S₀ and T(d,d) states, but a feature around 8337 eV in the difference spectra (Figure 2C) is a notable exceptions. A transient feature at 8337 eV rises rapidly to its maximum amplitude at 400 fs to 800 fs, and decays within ~2 ps (Figures 2B and 2C). After ~2 ps, the XANES difference reflects an increasing population of T(d,d) state, whose features are fully developed by 10 ps.

The ground state 1s → 4p_z peak depletion proceeds with an approximate time constant of ~1 ps, in contrast to the growth kinetics of the T(d,d) state 1s → 4p_z peak, which displays a sharp rise after ~200 fs followed by a slower rise to the maximum peak height, suggesting the presence of an additional transient state, which we denote T′ (Figure 1) preceding the relaxed T(d,d) state (Figure 2C, Figure 3A). The identity of the T′ state is considered in Results 2.1. Other dynamics of spectral features on the ps timescale include an apparent delay between the rise of the white line peak feature at 8353 eV, which is an indication of the Ni-N bond elongation as seen in the T(d,d) state, and the rise of the 1s → 4p_z transition peak associated with T(d,d). Though this region of the XANES spectrum suffers due to the drop off of the X-ray intensity at the upper limit of the SASE bandwidth, it is nonetheless clear that there is little growth of this feature until 2 ps delay time, suggesting a postponed nuclear geometry change, most likely the expansion of the Ni-N bond, relative to electronic configuration changes that lead to the blue shift of the 4p_z peak.

Figure 3.

(A) Single-energy delays scans at (left to right) 8337, 8338.5, and 8341 eV with fits to kinetic model (1) (dark blue line). (B) Decomposed signal contributions from each electronic state accounted for in the fit of model (1) to the delay scans at (left to right) 8337, 8338.5, and 8341 eV determined by numerical integration of the rate expression for each species, in this case for the assignment τ₁ = 1.0 ps, τ₂ = 0.08 ps (<300 fs). The resulting total signal for each energy (dark blue) was fit to the delay traces.

1.2 Excited state decay kinetics

Comparing time-delay scans at characteristic energies of 8338.5 eV (E2), 8341 eV (E3), and 8337 eV (E1), the spectral feature of the short-lived transient (Figures 2C & 3A) characterizes the decay kinetics of these electronic states along the proposed relaxation pathway (Figure 1).

As shown in Figure 3A, the bleach of the S₀ 1s → 4p_z signal at E2 appears to be slower than the initial rise of the T(d,d) state 1s → 4p_z at E3. The signal at E1 appears to rise almost instantaneously above that of the S₀ state then falls to the lower T(d,d) state absorption. This transient signal also interferes with the bleach of the S₀ 1s → 4p_z peak at E2, causing the kinetics of the ground state bleach to appear slower than the rise of the T(d,d) 1s → 4p_z peak intensity at E3. The weak transient signal again suggests that a short-lived transient species T′ contributes to the overall XTA signal at those energies, manifested most noticeably at E1.

Averaged traces at each energy were thus globally fit to the sequential kinetics model below using Equation 1 as described in Methods 3, which incorporates the formation of T′ from the initial S₁(π, π*) state and its decay into the T(d,d) state:

$$S_{\mathit{1}}(\pi ,\pi \ast )\stackrel{k_{\mathit{1}}}{\to }{T}^{\prime }\stackrel{k_{\mathit{2}}}{\to }T(d,d)\stackrel{k_{\mathit{3}}}{\to }GS$$ (2)

where k_i (i = 1 – 3) is the rate constant and its inverse 1/k_i is τ_i, the time constant for the i-th step of the reaction.

As shown by the fits to the delay scans in Figure 3A, the totality of the data can be well-described by the scheme of Equation 2 with three time constants; two short lifetimes, 1.0 ± 0.05 ps and 0.08 ± 0.22 ps, and one long lifetime, 400 ± 130 ps. The ~400 ps lifetime cannot be determined accurately due to the limit of the experimental 100 ps delay time window, but it is associated with a decay of the total difference signal and can be assigned to τ₃, the decay time constant of the T(d,d) state to the ground state. This time constant has been determined previously in optical and X-ray transient absorption experiments to be ~200 ps.^1,6 The 0.08 ps lifetime is within the temporal resolution of the experiment and hence cannot be precisely determined by the current data. Hence, we interpret it as less than the width of the instrument response function (FWHM, 0.29 ± 0.17 ps). Because the absorption of T′, A₂(E) (Equation 1), is treated as a variable in the fitting, the assignment of the 1.0 ps and <0.3 ps components to τ₁ and τ₂ is interchangeable kinetically, but can be distinguished by the very different absorption of T′ necessitated by the two alternatives. The scenario in which τ₁ = 1.0 ps and τ₂ <0.3 ps corresponds to a T′ intermediate that absorbs much more than the ground state at 8337 eV but has little accumulation due to its rapid τ₂ decay to T(d,d). The other possibility is that T′ appears with τ₁ <0.3 ps and decays with τ₂ = 1.0 ps. The alternatives have been distinguished based on the relative absorption of T′ at 8337 eV, where the transient XANES signal is most easily observed, and the former is preferred because with a slow decay relative to formation, T′ would accumulate significantly prior to decaying to T(d,d). As the computational results below show that T′ should have a large absorption at 8337 eV, then this would require a much larger positive difference signal at this energy within the first few ps, contrary to observation. The contributions of each species in the relaxation pathway along with the sum total fitted signal are presented along with the experimental traces in Figure 3 for τ₁ > τ₂ (Supporting Information 3 shows the fits for τ₁ < τ₂).

1.3 Ni 3d orbital configuration from pre-edge transitions

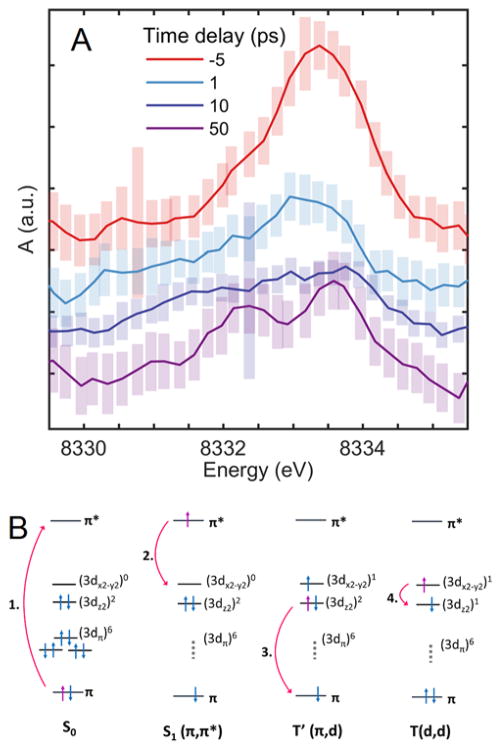
Pre-edge features corresponding to quadrupole-allowed transitions from 1s to vacant 3d orbitals in the nickel center provide insight into the electronic configuration of the 3d orbitals. In synchrotron experiments, the pre-edge region of S₀ contains a single peak for the 1s → 3d_x2-y2 transition arising from the electronic configuration of (3d_z2)²(3d_x2-y2)⁰ (Figure 4B, S₀).¹ By 50 ps after photoexcitation (Figure 4B, 1.), the T(d,d) excited state is fully populated and its pre-edge exhibits two peaks arising from the 1s → 3d_x2-y2 and 1s → 3d_z2 transitions available for the (3d_z2)¹(3d_x2-y2)¹ electronic configuration (Figure 4B, T(d,d)) which eventually decays to the ground state (Figure 4B, 4.). Looking at the time evolution of the d-orbital transition region (Figure 4A), at the negative delay representing 100% ground state population, we see a single peak corresponding to the transition to the sole 3d vacancy, 3d_x2–y2, consistent with previous synchrotron experiments. ^1,2 Following excitation, the d-orbital transitions are derived from a mixture of states which we interpret as evolving according to a series of processes represented in Figure 4B. At 1 ps delay time, the magnitude of this peak is diminished and slightly red shifted, while by 10 ps the pre-edge features are significantly broadened with some intensity growing in at lower energy. At 50 ps delay time, we see features associated with the T(d,d) state, where single vacancies in the 3d_x2–y2 and 3d_z2 lead to a split peak, although the splitting energy is 1 eV less than the 2.3 eV observed at 100 ps during synchrotron experiments. This splitting is not clearly discernable by 1 ps, but may influence the shape of the broadened features at 10 ps. The absence of a split peak by 1 ps is contradictory to the full conversion of the excited population to T(d,d) by 350 fs, as suggested by previous studies.⁷¹ Total population of the vibrationally hot T(d,d) state is more consistent with the 10 ps spectrum where the 1s → 3d_{x2- y2} and 1s → 3d_z2 transitions appear to be broadened with the 1s → 3d_{x2- y2} slightly higher in energy, possibly due to the shorter Ni-N bond length.

Figure 4.

(A) XANES scans in the 1s → 3d region (Figure 2A, E0), 5 pt smoothed and with the rising XANES edge background subtracted. Offset in A(a.u.) for clarity. (B) 3d-orbital occupations of electronic states in the NiTMP relaxation pathway resulting from: (1) excitation of the porphyrin macrocycle, (2) charge transfer from the macrocycle π* orbital to the Ni metal center, (3) reverse charge transfer from Ni to the macrocycle via relaxation of a 3dz2 electron into the π hole, (4) relaxation of the 3d_x2-y2 electron into the 3d_z2 to recover the ground state d-orbital configuration. Note naming convention w.r.t. spin state.⁵¹

Directly detecting T′ features for these weakly absorbing transitions is complicated by the fact that T′ appears to be short lived, present at low accumulation, and exists simultaneously with several other electronic states. Features at 1 ps are likely ascribable to a combination of the S1 state, T′, and broadened T(d,d) features.

2. Electronic structure and XANES calculation

2.1 TDDFT determination of excited state energies and geometries

DFT and TDDFT calculations identified possible electronic states participating in the relaxation pathway. Ground and excited state geometry optimizations of these potential intermediate electronic states provided their relative energies and structural characteristics. (see Methods: Computational Modeling for details of the calculation and Tables S1 – S4 for calculated excited states for each geometry optimized).

Using the optimized ground state geometry, the S₁(π, π*) state Frank-Condon excitation energy, which has B excitation symmetry, is computed to lie at 2.31 eV above the ground state. Any potential intermediate states in the singlet manifold should be rapidly populated according to Kasha’s rule and TDDFT excited state geometry optimizations performed on the lowest lying singlet excited states of both A and B symmetry found the lowest A state at 1.31 eV and the lowest B state at 1.81 eV. The lowest A singlet state, which possesses (π, 3d_x2-y2) orbital character, is chosen as a point of probable intersystem crossing and triplet states computed using the geometry optimized in this lowest A state reveal a corresponding triplet state with the same orbital character that lies close in energy at 1.25 eV. This A state provides an excellent candidate for the identity of T′ because 1) it is the lowest energy state in the singlet manifold and 2) the proximity of the singlet and triplet of (π, 3d_x2-y2) character in energy may enable rapid intersystem crossing.

For subsequent calculations, we identify T′ as a (π, d) state with the d-orbital configuration (3d_z2)²(3d_x2-y2)¹ as suggested by the experimental XANES pre-edges.

To determine any symmetry restrictions on intersystem crossing (ISC) between these electronic states, NiTMP was modeled without the mesityl substituents to obtain a higher symmetry group. Energies calculated for corresponding states of interest are very similar to those found in the lower symmetry geometry. Group theory considerations show that ISC from the singlet to triplet manifold is allowed, as the product of the irreducible representation of ¹(π, 3d_x2-y2) and ³(π, 3d_x2-y2) belong to the irreducible representation of the angular momentum operator R_z.

Relaxed geometries for the ground, S₁(π, π*), T′, and T(d, d) states show significant structural differences. Both the ground state and S₁(π, π*) state geometries have a short (1.94 Å) Ni-N distance and a significant out-of-plane ruffling distortion of the porphyrin macrocycle. This structural similarity is not surprising given the identical Ni electronic occupation in these two states. The T(d,d) state, on the other hand, exhibits 1s → π an expansion of the Ni-N distances by 0.1 Å, very similar to the 0.08 Å shift derived from 100 ps resolved EXAFS experiments,^1,2 and a flattening of the macrocycle conformation. A 0.8 Å Ni-N expansion is apparent in the T′ state, suggesting that a relaxed T′ geometry would have much the same structure as the T(d,d) state.

2.2 Modeling of inner shell XAS bound transitions

Solutions to the Self Consistent Field (SCF) equations that converge to at a higher energy than ground state solutions have long been recognized as useful approximations to excited state wave functions.^72–74 These solutions allow excited states to be treated in a single determinant framework whose response can be modeled with TDDFT. In order to obtain these higher-energy SCF solutions, a set of natural transition orbitals (NTOs)⁷⁵ for the state of interest was first generated at the excited state geometry. The initial guess for the SCF density of this higher-energy solution was then formed by a HOMO-LUMO swap of the dominant NTOs. A second-order optimization scheme was then used to converge to the state of interest.⁷⁶ The XANES spectra of these intermediate states were then calculated with ES-TDDFT at the same level of theory as the ground state (discussed in Computational Modeling).

Due to the neglect of scalar and spin-orbit relativistic effects in this simulation, the calculated transitions are much lower in energy than the experimental results. However, it has been shown that these operators have little effect on relative transition energies⁷⁷ and uniform shifts are routinely applied to calculated XANES spectra to better compare transition energies with experimental data.^77–79 A uniform shift of 172 eV is applied to all calculated spectra and all transitions are convoluted with Gaussian functions to match experimental lineshapes; 2.2 and 1.8 eV FWHM for the 4p_z and 3d transitions respectively.

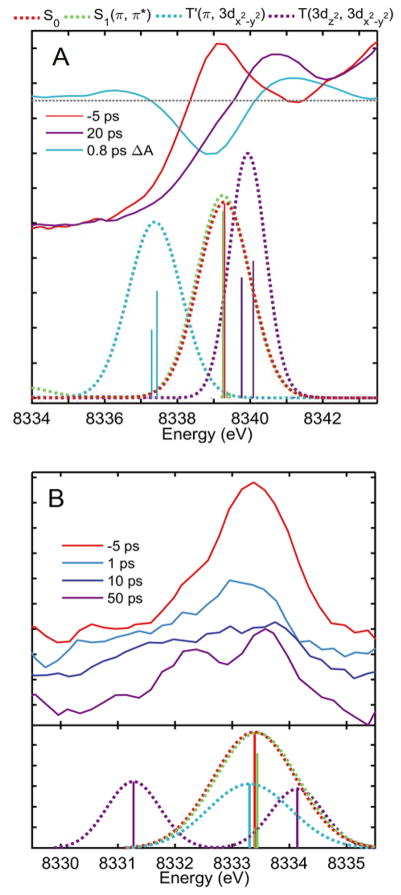
The dipole allowed 1s → 4p transitions are the dominant transitions in all calculated XAS (Table 1, Figure 5A). The electronic environment around the Ni atom has changed minimally between the S₀ and S₁(π, π*) states, so little change is seen in the 1s → 4p_z transition. However, a red and a blue shift is observed for the T′ and T(d,d) states respectively. These trends reproduce those of the experimental data where the T(d,d) 1s → 4p_z transition is clearly blue shifted compared to the S₀ and a short-lived rise and fall is evident red of the S₀ peak. It’s worth noting, however, that the calculated transitions are pure populations of their respective electronic states, which do not exist in the relaxation of the excited NiTMP and the experimental data reflects of a mixture of states.

Table 1.

Orbital energies for the electronic ground state and changes in those energies in various excited states.

	Inputs for excited-state XAS modeling
Wave function	S0	S1(π, π*)	T′	T(d,d)	S0	S0	T(d,d)	T(d,d)
Geometry	S0	S1(π,π*)	T′	T(d,d)	T′	T(d,d)	S0	S1
	Calculated Ni orbital energies
	eV	——— ΔeV ———
1s α	8167.47	−0.05	2.02	−1.17	0.37	−0.34	−0.67	−0.61
1s β	8167.47	−0.05	2.03	−1.17	0.37	−0.34	−0.67	−0.61
4pz α	1.39	−0.07	0.18	−0.23	0.06	−0.03	−0.15	−0.16
4pz β	1.39	−0.06	0.05	−0.44	0.06	−0.03	−0.34	−0.34

Figure 5.

Gaussian-broadened calculated XAS transitions of relevant excited electronic states compared to experimental spectra in (A) the rising edge regions where 1s → 4p_z transitions dominate and (B) the pre-edge region.

For this system, the modeled 1s → 3d transitions reflect the expected 3d-orbital occupation for the ground and T(d,d) states. Modeled transitions to 3d_z2 and 3d_x2-y2 roughly coincide with the two peaks apparent in the experimental XANES at 50 ps delay (Figure 5B) and are very similar to those observed in the pre-edge region at 100 ps during our previous synchrotron experiments.^1,2 The experimental 1s → 3d_x2-y2 peak at 1 ps is slightly red shifted compared to the ground state and this same behavior is seen for the modeled transition for the T′ state. This red shift is notable as it contrasts with the blue shift observed for the same transition at 50 ps and for the modeled T(d,d) state. A weakly dipole allowed 1s → π transition is apparent in the calculated spectra of the S₁(π, π*) and T′ states, although these are not plotted because their contribution is removed during background subtraction of the experimental data. Furthermore, these are relatively short-lived states, the contribution to the total signal is quite small, and this region of the spectrum is very noisy due to low XAS signal, so well-defined peaks for these weak dipole allowed transitions are not observed experimentally.

DISCUSSION

This study, which is among early examples of XTA measurements at LCLS, allows us to establish a kinetic scheme describing the decay of photo-excited NiTMP and to distinguish the short-lived Ni(I) state T′ as an intermediate preceding the formation of the previously characterized T(d,d) state. Inner-shell transitions characterized by the combined experimental and computational results are analyzed to derive properties not directly measureable using other ultrafast methods. Here, we discuss the evidence for the charge transfer nature of the short-lived T′ state, discuss the interpretation of the modeled XAS transitions towards discerning the impact of electronic occupation on Ni orbital energies, reflect on the role of structure in determining excited state properties, and present our views on the implications of our findings for potential applications.

1. Evidence for a transient Ni(I) center due to intramolecular electron transfer

In combination with calculated XAS transitions relating transient XANES features to corresponding electronic states, global analysis of the XTA signal as a function of the X-ray photon energy and delay time allowed us to overcome challenges in the assignment of T′ to a CT state: 1) the weak T′ state signal compared to those of the S₀ and T(d,d) states through the rising-edge; 2) the ambiguity of previous ultrafast optical absorption measurements with regards to changes in the Ni orbital occupation; and 3) the uncertainty of the correlation between the 3d electronic configuration and the energy of the prominent 1s → 4p_z transition.

Global fitting of kinetic traces at three characteristic X-ray energies obtained time constants for the three-step sequential model (Equation 2). However, the assignment of these time constants to specific processes requires an idea of the relative absorption properties of each state involved. This was determined with the DFT assignment of the difference XANES spectral feature at E1 to the 1s → 4p_z transition peak of the T′ state. This assignment would have been otherwise challenging due to evolving background signals near the rising edge and the lack of available XANES data for Ni(I) square planar systems. The decomposition of the total signal (Figure 3b) shows that the apparently faster rise at E2 compared to the decay at E1 arises from a small positive contribution to the signal from T′ at both energies that rises and decays quickly. The kinetics of the T′ state absorption (Figure 3B, cyan curves) initially appear to be the result of an ultrafast (< 300 fs) generation time constant τ₁ and a relatively slow (~1 ps) decay time constant τ₂ for the T′ species. However, taken by itself the integrated rate law for the T′ population (Equation S7) derived from the sequential kinetic model (Equation 2) cannot distinguish between this assignment and τ₁ = 1 ps, and τ₂ < 0.3 ps. This second case results in low T′ population accumulation. Given the expected large absorption of T′ at 8337 eV due to its red shifted 1s → 4p_z transition, the modest increase in signal at this energy supports the latter assignment.

Because the T′ state decays significantly faster than it forms, so-called “inverted kinetics” govern the T′ population. The 1 ps decay of the T′ population reflects the 1 ps decay of the S₁(π, π*) population from which T′ is being constantly generated, while the <0.3 ps decay of the T′ state limits T′ accumulation even when the population of S₁(π, π*) is large. This manifests as the population rise time and the rise of the T(d,d) state closely follows the rate of formation of this intermediate state, as this is essentially rate limiting. These population kinetics follow our observation that the transient T′ state is only detectable for 1–2 ps.

Relaxation through a charge transfer (CT) state that produces a transient Ni(I) intermediate has been previously hypothesized based on double-excitation optical methods that observed the relaxation of an excited π electron through d-orbital vacancies in the long-lived T(d,d) state in NiTPP.⁴⁰ Such a CT state has also been implicated as the route of excited porphyrin deactivation in Ni tetraphenylporphyrin (NiTPP), Ni octaethylporphyrin (NiOEP), heme⁸⁰, and several other open-shell metalloporphyrins⁸¹ by pump-probe photoelectron spectroscopy measurements in the gas phase, which report fast time constants for the evolution of the NiOEP excited state absorption very similar to this work (100 fs and 1.2 ps).

A short lived CT state, T′, is compatible with the population of the T(d,d) state on the picosecond time scale as observed by previous studies,^71,82 although these did not implicate a charge transfer state and depicted the S₁(π, π*) relaxation process as the direct transfer of the excitation to the metal center, resulting in a hot T(d,d) state. Vibrational relaxation of the hot T(d,d) state was observed within 10–20ps.

During this period, vibrational relaxation processes likely occur and these results do not preclude the involvement of an unrelaxed T(d,d) state in the S₁ decay. However, a purely vibrational model that does not assign T′ as a CT state is not as well supported by the current analysis of the 4p_z region, where XANES differences before T(d,d) is fully populated are ascribed to the rearrangement of the Ni electronic structure. Ni orbital energies calculated for a T(d,d) electronic configuration but an S₀ or S₁ geometry, approximating an unrelaxed T(d,d) state, show that such a state cannot account for the transient signal at 8337 eV due to an overall blue shift in the 1s → 4p_z transition (Table 1).

Nuclear movement during vibrational relaxation affects the 3d orbital energies, especially those involved in coordination to the porphyrin ring, which is reflected in the dynamics of the 1s → 3d transition region as general broadening of the 3d transitions in T(d,d). An increased linewidth for NiTMP 1s → 3d transitions due to conformational heterogeneity was previously observed for the NiTMP ground state.2 This may provide an explanation of the apparent broadening of 3d transitions at 10 ps when T(d,d) is fully populated although a full description of the relaxation processes in terms of nuclear movement requires additional measurement with more direct structurally sensitive techniques.

2. XAS transitions reflect photoinduced electronic structural changes in the metal center

Because it directly probes transient metal orbital energies and occupancy, XTA on the fs time scale can determine the dynamics of photoinduced metal electronic configuration and orbital energy changes well before thermalization of the excited states. While optical transient absorption measurements can clearly identify the kinetics of S₁(π,π*) state decay, they are not able to directly detect optically dark electronic states arising from changes in metal centered electronic occupation or metal orbital energy changes in subsequent excited states. This study has directly obtained energies of the transitions 1s → 3d and 1s → 4p_z in Ni for different electronic states, from which these properties have been obtained for short-lived transient states.

Changes in the observed Ni K-edge transition features, such as the red shift and subsequent blue shift of the 1s → 4p_z transition energy, agreed with the calculated inner shell transitions (Table 1) and their energies are interpreted in terms of the evolving electronic configuration. With the assignment of T′ to Ni(I), T′ state formation can be understood as the intramolecular charge transfer from the π* orbital to the 3d_x2-y2 orbital. Computational results indicate a rise of the 1s energy by ~2 eV for the T′ electronic configuration, where charge transfer results in greater nuclear shielding and therefore a lower electron binding energy. The rise of the 1s orbital energy in turn reduces the 1s → 4p_z transition energy in the T′ state. This is identical to the core-level shift seen in X-ray photoelectron spectroscopy (XPS)⁸³ and the effect of oxidation on K-edge spectra has also been observed in previous XAS experiments.^84,85

This computed red shift is seen experimentally as the rise and fall of intensity around E1 in <2 ps. Only about 0.2 eV of the ~2 eV shift in the 1s → 4p_z transition energy change from the ground state to the T′ state transition is due to the shift of the 4p_z orbital energy. Similarly, the blue shift in the 1s→4p_z transition energy of the T(d,d) state can be attributed to a change in the repulsive potential felt by the core electrons as the 3d_x2-y2 orbital is far more hybridized with the ligand orbitals than the 3d_z2 orbital (See Figure S7). Relative to the ground state, which has a doubly occupied 3d_z2 and an unoccupied 3d_x2-y2 orbital, the T(d,d) state has less electron density around the Ni atom, lowering the 1s orbital energy and blue-shifting the 1s → 4p_z transition by 1.5 eV.

As evidenced by the computed changes in the Ni 1s energy experimental 1s → 3d transition energies cannot be solely relied upon to determine changes in d-orbital splitting. Though the 1s → 3d_x2-y2 transitions, for example, are within half an eV of each other according to the experimental spectrum, we can expect the 3d_x2-y2 orbital energy to change much more significantly to remain consistent with the shifts in the Ni 1s energy. Calculated transition energies (see Supporting Information 4) are very similar to those experimentally observed with the possible exception of the T(d,d) state, though even here the trend in the movement of the transitions with respect to the ground state is preserved.

3. Macrocycle structural response to NiTMP electronic evolution

The identification by TDDFT of T′ as the lowest energy singlet as well as a state with a triplet state lying close in energy lends credence to the identification of T′ as a (π, d) state. The optimized geometries of the involved electronic states (Figure 6) provide insight into the behavior of the NiTMP structure in response to electronic changes and the subsequent energetic rearrangement of Ni orbitals.

Figure 6.

Relaxed geometries of each electronic state in the NiTMP decay pathway as calculated by TDDFT. Occupation of the Ni 3d_z2 orbital drives expansion of the Ni N bond length and subsequent flattening of the macrocycle.

Macrocycle expansion and flattening in the T(d,d) state is explained based on the net movement of electron density from 3d_z2 to 3d_x2-y2, which sits in the porphyrin plane and aligns well with the Ni-N bonds. This bond expansion is a repulsive response to additional electron density localized between the Ni and N atoms. Because the macrocycle need no longer accommodate the unusually short Ni-N bond length, the constrained ruffled geometry relaxes to a more energetically favorable flattened conformation that allows greater delocalization of π electrons. Interestingly, the majority of the Ni-N bond length expansion has already occurred in the relaxed geometry of the T′ state, which has a flattened porphyrin conformation and a Ni-N bond length expansion of 0.08 Å, suggesting that the occupation of 3d_x2-y2 is the main driver of porphyrin expansion.

Comparisons to 1s, 4p_z, and 3d orbital energies calculated for the T′ and T(d,d) optimized geometries but using the ground state wave function to describe the electronic state are used to separate electronic vs. structural effects on the excited-state XANES. In spite of the significant difference in structure between the ground state and the T′ and T(d,d) states, the difference in the 4p_z orbital energies is very modest and the shift in the 1s energy is only about −0.3 eV for both geometries (Table 1). We can therefore conclude that the 1s → 4p_z transition energy is largely determined by the electronic state of Ni, which is in line with the fact that the 1s shift dominates the observed transition shifts and that 4p_z has less interaction with ligand orbitals than other valence Ni orbitals. The relative insensitivity of the 1s → 4p_z energy to solely structural changes in the porphyrin conformation and Ni-N bond length also discounts the explanation of the short-lived transient signal as pure vibrational broadening of the T(d,d) state 1s → 4p_z feature.

Based on our observation of the Ni(I) state’s lifetime and the corresponding structural evolution, we can speculate on the participation of the ring structure and conformation on the stabilization of this species. Porphyrins with large out-of-plane ground state distortions generally have dramatically different photophysical properties compared to analogous planar porphyrins, exhibiting low fluorescence yield and shorter excited state lifetimes owing to an increase in accessible nonradiative decay pathways through a high degree of conformational flexibility.^42,86 A TDDFT survey of Ni porphine, NiTPP and NiOEP singlet and triplet states noted that the lowest energy singlet states in all cases are CT states of ¹(π, 3d_x2-y2) character, the energy of which increases for NiTPP which has a higher degree of macrocycle out-of-plane distortion, in this case ruffling.⁵⁵ Meanwhile, the lowest energy triplet state, the T(d,d) state, is destabilized to an even greater degree as ruffling increases, reducing the energy gap between these states and (π, 3d_x2-y2) states. This suggests that not only are more routes to radiation-less deactivation available for distorted porphyrins, but the relevant electronic states along the proposed route of deactivation are closer together in energy and the decay process is faster according to the energy gap law.

In the ground state, Ni porphyrins have a low barrier to interconversion between various distorted conformers of the macrocycle,^87,88 e.g., ruffled, domed, etc., as evidenced by the relative broadness of the 1s → 3d_x2-y2 transition peak.² The lowest in energy of these conformers is a ruffled geometry according to our own geometry optimization. Geometry optimizations of the T′ state indicate the Ni-N bond length should expand, and therefore flatten the macrocycle. Based on the delay in the rise of the white line feature at 8353 eV, closely related to the Ni-N bond length, with respect to the features associated with the 1s → 4p_z, this expansion is delayed compared to the change in the electronic state. Because the T′ state appears to initially retain a ruffled geometry while the molecular structure has yet to respond to the electronic change, its conversion to the T(d,d) may be accelerated by the structural effect mention above, causing relaxation to T(d,d) to occur before the molecule has time to flatten.

Out-of-plane distortions are structural factors that influence electronic state energies mainly through the destabilization of the π and 3d_x2-y2 orbitals, an effect that when taken to a greater extreme in substituted Ni phthalocyanines begins to lead to longer CT state lifetimes. While the CT state reported here and in previous studies of Ni porphyrins is very short-lived, on the order of <2 ps, octamethyl and octabutoxy substituted Ni phthalocyanines have been described as having long-lived LMCT states with lifetimes in the hundreds of picoseconds.^86,89 Here, ring substitution leads to the decrease of the relative CT state energy compared to the equivalent (3d_x2-y2, 3d_z2) state to the point where the CT state is the lowest energy triplet state, extending the lifetime of the Ni(I) to the point of potential catalytic utility.

CONCLUSION

Ultrafast XANES at the Ni K-edge was successfully measured for optically excited Ni(II)TMP on a previously unachievable sub-picosecond timescale, providing insight into its ultrafast electronic and structural relaxation processes. Importantly, a transient Ni(I) (π, d) electronic state (T′) is implicated as an intermediate through the interpretation of a short-lived excited state absorption. The assignment of this absorption is confirmed by agreement with calculated XAS transitions for the postulated (π, d) electronic states at this energy.

The observed and computed inner shell-to-valence orbital transition energies demonstrate and quantify the influence of electronic configuration on specific metal orbital energies. The strong influence of the valence orbital occupation on the inner shell orbital energies indicates that one should not use the transition energy from 1s alone to draw conclusions about the d-orbital energies of different states. A transient electronic configuration could influence d-orbital energies up to a few eV and any potential photocatalytic application should account for this to ensure that energy levels are well matched and that the photoexcitation can be used optimally in driving desirable processes.

NiTMP structural dynamics have been deduced from DFT optimized geometries and structurally sensitive features in the Ni K-edge XANES. Structural changes such as macrocycle expansion and flattening appear to have little impact on the energies of Ni axial orbitals observed in this study compared to the electronic changes that occur as the molecule relaxes. However, the influence of the porphyrin macrocycle conformation on relaxation kinetics may be significant enough to affect the kinetics that govern the limited population accumulation of Ni(I). The short lifetime of the T′ state and the delay of the nuclear rearrangement to a longer Ni-N bond length and flattened macrocycle with respect to its formation suggests the still-ruffled macrocycle expedites T′ decay.

ABBREVIATIONS

XTA

X-Ray Transient Absorption

XANES

X-ray Absorption Near Edge Structure

XAS

X-ray Absorption Spectroscopy

WAXS

Wide-Angle X-ray Scattering

EXAFS

Extended X-ray Absorption Fine Structure

NiTMP

Nickel(II) tetramesityl porphyrin

APS

Advanced Photon Source

LCLS

Linac Coherent Light Source

DFT

density functional theory

TDDFT

time dependent density functional theory

TMC

transition metal complex

XFEL

X-ray Free Electron Laser

SASE

spontaneously amplified stimulated emission

XPP

X-ray Pump Probe

CT

Charge Transfer

ISC

intersystem crossing