Abstract
Procedural learning of skills depends on dopamine-mediated striatal plasticity. Most prior work investigated single stimulus-response procedural learning followed by feedback. However, many skills include several actions that must be performed before feedback is available. A new procedural-learning task is developed in which three independent and successive unsupervised categorization responses receive aggregate feedback indicating either that all three responses were correct, or at least one response was incorrect. Experiment 1 showed superior learning of stimuli in position 3, and that learning in the first two positions was initially compromised, and then recovered. An extensive theoretical analysis that used parameter space partitioning found that a large class of procedural-learning models, which predict propagation of dopamine release from feedback to stimuli, and/or an eligibility trace, fail to fully account for these data. The analysis also suggested that any dopamine released to the second or third stimulus impaired categorization learning in the first and second positions. A second experiment tested and confirmed a novel prediction of this large class of procedural-learning models that if the to-be-learned actions are introduced one-by-one in succession then learning is much better if training begins with the first action (and works forwards) than if it begins with the last action (and works backwards).
Keywords: Computational cognitive neuroscience, Dopamine, Skill learning, Striatal plasticity, Parameter space partitioning
1. Introduction
Many skills are acquired via procedural learning, which is characterized by gradual improvements that require extensive practice and immediate feedback (Ashby & Ennis, 2006). Most motor skills fall into this class (Willingham, 1998), but also some cognitive skills, including certain types of category learning (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & Maddox, 2005, 2010; Maddox & Ashby, 2004). Much evidence suggests that procedural learning is mediated largely within the striatum, and is facilitated by a dopamine (DA) mediated reinforcement learning signal (Badgaiyan, Fischman, & Alpert, 2007; Grafton, Hazeltine, & Ivry, 1995; Jackson & Houghton, 1995; Knopman & Nissen, 1991). The well-accepted theory is that positive feedback that follows successful behaviors increases phasic DA levels in the striatum, which has the effect of strengthening recently active synapses, whereas negative feedback causes DA levels to fall below baseline, which has the effect of weakening recently active synapses (Schultz, 1998). In this way, the DA response to feedback serves as a teaching signal, with successful behaviors increasing in probability and unsuccessful behaviors decreasing in probability.
Experimental studies of DA neuron firing have focused on simple behaviors in which a single cue is followed by a single discrete response (e.g., button or lever press) or no response at all. The seminal finding from these experiments is that DA neurons fire to reward-predicting cues and unexpected reward (e.g. Schultz, 1998). Despite the importance of this work, it does not address the role of DA in the learning of skills that include multiple behaviors that must be precisely executed in response to discrete cues, and in which the feedback is delivered only after the final behavior is complete. Our goal is to investigate the putative role of DA in these more complex settings. We take an indirect approach by collecting behavioral data and then testing a wide variety of computational models that make qualitatively different assumptions about the role of DA in the learning of such multi-step behaviors.
Understanding how multistep behaviors are learned requires an understanding of how the feedback after the final behavior is used to learn the responses to each of the cues in the sequence. One possibility is that feedback propagates backward through each sub-behavior in the sequence, such that the learning of the response to a later cue in the sequence facilitates the learning of a preceding cue. A wealth of data show that once a cue comes to predict reward, it begins to elicit a vigorous response from DA neurons (Pan, Schmidt, Wickens, & Hyland, 2005; Schultz, 1998, 2006; Waelti, Dickinson, & Schultz, 2001). If a new cue is added before a learned cue that perfectly predicts reward, then the DA response to the learned cue shifts back (backpropagates1) to the new (earliest) cue (Schultz, Apicella, & Ljungberg, 1993). This works well when no response is required, as in classical conditioning, or in simple instrumental conditioning with only one available response (e.g. lever press), or in tasks requiring choices among different cues while navigating a maze. In such scenarios, DA release due to the reward prediction of the learned cue serves as a teaching signal to train the preceding, new cue, and in this way, sequences of cue-cue associations can be learned (Suri & Schultz, 2001). Importantly, such backpropagation of the DA response has only been demonstrated in tasks in which characteristics of later cues directly depend on decisions made to earlier cues (i.e., dependent decisions). Unfortunately, almost no empirical data exist on how DA neurons respond in tasks where a sequence of independent decisions must all be made correctly to earn positive feedback, nor have any models been proposed. If several independent decisions about unrelated cues are made in a row, and each has to be correct to earn positive feedback at the end of the sequence, then an earlier cue is not a predictor of a later cue.
Current efforts to study the learning of sequential, multistep decisions have focused on tasks in which the first-step choice predicts the available choices in the next step (Walsh & Anderson, 2011; Daw et al., 2011; Glascher et al., 2010). This is important work, and many real-life tasks include such dependencies between sequential cues. However, the demonstration in such work that the effect of the feedback backpropagates to earlier cues in the sequence confounds two issues. One possibility is that the backpropagation occurs only because of the perfect dependency, and another is that all sequential skills, including those with independent actions, benefit from such backpropagation. This article investigates the backpropagation of the feedback signal during the learning of a sequence of independent skills. Our results strongly contradict the latter of these two hypotheses. In fact, we show that virtually all models that predict any type of backpropagation of the DA signal to earlier independent cues are incompatible with our results. Furthermore, our results also suggest that any such backpropagation that did occur must have a detrimental effect on learning. Even models that use eligibility traces to update distant cues with the feedback signal (instead of the backpropagation) fail to account fully for our results.
To study how feedback provided at the end of multiple independent behaviors affects the learning of each behavior in the sequence, we developed a new experimental paradigm called the aggregate-feedback procedural category-learning task (for a similar declarative memory-based task, see Fu & Anderson, 2008). In this task, three highly discriminable visual images are presented sequentially, each requiring an A or B category response. Feedback is given only after all three responses are complete. Positive feedback is given if all three responses were correct, and negative feedback is given if any of the three responses were incorrect, without any information about which response or responses were in error.
This study addresses a number of fundamental questions regarding DA’s involvement in aggregate-feedback learning. These include the following: How do the DA reward prediction signals develop during learning to respond to multiple independent cues before feedback? How does the DA release to the reward prediction of a cue impact learning of cues earlier in the sequence? And do learning rates for cues depend on how far back in time they are from the feedback? We took a computational cognitive neuroscience approach to address these questions (Ashby & Hélie, 2011). First, we collected behavioral data from human participants in the aggregate-feedback category-learning task. Second, we used a computational approach called parameter space partitioning (PSP; Pitt, Kim, Navarro, & Myung, 2006) that allowed us to investigate the ability of a broad class of alternative procedural-learning models to account for our results. As we will see, none of these models successfully accounts for all aspects of our data. Third, we used these models to make novel predictions about which of two different training procedures is optimal with aggregate-feedback. Fourth, we tested these predictions with behavioral data from human participants, and identified the best training regime for procedural learning with aggregate feedback.
2. Experiment 1
Our goal was to extend behavioral neuroscience work on DA neuron firing properties to human behavioral experiments. The relevant behavioral neuroscience studies almost all used some form of classical or instrumental conditioning. So the ideal task would share properties with conditioning studies and present some nontrivial cognitive challenges. Our solution was to use an unstructured category-learning task in which highly unique stimuli are randomly assigned to each contrasting category, and thus there is no rule- or similarity-based strategy for determining category membership. This task is similar to instrumental conditioning tasks in which animals must learn to emit one response to one sensory cue and another response to a different cue (e.g., turn left in a T-maze to a high-pitched tone and turn right to a low-pitched tone). But it is also similar to high-level categorization tasks that have been studied for decades in the cognitive psychology literature. For example, Lakoff (1987) famously motivated a whole book on a category in the Australian aboriginal language Dyirbal that includes seemingly unrelated exemplars such as women, fire, dangerous things, some birds that are not dangerous, and the platypus. Similarly, Barsalou (1983) reported evidence that ‘ad hoc’ categories such as “things to sell at a garage sale” and “things to take on a camping trip” have similar structure and are learned in similar ways to other ‘common’ categories. Thus, the unstructured category-learning task that forms the foundation of our studies is simple enough that we should be able to relate our results to those from instrumental conditioning studies, while resembling the structure of ad hoc categories.
Although intuition might suggest that unstructured categories are learned via explicit memorization, there is now good evidence – from both behavioral and neuroimaging experiments – that the feedback-based learning of unstructured categories is mediated by procedural memory. First, several neuroimaging studies of unstructured category learning found task-related activation in the striatum, as one would expect from a procedural-learning task, and not in the hippocampus or other medial temporal lobe structures, as would be expected if the task was explicit (Lopez-Paniagua & Seger, 2011; Seger & Cincotta, 2005; Seger et al., 2010). Second, Crossley, Madsen, and Ashby (2012) reported behavioral evidence that unstructured category learning is procedural. A hallmark of procedural learning is that it includes a motor component. For example, switching the locations of the response keys interferes with performance in the most widely studied procedural-learning task – namely the serial reaction time task (Willingham, Wells, Farrell, & Stemwedel, 2000). In addition, several studies have shown that switching the response keys interferes with performance of a categorization task known to recruit procedural learning (i.e., information-integration categorization) but not with performance in a task known to recruit declarative memory (i.e., rule-based categorization; Ashby et al., 2003; Maddox et al., 2004; Maddox, Glass, O’Brien, Filoteo, & Ashby, 2010; Spiering & Ashby, 2008). Crossley et al. (2012) showed that switching the locations of the response keys interfered with unstructured categorization performance but not with performance in a rule-based categorization task that used the same stimuli. Thus, feedback-mediated unstructured category learning seems to include a motor component, as do other procedural-learning tasks.
Stimuli in the experiments described here were perceptually distinct fractal images (Experiment 1a and 2) or real life scenes (Experiment 1b). High perceptual dissimilarity is important in order to minimize the possibility that performance for an item early in the sequence improves because it is highly similar to an item later in the sequence, rather than because of its ability to make use of the aggregate feedback that is provided.
Experiment 1a examined aggregate-feedback category learning using 12 highly discriminable fractal patterns as stimuli. Half of the 12 fractal images were randomly assigned to category A and half to category B. Participants received enough single-trial fully supervised training to achieve single-stimulus performance of about 80% correct. On these single-trial fully supervised trials, feedback followed every response. This was followed by an extended period of aggregate-feedback training in which participants made categorization responses to three successive stimuli with aggregate feedback after the third response. The single-trial pre-training was included so that once aggregate feedback began, participants would receive positive feedback with probability approximately equal to 0.5 (i.e., 0.83). Without such pre-training, the positive feedback rate under aggregate feedback would be only 0.125 (i.e., 0.53), and pilot studies showed that under such conditions many participants never learn2.
At the start of the experiment, 4 of the 12 stimuli (2 from category A and 2 from category B) were randomly assigned to appear in position 1, another 4 (2 from A and 2 from B) were randomly assigned to appear in position 2, and the remaining 4 appeared in position 3. A full-feedback control condition with a separate set of participants was also included for which feedback was presented on a trial-by-trial basis following each response.
2.1. Methods – Experiment 1a
2.1.1. Participants
Forty-eight participants completed the aggregate-feedback task and 28 participants completed the full-feedback control task. All participants received course credit or payment of $10 for their participation. All participants had normal or corrected to normal vision.
2.1.2. Stimuli and Stimulus Generation
For each participant, we randomly selected 12 fractal patterns (Figure 1a) from a pool of 100. On each trial, a single stimulus was presented in the center of a 1280 × 1024 pixel computer screen (subtending approximately 3° of visual angle).
Figure 1.
A. Two sample fractal stimuli used in Experiment 1a. B. Two sample real-world stimuli (indoor scenes) used in Experiment 1b. A. and B. At the start of both experiments 12 stimuli were randomly sampled from a pool of 100 independently for each participant. Four of these 12 stimuli (2 from category A and 2 from category B) were randomly assigned to appear in position 1, another 4 (2As and 2Bs) were randomly assigned to appear in position 2, and the remaining 4 (2As and 2Bs) appeared in position 3.
2.1.3. Procedure
Participants were informed that there were two equally likely categories and that they should be accurate and not to worry about speed of responding. The experiment consisted of 15 24-trial blocks with each stimulus being presented twice in each block. To facilitate initial learning, the first four blocks included trial-by-trial feedback. We denote these as “full-feedback blocks 1 – 4”. On each trial, the stimulus appeared until the participant generated an “A” (“z” key) or “B” (“/” key) response, followed by the word “correct” or “incorrect” for 1000ms, a 500ms blank-screen inter-trial interval (ITI), and the next trial. The 4 full-feedback blocks were followed by 11 aggregate-feedback blocks, denoted as “aggregate-feedback blocks 1 – 11”. On aggregate-feedback trials, feedback was presented only following every third response. Specifically, the first stimulus appeared until the participant generated an “A” or “B” response, followed by a 500ms blank screen ITI, and then presentation of the second stimulus. The second stimulus appeared until the participant generated an “A” or “B” response, followed by a 500ms blank screen ITI, and presentation of the third stimulus. The third stimulus appeared until the participant generated an “A” or “B” response, followed by the words “All responses were correct” or “At least one response was incorrect” for 1000ms, a 500ms blank screen ITI, and the next triple of trials. In the full-feedback control task, trial-by-trial feedback was included on every trial in all 15 blocks.
2.2. Results – Experiment 1a
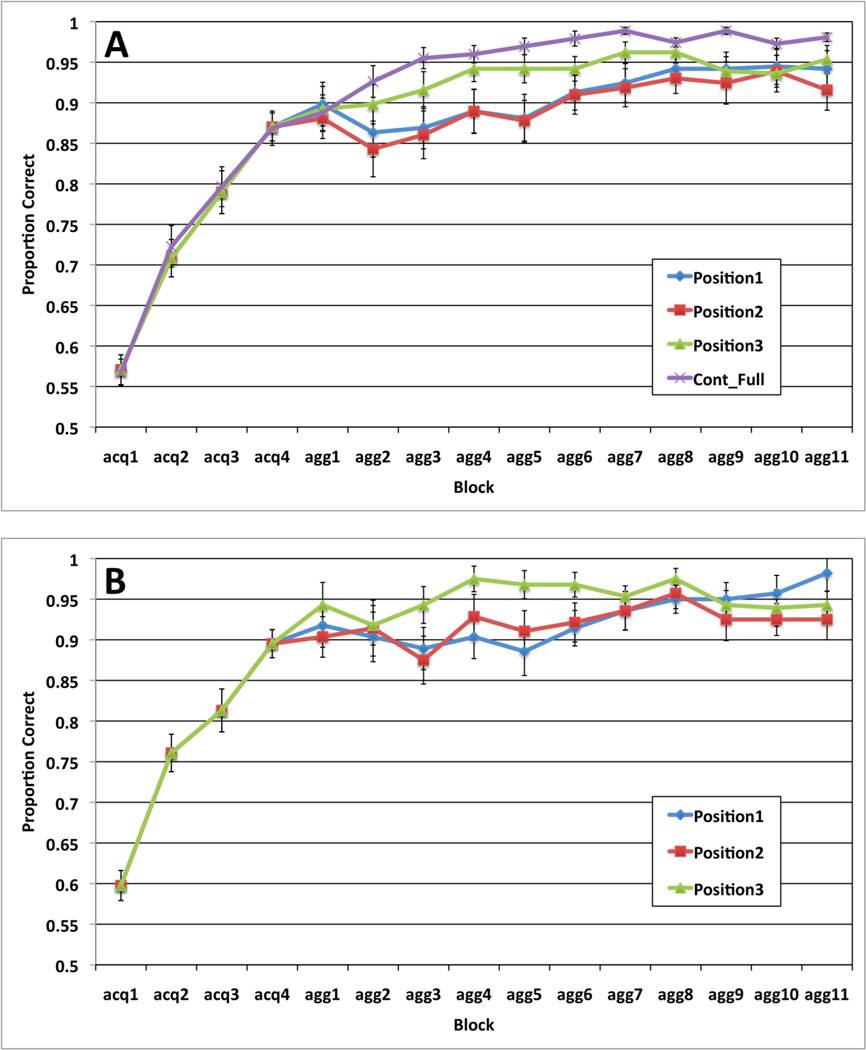
To exclude non-learners, we included only participants who exceeded 60% correct in the final full-feedback block of the aggregate-feedback task3 (i.e., full-feedback block 4). This excluded 5 participants from the aggregate-feedback condition (43 remaining). For consistency, the same criterion (>60%) was applied in the full-feedback condition’s fourth block, excluding 2 from the full-feedback condition (26 remaining). Average accuracy in the four full-feedback and 11 aggregate-feedback blocks by position in the aggregate-feedback task are displayed in Figure 2a, along with the average accuracy rates for the full-feedback control task.
Figure 2.
A. Proportion correct (averaged across participants) from the aggregate-feedback and full-feedback control tasks across blocks in A) Experiment 1a, and B) Experiment 1b. Standard error bars included. (acq: acquisition, agg: aggregate).
2.2.1. Aggregate-Feedback Task
A repeated-measures ANOVA on the accuracy rates across the four full-feedback blocks suggests learning [F(3, 126) = 82.84, p < .001, η2 = .664] with performance reaching 87% by the fourth block. Next we conducted a 3 position × 11 block repeated-measures ANOVA on the accuracy rates in the aggregate-feedback blocks. The main effects of block [F(10, 420) = 6.28, p < .001, η2 = .130] and position were significant [F(2, 84) = 6.14, p < .005, η2 = .128]. Post hoc tests with Bonferroni correction for multiple comparisons showed that position 3 accuracy was superior to both position 2 accuracy (p < .05), and to position 1 accuracy (p < .05), with no significant difference in positions 1 and 2 accuracy. The position × block interaction was not significant [F(20, 840) = 1.00, p = .45, η2 = .023].
2.2.2. Comparing Full-Feedback Control and Aggregate-Feedback Accuracies
To verify that initial learning did not differ between the aggregate-feedback and full-feedback tasks, we conducted a mixed design ANOVA comparing task performance across the four full-feedback blocks from the aggregate-feedback and full-feedback tasks. As a visual examination of Figure 2 suggests, the main effect of block was significant [F(3, 201) = 136.03, p < .001, η2 = .670], but the main effect of task [F(1, 67) = 0.023, p = .88, η2 = .001] and the task × block interaction [F(3, 201) = 0.14, p = .94, η2 = .002] were not.
To determine whether position 3 accuracy in the aggregate-feedback task was as good as that observed in the full-feedback control task, we conducted a mixed design ANOVA comparing the position 3 aggregate-feedback accuracy rates across the 11 aggregate-feedback blocks with the overall full-feedback control accuracy rates across the final 11 blocks of that task. The main effect of block was significant [F(10, 670) = 6.78, p < .001, η2 = .092], but the main effect of task [F(1, 67) = 2.192, p = .14, η2 = .032] and the task × block interaction [F(10, 670) = .54, p = .74, η2 = .008] were non-significant. Despite the lack of a significant main effect of task, the full-feedback learning curve is significantly higher than the position 3 learning curve during aggregate-feedback blocks by a sign test (p < 0.01).
2.3. Methods – Experiment 1b
Experiment 1b was identical to Experiment 1a except that the fractal stimuli were replaced with real-world stimuli, and the full-feedback control condition was excluded.
2.3.1. Participants, Stimuli and Stimulus Generation
Thirty-nine individuals participated. All aspects of participants, stimuli and stimulus generation were identical to those from Experiment 1a, except that the stimuli were real-world indoor scenes (Figure 1b).
2.3.2. Procedure
The procedure was identical to that from Experiment 1a.
2.4. Results – Experiment 1b
We applied the same exclusion criteria used in Experiment 1a to the Experiment 1b data and were left with data from a total of 35 participants. Figure 2b displays the average accuracy rates for the four full-feedback and the 11 aggregate-feedback blocks separately by position. A repeated measures ANOVA on the accuracy rates across the four full-feedback blocks suggests learning [F(3, 102) = 59.38, p < .001, η2 = .636] with performance reaching 90% by the fourth block. Next we conducted a 3 position × 11 block repeated measures ANOVA on the accuracy rates in the aggregate-feedback blocks. The main effects of block [F(10,340) = 2.42, p < .01, η2 = .066] and position were significant [F(2, 68) = 4.84, p < .01, η2 = .125]. There was also a significant position × block interaction [F(20,680) = 2.11, p < .005, η2 = .058]. To further characterize these results, we ran post hoc tests with Bonferroni correction for multiple comparisons. Position 3 accuracy was superior to both position 2 accuracy (p < .05), and to position 1 accuracy (p < .05) with no significant difference between positions 1 and 2 accuracy; and the interaction was characterized by effects of position during aggregate-feedback blocks 3 – 6, and no effect of position in the remaining blocks.
2.5. Discussion – Experiment 1
We developed a novel task for studying how aggregate feedback is used to learn three separate categorization responses to an independent sequence of stimuli. The paradigm allowed us to compare the learning profiles of stimuli that were far, intermediate, or near the aggregate feedback. Results from two qualitatively different types of stimuli (fractal images and real-world scenes) were qualitatively similar, which establishes the generalizability of the aggregate-feedback task.
Full-feedback control learning was slightly better than Position 3 aggregate-feedback learning. The full-feedback advantage may occur because the feedback is perfectly contingent on full-feedback trials, whereas incorrect feedback on an aggregate-feedback trial could occur because of an error in one or more of the earlier positions despite a correct response to the stimulus in Position 3. In other words, given equal single-stimulus accuracy, the overall positive feedback rate is necessarily higher on full-feedback trials than with aggregate feedback.
Learning in Positions 1 and 2 was worse than in Position 3 during the early aggregate-feedback blocks. In fact, for the first 5 aggregate-feedback blocks, there was no apparent learning at all in Positions 1 and 2, and accuracy in Positions 1 and 2 even dipped by the second or third aggregate-feedback block (by 3.6% and 3% for Experiment 1a and 1b, respectively). After the learning curve in Position 3 plateaued, accuracy gradually increased (by 6% and 7% for Experiment 1a and 1b, respectively) in Positions 1 and 2.
Fu and Anderson (2008) also investigated sequential learning with aggregate feedback, but their task required explicit, rather than procedural learning (and two, rather than three independent responses). They found faster learning in position one than two, consistent with a primacy effect in declarative memory. However, a dual-task reversed this dominance ordering, which they interpreted as suggesting a switch to implicit learning mechanisms. Learning in position one gradually caught up to position two, which they took as evidence that the feedback signal propagated back to the first stimulus.
Unlike Fu and Anderson, we did not observe a first-position primacy advantage, so this difference supports the assumption that our unstructured category-learning task recruits procedural, rather than declarative memory. Instead, we found a recency effect, with better learning for the stimulus closest to the feedback. The eventual learning in positions 1 and 2 could indicate a backpropagation of the feedback signal, although the initially compromised learning seems incompatible with this hypothesis. An alternate hypothesis is that procedural learning of sequential skills composed of independent actions do not benefit from DA signal backpropagation to the stimuli.
3. Theoretical Analysis
This section examines the theoretical implications of our results for models of DA-mediated synaptic plasticity. Our focus will be on learning in positions 1 and 2 during aggregate feedback. There are several reasons for this. First, the primary motivation for developing the aggregate-feedback task was to study the possible backpropagation of the feedback signal to earlier actions in a sequence. Only positions 1 and 2 require backpropagation, since the response to the stimulus in position 3 is followed immediately by feedback. Second, many different models can account for learning in the single-stimulus control condition, and these same models can account for learning to the stimulus in position 3 during aggregate-feedback training because of its proximity to the feedback. Preliminary modeling though, showed that these same models have much greater difficulty accounting for learning to the stimuli in positions 1 and 2 during aggregate-feedback training. Thus, instead of pursuing a traditional model-fitting approach that would likely be unsuccessful, we took a less common approach to this problem that allows us to make stronger inferences.
The traditional approach is to propose a model and then show that it provides reasonable fits to the data of interest. Our more ambitious goal is to begin with a large class of models and then identify subsets within this class that are and are not qualitatively consistent with our results. If successful, we should then be able to identify the critical qualitative property or properties that any successful model must have to account for our results. Because of this rather unique modeling goal, our primary methodology was parameter-space partitioning (PSP; Pitt et al., 2006).
Figure 3 offers a schematic representation of a generic PSP analysis. In this example, a hypothetical class of models is characterized by two free parameters (a1 and a2). The goal of PSP is to determine what different kinds of qualitative behaviors this class of models can produce. For example, suppose these are learning models and we are interested in whether there are models within the class that can account for good learning (say two-alternative accuracy above 80%), poor learning (accuracy between say 55% and 80%), or no learning (accuracy below 55%). In the hypothetical Figure 3 example, the PSP analysis systematically explored the (a1, a2) parameter space and discovered that by simultaneously varying these parameters, it was possible to construct models that could only account for two different possibilities: either poor learning or no learning. The PSP analysis then measured the area (or volume when there are 3 or more parameters) of the parameter space that predicts each of these two outcomes. In this case, the analysis revealed that for most parameter combinations, no learning occurs, but for more restricted sets of parameters, some learning is possible. Thus, this hypothetical PSP analysis tells us that there is no model in this class that can account for good learning and that most models predict no learning
Figure 3.
A hypothetical example of parameter space partitioning (PSP) for a model with two parameters (a1 and a2). Note that in this example, much more of the model’s parameter space is partitioned into the “No learning” than the “Poor Learning” data pattern.
3.1 Overview of the PSP Analysis
Standard modeling approaches work well when some version of the model of interest provides a good fit to the available data, but not when all versions of the model are inconsistent with the data. It is in this latter case where a PSP analysis is most valuable. Our preliminary attempts to follow the standard modeling approach failed, which made us suspect that no currently popular procedural-learning model would be able to account for the results of Experiment 1. So we turned to PSP to test this hypothesis.
The first step in preparing for a PSP analysis is to define qualitative properties of the data that may be a challenge for the models to reproduce. We focused on two aspects of the Experiment 1 data that seemed potentially problematic for procedural-learning models. The first property was the good learning that occurred in positions 1 and 2, which seemed potentially problematic because the stimuli in positions 1 and 2 are so far removed from the feedback. So we used PSP to ask whether any of a large class of procedural-learning models could account for good learning in positions 1 and 2, and if some were successful, to identify the mechanisms that allowed them to learn. The second property was that the learning that did occur in these positions occurred near the end of the session. During the early aggregate-feedback blocks there was little or no learning in positions 1 and 2. So we used PSP to explore whether any of our procedural-learning models that were able to learn in positions 1 and 2 were able to reproduce this late-learning profile.
Note that a standard modeling approach cannot address these questions. For example, suppose we used a standard approach to fit a set of alternative models that included procedural-learning models and models that were incompatible with procedural learning. Further suppose that the procedural-learning models were unable to match either of these qualitative properties of our data, whereas at least one model incompatible with procedural learning was able to match both properties. Unfortunately, goodness-of-fit statistics penalize for a poor quantitative fit, not a poor qualitative fit. As a result, it is easily possible that one of the qualitatively mismatching procedural-learning models would provide the best overall fit to the data, thereby supporting the incorrect conclusion that our results are consistent with current theories of procedural learning.
The next step in any PSP analysis is to construct the general class of models to be explored. The more general this class, the stronger the conclusions. Our approach to this problem exploited the fact that there is good evidence that: 1) unstructured category learning recruits procedural learning and memory (Crossley, Madsen, & Ashby, 2012; Lopez-Paniagua & Seger, 2011; Seger & Cincotta, 2005; Seger et al., 2010); 2) procedural learning depends critically on the basal ganglia (Ashby & Ennis, 2006; Doyon & Ungerleider, 2002; Packard & Knowlton, 2002; Willingham, 1998; Yin & Knowlton, 2006); and 3) reinforcement learning within the basal ganglia is based on DA-mediated synaptic plasticity, for which the actor-critic architecture4 is a popular computational metaphor (Houk, Adams, & Barto, 1995; Joel, Niv, & Ruppin, 2002). In the present application, the actor-critic architecture included two components: (1) a procedural category-learning network (actor), and (2) a reward-learning algorithm that predicts DA release (critic) at the times of stimulus presentation and feedback during full- and aggregate-feedback training. The critic determines the value of the feedback based on the current reward prediction, and the actor is updated by using information from the critic.
Our theoretical analysis focused on the critic, and specifically, on what we can learn about the critic from our results. Even so, our analyses require that we specify a model of the actor. Fortunately, an extensive literature has rigorously tested neurobiologically detailed network models of procedural (category) learning (e.g., Ashby et al., 1998; Ashby & Waldron, 1999; Ashby, Ennis, & Spiering, 2007; Ashby & Crossley, 2011; Crossley, Ashby, & Maddox, 2014; Gurney, Humphries, & Redgrave, 2015; for a review see Hélie, Chakravarthy, & Moustafa, 2013). So our approach was to model the actor with a simple, non-controversial version of these validated models that makes minimal assumptions. This model is elaborated below.
The final step in the PSP analysis is to examine all possible predictions of this general model. As in the Figure 3 example, this is done by an exhaustive search of the parameter space that defines the general model with the goal of mapping out regions (i.e., specific parameter combinations) that lead to predictions that are qualitatively consistent with our results, as well as regions leading to predictions that are qualitatively inconsistent with our findings. Because the computational demands of searching the parameter space increase dramatically with the number of parameters, PSP uses an efficient Markov chain Monte Carlo search algorithm (Pitt et al., 2006). We performed two separate PSP analyses – one for each of the key data properties described above.
The next two sections describe the procedural-learning (actor) and reward-learning (critic) components of the model, respectively. Then we describe the results of the PSP analyses.
3.2. Procedural Category Learning (Actor) Component
The procedural-learning component is a simple two-layer connectionist network that learns to associate a response to each stimulus via reinforcement learning (Ashby & Waldron, 1999). Details are given in the appendix, but basically the model simply assumes that every stimulus has an association strength with each of the two response alternatives. Initially these strengths (i.e., synaptic weights) are random, but they are adjusted during learning via a biologically-motivated model of reinforcement learning. Following standard approaches, the model assumes that the stimulus-response (i.e., cortical-striatal) synaptic weights are increased if three conditions are met: 1) strong presynaptic activation, 2) strong postsynaptic activation (i.e., above threshold), and 3) DA levels above baseline (Arbuthnott, Ingham, & Wickens, 2000; Calabresi et al, 1996; Reynolds & Wickens, 2002). If the first two conditions hold but DA levels are below baseline, then the synaptic weight is decreased.
More specifically, let wKJ(n) denote the synaptic strength or connection weight between input unit K and output unit J following the nth presentation of stimulus K. We assume these weights are updated after each trial using the following reinforcement learning rule:
| (1) |
where DK(n) is the amount of DA released on the trial when the nth presentation of stimulus K occurs (described in detail below), IK(n) is the input to unit K, and SJ|K(n) is the amount of activation in striatal unit J on the nth trial that stimulus K was presented. The function [g(n)]+ = g(n) if g(n) > 0, and otherwise g(n) = 0 (e.g., [DK(n)-Dbase]+ = DK(n)–Dbase when DA is above baseline and 0 otherwise). Equation 1 includes two constants: Dbase represents the baseline DA level and was set to 0.2 in all applications (see Eq. 4), and θNMDA represents the activation threshold for postsynaptic NMD A glutamate receptors. This threshold, which was set to 0.0118 in all applications, is critical because NMDA receptor activation is required to strengthen cortical-striatal synapses (Calabresi, Maj, Pisani, Mercuri, & Bernardi, 1992). The terms α and β are free parameters that were manipulated during the PSP analysis.
The first line in Eq. 1 describes the conditions under which synapses are strengthened (i.e., striatal activation above the NMDA threshold and DA above baseline, as on a correct trial) and line 2 describes conditions that cause the synapse to be weakened (postsynaptic activation is above the NMDA threshold but DA is below baseline, as on an error trial). Note that synaptic strength does not change if postsynaptic activation is below the NMDA threshold.
The critic described in the next section specifies exactly how much DA is released on each trial [i.e., the value of DK(n) in Eq. 1]. Note that the parameters α and β in Eq. 1, which are the focus of the PSP analysis, act as gains on this DA response. Specifically, we will explore predictions of a wide variety of alternative models of how the DA system responds in our aggregate-feedback task over a large range of possible α and β values.
As mentioned above, many previous studies have validated this general model of procedural category learning (e.g., Ashby et al, 1998, 2007; Ashby & Waldron, 1999; Ashby & Crossley, 2011; Crossley et al, 2014). In the current application, procedural learning of the stimulus-response associations occurs independently in the three stimulus positions according to the constraints on DA release specified by the critic. As described in section 4.2.3 below, this is done by allowing different α and β values for each stimulus position.
3.3. Reward-Learning (Critic) Component
The learning model used by the procedural component requires specifying exactly how much DA is released on every trial [i.e., DK(n) in Eq. 1]. These computations are performed by the reward-learning component of the model (i.e., the critic). The amount of DA released serves as a learning rate on the association strengths in the actor. The more DA deviates from baseline, the greater the learning. On trials when DA remains at baseline, no learning occurs.
When building a general model of the critic, there are two separate questions to consider. First, what do the DA neurons do when each of the three categorization stimuli are presented, and second, what do DA neurons do when the aggregate feedback is presented? There is strong consensus in the literature on the answer to the second question, but the first question is novel to this research. Thus, our goal is to build a general model of the critic that allows for a wide variety of different possible DA responses to the categorization stimuli. We begin with the more straightforward question of how the DA neurons respond to the feedback.
3.3.1. DA Response to the Feedback
An extensive literature suggests that over a wide range, the DA response to feedback increases with the reward prediction error (RPE; e.g., Schultz, 1998, 2006) – that is, with the difference between obtained and predicted reward. During single-stimulus full-feedback trials, the RPE following feedback to the nth presentation of stimulus K equals
| (2) |
where RK(n) is the value of the feedback (i.e., reward) received on this trial (0 or 1 depending on whether the feedback was negative or positive, respectively) and RPK(n) is the predicted value of the feedback computed after the nth presentation of stimulus K (where K ∈ {1,2,….,12}). Note that RPK(n) equals the predicted reward probability (because negative feedback has a value of 0 and positive feedback has a value of 1). On aggregate-feedback trials, RPK(n) is replaced in Eq. 2 by a prediction that depends on all three presented stimuli. Consider an aggregate feedback trial where stimulus K1 appears in position 1, stimulus K2 appears in position 2, and stimulus K3 appears in position 3. Then we denote the overall estimate of the probability that all three responses were correct by RPOverall|K1,K2,K3(n1, n2, n3), where n1, n2, and n3 are the numbers of times that each of the three stimuli have been presented in the experiment up to and including the current trial.
The next task in our model construction is to specify exactly how predicted reward is computed. In the full-feedback control conditions this is a straightforward exercise. Following the current literature, we assume predicted reward is computed using standard temporal discounting methods (e.g., Sutton & Barto, 1998). More specifically, we assume that the predicted value of the feedback that follows the response to the (n +1)th presentation of stimulus K equals5
| (3) |
where , and γ is a constant that specifies the amount of discounting (e.g., γ = .2). The initial value [i.e., RPK(0)] for all stimulus-specific reward predictions is 0.5 (chance accuracy). Equation 3 states that predicted reward is just a weighted average of all previous rewards, with the weight given to a trial diminishing exponentially as it recedes further away in time from the present trial.
In the aggregate-feedback category-learning task, the stimulus presented in each position is selected independently on each trial. Thus, the probability that all three responses are correct, and therefore the probability that positive feedback is received, equals the product of the 3 probabilities of a correct response in each position. Thus, we assumed that RPOverall|K1,K2,K3 (n1,n2,n3)is the product of the three RPK(n) values that are associated with the three stimuli6 presented on trial n. Consequently, as it should, RPOverallK1,K2,K3 (n1,n2,n3)will be less than each stimulus-specific RPK(n) (provided each is less than 1). Note that this model assumes participants compute RPOverallK1,K2,K3 (n1,n2,n3)in an optimal fashion. Other, suboptimal models could also be constructed. Fortunately, however, this is not a critical issue. As will be elaborated in the next section, the PSP analysis explores such a wide range of Eq. 1 α and β values that our results would not appreciably change if we assumed participants computed RPOverallK1,K2,K3 (n1,n2,n3) using some (moderately) suboptimal method.
Finally, following Ashby and Crossley (2011), we assumed that the amount of DA release is related to the RPE in accord with a simple model that accurately accounts for the single-unit DA cell firing data reported by Bayer and Glimcher (2005):
| (4) |
Note that the baseline DA level is .2 (i.e., when the RPE = 0) and that DA levels increase linearly with the RPE between a floor of 0 and a ceiling of 1.
3.3.2. DA Response to the Categorization Stimuli
In classical conditioning studies, the DA response to a cue or stimulus is an increasing function of the predicted probability that the stimulus will be followed by reward (Schultz, 1998; Fiorillo, Tobler, & Schultz, 2003). Perceptual categorization is more similar to instrumental conditioning than to classical conditioning, and we know of no studies that have examined DA response in an instrumental conditioning analogue of our aggregate-feedback category-learning task. Even so, one obvious possibility is that DA neurons will respond to the stimuli in our task in a similar manner to the way they respond to cues that predict reward in classical conditioning tasks – that is, proportionally to the predicted reward associated with each stimulus. Another possibility, however, is that the DA neurons will not respond to the stimuli in our task, and instead will only respond to the feedback. For this reason, we explored models in which the DA response to each stimulus is proportional to predicted reward, and models in which the DA neurons do not respond to the stimuli. For models in the first class, we were not interested here in how this DA response develops (e.g., via temporal-difference learning; Sutton & Barto, 1998) – only in whether any models within this class are compatible with our results. The PSP analysis explored predictions of this model class over the entire range of possible values of α and β in Eq. 1. Thus, included in this class are models in which the DA neurons respond strongly to an expectation of reward and models in which the DA neurons respond weakly to the same expectation.
On either single-stimulus or aggregate-feedback trials, an obvious prediction is that if there is a DA response to the presentation of a stimulus, then it should be proportional to predicted reward. We do not need to account for this possible source of DA release during single-stimulus feedback training because any DA released to the stimulus would precede the response and each response is followed immediately by feedback, so learning should be mediated by DA released to the feedback and the DA released to the stimulus should play little or no role. However, during aggregate-feedback training, DA released to each stimulus could have significant effects on learning. For example, consider the stimulus in position 1. After the participant responds to this stimulus, the next DA released will be to the presentation of the stimulus in position 2, and the DA released to the feedback will occur several seconds in the future. For these reasons, our primary modeling task was to build a reasonable model of how much DA might be released to each stimulus during aggregate-feedback training.
Chance accuracy on every stimulus is 0.5, so chance accuracy on any aggregate-feedback trial is 0.125 (i.e., .53 = .125 = probability of receiving positive feedback if the participant is at chance on every stimulus). Crossley, Ashby, and Maddox (2013) reported behavioral and computational modeling evidence from a similar perceptual categorization task suggesting that DA levels remain at baseline during random feedback. Thus, we assumed that DA levels would rise above baseline when RPOverall|K1,K2,K3(n1,n2,n3) > 0.125, and remain at baseline when RPOverall|K1K2K3(n1,n2,n3) = 0.125. Fortunately, we do not need to be concerned with values of RPOverall below 0.125 because this never occurred since the single-stimulus feedback training guaranteed that all RPK were well above chance at the beginning of aggregate-feedback training. Therefore, following Eq. 4 we assumed that
| (5) |
Note that the baseline DA level is again 0.2 (i.e., when the RPOverall = 0.125) and that DA levels increase linearly from 0.2 to a ceiling of 1 (when RPOverall = 1).
3.3.3. Creating a General Critic Model
In any PSP analysis, the model classes are defined both by their architecture and by the parameters that are explored. Including every possible parameter in the analysis is impractical because the dimensionality of the parameter space would be so large that the computational costs would be prohibitive. For this reason, our analysis focused only on the α and β parameters of Eq. 1 since these are the parameters most relevant to our main research question – namely, what is the effect of the DA response on the earliest stimulus positions during aggregate-feedback training. All other parameters were set to values that allowed the model to provide good fits to the single-trial control data, and the position 3 data. To simplify the analysis even further, we assumed no difference in α and β parameter values for positions 1 and 2 because the results of Experiment 1 showed no learning differences between these two positions.
Using this general framework, we constructed three qualitatively different types of models – one type assumed that the DA neurons respond to the feedback but not to the stimuli (referred to as feedback-update models below), and two types assumed the DA neurons respond both to the stimuli and to the feedback (referred to as stimulus-feedback-update models and immediate-update models below).
The feedback-update models assume that the DA neurons respond to the feedback but not to the categorization stimuli. These models allow the DA response to the feedback to have a scalable effect on the position 1 and 2 synaptic weights, and therefore they include as special cases models that postulate an eligibility trace (i.e., a sort of memory trace that facilitates the backpropagation of the feedback signal). The idea here is that position 3 stimuli should always benefit from a full DA response to the feedback (because of temporal adjacency), whereas positions 1 and 2 have limited access to this DA signal due to the temporal separation and masking from intervening trial events. The PSP explored the full range of possible DA magnitudes available for updating position 1 and 2 weights, and therefore it explored the predictions of models that postulate an eligibility trace of almost any magnitude. This was done by separately exploring all possible values of the position 1 and 2 (Eq. 1) α and β parameters that are associated with DA release to the feedback (the position 3 α and β were fixed). Thus, this PSP analysis explored a 2-dimensional parameter space (since we assumed that both stimulus positions were characterized by the same values of α and β).
The stimulus-feedback-update models assume that the DA neurons respond to the feedback and to each stimulus. These models require position 1 weights to be updated three times and position 2 weights to be updated twice on each trial – once after DA release to each later stimulus, and again after DA release to feedback. For example, the position 1 weights are updated after presentation of: the stimulus in position 2, the stimulus in position 3, and the aggregate feedback. This class also assumes a scalable DA response. The PSP explored 4 DA-scaling parameters – one α to scale the above-baseline DA response to the next stimulus (for position 1: the DA response to the stimulus in position 2; for position 2: the DA response to the stimulus in position 3), one α to scale the position 1 effects of the DA response to the stimulus in position 3, and an α and a β to scale the effects of the feedback.
The immediate-update models generate a DA response to each stimulus and to the feedback, but each DA burst could update synaptic weights only for temporally adjacent responses. This means that the synapses currently active are strengthened by whatever DA release immediately follows, whether due to feedback, or a reward-predicting stimulus. More specifically, position 1 weights are updated by the DA response to position 2 stimuli, position 2 weights are updated by the DA response to position 3 stimuli, and position 3 weights are updated by the DA response to feedback. Note that this class of models assumes that the traces activated by stimuli in positions 1 and 2 decay before aggregate feedback is available, and therefore they are no longer eligible for synaptic modification. Because the PSP analyses only explored parameters that could affect learning in positions 1 and 2, this analysis only explored one parameter, α, which scales the DA response above baseline to the stimulus that follows the position 1 and 2 responses7.
3.4. Methods – PSP Analysis
For technical details of the PSP analysis, see the Appendix. As mentioned earlier, we completed two separate PSP analyses that focused on different behaviors. For PSP Analysis 1, we chose three outcomes defined by the mean amount of procedural learning in positions 1 and 2: (1) “No Learning” (accuracy increases less than 2% during aggregate-feedback training), (2) “Limited Learning” (accuracy increases between 2% and 4%), and (3) “Full Learning” (accuracy increases by at least 4%). These values were based on qualitative trends in the data. The average standard error was 2, therefore less than a 2% accuracy change was considered to be no learning. The Experiment 1 data showed “Full Learning” because the mean accuracy increase in positions 1 and 2 was 5.6% (ranging from 4.7–6.4% depending on the condition) during aggregate-feedback training. For PSP Analysis 2 we focused on four different learning profiles for positions 1 and 2 only: (1) “Early Learning”, which we defined as an accuracy increase of at least 2% only during aggregate-feedback blocks 2 – 5 compared to aggregate-feedback block 1, (2) “Late Learning”, defined as an accuracy increase of at least 2% only during aggregate-feedback blocks 6 – 11 compared to aggregate-feedback block 5, (3) “Learning Throughout”, defined as accuracy increases of at least 2% during both aggregate-feedback blocks 2 –5 and 6 – 11, and (4) “No Learning”, defined as accuracy increases less than 2% during early and late aggregate-feedback blocks. Our empirical results were consistent with “Late Learning”, because the mean accuracy increase in positions 1 and 2 was 0.27% (ranging from −1.4% to 2.5%) for early, and 6.7% (ranging from 4.6–9.6%) for late aggregate-feedback blocks.
The results of each PSP analysis were the percentages of the parameter space volume that allowed the model to produce each of the 3 qualitative behavioral outcomes from PSP Analysis 1 or 4 qualitative behavioral outcomes from PSP Analysis 2, plus a specific set of parameter values that could generate each outcome. We ran each PSP Analysis three times to check for reproducibility, and averaged the resulting volume percentages, which we report below. Following each PSP analysis, we also evaluated the robustness of each identified data pattern to ensure that the pattern was representative of the model’s predictions and not an artifact of the (200) random configurations that were chosen for the analysis. During the robustness stage, we further tested each model in 30 simulations of 200 new random stimulus orderings, guesses and weight initializations using the parameters returned for each discovered pattern. Below, we summarize the results and indicate all cases when this subsequent test failed to replicate the data pattern identified by the PSP.
3.5 Results – PSP Analysis
This section describes the results of PSP Analyses 1 and 2 together.
3.5.1. Feedback-Update Models
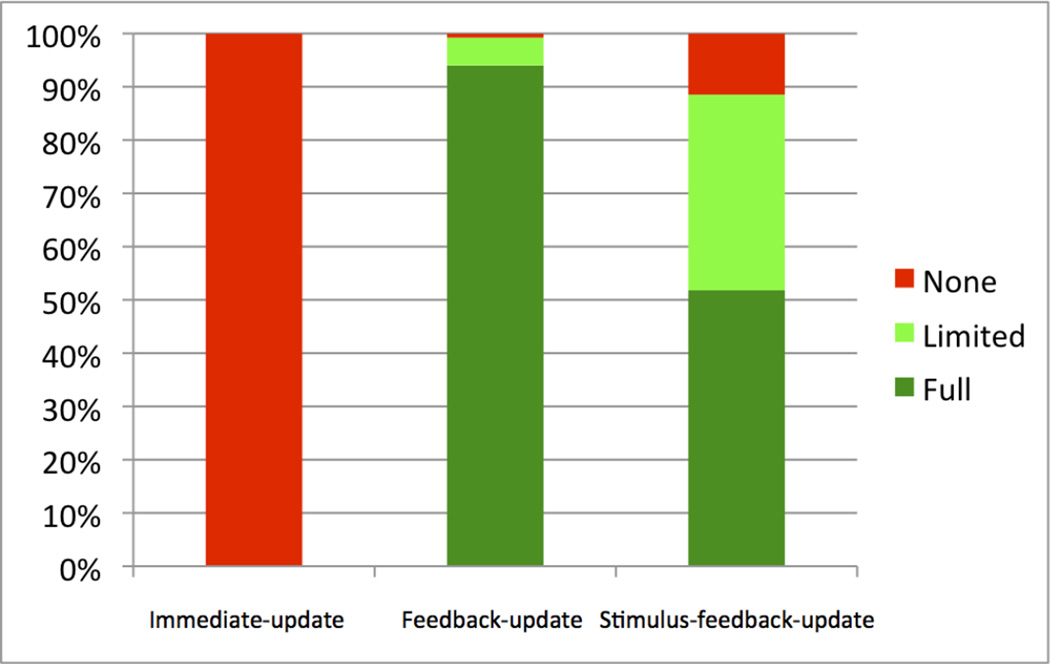
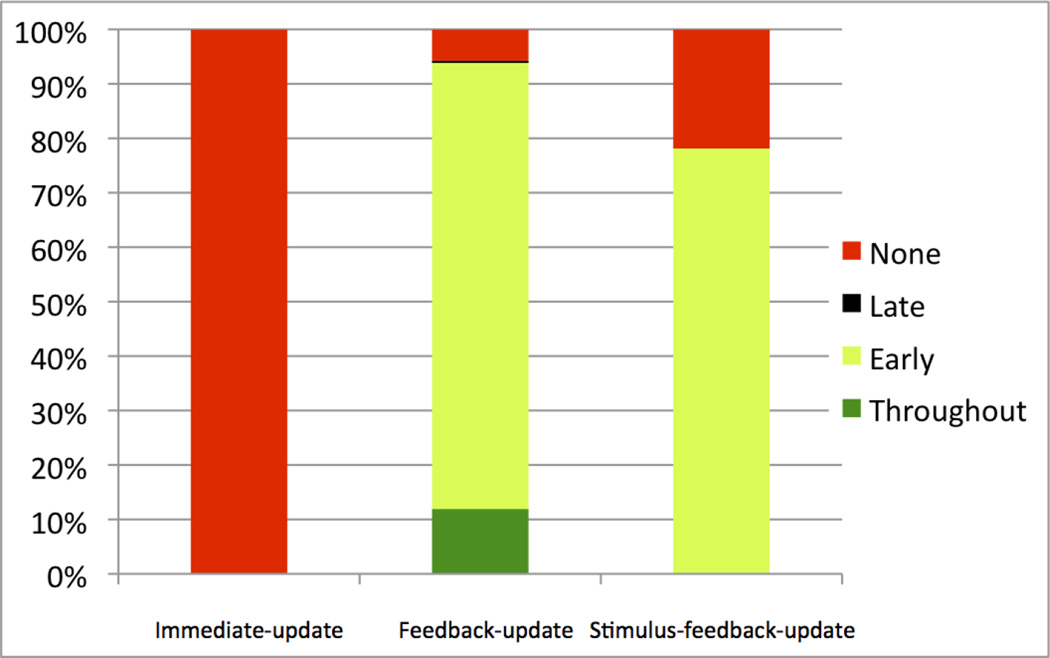
The feedback-update models allow a graded DA response to the feedback (e.g., as in models that include an eligibility trace), but no DA response to the stimuli. The PSP results are summarized in Figures 4 and 5. Note that the feedback-update models produced “Full Learning” over 94.02% of the parameter space, “Limited Learning” over 5.22%, and “No Learning” over 0.77% of the space (Figure 4). The profile analysis of PSP Analysis 2 yielded “Learning Throughout” over 11.94% of the parameter space, “Early Learning” over 82.12%, “Late Learning” over 0.18%, and “No Learning” over 5.78% of the space (Figure 5). The “No Learning” pattern produced the lowest α parameters, and was reproduced in 20 out of 30 simulations with new randomizations (with an average of 1.2% early, and 1.5% late accuracy increases), and the rest produced the “Late Learning” pattern (slightly surpassing 2%). The “Late Learning” pattern was reproduced in only 16 out of the 30 simulations with new randomizations, and the rest produced the “Learning Throughout” pattern (with both early-learning and late-learning slightly surpassing 2%). In addition, the “Late Learning” pattern of the model showed only limited learning (2.3% accuracy increase on average, 3.6% at best) in late aggregate-feedback blocks, unlike the mean empirical data’s 6.7%, and in early aggregate-feedback blocks, model accuracy increase (1.5% on average, 0.5% at best) was more than the mean empirical data’s 0.27%. Furthermore, this limited early learning still does not capture the empirical data’s slight dip in position 1 and 2 accuracy in the second or third aggregate-feedback block (−2.9% to −3.8% depending on condition). Overall the feedback-only model nearly always produced “Full Learning”, and it nearly always began at the first aggregate-feedback block and finished almost always by the fifth aggregate feedback block.
Figure 4.
Results of PSP Analysis 1. Percentage of parameter space volume for “None” (red), “Limited” (light green), and “Full” (dark green) learning data patterns, using the immediate-update, feedback-update, and stimulus-feedback-update model versions. Each color corresponds to a unique data pattern discovered by PSP. The height of each colored rectangle corresponds to the volume of parameter space of the specified data pattern.
Figure 5.
Results of PSP Analysis 2. Percentage of parameter space volume for “None” (red), “Late” (black), “Early” (light green), and “Throughout” (dark green) learning data patterns, using the immediate-update, feedback-update, and stimulus-feedback-update model versions. The height of each colored rectangle corresponds to the volume of parameter space of that data pattern.
3.5.2. Stimulus-Feedback-Update Models
The stimulus-feedback-update models allow graded DA responses to the stimuli and the feedback. These models produced “Full Learning” over 51.80% of the parameter space, “Limited Learning” over 36.73% of the space, and “No Learning” over 11.47% of the space (Figure 4). The profile analysis of PSP Analysis 2 produced “Early Learning” over 78.13% of the space, and “No Learning” over 21.87% of the space (Figure 5). “Late Learning” or “Learning Throughout” profiles were not discovered. Overall, the additional DA responses to the stimuli resulted in much less learning than when DA responded only to the feedback. The parameter combination that produced “No Learning” had feedback-related α and β values much smaller than the one that produced “Early Learning”, therefore diminishing the contribution of the feedback to learning. In other words, there was no learning when the available DA was mainly due to the presentation of an ensuing stimulus. As with the model in which there is only DA release to the feedback, when this combined model learns, it almost always learns gradually from the start of the aggregate-feedback blocks, unlike the empirical data.
3.5.3. Immediate-Update Models
The immediate update models allow DA responses to the stimuli and the feedback, but these responses only affect learning of the immediately preceding response. The PSP analysis showed that 100% of the parameter space yielded “No Learning” in positions 1 and 2 (Figure 4). Thus, all versions of the model failed to learn. This conclusion was verified by the profile analysis of PSP Analysis 2, which showed that 100% of the parameter space produced “No Learning” throughout the aggregate-feedback blocks, and no other learning profiles were found (Figure 5). Overall, this is powerful evidence that learning cannot occur if the only available DA is due to the stimulus presentations.
3.5.4. Best-Fitting Model
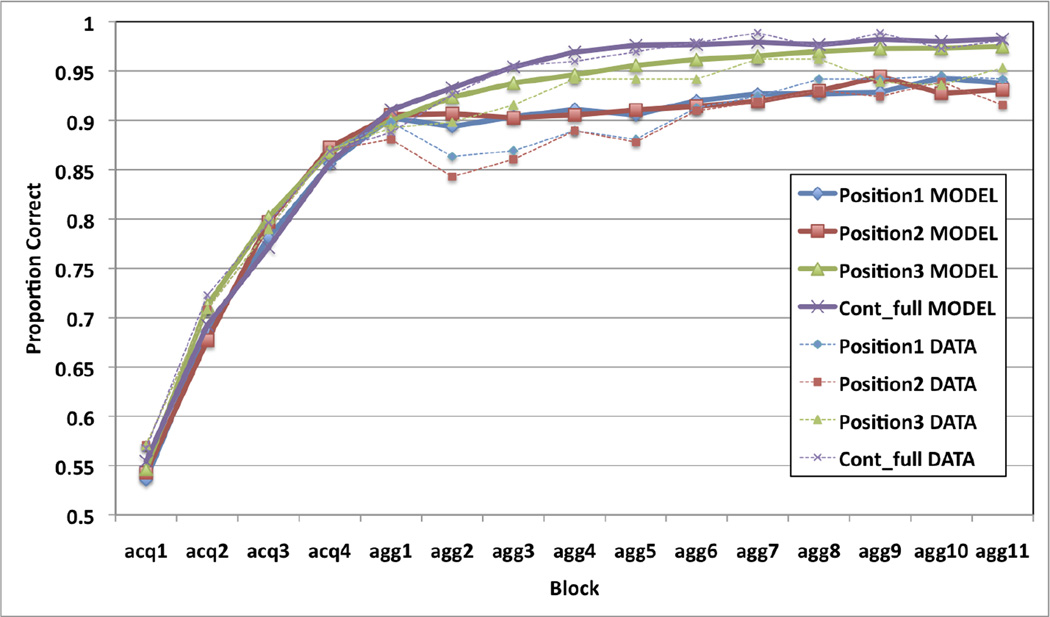
Using the results of the PSP analysis, we identified the single model that best fit the data from Experiment 1a. This was a feedback-update model that includes a DA response to the feedback but not the stimuli, and allows for a weak eligibility trace. One set of learning rate parameters provided by the PSP (feedback-related α and β values of 0.158 and 0.175, respectively) for the “Late Learning” data pattern was used. The model’s performance was simulated in 200 independent replications of Experiment 1a, and the results were averaged. This was repeated 30 times (robustness stage) and we selected the model output that matched the empirical data best, shown in Figure 6. Note that the model captures many qualitative properties of the data. First, it learns at about the same rate as the human participants in the single-stimulus immediate-feedback training. Second, it correctly predicts that learning with aggregate feedback is better in position 3 than in positions 1 or 2. Third, it correctly predicts that position 3 learning gradually increases throughout aggregate-feedback blocks, unlike the position 1 and 2 learning, which is initially impaired, but continues in the last half of the aggregate-feedback blocks.
Figure 6.
Result of 200 simulations of Experiment 1a by the feedback-update procedural learning model that includes DA release only to the feedback and very low learning rates for positions 1 and 2 (weak eligibility trace, perhaps due to the temporal separation from stimuli to feedback).
Quantitatively, the model successfully accounts for 98.85% of the variance in the data of Experiment 1a, but much of this good fit is due to the single-trial data. If we consider only the aggregate-feedback trials, the model accounts for only 83.94% of the variance of the data. For example, the model accounts for “Late Learning” in positions 1 and 2, but it under predicts the amount of this learning (3.6% model versus 6.3% data, Figure 6). The model also accounts for a relatively impaired early-learning in positions 1 and 2, but even the lowest possible accuracy increase is an over prediction (0.5% model versus ~0% data, Figure 6). It is also important to note that this model came from a (“Late Learning”) data pattern associated with only 0.18% of the parameter space. Even miniscule changes in the learning rate parameters qualitatively change the model’s predictions. Almost any decrease in the learning rates abolishes all learning in positions 1 and 2, whereas almost any increase produces immediate learning in the early blocks of aggregate feedback.
3.6. Discussion – PSP Analysis
The PSP analysis allowed us to explore predictions of a wide variety of alternative models of how the DA system responds during aggregate feedback. This included virtually all models that assume the DA response to the feedback is an increasing function of RPE and the DA response to the stimuli is an increasing function of predicted reward. Our results showed that none of these models can perfectly account for all major properties of the data.
The majority of the models either predict no learning at all in positions 1 and 2, or gradual learning that starts in the first block of aggregate feedback in all positions. In contrast, the data showed no learning in positions 1 and 2 for the first 5 blocks of aggregate feedback, but learning during aggregate-feedback blocks 6–11. But how much should we trust this apparent late learning? First, note that the data from Experiment 1b (bottom panel of Figure 2) show a similar, albeit less dramatic effect – late but not early learning in positions 1 and 2. The appearance of this effect across both experiments suggests it might not be a statistical artifact. In fact, t-tests that compare averaged position 1 and 2 accuracy in aggregate-feedback blocks 1–5 versus aggregate-feedback blocks 6–11 are significant in both experiments (Experiment 1a: ~0% versus 6.3% – t(42) = 4.03, p < .001; Experiment 1b: 0.54% versus 7.1% – t(34) = 2.68, p = .011). Even so, because the effect is somewhat small, more research is needed before any strong statistical conclusions can be drawn.
Only the feedback-update model, with highly restricted parameter settings, accounted for the position 1 and 2 late learning profile, and only qualitatively, because the model improved in accuracy during the latter half of aggregate-feedback training only about half as much as the humans, and during the earlier half the improvement was more than that of humans. This feedback-update model assumes no DA release to the stimuli and that a trace of the striatal activation (or synaptic eligibility) produced by the position 1 and 2 categorization responses overlapps with the DA released to the feedback. The assumption that a trace of the striatal activation produced by the position 1 and 2 categorization responses overlaps with the DA released to the feedback seems highly unlikely given that such traces are thought to persist for only a few seconds (Yagishita et al., 2014; Worthy, Markman, & Maddox, 2013; Maddox, Ashby, & Bohil, 2003). Thus, this assumption seems questionable, especially for position 1. The late position 1 and 2 learning produced by the model was also restricted to a tiny range of learning rates. Increasing or decreasing these rates even by the smallest amount caused the late learning to disappear. Of course, we cannot rule out that the narrow range of learning rates required for this result may coincide with some biological constraint on procedural learning. If this is not true however, then our results suggest that current models of procedural learning are incomplete.
So why should DA release to the stimuli impair learning in positions 1 and 2? Following well-replicated results from the classical conditioning literature (e.g., Schultz, 1998; Fiorillo et al., 2003) and standard (e.g., TD) models, we assumed that DA release to the stimuli, if it occurred at all, was proportional to the predicted reward probability (see Eq. 5). Our PSP analysis showed that virtually any model based on this assumption is of questionable validity because after any learning at all, predicted reward probability is necessarily above chance, so all these models predict that DA levels will always rise above baseline when each new stimulus is presented. This increase is helpful on trials when positive feedback is given because it facilitates the strengthening of synapses that were responsible for the accurate responding. The problem occurs on error trials. In the full model, DA levels rise above baseline on error trials when each successive stimulus appears and then fall below baseline after the error feedback is given. The DA depression to the feedback helps position 3, but is too far removed in time from the stimuli in positions 1 and 2 to reduce their weights. Instead, the increased DA released to the stimuli increases synaptic strengths for the position 1 and 2 responses, despite the error(s). One significant advantage of the PSP analysis is that these conclusions are robust, in the sense that they should hold for any model that predicts DA release to cues that predict reward.
3.7. Procedural-Learning Model Predictions for Experiment 2
The failure of the wide class of procedural models considered here to learn multiple actions with aggregate feedback raises the question: Under what conditions can procedural learning accomplish multistep learning with aggregate feedback without augmentation by other (e.g., explicit) mechanisms? The Experiment 1 task design jump-starts learning by pre-training individual actions before aggregate-feedback training on the entire sequence begins. An alternative training procedure may be to first train up one of the actions and then introduce another with aggregate feedback to create a sequence of two actions, and finally add in the third action with aggregate feedback to create a sequence that includes all three. There are two obvious ways this might be done. One is to begin with the first action and then add successive actions to the end of the sequence. Thus, participants would train on action 1 alone, then on the sequence 12, and finally on the sequence 123. We denote this as 123 training (reflecting the order in which each action is introduced). The opposite strategy is to employ 321 training that begins on action 3 alone, then on the sequence 23, and finally on the sequence 123.
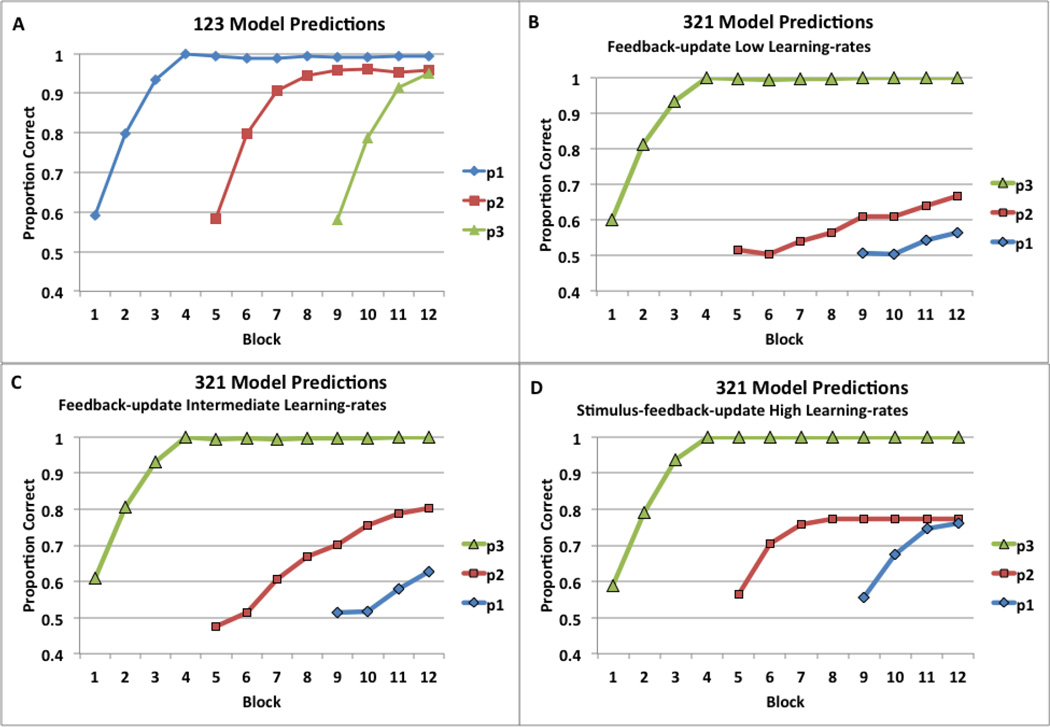
The PSP analysis suggested that the procedural-learning models make a strong a priori prediction that 123 training should be superior to 321 training. Figure 7 shows predictions from different procedural-learning models, averaged over 200 replications of 123 versus 321 training. All model versions learned equally well in the 123 condition, and while Figure 7a shows predictions of the feedback-update model, the predictions were identical for the other model types with all possible data patterns discovered by PSP. On the other hand, almost all model versions predict that in 321 training, learning is compromised in positions 1 and 2, but not 3. The feedback-update model predicts equally perfect learning in all 3 positions (output not shown) with high learning rates (α = 2.4, β = 0.7; perfect eligibility trace), but it predicts little learning in position 1 and 2 (Figure 7b) with low learning rates (α = 0.158, β = 0.175; weak eligibility trace). This was the best-fitting model for Experiment 1, which corresponded to the “Late Learning” data pattern associated with only 0.18% of the parameter space. A full 82% of the parameter space predicted “Early Learning” and representative parameter values from this volume (intermediate learning rates of α = 0.307 and β = 0.397) leads to somewhat better 321 learning (Figure 7c). Figure 7d shows the compromised learning prediction of the stimulus-feedback-update model, with high learning rates (α = 2.4, β = 0.7), updating with DA release to stimuli, and updating with DA release to feedback (perfect eligibility trace). Finally, with DA release to stimuli in the immediate-update model (without eligibility trace), there is no learning at all (output not shown), just as in the PSP result for Experiment 1.
Figure 7.
Predictions of procedural-learning models in Experiment 2. A) Feedback-update model predictions for 123 training. B) Feedback-update model predictions for 321 training with low learning rates. C) Feedback-update model predictions for 321 training with moderate learning rates. D) Stimulus-feedback-update model predictions for 321 training with high learning rates. (Note. In the legends p1, p2, and p3 signify stimulus positions 1, 2, and 3, respectively.)
These model predictions reveal that procedural learning is most optimal if an action is followed by immediate feedback, and therefore chaining actions into a sequence works best if immediate feedback follows the to-be-learned new action, which follows a mastered action. With 123 training, the untrained action is always nearest the feedback, whereas with 321 training the untrained action is always at the beginning of the sequence, and thus, in the furthest possible position from the feedback. The prediction that 123 training is better than 321 training will be tested next in Experiment 2.
4. Experiment 2
In 123 training, immediate feedback always follows the to-be-learned stimulus, with sequences of 12, and 123 receiving aggregate feedback. For example, during position 1 training, immediate feedback always follows the response to the item in position 1. Once the position 1 item is well learned then items in position 2 are added. During this 12 training the novel to-be-learned position 2 items are always followed by immediate feedback. Once the position 1 and 2 items are well learned then items in position 3 are added. During this 123 training the novel to-be-learned position 3 items are always followed by immediate feedback. However, in 321 training, feedback gets farther and farther removed from the to-be-learned stimulus as more stimuli are added into the sequence. For example, if the position 3 stimulus is learned perfectly, the sequence of 23 will be followed by aggregate feedback, which, if incorrect, most likely reflects an error in response to the position 2 stimulus. However, this feedback does not immediately follow the position 2 stimulus, but instead, the position 3 stimulus presentation and response occurs before the aggregate feedback.
To our knowledge, within the domain of classical conditioning, only 321 training has been previously investigated, and the backpropagation of the DA signal from learned to new stimulus was demonstrated with electrophysiology and computational analyses (Schultz, Apicella, & Ljungberg, 1993; Suri & Schultz, 1998). However, in that work, the new stimulus perfectly predicted the upcoming learned stimulus (i.e., the cues were dependent), while in the current task, the learned stimulus followed both correct and incorrect responses to the new (and previously presented) stimulus (i.e., the cues were independent), therefore DA release to the learned stimulus cannot serve as a teaching signal for learning the appropriate response to the new stimulus.
Our PSP analysis showed that a huge class of popular procedural-learning models fail to account for the results of the aggregate-feedback training used in Experiment 1. However, that analysis also suggested that the models would successfully learn with aggregate feedback if the training followed a 123 format. Experiment 2 tested this prediction.
4.1. Methods – Experiment 2
4.1.1. Participants, Stimuli, and Stimulus Generation
Twenty-seven participants completed the 123 task and 22 participants completed the 321 task. All aspects of participants and stimuli and stimulus generation were identical to those from Experiment 1a.
4.1.2. Procedure
Participants were informed that there were two equally likely categories and that they should be accurate and not to worry about speed of responding. The experiment consisted of 12 12-trial blocks divided into 3 phases of 4 blocks each. The design is described in Table 1. The 123 task had three training components: single position 1, then pairs of position 1 and 2, then triplets of position 1, 2, and 3 stimuli. In the first phase, only the position 1 stimuli were shown followed by trial-by-trial full feedback. On each trial, a position 1 stimulus appeared until the participant generated an “A” (“z” key) or “B” (“/” key) response, followed by the word “correct” or “incorrect” for 1000ms, a 500ms blank screen ITI, and then the next trial. During phase 2 (blocks 5–8), each trial consisted of the presentation of a position 1 and 2 stimulus followed by aggregate feedback. Specifically, the first stimulus appeared until the participant generated an “A” or “B” response, followed by a 500ms blank screen ITI, and then presentation of the second stimulus. The second stimulus appeared until the participant generated an “A” or “B” response, followed by the words “All responses were correct” or “At least one response was incorrect” for 1000ms, then a 500ms blank screen ITI, and then the next stimulus-pair trial. During phase 3 (blocks 9–12), each trial consisted of the presentation of a position 1, 2, and 3 stimulus followed by aggregate feedback. The specific timing of the trial events was the same as previous blocks, except that the second stimulus’ response was followed by a 500ms blank screen ITI, and then presentation of the third stimulus. The third stimulus appeared until the participant generated an “A” or “B” response, followed by the words “All responses were correct” or “At least one response was incorrect” for 1000ms, a 500ms blank screen ITI, and then the next triple-stimulus trial. Note that in the 123 task, new learning was always to the stimulus closest to the feedback. The 321 task mirrored the 123 task in all aspects of the procedure, except the order of the three training components: during phase 1, single position 3, then pairs of position 2 and 3 during phase 2, and finally triplets of positions 1, 2, and 3 stimuli during phase 3. This way, in the 321 task, new learning was always to the stimulus farthest away in time from the feedback.
Table 1.
Design of the 123 and 321 Conditions of Experiment 2.
| 123 Condition | 1st Stimulus | 2nd Stimulus | 3rd Stimulus |
|---|---|---|---|
| Phase 1 | Position 1 (NEW) | none | none |
| Phase 2 | Position 1 | Position 2 (NEW) | none |
| Phase 3 | Position 1 | Position 2 | Position 3 (NEW) |
| 321 Condition | 1st Stimulus | 2nd Stimulus | 3rd Stimulus |
|---|---|---|---|
| Phase 1 | Position 3 (NEW) | none | none |
| Phase 2 | Position 2 (NEW) | Position 3 | none |
| Phase 3 | Position 1 (NEW) | Position 2 | Position 3 |
4.2. Results – Experiment 2
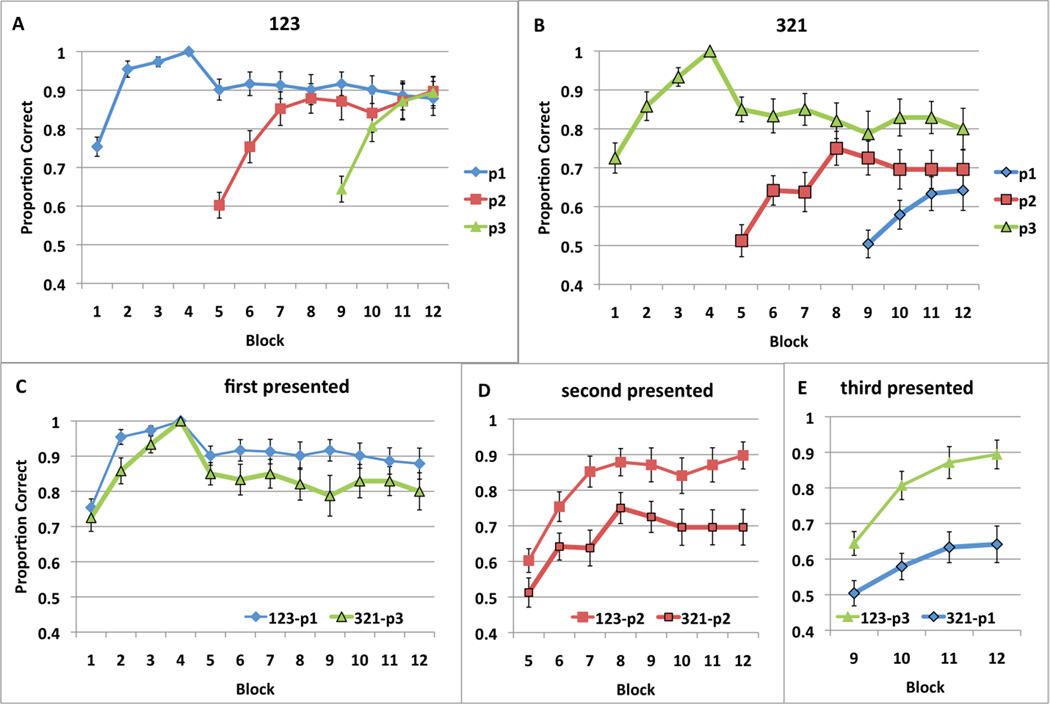
To ensure that both conditions (123 and 321) began with equal amounts of learning in the first 4 single-stimulus full-feedback blocks, we included only participants who reached 100% correct by the fourth block of the task. This criterion excluded 5 participants from the 123 condition (22 remaining), and 2 from the 321 condition (20 remaining). The average accuracies across the 12 blocks for each stimulus position are displayed in Figure 8a for the 123 condition, and in Figure 8b for the 321 condition. Figure 8 panels, c, d, and e show direct comparisons of each position from the two different conditions.
Figure 8.
Proportion correct (averaged across participants) from Experiment 2 across blocks for A) 123 training and B) 321 training. C) Accuracy to first stimulus presented during 123 training (position 1) and during 321 training (position 3), D) Accuracy to second stimulus presented during 123 and 321 training (position 2 in both cases), and E) Accuracy to third stimulus presented during 123 training (position 3) and during 321 training (position 1). Standard error bars included.
Repeated-measures ANOVAs on the accuracy rates across blocks suggest learning in each position of both tasks. In the 123-task, the main effects of block for position 1 [F(11, 231) = 6.884, p < .001, η2 = .247], position 2 [F(7, 147) = 14.291, p < .001, η2 = .405], and position 3 [F(3, 63) = 22.094, p < .001, η2 = .513] were all significant, with performance at 90% in block 12 for all positions. In the 321-task, the main effects of block for position 3 [F(11, 209) = 5.098, p < .001, η2 = .212], position 2 [F(7, 133) = 5.504, p < .001, η2 = .225], and position 1 [F(3, 57) = 3.001, p = .038, η2 = .136] were all significant, but block 12 performance was best in position 3 (80%), worse in position 2 (70%), and worst in position 1 (65%).
We conducted a 3 position × 4 block mixed ANOVA on the accuracy rates over blocks 9–12. In the 123-task the main effects of block [F(3, 63) = 6.448, p < .001, η2 = .235] and position were significant [F(2, 42) = 10.338, p < .001, η2 = .330], as well as the position × block interaction [F(6, 126) = 14.169, p < .001, η2 = .403]. To decompose the interaction, we compared the positions in each block. The main effect of position in block 9 [F(2, 42) = 27.834, p < .001, η2 = .570], and block 10 [F(2, 42) = 4.023, p=.025, η2 = .161] were significant, but not in block 11 [F(2, 42) = .241, p=787, η2 = .011], and block 12 [F(2, 42) = .385, p=683, η2 = .018], therefore by blocks 11 and 12, position 1 accuracy caught up with position 2 and 3 accuracy. In the 321-task the main effect of position [F(2, 38) = 17.664, p < .001, η2 = .482] was significant, but not that of block [F(3, 57) = 2.031, p=.120, η2 = .097], or the position × block interaction [F(6, 114) = 1.949, p = .079, η2 = .093].
Next we examined the data grouped by order of presentation. The first, second, and third presented stimuli were compared with a 2 task × n block mixed ANOVA (where n = 12 for first, n = 8 for second, and n = 4 for third presented stimuli). For the first presented stimuli (position 1 for 123-task, and position 3 for 321-task), the effect of block [F(11, 440)=10.974, p<001, η2 = .215] was significant, and the effect of task [F(1, 40)=3.445, p=.071, η2 = .079] was marginally significant, but not the task × block interaction [F(11, 440)=.776, p=664, η2 = .019]. For the second presented stimuli (position 2 in both tasks), the effect of task [F(1, 40)=9.183, p=.004, η2 = .187], and the effect of block [F(7, 280)=17.282, p<.001, η2 = .302] were both significant, but not the task × block interaction [F(7, 280)=1.133, p=342,, η2 = .028]. For the third presented stimuli (position 3 for 123-task, and position 1 for 321-task), the effect of task [F(1, 40)=23.241, p=.000, η2 = .367], and block [F(3, 120)=16.742, p<.001, η2 = .295] were significant, but not the task × block interaction [F(3, 120)=1.395, p=248, η2 = .034].
4.3. Discussion – Experiment 2
The results of Experiment 2 showed that learning can occur in each position, regardless of whether training is via the 123 or 321 order; however, learning was near complete and equal in magnitude for all positions in the 123-task, but compromised in the 321-task, especially in positions 1 and 2. We observed significantly better learning for the second and third presented items in the 123-task than in the 321-task. Overall, learning was better with 123 than with 321 training. Thus, Experiment 2 suggests that learning is better when the feedback follows immediately after the untrained action.
The 123 training results from Experiment 2 (Figure 7a) were consistent with almost all versions of the procedural-learning model (Figure 7a). The compromised position 1 and 2 learning in 321 training was predicted by 3 different versions of the model (Figure 7b–d). Perhaps the best prediction was from the stimulus-feedback update model (Figure 7d), which shows how DA release to stimuli compromises learning, even with the full benefit of the distant feedback (perfect eligibility trace). Note that all versions of the model that predicted some, but not full learning in positions 1 and 2 assumed an eligibility trace. Furthermore, note that the procedural-learning models we considered all failed to account for the pronounced dip in accuracy of the first presented stimulus that occurred when the second stimulus was first introduced (block 5), and that was seen in both conditions.
5. General Discussion
We developed a novel aggregate-feedback category-learning task to study the learning of a sequence of independent actions under aggregate-feedback conditions. The results of Experiment 1a and 1b confirmed that the stimulus nearest to the feedback was learned best, whereas the stimuli further removed from the feedback showed much poorer learning, especially during early aggregate-feedback training. Our modeling analysis showed that currently popular actor-critic conceptions of procedural category learning account for many qualitative properties of the data, most importantly that learning was compromised for stimuli early in the sequence. Even so, no version of currently popular actor-critic procedural-learning models can account for all properties of the data. The models either predict continual learning in positions 1 and 2 or no learning in either of these positions. A restricted set of models showed poor learning in positions 1 and 2 during the first 5 blocks, and limited learning thereafter. In contrast, the data of both Experiment 1a and 1b showed no learning in positions 1 and 2 initially, and good delayed learning.
The modeling analysis also indicated that any DA released to the stimuli necessarily impairs category learning, at least if the DA response is in accord with current reward-learning models, which predict that, if there is a DA response to stimulus presentation, it should be an increasing function of predicted reward. When accuracy is above chance, predicted reward probability is necessarily high, so DA release in all of these models is high on every trial. This is problematic on error trials because the high DA levels strengthen synapses that led to the error.
Note that the deleterious effects of DA release to the stimuli are limited to early stimuli in the sequence and to error trials. Thus, DA release to stimuli should cause no detrimental effects if early stimuli require no response, or if there are no errors. The aggregate-feedback category-learning task requires a response to each stimulus and errors are unavoidable. This is in sharp contrast to second-order conditioning, in which each cue in a sequence is perfectly predictive of the next cue and there is either no response to learn (e.g., as in classical conditioning) or only one response is required (e.g., in instrumental conditioning). So in second-order conditioning, one would not expect DA release to the cues to cause any learning problems.
The detrimental effects of DA release to early stimuli in independent, multi-action tasks may be overcome by altering the learning regime. Introducing the to-be-learned components one-by-one in order to link together a chain of actions of a skill is common in the real world. Procedural-learning models make a strong prediction about what the order of introducing the actions must be for procedural learning to proceed under aggregate feedback. Training the first action first, and then adding the second and then the third, one-by-one, allows for the unlearned action to always be followed by feedback (123 training). The reverse order, in which the final action is trained first, and then new actions are successively added to the beginning of the sequence (321 training) places unlearned actions as far from the feedback as possible, and therefore is not ideal for procedural learning. Results from Experiment 2 confirmed this prediction.
If DA release to the stimulus impairs aggregate-feedback learning, then what is its adaptive value? The backpropagation of the DA response seems to facilitate second-order conditioning, so evolution may have favored this benefit over the problems that backpropagation causes in aggregate-feedback tasks. But it is also important to note that DA has two different effects. We have focused on the slow-acting effects of DA on synaptic plasticity. But DA also has well documented fast effects on the post-synaptic response. More specifically, DA acts to increase the signal-to-noise ratio in neurons that are targets of glutamate neurons. In particular, increasing DA levels potentiate the response of strong glutamate signals and dampen the response of weak glutamate signals (Ashby & Casale, 2003; Cohen & Servan-Schreiber, 1992). Visual cortex sends prominent projections to the striatum and to many areas of frontal cortex, all of which are targets of DA neurons. Thus, even in aggregate-feedback tasks, a DA response to the stimuli should have the function of making frontal cortex and the striatum more responsive to the visual cortical activation initiated by stimulus presentation. This benefit may outweigh the detrimental effects on cortical-striatal synaptic plasticity. As a very speculative example, the increasing DA release to stimuli may reach a critical threshold that in turn enhances the eligibility trace, and allows for the late learning in our task. Simultaneously modelling DA’s parallel effects in functionally different networks may prove to be an especially fruitful approach (e.g., Collins & Frank, 2014).
The assumption of an eligibility trace better predicted the results of all Experiments (1a, 1b, and 2). The biological mechanism underlying the procedural-learning models we considered is DA-mediated synaptic plasticity (dendritic spine enlargement), which has been shown to occur only if DA arrives within a few seconds after stimulus presentation (Yagishita et al., 2014). In the aggregate-feedback task, this time window is too short to allow for learning in positions 1 or 2. A biological mechanism that might mediate an eligibility trace of longer than 2s has not been identified. Even so, some recent evidence suggests a possible prefrontal-based explicit mechanism. In particular, recurrent neural networks in visual and prefrontal cortices have been discovered that support synaptic eligibility traces that persist between 5–10 seconds (He et al. 2015). These cortical transient traces are thought to develop via Hebbian learning and can remain active until feedback arrives. Note that this mechanism does not require DA. These data then suggest a model in which DA mediates the synaptic plasticity that occurs immediately after the feedback and prefrontal (explicit) mechanisms mediate the eligibility traces that allow learning with feedback delays longer than a few seconds8.
However, at least one feature of the Experiment 1 results argues against explicit memory as the primary driver of performance, namely the absence of a primacy effect. In particular, position 1 accuracy was the same as position 2, and less than position 3 accuracy. Previous research indicates strong primacy effects in sequential learning tasks that depend on explicit memory (e.g., Fu & Anderson, 2008; Drewnowski & Murdock, 1980; Ward, 1937), suggesting that our task design did not evoke explicit memorization. In addition, an explicit-memory explanation would predict no difference between learning in the 123 and 321 tasks of Experiment 2, which is the opposite of the procedural-learning model predictions and the behavioral results. This is based on previous findings that working-memory based category learning is unaffected by 5s feedback delays that include an intervening irrelevant stimulus, while procedural-learning based category learning is compromised (Maddox, Ashby & Bohil, 2003; Maddox & Ing, 2005). The fact that learning is compromised in the 321 task (in which feedback is delayed and there is an intervening stimulus), suggests that learning is procedural in this task. On the other hand, the procedural models examined here were not equipped to account for some qualitative features of the data in both experiments, such as the accuracy dips with the introduction of multi-stimulus aggregate feedback. One possibility is that explicit strategies aid or interfere with procedural learning, which makes sense in a brain where memory systems do not act in isolation.
When building the models investigated in this article, the most significant limitation was that almost no data existed on how DA neurons might respond in the aggregate-feedback task. Instead, when building this portion of the model, we relied on standard models of reward learning (e.g., TD) and empirical results from first- and second-order conditioning tasks (e.g., Schultz, 1998). On the other hand, the category-learning component of the models we considered is much less speculative, since some version of this model has been used successfully in many previous applications (e.g., Ashby, et al., 1998; Ashby & Crossley, 2011; Ashby, Ennis, & Spiering, 2007; Hélie, Paul, & Ashby, 2012a, 2012b). Investigating various reward-learning models within the context of a reasonably well-understood task makes for stronger inferences and more rigorous tests. For example, this combination allowed us to conclude that DA release to later stimuli is likely to interfere with the learning of responses to earlier stimuli. At the same time, however, our results also identified a number of new questions that will require further research to answer. Perhaps the most important of these are: What is the function of DA released to the stimuli during aggregate feedback training? And what other mechanisms augment procedural learning in the type of skills studied in this article?
Highlights.
A novel task was developed with three independent, unsupervised categorization responses that receive aggregate feedback.
Stimuli closest to the feedback were learned best, while earlier ones were initially compromised.
A theoretical analysis using parameter space partitioning showed that procedural-learning models fail to fully capture the data and that any dopamine released to the stimuli must necessarily impair learning in the early positions.
A novel prediction of procedural-learning models regarding the optimal order of presentation for training sequences was tested and confirmed.
Acknowledgments
This research was supported in part by AFOSR grant FA9550-12-1-0355 to WTM and FGA and by NIDA grant 1 R01 DA032457 to WTM. We thank Robert Musgrave for the simulations he performed on an early version of the procedural-learning model, the MaddoxLab RAs for all data collection and especially Micajah Spoden for programming all of the experiments, and Russ Poldrack and Marissa Gorlick for providing the stimuli.
Appendix.
The Procedural-Learning Model
The input layer includes 12 units, one for each of the visually distinct fractals. The input activation in visual cortical unit K, denoted by IK, is a constant set to 1 when stimulus K is present and 0 when stimulus K is absent. The output layer is assumed to represent the striatum and all downstream structures (e.g., GPi, thalamus, premotor cortex). The model i ncludes two output units for the two alternative responses (A and B). Activation of striatal unit J in the output layer on trial n, SJ(n), equals:
where wK,J(n) is the strength of the synapse between cortical unit K and striatal cell J on trial n. On trial 1, the initial value of each of the 24 weights is set to a value randomly drawn from a uniform distribution over the range [.011 .035]. The decision rule is: respond A on trial n if SA(n) – SB(n) > 0.02, and respond B if SB(n) – SA(n) > 0.02, otherwise the model randomly selects between A and B. The relative activity between striatal units changes as the model learns, and learning is accomplished by adjusting the synaptic weights, wK,J(n), up and down as specified by Eq. 1.
For simplification, a strong form of lateral inhibition at the level of the striatum was assumed (activity in the striatal unit associated with the unselected response is forced to zero). Computationally, this amounts to updating only the weights associated with the striatal unit matching the response suggested by the procedural system. For example, if the procedural system suggests an “A” response, only the weights associated with the “A” striatal unit are modified. This simplification effectively serves a dual-purpose: it accelerates learning because only the weights relevant to that trial are updated and improves computational efficiency.
PSP Analysis
The PSP analysis was conducted using MATLAB code obtained from J. I. Myung’s website (http://faculty.psy.ohio-state.edu/myung/personal/psp.html). Any PSP analysis requires the model to produce deterministic output for each set of parameters. To accomplish this, all randomized features of the model must be fixed. All models used here omitted the noise terms typically included in models of this type. The only remaining probabilistic features are the initial random weights at each cortical-striatal synapse, the random guesses that are made on trials when both output units are nearly equally activated, and the random stimulus presentation order.
As mentioned earlier, our analysis focused on the DA gains, α and β of Eq. 1, for positions 1 and 2, and all other parameters were set to values that allowed the model to provide good fits to the single-trial control data, and the position 3 data (i.e., IK = 1; α = 2.4 and β = 0.7 of Eq. 1). The search range for the manipulated parameters was between 0 and the value of the original learning parameter values (α = 2.4 and β = 0.7). This is because the search was for parameter values that could produce accuracies in the range of 0 to optimal (position 3). Every other parameter was fixed to the optimal value (note, position 3 was always updated with the original α and β). During the PSP search, the updating parameters for positions 1 and 2 were set to be equal, because the empirical data did not reveal any significant differences in learning rates. The PSP evaluated each step in the parameter space on all 200 random initializations of weights, stimulus orderings, and guesses. The performance of the model was averaged over all 200 initializations to determine the final data pattern for each step in the parameter space. The PSP algorithm proceeded for six search cycles to obtain a reliable partitioning of the parameter space. The complete PSP search returned the volume of parameter space that was associated with each of the 3 or 4 data patterns, and a specific set of parameter values that could generate each discovered pattern.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Note, our use of the word “backpropagate” refers to the phenomenological dynamics of DA firing to reward predicting events, and not to the popular backpropagation algorithm that is commonly used to train artificial neural networks.
There are at least two prominent and competing accounts of this failure. One possibility is that the failure is mostly motivational. At the beginning of the session, all participants are told they are incorrect on 7 out of every 8 trials (on average). This can be discouraging and cause many participants to give up. Of course, we cannot learn much about procedural learning from this group. The second, and much more theoretically interesting possibility is that procedural learning is defeated when the positive feedback rate is so low. Unfortunately, it is not clear how to determine whether the poor performance of an individual participant is due to the first or second of these possibilities. Thus, considerable research would be required to fully understand the effects of providing aggregate feedback from trial 1.
This is a conservative criterion, because any participant failing to reach 60% correct would not be performing significantly above chance.
For our purposes, the important characteristic of actor-critic models is that they postulate two separate neural networks – one network that categorizes the stimulus (the actor) and another that uses the feedback to determine how much DA is released (the critic), which is then used to improve the performance of the actor. Actor-critic models are contrasted with other models in which both of these tasks are mediated within the same network. For more details see Sutton and Barto (1998).
Of course, when the stimulus in position 1 is presented, the stimuli that will appear in positions 2 and 3 are not yet known. Therefore, when calculating RPOverall for position 1, to compute the RP for position 2, we averaged the RPK of all stimuli that could appear in position 2, and to compute the RP for position 3, we averaged the RPK of all stimuli that could appear in position 3. Similarly, to compute RPOverall for position 2, we used the RPK of the actual stimuli presented in positions 1 and 2 and the average RPK of all possible position 3 stimuli.
Note that there is no need to explore predictions for a β parameter because DA levels always rise when the stimulus in position 2 or 3 is presented. This is because performance and predicted reward probability are well above chance by the time aggregate feedback begins.
Exploring whether such an augmented model could successfully account for our results is beyond the scope of this article. Unfortunately, so little is known about these possible cortically-mediated eligibility traces that many alternative versions of such a model could be constructed, and each one would be highly speculative. On the other hand, it is straightforward to construct augmented models that can account for the results of Experiment 1. For example, we were able to obtain good fits to the Experiment 1 data via a model that assumed that when the procedural strategy started to fail, control switched to a simple explicit strategy (i.e., memorization). Our main point is that currently popular models of procedural learning fail to account for the successful learning we observed in Experiment 1, but do accurately predict the 123 training advantage seen in Experiment 2.
References
- Arbuthnott BW, Ingham CA, Wickens JR. Dopamine and synaptic plasticity in the neostriatum. Journal of Anatomy. 2000;196:587–596. doi: 10.1046/j.1469-7580.2000.19640587.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Casale MB. A model of dopamine modulated cortical activation. Neural Networks. 2003;16:973–984. doi: 10.1016/S0893-6080(03)00051-0. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Crossley MJ. A computational model of how cholinergic interneurons protect striatal-dependent learning. Journal of Cognitive Neuroscience. 2011;23:1549–1566. doi: 10.1162/jocn.2010.21523. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ell SW, Waldron EM. Procedural learning in perceptual categorization. Memory & Cognition. 2003;31:1114–1125. doi: 10.3758/bf03196132. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ennis JM. The role of the basal ganglia in category learning. The Psychology of Learning and Motivation. 2006;47:1–36. [Google Scholar]
- Ashby FG, Ennis JM, Spiering BJ. A neurobiological theory of automaticity in perceptual categorization. Psychological Review. 2007;114:632–656. doi: 10.1037/0033-295X.114.3.632. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Hélie S. A tutorial on computational cognitive neuroscience: Modeling the neurodynamics of cognition. Journal of Mathematical Psychology. 2011;55:273–289. doi: 10.1016/j.jmp.2011.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT. Relations between prototype, exemplar, and decision bound models of categorization. Journal of Mathematical Psychology. 1993;37:372–400. [Google Scholar]
- Ashby FG, Maddox WT. Human category learning. Annual Review of Psychology. 2005;56:149–178. doi: 10.1146/annurev.psych.56.091103.070217. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT. Human category learning 2.0. Annals of the New York Academy of Sciences. 2010;1224:147–161. doi: 10.1111/j.1749-6632.2010.05874.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badgaiyan RD, Fischman AJ, Alpert NM. Striatal dopamine release in sequential learning. Neuroimage. 2007;38:549–556. doi: 10.1016/j.neuroimage.2007.07.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barsalou LW. Ad hoc categories. Memory & Cognition. 1983;11:211–227. doi: 10.3758/bf03196968. [DOI] [PubMed] [Google Scholar]
- Bayer HM, Glimcher PW. Midbrain dopamine neurons encode a quantitative reward prediction error signal. Neuron. 2005;47(1):129–141. doi: 10.1016/j.neuron.2005.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown J, Bullock D, Grossberg S. How the basal ganglia use parallel excitatory and inhibitory learning pathways to selectively respond to unexpected rewarding cues. Journal of Neuroscience. 1999;19:10502–10511. doi: 10.1523/JNEUROSCI.19-23-10502.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabresi P, Maj R, Pisani A, Mercuri NB, Bernardi G. Long-term synaptic depression in the striatum: physiological and pharmacological characterization. Journal of Neuroscience. 1992;12:4224–4233. doi: 10.1523/JNEUROSCI.12-11-04224.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabresi P, Pisani A, Centonze D, Bernardi G. Role of Ca²+ in striatal LTD and LTP. Seminars in the Neurosciences. 1996;8:321–328. [Google Scholar]
- Cohen JD, Servan-Schreiber D. Context, cortex, and dopamine: a connectionist approach to behavior and biology in schizophrenia. Psychological Review. 1992;99:45–77. doi: 10.1037/0033-295x.99.1.45. [DOI] [PubMed] [Google Scholar]
- Crossley MJ, Ashby FG, Maddox WT. Erasing the engram: The unlearning of procedural skills. Journal of Experimental Psychology: General. 2013;142:710–741. doi: 10.1037/a0030059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley MJ, Ashby FG, Maddox WT. Context-dependent savings in procedural category learning. Brain & Cognition. 2014;92:1–10. doi: 10.1016/j.bandc.2014.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley MJ, Madsen NR, Ashby FG. Procedural learning of unstructured categories. Psychonomic Bulletin & Review. 2012;19:1202–1209. doi: 10.3758/s13423-012-0312-0. [DOI] [PubMed] [Google Scholar]
- Daw ND. Model-based reinforcement learning as cognitive search: Neurocomputational theories. In: Todd PM, Hills TT, Robbins TW, editors. Cognitive search: Evolution, algorithms and the brain. Cambridge, MA: MIT Press; 2012. pp. 195–208. [Google Scholar]
- Daw ND, Gershman SJ, Seymour B, Dayan P, Dolan RJ. Model-based influences on humans' choices and striatal prediction errors. Neuron. 2011;69:1204–1215. doi: 10.1016/j.neuron.2011.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doya K, Samejima K, Katagiri K, Kawato M. Multiple model-based reinforcement learning. Neural Computation. 2002;14:1347–1369. doi: 10.1162/089976602753712972. [DOI] [PubMed] [Google Scholar]
- Drewnowski A, Murdock BB. The role of auditory features in memory span for words. Journal of Experimental Psychology: Human Learning and Memory. 1980;6:319–332. [PubMed] [Google Scholar]
- Doyon J, Ungerleider LG. Functional anatomy of motor skill learning. In: Squire LR, Schacter DL, editors. Neuropsychology of memory. Guilford Press; 2002. pp. 225–238. [Google Scholar]
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Computation. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Fabiani M, Buckley J, Gratton G, Coles MG, Donchin E, Logie R. The training of complex task performance. Acta Psychologica. 1989;71:259–299. [Google Scholar]
- Fiorillo CD, Tobler PN, Schultz W. Discrete coding of reward probability and uncertainty by dopamine neurons. Science. 2003;299(5614):1898–1902. doi: 10.1126/science.1077349. [DOI] [PubMed] [Google Scholar]
- Frederiksen JR, White BW. An approach to training based upon principled task decomposition. Acta Psychologica. 1989;71:147–177. [Google Scholar]
- Fu WT, Anderson JR. Solving the credit assignment problem: Explicit and implicit learning of action sequences with probabilistic outcomes. Psychological research. 2008;72(3):321–330. doi: 10.1007/s00426-007-0113-7. [DOI] [PubMed] [Google Scholar]
- Gläscher J, Daw N, Dayan P, O'Doherty JP. States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron. 2010;66:585–595. doi: 10.1016/j.neuron.2010.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafton ST, Hazeltine E, Ivry RB. Functional mapping of sequence learning in normal humans. Journal of Cognitive Neuroscience. 1995;7:497–510. doi: 10.1162/jocn.1995.7.4.497. [DOI] [PubMed] [Google Scholar]
- Gurney KN, Humphries MD, Redgrave P. A New Framework for Cortico-Striatal Plasticity: Behavioural Theory Meets In Vitro Data at the Reinforcement-Action Interface. PLoS biology. 2015;13(1):e1002034. doi: 10.1371/journal.pbio.1002034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpain S, Girault JA, Greengard P. Activation of NMDA receptors induces dephosphorylation of DARPP-32 in rat striatal slices. Nature. 1990;343:369–372. doi: 10.1038/343369a0. [DOI] [PubMed] [Google Scholar]
- He K, Huertas M, Hong SZ, Tie X, Hell JW, Shouval H, Kirkwood A. Distinct Eligibility Traces for LTP and LTD in Cortical Synapses. Neuron. 2015;88(3):528–538. doi: 10.1016/j.neuron.2015.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hélie S, Chakravarthy S, Moustafa AA. Exploring the cognitive and motor functions of the basal ganglia: An integrative review of computational cognitive neuroscience models. Frontiers in computational neuroscience. 2013:7. doi: 10.3389/fncom.2013.00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hélie S, Paul EJ, Ashby FG. A neurocomputational account of cognitive deficits in Parkinson's disease. Neuropsychologia. 2012a;50:2290–2302. doi: 10.1016/j.neuropsychologia.2012.05.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hélie S, Paul EJ, Ashby FG. Simulating the effects of dopamine imbalance on cognition: From positive affect to Parkinson’s disease. Neural Networks. 2012b;32:74–85. doi: 10.1016/j.neunet.2012.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemmings HC, Jr, Greengard P, Tung HY, Cohen P. DARPP-32, a dopamine-regulated neuronal phosphoprotein, is a potent inhibitor of protein phosphatase-1. Nature. 1984;310:503–505. doi: 10.1038/310503a0. [DOI] [PubMed] [Google Scholar]
- Houk JC, Adams JL, Barto AG. A model of how the basal ganglia generate and use neural signals that predict reinforcement. In: Houk JC, Davis JL, Beiser DG, editors. Models of information processing in the basal ganglia. Cambridge, MA: MIT Press; 1995. pp. 249–270. [Google Scholar]
- Izhikevich EM. Dynamical systems in neuroscience: The geometry of excitability and bursting. Cambridge MA: MIT Press; 2007. [Google Scholar]
- Jackson S, Houghton G. Sensorimotor selection and the basal ganglia: A neural network mode. Cambridge, MA: MIT Press; 1995. [Google Scholar]
- Joel D, Niv Y, Ruppin E. Actor-critic models of the basal ganglia: New anatomical and computational perspectives. Neural networks. 2002;15:535–547. doi: 10.1016/s0893-6080(02)00047-3. [DOI] [PubMed] [Google Scholar]
- Knopman D, Nissen MJ. Procedural learning is impaired in Huntington's disease: evidence from the serial reaction time task. Neuropsychologia. 1991;29:245–254. doi: 10.1016/0028-3932(91)90085-m. [DOI] [PubMed] [Google Scholar]
- Lakoff G. Women, fire, and dangerous things. Chicago: The University of Chicago Press; 1987. [Google Scholar]
- Li J, Delgado MR, Phelps EA. How instructed knowledge modulates the neural systems of reward learning. Proceedings of the National Academy of Sciences. 2011;108:55–60. doi: 10.1073/pnas.1014938108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Paniagua D, Seger CA. Interactions within and between corticostriatal loops during component processes of category learning. Journal of Cognitive Neuroscience. 2011;23:3068–3083. doi: 10.1162/jocn_a_00008. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG. Dissociating explicit and procedural-learning based systems of perceptual category learning. Behavioural Processes. 2004;66:309–332. doi: 10.1016/j.beproc.2004.03.011. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Bohil CJ. Delayed feedback effects on rule-based and information-integration category learning. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2003;29:650–662. doi: 10.1037/0278-7393.29.4.650. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Glass BD, O'Brien JB, Filoteo JV, Ashby FG. Category label and response location shifts in category learning. Psychological Research. 2010;74:219–236. doi: 10.1007/s00426-009-0245-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddox WT, Ing AD. Delayed Feedback Disrupts the Procedural-Learning System but Not the Hypothesis-Testing System in Perceptual Category Learning. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2005;31(1):100–107. doi: 10.1037/0278-7393.31.1.100. [DOI] [PubMed] [Google Scholar]
- Naylor JC, Briggs GE. Effects of task complexity and task organization on the relative efficiency of part and whole training methods. Journal of Experimental Psychology. 1963;65:217–224. doi: 10.1037/h0041060. [DOI] [PubMed] [Google Scholar]
- Nissen MJ, Bullemer P. Attentional requirements of learning: Evidence from performance measures. Cognitive Psychology. 1987;19:1–32. [Google Scholar]
- Packard MG, Knowlton BJ. Learning and memory functions of the basal ganglia. Annu. Rev. Neurosci. 2002;25:563–593. doi: 10.1146/annurev.neuro.25.112701.142937. [DOI] [PubMed] [Google Scholar]
- Pan WX, Schmidt R, Wickens JR, Hyland BI. Dopamine cells respond to predicted events during classical conditioning: evidence for eligibility traces in the reward-learning network. Journal of Neuroscience. 2005;25:6235–6242. doi: 10.1523/JNEUROSCI.1478-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitt MA, Kim W, Navarro DJ, Myung JI. Global model analysis by parameter space partitioning. Psychological Review. 2006;113:57–83. doi: 10.1037/0033-295X.113.1.57. [DOI] [PubMed] [Google Scholar]
- Rall W. Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. Journal of Neurophysiology. 1967;30:1138–1168. doi: 10.1152/jn.1967.30.5.1138. [DOI] [PubMed] [Google Scholar]
- Reynolds JN, Wickens JR. Dopamine-dependent plasticity of corticostriatal synapses. Neural Networks. 2002;15:507–521. doi: 10.1016/s0893-6080(02)00045-x. [DOI] [PubMed] [Google Scholar]
- Schultz W. Predictive reward signal of dopamine neurons. Journal of Neurophysiology. 1998;80:1–27. doi: 10.1152/jn.1998.80.1.1. [DOI] [PubMed] [Google Scholar]
- Schultz W. Behavioral theories and the neurophysiology of reward. Annual Review of Psychology. 2006;57:87–115. doi: 10.1146/annurev.psych.56.091103.070229. [DOI] [PubMed] [Google Scholar]
- Schultz W, Apicella P, Ljungberg T. Responses of monkey dopamine neurons to reward and conditioned stimuli during successive steps of learning a delayed response task. Journal of Neuroscience. 1993;13:900–913. doi: 10.1523/JNEUROSCI.13-03-00900.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seger CA, Cincotta CM. The roles of the caudate nucleus in human classification learning. Journal of Neuroscience. 2005;25:2941–2951. doi: 10.1523/JNEUROSCI.3401-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger CA, Peterson EJ, Cincotta CM, Lopez-Paniagua D, Anderson CW. Dissociating the contributions of independent corticostriatal systems to visual categorization learning through the use of reinforcement learning modeling and Granger causality modeling. Neuroimage. 2010;50:644–656. doi: 10.1016/j.neuroimage.2009.11.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- Spiering BJ, Ashby FG. Initial training with difficult items facilitates information-integration but not rule-based category learning. Psychological Science. 2008;19(11):1169–1177. doi: 10.1111/j.1467-9280.2008.02219.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suri RE, Schultz W. Learning of sequential movements by neural network model with dopamine-like reinforcement signal. Experimental Brain Research. 1998;121:350–354. doi: 10.1007/s002210050467. [DOI] [PubMed] [Google Scholar]
- Suri RE, Schultz W. Temporal difference model reproduces anticipatory neural activity. Neural Computation. 2001;13:841–862. doi: 10.1162/089976601300014376. [DOI] [PubMed] [Google Scholar]
- Surmeier DJ, Plotkin J, Shen W. Dopamine and synaptic plasticity in dorsal striatal circuits controlling action selection. Current opinion in neurobiology. 2009;19:621–628. doi: 10.1016/j.conb.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: An introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Sweller J. Cognitive load during problem solving: Effects on learning. Cognitive Science. 1988;12:257–285. [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Waelti P, Dickinson A, Schultz W. Dopamine responses comply with basic assumptions of formal learning theory. Nature. 2001;412:43–48. doi: 10.1038/35083500. [DOI] [PubMed] [Google Scholar]
- Walsh, Anderson Learning from delayed feedback: neural responses in temporal credit assignment. Cogn Affect Behav Neurosci. 2011;11:131–143. doi: 10.3758/s13415-011-0027-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward LB. Reminiscence and rote learning. Psychological Monographs. 1937;49:64. [Google Scholar]
- Willingham DB. A neuropsychological theory of motor skill learning. Psychological Review. 1998;105:558–584. doi: 10.1037/0033-295x.105.3.558. [DOI] [PubMed] [Google Scholar]
- Willingham DB, Wells LA, Farrell JM, Stemwedel ME. Implicit motor sequence learning is represented in response locations. Memory & Cognition. 2000;28(3):366–375. doi: 10.3758/bf03198552. [DOI] [PubMed] [Google Scholar]
- Worthy DA, Markman AB, Maddox WT. Feedback and stimulus-offset timing effects in perceptual category learning. Brain and Cognition. 2013;81(2):283–293. doi: 10.1016/j.bandc.2012.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yagishita S, Hayashi-Takagi A, Ellis-Davies GC, Urakubo H, Ishii S, Kasai H. A critical time window for dopamine actions on the structural plasticity of dendritic spines. Science. 2014;345(6204):1616–1620. doi: 10.1126/science.1255514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ. The role of the basal ganglia in habit formation. Nature Reviews Neuroscience. 2006;7:464–476. doi: 10.1038/nrn1919. [DOI] [PubMed] [Google Scholar]