GIST 2.0: A Scalable Multi-trait Metric for Quantifying Population Representativeness of Individual Clinical Studies

Abstract

The design of randomized controlled clinical studies can greatly benefit from iterative assessments of population representativeness of eligibility criteria. We propose a multi-trait metric - GIST 2.0 that can compute the a priori generalizability based on the population representativeness of a clinical study by explicitly modeling the dependencies among all eligibility criteria. We evaluate this metric on twenty clinical studies of two diseases and analyze how a study’s eligibility criteria affect its generalizability (collectively and individually). We statistically analyze the effects of trial setting, trait selection and trait summarizing technique on GIST 2.0. Finally we provide theoretical as well as empirical validations for the expected properties of GIST 2.0.

Graphical abstract

1. Introduction

Randomized controlled trials generate medical evidence of the highest quality. Hence it is of great importance that clinical studies benefit a representative proportion of the population under consideration. The representativeness of a trial affects its generalizability [1, 2, 3, 4], which indicates whether the findings of a trial can be extended to patients of the same disease who are not trial participants but for whom the treatment is intended. This becomes of prime importance when the results of a clinical trial are disseminated to other patients since the lack of generalizability can lead to serious negative consequences in some subgroups of the diseased population that may have been underrepresented in the trial. A key contributing factor for generalizability is the trial eligibility criteria, which define constraints on the various study traits. Study traits are attributes of a patient that are relevant for the study (either to determine eligibility or to measure outcome). They include conditions (e.g. type 2 diabetes), procedures (e.g. colonoscopy), medications (e.g. metformin), laboratory tests (e.g. glucose) or demographic information (e.g. ethnicity).

Inappropriate eligibility criteria can result in studies that either exclude patients who might benefit from the intervention or, conversely, threaten patient safety by causing unforeseeable post-marketing adverse drug effects [5, 6, 7]. Resources that assist clinical investigators make better eligibility criteria choices are very limited. Clinical research eligibility criteria often suffer from ambiguity, complexity or over-restrictiveness [8, 9]. The lack of interoperability with different data sources is another concern with current eligibility criteria [4]. Study designers often reuse eligibility criteria from previous clinical trials with minimal modifications [10], which may lead to a concordant bias in sampling and under-representation of certain subgroups. Some other researchers rely on past experience for patient selection. However, this type of selection process is highly subjective with limited justification [11]. Another popular practice in eligibility criteria design is through trial and error, which can be unstable and can entail frequent and costly protocol amendments. Hence, optimization of eligibility criteria is a topic of great interest.

To address these concerns with eligibility criteria, we propose a metric to calculate a priori generalizability of a single trial based on its population representativeness. Currently, the lack of population representativeness in clinical studies remains largely undiscovered until after study publications (e.g. [12]-details in Sec. 1.2). With our metric we aim to provide a decision aid for eligibility criteria designs by answering important questions such as: (1) Are the eligibility criteria too restrictive (when multiple traits are considered together)? (2) Is there a particular eligibility trait (or traits) that decreases the study’s population representativeness? (3) How would small changes in the eligibility criteria affect overall population representativeness of the study? The answers to these questions can potentially optimize population representativeness of the study within the constraints of patient safety and other Food and Drug Administration (FDA) regulations [13].

1.1. Populations in a clinical trial

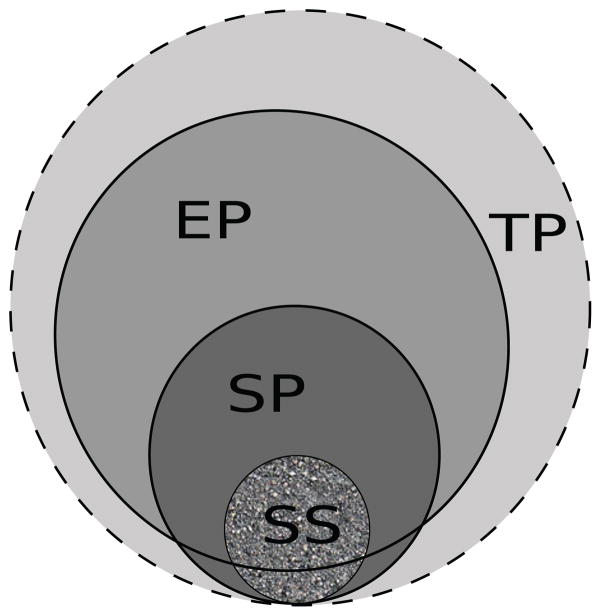
For any clinical trial, there are typically four associated populations. The target population (TP) corresponds to the entire universe of patients (suffering from the disease under consideration) for whom the results of the clinical trial are intended. It includes patients who are unaware of the presence of the disease and those who do not seek medical treatment. The Electronic Health Record population (EP) includes those patients (suffering from that disease) who visit medical facilities to receive treatment and consultation from clinicians. A study population (SP) is the set of all patients who satisfy the eligibility criteria of a particular trial. Finally, the patients who actually enroll for the clinical trial constitute the study sample (SS).

The relationships among these populations are shown schematically in Figure 1. The TP subsumes all other populations. It is impossible to characterize this population exactly, but it can often be approximated by the EP [14]. The dashed outline around the TP in Figure 1 indicates that the TP is not exactly defined. The SP is determined solely by eligibility criteria, and may exclude specific subpopulations (e.g. elderly patients, children, patients with comorbidities etc.) who may potentially benefit from the trial. The SP subsumes the SS but both these populations may include patients from outside the EP. In the scenario of perfect recruitment (the SS being a random sample from the SP) all subgroups within the SP are represented in the SS. However, this may not be the case as the SS is constrained by informed consent, geographical locations, ability to adhere to the conditions set by the trial, etc.

Figure 1.

Relationship between various populations associated with a clinical trial: Target Population (TP), EHR Population (EP), Study Population (SP) and Study Sample (SS).

Generalizability can be measured before the commencement of a trial (a priori) or after its completion (a posteriori). A priori generalizability is calculated on the basis of eligibility criteria and we refer to this as eligibility-driven generalizability. Since the SP is defined precisely by the eligibility criteria, this is measuring the representativeness of the SP within the TP. A posteriori generalizability is determined by the actual patients enrolled in the study, i.e. the SS. This is sample-driven generalizability, which measures the representativeness of the SS within the TP. For this paper we focus on the former, which is affected by population representativeness.

1.2. Previous Work and its Limitations

A detailed literature review for clinical trial generalizability was discussed by Kennedy-Martin et al. [15]. As mentioned above, most of the generalizability assessments have been performed after the completion of a trial. For example, in a technical report by Buchanan et al. [12], a generalizability study was performed for HIV treatment clinical trials. The majority of the results presented in this study were simulation-based and only two clinical trials were evaluated. Bress et al. studied the generalizability of the Systolic Blood Pressure Intervention Trial (SPRINT) in detail [16]. Although the analysis was comprehensive, it was limited to a single trial. The concept of a priori generalizability has been mentioned by several authors but there have been relatively few efforts at a rigorous quantitative assessment. Such assessments have been restricted to visualization techniques (e.g. comparison of histograms by Schoenmaker et al.[5]) and statistical tests (e.g. assessment of generalizability bias [17, 18]).

One of the first efforts at quantification of generalizability used receiver operator characteristic analysis [19]. A binary classifier evaluated infants with fever for presence of bacterial infection. Training and validation sets consisted of patients from two time periods in different hospitals. This type of supervised study is different from a clinical trial as prior knowledge about the outcome (bacterial infection in this case) was known. Intervention outcomes cannot be assumed in clinical trial settings. Some studies have analyzed the generalizability of one trial in detail but their methods remain untested with a broader class of clinical studies. For example, (1) Wang et al. computed the representativeness of the ‘Relaxin for the Treatment of Acute Heart Failure (RELAX-AHF) trial’ by calculating the fraction of patients in international registries who would satisfy the eligibility criteria [20]. (2) Cole et al. [21] used inverse-probability selection weights to calculate the generalizability of the AIDS clinical trial group (ACTG) 320 trial (for HIV) to a target population (of all HIV patients in the USA) defined by state registries.

In most of the above cases, studies with multiple eligibility criteria had each criterion evaluated independently. However, there could be functional relationships between two or more traits. We refer to such relationships between traits as trait dependencies. Furthermore, every trait was treated as equally important in the computation of generalizability. In actual practice the importance of a trait may be disease-specific (e.g. HbA1C is more important in type two diabetes than it is in chronic kidney disease) as well as trial-specific (e.g. HbA1C >6.5% is less important than HbA1C within 9–11% - see Sec. 2.3). We refer to a quantification for the importance of a study trait as trait-significance (this should not be confused with ‘statistical significance’ later in the paper). Hence, the two major limitations of all the studies mentioned above were: (a) the trait dependencies were not explicitly modeled (b) the significance of traits was not accounted for. In addition, most of the studies (with the exception of [16]) restricted their generalizability analyses to continuous traits and did not consider categorical traits, which are often critical in clinical study designs.

Weng et al. previously introduced the generalizability index for study traits (GIST) to quantify generalizability [22] (validated in [23]). Though initially presented only for individual traits, GIST is capable of computing generalizability with multiple traits [14]. However, as with the other studies mentioned above, GIST did not account for the dependencies and significance of traits. Due to the limited number of traits considered in these implementations, it was impossible to compute the generalizability of individual trials (since each trial contains multiple eligibility traits). With the design of GIST 2.0 we aim to overcome these limitations. The suffix 2.0 represents a newer version of the initial GIST metric, which is henceforward referred to as GIST 1.0 for disambiguation. Also, the shorthand GIST henceforward refers to GIST 2.0.

1.3. Our Vision

The generalizability of a clinical study is inversely related to its internal validity [24]. In fact, generalizability is often compromised to maximize internal validity [24]. The tradeoff between study generalizability and internal validity is an optimization problem that can benefit from data-driven transparency. The emergence of vast electronic health records (EHRs), clinical data warehouses, and data networks have made available enormous amounts of electronic patient data. Some examples include public medical record databases such as MIMIC II [25], electronic health records for specific institutions and international collaborative consortia such as Observational Health Data Sciences and Informatics (OHDSI - http://www.ohdsi.org/). Also, clinical trial registries (e.g Clinical-Trials.gov) are becoming increasingly available publicly. These provide in depth summaries of clinical trials including eligibility criteria. The concurrent availability of EHRs and clinical trial summaries provides a unique opportunity to explore data-driven eligibility criteria design.

An immediate advantage of patient-level big data resources is that clinical investigators can be informed about the approximate distributions of the real-world patient profiles. This is crucial for the estimation of a priori generalizability. It has been previously suggested that the suboptimality of eligibility criteria may be caused by poor understanding of patient profiles [13]. The quantification of generalizability can provide important decision aids to clinical investigators before and during the design of eligibility criteria by: (1) providing early estimates about the relative generalizability of clinical trials (2) enabling iterative refinements of eligibility criteria based on data-driven population representativeness feedback. However, it must be noted that by reusing EHRs for clinical research, we are using data for a purpose for which it was not acquired. This creates major challenges such as data completeness and sampling bias [26]. That is why we emphasize the use of GIST 2.0 to indicate relative population representativeness only.

2. Methods

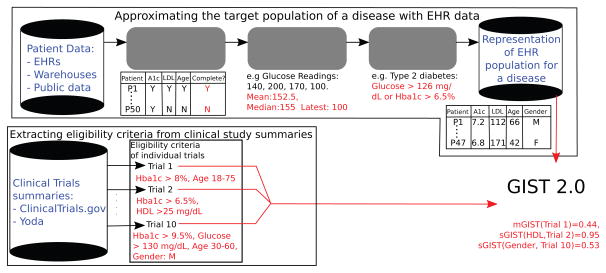
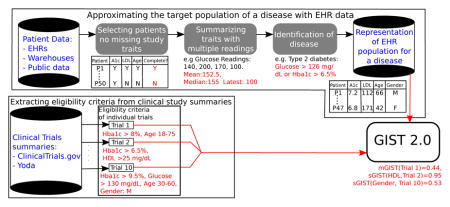
As per our vision, a schematic representation for our methodology is shown in Figure 2. In our vision the availability of Big Data in the form of EHRs (the top arm of Figure 2) promises to reduce the bias in the approximation of the TP. From the EHR data the patients containing readings for all study traits are filtered. Since continuous traits may have multiple readings, summarizing these readings into a single value is an important aspect of our experiments. We refer to this as trait summarization. The summarization creates a multi-dimensional representation of patients with each dimension representing a summarized study trait. From these vector representations, the patients of the disease under consideration are identified by suitable phenotyping algorithms. Population representativeness can then be quantified based on patient characteristics. The extraction of eligibility criteria from clinical trial summaries is a complex process that uses natural language processing (NLP) techniques. Those details are beyond the scope of this paper but can be found in [27] or substituted by other related NLP methods. With an approximation of the real-world patient population and eligibility criteria for a clinical trial we are in a position to define GIST 2.0.

Figure 2.

A schematic representation of our vision for the development of a generalizability metric from patient and clinical trial data

2.1. Summarizing study traits and Identification of diseased patients

For this study we focused on diseases that are widely prevalent in the EHRs and can be quantified by lab values. Use of widely prevalent diseases ensured we had a sufficiently large number of patients for our experiments. The restriction to lab values was aimed at keeping the dimensions of the data within manageable limits as there can be hundreds of categorical traits. After consultations with a medical expert (author A.G.) we chose type 2 diabetes mellitus and iron deficiency anemia.

As mentioned above summarizing the different readings of continuous traits into a single value is an important part of our experiments. Using measures of central tendency such as mean or median is one possible way to summarize continuous traits. Another viewpoint is that only the most recent measurement should be tested for satisfaction of the eligibility criteria. For volatile traits such as glucose, a single reading for summarizing statistics causes high variance. Hence, using several of the most recent readings may be preferable. We compared four summarization statistics to represent patient level data - (1) the mean of all readings (2) the latest reading (3) the mean of up to the last three readings (4) the median of all readings, for type 2 diabetes and iron deficiency anemia patients.

To identify diabetic patients we used the World Health Organization (WHO) criteria for diabetes, which states - a person is diabetic if s/he has a (a) a glucose level greater than 126 mg/dL OR (b) an HbA1C measurement of greater than 6.5%.

The identification of iron-deficiency anemia patients is trickier due to different protocols being followed at different practices. We have used the case definition from [28]. According to this definition anemia is characterized by low hemoglobin - less than 13.8 g/dL for males and less than 11.5 g/dL for females. Serum ferretin concentration is the most powerful test to determine iron deficiency. A ferretin level of less than 120 μg/dL is a sufficient condition for iron deficiency. However, in combination with some other conditions ferretin may rise above this limit despite iron deficiency. Hence a second test for transferrin saturation (TSAT) may be required. A TSAT level of less than 30% is an indicator for iron deficiency as long as ferretin levels are below iron excess levels (300 μg/dL).

2.2. Defining the EHR population

We approximate the TP by the EP. Our EHR data set consists of 30,000 randomly selected patients out of the 4.5 million patients in the Columbia Data Warehouse (CDW) [29]. These include both inpatients and outpatients. Data quality assessment was performed by Weiskopf et al. [26] and comparisons with survey data were presented by Fort et al. [30]. For each of the two diseases, we defined a set of traits based on their (1) frequency of usage in the eligibility criteria - determined after discussions with a medical expert (author A.G) and (2) availability for patients in our EHR data. For example, c-peptide is frequently used in diabetes trials but was available for only 0.3% patients in the EHR data set, and hence was not selected. We focused on trials where the majority of the lab eligibility traits were among the disease-specific traits listed below and selected ten such trials for each disease. Of the ten trials, we made sure that the frequent traits for each disease had eligibility constraints in at least two trials. To illustrate our methodology for categorical variables, we selected at least two trials for each disease that had gender constraints-one on males and one on females.

We identified seven traits that are frequently used in type 2 diabetes trials and are adequately represented in the EHR data set. These traits were: HbA1C, glucose, low density lipoprotein (LDL), high density lipoprotein (HDL), triglycerides, creatinine and glomerular filtration rate (GFR). In addition, age and gender are eligibility traits in most trials. Beside these nine traits, two of the selected trials also had eligibility conditions on total cholesterol and hemoglobin respectively. Since these two traits are also well represented in the EHR, they formed a part of our trait set (increasing the total number of traits to eleven). Similarly we identified eight traits that are frequently used in iron deficiency anemia: hemoglobin, ferretin, TSAT, phosphorus, vitamin B12, folate, iron and GFR. Two trials also had conditions on creatinine and total iron binding capacity (TIBC), which increased the total number of traits to twelve (including age and gender). Traits other than the ones mentioned above were not considered.

For each disease, patients having at least one reading for each of these traits (in its trait set) were extracted from the EHR data (irrespective of the number or lengths of stays). After summarizing each lab trait for each patient, the disease identification criterion for the respective disease (described above) was applied to every patient and the patients satisfying it formed our EP of that disease. Since we are using four summary statistic types, there are four possible representations for each patient. Hence, the EP corresponding to each summary statistic may be different.

Let the EHR population of size N consist of patients P₁, P₂, . . . , P_N, where each patient P_i is represented by an n-dimensional vector of study traits f₁, f₂, . . . , f_n, i.e. $P_i=(f_1^i,f_2^i,\dots ,f_n^i)$. Throughout the rest of this section we will index patients by i and traits by j. Hence, $f_j^i$ represents the summarized trait f_j of the ith patient.

2.3. Significance Assessment

The clinical significance of each eligibility trait is different and may vary by trial. We use a trial-specific significance scale based on stringency where the traits with greater stringency had higher significance. For example, in a trial with HbA1C criterion greater than 6.5% the significance of HbA1C is lower than a trial requiring HbA1C between 9 and 11% [31]. While the former criterion is aimed at ascertaining that a prospective patient is indeed diabetic, the latter plays the additional role of further restricting the diabetic patient population to a smaller subgroup, relevant to the objective of the trial. Formally, in a trial T and for trait f_j, let the fraction of patients in the EP satisfying its eligibility criteria be r_j. Then the significance of f_j is calculated as s_j = 1 − r_j.

2.4. Algorithm for computing GIST 2.0

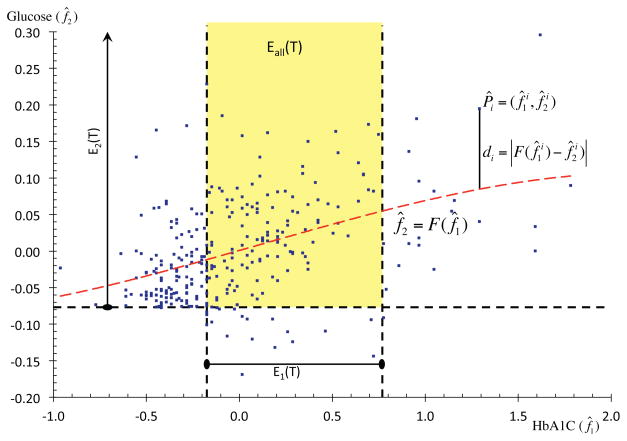
In addition to the formal description of the GIST algorithm, we explain each step with a simple example. In this example we use only two study traits, HbA1C and glucose (referred to as f₁ and f₂) of a clinical trial (Clinical trial ID: NCT00570739, referred to as T3 later in the paper). Figure 3 is used to visualize some steps of the algorithm. An EP of 1290 patients was identified as described above (with median as the summarizing statistic). As continuous study traits have different ranges, we begin by standardizing them.

Figure 3.

An example illustrating the GIST 2.0 methodology with two traits. The regression curve of dependency is shown by the red dashed curve. The eligibility criteria are marked by black dashed lines and points in the yellow region represent eligible patients.

1. Standardize the summarized continuous traits of every patient using the mean and the standard deviation (SD). For any continuous trait f_j, let μ_j and σ_j denote its mean and SD over the EP patients. Then the standardized patient is ${\stackrel{\sim }{P}}_i=({\stackrel{\sim }{f}}_1^i,{\stackrel{\sim }{f}}_2^i,\dots ,{\stackrel{\sim }{f}}_n^i)$, with ${\stackrel{\sim }{f}}_j^i=\frac{f_j^i-{\mu }_j}{{\sigma }_j}$ for continuous traits and categorical traits remaining unchanged ( ${\stackrel{\sim }{f}}_j^i=f_j^i$).

   In the example - The means and standard deviations of f₁ and f₂ were calculated: μ₁ = 7.14, σ₁ = 1.65, μ₂ = 165.81, σ₂ = 41.15 and used for the standardization.

2. Use the stringency-based method described above to calculate the significance s_j, of each trait. For a patient with standardized traits P̃_i, compute its significance-scaled form by ${\widehat{P}}_i=({\stackrel{\sim }{f}}_1^i,\dots ,{\widehat{f}}_n^i)=(s_1{\stackrel{\sim }{f}}_1^i,\dots ,s_n{\stackrel{\sim }{f}}_n^i)$.

   In the example - The significance scales s₁ and s₂ were calculated to be 0.45 and 0.08 respectively. These were used to compute f̂₁ and f̂₂. The scatter plot between the standardized and significance-scaled patients (f̂₁ and f̂₂) is shown in Figure 3. For visual clarity only a random sample of 300 patients are displayed in this figure. Note that due to the lower significance of f₂, its range is much lower than that of f₁.

3. Use the standardized and significance-scaled patients P̂_i to compute a non-linear regression hyper-surface F with one of the continuous traits (e.g. f̂_n) designated as the dependent variable (and all other traits as independent variables), i.e. f̂_n = F (f̂₁, . . . , f̂_n−1).

   In the example - The hyper-surface f̂₂ = F (f̂₁) was calculated in Matlab 2015b. It is shown by the red dashed curve in Figure 3.

4. For every patient (standardized and significance-scaled) P̂_i, calculate its residual distance d_i = |F (f̂₁, . . . , f̂_n−1) − f̂_n| from the hyper-surface F .

   In the example - In Figure 3, this distance is shown for one patient P_i. For this patient d_i = 0.13.

5. Assign a weight w_i to every patient P_i that is inversely proportional to the patient’s distance d_i from F, i.e. $w_i=\frac{1}{1+d_i}$. (Note that w_i = 1 when d_i = 0).

   In the example - For the patient P_i in Figure 3 the corresponding d_i would be 0.88.

6. For a trial T, let the inclusion range (as given in the eligibility criteria) for trait f_j be denoted by the set E_j(T). The notation $f_j^i\in E_j(T)$ implies that the jth trait of patient P_i falls within the corresponding inclusion range of the eligibility criteria. Now, the single-trait GIST score sGIST_j for trait f_j is computed as,

   $${\mathit{sGIST}}_j(T)=\frac{{\displaystyle \sum _{f_j^i\in E_j(T)}}{w}_i}{{\displaystyle \sum _{f_j^i}}{w}_i}$$ (1)

   In the example - The eligibility criteria for HbA1C and glucose were 6.5 ≤ f₁ ≤ 10.5 and f₂ ≥ 126 respectively. In the standardized and significance-scaled coordinates these transform to −0.17 ≤ f̂₁ ≤ 0.78 and f̂₂ ≥ −0.07 respectively. These intervals form the sets E₁(T) and E₂(T). They are marked in Figure 3 with capped dashed lines. Elliptical caps imply bounded range and arrow-head caps imply unbounded range.

   701 patients satisfied the criteria for f₁ and 1213 for f₂. The total weight of patients lying in E₁ was 642.75 and for those lying in E₂ was 1130.20. The total weight of all patients was 1231.71. Hence, ${\mathit{sGIST}}_1(T)=\frac{642.75}{1231.71}=0.52$ and ${\mathit{sGIST}}_2(T)=\frac{1130.20}{1231.71}=0.92$.

7. The multi-dimensional (overall) eligibility criteria of T is the logical combination of the eligibility criteria of the individual traits. Let the volume defined by the multi-dimensional eligibility criteria be denoted by E_all(T) (e.g. E_all(T) = E₁(T) AND [E₂(T) OR E₃(T)]). A patient P_i satisfying the overall eligibility criteria for T is said to belong to this volume i.e. P_i ∈ E_all(T). Now, the multiple-trait GIST score mGIST of T is computed as,

   $$\mathit{mGIST}(T)=\frac{{\displaystyle \sum _{P_i\in E_{\mathit{all}}(T)}}{w}_i}{{\displaystyle \sum _{P_i\in EP}}{w}_i}$$ (2)

   In the example - The set E_all(T) is the intersection of E₁(T) and E₂(T). 492 patients lie within E_all(T) with a combined weight of 448.33. As the total weight of all patients was 1231.71, we get $\mathit{mGIST}(T)=\frac{448.33}{1231.71}=0.36$. Note that this value is different from the one reported for T3 later in the paper as only two study traits were considered here.

The GIST scores are always between zero and one with higher scores implying greater population representativeness. For a clinical study with n study traits this algorithm outputs n + 1 values: the sGIST of the n study traits and the mGIST of the study. An mGIST score (for both versions 1.0 and 2.0) estimates the fraction of TP patients that would be eligible for a particular clinical study. This is only an estimate as the TP is not well defined and is being approximated by the EP. While GIST 1.0 estimated this by simply calculating the fraction of EP patients within the SP, GIST 2.0 uses patient weights to compute a weighted fraction. Moreover, it should also be noted that this calculated mGIST score only accounts for the selected study traits and the true mGIST score (which would include all traits) may be lower. In fact, later in the paper we will prove that the calculated mGIST score is an upper bound of the true mGIST score.

2.5. Statistical Analysis

As the GIST scores are dependent on eligibility criteria we expect trials with different eligibility criteria to have significantly different GIST scores. Similarly each trait has different levels of restrictions and hence should have significantly different sGIST scores. Finally, we would expect our algorithm for computing GIST scores to be robust to the choice of a reasonably-defined summary statistic. We thus conducted statistical analysis to examine if (1) different trials have different mGIST scores when a certain patient-level summary statistic is used; (2) if different traits have different sGIST scores within a trial when a certain patient-level summary statistic is used; and (3) if different patient-level summary statistics have different mGIST/sGIST scores within a trial/trait. More specifically, to compare mGIST scores, we performed a two-way analysis of variance (ANOVA) with trial and summary statistic type as the factors. To compare sGIST scores, we performed a three-way ANOVA with trial, trait and summary statistic type as the factors. Statistical significance was tested at the 0.05 level. We further examined which levels within the summary statistic type factor were significantly different using the Tukey honest significant difference (HSD) multiple comparison test [32].

3. Results

3.1. Evaluation of GIST 2.0 on Individual Trials

We illustrate the GIST 2.0 methodology for the two diseases using ten trials of each. We denote trials by T1, T2,..., T20. The Clinicaltrials.gov trial identifiers for these trials are given below and detailed eligibility criteria can be found in the corresponding web pages.

Type 2 diabetes mellitus: T1 - NCT00287404; T2 - NCT00695526; T3 -NCT00570739; T4 - NCT01414556; T5 - NCT00747149; T6 - NCT00157482; T7 - NCT01835678; T8 - NCT02231736; T9 - NCT00108485; T10 - NCT02330406.

Iron deficiency anemia: T11 - NCT00520780; T12 - NCT01736397; T13 -NCT00994318; T14 - NCT01340872; T15 - NCT00810030; T16 - NCT01052779; T17 - NCT02492620; T18 - NCT01991600; T19 - NCT00498511; T20 - NCT02631668.

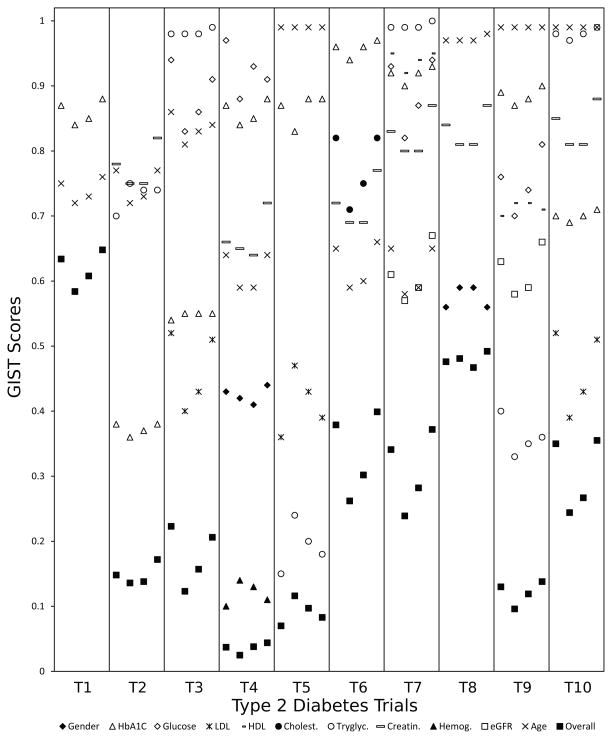
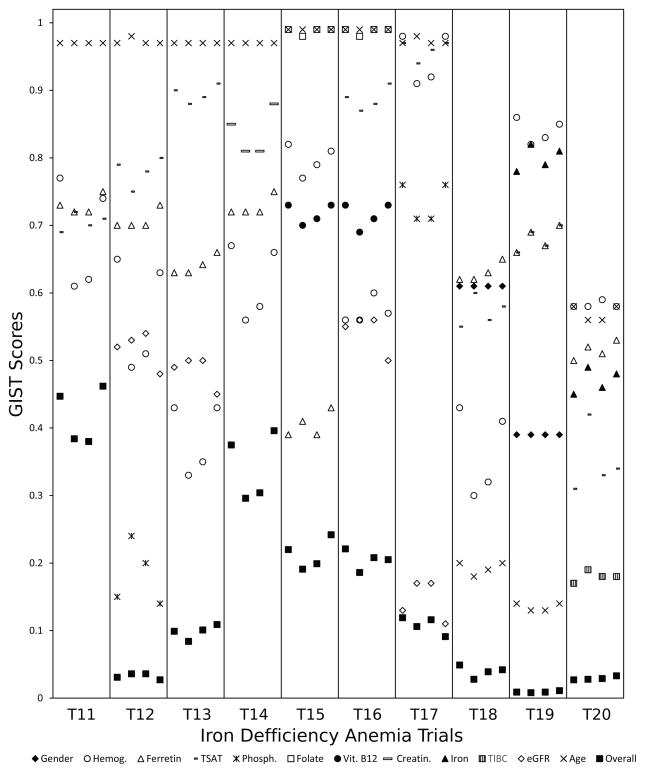
Detailed results are shown in Figure 4 for type 2 diabetes trials and in Figure 5 for iron deficiency anemia trials. The horizontal axis contains various trials in swim lanes. Within each lane the four sublanes represent the four summarizing statistics described in 2.1 - from left to right: (a) the mean of all readings (b) the latest reading (c) the mean of up to the last three readings (d) the median of all readings. Study traits are specified by markers. The last marker ‘Overall’ refers to all traits taken together. The vertical axis is for the GIST scores (sGISTs for the individual traits, mGIST for ‘Overall’).

Figure 4.

GIST scores for 10 type 2 diabetes trials. Each swim lane represents a trial and the four sublanes represent the four summarizing statistics (for study traits) from left to right: (a) the mean of all readings (b) the latest reading (c) the mean of up to the last three readings (d) the median of all readings.

Figure 5.

GIST scores for 10 iron deficiency anemia trials. Each swim lane represents a trial and the four sublanes represent the four summarizing statistics (for study traits) from left to right: (a) the mean of all readings (b) the latest reading (c) the mean of up to the last three readings (d) the median of all readings.

We categorize the study traits broadly into three groups. The defining traits are the ones that determine the presence or severity of the disease. Exclusion criteria exclude certain patients (e.g. patients with comorbidities). The last category of criteria are the refining criteria that narrow the TP to a sub-population. For type 2 diabetes, the primary defining trait was HbA1C (sometimes in combination with glucose). One trial - T8 - had no eligibility conditions on these traits. This implied that as long as it was predetermined that the patient was diabetic, the actual HbA1C and glucose measurements did not affect eligibility. The sGIST scores for these traits were generally high (> 0.7) since the EP consisted only of diabetic patients. The two exceptions were T2 and T3. In both these trials the acceptable HbA1C value range had both lower and upper bounds, which caused patients at both ends to be excluded. In iron deficiency anemia the defining traits were hemoglobin, ferretin and TSAT. Gender was also a defining trait in some of the trials as the hemoglobin criterion was dependent on gender. As compared to diabetes trials the sGIST scores for these trials were substantially lower, which was primarily due to most of these trials excluding severe anemia patients (except T17 and T19).

The two major exclusion criteria in diabetes trials were chronic kidney disease and hypertriglyceridemia. While the trials T3, T7 and T10 excluded patients with hypertriglyceridemia, T7 and T9 excluded patients with chronic kidney disease. For iron deficiency anemia, folate and vitamin B12 deficiency were excluded in T15 and T16. The traits associated with these criteria again had high sGIST values as the fraction of patients with comorbidities was relatively small. The actual number was dependent on the severity at which a patient was excluded. The exclusions due to hypertriglyceridemia and abnormal folate were only for the most severe cases, which led to sGISTs very close to 1. The chronic kidney disease and abnormal vitamin B12 exclusions contained even the less severe cases, resulting in relatively lower sGISTs. Most trials had a lower bound on age as 18 and some also had upper bounds. This was also an exclusion criterion for excluding children and the elderly.

A typical refining criteria was the restriction to a particular gender (e.g. T4 and T8 for diabetes, T18 and T19 for anemia). The presence of additional conditions was also a refining criteria. For example, among the diabetes trials, T4 had anemia as an added condition, T10 had high LDL cholesterol alongside diabetes, T5 required hypertriglyceridemia, etc. For the iron deficiency anemia trials, T17 had chronic kidney disease as an added condition. The sGISTs for these traits varied depending upon the level of refinement. In T4 the anemia condition for males was applied which automatically excluded most females and had a low (~0.1) sGIST. The condition on high LDL (in T10) however, covered a larger group of patients. The restriction to a gender resulted in moderate sGISTs due to a more even distribution between the two genders. Sometimes age was also used as a refining criterion to assess benefits of the intervention in a particular age group (e.g. T7).

The mGIST score accounted for all these criteria. The score depended on the number of traits that were part of the eligibility criteria, their restrictiveness and the logical relations among them. Among the diabetes trials, T1 only had one defining criterion (on HbA1C) and hence the highest mGIST. T5 had exclusion criteria (for LDL and triglycerides) with moderately high (> 0.7) sGISTs and hence had a moderate mGIST. Despite a refining criteria on gender, T8 had a moderately high mGIST as the only exclusion criteria on creatinine had a high sGIST. In contrast, T4 (which also had a refining criteria on gender) had a very low mGIST due a further highly restrictive refinement on hemoglobin (sGIST ~0.10). Among the iron deficiency anemia trials, T11 only had defining traits and hence the highest mGIST. The refining criteria on phosphorus resulted in a low mGIST for T12. In contrast T14, which had similar sGISTs for ferretin and hemoglobin, had a much higher mGIST as the exclusion criteria for creatinine had a high sGIST. In T18 and T19 the low mGISTs were primarily due to the strict refinements on age.

3.2. ANOVA Findings

A three-way ANOVA on diabetes (T2DM) trials’ sGISTs yielded trial and trait as a statistically significant factors (p-values of 0.00127 and < 0.0001 respectively). The summary statistic type was not a significant factor for sGIST. The results were similar for the iron deficiency anemia (IDA) trials with the trial and trait factors yielding statistically significant p-values of < 0.0001. Since there were five traits common to both diseases (gender, age, hemoglobin, creatinine, eGFR) we also conducted a three-way ANOVA for sGIST with all 20 trials and the three factors mentioned above. Trial and trait were again the statistically significant factors with p-values < 0.0001.

A two-way ANOVA on the diabetes trials yielded both trial and summary statistic type as statistically significant factors for mGIST with p-values < 0.0001 and 0.0002 respectively. For iron deficiency anemia the corresponding p-values were < 0.0001 and 0.0127. All the p-values from the five described ANOVAs are summarized in Table 1.

Table 1.

Results from ANOVAs conducted on the mGIST and sGIST scores with trial, trait (only for sGIST) and summary statistic type as factors. Significant p-values (at significance level 0.05) are marked in bold.

Tested Variable	Disease	p-value
		Trial	Trait	Summ. Stat.
sGIST	T2DM	0.0010	<0.0001	0.6948
sGIST	IDA	<0.0001	<0.0001	0.9534
sGIST	Both	<0.0001	<0.0001	0.7179
mGIST	T2DM	<0.0001	-	0.0002
mGIST	IDA	<0.0001	-	0.0127

The summary statistic does not affect sGIST significantly but affects mGIST significantly. A Tukey HSD test on the mGISTs showed that the summary statistic ‘latest measurement’ was significantly different from ‘mean’ and ‘median’. The pairwise p-values for the mean-latest and median-latest pairs were 0.0460 and 0.0272, respectively. There were no statistically significant differences between the categories ‘mean’, ‘median’ and ‘mean of the last 3’.

4. Validation of GIST 2.0

4.1. Theoretical Validation

The GIST 2.0 metric satisfies several of the desired mathematical properties. In this section we state these properties and provide brief set theoretic proofs for two of the major properties (distributivity and monotonicity). The properties below hold for both mGIST and sGIST. Though they are stated for mGIST only, the corresponding sGIST properties can be stated and proven in an almost identical manner.

Property 1. (nullity)

For a trial T if no patient of the EP satisfies all eligibility criteria of T the mGIST (T) = 0.

Property 2. (identity)

For a trial T if all patients of the EP satisfy all eligibility criteria of T the mGIST (T) = 1.

Property 3. (distributivity or additivity)

For a trial T if E_all(T) is partitioned into eligible populations of more specific trials E_all(T₁), E_all(T₂), . . . , E_all(T_m), then mGIST (T) = mGIST (T₁) + mGIST (T₂) + . . . + mGIST (T_m).

Proof

By the definition of a partition,

$$E_{\mathit{all}}(T)=E_{\mathit{all}}(T_1)\cup E_{\mathit{all}}(T_2)\cup \dots E_{\mathit{all}}(T_m)$$ (3)

$$E_{\mathit{all}}(T_u)\cap E_{\mathit{all}}(T_v)=\varnothing \text{for}\text{any}u,v\in \{1,2,\dots ,m\}$$ (4)

Hence, any P_i ∈ E_all(T) belongs to exactly one of the sets E_all(T_u) with u ∈ {1, 2, . . . , m}. This gives,

$$\sum _{P_i\in E_{\mathit{all}}(T)}{w}_i=\sum _{P_i\in E_{\mathit{all}}(T_1)}{w}_i+\sum _{P_i\in E_{\mathit{all}}(T_2)}{w}_i+\dots +\sum _{P_i\in E_{\mathit{all}}(T_m)}{w}_i$$ (5)

Dividing throughout by the term ${\displaystyle \sum _{P_i\in EP}}{w}_i$,

$$\mathit{mGIST}(T)=\mathit{mGIST}(T_1)+\mathit{mGIST}(T_2)+\dots +\mathit{mGIST}(T_m)$$ (6)

Property 4. (monotonicity)

For two trials T₁ and T₂ with the same EP, if E_all(T₁) ⊆ E_all(T₂) (the eligibility criteria of T₂ subsumes the eligibility criteria of T₁) then mGIST (T₁) ≤ mGIST (T₂).

Proof

By given condition P_i ∈ E_all(T₁) ⇒ P_i ∈ E_all(T₂).

Hence, ${\displaystyle \sum _{P_i\in E_{\mathit{all}}(T_1)}}{w}_i\le {\displaystyle \sum _{P_i\in E_{\mathit{all}}(T_2)}}{w}_i$.

Dividing throughout by the term ${\displaystyle \sum _{P_i\in EP}}{w}_i$, we get mGIST (T₁) ≤ mGIST (T₂).

The monotonicity property has several other implications especially regarding the logical combinations of eligibility criteria. Using the properties of the conjunction (AND) operator we get the following corollary.

Corollary 5

For two trials T₁ and T₂ with the same EP, if the eligibility criteria of T₂ is obtained by a conjunction (AND) operation on the eligibility criteria of T₁ then mGIST (T₂) ≤ mGIST (T₁).

From this corollary it immediately follows that the mGIST calculated using a subset of the eligibility criteria is an upper bound for the true mGIST score.

4.2. Simulation-based Empirical Validation

Next we provide numerical examples to verify these properties. For all numerical experiments it should be noted that in fitting hyper-surfaces there is some amount of randomness involved. The non-linear regression uses a Levenberg-Marquardt optimization algorithm, which requires a random initial guess. Since this initial guess is different for every execution there may be small differences in the calculated GIST scores. For our experiments, these differences were generally to the order of 10⁻³. In this section we have used the median for summarizing traits. Since the nullity and identity properties are trivial we focus on the monotonicity and distributivity properties.

For distributivity we perform a simple test of splitting the EP by the gender trait into males and females. We use five trials from Figure 4 (for which both genders are eligible) to demonstrate this. We restrict the eligibility to males and females (referred as mGIST^M and mGIST^F respectively) separately and test how the sum of these mGISTs differ from the overall mGIST. The obtained results are shown in Table 2.

Table 2.

Demonstration of distributivity with gender as the splitting trait. The difference column refers to the quantity mGIST(T)-(mGIST^M (T)+mGIST^F(T)).

	mGIST	mGISTM	mGISTF	Difference
T1	0.648	0.309	0.337	0.002
T2	0.172	0.070	0.102	0.000
T3	0.206	0.065	0.141	0.000
T5	0.083	0.043	0.039	0.001
T6	0.399	0.175	0.225	−0.001

We observe that the sum of the mGISTs for individual genders is not significantly different from the overall mGIST. A Friedman’s test [33] on the respective values of mGIST and mGIST^M+mGIST^F (column 2 and column 3 + column 4 in Table 2) yielded an insignificant p-value of 0.563. Note that distributive law would hold for splitting on any variable (e.g. HbA1C > 8% and HbA1C ≤ 8%), into several groups (e.g. age below 30 years, 30–60 years and over 60 years) as well as across more than one variable (e.g. males over 50 years, males under 50 years, females over 50 years, females under 50 years).

Our evaluation of monotonicity is indirect. Instead of testing containment of eligibility criteria (which is trivial), we extend the idea of monotonicity to ‘wider’ and ‘narrower’ eligibility criteria. We hypothesize that narrow or restrictive eligibility criteria even for a single trait result in a very low value of mGIST. To verify this (for the diabetes trials), we set the eligibility criteria of the trait f_j under consideration to greater than μ_j + 2.5σ_j (Test 1) and then to less than μ_j -2.5σ_j (Test 2). All other traits had no restrictions in eligibility criteria, (and hence have an sGIST of 1) which implied that the mGIST of the hypothetical trial was completely determined by the trait under consideration. Hence, in Table 3 the displayed values are the sGISTs for the particular trait as well as the mGISTs for the hypothetical trials.

Table 3.

Effect of low representation of one trait on mGIST scores

	HbA1C	Gluco.	LDL	HDL	Chol.	Triglyc.	Creatin.	eGFR	Hemog.	Age
Test 1	0.027	0.025	0.011	0.013	0.010	0.024	0.047	0.007	0.004	0.004
Test 2	0.000	0.000	0.001	0.008	0.007	0.000	0.000	0.000	0.001	0.000

As can be seen in Table 3 all tests result in an mGIST score of less than 0.05. Hence a low representation of even one trait degenerates the mGIST of a trial. A closer observation indicates that the scores for Test 2 are significantly lower than the scores of Test 1 for all traits. A Friedman’s test found statistically significant difference between the Test 1 and Test 2 scores (p-value=0.0016). This implies a positive skewness for most of the individual trait distributions.

5. Discussion

In contrast to GIST 1.0, which computes the multiple-trait generalizability by simply aggregating the single-trait generalizabilities, GIST 2.0 explicitly models the trait-dependencies. Moreover, even for a single trait GIST 1.0 is simply a counting measure where every patient is equally weighted. The weighting scheme for the patients introduced in GIST 2.0 minimizes the effects of outliers (in the context of typical dependencies among study traits) as they are associated with lower weights. This also implicitly accounts for the goodness of the hyper-surface fit. In cases of good fits, the outlier patients have a much lower weight (relative to other patients) than in cases of poor fit. The non-linear regression model for trait dependencies is capable of handling both categorical and continuous traits with different significance.

An important issue in the a priori generalizability quantification is when should it be deemed necessary to modify eligibility criteria to improve generalizability. The answer to this is dependent on several study constraints such as patient safety, budget, desired enrollment, etc. The mGIST score could possibly be a decision aid but must be treated with caution. As mentioned above, data incompleteness is invariably an issue in the EHRs (for example, a very common eligibility criterion is informed consent and that is rarely recorded in the EHRs). Hence, the calculated mGIST score is an upper bound that is always greater than the true mGIST score (Corollary 5). This upper bound can still provide valuable information (e.g. a low calculated mGIST definitely points to restrictive eligibility criteria). An investigator must account for the volume of missing data if the mGIST is used for this decision.

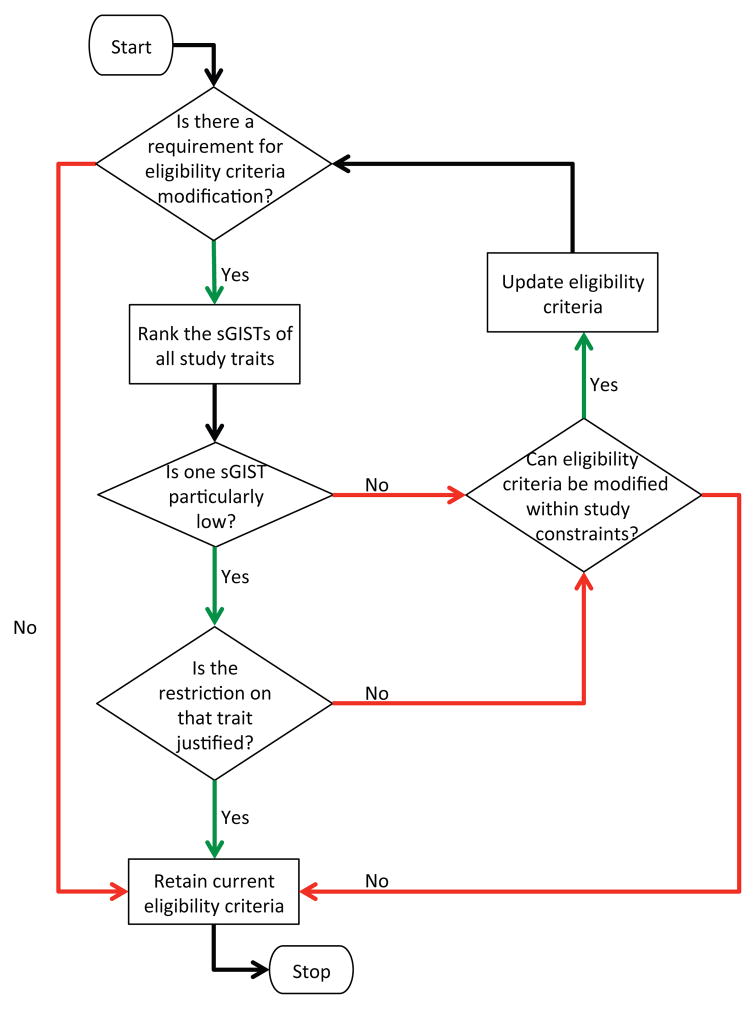
On the other hand, the sGIST scores can be a powerful indicator for guiding the loosening of eligibility criteria. Once it has been determined that modification may be beneficial, the sGISTs of the individual traits are ranked from highest to lowest. Now there may be two cases (1) there is one trait with substantially lower sGIST than all other traits (2) there are two or more traits with low/moderately low sGISTs. In the first case, a clinical investigator has to determine whether such a strong restriction on a particular trait is justified. In the latter case, since the restrictions on individual traits are not that strong, the eligibility criteria may potentially be altered within study constraints to improve generalizability. This workflow of iterative modification of eligibility criteria is shown in Figure 6.

Figure 6.

A flowchart for the use of relative GIST scores for eligibility criteria modification

Two major aspects of clinical research are patient outcomes and subgroup analysis. Patient outcomes include adverse events, all cause mortality, length of hospital stay, etc. It is important to note how generalizability assessment can influence patient outcomes and whether these are consistent with previously published literature. Though not presented here we previously showed how generalizability is related to serious adverse events in sepsis trials [34]. Further development of GIST 2.0 will enable us to study the relation between generalizability and other types of patient outcomes. Subgroup analysis is important in identifying underrepresented populations in clinical studies. The GIST methodology is capable of computing the population representativeness of specific subgroups by restricting the EP to that particular subgroup. Subgroup analysis with GIST 2.0 remains a part of our future plans.

The rationale behind trait significance for this study was derived from [31], where significance is directly proportional to the stringency of the eligibility criteria. We currently have not verified whether this is the best way to define significance. Another way of defining significance is through expert consensus [35] but such a definition might be highly subjective. We have previously explored the use of trait prevalence within the EP to define significance [34]. While prevalence works well for the traits in the disease defining criteria, it also inflates the significance of traits such as age and gender, which are prevalent in almost all patients.

5.1. Limitations

Our study has certain limitations. It is debatable how well the EP can approximate the TP. Certain subgroups may be underrepresented in the EP such as patients with a minor form of the disease, patients who cannot afford healthcare due to socio-economic constraints, patients who are unaware of the disease being present, etc. It has previously been shown that the EP is younger [5] (due to higher number of medical records of recent patients) and sicker [36].

Our methodology for defining the EP required at least one reading of all disease-specific traits to be present in the EHRs. However, such a pre-conditioning may introduce biases within the EP. Imputation and interpolation are possible ways for dealing with patients with missing traits. Further, EPs are inherently local. Therefore, in the future we plan to use bigger and wider data sets, which encompass a far greater variety of patients. In addition, we plan to use the OHDSI Common Data Model to standardize our algorithm for GIST 2.0 and make it portable across EHR datasets.

Larger data sets will also enable more fine-grained definitions of the EP such as by procedure (e.g. colorectal surgery [37]), medications (e.g. chronic use of prescription medication [38]) or clinical trial interventions already in the market (e.g. all phase four trials). Due to its relatively smaller size, one institution’s EHR data is often limited in defining such EPs with adequate sample size. For example [39] requires an EP of diabetic patients undergoing dialysis but our 30,000-patient EHR data has just four such patients (<0.1% of its size).

Though our methodology for GIST 2.0 can handle categorical variables, in this study the main focus was on continuous lab values and gender was the only categorical variable. Typically clinical studies contain several eligibility conditions that are categorical. In future studies we plan to use more complex categorical variables such as medication, therapies, procedures, etc.

The eligibility-driven generalizability as defined here, depends only on the traits that are part of the eligibility criteria and not on several latent traits that may be clinically relevant. This raises the question ‘how can we use a generalizability metric to account for differences among latent variables?’ In some cases these differences may be supremely important, while in others they may be unimportant. Evidence appraisers can help us estimate the boundaries and confidence for this, but ultimately we require empirical validation so that the latent variable differences do not matter (via outcome tracking, replications in previously unstudied populations, or implementations that include unstudied populations). This lack of knowledge about latent variables can cause the SP to be very different from the EP and the TP.

6. Conclusions

We have introduced a metric GIST 2.0 for evaluating the eligibility-driven generalizability of a clinical trial during the design phase of the trial. We have provided rigorous mathematical proofs for the properties of GIST 2.0 and validated them with simulation-based experiments. We plan on further development and evaluation of this metric and present it in a user-friendly interface to engage stakeholder-driven clinical research design optimization in the near future.

Highlights.

1. An a priori generalizability metric GIST 2.0 for individual trials is proposed

2. GIST 2.0 indicates relative restrictiveness of clinical eligibility criteria

3. The dependencies and significance of traits are explicitly modeled

4. GIST 2.0 is evaluated on twenty trials and the scores are statistically analyzed

5. GIST 2.0 is validated with set-theoretic analysis and simulations

Abbreviations

GIST

Generalizability Index for Study Traits

EHR

Electronic Health Record

TP

Target Population

EP

EHR Population

SP

Study Population

SS

Study Sample

sGIST

Single-trait GIST

mGIST

Multiple-trait GIST

T2DM

Type 2 Diabetes Mellitus

IDA

Iron Deficiency Anemia

HbA1C

Glycated Hemoglobin

ANOVA

Analysis of Variance