The Role of Local Ancestry Adjustment in Association Studies Using Admixed Populations

Abstract

Association analysis using admixed populations imposes challenges and opportunities for disease mapping. By developing some explicit results for the variance of an allele of interest conditional on either local or global ancestry and by simulation of recently admixed genomes we evaluate power and false-positive rates under a variety of scenarios concerning linkage disequilibrium (LD) and the presence of unmeasured variants. Pairwise LD patterns were compared between admixed and nonadmixed populations using the HapMap phase 3 data. Based on the above, we showed that as follows:

1. For causal variants with similar effect size in all populations, power is generally higher in a study using admixed population than using nonadmixed population, especially for highly differentiated SNPs. This gain of power is achieved with adjustment of global ancestry, which completely removes any cross-chromosome inflation of type I error rates, and addresses much of the intrachromosome inflation.

2. If reliably estimated, adjusting for local ancestry precisely recovers the localization that could have been achieved in a stratified analysis of source populations. Improved localization is most evident for highly differentiated SNPs; however, the advantage of higher power is lost on exactly the same differentiated SNPs.

3. In the real admixed populations such as African Americans and Latinos, the expansion of LD is not as dramatic as in our simulation.

4. While adjustment for global ancestry is required prior to announcing a novel association seen in an admixed population, local ancestry adjustment may best be regarded as a localization tool not strictly required for discovery purposes.

Introduction

Major racial groups in the world originated because of continental-scale geographical separation. Allele frequencies diverged as a result of genetic drift and natural selection under different environmental pressures. Starting generally from genome-wide association studies (GWAS) in European-originated populations, collaborative efforts have been made to evaluate phenotypic associations using non-European populations [Matise et al., 2011]. The motivation for expanding the population diversity for association studies includes: (1) Evaluation of the generalizability of risk variants of complex diseases in all populations. (2) Better mapping and localization of the true variants by leveraging the varied linkage disequilibrium (LD) across different populations. For (1), association studies have revealed that the significance of risk variants can vary profoundly in different populations [Ioannidis et al., 2004]. Many association signals originally found in European-based studies failed to replicate in other non-European populations [Waters et al., 2009; Yamada et al., 2009] and vice versa; for example populations with African ancestry harbor prostate cancer risk variants at 8q24 with notably higher frequencies compared to other populations [Haiman et al., 2007]. Possible explanations for these observed disparities include altered frequency of causal variants due to genetic drift combined with varying LD between marker and causal alleles, or different environmental/genetic modifiers that amplify the effects of the causal variants in certain populations more than in others. The full scope of risk variants across populations is a fundamental piece of knowledge about human disease, and requires more detailed investigations in diverse populations. Focusing on solely one population may ignore associations with SNPs that are common overall, but rare in certain individual populations, and misleadingly highlight some population-specific ones. For (2), the philosophy is that, as different populations drifted from the original common ancestry of all human beings at different historical time points, accumulated recombination would produce LD that varies in length and boundaries across populations, and working with multiple populations could hopefully narrow down the signal over the risk region, by leveraging the variation of LD in different populations [Franceschini et al., 2012; Haiman et al., 2007; Morris, 2011; Udler et al., 2009].

A key requirement for success in exploring multiple populations in an association study is attending to population heterogeneity. Many modern populations especially in the New World have undergone admixture during the past several hundred years. Within the United States the largest admixed populations are African-Americans and Latinos. Individuals self-identified to belong to the same racial population could have very different ancestral origins. Among groups of self-identified African-Americans, average proportions of European ancestry vary from 3.5% to 22.5%, and within population differences are much greater [Chen et al., 2010; Parra et al., 1998, 2001]. Latinos living in the United States are believed to have derived from three major ancestral populations: European, Native American, and Africans, with the contribution of each group varying according to the region of residency [Hanis et al., 1991].

The study of admixed populations allow for analyses that can not always be performed within homogeneous groups, even when data for more than one such group is present. For example, several SNPs related to skin pigmentation have different alleles fixed or nearly fixed in Northern European (HapMap CEU) vs. sub-Saharan African (as in HapMap YRI) populations [Beleza et al., 2013; Sturm, 2009]. Since these SNPs do not vary within the ancestral populations, it requires either a historically or recently admixed population to detect their relationship to skin pigmentation.

Recent admixture can be exploited to identify candidate regions of the genome that are likely to contain variants involved in disease susceptibility. Admixture mapping searches for regions of the genome where ancestral population origin with the higher disease prevalence is present with higher proportion in diseased individuals [Chakraborty and Weiss, 1988; Freedman et al., 2006; Kopp et al., 2008; Manichaikul et al., 2012; Stephens et al., 1994]. This analysis can be done with a relatively small panel of ancestry-informative SNPs, but the regions identified tend to be large in extent compared to GWAS, which provides more definitive localization.

In GWAS with multiethnic and admixed populations, one should be aware of the issues raised by “population stratification.” Spurious association occurs for SNPs with different allele frequencies in the mixing subpopulations, when disease risk also differs by population. Even if two SNPs are in perfect linkage equilibrium in both ancestral populations, as long as their allele frequencies are different in two subpopulations, linkage disequilibrium will be created as the two populations admix [Chakraborty and Weiss, 1988], we term this as admixture-induced LD (ALD) here after. With recombination taking place every generation, the genome of an admixed individual is a mosaic consisting of chromosomal segments with different ancestral origins. In a recently admixed population, the fraction of ancestry from each population varies across each individual, which is termed variation in global ancestry. For a single person, the proportions of ancestries vary across the genome, which is termed variation in local ancestry.

Motivated by the advantages and challenges of using multiethnic, and admixed populations for GWAS studies, discussions aiming to find optimal association tests abound. In terms of controlling of type I error inflated with population stratification, a basic but useful practice is genomic control [Devlin and Roeder, 1999]. Price et al. suggested estimating and then adjusting for top principal components [Price et al., 2006], because the top eigenvectors are shown to be effective in capturing the demographic uniqueness of a population. The above two are accepted as standard practice nowadays, but Qin et al. argued that in direct SNP association test, adjusting only for global population structure is insufficient when local population stratification is the dominating confounder, and suggested the calculation and correction of local principal components in such cases [Qin et al., 2010]. Wang et al. made similar points but suggested adjusting for estimated local ancestry, instead of local principal components [Wang et al., 2011]. Another direction of active efforts is to increase power by unifying admixture mapping and single variant association tests. Tang et al. proposed that the signals from admixture mapping and single SNP associations provide independent information and could complement each other, and suggested a joint test under a family design [Tang et al., 2010]. Two joint tests (MIXSCORE) were developed in the context of case/control GWAS study, and a gain of power was reported [Pasaniuc et al., 2011]. A Bayesian method (BMIX) has also been proposed [Shriner et al., 2011].

When the causal variants are not directly typed, the effects of surrogate markers might vary across populations due to heterogeneity of LD. Liu et al. proposed to include local ancestry and an interaction term in logistic regression model, which may increase power when LD varies greatly between mixing populations [Liu et al., 2013].

Despite the interest in local ancestry and in the correct use of admixed populations in GWAS, the type I error and power of these proposed methods were only evaluated in the original papers with individually different and sometimes oversimplified simulations. The lack of consistency in the evaluation measures and results has lead to conflicting advice to the researchers needing to choose the strategies to deal with admixed populations in GWAS practice. Here, we attempt to discuss the following basic questions:

1. Can an admixed population provide good power for association tests relative to studies within an ancestral population, or combinations of ancestral populations?

2. Should correction for local ancestry be generally required when evaluating statistical significance found in studies using admixed populations?

3. How much power for localization is lost due to admixture, and can mapping be improved by using local ancestry adjustment?

To answer the above questions, we started with deriving the conditional variances of candidate allele counts in association strategies being discussed, and showed in simulation that the conditional variance largely determines power. Further, we simulated simple but illustrative admixture processes and a polygenic disease model to evaluate the false-positive rate. The advantage of our simulation over many of the others is that (1) the global and local ancestry was fully known, so the bias introduced by ancestry inference was avoided; (2) the contribution from global or local ancestry to disease risk in the admixed population was a result of risk allele differentiation, rather than an effect assigned arbitrarily as in some other simulations [Qin et al., 2010; Wang et al., 2011]; (3) the disease risk differentiation could be due to an overall differentiation of the polygene, instead of due to one single causal variant only; (4) null SNPs could be in LD with causal SNPs, which enables us to compare type I error in a more practical sense, and to visualize association signals in a genome-wide scan. Finally, we investigated the pairwise SNP correlation patterns in actual admixed and nonadmixed populations using HapMap Phase III data, to inspect the real extent of LD expansion in major admixed populations, as a reference when addressing the necessity of adjusting for local ancestry in actual practice.

Methods

Theoretical Derivations

Notation

Without loss of generality, we consider a simple but illustrative two-way admixture model. Suppose there are two ancestral populations in which the risk of the polygenic disease of interest differs, and the allele frequency of a candidate SNP in each population is p₁ and p₂, respectively; and a new admixed population derives from these two ancestral populations with an initial proportion a of population 1 and 1-a of population 2 and K generations of subsequent random mating. For each admixed offspring, the proportion of his/her ancestors originating from ancestral subpopulation 1 is termed “global ancestry” or G here after. For each SNP of each admixed offspring, the number of alleles (0, 1, or 2) originating from ancestral population 1 is termed “local ancestry” or L. The allele count of the candidate SNP is termed as M.

Under the above setting, the probability distribution of G and L can be readily written down as:

$$\mathrm{Pr}(G=g)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill g\times n\hfill \end{array}\right)a^{g\times n}(1-a{)}^{(1-g)\times n};$$ (1)

$$\mathrm{Pr}(L=l\mid G=g)=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill l\hfill \end{array}\right)g^l(1-g{)}^{2-l};$$ (2)

where n = 2^K is the number of ancestors of an admixed individual.

For purposes of comparison, we also consider a study using stratified ancestral populations. Suppose there is a stratified population with proportion a from ancestral population 1 and 1-a from ancestral population 2. We term the subpopulation indicator of each individual that will later be used for stratified analysis as P, which follows a simple binomial distribution:

$$\mathrm{Pr}(P=p)=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill p\hfill \end{array}\right)a^p(1-a{)}^{1-p}.$$

Conditional Variance of the Candidate SNP Allele Count Given Certain Population Stratification Controlling Variables

Global and local ancestry for analysis of an admixed population, and subpopulation indicator for analysis of a combined ancestral population are possible covariates to control for population stratification, and we inspect the variance of the candidate allele count conditioning on each of these covariates, which, for studies of a constant sample size, largely determines the power to detect the effect of the candidate SNP when using an adjusted Armitage test.

Some derivations (details shown in Appendix) reveal that:

$$\begin{array}{cc}\hfill E\left(\mathit{Var}\right(M\mid G\left)\right)=& 2{\mathit{ap}}_1(1-p_1)+2(1-a)p_2(1-p_2)\hfill \\ \hfill & +(p_1-p_2{)}^2\times 2a(1-a)\left(1-\frac{1}{n}\right);\hfill \end{array}$$

$$\begin{array}{cc}\hfill E\left(\mathit{Var}\right(M\mid P\left)\right)& =E\left(\mathit{Var}\right(M\mid L\left)\right)=E\left(\mathit{Var}\right(M\mid L,G\left)\right)\hfill \\ \hfill & =2{\mathit{ap}}_1(1-p_1)+2(1-a)p_2(1-p_2);\hfill \end{array}$$

Note that $E\left(\mathit{Var}\right(M\mid G\left)\right)-E\left(\mathit{Var}\right(M\mid L\left)\right)=(p_1-p_2{)}^2\times 2a(1-a\left)\right(1-\frac{1}{n})\ge 0$, so the conditional variance of candidate SNP allele count could be ordered as follows: $E\left(\mathit{Var}\right(M\mid G\left)\right)\ge E\left(\mathit{Var}\right(M\mid G,L\left)\right)=E\left(\mathit{Var}\right(M\mid L\left)\right)=E\left(\mathit{Var}\right(M\mid P\left)\right)$. The first equality holds only when p₁ = p₂, and the difference of expected variance is a function of (p₁ – p₂)², so it increase as the difference of allele frequencies in two ancestral populations gets larger.

Impact on Power

For a continuous trait Y, the noncentrality parameter for detecting the effect of a variable X in the presence of a control variable C equals: $\frac{{\beta }^2}{{\sigma }_{Y\mid X,C}^2}N\mathit{Var}(X\mid C)$, where $\mathit{Var}(X\mid C)=(1-R_{X,C}^2)\times \mathit{Var}\left(X\right)$. Assuming that X explains only a modest proportion of the variance of Y, so that σ_Y|X,C² is almost equal to the variance of Y given only C we can see that the noncentrality parameter and hence power is determined by Var(X|C). For a binary outcome we consider the Armitage test, which is equivalent to the score test of logistic regression. While it is not as easy to derive a closed-form expression of the noncentrality parameter we find in simulations that the concept for linear regression largely generalizes to logistic regression and the power of detecting the effect of a risk allele increases with its expected conditional variance. An additional consideration for logistic regression is that greater variance of omitted covariates (e.g., other elements in polygene) leads to greater bias toward the null [Neuhaus and Jewell, 1993], which would reduce power under alternative hypothesis. This is discussed more fully below.

Power

Let Y_i denote the disease status of each individual, W_i denote the score of polygene (i.e., the weighted sum of risk alleles of all causal SNPs M_is of each individual), and assuming that risk of polygenic disease can be modeled as

$$\mathrm{logit}\left(E\right(\mathit{Yi}\left)\right)=\alpha +W_i,i=1,2,\dots ,N\text{for each individual};$$

$$\text{where},W_i=\sum _{s=1}^S{\beta }_s\times M_{\mathit{is}},s=1,2,\dots ,S\text{for each causal}\mathrm{SNP}.$$

We are interested in evaluating the power (and type I error) of detecting the effect of any single M_is, in association studies using an admixed population with global ancestry adjustment (referred to as Adx|G here after), or with local ancestry adjustment (Adx|L), in comparison with stratified analysis of combined ancestral populations (Anc|P).

Single Causal Variant

We started with a very simple model of single causal variant disease, with disease model parameters specified as S = 1, α = log (0.1), β_s = 0.3∀s. Allele frequencies of the causal variant in two ancestral populations were arbitrarily assigned for comparison purposes (sets of frequencies: 0.01 vs. 0.99, 0.01 vs. 0.5, 0.5 vs. 0.5, and 0.3 vs. 0.7 were used). A combined ancestral population was simulated by sampling a number of subjects from subpopulation 1 and subpopulation 2, respectively, with the prespecified proportion a. The genotype of the causal variant in each subject was sampled according to the conditional probabilities, given local and global ancestry, as described in the Appendix. An admixed population after five generations with original admixture proportion a was simulated by sampling global ancestries, local ancestries, and genotypes according to the probabilities listed in Theoretical Derivation and Appendix.

Multiple Causal Variants (Polygenic Disease)

We next investigated whether the result of the single variant disease could be generalized to polygenic disease, by simulating another 100 causal variants in addition to the causal variant of interest. The allele frequency of the causal variant of interest is assigned arbitrarily as before, and the allele frequencies of the other 100 variants in two ancestral populations were generated following Balding–Nichols model [Balding and Nichols, 1995] with Fst set to 0.2. Disease model was specified with parameters S = 101, α = log(10⁻¹³), β_s = 0.3∀s (the very small α was assigned because only a vanishingly small proportion of individuals will carry no risk alleles at all). We assumed the causal variants are independent of each other, and the genotypes were again sampled according to the probabilities listed in Theoretical Derivation and Appendix.

Power Evaluation

Disease statuses in the stratified ancestral population and admixed population were assigned according to same pre-specified disease models. For each replication 1,000 case-control pairs were sampled, and Armitage tests were performed using the sampled subjects. χ² statistics were averaged over 1,000 replicates.

Positive Rate

Simulation of Ancestral Genomes With LD

Two established populations with Fst of 0.2 were generated following Balding–Nichol’s model [Balding and Nichols, 1995]. The allele frequencies (vector p) of SNPs of an original population ancestral to all modern populations were drawn i.i.d. from uniform [0.1, 0.9]. Then, the allele frequencies of population 1 and 2 were each drawn from a Beta($\frac{p(1-F_{\mathit{st}})}{F_{\mathit{st}}}$, $\frac{(1-p)(1-F_{\mathit{st}})}{F_{\mathit{st}}}$) distribution. Two scenarios of ancestral LD were simulated (i) without, and (ii) with, ancestral LD between the SNPs used for the association study: For (i), the allele counts on a single chromosome was generated as independent Bernoulli random variables with expectations equal to corresponding allele frequencies. For (ii), the correlated Bernoulli variables were simulated through the following procedure:

1. M (number of SNPs on each chromosome) multivariate normal variables Vs were simulated, such that V₁,V₂, …, V_M ~ N (0,Σ), where Σ = (ρ_{j k}), ρ_{j k} = exp (− |j – k| · d) ∀j , k.

2. Hs were created as $\{\begin{array}{cc}{H}_j=0,\hfill & \text{if}{V}_j\le {\varphi }^{-1}\left(p_j\right)\hfill \\ H_j=1,\hfill & \text{if}{V}_j>{\varphi }^{-1}\left(p_j\right)\hfill \end{array}\phantom{\}}$.

So that the each vector of H consists of binary counts with E(H_j) = p_j and $\mathit{corr}(H_j,H_k)=\frac{\left(\varphi \right[z\left(p_j\right),z\left(p_k\right),{\rho }_{jk}]-p_j{p}_k)}{\sqrt{p_j{p}_k{q}_j{q}_k}}$, which make up allele counts on a single chromosome. Each chromosome was generated independently, and then allele counts on two chromosomes were collapsed to genotypes. Two ancestral populations were simulated respectively.

For the purpose of our discussion, we simulated both sparsely typed SNPs and densely typed SNPs. For sparsely typed SNPs, genomes of the ancestral populations were simulated as 22 autosomes with 500 SNPs on each chromosome. SNPs were simulated to be moderately correlated by setting d = 0.3 in ρ_{j k} = exp (− |j − k| · d), and the pairwise correlation R² dies off below 0.36 within about 1–2 SNPs. For the densely typed SNPs, two chromosomes with 10,000 SNPs on each chromosome were simulated; d = 0.01 was used to make the pairwise correlation R² die off below 0.36 within about 30 SNPs.

Simulation of Admixture Process and Disease Status

A simple admixture process was simulated for each scenario we have described above. Two established ancestral populations were mixed with equal proportions to form one mixing population. Then a simulation of random mating was implemented within this mixing population: In each generation we forced one recombination between each pair of parental chromosomes at a randomly selected position. This is a simplification of the fact that at least one crossover takes place as the chiasmata is formed in meiosis [Creighton and McClintock, 1931]. To illustrate a scenario of very recent admixture, only two generations of random mating were performed. Offspring of this admixture process makes up the simulated admixed population. To ensure comparability between the ancestral and admixed populations, the random mating process was also implemented respectively within the two original populations, and resulted in a slight reduction in ancestral LD. Subjects from these two nonadmixed populations were sampled with equal proportion to make up the combined ancestral population.

In each set of simulated genomes, a set of SNPs were randomly sampled and made causal to constitute the polygene. To focus on situations where the disease risks are at least moderately differentiated between ancestral populations, a paired t-test of the polygene allele frequencies in the two ancestral populations were performed and we refrained from proceeding unless the p value was less than 0.10. Two patterns of polygene locations were simulated: (i) Many causal SNPs spread randomly across the genome. (ii) Causal SNPs clustered around a few causal loci. For (i), causal SNPs were selected by simple random sampling, for (ii), centers of causal loci were selected by simple random sampling, and then two SNPs on each side were made causal.

We selected 100 causal SNPs from 22 chromosomes of the sparsely typed SNPs; and 10 causal SNPs from one chromosome of the densely typed SNPs. Case/control status of each individual was assigned as a binary outcome according to the disease model described above with β = 0.3. Then 750 cases and 750 controls from each ancestral population, and 1,500 cases and 1,500 controls from the admixed population were selected by simple random sampling.

False Positive Rate and Significance Rate

False positive rates were calculated over 500 replicates as the proportion of simulations in which a noncausal SNP was claimed significant falsely with P ≤ 0.05 without Bonferroni adjustment.

Armitage Trend χ² Test and Adjusted Armitage Test

The association between a given SNP and the disease of interest was calculated using the Armitage trend χ² test [Armitage, 1955]. This test is equivalent to score test of logistic regression, and the statistic χ² was calculated as the Pearson squared correlation between the genotype of this SNP and the disease status, multiplied by N, the number of samples.

To adjust for a variable (such as G, L, or P) in the association tests, we performed linear regression of disease status and the SNP genotype, respectively, on the adjusted variable, and retained the residuals of the disease status and genotype. Then the statistic χ² of an adjusted Armitage trend test was calculated as the Pearson squared correlation between the two residuals, multiplied by (N-k-1), where N was the number of samples, k the number of variables adjusted. This is a generalization of Armitage test for discrete phenotype and genotypes, based on the idea that to test for the partial correlation of two vectors is equivalent to test correlation between their projections in a space with reduced dimension [Price et al., 2006].

Pairwise Correlation Patterns of Real GWAS Data

The Armitage trend test statistic is proportional to the Pearson R² correlation coefficient between marker and case-control status. Therefore for any other adjacent marker SNP with a correlation R² with a causal locus with a large noncentrality parameter T (if we test the locus directly), the noncentrality parameter is approximately T × R². So in a region with an unobserved causal variant, the strength of association signals we would detect is a function of the Pearson correlation between that variant and nearby SNPs residing within that region.

We used HapMap phase III data to evaluate the pairwise R² correlation pattern in continental and admixed populations. We randomly selected 100 subjects from the founders in American Europeans (CEU), Western Africans (YRI), and East Asian (pooled CHB and JPT, referred to as ASN here after), respectively. The pairwise Pearson R² between SNPs was calculated for the 11,485 common SNPs (MAF > 0.05 in all populations) on chromosome 21. Similarly, 48 subjects (the available size of MEX panel) were sampled from African Americans (ASW), and Latinos (MEX), respectively, and the pairwise Pearson R² between SNPs was calculated for the 12,099 common SNPs (MAF > 0.05 in all populations) on chromosome 21.

The global ancestry of the admixed population ASW and MEX was estimated as top principal components, local ancestry of ASW was estimated by program LAMP [Sankararaman et al., 2008]. Partial correlations conditioning on G or L were calculated to investigate the LD pattern after adjustment of G or L.

By examining the distributions of pairwise R² correlation in the HapMap continental panels (CEU, YRI, and ASN), we found the 99-percentile cutoff is 0.36. Thus we define a SNP that correlates with a causal variant with R² ≥ 0.36 as a surrogate of this variant, and therefore the surrogates of a causal variant correspond to the top 1 percent strongest signals we would detect in a well-powered association test scanning for this causal variant.

One SNP (not necessarily differentiated between ancestries) was randomly sampled to be the causal variant, and its surrogates within 7.5 Mb neighboring region (on each side) were identified. The number of surrogates, and the distance between the farthest surrogate and the variant of interest were recorded; empirical distributions were generated over 1,000 independent samplings. The causal variants were stratified by their allele frequency difference in ancestral populations, which refer to CEU and YRI for ASW, CEU, and ASN for MEX.

The pairwise correlations and partial correlations were also calculated for the simulated data with densely typed SNPs. To make the pattern in simulated data comparable to that in HapMap data, we assigned a constant interval of 1.8 Kb between SNPs in simulated data, so that the correlations die off below 0.36 in roughly 55 Kb, as in HapMap CEU panel.

Results

Power

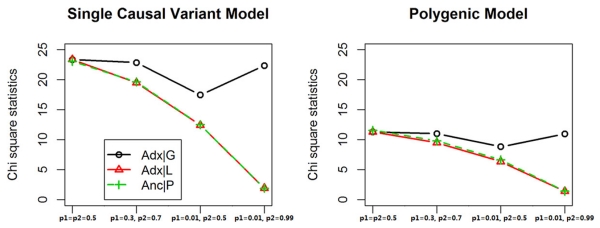
A major motivation of this paper is to understand whether using an admixed population for an association study is at least as powerful as using its ancestral populations, and a quick answer is that using admixed populations with adjustment of global ancestry could yield even higher power. As shown in Tables 1 and 2, and illustrated in Figure 1, it is evident that as long as the allele frequency of a causal variant differs between ancestral populations Adx|G yields higher power than Anc|P or Adx|L with the difference in power dependent on the difference in allele frequency.

Table 1. Mean χ² statistics for single variant association tests.

Pop1: Pop2 = 1:1	Anc|P	Adx	Adx|G	Adx|L
p1 = 0.01, p2 = 0.99	1.914	23.706	22.372	1.941
p1 = 0.5, p2 = 0.5	23.070	23.374	23.373	23.374
p1 = 0.01, p2 = 0.5	12.505	17.784	17.472	12.433
p1 = 0.3, p2 = 0.7	19.652	23.078	22.867	19.518

Pop1: Pop2 = 1:4	Anc|P	Adx	Adx|G	Adx|L
p1 = 0.01, p2 = 0.99	1.796	16.074	15.214	1.887
p1 = 0.5, p2 = 0.5	23.978	22.995	23.005	23.011
p1 = 0.01, p2 = 0.5	6.217	9.786	9.563	6.421
p1 = 0.3, p2 = 0.7	19.483	21.976	21.837	19.680

Single variant disease and polygenic disease were simulated, and the power of association tests we have discussed were evaluated as the χ² statistics averaged over 10,000 replicates. The disease model is specified with S = 1, α = log (0.1) , β_s = 0.3∀s in disease model. Two sets of admixture proportion were simulated.

Table 2. Mean χ² statistics for association tests in polygenic disease.

Pop1: Pop2 = 1:1	Anc|P	Adx	Adx|G	Adx|L
p1 = 0.01, p2 = 0.99	1.4511	9.7939	10.9613	1.4069
p1 = 0.5, p2 = 0.5	11.5825	11.2928	11.3032	11.2938
p1 = 0.01, p2 = 0.5	6.6472	8.0579	8.8355	6.3579
p1 = 0.3, p2 = 0.7	9.8238	10.3922	11.034	9.5108

The disease model is specified with S = 101, α = log(10⁻¹³), β_s = 0.3∀s. Allele frequencies of the candidate variant were arbitrarily assigned as below for comparison. The average allele frequency of the other 100 causal variants is 0.491 and 0.476, respectively, in two ancestral populations.

Figure 1.

Power comparison with adjustment of local or global ancestry. The mean χ² statistics of detecting a causal variant with certain degree of allele frequency differentiation were compared. The left panel shows the power comparison when the disease is caused by this single variant; the right panel shows the power when the disease is polygenic (i.e., other unmeasured causal variants exist).

When the candidate SNP is the only causal variant, power using either Adx|L or Anc|P is very similar (Table 1). However, when a causal polygene is simulated, a subtle but perceptible deficit of power in ADX|L comparing to Anc|P is observed (Table 2). This can be explained by the fact that the conditional variance of the other elements in polygene is larger in Adx|L than Anc|P, which leads to larger bias toward null and interferes with the power of detecting the effect of the candidate SNP [Neuhaus and Jewell, 1993].

It is worth being noted that our comparison is between an admixed population with admixture proportion a, and a stratified analysis of a population consisting of subjects from the two ancestral populations (of the studied admixed population) with the same proportion. For all the three tests we have discussed, the expected conditional variance of a candidate variant is maximized when the proportions subjects deriving from the ancestral populations are equal.

False-Positive Rates

The immediate following goal was to compare the performance of the tests discussed above in terms of controlling spurious association. An oversimplified measure of type I error would be the proportion of times of rejection for a candidate SNP with β = 0. However, in the real practice of disease mapping it is not appropriate to use the very strict definition of false positive because in a sense all GWAS are based on LD instead of complete genotypes. On the other hand, it is also not desirable to detect an association when candidate SNPs and causal SNPs are in very weak LD, such as on two ends of one chromosome or on different chromosomes.

To accommodate this practical consideration, we compared the rate of false positives using the strict definition when applied in the admixed population to when the same definition was applied to a stratified analysis of the combined ancestral populations. The noncausal SNPs were categorized by their proximity to members of the polygene, and the observed positive rates were compared within categories.

As expected (Table 3), the näive test using the admixed population without any adjustment of ancestry information suffers spurious association even for noncausal SNPs physically residing on chromosomes where no causal locus exist. Adx|G sufficiently controls this kind of inflation, no matter whether the SNPs are independent, or in considerable LD in the ancestral populations. For noncausal SNPs that reside on the chromosomes harboring elements of the polygene, Adx|G removes a substantial amount of the spurious associations: the positive rate level is almost identical to Anc|P for SNPs that are distant from the polygene; while for SNPs that are close to the polygene the positive rate level is higher than that in Anc|P, especially when the SNPs are dense. Adx|L always controls the inflation of the null SNPs to the level that is almost identical to Anc|P, even for SNPs in strong LD with the polygene. The result of the Armitage test adjusted for both global and local ancestry were also examined, and the type I error is almost identical to that of Adx|L (data not shown), which is expected since conditioning on global ancestry as well as local ancestry does not further reduce the variance of the candidate allele, as shown in Methods.

Table 3. False-positive rate comparison.

a. Sparse SNPs
	Overall	Close to polygene (d≤5 SNPs)	Far from polygene (d>5 SNPs)	Overall	Close to polygene (d≤10 SNPs)	Far from polygene (d>10 SNPs)	Off-Chr
	Causal variants scattered			Causal variants clustered
				No ancestral LD
Anc | P	0.050	0.050	0.050	0.050	0.050	0.050	0.050
Adx	0.509	0.519	0.508	0.484	0.511	0.485	0.480
Adx | G	0.056	0.059	0.056	0.059	0.082	0.063	0.051
Adx | L	0.051	0.051	0.051	0.052	0.051	0.052	0.051
				Moderat ancestral LD
Anc | P	0.064	0.120	0.052	0.063	0.344	0.053	0.052
Adx	0.567	0.577	0.566	0.482	0.571	0.479	0.477
Adx | G	0.068	0.115	0.058	0.064	0.319	0.054	0.051
Adx | L	0.061	0.107	0.052	0.061	0.311	0.052	0.051

b. Dense SNP with ancestral LD
	Overall	Close to polygene (d≤100 SNPs)	Far from polygene (d>100 SNPs)	Off-Chr
		Causal variants scattered
Anc | P	0.067	0.194	0.056	0.050
Adx	0.339	0.405	0.382	0.292
Adx | G	0.084	0.206	0.097	0.050
Adx | L	0.066	0.183	0.055	0.050
		Causal variants clustered
Anc | P	0.080	0.151	0.099	0.051
Adx	0.269	0.329	0.317	0.220
Adx | G	0.104	0.198	0.147	0.051
Adx| L	0.080	0.157	0.098	0.051

False-positive rate of association tests using admixed population were compared as follow. For the admixed population, un-adjusted Armitage test (ADX), Armitage test adjusted for global ancestry (ADX|G) and for local ancestry (ADX|L). As reference, subpopulation variable was adjusted in the mixed ancestral populations (ANC | P). The noncausal SNPs were categorized by their distance to polygene.

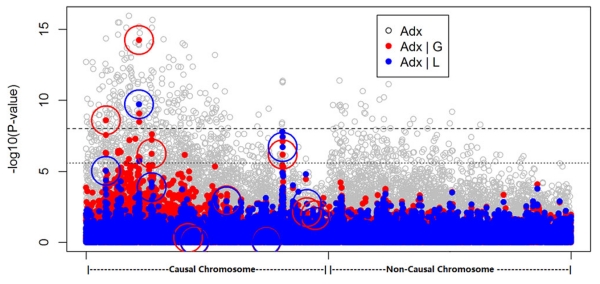
To visualize the trade-off of power and false-positive rates by adjusting for local or global ancestry, we produced a Manhattan plot using one set of simulated association results (Fig. 2). It is seen that the näive test without any adjustment of ancestry suffers severe inflation even on a chromosome that does not harbor any causal variant, while adjustments for global ancestry or local ancestry perform similarly well in getting rid of this kind of gross inflation. Adjusting for global ancestry generally yields more significant results than adjusting for local ancestry, with relatively more inflation on regions immediately proximal to the true causal variants.

Figure 2.

Manhattan plot of simulated association results. The P-values of association tests with adjustment of local or global ancestry was plotted in minus log10 scale. Each test is represented by a red (global ancestry adjustment) or blue (local ancestry adjustment) dot, and circles of corresponding color pinpoint the tests detecting the causal variants. The upper dash line represents the conventional genome-wide significance level of 10⁻⁸, the lower dash line represents the significance level after Bonferroni correction for the number of tests performed (20,000).

Global and Local Ancestry Estimation

The above comparison was performed in the ideal situation that the ancestry attribution of each admixed individuals on each SNP was completely known. In real practice of GWAS using admixed populations, one would need to estimate the global and local ancestry. Based on our simulated data (see Supplementary Fig. S1), we found that as recommended by Price et al. [Price et al., 2006], top PCs capture the variation in global ancestry very well. For local ancestry estimation we found that estimates using LAMP were highly correlated (R² > 0.99) with the true local ancestry of the simulated admixed individuals.

Pairwise SNP Correlation Patterns in Real GWAS Data

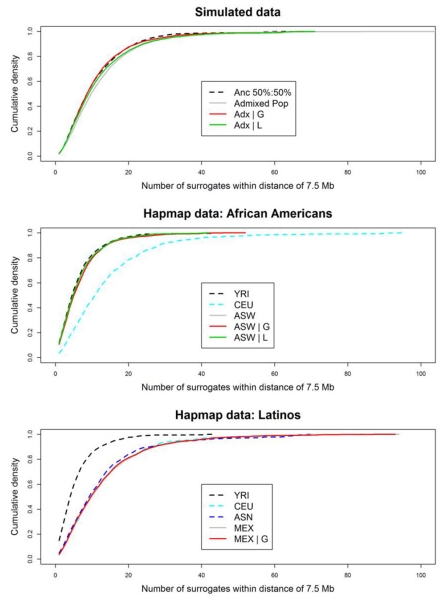
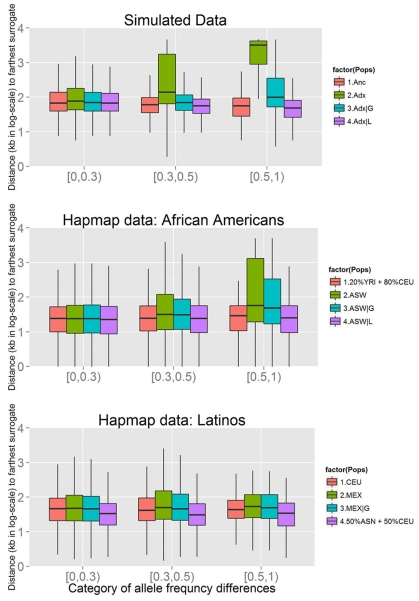
As described in Methods, we define surrogates of a variant as the SNPs that have correlation R² > 0.36 with that given variant. In the HapMap African American panel (ASW), the number of surrogates is not substantially increased when compared to a stratified reference panel (20% ASW + 80% CEU), the medians of both are 5. Conditioning on local ancestry estimation for ASW reduced the median to 4 (Table 4, Fig. 3). The distance to the farthest surrogates is extended in ASW (with median 26.02 Kb), but is still comparable to the reference panel (with median 24.46 Kb). Conditioning on global ancestry reduces the median very slightly to 25.98 Kb, and conditioning on local ancestry reduces the median to 22.95 Kb (Table 4). When the allele frequency for the causal variant differs greatly between CEU and YRI (difference > 0.5), the effect of admixture is more pronounced: surrogates may be more than 1 Mb away for a quarter of all such loci. Conditioning on global ancestry narrowed the signals down by more than 900 Kb, while conditioning on local ancestry almost recovered the signal pattern in the reference panel, which is another 300 Kb narrower than adjusting for global ancestry. For more moderately differentiated variants (difference is within 0.3~0.5), one quarter of the signals could expand 60 Kb away compared to that in the reference panel, conditioning on global ancestry could narrow down the region by 30 Kb, and conditioning on local ancestry further localized the signal by another 30 Kb narrower. For variants that are not differentiated to a noticeable level (difference < 0.3) that consists more than 77% of all the SNPs, the signals expand for less than 10 Kb in ASW, conditioning on either global or local ancestry recovered the signal pattern to that in the reference panel (Fig. 4, Supplementary Table S2). However, the ratio of variances Var(ASW|L)/Var(ASW|G), which is equivalent to the proportionate loss of effective sample size when adjusting for L rather than G, gets larger as the differentiation of allele frequency increases (Supplementary Tables S1, S2). For slightly differentiated causal alleles (differentiation [0, 0.3]) this loss of effective size is quite minor (mean of 2 percent) but large differences (e.g. [0.5, 1]) imply losses of roughly 25 percent and sometimes much more (Supplementary Table S1). Note that a 2 percent loss in effective sample size reduces power from 80 percent to 78 percent (at type I error rate 5 × 10⁻⁸) while a 25 percent reduction in sample size reduces the power from 80 to 50 percent. Put another way, a 25 percent reduction in sample size may be expected to change a P value of 5 × 10⁻⁸ (generally regarded as globally significant in GWAS) to a much less remarkable 2.4 × 10⁻⁶.

Table 4. Quartiles of the number of surrogates, and the distance of the farthest surrogate to the causal variant.

	Number of surrogates			Distance (Kb) to the furthest surrogate
	1st Q	Median	3rd Q	1st Quartile	Median	3rd Quartile
CEU	5	10	18	20.82	45.73	93.35
YRI	2	4	8	8.58	22.99	55.07
ASN	4	9	15	16.62	35.46	71.99
80%YRI + 20% CEU	2	5	10	10.08	24.46	53.34
ASW	2	5	8	9.81	26.02	67.97
ASW | G	2	5	8	9.97	25.98	66.09
ASW | L	2	4	8	8.92	22.95	54.32
50%ASN + 50%CEU	4	8	15	15.58	32.99	65.19
MEX	5	9	17	20.89	47.81	118.3
MEX | G	4	9	16	20.38	45.76	107.6
Sim Anc	4	8	14	37.5	63.75	121.9
Sim Adx	5	9	16	48.75	93.75	991.9
Sim Adx| G	4	8	14	41.25	71.25	138.8
Sim Adx | L	4	9	15	37.5	63.75	110.6

In each population, one SNP was randomly sampled to be the causal variant, and its surrogates (R² > 0.36) were found within 7.5 Mb neighboring region (either side). The distributions were generated based on 1,000 repeats.

Figure 3.

Cumulative density of the number of surrogates. The empirical cumulative densities of the number of surrogates within a neighboring region of 7.5 Mb (on either side) were plotted. The upper panel represents the simulated data, the middle panel African Americans, and lower panel Latinos.

Figure 4.

Distribution of distance from the farthest surrogate to the causal variant. The empirical distributions of the distance from the farthest surrogates to the causal variants were compared using boxplot, stratified by allele frequency difference of the causal variant. The upper panel represents the simulated data, the middle panel African Americans, and lower panel Latinos. Because of the great numerical difference, the y-axis is in log scale. The exact values are listed in Supplementary Table S2.

In the HapMap Mexican panel MEX, due to the lack of reliable local ancestry estimation for Latinos, currently we have not assessed the effect of adjusting for local ancestry in MEX. But we used a reference panel with equal proportion of CEU and ASN (pooled CHB and JPT as described in Methods) to get an idea of the possible association signal span. The number of surrogates in MEX (with median 9) is comparable to that in European panel CEU with median 10 and the mixed panel of CEU and ASN with median 8 (Table 4, Fig. 3). The distance to the farthest signal with median 47.81 Kb is not obviously expanded compared with CEU, in which the distance has median 45.73 Kb; in the mixed panel of CEU and ASN the median is 32.99 Kb. Conditioning on global ancestry estimation reduces the median to 45.76 Kb (Table 4). We should be aware that the LD in the mixed panel used as a reference here is likely shorter than that in the real ancestral populations of MEX since the Native Americans are a younger population than Asian. One quarter of the signals extend over 25 Kb greater than in CEU, and adjusting for global ancestry narrowed the third quartile cut-point to 14 Kb wider than in CEU (Table 4). The expansion of signals is not particularly dramatic for the highly differentiated loci (Fig. 4, Supplementary Table S2). This may in part reflect the poor performance of the ASN reference panel compared to having a true Native American reference.

In contrast, the expansion in simulated data was also examined. The number of surrogates does not increase notably in admixed populations when compared to ancestral populations, and adjusting for global or local ancestry reduced that small increment to the level of the reference panel Anc|P, which is similar with what we have seen in HapMap data (Table 4, Fig. 3). Nevertheless, the regions encompassed by the signals expand tremendously in the admixed populations (with median 93.75 Kb, 3rd quartile cut point 991.0 Kb) compared with that in the reference (with median 63.75 Kb, 3rd quartile cut point 121.9 Kb), conditioning on global ancestry reduced the median to 71.25 Kb, 3rd quartile cut point 138.80 Kb, while conditioning on local ancestry reduced the median to 63.75 Kb, 3rd quartile cut point 110.6 Kb (Table 4). The expansion is prominent in not only largely differentiated loci, but also moderately differentiated ones (Fig. 4, Supplementary Table S2). Comparing this to the HapMap III results implies that ALD in real admixed population is much less expanded than in the very recent admixture that we have simulated.

Discussion

Correction for population stratification is critical for the success of GWAS using admixed populations. We showed via theoretical derivation and simulations that adjusting for global ancestry provides higher power to discover associations than adjusting for local ancestry. Correcting for local ancestry improves localization with the trade off of power loss for discovery. Examination of HapMap III ASW and MEX data reveals that the gain of localization by adjusting for local ancestry is expected to be moderate in practice except for the most highly differentiated alleles, where the power loss is also the greatest. While we have focused mainly on analysis of case-control data in our simulations, our results also apply to analysis of continuous phenotype data under the assumptions given in the Methods section. We have simulated a model in which disease risk differs between populations due only to genetic factors (i.e., the differentiation of genes related to disease). It is worth noting that if there are environmental factors that differ between ancestral populations that contribute to the disease risk, the cultural inheritance pattern of these environmental factors in an admixed population is far more likely to be related to global ancestry than to local ancestry at a particular SNP. In such a case, adjusting for local ancestry will not help improve the statistical behavior of the association tests used in evaluating the effect of the candidate SNP.

Assuming constant effect (the β parameter above) across populations, the expected variance of a candidate SNP allele count in admixed population is larger than that in a single or combined ancestral population, even allowing for global ancestry adjustment (shown in Theoretical Derivation). This is an advantage of association studies using admixed population, which improves power in detecting differentiated variants, and especially benefit variants with different alleles nearly fixed in different populations, compared to the study carried on either one ancestral population, or a combination of them. It should be emphasized that the gain of power is only achieved in Adx|G; if Adx|L is used, the power drops to the level that is similar to Anc|P.

Adx|L and Anc|P yields the same power when the candidate SNP is the only causal variant, which is expected given that the conditional variances of the candidate allele counts are equal in the two tests. However, when there is an unmeasured polygene, the power yielded by Adx|L is slightly but consistently lower than Anc|P. This can be explained by the fact that the conditional variance of the other elements in the polygene is larger in Adx|L than in Anc|P. That is if we condition on the local ancestry of the candidate variant this reduces the variance of that candidate to the value in the stratified analysis, however this conditioning does not affect the variance of other causal variants, since their local ancestry is largely independent of that of the candidate variant. On the other hand in the stratified analysis all the other causal variants for an individual have the same ancestry and hence have smaller variance in Anc|P compared to Adx|L (since L refers only to the local ancestry of the candidate variant). Neuhaus et al has shown that omitting causal covariates in logistic regression leads to bias towards the null, and the attenuation of main effect estimate gets larger as the variation of omitted covariate increase [Neuhaus and Jewell, 1993].

We have simulated a very simple model of admixture (the hybrid isolation model HI) for illustrative purposes. This model is unrealistic compared to the gradual admixture (GA) or continuous gene flow (CGF) models as a description of the history of modern-day admixed populations. One of the most important differences between HI, GA, and CGF is in the distribution of the lengths of chromosomal segments of distinct ancestry (CSDAs) [Jin et al., 2012]. After the same number of generations of mixing, HI generally yields relatively shorter CSDAs than CGF, or GA. However, note that we have only simulated two generations of admixture, which will lead to much longer CSDAs than if the admixture had occurred over several hundred years as in African Americans or Latinos. Our simulation is clearly more extreme with larger and less variable lengths of CDSAs than is the reality for most populations and hence we have simulated an extreme amount of ALD; this is also clear from the data, presented in Table 4, of the extent of ALD in the HapMap data compared to our simulated data. The basic principle that the expected variance of the allele of interest (which determines power) is greater after correcting for global ancestry than for local ancestry still holds for these other admixture models. There is a dependence of the expected variance E(Var(M|G)), of the allele count, M, given global ancestry G, on the distribution of G. (In our simulation the distribution of G is binomial with index n while the other models would lead to mixtures of binomial random variables with varying indices.) Crudely speaking, E(Var(M|G)) will decline (but will remain larger than E(Var(M|L)) as the variance of G increases. Because we have simulated only two generations of HI admixture we are using quite a large variance of G in our calculations, therefore in real populations where the variance of global ancestry G is likely to be considerably less than in our simulations, the loss of power in correcting for local rather than global ancestry is actually somewhat greater than we have simulated.

By increasing population diversity in association studies, the populations with shorter LD, such as Africans, can help to narrow down the signals, compared to using populations with longer LD, such as Europeans. When an admixed population is used, there is a concern that extended ALD would counter balance this benefit, or even produce spurious associations on regions that are unlinked with disease. On the other hand, the causal variants are usually not directly geno-typed in practice, and we actually depend on LD between neighboring SNPs and true variants to map the disease. The simulation results revealed that adjusting for global ancestry alone was sufficient to remove inflation induced by admixture on the noncausal chromosomes, as well as greatly reduce type I error rates for regions distant from a causal variant on the same chromosome. On regions that are close to causal variants, Adx|L yields relatively fewer inflated signals compared to Adx|G so that adjusting for local ancestry can improve localization. As described above however better localization by using local ancestry adjustment comes with a loss of discovery power specifically for SNPs that are highly differentiated. For situations where adjusting for local ancestry could truly improve signal localization, the challenge lies in the accurate local ancestry inference. Methods of local ancestry estimation developed for the purpose of admixture mapping (e.g., ANCESTRYMAP [Patterson et al., 2004], ADMIXMAP [Hoggart et al., 2004], ADMIXPROGRAM [Zhu et al., 2004], and MALDsoft [Montana and Pritchard, 2004]) use ancestry informative markers to track the ancestry variation across genome. LAMP [Sankararaman et al., 2008] and WINPOP [Pasaniuc et al., 2009] incorporated unlinked GWAS chip genotypes. SABER [Tang et al., 2006] accounted for ancestral LD and allowed denser SNPs. HAPMIX [Price et al., 2009] and HAPAA [Sundquist et al., 2008] employed phased haplotypes, which largely improved the accuracy at the price of considerable computational complexity. The current methods are reported to be relatively successful only in African Americans, who have a clear genetic background that could be modeled as a combination of African and European ancestry. For Latinos, due to the complex admixture history and the lack of reliable genotype data of ancient Native Americans, it is difficult to explicitly define their ancestral populations, and the inferences are more susceptible to miss-call bias [Seldin et al., 2011]. Noticeably larger than expected Mendelian error rates in local ancestry estimation of Latinos were reported by evaluating the most popular current methods [Pasaniuc et al., 2013].

Global ancestry could be inferred by program STRUCTURE [Pritchard et al., 2000], or estimated as the average of local ancestries across genome, which is highly correlated with true global ancestry based on our preliminary results. Another widely used approach to correct for global population stratification is adjusting for top principal components [Price et al., 2006]. Our preliminary data showed that adjusting for either top PCs or true global ancestry results in similar association signals.

The assumption of constant effect is commonly made but not always guaranteed. Population variation in effect sizes could be due to modification by other variants or by environmental exposures that vary in frequency by ethnicity. Modeling interaction in secondary follow-up could potentially reveal such variants, as has been shown by Liu et al. [Liu et al., 2013]. However, if the inconsistent effect is merely due to LD heterogeneity, increasing the SNP density could resolve the issue.

Owing to their relatively clear genetic background the best known findings of admixture mapping, such as 6q21 for hypertension [Zhu et al., 2005], 8q24 for prostate cancer [Freedman et al., 2006], and MYH9 for focal segmental glomerulosclerosis [Kopp et al., 2008] have been obtained in studies of African Americans. Furthermore, GWAS analysis using African Americans has identified many risk variants for a wide range of disease [Adeyemo et al., 2009; Lettre et al., 2011]. Compared with reference panel of 80%YRI and 20% CEU, obvious LD expansion was observed in the HapMap III data for highly differentiated SNPs; adjusting for global ancestry narrows down the signal by more than 900 Kb and adjusting for local ancestry further narrows the signals by another 300 Kb to a level comparable to reference panel. But it is noteworthy that in most cases the LD sizes in ASW are actually still lower than CEU even without any ancestry adjustment.

The inadequacies of current algorithms make the discussion about local ancestry correction in Latinos an impractical one for now. In Hapmap III MEX data, a very slight association expansion was observed compared to CEU; and the expansion is not particularly more dramatic in variants with allele frequency that differ between European and Asian populations. Adjusting for global ancestry generally narrows down the associations to a region very close to that in CEU. In GWAS practice, many reported studies have shown that global ancestry adjustment is useful in controlling for population stratification in Latinos [Graff et al., 2013; Manichaikul et al., 2012; Waters et al., 2009].

Taking these factors into consideration, it seems to us that it is efficient and practical to scan the genomes of admixed individuals with global ancestry adjustment first, in order to discover causal loci with highest power. If multiple association peaks abound over a relatively large region, a follow-up analysis of this region with local ancestry adjustment could hopefully help in localizing causal variants by eliminating ALD. On the other hand if an association originally implicated using global ancestry adjustment no longer remains significant after local ancestry adjustment it may be unreasonable to discard it as spurious. A more advised interpretation is that the underlying causal variants may be highly differentiated across populations, leading to power loss when adjusting for local ancestry. While adjustment for global ancestry is required prior to announcing a novel association seen in an admixed population, local ancestry adjustment may best be regarded as a localization tool not strictly required for discovery purposes.

Appendix

In combined ancestral population, conditional variation of candidate SNP allele count given P

With the relationship between P and M described as in Method, we could list the conditional probabilities of observing a certain number of allele counts.

Pr(P = p)	p = 0 1−a	p = 1 a
Pr(M = m | P = p)
m = 0	(1 − p2)2	(1 − p1)2
m = 1	2p2 (1 − p2)	2p1 (1 − p1)
m = 2	p22	p12
E(M | P = p)	2p2	2p1
Var(M | P = p)	2p2 (1 − p2)	2p1 (1 − p1)

With the above table, we could easily calculate the expected conditional variation

$$E\left(\mathit{Var}\right(M\mid P\left)\right)=\sum _{p=0,1}\mathit{Var}(M\mid P=p)\times \mathrm{Pr}(P=p).$$

Plugging the Pr (P = p) into E (Var (M|P)) will get the expressions in Method.

In admixed population, conditional variation of candidate SNP allele count, given G or L

With the relationship between G, L, and M described as in Method, we could list the conditional probabilities of observing a certain number of allele counts.

Pr(L = l | G = g)	l = 0 (1 − g)2	l = 1 2g(1 – g)	l = 2 g2
Pr(M = m | L = l)
m = 0	(1 – p2)2	(1 − p1)(1 − p2)	(1 − p1)2
m = 1	2p2(1 − p2)	p1(1 − p2 ) + p2 (1 − p1)	2p1(1 − p1)
m = 2	p22	p1p2	p12
E(M | L = l)	2p2	p1 + p2	2p1
Var(M | L = l)	2p2(1 − p2)	p1(1 − p1 ) + p2 (1 − p2)	2p1(1 − p1)

With the above table, we could calculate

$$\begin{array}{cc}\hfill E(M\mid G=g)& =\sum _{l=0,1,2}E(M\mid L=l)\times \mathrm{Pr}(L=l\mid G=g)=2p_2\hfill \\ \hfill & (1-g)+2p_{1}g\hfill \end{array}$$

$$\begin{array}{cc}\hfill E(M^2\mid G=g)& =\sum _{l=0,1,2}E(M^2\mid L=l)\times \mathrm{Pr}(L=l\mid G=g)\hfill \\ \hfill & =2p_2(1+p_2)(1-g{)}^2+2(p_1+p_2+2p_1{p}_2)\hfill \\ \hfill & (1-g)g+2p_1(1+p_1)g^2\hfill \end{array}$$

therefore,

$$\begin{array}{cc}\hfill \mathit{Var}(M\mid G=g)& =E(M^2\mid G=g)-E^2(M\mid G=g)\hfill \\ \hfill & =2p_2(1-p_2)(1-g{)}^2+2(p_1+p_2-2p_1{p}_2)\hfill \\ \hfill & (1-g)g+2p_1(1-p_1)g^2.\hfill \end{array}$$

With the above elements, the expected conditional variation could be calculated through

$$E\left(\mathit{Var}\right(M\mid L\left)\right)=\sum _{l=0,1,2}\mathit{Var}(M\mid L=l)\times \mathrm{Pr}(L=l);$$

$$E\left(\mathit{Var}\right(M\mid G\left)\right)=\sum _{g=0,\frac{1}{n},\dots ,1}\mathit{Var}(M\mid G=g)\times \mathrm{Pr}(G=g).$$

$$\text{Where}\mathrm{Pr}(L=l)=\sum _{g=0,\frac{1}{n},\dots ,1}\mathrm{Pr}(L=l\mid G=g)\times \mathrm{Pr}(G=g)$$

and a little work could show that

$$\mathrm{Pr}(L=0)=(1-a{)}^2+a(1-a)∕2^K;$$

$$\mathrm{Pr}(L=1)=2a(1-a)+2a(1-a)∕2^K;$$

$$\mathrm{Pr}(L=2)=a^2+a(1-a)∕2^K.$$

Plugging the Pr (L = l) or Pr (G = g) into E (Var (M|L))orE (Var (M|G)), and with some basic algebra and a bit bookkeeping, one will get the expressions in Method.