Abstract
A new method is presented to denoise 1-D experimental signals using wavelet transforms. Although the state-of- the-art wavelet denoising methods perform better than other denoising methods, they are not very effective for experimental signals. Unlike images and other signals, experimental signals in chemical and biophysical applications for example, are less tolerant to signal distortion and under-denoising caused by the standard wavelet denoising methods. The new method 1) provides a method to select the number of decomposition levels to denoise, 2) uses a new formula to calculate noise thresholds that does not require noise estimation, 3) uses separate noise thresholds for positive and negative wavelet coefficients, 4) applies denoising to the Approximation component, and 5) allows the flexibility to adjust the noise thresholds. The new method is applied to continuous wave electron spin resonance (cw-ESR) spectra and it is found that it increases the signal-to-noise ratio (SNR) by more than 32 dB without distorting the signal, whereas standard denoising methods improve the SNR by less than 10 dB and with some distortion. Also, its computation time is more than 6 times faster.
Index Terms: Wavelet Transform, Wavelet Denoising, Noise Thresholding, Noise Reduction, Magnetic Resonance Spectroscopy
I. Introduction
Experimental signals are often difficult to study because weak signals have a low Signal-to-Noise Ratio (SNR). Based on the discrete wavelet transform (DWT), various wavelet denoising methods like wavelet shrinkage [1]–[16], wavelet coefficient modeling [17]–[20], and wavelet transform modulus maxima (WTMM) [21]–[23] denoising methods have been developed and shown to be more effective than filtering methods [24], [25].
Although denoising increases SNR, many experimentalists are skeptical of the denoised signal as they fear inadequate noise removal and/or unknown signal distortion. More importantly, the current wavelet-based denoising methods are not very reliable in accurately retrieving the signal components, especially for weak signals that have magnitude close to noise. Also, these methods try to eliminate random noise and are not tested against systematic (or coherent) noise generated by the instrument or (e.g. biological) sample. Another problem with current wavelet denoising methods is their practical implementation. They do not provide information regarding the choice of wavelets to use, the number of decomposition levels to denoise, nor do they have the flexibility to adjust the thresholds. A noisy signal clearly indicates its degree of uncertainty, whereas a denoised signal lacks such information. Therefore, to reduce noise, signal averaging [26] is widely used to improve experimental data. In this paper, experimental data from electron spin resonance (ESR) spectroscopy [27] is used, where signal averaging is currently the most reliable method to reduce noise. Although some signal denoising methods like filtering [28] and the traditional wavelet denoising [29] methods have been applied to ESR spectra [30], they have not yet yielded the desired results.
In this paper, a new wavelet denoising approach is presented which is based on wavelet shrinkage, that significantly improves denoising and provides clearer implementation compared to previous methods. It can be reliably used for denoising experimental signals. The paper is organized as follows. First, a brief description of the wavelet shrinkage method is provided. Second, the issues of estimating the choice of wavelets and accurately selecting decomposition levels to denoise are discussed. Third, the new denoising method is presented. Fourth, examples of denoising using experimental results from ESR spectroscopy are presented and compared with other wavelet shrinkage denoising methods. Finally, brief comments are given on the findings and future extensions.
II. Wavelet Shrinkage Denoising Method
Wavelet shrinkage methods provide effective signal denoising with minimum computational complexity. In the wavelet domain, the signal is coherent and has concentrated “energy” residing in just a few high magnitude coefficients, whereas incoherent noise is represented by a large number of coefficients with small magnitudes. This sparsity of wavelet coefficients representing the signal is exploited by wavelet shrinkage methods to separate noise from signal coefficients. Figure 1 displays a block diagram of the denoising process. Algorithm 1 summarizes the wavelet shrinkage denoising method.
Fig. 1.
Block Diagram of a Standard Wavelet Shrinkage Method.
The noise threshold for the selected Detail components is obtained either using the universal threshold [31] , or decomposition level dependent thresholds [32] or [33], where Nj is the length of the jth Detail component, and is an estimate of noise level [31]–[33]. However, state-of-the-art level-dependent noise threshold selection methods like Stein’s Unbiased Risk Estimate (SURE) threshold [34], [35] and Minmax threshold [31] are more widely used for their better performance.
Algorithm 1.
Wavelet Shrinkage Denoising
|
Thresholding functions are then applied to remove noise using noise thresholds. Hard and soft thresholding are the most common thresholding techniques defined in equations 1 and 2, respectively:
| (1) |
| (2) |
where wj,i and are noisy and denoised wavelet coefficients, respectively, at the jth decomposition level and the ith location of the Detail component and j ≤ k. Hard thresholding is better suited when a Detail wavelet coefficient is either a signal or a noise coefficient. On the other hand, soft thresholding performs better when a Detail wavelet coefficient contains both signal and noise. There are other thresholding functions in the literature that can also be used; for example, see [9], [36]–[39].
A. Limitations of Current Shrinkage Methods
The choice of k, the number of decomposition levels to be denoised, is arbritary.
The choice of greatly influences the noise threshold λ, but there is no definitive way to estimate the noise value . Although widely used, different noise estimates yield different noise thresholds [31], [32], [35].
Assuming white gaussian noise (WGN), a single noise threshold is selected and applied to the magnitudes of both the negative and positive Detail coefficients. Other noise such as Poisson noise, Rician noise, and coherent noise are not considered for positive or negative bias in noise. Even for WGN, the assumption of no distribution bias is often flawed as will be discussed in section III.
The methods used result in fixed thresholds that are not adjusted. Flexiblity in adjusting thresholds enables users to reach accurate or optimal thresholds for signals, especially when the wavelet coefficients of weak signals are close to the maximum magnitude of noise.
Apart from the above reasons, the current denoising methods do not emphasize the choice of wavelets that is necessary to create sparsity, and separate noise and signal in the Detail components. One possible reason is that these methods are mostly applied in image processing applications which already use customized wavelets.
III. Noise in Wavelet Domain
It is assumed that random WGN translates into random WGN in the wavelet domain. Ideally, random white gaussian noise with zero mean should be symmetric with no overall positive and negative bias, and the magnitude of minimum and maximum values should be approximately the same. Note that the minimum is the largest magnitude among negative coefficient values (max(|wj,i < 0|)). To test this noise behavior in the wavelet domain, simulations were run in MATLAB using the following steps:
Generate random WGN with zero mean, call it X, and length N.
Take the full scale DWT of X that results in ⌊log2(N)⌋ Detail components.
Calculate the skewness of each Detail component. The skewness is a parameter that measures positive or negative bias in a distribution with respect to the mean. For WGN (i.e. normal distribution), the skewness should be zero.
Find the magnitude of minimum and maximum value of each Detail Component.
-
Calculate the percentage difference between the magnitude of minimum and maximum value with respect to the minimum value between them, i.e.
The percentage values should be close to zero as the magnitude of minimum and maximum values would be expected to be almost the same.
The following are the simulation parameters:
Number of Simulations: 1000–5000.
Noise Length N: 1024–4096.
Wavelet Families: Coiflet, Daubechises, and Symlet.
Findings:
The wavelet coefficient distribution for each Detail component has either positive or negative bias. The positive and negative bias is not correlated amongst successive Detail components.
There is a substantial difference between the magnitude of minimum and maximum values, and it increases monotonically from decomposition level 1 to M. For decomposition level 1, it is already more than 10 percent.
We believe that this behavior is due to the finite nature of discrete values and the DWT. There seems to be no correlation between the choice of wavelet and the distribution bias. Experimental signals do not necessarily have simple WGN; their noise content is liable to be more complex and may have inherent positive or negative bias.
IV. Wavelet Bases
It is difficult to apply the DWT without selecting an appropriate choice of wavelets. In general, standard wavelets that resemble the signal or its properties yield better signal and noise separation as well as sparsity. For example, we found that the coiflet wavelet family is better suited for cw-ESR spectra, compared to other wavelet families such as daubechies and symlets. However, a trial and error method to select the appropriate wavelet can be tedious and challenging in finding an appropriate wavelet. We recommend developing customized wavelets corresponding to the signal properties. For example, cw-ESR spectra are typically represented as blends of functions of Gaussian and Lorentzian functions [27], and hence, a specific wavelet could be designed and used for such spectra.
To effectively eliminate noise from signal coefficients, the wavelets should be designed to satisfy the following conditions:
| (3) |
| (4) |
The above conditions eliminate the need for thresholding methods (like soft-thresholding) that assume a wavelet cofficient as a sum of signal and noise coefficient, i.e. . In other words, either or .
V. New Denoising Method
The new denoising method applies the wavelet shrinkage approach with the following novel features:
The decomposition levels to denoise can be determined by the user through visual inspection of the Detail and Approximation components as described below. Alternatively, an objective measure to select the k decomposition levels is provided.
Then a new noise threshold selection formula is presented that allows the user automatic adjustment of the noise thresholds. Such noise thresholds do not require the use of a noise estimation formula.
Two distinct noise thresholds are used in the thresholding function for negative and positive wavelet coefficients, respectively.
The kth Approximation component is noise thresholded along with the k Detail Components.
These features are discussed below. Figure 2 illustrates the new denoising method.
Fig. 2.
Block Diagram of the New Method.
A. Decomposition Level Selection
Selecting decomposition levels to denoise is a major challenge to which current methods do not provide guidance. Generally decomposition levels between 2–5 are arbitrarily selected without first examining the Detail components. A poor choice can result either in signal under-denoising or distortion, similar to that caused by poor noise thresholding. For experimental signals, this can lead to misleading analysis because the accuracy of denoising cannot be verified for every signal. A subjective and an objective method are provided to select the decomposition level k.
1) Subjective Method
As all the Detail components and their corresponding Approximation components are correlated, visually observing all the components can easily allow one to select the correct decomposition level. In the new method, the user determines the Detail components to be denoised with the help of visual correlation. An easy way is to select decomposition levels until one is reached in which noise is almost indistinguishable. The location and magnitude of signal and noise in the wavelet component are also useful sources of information, especially for identifying systematic noise. In all the Detail components, signals occur in the same locations with large magnitudes, whereas random noise appears inconsistently with small magnitudes, and systematic noise usually occurs at a specific location with low magnitude. The amount of noise present in the Detail components reduces from decomposition level 1 to decomposition level M because noise ususally contains more high frequencies than low frequencies. For very low SNR, initial decomposition levels like 1 and 2 may contain just noise, whereas for very high SNR, the last decomposition levels may only contain signal. Through Figure 3, decomposition level selection is illustrated by an example from ESR. Examining the figure, one can see that the Detail components at decomposition levels 1–5 contain varying amount of noise, whereas the noise (low frequency) from decomposition level 6 is extremely small and indisguishable. The noise at and above decomposition level 6 is represented in the Approximation component at decomposition level 5. Hence, the decomposition level k = 5 can be confidently selected.
Fig. 3.
All the Detail and Approximation components of a cw-ESR spectrum. DL is the decomposition level. After examining the figure, k = 5 can be confidently selected.
After selecting decomposition level k, k Detail components and the kth Approximation component are noise thresholded as shown in Figure 2. Coupled with noise thresholding, the decomposition level selection process also acts as a feedback for optimal thresholds and correct denoising by allowing visual comparison between the thresholded and non-thresholded wavelet components. Based on the feedback, the κj,L and κj,H values (discussed below) can be adjusted to desired thresholds. The standard state-of-the-art wavelet shrinkage methods do not exploit the correlation amongst wavelet components nor use this approach. They use non-adjustable thresholds which are optimized only for random Gaussian noise.
This subjective method is useful when a single set of experimental data needs to be denoised. It provides control to the experimentalist in selecting the decomposition levels as well as insights about the signal observed for analysis.
2) Objective Method
The objective measure of selecting k is more appropriate for real time denoising and where extensive experimental data needs to be denoised. To obtain the decomposition levels for noise thresholding, first calculate the “peak-to-sum ratio” (Sj ) of the Detail components,
| (5) |
Sj reflects the sparsity of a Detail component and allows the identification of noise presence in a Detail component. A large Sj implies signal presence with only a few large coefficient values, whereas a small Sj reveals noise presence with a large number of small coefficient values.
Now the determination of the decomposition levels 1, 2, 3, …, k to noise threshold is described with reference to the four categories:
Detail components that only contain noise coefficients (see DL1 in Figure 3), Sj ≤ 0.01.
Detail components that mainly contain noise with very few high magnitude signal coefficients (see DL2 and DL3 in Figure 3), 0.01 < Sj ≤ 0.1.
Detail components dominated by signal coefficients with noise coefficients having small magnitudes (see DL4 and DL5 in Figure 3), 0.1 < Sj ≤ Tr.
Detail components that only contain signal coefficients, i.e. noise is no longer distinguishable (see DL6 – DL10 in Figure 3), Sj > Tr.
Here Tr is a criterion to distinguish between the Detail components of types 3 and 4 having some noise and almost no noise. Therefore, k = j where Sj ≤ Tr and Sj+1 > Tr. We find that the choice of Tr ≈ 0.2 leads to an effective criterion between cases 3 and 4 (More generally, 0 ≤ Tr < 1 given that Sj of equation 5 is limited by 0 ≤ Sj < 1). Note that the Detail components in the above-mentioned categories occur in sequential order (see Figure 3). Depending on the noise level in a signal, the initial Detail component categories may or may not be present.
B. Threshold Selection
Wavelet shrinkage denoising depends greatly on the noise threshold value because a poor choice of threshold can result in unremoved noise or distorted signal. The presence of signal and noise coefficients in a Detail component may not result in a symmetric distribution of coefficients and zero mean. The coefficients of signal, systematic noise, and other nonsymmetric noise, like Poisson noise, can create positive or negative bias in the Detail component and result in nonzero mean. Even random Gaussian noise is likely to have coefficient distribution bias due to the Detail components’ discretization and finite length as was noted in section III. In fact, it was found that symmetric Gaussian noise with zero mean has substantial differences in magnitudes of minimum and maximum noise values in the discrete wavelet domain, and the difference increases with the decomposition level (cf. section III).
Therefore, one selects two noise thresholds (λL and λH) in the following way,
| (6) |
| (7) |
where λj,L and λj,H are the lower and upper thresholds at decomposition level j; κj,L and κj,H are adjustable parameters for each threshold; and μj and σj are the mean and standard deviation, respectively, of the wavelet component at decomposition level j, and are defined here as,
| (8) |
| (9) |
The two noise thresholds in equations 6 and 7 do not require the calculation of the noise level in a Detail component. They use the mean (μj ) and standard deviation (σj ) of the jth Detail component, which includes both signal and noise coefficients, and κj,L and κj,H are used to accurately scale σj in eliminating noise coefficients. Also, the two thresholds include the mean value μj, and do not assume it to be zero.
To obtain appropriate κ values, we first find the minimum values of κj,L and κj,H that cover the all the coefficients in the jth Detail component. Substituting minimum (peak negative value) and maximum (peak positive) values of the Detail component in equations 6 and 7, respectively, one can express them as:
| (10) |
| (11) |
Since all the decomposition levels j (1 ≤ j ≤ k) where Sj ≤ 0.01 (i.e., case 1) contain only noise coefficients, for these cases we can set κj,L = κj,Lmin and κj,H = κj,Hmin. In other words, all the coefficients of the Detail component are assigned zero.
For all the decomposition levels j (1 ≤ j ≤ k) where 0.01 < Sj < Tr (i.e., cases 2 and 3), both signal and noise coefficients are present. Knowing that the magnitude of a noise coefficient is less than that of the signal coefficients (cf. equations 3 and 4), κj,L < κj,Lmin and κj,H < κj,Hmin. One then obtains κj,L and κj,H from κj,Lmin and κj,Hmin using the peak positive and negative coefficient values in the following way,
| (12) |
| (13) |
where Sr,L and Sr,H are the reference peak-to-sum coefficient values and are defined as and . Sj,L and Sj,H are the peak-to-sum ratios of the negative and positive coefficient values, respectively. They are calculated from equation 5 as,
| (14) |
| (15) |
By separating the wavelet coefficients at a decomposition level into two groups, one having negative values and other having positive values, the number of coefficient values as well as their sum in each category is reduced. However, the peak value remains at a similar level. In other words, one expects max(|wj < 0|) ≈ max(|wj ≥ 0|), and one of them is in fact max(|wj |), whereas and are both less than their sum . Thus Sj,L; Sj,H > Sj. Instead of manually selecting the kappa values, it is found that equations 12 and 13 accurately estimate the required κj,L and κj,H values.
The Detail components at decomposition levels j > k (i.e., Sj > Tr) are not noise thresholded as they contain only signal coefficients or signal and indistinguishable low frequency noise coefficients.
Although κj,L and κj,H will optimally select the noise thresholds, they may require minor adjustment by user intervention for the following three exceptions:
Even for Sj ≥ 0.01, a Detail component can have only noise coefficients due to one or more large random noise spikes. In this case, κj,H = κj,Hmin and κj,H = κj,Hmin, instead of equation 12 and 13.
In a noise-dominated Detail component, either positive or negative coefficients are all noise, requiring readjustment κj,H = κj,Hmin or κj,H = κj,Hmin, respectively.
When small signal and large noise coefficient values are comparable, κj,L and/or κj,H may require a slight increase or decrease in their values to separate signal and noise coefficients.
C. Thresholding Function
This new approach to denoise the signal uses hard thresholding coupled with the above noise threshold selection method. Unlike other thresholding techniques, hard thresholding ensures that the signal wavelet coefficients are not distorted by the noise thresholds, especially when signal and noise coefficients are disjoint and not superimposed. With appropriate wavelet selection, the noise present at a signal location is separated in the initial decomposition levels and is removed using noise thresholding. Hard thresholding is now carried out in the following way,
| (16) |
wj,i is the ith Detail coefficient at jth decomposition level, is the thresholded wavelet coefficient, and λj,L and λj,H are the two noise thresholds obtained from equations 6 and 7. The above equation is a generalized form of the hard thresholding function shown in equation 1. If κj,L = κj,H and μ = 0, then |λj,L| = |λj,H | = λj, and equation 16 becomes equation 1.
D. Denoising the Approximation Component
Current wavelet shrinkage methods do not denoise the Approximation component because the noise thresholding relies on sparsity of wavelet coefficients for estimating noise and selecting thresholds. Experimental signals often contain substantial low frequency noise, especially at low SNR, that impedes analysis. The Detail components that represent low frequency noise are non-sparse, restricting the effectiveness of noise thresholding. However, the Approximation component can also contain low frequency noise. Thus, it would be desirable to remove the Approximation component’s low frequency noise. Depending on the signal properties and the choice of wavelet, the kth Approximation component can represent low frequency noise and signal coefficients in a relatively sparse manner. The signal coefficients will have larger values than the noise coefficients. This new approach denoises the kth Approximation component to eliminate low frequency noise. Similar to the Detail components, the noise thresholds for the Approximation component is selected using the Approximation coefficients in equations 6 and 7, where κ values are obtained from equations 12 and 13. The thresholding function in equation 16 is then applied to remove the noise. This is shown in the block diagram of Figure 2.
VI. ESR Experiments and Results
A. ESR Methodology and Sample Preparation
Most of the ESR experiments were performed at 20°C on a commercial spectrometer (BRUKER ELEXYS-II E500) at a standard microwave frequency of 9.4 GHz (X-band) corresponding to a dc magnetic field of 0.34 Tesla (cf. Figs. 3–8). These results are referred to as example 1. In these experiments the microwave frequency is held constant, while the magnetic field is swept through resonance to obtain the ESR spectrum [27]. The sample consisted of 4 μL of a 100 μM aqueous solution of the commonly used spin-probe molecule Tempol (4-Hydroxy-2,2,6,6-Tetramethylpiperidine 1-oxyl) [27], [40]–[43]. It was placed in a glass capillary of 0.8 mm ID, which was then introduced into the microwave cavity situated between the pole caps of the dc magnet. The magnetic field was then swept over a range of 60 G corresponding to the resonant spectral range which took 2 minutes, and a 82 ms time constant was used. The spectral data consisted of 4096 points along the magnetic-field sweep. In addition, small coils placed at the sides of the resonator provided a small magnetic field modulation of ±0.02 G at a frequency of 100 kHz. The 100 kHz modulated ESR signal was detected with a lock-in detector at this frequency, providing the first derivative of the absorption signal [27], [44]. Low power (0.2 mW) microwave radiation was used to avoid saturating the ESR signal. Multiscan experiments were performed with a delay of 4 s between scans. The results of these scans were then averaged. The ESR spectrum in Figure 3 was obtained under very similar conditions, also for the Tempol spin-probe.
Fig. 8.
Example 1: Comparison of New Method with Denoising methods [9], [37]–[39] other than soft and hard thresholding at 16 scans.
In example 2, an ESR spectrum (Figure 9) was obtained under different conditions to provide a more complex spectrum for denoising. It was obtained on a home-built (ACERT) 95 GHz ESR spectrometer [43] with a dc magnetic field of 3.3 Tesla at 25°C. The sample here contained ca. 5 μL of phospholipid vesicles doped with 0.5% of a lipid spin label: 16-PC (1-acyl-2-[16-(4,4-dimethyloxazolidine-N-oxyl) stearoyl]-sn-glycero-3-phosphocholine) in the fluid phase that had been suspended in water. It was placed in a disc-like sample holder utilized for millimeter-wave ESR methodology [43], [45]. The acquisition parameters were: sweep width of 250 G, sweep time of 2 min with a time constant of 100 ms. The millimeter-wave power was 16 mW and the spectrum consists of 512 points. The field modulation parameters were: 6 G modulation amplitude and 100 kHz modulation frequency. The spectrum in Figure 9 is the average of 100 scans. The time between scans was 3 s.
Fig. 9.
Example 2: Comparison of New Method with other standard denoising methods. The cw-ESR spectrum was obtained from a sample of a nitroxidelabeled lipid in lipid vesicles.
B. Experiment
These experimental cw-ESR spectra were used to test and compare the denoising methods. By averaging different numbers of scans, different SNRs were obtained. In the case of typical cw-ESR spectra, such as those in Figures 3–9, they have regions with zero signal, aiding in the estimation of noise. The noise in these experiments is predominantly random Gaussian noise, as is typical in ESR. Hence, the cw-ESR spectra reveal the effectiveness of denoising methods at places where the signal is present as well as absent. In Figure 4 two noisy spectra from a single sample are shown, but at different SNRs obtained by signal averaging 4 and 16 scans, respectively. As a reference, the signal averaged over 500 scans is used for comparison with the denoised signals. The SNR was calculated as,
Fig. 4.
Example 1: New Method Denoising results at 16 and 4 scans, respectively. The cw-ESR spectrum was obtained from a sample of the nitroxide spin probe tempol in a 0.1 mM solution in water [47]. The signal amplitude is in arbitrary units (a.u.) and the abscissa is in Gauss.
| (17) |
or in decibels (dB)
| (18) |
where rms is the root mean square. The SNR measures both distorting (i.e., structural) and non-distorting (i.e., nonstructural) noise in the signal, but it cannot differentiate between them. Usually, the structural fidelity of the noisy or denoised signal with respect to a reference signal can be visually observed. Of course, the retention of signal structure is important. Apart from visually observing and comparing the noisy or denoised signal with a reference signal, an objective measure, the structure similarity index measure (SSIM) [46] was used. It enabled the estimation of the structural similarity or fidelity of the noisy and of the denoised signals at 4 and 16 scans with respect to the reference 500 scan signal. The SSIM is calculated as,
| (19) |
where X is either the noisy or denoised signal; Y is the reference signal; μX and μY are the mean values of X and Y, respectively; σX and σY are the standard deviation values of X and Y, respectively; σXY is the covariance of X and Y; and c1 and c2 are small positive constants used for stabilizing each term. The SSIM value ranges within [−1, 1], and achieves 1 when X is identical to Y (SSIM(X, Y ) = SSIM(X,X) = SSIM(Y, Y) = 1). The more that X structurally resembles Y, the SSIM value will be closer to 1. MATLAB was used to calculate the SSIM.
An ESR spectrum is frequently composed of Lorentzian and Gaussian functions, or mixtures of both. The examples of Figures 3–8 are simple Lorentzians, whereas that of Figure 9 is more complex. If the cw-ESR spectra match the wavelets, the denoising can be extremely effective. Thus, we used coiflet 3 as the wavelet because it best resembles the spectra. Other coiflets and wavelets such as daubechies and symlet did not perform as well as coiflet 3.
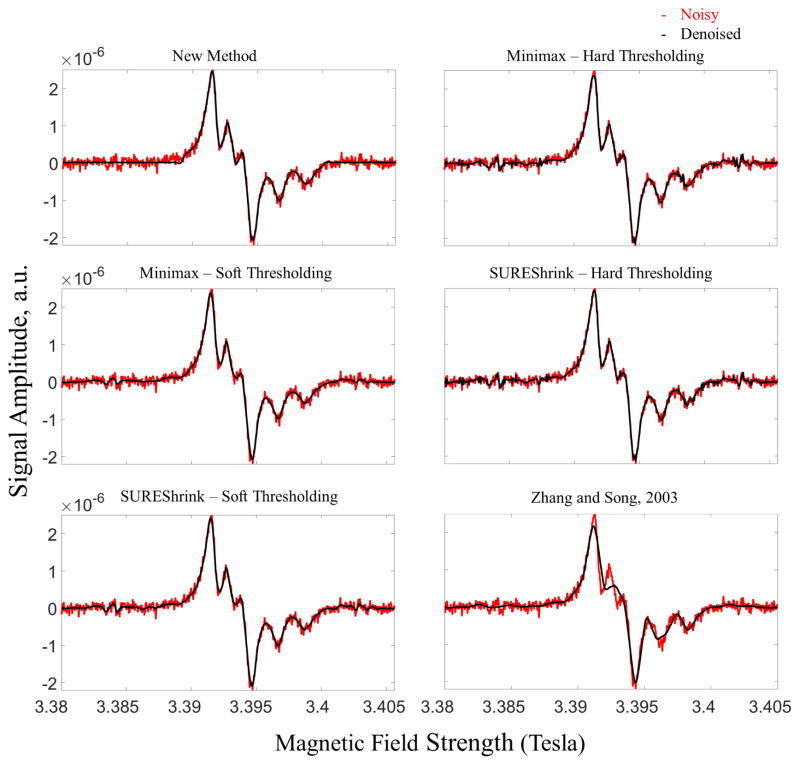
The new method is compared with the standard SUREShrink and Minimax methods [29], [31] using both hard and soft thresholding as well as other wavelet denoising methods. We used the two different examples (Figures 5–8 and Figure 9) to show and compare the denoised results. The SUREShrink and Minimax methods are the optimized hybrid scale dependent threshold selection schemes in the current literature [24], [48], whereas other newer methods [9], [37]–[39] use a thresholding function other than hard and soft in an effort to obtain better denoising. Filtering methods are not compared with the new method because standard wavelet denoising methods perform better than them as shown in ESR [30] and in general [24], [25]. The decomposition level k that yields maximum SNR compared to other decomposition levels is selected for the standard denoising methods. In the new method, Tr = 0.20 was used for all the examples. We have extensively tested (both experimental and model data sets) this value of Tr as the criterion for noise thresholding and find it succeeds in virtually all cases.
Fig. 5.
Experimental Data Example 1: Comparison of New Method with Minimax and SUREShrink Denoising at 4 scans.
C. Results
In example 1 (cf. Figures 3–8), the denoised spectra by the new method at 16 and 4 scans in Figure 4 are shown overlapped with the noisy and reference spectra for comparison and analysis. As can be seen, the new method successfully recovers the signal peaks and removes the baseline noise. Also, the new method retrieves the small satellite peaks (adjacent to large peaks) that were submerged in noise. Comparing the spectra of 16 and 4 scans, the denoised 16 scan spectrum recovers the satellite peaks more accurately than the 4 scan denoised spectrum, as expected. In Figures 5–8 the new method is compared with the denoised spectra of other denoising methods.
Similarly in example 2 (see Figure 9), the new method effectively removes the baseline noise and is better able to retrieve the peaks compared to other denoising methods. Note that the results of non-soft and non-hard thresholding function methods [9], [37]–[39] were similar for example 2, and hence, only Zhang and Song’s method [39] is shown. As can be seen, the current state-of-the-art methods are either not very effective at removing baseline noise and/or they distort the signal peak heights.
Tables I and II show the SNR of the original noisy and denoised spectra, along with decomposition levels selected for noise thresholding. In example 1, it can be seen that the new method doubles the SNR (in dB) from the noisy spectrum and is more than 20 dB greater than other denoising methods. In example 2, which is a more complex but much broader spectrum, the new method increases the SNR by a huge amount, almost reaching the noiseless state. This is likely due to the low frequency nature of the spectrum versus the higher frequency noise.
TABLE I.
Example 1 - Signal to Noise Ratio (SNR): Comparison of New Method with other standard wavelet denoising methods at 16 and 4 scans. Hard and Soft represent hard and soft thresholding, respectively; dB is SNR in decibels; and DL is Decomposition Level (cf. Figures 3–8).
| Method | 16 scans | 4 scans | ||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| SNR (dB) | SNR | SSIM | DL | SNR (dB) | SNR | SSIM | DL | |
|
| ||||||||
| Noisy | 35 | 57 | 0.9903 | - | 30 | 32 | 0.9684 | - |
| Minimax-Hard | 43 | 146 | 0.9959 | 7 | 38 | 81 | 0.9880 | 7 |
| Minimax-Soft | 46 | 201 | 0.9954 | 7 | 41 | 114 | 0.9890 | 12 |
| SUREShrink-Hard | 38 | 82 | 0.9938 | 9 | 32 | 41 | 0.9779 | 9 |
| SUREShrink-Soft | 44 | 157 | 0.9966 | 7 | 37 | 77 | 0.9905 | 12 |
| Zhao [9] | 46 | 209 | 0.9821 | 6 | 38 | 80 | 0.9790 | 6 |
| Poornachandra [38] | 44 | 167 | 0.9825 | 6 | 37 | 73 | 0.9803 | 6 |
| Zhang [39] | 46 | 209 | 0.9821 | 6 | 38 | 80 | 0.9778 | 6 |
| Lin [37] | 44 | 167 | 0.9825 | 6 | 38 | 79 | 0.9800 | 6 |
| New Method | 73 | 4438 | 0.9969 | 6 | 64 | 1567 | 0.9957 | 6 |
TABLE II.
Example 2 - Signal to Noise Ratio (SNR): Comparison of New Method with other standard wavelet denoising methods. dB is SNR in decibels; and DL is Decomposition Level (cf. Figure 9).
| Method | SNR (dB) | SNR | DL |
|---|---|---|---|
|
| |||
| Noisy | 33 | 49 | - |
| Minimax-Hard | 38 | 81 | 10 |
| Minimax-Soft | 43 | 149 | 6 |
| SUREShrink-Hard | 37 | 76 | 7 |
| SUREShrink-Soft | 41 | 115 | 9 |
| Zhang [39] | 44 | 167 | 6 |
| New Method | 165 | 191 × 106 | 4 |
For example 1, since there is a good reference signal, the SSIM is also calculated and shown in Table I. It can be seen that the noisy signal at 16 scans is structurally very similar to the reference signal, revealing that the noise hardly distorts the signal. But the 4 scan noise possesses some structural distortion. For 16 scans, the new method along with SUREShrink and Minimax soft and hard thresholding methods increases the SSIM, while the other methods decrease it. The increase is highest for the new method. For 4 scans, the new method significantly increases the SSIM, while other denoising methods slightly improve it. At both 16 and 4 scans, the new method not only regains the reference signal maximally but it also resembles it very closely.
Both qualitatively and quantitatively, the new method outperforms the current denoising methods and successfully recovers the desired spectrum.
D. Computational Complexity
For the new method as well as the other methods, the computational complexity of DWT, IDWT, plus application of the thresholding function is 𝒪(N). However, the new method takes 𝒪(N) operations to calculate thresholds, as it requires only simple arithmetic operations for calculating mean, standard deviation, and ratios. On the other hand, the thresholds obtained from SURE and Minimax optimization can take 𝒪(N logN) operations. Therefore, overall the new method has computational complexity (𝒪(N)) which is less than the other denoising methods (𝒪(N logN)).
Table III shows the actual computation times of the new method and other denoising methods for example 1. The computation time was calculated in MATLAB on a 64-bit operating system with 16 GB RAM and a 3.30 GHz processor. To overcome any processing variation in the computer, the computation time was measured 5000 times and then averaged. It can be seen that the new method is more than 6 times faster than other denoising methods.
TABLE III.
Example 1 - Computation Time: Comparison of New Method with other standard wavelet denoising methods.
VII. CONCLUSIONS
This paper presents a comprehensive framework for wavelet transform denoising illustrating it with denoising of cw-ESR spectra, and it shows the limitations of current wavelet denoising methods. The two examples were chosen as illustrative from over 100 examples of model and experimental data. This new denoising method enables the selection of appropriate thresholds for noise removal. It is shown that this new method is able to effectively denoise and especially retrieve the signal peaks accurately.
There are two advantages of the proposed method. First, it allows the analysis of a low SNR signal by effectively retrieving the relevant information. This is especially beneficial where signals are obtained at low SNR. Second, the new method can be used to minimize the number of scans needed for signal averaging, resulting in large savings in experimental time. In the application of the new method to extensive cw-ESR spectra, we found it to be consistently successful in accurately retrieving the original signal. Theoretically, very extensive signal averaging would remove all the random noise, but due to time constraints, the number of scans that are practical is often limited.
We believe that our new denoising method can be applied to other spectroscopies such as nuclear magnetic resonance (NMR) spectroscopy [49], Infrared spectroscopy [49], Ultraviolet spectroscopy [49], Raman spectroscopy [50], mass spectroscopy [49], and others that yield 1D spectra. We currently are developing this approach for time domain signals as well as for two- and higher-dimensional spectroscopies.
Fig. 6.
Example 1: Comparison of New Method with Denoising methods [9], [37]–[39] other than soft and hard thresholding at 4 scans.
Fig. 7.
Example 1: Comparison of New Method with Minimax and SUREShrink Denoising at 16 scans.
Acknowledgments
The authors would like to thank Boris Dzikovski for generating the ESR spectra and useful discussions. This research is supported by NIGMS/NIH Grant Number P41GM103521 and is covered by U.S. Provisional Patent Application No. 62/334,626.
Contributor Information
Madhur Srivastava, Email: ms2736@cornell.edu, National Biomedical Center for Advanced ESR Technology (ACERT) and the Nancy E. and Peter C. Meinig School of Biomedical Engineering, Cornell University, Ithaca, NY, 14853 USA.
C. Lindsay Anderson, Email: cla@cornell.edu, Department of Biological and Environmental Engineering, Cornell University, Ithaca, NY, 14853 USA.
Jack H. Freed, Email: jhf3@cornell.edu, National Biomedical Center for Advanced ESR Technology (ACERT) and the Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, 14853 USA
References
- 1.Cai T, Silverman B. Incorporating information on neighboring coefficients into wavelet estimation. Sankhya: The Indian Journal of Statistics B. 2001;63(2):127–148. [Google Scholar]
- 2.Jang J, Guo J, Fan W, Chen Q. An improved adaptive wavelet denoising method based on neighboring coefficients. Proc. 8th World Congress Intelligent Control and Automation; July 2010. [Google Scholar]
- 3.Chen G, Bui T. Multiwavelets denoising using neighboring coefficients. IEEE Signal Process Lett. 2003 Jul;10(7):211–214. [Google Scholar]
- 4.Chen G, Bui T, Krzyzak A. Image denoising using neighboring wavelet coefficients. Integrated Computer-Aided Engineering. 2005;12(1):99–107. [Google Scholar]
- 5.Zhou D, Cheng W. Image denoising with an optimal threshold and neighbouring windows. Pattern Recognition Letters. 2008;29(11):1694–1697. [Google Scholar]
- 6.Madhu S, Bhavani HB, Sumathi S, Vidya HA. A novel algorithm for denoising of simulated partial discharge signals using adaptive wavelet thresholding methods. Electronics and Communication Systems (ICECS), 2015 2nd International Conference on; 2015; pp. 1596–1602. [Google Scholar]
- 7.Hussein R, Shaban KB, El-Hag AH. Histogram-based thresholding in discrete wavelet transform for partial discharge signal denoising. Communications, Signal Processing, and their Applications (ICCSPA), 2015 International Conference on; 2015; pp. 1–5. [Google Scholar]
- 8.Cetin AE, Tofighi M. Projection-based wavelet denoising [lecture notes] IEEE Signal Processing Magazine. 2015;32(5):120–124. [Google Scholar]
- 9.Zhao RM, Cui Hm. Improved threshold denoising method based on wavelet transform. 2015 7th International Conference on Modelling, Identification and Control (ICMIC); 2015; pp. 1–4. [Google Scholar]
- 10.Ding Y, Selesnick IW. Artifact-free wavelet denoising: Non-convex sparse regularization, convex optimization. IEEE Signal Processing Letters. 2015;22(9):1364–1368. [Google Scholar]
- 11.Zhao Q, Dai W. A wavelet denoising method of new adjustable threshold. 2015 IEEE 16th International Conference on Communication Technology (ICCT); 2015; pp. 684–688. [Google Scholar]
- 12.Madadi Z, Anand GV, Premkumar AB. Signal detection in generalized gaussian noise by nonlinear wavelet denoising. IEEE Transactions on Circuits and Systems I: Regular Papers. 2013;60(11):2973–2986. [Google Scholar]
- 13.Deng G, Liu Z. A wavelet image denoising based on the new threshold function. 2015 11th International Conference on Computational Intelligence and Security (CIS); 2015; pp. 158–161. [Google Scholar]
- 14.Bibina VC, Viswasom S. Adaptive wavelet thresholding amp; joint bilateral filtering for image denoising. 2012 Annual IEEE India Conference (INDICON); 2012; pp. 1100–1104. [Google Scholar]
- 15.Guo S, Wu F, Wei W, Guo J, Ji Y, Wang Y. A novel wavelet denoising method used for droplet volume detection in the microfluidic system. 2013 IEEE International Conference on Mechatronics and Automation; 2013; pp. 1732–1737. [Google Scholar]
- 16.Chen G, Xie W, Zhao Y. Wavelet-based denoising: A brief review. Intelligent Control and Information Processing (ICICIP), 2013 Fourth International Conference on; 2013; pp. 570–574. [Google Scholar]
- 17.Chang S, Yu B, Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising. Image Processing, IEEE Transactions on. 2000 Sep;9(9):1522–1531. doi: 10.1109/83.862630. [DOI] [PubMed] [Google Scholar]
- 18.Sendur L, Selesnick I. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans on Signal Process. 2002 Nov;50(11):2744–2756. [Google Scholar]
- 19.Pizurica A, Philips W. Estimating the probability of the presence of a signal of interest in multiresolution single- and multiband image denoising. IEEE Trans Image Process. 2006;15(3):654–665. doi: 10.1109/tip.2005.863698. [DOI] [PubMed] [Google Scholar]
- 20.Jansen M, Bulthel A. Empirical bayes approach to improve wavelet thresholding for image noise reduction. Journal of the American Statistical Association. 2001 Jun;96(454):629–639. [Google Scholar]
- 21.Liu Y, Cheng X. A new signal denoising algorithm from wavelet modulus maxima. Fourth International Conference on Fuzzy Systems and Knowledge Discovery; August 2007; pp. 32–35. [Google Scholar]
- 22.Mallat S. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans Patter Anal Mach Intell. 1989;11:674–693. [Google Scholar]
- 23.Meng X, He Z, Feng G, Xiao B. An improved wavelet denoising algorithm for wideband radar targets detection. Circuits Syst Signal Process. 2013;32:2003–2026. [Google Scholar]
- 24.Fodor I, Kamath C. Denoising through wavelet shrinkage: an empirical study. Journal of Electronic Imaging. 2003;12(1):1200–1224. [Google Scholar]
- 25.Wink AM, Roerdink JBTM. Denoising functional mr images: a comparison of wavelet denoising and gaussian smoothing. Medical Imaging, IEEE Transactions on. 2004 Mar;23(3):374–387. doi: 10.1109/TMI.2004.824234. [DOI] [PubMed] [Google Scholar]
- 26.Ernst R. Sensitivity enhancement in magnetic resonance. i. analysis of the method of time averaging. Review of Scientific Instruments. 1965;36(12):1689–1695. [Google Scholar]
- 27.Weil J, Bolton J, Wertz JE. Electron paramagnetic resonance: elementary theory and practical applications. Wiley and Sons; New York: 1994. [Google Scholar]
- 28.Kak AC, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press; 1988. [Google Scholar]
- 29.Donoho D. De-noising by soft-thresholding. Information Theory, IEEE Transactions on. 1995 May;41(3):613–627. [Google Scholar]
- 30.Bryant JH. PhD dissertation. The University of Chicago; 2011. Electron paramagnetic resonance image reconstruction for arbitrary projection sampling and regions of interest. [Google Scholar]
- 31.Donoho DL, Johnstone IM. Ideal spatial adaptation via wavelet shrinkage. Biometrika. 1994;81(3):425–455. [Google Scholar]
- 32.Johnstone I, Silverman B. Wavelet threshold estimators for data with correlated noise. J Roy Statist Soc D. 1997;59:319–351. [Google Scholar]
- 33.Chang F, Hong W, Zhang T, Jing J, Liu X. Research on wavelet denoising for pulse signal based on improved wavelet thresholding. Pervasive Computing Signal Processing and Applications (PCSPA), 2010 First International Conference on; Sept 2010; pp. 564–567. [Google Scholar]
- 34.Stein CM. Estimation of the mean of a multivariate normal distribution. The Annals of Statistics. 1981;9(6):1135–1151. [Google Scholar]
- 35.Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association. 1995;90(432):1200–1224. [Google Scholar]
- 36.Gao HY. Wavelet shrinkage denoising using the non-negative garrote. Journal of Computational and Graphical Statistics. 1998;7(4):469–488. [Google Scholar]
- 37.Lin Y, Cai J. A new threshold function for signal denoising based on wavelet transform. 2010 IEEE International Conference on Measuring Technology and Mechatronics Automation; 2010; pp. 200–203. [Google Scholar]
- 38.Poornachandra S, Kumaravel N, Saravanan TK, Somaskandan R. Waveshrink using modified hyper-shrinkage function,” in. Engineering in Medicine and Biology Society, 2005. IEEE-EMBS 2005. 27th Annual International Conference of the; Jan 2005; pp. 30–32. [DOI] [PubMed] [Google Scholar]
- 39.Zhang D, Bao P. Denoising by spatial correlation thresholding. Circuits and Systems for Video Technology, IEEE Transactions on. 2003 Jun;13(6):535–538. [Google Scholar]
- 40.Freed J. New technologies in electron spin resonance. Annual review of physical chemistry. 2000;51(1):655–689. doi: 10.1146/annurev.physchem.51.1.655. [DOI] [PubMed] [Google Scholar]
- 41.Freed J. Biomedical EPR, Part B: Methodology, Instrumentation, and Dynamics. Springer; 2005. Esr and molecular dynamics; pp. 239–268. [Google Scholar]
- 42.Zhang Z, Fleissner M, Tipikin D, Liang Z, Moscicki J, Earle K, Hubbell W, Freed J. Multifrequency electron spin resonance study of the dynamics of spin labeled T4 lysozyme. The Journal of Physical Chemistry B. 2010;114(16):5503–5521. doi: 10.1021/jp910606h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hofbauer W, Earle K, Dunnam C, Moscicki J, Freed J. High-power 95 ghz pulsed electron spin resonance spectrometer. Review of scientific instruments. 2004;75(5):1194–1208. [Google Scholar]
- 44.Poole C. Electron spin resonance: a comprehensive treatise on experimental techniques. Courier Corporation; 1996. [Google Scholar]
- 45.Earle K, Dzikovski B, Hofbauer W, Moscicki J, Freed J. High-frequency esr at acert. Magnetic Resonance in Chemistry. 2005;43(S1):S256–S266. doi: 10.1002/mrc.1684. [DOI] [PubMed] [Google Scholar]
- 46.Wang Z, Bovik A, Sheikh H, Simoncelli E. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 47.Dzikovski B, Livshits V. Epr spin probe study of molecular ordering and dynamics in monolayers at oil/water interfaces. Phys Chem Chem Phys. 2003;5:5271–5278. [Google Scholar]
- 48.Cohen R. Technion, Israel Institute of Technology, Tech Rep. 2012. Signal denoising using wavelets. [Google Scholar]
- 49.Pavia D, Lampman G, Kriz G, Vyvyan J. Cengage Learning. 2008. Introduction to spectroscopy. [Google Scholar]
- 50.Galloway C, Ru EL, Etchegoin P. An iterative algorithm for background removal in spectroscopy by wavelet transforms. Applied spectroscopy. 2009;63(12):1370–1376. doi: 10.1366/000370209790108905. [DOI] [PubMed] [Google Scholar]