Comparison of unsupervised classification methods for brain tumor segmentation using multi-parametric MRI

Abstract

Tumor segmentation is a particularly challenging task in high-grade gliomas (HGGs), as they are among the most heterogeneous tumors in oncology. An accurate delineation of the lesion and its main subcomponents contributes to optimal treatment planning, prognosis and follow-up. Conventional MRI (cMRI) is the imaging modality of choice for manual segmentation, and is also considered in the vast majority of automated segmentation studies. Advanced MRI modalities such as perfusion-weighted imaging (PWI), diffusion-weighted imaging (DWI) and magnetic resonance spectroscopic imaging (MRSI) have already shown their added value in tumor tissue characterization, hence there have been recent suggestions of combining different MRI modalities into a multi-parametric MRI (MP-MRI) approach for brain tumor segmentation. In this paper, we compare the performance of several unsupervised classification methods for HGG segmentation based on MP-MRI data including cMRI, DWI, MRSI and PWI. Two independent MP-MRI datasets with a different acquisition protocol were available from different hospitals. We demonstrate that a hierarchical non-negative matrix factorization variant which was previously introduced for MP-MRI tumor segmentation gives the best performance in terms of mean Dice-scores for the pathologic tissue classes on both datasets.

Highlights

• •Unsupervised classification algorithms are applied for brain tumor segmentation on multi-parametric MRI datasets.
• •Reported mean Dice-scores are in the range of state-of-the-art segmentation algorithms.
• •Hierarchical NMF obtained the best segmentation results in terms of mean Dice-scores for most of the tissue classes.

1. Introduction

High-grade gliomas (HGGs) are the most common type of malignant primary brain tumors (Goodenberger and Jenkins, 2012). Despite considerable advances in understanding their biological behavior, patient prognosis remains poor due to their rapid infiltrative growth into the surrounding healthy tissue. Anaplastic astrocytomas (WHO grade III) have a 5-year survival rate of approximately 30%, whereas glioblastoma multiforme (GBM, WHO grade IV), the most malignant type, has a 5-year survival rate of only 5% (Ostrom et al., 2014). HGGs are among the most heterogeneous tumors in oncology. They are diffuse, exhibiting unclear and irregular boundaries, preferentially invading the surrounding tissue along white matter tracts (Price et al., 2006). Different stages of the disease can occur within the same lesion (Paulus and Peiffer, 1989), with varying degrees of tumor enhancement, mitotic activity and necrosis. Furthermore, tumor structures vary considerably in terms of size, shape and location. This makes tumor segmentation, i.e. the imaging-based delineation of the tumor and its subcomponents, particularly challenging in HGGs.

Tumor segmentation is a crucial task in the treatment planning and follow-up of HGG patients. Manual segmentation by a neuro-radiologist, usually based on conventional MRI, is currently still the gold standard. It is a tedious and time-consuming task, and it is susceptible to subjective interpretation. Intra- and inter-observer variabilities of 20% and higher have been reported for manual tumor delineation (Weltens et al., 2001, Menze et al., 2015). To alleviate these limitations and due to the high clinical relevance, there has been an increasing interest for automated brain tumor segmentation. Classification methods, which rely primarily on voxel intensity-based features for differentiating tissue types, have been receiving the most attention (Menze et al., 2015). They have the advantage of being able to deal with multi-parametric imaging datasets, combining voxel-wise information from different MRI modalities. Classification methods can be further categorized into supervised and unsupervised methods. Supervised classification methods naturally incorporate large amounts of prior knowledge in the form of a training dataset with known tissue labels. From this training dataset, the algorithm learns decision boundaries between tissue classes in high-dimensional feature space, which can then be applied to unlabeled test data. Supervised classification methods require extensive training datasets, to account for the wide heterogeneity in tumor appearance among glioma grades and occasional labelling errors. Unsupervised classification methods reveal structure in a dataset by modelling the similarity within the data itself. These methods can directly be applied to any imaging dataset, irrespective of the acquisition protocol and without the need for any training data. Due to the lack of manually annotated ground truth, unsupervised methods depend more strongly on the incorporation of additional prior knowledge, e.g. by imposing spatial coherence (Nie et al., 2009) or feature-specific knowledge (Kazerooni et al., 2015), to achieve a valid tissue segmentation.

Fuzzy C-means clustering (FCM) is one of the most popular unsupervised algorithms for brain tumor segmentation (Gordillo et al., 2013). FCM takes into account the MRI feature overlap between tissue classes, assigning fuzzy membership values to different tissue types. FCM was introduced for brain tumor segmentation by Phillips et al. (1995) and was later combined with knowledge-based techniques for improved performance (Kazerooni et al., 2015, Fletcher-Heath et al., 2001). Several studies have applied finite mixture modelling for unsupervised tumor segmentation. Mostly, each tissue type is modelled by a multi-variate Gaussian distribution, resulting in a Gaussian mixture model (GMM) (Menze et al., 2010, Zhang et al., 2001). Recently, GMM has been shown to be competitive with state-of-the-art supervised classification algorithms for GBM segmentation based on cMRI data (Juan-Albarracín et al., 2015). Over the last years graph-cut based methods have become popular as well. A semi-supervised procedure based on graph-cut has been presented to differentiate tumor tissue from healthy brain using MRSI data (Görlitz et al., 2007). Padole et al. have initiated a normalized-cut method using the mean-shift algorithm for increased computational efficiency (Padole and Chaudhari, 2012).

Nearly all of the proposed segmentation algorithms have so far mainly been applied to cMRI data (Phillips et al., 1995, Fletcher-Heath et al., 2001, Menze et al., 2010, Zhang et al., 2001, Juan-Albarracín et al., 2015). However, along with the recent emergence of advanced MRI modalities such as diffusion-weighted MRI (DWI), perfusion-weighed MRI (PWI) and magnetic resonance spectroscopic imaging (MRSI), numerous studies have suggested that tumor characterization might benefit from the additional structural, biological and biochemical information provided by these advanced MRI modalities (Bauer et al., 2013, Cha, 2006, Padhani and Miles, 2010).

DWI probes diffusion of water molecules and its interaction with a local microstructure. Minimal apparent diffusion coefficient (ADC) values have been shown to inversely correlate with tumor cellularity (Sugahara et al., 1999). Diffusion tensor imaging (DTI) models the diffusion process three-dimensionally, providing insight in diffusion directionality and tissue structure through mean diffusivity (MD) and fractional anisotropy (FA) (Abdullah et al., 2013). DTI has been shown to better delineate tumor margins in gliomas than cMRI (Price et al., 2006). Jones et al. presented a DTI based segmentation to delineate tumor volumes of interest using isotropic and anisotropic components of the diffusion tensor (Jones et al., 2015). Diffusion kurtosis imaging (DKI) is a recent extension of DTI, quantifying the non-Gaussian component of diffusion by the mean kurtosis (MK) (Van Cauter et al., 2012). The additional information from DKI is thought to indicate the complexity of the microstructural environment (Steven et al., 2014).

PWI is widely used for studying tumor angiogenesis, mainly through the quantification of relative cerebral blood volume (rCBV) (Cha et al., 2002). HGGs are known to promote vascular ingrowth under hypoxic conditions (Mukhopadhyay et al., 1995). Strong correlations have been reported between rCBV and cell density, and between rCBV and microvessel density in HGGs (Sadeghi et al., 2008). PWI has been reported to detect tumor recurrence at an earlier stage than cMRI (Ion-Margineanu et al., 2015) and has been shown to be useful in differentiating active glioma from radiation necrosis (Hu et al., 2012).

Proton MRSI (¹H MRSI) provides biochemical information about the spatial distribution of metabolites in a localized region of the brain. The principal metabolites seen in brain tumors include lactate (Lac), lipids (Lip), N-acetyl-aspartate (NAA), glutamine + glutamate (Glx), total creatine (Cre), total choline (Cho), glycine (Gly) and myo-inositol (mI). NAA levels progressively decrease with increasing glioma grade, as it is a marker of neuronal cell density (Bulik et al., 2013). Cho indicates cell membrane density and integrity, showing elevated levels in HGGs with increased cell density. Elevated levels of Lip are mostly seen in GBM, as it is a hallmark of necrosis (Kuesel et al., 1994). ¹H MRSI has been reported to detect metabolically active tumor beyond the radiological boundaries defined by cMRI (Pirzkall et al., 2001).

Thus far, only few studies have combined different MRI modalities for glioma segmentation. Di Costanzo et al. used DWI, PWI and ¹H MRSI to classify a set of manually delineated regions of interest (ROIs) in the non-necrotic part of the tumor and the peritumoral region (Di Costanzo et al., 2006). Step-wise linear discriminant analysis was applied to the ROI averaged MP-MRI parameters to differentiate between regions of gross tumor, edema, tumor/edema, tumor infiltration and normal tissue. Highest classification accuracy was reported when all MRI modalities were included. Verma et al. applied support vector machines to a combined set of cMRI and DTI parameters to segment intensity-based tissue profiles on a voxel-wise basis (Verma et al., 2008). They provide tissue probability maps as well as hard segmentation of enhancing tumor, non-enhancing tumor and edema in the pathologic region. Zikic et al. applied a decision forest classifier on a set of voxel-wise intensities and context-aware features from cMRI and DTI (Zikic et al., 2012). They report an improvement of the segmentation accuracy when DTI is included compared to using only cMRI data. As extensive MP-MRI datasets might be more prone to variations in the acquisition protocol, unsupervised methods benefit from not requiring a uniform training dataset. Kazerooni et al. are among the first to explore unsupervised classification methods for MP-MRI based glioma segmentation (Kazerooni et al., 2015). They employed spatial fuzzy C-means clustering to a combination of cMRI, DWI and PWI data, followed by a region growing step. Unsupervised classification based on non-negative matrix factorization (NMF) has been proposed for differentiating brain tumor from healthy tissue in MRSI data (Li et al., 2013, Ortega-Martorell et al., 2012). In a previous study, we applied hierarchical NMF (hNMF) for tumor segmentation to an MP-MRI dataset combining cMRI, DWI, PWI and MRSI data (Sauwen et al., 2015). Segmentation results were shown to be significantly better when using the MP-MRI data compared to using cMRI data only.

In this paper, we present an hNMF variant with improved computational efficiency, making it approximately 10 times faster while maintaining segmentation performance compared to (Sauwen et al., 2015). We compare its performance to 5 other state-of-the-art unsupervised classification algorithms for brain tumor segmentation using MP-MRI data, namely 2 single-level NMF methods (hierarchical alternating least-squares NMF and convex NMF) and 3 clustering methods (fuzzy C-means, Gaussian mixture modelling and spectral clustering). In order to make our conclusions more general, all methods are applied to 2 independent MP-MRI datasets, acquired at different hospitals and using a different acquisition protocol. To assess the added value of the advanced MRI modalities, all methods were also applied when considering only cMRI data.

2. MP-MRI datasets

Two independent MP-MRI datasets were acquired at the university hospitals of Ghent (UZ Gent) and Leuven (UZ Leuven). Both datasets included cMRI, DWI, PWI and ¹H MRSI, but the acquisition protocols and the resulting sets of MRI features were different. Table 1 gives a concise overview of the acquisition protocols and MP-MRI features from both datasets.

Table 1.

Schematic overview of the MP-MRI protocols and derived parameters of the 2 datasets acquired at UZ Gent and UZ Leuven.

	UZ Gent dataset (21 patients)	UZ Leuven dataset (14 patients)
cMRI	T1, T1c, FLAIR	T2, T1c, FLAIR
DWI	DWI (3 b-values, 1 + 3 + 3 directions) ADC, b0	DKI (4 b-values, 10 + 25 + 40 + 75 directions) MD, MK, FA
1H MRSI	3D long echo1H MRSI Lac, Lip, NAA, Glx, Cre, Cho	2D short echo1H MRSI Lac, Lip, NAA, Glx, Cre, Cho, Gly, mI
PWI	DSC-MRI rCBV	DSC-MRI rCBV

2.1. UZ Gent

21 HGG patients (12 GBMs, 1 grade III astrocytoma, 1 grade III oligodendroglioma, 7 grade III oligoastrocytomas) were included in the study. The lesions were classified according to grade using the 2007 WHO classification (Louis et al., 2007). Retrospective analysis of the data was approved by the local ethics committee. MR examinations were performed on a 3 T scanner (Siemens Trio Tim, Erlangen, Germany), using a standard 12-channel phased array head coil. cMRI included T1 with and without contrast (T1c and T1, voxel size 0.9 × 0.85 × 0.85 mm³) and fluid-attenuated inversion recovery (FLAIR, voxel size 1 × 0.98 × 0.98 mm³) imaging. Axial DWI images were acquired using a fast single-shot gradient echo echo-planar imaging sequence (voxel size 2 × 2 × 3 mm³). The raw DWI data were averaged over 3 orthogonal directions and ADC maps were calculated using weighted linear least-squares fitting (Veraart et al., 2013). The T2-weighted b0 images were also added to the feature set. PWI was performed by using a T2*-weighted dynamic susceptibility-weighted contrast-enhanced MRI (DSC-MRI) sequence (voxel size 1.8 × 1.8 × 5 mm³). rCBV maps were quantified from the dynamic signal intensity curves using the method proposed by Boxerman et al., which accounts for leakage correction (Boxerman et al., 2006). A 3D ¹H MRSI protocol with long echo-time was included (voxel size 10 × 10 × 15 mm³). In the two-slice MRSI examination, a volume of interest was positioned manually to include tumor, perilesional edema and normal brain tissue. Metabolite quantification was performed using AQSES-MRSI (Croitor Sava et al., 2011), resulting in Lac, Lip, NAA, Glx, Cre and Cho maps. A detailed description of the UZ Gent MP-MRI acquisition protocol and post-processing of the MRI features can be found in (Sauwen et al., 2016)

2.2. UZ Leuven

14 HGG patients were enrolled in the study (11 GBMs, 2 grade III astrocytomas and 1 grade III oligoastrocytoma). Written informed consent was obtained from every patient before participation. MRI acquisition was performed on a 3 T MR system (Philips Achieva, Best, The Netherlands), using a body coil for transmission and an 8-channel head coil for signal reception. cMRI consisted of T2-weighted imaging (voxel size 0.45 × 0.45 × 4 mm³), T1-weighted imaging after contrast administration (0.98 × 0.98 × 1 mm³) and FLAIR (0.45 × 0.45 × 4 mm³). An extensive DWI echo-planar imaging sequence was used to acquire DKI data (voxel size 2.5 × 2.5 × 2.5 mm³). Diffusion and kurtosis tensors were estimated in each voxel using a constrained weighted linear least-squares algorithm (Veraart et al., 2013). MD, FA and MK maps were calculated according to (Le Bihan et al., 2001, Poot et al., 2010). PWI consisted of a DSC-MRI sequence (voxel size 1.56 × 1.56 × 3 mm³). rCBV maps were derived from the dynamic signal intensity curves using the method by Boxerman et al. (2006). Short echo-time ¹H MRSI data were acquired for a 2-dimensional ROI positioned in the center of the tumor (voxel size 10 × 10 × 10 mm³). AQSES-MRSI was used to quantify Lac, Lip, NAA, Glx, Cre, Cho, Gly and mI. For a detailed description of the UZ Leuven acquisition protocol and post-processing of the MRI features, the reader is referred to Sauwen et al. (2015).

2.3. Image coregistration and voxel selection

To allow for voxel-wise segmentation, all MP-MRI parameters were coregistered and resampled to the same spatial resolution of 1 × 1 × 3 mm³. cMRI data were skull-stripped and T1c served as a reference for rigid coregistration in SPM8 (Wellcome Trust Centre for Neuroimaging, University College London), using the normalized mutual information criterion (Maes et al., 1997) and cubic B-spline interpolation for reslicing. The MRSI data were spatially aligned and resliced to the T1c reference without coregistration, due to their low spatial resolution and limited spatial extent. Only voxels within the MRSI ROI have a full set of MP-MRI features, so only those voxels were included in the segmentation analyses. For the UZ Gent dataset, voxels from 10 slices located within the 3D MRSI ROI were included. For the UZ Leuven dataset, voxels in a central slice intersecting the 2D MRSI ROI were considered. Additional intensity-based features were added to the feature set to include localized spatial information. An in-plane local neighbourhood of 3 × 3 and 5 × 5 voxels was used to calculate average intensity values that were assigned to the central voxel. These spatially averaged intensity values were added for all MP-MRI features except for the MRSI data, because of the low spatial MRSI resolution. Finally, each feature's full range was rescaled linearly to [0–1].

3. Methods

In this paper, several state-of-the-art unsupervised MP-MRI classification methods were applied and evaluated on the UZ Gent and UZ Leuven datasets for brain tumor segmentation, 3 of which are based on NMF and 3 are based on clustering.

3.1. Non-negative matrix factorization

Given a non-negative input matrix X, NMF will provide a low-rank (rank r) approximation of X as the product of 2 non-negative factor matrices W and H:

$$X\approx \mathit{WH}\text{with}X\in R_{+}^{m\times n},W\in R_{+}^{m\times r}\mathrm{and}H\in R_{+}^{r\times n}$$ (1)

NMF aims at finding meaningful basic components which are present in a dataset, using an additive parts-based representation to model the data. As we are dealing with image intensities, the non-negativity constraint applies naturally. Each column of X corresponds to one data point, i.e. one voxel's MP-MRI feature vector. The columns of W, the so-called sources, will represent tissue-specific MP-MRI signatures. Each row of H will then contain the relative weights (the so-called abundances) of the corresponding source in W for all voxels. As such, each data point is modelled as a weighted sum of the tissue-specific signatures. The abundances in H tell us which tissue types are most prominent in each voxel. To convert the multi-linear NMF result into a hard segmentation, k-means clustering is applied to the abundance values in H. As we assume the NMF sources to correspond to the tissue classes, we initialize each cluster centroid with a different abundance value set to 1, and all other abundance values set to 0. The most commonly used cost function to assess the factor approximation is the Frobenius norm, which is based on the squared Euclidian distance as a similarity metric:

$$\underset{W,H}{min}f\left(W,H\right)=\frac{1}{2}X-W{H}_F^2,\text{such}\text{that}\forall i,j:W_{i,j}\ge 0,H_{i,j}\ge 0$$ (2)

Many algorithms have been developed to solve this non-convex optimization problem. In the next sections, we will propose 2 commonly used NMF algorithms for brain tumor segmentation, along with the hNMF algorithm (Sauwen et al., 2015).

3.1.1. HALS NMF

Hierarchical alternating least-squares (HALS) NMF belongs to the family of alternating least-squares algorithms (ALS) (Cichocki et al., 2007). These methods rely on the observation that optimizing W when H is fixed, and optimizing H when W is fixed are convex problems, as opposed to the original non-convex NMF problem as defined in Eq. (2). ALS NMF methods iteratively update W and H by solving the normal equations:

$$H^{\left(k\right)}{H}^{{\left(k\right)}^T}{W}^{{\left(k+1\right)}^T}=H^{\left(k\right)}{X}^T\mathrm{for}\text{updating}W$$ (3)

$$W^{{\left(k\right)}^T}{W}^{\left(k\right)}{H}^{k+1}=W^{{\left(k\right)}^T}X\mathrm{for}\text{updating}H$$ (4)

HALS NMF successively updates the individual columns of W and the individual rows of H, as one obtains a computationally efficient closed-form solution when decoupling the variables in this way. In the current study we apply an accelerated HALS NMF algorithm because of its fast convergence compared to other ALS based methods (Gillis and Glineur, 2012).

3.1.2. Convex NMF

Convex NMF imposes the source vectors (columns) of W to lie within the column space of X (Ding et al., 2010). Moreover, each source must be a weighted sum of some of the data points. An auxiliary non-negative matrix A is introduced to enforce this additional constraint:

$$W=\mathit{XA}\text{such}\text{that}X\approx \mathit{XAH}$$ (5)

Multiplicative update rules are defined to alternatingly revise A and H towards convergence. Convex NMF naturally leads to a sparse abundance matrix H.

3.1.3. Hierarchical NMF

Hierarchical NMF variants have been previously used for document clustering (Kuang and Park, 2013), for unmixing hyperspectral images (Gillis et al., 2015) and for tumor tissue differentiation based on MRSI data (Di Costanzo et al., 2006). Our hNMF method was introduced in a previous paper for MP-MRI based glioma segmentation (Sauwen et al., 2015). We have currently adapted the original hNMF algorithm, making it computationally more efficient while maintaining similar performance. The hNMF method consists of 2 levels of NMF, using HALS NMF at both levels. First, rank-2 NMF is applied to the input matrix X, resulting in 2 sources (W₁ and W₂) and corresponding abundance maps (H₁ and H₂). It is assumed that each tissue class is mainly represented by one source, such that we can assign each tissue type to either W₁ or W₂. The voxels are then divided over the 2 sources based on their abundance values H₁ and H₂. Whereas hNMF originally used iterative thresholding for dividing the voxels, the algorithm has been adapted such that k-means clustering is applied to the H₁ and H₂ values for efficient voxel assignment. The clusters are initialized at [1 0] and [0 1], i.e. we expect to find one cluster (X₁) with high H₁ and low H₂ values, and another cluster (X₂) with low H₁ and high H₂ values. By doing so, we were able to make the hNMF computation approximately 10 times faster while maintaining segmentation performance. A second level of NMF is then applied to X₁ and X₂ separately, with the rank set to the number of tissue types represented by each cluster, k₁ and k₂. k₁ and k₂ are determined based on visual inspection of the abundance maps H₁ and H₂ in combination with T1c: each tissue class is assigned to the source for which it has the highest abundance values. The sources found at this second level are the actual tissue signatures. Finally, we recombine all the voxels and use non-negative least-squares fitting (NNLS) with the tissue signatures to obtain abundance maps for each tissue type over the full ROI. A schematic overview of the hNMF procedure is shown in Fig. 1.

Fig. 1.

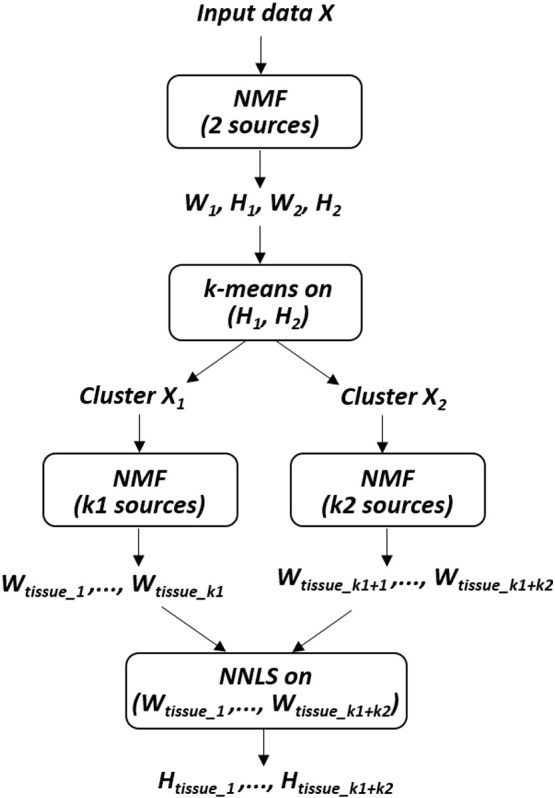
Schematic overview of the hNMF algorithm.

3.2. Clustering

3.2.1. Fuzzy C-means clustering

FCM is a clustering method that allows each data point to belong to multiple clusters with varying degrees of membership. These membership grades indicate the degree to which data points belong to each cluster. FCM aims at minimizing the following objective function:

$$\underset{w,c}{\text{argmin}}\sum _{i=1}^n\sum _{j=1}^k{w}_{i,j}^m{||x_i-c_j||}^2$$ (6)

where m is the fuzziness exponent which determines the level of fuzziness, w_i,j is the degree of membership of data point x_i to cluster C_j. Here, the data points are the columns of the input matrix X, representing the MP-MRI features per voxel. The cluster centroids c_j and the degrees of membership w_i,j are calculated by:

$$c_j=\frac{{\displaystyle {\sum }_{i=1}^n}{w}_{i,j}^m{x}_i}{{\displaystyle {\sum }_{i=1}^n}{w}_{i,j}^m}$$ (7)

$$w_{i,j}=\frac{1}{{\displaystyle {\sum }_{l=1}^k{\left(\frac{||x_i-c_j||}{||x_i-c_l||}\right)}^{\frac{2}{m-1}}}}$$ (8)

FCM is carried out through an iterative optimization of the objective function in Eq. (6), with the update of cluster centroids c_j and cluster memberships w_i,j through Eqs. (7), (8), respectively. In the current study we have set the fuzziness exponent m to 2. Hard segmentation is obtained from FCM by assigning each data point to the cluster for which it has the highest membership value.

3.2.2. Gaussian mixture modelling

GMM aims at finding the maximum likelihood parameters of a mixture of Gaussians fitting the input data. This comes down to maximizing the posterior probability of a parameter set Θ of k Gaussian components, given the input data X:

$$p\left(\Theta |X\right)={\displaystyle \sum _{i=1}^k}{\phi }_i\mathcal{N}\left(X|{\mu }_i,{\sigma }_i\right)$$ (9)

with φ_i the weight of the ith Gaussian component and $\mathcal{N}\left(x|{\mu }_i,{\sigma }_i\right)$the probability of a data point x (i.e. columns of the data matrix X containing MP-MRI features) belonging to a normal distribution with mean μ_i and standard deviation σ_i. The Expectation Maximization (EM) algorithm (Dempster et al., 1977) is the most popular technique to solve this optimization problem. EM alternates between an expectation step (E-step) and a maximization step (M-step) until convergence. In the E-step an estimation of the posterior probability p(Θ | X) is computed given the current estimation of the model parameters. In the M-step a maximum likelihood update of the model parameters is performed based on the posterior probability computed in the E-step. GMM is a soft clustering technique, i.e. it will provide probabilities of the voxels belonging to the different tissue classes. Hard segmentation is obtained by assigning each voxel to the tissue class with the highest probability. In order to recover from singular covariance matrices, a regularization constant of 1e^− 3 was added to the diagonal elements of the covariance matrices (Diehl et al., 2011).

3.2.3. Spectral clustering

Spectral clustering (SC) has become a popular tool for image segmentation. Several studies have applied SC for automated brain tumor and lesion detection (Yang and Grigsby, 2010, Manoj and Padmasuresh, 2016). SC refers to a family of graph partitioning methods which make use of the eigenvalue decomposition of a graph Laplacian matrix for dimensionality reduction prior to the actual clustering step (Von Luxburg, 2007). Its success is mainly based on the fact that SC does not make any strong assumptions about the cluster shape nor about the density distribution of the data points. The aim of SC is to find a partitioning of the similarity graph such that the edge weights between the data clusters are very low. The graph Laplacian matrix L is derived from the adjacency matrix W, which defines the edge weights between the graph nodes. We used a k-nearest neighbour graph to obtain a sparse adjacency matrix, for efficiently performing the eigenvalue decomposition. The Gaussian similarity function $exp\left((-x_i-{x_j}^2/\left(2{\sigma }^2\right)\right)$, where x_i and x_j stand for columns of the data matrix X, was used to calculate the weights in W (Von Luxburg, 2007). Careful selection of the connectivity parameters is crucial in constructing the adjacency matrix, such that the connected components are well separable. We set the number of k nearest neighbours to 50, being in the order of the logarithm of the number of data points for both the UZ Leuven and UZ Gent datasets (Brito et al., 1997). For the Gaussian similarity function, σ was set to 0.5, being in the order of the mean distance of the data points to their k-nearest neighbour (Von Luxburg, 2007). Several graph Laplacian matrices have been proposed in literature. We used the normalized Laplacian proposed by Shi and Malik (2000):

$$L=I-D^{-1}W$$ (10)

where I is the identity matrix and D is a diagonal matrix with its diagonal elements equal to the sums of the rows of W. Eigenvalue decomposition is then applied to L and a matrix U is created with the first k eigenvectors as its columns. Finally, k-means clustering is applied to the rows of U to obtain the k clusters.

3.3. Initialization

Except for SC, all of the proposed unsupervised classification methods are non-convex, i.e. the obtained solution will be a local rather than a global optimum, depending on the initialization conditions. A wide range of initialization methods have been developed for NMF and clustering. As NMF and clustering assume different data models, their most common initialization strategies (besides random initialization) also differ. To avoid favouring either method, we have performed segmentation using 2 initialization strategies: the successive projection algorithm (SPA), which has been suggested for NMF source detection, and kmeans ++, a popular initialization method for clustering. SPA is a forward selection method which minimizes collinearity of the selected variables in vector space (Araújo et al., 2001). It has been commonly used as an endmember extraction tool for hyperspectral unmixing. SPA aims at finding the vertices of a convex hull spanning the dataset, under the assumptions of near-separable NMF (Gillis, 2014). SPA iteratively adds data points to the set of initial sources, at each step selecting the data point with the highest l2-norm in the orthogonal subspace of the already selected sources. Kmeans ++ is a recently proposed method for initializing the cluster centroids (Arthur and Vassilvitskii, 2007). The intuition behind this approach is that it is favorable to spread out the initial centroids. The first cluster center is chosen randomly from the data points, after which each subsequent centroid is chosen from the remaining data points with probability proportional to its squared distance from the point's closest existing cluster center. As kmeans ++ is not a deterministic algorithm, we successively ran it 20 times and withheld the result with the best (= highest or lowest) objective function value for the considered classification method. SC does not require any initialization, but we applied both initialization methods to the k-means clustering step in the final part of the algorithm.

3.4. Validation

The unsupervised classification methods were applied to each patient's MP-MRI dataset individually. Segmentation results obtained from the NMF and clustering methods were validated based on manual expert labelling. Manual delineations of the pathologic tissue regions were obtained at the 2 hospitals from an experienced radiologist, each of them having > 5 years of experience in neuro-radiology. The number of tissue classes present within each patient's ROI was determined based on visual inspection by the radiologists. The Dice-score (Menze et al., 2015) was used to quantify the spatial alignment between each method's automated segmentation and the manual segmentation. Dice-scores were calculated for the main pathologic tissue types: actively proliferating tumor (active tumor), necrosis and edema. Furthermore, to be consistent with the results reported for the BRATS challenge (Menze et al., 2015), Dice-scores were also reported for the tumor core (active tumor + necrosis) and the whole tumor (tumor core + edema). To evaluate the added value of including PWI, DWI and MRSI in terms of segmentation performance, all unsupervised algorithms were also applied to the UZ Gent dataset when considering cMRI data only. Average computation times were calculated for the different methods to compare their computational cost. We also wanted to assess how well the built-in modelling assumptions of the different methods align with the actual data in feature space, e.g. in terms of spatial distribution, the shape of the tissue clusters and the overlap between them. Principal component analysis was applied to the pathologic data of each patient and the data points were projected onto the 2 main principal components to allow for visual inspection of the data distribution.

4. Results

4.1. UZ Gent

A comparison of the segmentation results of the unsupervised algorithms on the UZ Gent MP-MRI dataset is given in Table 2 for kmeans ++ initialization and in Table 3 for SPA initialization. The highest mean Dice-score is marked in bold for each tissue class. With both initialization methods, hNMF has the highest mean Dice-score for all tissue classes except for necrosis, for which SC performs best. We also report for each method the number of times it did not detect a pathologic tissue class which was annotated by the radiologist. The number of cases with undetected tissue classes ranged from 0 to 1 out of 21 patients for active tumor, from 0 to 3 out of 12 patients for necrosis and from 2 to 7 out of 15 patients for edema. The high number of cases of undetected edema is also reflected in its low Dice-scores. This is mainly attributed to the relatively high number of grade III patients in the UZ Gent dataset, many of them exhibiting non-enhancing tumor that is hard to differentiate from the peri-tumoral edema. Neither initialization method gave clearly better performance for any of the segmentation algorithms. For edema, we see that kmeans ++ achieves Dice-scores which are at least as high as with SPA and the number of undetected edema cases are also generally lower.

Table 2.

Segmentation results for the UZ Gent MP-MRI dataset when using kmeans ++ initialization. Mean Dice-score ± standard deviation is reported for active tumor, necrosis, edema, the tumor core (active tumor + necrosis) and the whole tumor (core + edema). The number of undetected cases is reported for active tumor, necrosis and edema.

		NMF			Clustering
		HALS	Convex	hNMF	FCM	GMM	SC
Dice [%]	Tumor	66 ± 13	61 ± 22	70 ± 14	61 ± 21	66 ± 19	69 ± 14
	Necrosis	56 ± 28	54 ± 31	62 ± 25	41 ± 33	58 ± 32	66 ± 33
	Edema	33 ± 24	37 ± 27	46 ± 22	38 ± 23	36 ± 26	43 ± 24
	Core	76 ± 11	73 ± 15	79 ± 12	71 ± 19	77 ± 18	76 ± 16
	Whole	78 ± 13	82 ± 10	86 ± 8	78 ± 17	85 ± 10	85 ± 10
Undetected [#]	Tumor	0/21	1/21	0/21	0/21	0/21	0/21
	Necrosis	1/12	2/12	0/12	3/12	2/12	2/12
	Edema	4/15	4/15	2/15	3/15	3/15	3/15

Table 3.

Segmentation results for the UZ Gent MP-MRI dataset when using SPA initialization. Mean Dice-score ± standard deviation is reported for active tumor, necrosis, edema, the tumor core and the whole tumor. The number of undetected cases is reported for active tumor, necrosis and edema.

		NMF			Clustering
		HALS	Convex	hNMF	FCM	GMM	SC
Dice [%]	Tumor	65 ± 13	64 ± 18	71 ± 15	60 ± 21	66 ± 21	68 ± 14
	Necrosis	55 ± 27	60 ± 28	60 ± 28	41 ± 34	48 ± 33	65 ± 29
	Edema	28 ± 23	18 ± 18	46 ± 23	38 ± 23	27 ± 26	43 ± 24
	Core	76 ± 11	74 ± 14	79 ± 12	70 ± 18	77 ± 18	76 ± 15
	Whole	78 ± 12	84 ± 10	86 ± 8	77 ± 15	84 ± 10	85 ± 11
Undetected [#]	Tumor	0/21	0/21	0/21	0/21	0/21	0/21
	Necrosis	1/12	1/12	1/12	3/12	3/12	1/12
	Edema	5/15	7/15	2/15	3/15	6/15	3/15

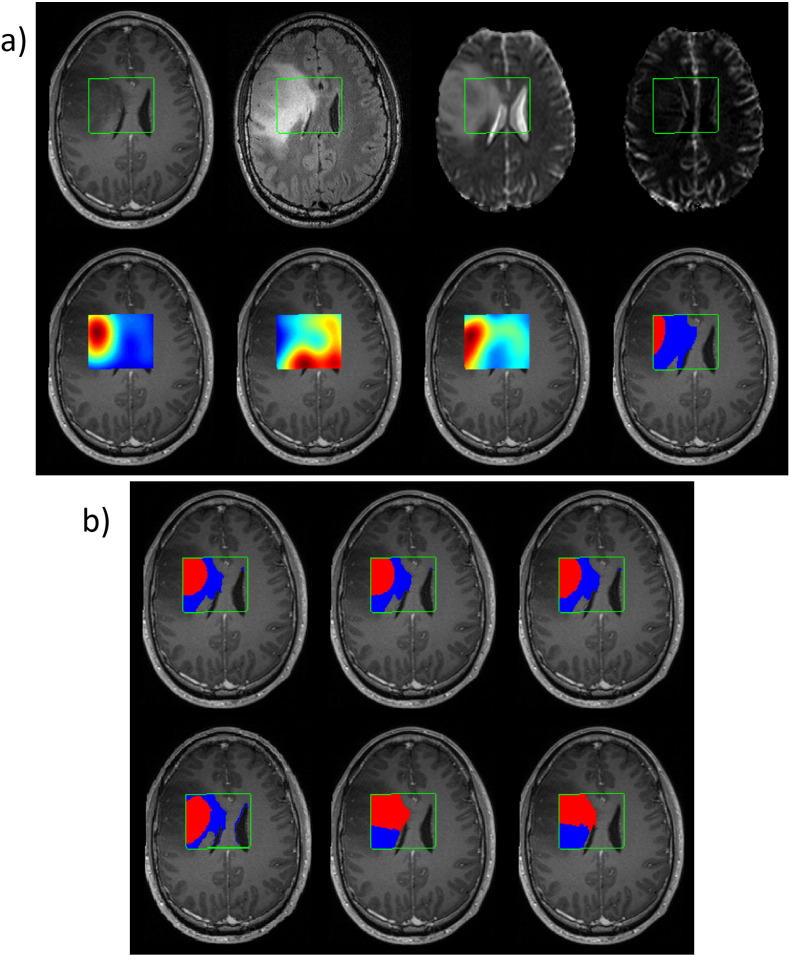
Fig. 2 gives an example of some of the MP-MRI input maps and the segmentation results for a grade III oligo-astrocytoma patient from UZ Gent. No necrotic region was present but the main challenge was the differentiation of non-enhancing tumor from edema. Comparing with the manual segmentation, all classification methods overestimate the active tumor region. hNMF gives the best segmentation for active tumor, slightly better than HALS NMF and Convex NMF. All of the methods obtain a good estimation of the whole tumor region.

Fig. 2.

a) Some of the MP-MRI images of a grade III oligo-astrocytoma patient from the UZ Gent dataset. First row, left to right: T1c, FLAIR, ADC, rCBV. Second row, left to right: Cho, NAA, Lac, and manual segmentation of active tumor (red) and edema (blue). The ROI is delineated in green. b) Segmentation results (using kmeans ++ initialization), top row left to right: HALS NMF, Convex NMF, hNMF. Second row, left to right: FCM, GMM, SC. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 4 compares segmentation performance on the UZ Gent dataset when considering only cMRI data with SPA initialization. hNMF has the highest mean Dice-score for all tissue classes except for necrosis, for which SC performs better. Compared to the MP-MRI results with SPA initialization in Table 3, Dice-scores are lower or at best equal when using cMRI data only. The reduction in mean Dice-score is between 0 and 4% for active tumor, between 2 and 11% for necrosis, between 0 and 12% for edema, between 1 and 8% for the tumor core and between 0 and 6% for the whole tumor region. The number of cases with undetected tissue classes ranged from 1 to 3 out of 12 patients for necrosis and from 5 to 10 out of 15 patients for edema. None of the methods showed a case of undetected active tumor.

Table 4.

Segmentation results for the UZ Gent cMRI data when using SPA initialization. Mean Dice-score ± standard deviation is reported for active tumor, necrosis, edema, the tumor core and the whole tumor. The number of undetected cases is reported for active tumor, necrosis and edema.

		NMF			Clustering
		HALS	Convex	hNMF	FCM	GMM	SC
Dice [%]	Tumor	64 ± 16	60 ± 21	68 ± 18	60 ± 20	64 ± 21	66 ± 20
	Necrosis	51 ± 29	49 ± 31	55 ± 29	39 ± 31	46 ± 30	58 ± 27
	Edema	28 ± 25	18 ± 27	43 ± 25	31 ± 28	15 ± 28	40 ± 26
	Core	72 ± 17	69 ± 21	74 ± 16	69 ± 19	69 ± 20	69 ± 17
	Whole	78 ± 14	78 ± 17	81 ± 12	77 ± 17	79 ± 17	80 ± 14
Undetected [#]	Tumor	0/21	0/21	0/21	0/21	0/21	0/21
	Necrosis	2/12	2/12	2/12	3/12	2/12	1/12
	Edema	7/15	9/15	5/15	7/15	10/15	5/15

4.2. UZ Leuven

The segmentation results for the UZ Leuven dataset are shown in Table 5 for kmeans ++ initialization and in Table 6 for SPA initialization. With both initialization methods, hNMF has the highest mean Dice-score for all tissue classes except for the tumor core, for which Convex NMF has a slightly higher mean Dice using kmeans ++ initialization. HALS NMF matches hNMF with equal mean Dice-score for active tumor using kmeans ++, HALS NMF and SC match hNMF performance for the tumor core using SPA and SC matches hNMF for necrosis with both initialization methods. Globally, GMM has the worst performance on this dataset, with the lowest mean Dice in 6 out of 10 classes from both tables. Neither kmeans ++ nor SPA clearly showed better performance for any of the unsupervised methods or for any of the tissue classes. The number of undetected cases ranged from 0 to 2 out of 14 patients for active tumor, from 0 to 3 out of 9 patients for necrosis and from 0 to 2 out of 9 patients for edema. hNMF matches the lowest number of undetected cases for all tissue classes, except for necrosis with SPA initialization, where Convex NMF has no undetected cases and hNMF has one.

Table 5.

Segmentation results for the UZ Leuven MP-MRI dataset when using kmeans ++ initialization. Mean Dice-score ± standard deviation is reported for active tumor, necrosis, edema, the tumor core and the whole tumor. The number of undetected cases is reported for active tumor, necrosis and edema.

		NMF			Clustering
		HALS	Convex	hNMF	FCM	GMM	SC
Dice [%]	Tumor	73 ± 16	67 ± 26	73 ± 15	66 ± 26	57 ± 26	72 ± 17
	Necrosis	56 ± 28	49 ± 29	57 ± 29	45 ± 31	35 ± 28	57 ± 35
	Edema	51 ± 23	60 ± 16	62 ± 21	60 ± 15	50 ± 29	56 ± 20
	Core	84 ± 9	85 ± 9	84 ± 9	83 ± 12	82 ± 10	84 ± 9
	Whole	80 ± 12	83 ± 11	85 ± 11	82 ± 10	83 ± 10	83 ± 11
Undetected [#]	Tumor	0/14	1/14	0/14	1/14	2/14	0/14
	Necrosis	1/9	2/9	1/9	2/9	3/9	2/9
	Edema	1/9	0/9	0/9	0/9	2/9	0/9

Table 6.

Segmentation results for the UZ Leuven MP-MRI dataset when using SPA initialization. Mean Dice-score ± standard deviation is reported for active tumor, necrosis, edema, the tumor core and the whole tumor. The number of undetected cases is reported for active tumor, necrosis and edema.

		NMF			Clustering
		HALS	Convex	hNMF	FCM	GMM	SC
Dice [%]	Tumor	68 ± 24	72 ± 15	73 ± 15	66 ± 26	63 ± 16	72 ± 17
	Necrosis	55 ± 28	55 ± 17	57 ± 29	45 ± 31	33 ± 27	57 ± 35
	Edema	50 ± 23	40 ± 28	62 ± 21	60 ± 15	52 ± 22	56 ± 20
	Core	84 ± 9	80 ± 11	84 ± 9	82 ± 12	81 ± 9	84 ± 10
	Whole	79 ± 13	82 ± 11	85 ± 11	82 ± 10	82 ± 9	84 ± 11
Undetected [#]	Tumor	1/14	0/14	0/14	1/14	0/14	0/14
	Necrosis	1/9	0/9	1/9	2/9	3/9	2/9
	Edema	1/9	2/9	0/9	0/9	1/9	0/9

4.3. Computational cost

Table 7 reports the average computation times per patient for the UZ Gent dataset using kmeans ++ initialization. These were the computationally most expensive analyses, as the UZ Gent data were 3D (UZ Leuven dataset has 2D ROI) and the analyses are repeated 20 times with kmeans ++ to come to the final result. Segmentations were computed in Matlab R2015a (The MathWorks, Natick, MA, USA) with an Intel Core i7-3720QM processor and 8 GB of RAM. The input data matrix typically consisted of approximately 30,000 voxels by 24 MRI features. HALS NMF and in particular FCM clustering, both known for their computational efficiency, have relatively low computational costs. SC has a computational cost similar to HALS NMF as we have defined a sparsely connected k-nearest neighbours graph, allowing efficient calculations. Computation times for hNMF and GMM are 2 to 4 times higher compared to HALS NMF and SC. For hNMF, this is partly explained by its hierarchical structure, requiring 3 HALS NMF analyses at each run, but the main expense comes from the NNLS recombining step to calculate the abundance maps at the final stage of the algorithm. Convex NMF has the highest computation time, approximately twice as high as for hNMF, due to its low convergence rate.

Table 7.

Average computation time (in seconds) per patient on the UZ Gent dataset using kmeans ++ initialization.

	Average computation time [s]
HALS NMF	80
Convex NMF	429
hNMF	208
FCM	31
GMM	266
SC	74

4.4. Data distribution

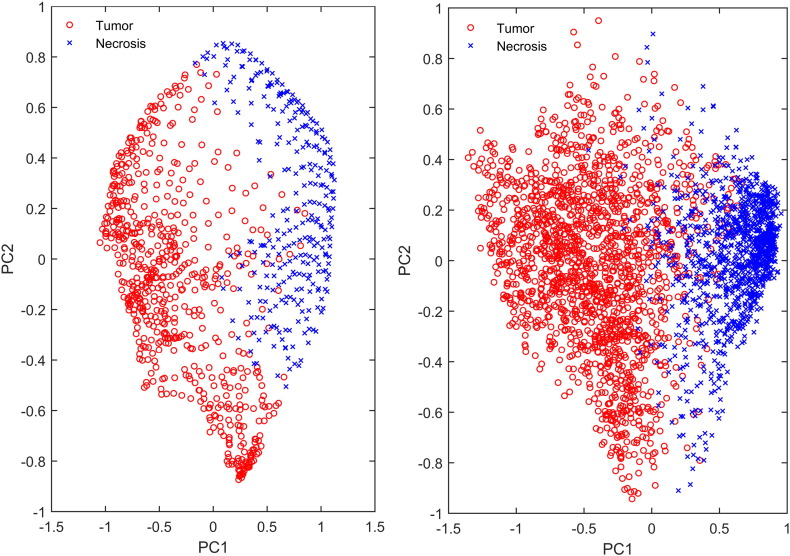
To gain some insight into the spatial distribution of the data points in feature space, the shape of the tissue clusters and their overlap, we performed a principal component analysis on the active tumor and necrosis data points of a single GBM patient from each hospital. The projections of the data points onto the first and second principal component are plotted against each other in Fig. 3, providing insight into the data spread along the 2 main directions of data variance. We can see that the first principal component separates tumor and necrosis, but there is a distinct difference in the data spread of both patients. For the UZ Leuven patient, there is a structured pattern in the data and distinct curves of data points can be observed. Such patterns are not seen in the data of the UZ Gent patient, for which data points appear more randomly distributed. The structure in the UZ Leuven data can be explained by the limited number of voxels within the 2D ROI in combination with the large MRSI voxel size. Often only a few MRSI voxels fully cover the tumor and the necrotic tissue class. The MRSI data have been upsampled to the spatial resolution of 1 × 1 × 3 mm³, generating a high number of interpolated and noiseless data points. The structure that can be seen in the data are interpolation patterns within the highly upsampled MRSI data. This explains why SC performs very well and almost as good as hNMF on the UZ Leuven data: it can easily model this kind of structured data as the SC similarity matrix is based on a distance metric among the nearest neighbours of each data point. It also explains why GMM underperforms on the UZ Leuven dataset, as its assumptions of a Gaussian within-class data distribution and ellipsoidal cluster shapes does not hold. For the UZ Gent data, the structured upsampling effect is not relevant as we are analyzing a sufficiently large (3D) ROI, with about 10 times more data points compared to the UZ Leuven patients.

Fig. 3.

Active tumor and necrosis data points projected onto the plane formed by the first and second principal component for an UZ Leuven GBM patient (left) and for an UZ Gent GBM patient (right).

5. Discussion

5.1. NMF vs clustering

So far only few studies have considered MP-MRI for brain tumor segmentation, although it has been commonly suggested in literature (Juan-Albarracín et al., 2015, Bauer et al., 2013, Dhermain, 2014). We have shown in a previous study that significantly higher segmentation accuracy could be achieved by applying hNMF to MP-MRI data compared to using only cMRI data (Sauwen et al., 2015). For the whole tumor region, segmentation algorithms already achieve Dice-scores in the range of inter-rater variability, which has been reported to be between 80 and 85% (Menze et al., 2015). Such Dice-scores were also achieved by most algorithms in the current study. Lower Dice-scores are commonly reported for the individual pathologic tissue types. There are several reasons why it is particularly difficult to differentiate the tumor subregions. First of all, HGGs show a high degree of within-tissue heterogeneity. Clustering methods explain the data variability in this way, by incorporating within-class variability into their model. On the other hand, the pathologic region contains a continuum of tissue mixtures rather than absolute tissue boundaries: e.g. active tumor in HGGs contains foci of microscopic necrosis (Bell et al., 2001) and edema will often be invaded by active tumor cells (Price et al., 2006). These tissue mixtures are further enhanced at the voxel level due to the partial volume effect. Clinical MRI is often acquired in a highly anisotropic way, with relatively low inter-slice resolution. Furthermore, advanced MRI modalities usually have lower spatial resolution than cMRI, causing even more partial volume effects. NMF has this concept of class mixtures built into its model. As such, clustering methods and NMF methods each model only one aspect of the data variability: clustering does not incorporate tissue mixtures and NMF does not consider within-tissue variability. In the current study we did not see either type of methods outperforming the other, suggesting that both aspects of data variability play a considerable role in glioma segmentation.

5.2. hNMF performance

Segmentation performance was compared among the different methods by reporting mean Dice-scores for 5 tissue classes, on 2 independent MP-MRI datasets, using 2 different initialization methods. The hNMF method globally performed best, with the highest mean Dice-score in 17 out of the 20 comparisons on the MP-MRI datasets. When considering only cMRI data of the UZ Gent dataset, hNMF also had the highest mean Dice-score for 4 out of 5 tissue classes. Additionally, hNMF provided robust segmentation, with relatively low standard deviations and the lowest number of undetected cases for nearly all tissue classes. The hierarchical structure of hNMF gives it some advantages over the other methods. At the first (rank-2) NMF level, the tissue classes are divided over 2 sources, with tissues that are most similar in terms of MP-MRI feature vectors being assigned to the same source. At the second level, NMF can focus on the more subtle differences between the similar tissue classes. This property has allowed hNMF to better separate edema from non-enhancing tumor in the UZ Gent dataset, resulting in the highest mean Dice-scores and the lowest number of undetected sources for edema in Table 2, Table 3. Another challenging problem for most unsupervised methods is how to cope with data imbalance. Unsupervised methods have to model a large amount of data with a limited number of degrees of freedom, based on a global optimization criterion. This does not favour the detection of small lesions. In the current study this was mainly an issue in detecting small necrotic regions. As the input data are divided into 2 groups after the first NMF level, hNMF might be able to detect small tissue regions more easily at the second NMF level. This has allowed hNMF to detect some small necrotic areas that other methods were not able to differentiate. An important drawback of the original hNMF algorithm as proposed in Sauwen et al. (2015) was its computational expense. This was mainly attributed to the iterative mask selection step after the first NMF level, using hard thresholding to subdivide the voxels over both sources. We have adapted the hNMF algorithm, using k-means clustering after the first NMF level for the voxel assignment. This has brought the computation time of hNMF within the range of the other methods evaluated in the current study, as shown in Table 7. It must be noted that we did not directly explore the effect of inter-observer variability on the segmentation results. However, all methods were applied to 2 independent datasets with manual segmentation by 2 different raters. Similar results were obtained for both datasets, suggesting that the drawn conclusions are general.

5.3. Spatial regularization

Many classification based segmentation algorithms incorporate some kind of spatial regularization to obtain spatially consistent results. It is to be expected that most neighbouring voxels will belong to the same tissue class, except at the tissue boundaries. Common techniques to encourage spatially consistent segmentation include Markov random fields (Menze et al., 2010) and spatial smoothness regularization on the NMF abundance matrix H (Xie et al., 2011). We did not apply spatial regularization to any of the unsupervised methods, as it would bias the comparison to the other methods. In general, we did obtain spatially consistent segmentations, as is illustrated in Fig. 2. This is partly explained by the fact that we combined many MP-MRI features, thereby increasing the specificity of the feature set. Secondly, the inclusion of locally averaged MRI features further improved robustness of the segmentation in terms of spatial coherence. Zikic et al. also reported naturally smooth segmentation results by combining cMRI with DWI and including spatial and context-aware features (Ortega-Martorell et al., 2012). Nevertheless, the hNMF algorithm might benefit from adding spatial regularization, especially when reducing the number of MRI features or extending the region of interest to full brain slices.

5.4. UZ Gent and UZ Leuven datasets

For the UZ Gent dataset edema is clearly showing the lowest Dice-scores. 8 out of 21 patients in the UZ Gent dataset (6 grade III and 2 GBM) exhibited non-enhancing tumor in combination with vasogenic edema in the ROI. Distinction of both tissue types is often difficult on conventional MRI due to the diffuse infiltrative nature of many gliomas, lacking a well-defined margin. The perilesional environment often contains not only T2/FLAIR hyperintense vasogenic edema but also tumor components which appear less hyperintense on T2/FLAIR weighted images due to hypercellularity. The differences in signal intensity on T2/FLAIR can be subtle making the segmentation in these cases susceptible to subjective interpretation. Even when using MP-MRI, the tissue signatures of both tissue types are similar and proper differentiation remains challenging (see Fig. 2). The UZ Leuven dataset only contained 3 (out of 14) grade III patients, and none of the patients showed non-enhancing tumor with edema in the ROI. Due to this clear bias across the patient cohorts, higher Dice-scores were found for edema in the UZ Leuven dataset. Looking at the distribution of the data points of the pathologic tissue classes as shown in Fig. 3, we did find a marked difference between both datasets. A structured pattern is seen in the UZ Leuven data, which is explained by the limited extent of the 2D ROI in combination with the low spatial resolution of MRSI compared to the other MRI modalities. SC, which is known to cope well with complex cluster shapes, performs well on the UZ Leuven data, almost as good as hNMF. GMM, due to its strong assumption of Gaussian within-class data distribution, is not able to model the structured data well and has the lowest Dice-scores. However, for the 3D ROI of the UZ Gent dataset, these structured patterns are no longer appearing. Therefore, SC and GMM perform comparably to most of the other methods on the UZ Gent dataset. The added value of including PWI, DWI and MRSI was assessed on the UZ Gent dataset by considering only the cMRI data with SPA initialization (see Table 4). Mean Dice-scores were lower or at best equal for all tissue classes and for all the methods when considering only cMRI data. Sensitivity to this reduction of the MP-MRI dataset was found to be similar across the different methods. The decrease in performance was in general more pronounced for necrosis and edema than for active tumor. On the UZ Leuven dataset, segmentation results for hNMF when considering only cMRI data have been previously reported in (Sauwen et al., 2015). Significantly lower Dice scores were found for active tumor, the tumor core and the whole tumor region compared to the full MP-MRI dataset.

5.5. Initialization methods

We have performed tissue segmentation using 2 initialization methods: kmeans ++ which is commonly used for clustering and SPA which is commonly used for NMF. No bias was seen in the results with both types of initialization: kmeans ++ did not improve segmentation results for the clustering methods nor did SPA show better results for the NMF methods. SPA provides a deterministic initialization, such that the obtained segmentation results are reproducible. Kmeans ++ on the other hand provides a different initialization at each run. Analyses using kmeans ++ were repeated 20 times, withholding the result with the best (= highest or lowest) objective function value for the considered classification method. 20 repetitions was found to be sufficient to give reproducible results, i.e. to obtain Dice-scores differing by < 1% for each patient upon repeating the analyses. In general, similar performance was found using both types of initialization. The main difference was seen in the segmentation of edema in the UZ Gent dataset: mean Dice-scores for edema were higher with kmeans ++ than with SPA for 4 out of 6 classification methods, and were equal for the other 2 methods. The number of undetected cases for edema was also at least as high with SPA as with kmeans ++. SPA minimizes collinearity between the initialized sources by successively selecting data points with maximal l2-norm in the orthogonal subspace of the previously selected sources. As such, SPA might have difficulty in correctly initializing tissue classes with similar sources, such as non-enhancing tumor and edema. Indeed, we noticed that SPA often seeded only one source for the combined region of non-enhancing tumor and edema, whereas kmeans ++ often obtained at least 2 sources. kmeans ++ is more likely to select data points which are further apart in Euclidian space, but it does not explicitly look for the extremal points in a dataset. As we run kmeans ++ a sufficient number of times, it is likely that both non-enhancing tumor and edema get a seeding point in at least one of those runs. At the individual patient level, SC, HALS NMF and hNMF gave very similar results with both initialization methods, which is reflected in the similar mean Dice-scores for most tissue classes. HALS NMF has previously been shown to be insensitive to the initialization strategy, and the same goes for hNMF as it consists of 2 levels of HALS NMF (Sauwen et al., 2016). SC does not require an initialization, but it applies k-means clustering to the matrix of eigenvectors in the final stage of the algorithm. This k-means step however does not seem sensitive to the initialization method, probably because the complexity of the classification problem is already reduced by withholding only the k main eigenvectors to find k tissue classes.

5.6. Supervised vs unsupervised classification

Recently, supervised classification methods have been receiving most attention for automated brain tumor segmentation (Menze et al., 2015). However, unsupervised methods remain competitive, e.g. Juan-Albarracin et al. have recently combined some dedicated cMRI pre-processing steps with several unsupervised methods, including FCM, GMM and hidden Markov random fields. Their results ranked among the best supervised algorithms in the BRATS challenge (Juan-Albarracín et al., 2015). A direct comparison between our results and those from the BRATS challenge is not in place, as we are combining cMRI data with PWI, DWI and MRSI in a multi-parametric approach, whereas BRATS only considers cMRI data. Furthermore, we restricted our study to the limited region of interest of the MRSI data, whereas full 3D imaging data of the brain are considered in the BRATS challenge. Nevertheless, several of the unsupervised algorithms reported in this study, and in particular hNMF achieved mean Dice-scores which are higher than the best performing algorithms participating in the BRATS challenge (Menze et al., 2015), showing the potential of these methods. Unsupervised methods are more flexible as they don't require an extensive set of training data, which is only valid for segmentation under a particular data acquisition and processing protocol. This limitation might be more restrictive when considering MP-MRI data, as there is a wide variability and fast evolution in acquisition protocols and post-processing methods for PWI, MRSI and DWI (Young, 2007). Furthermore, unsupervised methods are not susceptible to overfitting, and they don't require intensity calibration, which can be challenging in the presence of pathologic tissue (Bauer et al., 2013). On the other hand, an attractive feature of supervised methods is that they don't require a rank estimation step for determining the number of tissue types, and they automatically apply voxel labelling based on the training data. The unsupervised methods presented in this study are not fully automatic: they require the user to specify the number of tissue types to be found within the region of interest. Therefore, further research will focus on automation by incorporating prior knowledge, e.g. tissue probability maps based on an image atlas (Juan-Albarracín et al., 2015), feature-specific knowledge (Kazerooni et al., 2015) or user input (Menze et al., 2015).

6. Conclusion

This study explored the usage of unsupervised classification methods applied to MP-MRI data for segmenting the tumor subregions in HGGs. We have proposed a hierarchical 2-level hNMF method and compared its performance to 5 common unsupervised classification algorithms. hNMF achieved the best segmentation results in terms of mean Dice-scores on 2 independent MP-MRI datasets acquired at different hospitals. This trend was confirmed using both kmeans ++ and SPA initialization. Unsupervised methods can be applied to any MP-MRI dataset at the individual patient level, irrespective of the acquisition protocol or image processing methods used. Future work will focus on further automation of unsupervised segmentation methods by incorporating prior knowledge.